四川省泸县第一中学2019-2020学年高二下学期期末模拟考试数学(理)试题word版含答案
文档属性
| 名称 | 四川省泸县第一中学2019-2020学年高二下学期期末模拟考试数学(理)试题word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 521.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-13 00:00:00 | ||
图片预览




文档简介
2020年春四川省泸县第一中学高二期末模拟考试
理科数学
注意事项:
1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第I卷 选择题(60分)
一、选择题:本题共12小题,每小题5分,共60分。在每小题给的四个选项中,只有一项是符合题目要求的。
1.设是虚数单位,则复数在复平面内对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知命题:,;命题:若<,则>,则下列为真命题的是
A. B.
C. D.
3.若a>b,c>d,则下列不等关系中不一定成立的是
A.a?b>d?c B.a+d>b+c C.a?c>b?c D.a?c4.设,则
A. B. C. D.
5.已知双曲线的右焦点到渐近线的距离等于实轴长,则此双曲线的离心率为A. B. C. D.
6.已知随机变量X服从正态分布N(3.1),且=0.6826,则p(X>4)=
A.0.1588 B.0.1587 C.0.1586 D.0.1585
7.在的展开式中,含项的系数为
A. B. C. D.
8.五名同学进行百米赛跑比赛,先后到达终点,则甲比乙先到达的情况有
A.240种 B.120种 C.60种 D.30种
9.函数f(x)=sin(ωx+π4)(ω>0)的图象在[0,π4]内有且仅有一条对称轴,则实数ω的取值范围是
A.(1,5) B.(1,+∞) C.[1,5) D.[1,+∞)
10.一张储蓄卡的密码共有位数字,每位数字都可以从中任选一个,某人在银行自动提款机上取钱时,忘记了密码最后一位数字,如果任意按最后一位数字,不超过次就按对的概率为
A. B. C. D.
11.已知焦点在轴上的双曲线的左、右焦点分别为,,其右支上存在一点满足,且的面积为2.若双曲线的两条渐近线与抛物线的准线分别交于、两点,为坐标原点,且的面积为,则
A.2 B. C. D.24
12.定义在上可导函数的导数为,且,则下列判断中,一定正确的是
A. B. C. D.
第II卷 非选择题(90分)
填空题:本题共4小题,每小题5分,共20分。
13.将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91.现场作的9个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以表示,则7个剩余分数的方差为______.
14.设曲线在点处的切线与直线垂直,则_________.
15.非负实数,,满足,则的最小值为__________.
16.设函数,其中,若存在唯一的整数,使得,则实数的取值范围是__________.
三.解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分
17.(12分)已知函数f(x)=lnx,其中a>0.曲线y=f(x)在点(1,f(1))处的切线与直线y=x+1垂直.
(1)求函数f(x)的单调区间;
(2)求函数f(x)在区间[1,e]上的极值和最值.
18.(12分)一次数学考试后,对高三文理科学生进行抽样调查,调查其对本次考试的结果满意或不满意,现随机抽取名学生的数据如下表所示:
满意
不满意
总计
文科
22
18
40
理科
48
12
60
总计
70
30
100
(1)根据数据,有多大的把握认为对考试的结果满意与科别有关;
(2)用分层抽样方法在感觉不满意的学生中随机抽取名,理科生应抽取几人;
(3)在(2)抽取的名学生中任取2名,求文科生人数的期望.(其中)
0.100
0.050
0.025
0.010
0.001
2.706
3.841
5.024
6.635
10.828
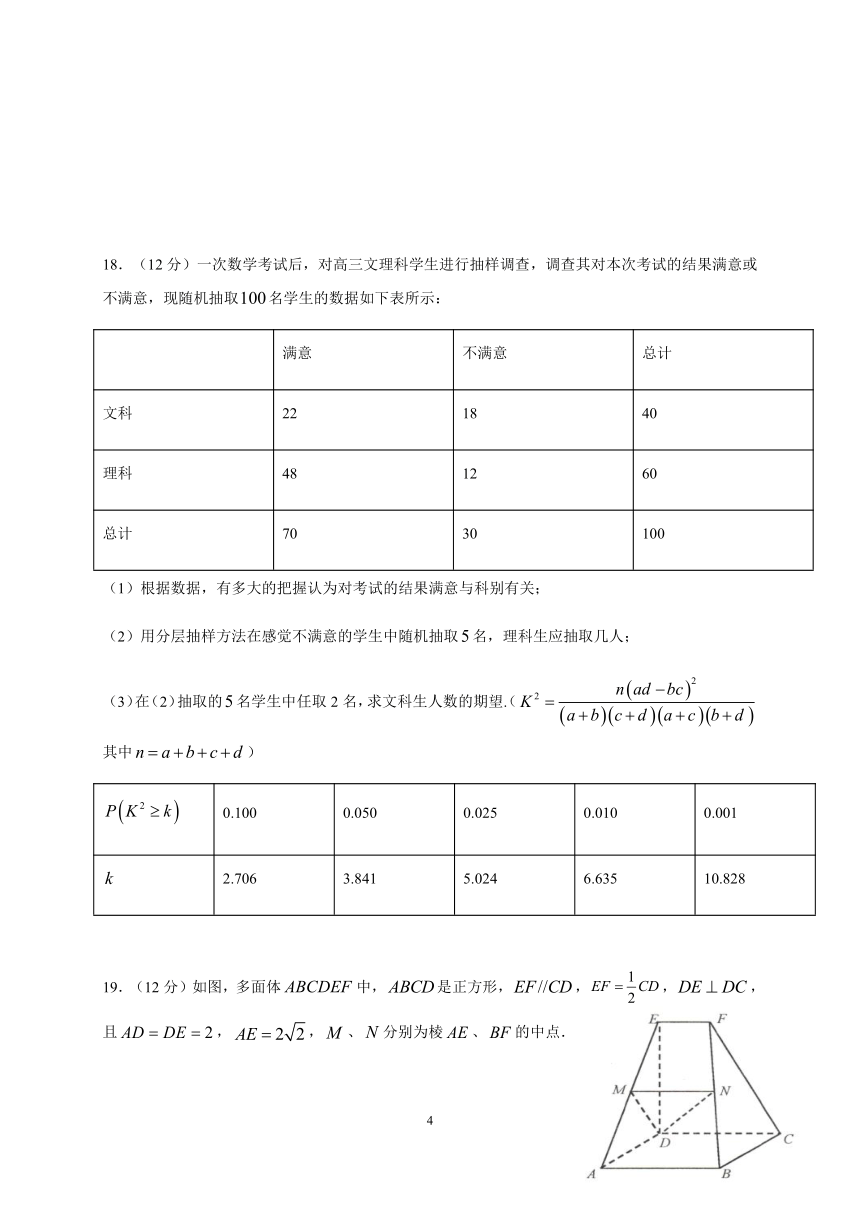
424815036957019.(12分)如图,多面体中,是正方形,,,,且,,、分别为棱、的中点.
(1)求证:平面;
(2)求平面和平面所成锐二面角的余弦值.
435292548958520.(12分)已知抛物线C:y2=4x与椭圆E:1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|.
(1)求椭圆E的标准方程;
(2)过点P(1,)的直线交抛物线C于A、B两点,直线PO交椭圆
E于另一点Q.若P为AB的中点,求△QAB的面积.
21.(12分)已知函数,其中.
(1)当时,求函数的单调性;
(2)若函数有两个极值点,,且,求证:.
(二)选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
22.[选修4-4:坐标系与参数方程](10分)
在平面直角坐标系xOy中,曲线的参数方程为(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程是,曲线的极坐标方程是.
(1)求直线l和曲线的直角坐标方程,曲线的普通方程;
(2)若直线l与曲线和曲线在第一象限的交点分别为P,Q,求的值.
23.[选修4-5:不等式选讲](10分)
设函数的最小值为.
(1)求的值;
(2)若,,求的取值范围.
2020年春四川省泸县第一中学高二期末模拟考试
理科数学参考答案
1.C 2.B 3.B 4.B 5.C 6.B 7.B 8.C 9.C 10.C 11.A 12.A
13. 14. 15.3 16.
17.(1)由题,(x>0),因为曲线在点处的切线与直线垂直,
所以,解得a=2,所以,令得0<x<2,令得x>2,
所以f(x)的单调减区间为(0,2),增区间为[2,+∞)
(2)由(1)可得f(x)在(1,2)上递减,在(2,e)上递增,
故f(x)的极小值为f(2)=ln2,无极大值;
又因为f(1)=1,f(e),f(2)=ln2,所以f(x)的最小值为ln2,最大值为1.
18.解:(1)由题意有:,所以有的把握认为对考试的结果满意与科别无关.
(2)感觉不满意的学生共有人,抽取的比例为,所以理科生应抽取人.
(3)记抽取的名学生中,有名文科生名理科生,设抽出的文科生的人数为,
则.所以 .
所以的期望为.所以抽出的文科生人数的期望为1.2.
19.(1)因为,,所以,即.
平面.又因为平面,所以.
因为四边形是正方形,所以.平面.
因为,四边形是正方形,所以.
又因为、分别为棱、的中点,所以.
所以平面.
又因为平面,所以.
因为,是中点,所以.平面.
(2)以为原点,,,分别为,,轴建立空间直角坐标系,
如图所示:
则,,,,所以,
472440040005平面的一个法向量为,
由,得,令,则.
由(1)可知平面所以平面的一个法向量为,
设平面和平面所成锐二面角为,
则
所以平面和平面所成锐二面角的余弦值为.
(1)由抛物线方程可得F(1,0),则椭圆的另一个焦点,因为,∴M(,),则2a4,则a=2,所以,
椭圆E的标准方程为.
(2)设A(x1,y1),B(x2,y2),点P(1,)在椭圆上,则Q(﹣1,),
因为P为AB的中点,且,则kAB,
故直线AB的方程为y(x﹣1),即8x﹣6y+1=0,∴Q到直线AB的距离,
联立,整理得64x2﹣128x+1=0,故x1+x2=2,x1x2,
则,
所以.
21.解:(1),
当时,,即时,令,得:
,,
的单调递增区间和,单调递减区间.
(2)由(1)可知,
①当即时,,
的单调递增区间是,此时不存在极值,
②当时,即时,令得,;
的单调递增区间是和,单调递减区间.
则在处取得极大值,在处取得极小值,
因为,所以,,所以
证明:在单调递增,且,,
有两个极值点,,,.
,令,,
在单调递增,,
,综上可知:.
22.解:(1)由,得,代入,得,
故直线l的直角坐标方程是.由,得,
代入,得,即,
故曲线的直角坐标方程是.由,得
即.故曲线的普通方程是.
(2)把代入中,化简整理,
曲线的极坐标方程为,曲线的极坐标方程为,
因为,所以
所以,.所以
23.(1),显然当时,取得最小值.
(2)∵,
∴.
理科数学
注意事项:
1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第I卷 选择题(60分)
一、选择题:本题共12小题,每小题5分,共60分。在每小题给的四个选项中,只有一项是符合题目要求的。
1.设是虚数单位,则复数在复平面内对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知命题:,;命题:若<,则>,则下列为真命题的是
A. B.
C. D.
3.若a>b,c>d,则下列不等关系中不一定成立的是
A.a?b>d?c B.a+d>b+c C.a?c>b?c D.a?c
A. B. C. D.
5.已知双曲线的右焦点到渐近线的距离等于实轴长,则此双曲线的离心率为A. B. C. D.
6.已知随机变量X服从正态分布N(3.1),且=0.6826,则p(X>4)=
A.0.1588 B.0.1587 C.0.1586 D.0.1585
7.在的展开式中,含项的系数为
A. B. C. D.
8.五名同学进行百米赛跑比赛,先后到达终点,则甲比乙先到达的情况有
A.240种 B.120种 C.60种 D.30种
9.函数f(x)=sin(ωx+π4)(ω>0)的图象在[0,π4]内有且仅有一条对称轴,则实数ω的取值范围是
A.(1,5) B.(1,+∞) C.[1,5) D.[1,+∞)
10.一张储蓄卡的密码共有位数字,每位数字都可以从中任选一个,某人在银行自动提款机上取钱时,忘记了密码最后一位数字,如果任意按最后一位数字,不超过次就按对的概率为
A. B. C. D.
11.已知焦点在轴上的双曲线的左、右焦点分别为,,其右支上存在一点满足,且的面积为2.若双曲线的两条渐近线与抛物线的准线分别交于、两点,为坐标原点,且的面积为,则
A.2 B. C. D.24
12.定义在上可导函数的导数为,且,则下列判断中,一定正确的是
A. B. C. D.
第II卷 非选择题(90分)
填空题:本题共4小题,每小题5分,共20分。
13.将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91.现场作的9个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以表示,则7个剩余分数的方差为______.
14.设曲线在点处的切线与直线垂直,则_________.
15.非负实数,,满足,则的最小值为__________.
16.设函数,其中,若存在唯一的整数,使得,则实数的取值范围是__________.
三.解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分
17.(12分)已知函数f(x)=lnx,其中a>0.曲线y=f(x)在点(1,f(1))处的切线与直线y=x+1垂直.
(1)求函数f(x)的单调区间;
(2)求函数f(x)在区间[1,e]上的极值和最值.
18.(12分)一次数学考试后,对高三文理科学生进行抽样调查,调查其对本次考试的结果满意或不满意,现随机抽取名学生的数据如下表所示:
满意
不满意
总计
文科
22
18
40
理科
48
12
60
总计
70
30
100
(1)根据数据,有多大的把握认为对考试的结果满意与科别有关;
(2)用分层抽样方法在感觉不满意的学生中随机抽取名,理科生应抽取几人;
(3)在(2)抽取的名学生中任取2名,求文科生人数的期望.(其中)
0.100
0.050
0.025
0.010
0.001
2.706
3.841
5.024
6.635
10.828
424815036957019.(12分)如图,多面体中,是正方形,,,,且,,、分别为棱、的中点.
(1)求证:平面;
(2)求平面和平面所成锐二面角的余弦值.
435292548958520.(12分)已知抛物线C:y2=4x与椭圆E:1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|.
(1)求椭圆E的标准方程;
(2)过点P(1,)的直线交抛物线C于A、B两点,直线PO交椭圆
E于另一点Q.若P为AB的中点,求△QAB的面积.
21.(12分)已知函数,其中.
(1)当时,求函数的单调性;
(2)若函数有两个极值点,,且,求证:.
(二)选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
22.[选修4-4:坐标系与参数方程](10分)
在平面直角坐标系xOy中,曲线的参数方程为(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程是,曲线的极坐标方程是.
(1)求直线l和曲线的直角坐标方程,曲线的普通方程;
(2)若直线l与曲线和曲线在第一象限的交点分别为P,Q,求的值.
23.[选修4-5:不等式选讲](10分)
设函数的最小值为.
(1)求的值;
(2)若,,求的取值范围.
2020年春四川省泸县第一中学高二期末模拟考试
理科数学参考答案
1.C 2.B 3.B 4.B 5.C 6.B 7.B 8.C 9.C 10.C 11.A 12.A
13. 14. 15.3 16.
17.(1)由题,(x>0),因为曲线在点处的切线与直线垂直,
所以,解得a=2,所以,令得0<x<2,令得x>2,
所以f(x)的单调减区间为(0,2),增区间为[2,+∞)
(2)由(1)可得f(x)在(1,2)上递减,在(2,e)上递增,
故f(x)的极小值为f(2)=ln2,无极大值;
又因为f(1)=1,f(e),f(2)=ln2,所以f(x)的最小值为ln2,最大值为1.
18.解:(1)由题意有:,所以有的把握认为对考试的结果满意与科别无关.
(2)感觉不满意的学生共有人,抽取的比例为,所以理科生应抽取人.
(3)记抽取的名学生中,有名文科生名理科生,设抽出的文科生的人数为,
则.所以 .
所以的期望为.所以抽出的文科生人数的期望为1.2.
19.(1)因为,,所以,即.
平面.又因为平面,所以.
因为四边形是正方形,所以.平面.
因为,四边形是正方形,所以.
又因为、分别为棱、的中点,所以.
所以平面.
又因为平面,所以.
因为,是中点,所以.平面.
(2)以为原点,,,分别为,,轴建立空间直角坐标系,
如图所示:
则,,,,所以,
472440040005平面的一个法向量为,
由,得,令,则.
由(1)可知平面所以平面的一个法向量为,
设平面和平面所成锐二面角为,
则
所以平面和平面所成锐二面角的余弦值为.
(1)由抛物线方程可得F(1,0),则椭圆的另一个焦点,因为,∴M(,),则2a4,则a=2,所以,
椭圆E的标准方程为.
(2)设A(x1,y1),B(x2,y2),点P(1,)在椭圆上,则Q(﹣1,),
因为P为AB的中点,且,则kAB,
故直线AB的方程为y(x﹣1),即8x﹣6y+1=0,∴Q到直线AB的距离,
联立,整理得64x2﹣128x+1=0,故x1+x2=2,x1x2,
则,
所以.
21.解:(1),
当时,,即时,令,得:
,,
的单调递增区间和,单调递减区间.
(2)由(1)可知,
①当即时,,
的单调递增区间是,此时不存在极值,
②当时,即时,令得,;
的单调递增区间是和,单调递减区间.
则在处取得极大值,在处取得极小值,
因为,所以,,所以
证明:在单调递增,且,,
有两个极值点,,,.
,令,,
在单调递增,,
,综上可知:.
22.解:(1)由,得,代入,得,
故直线l的直角坐标方程是.由,得,
代入,得,即,
故曲线的直角坐标方程是.由,得
即.故曲线的普通方程是.
(2)把代入中,化简整理,
曲线的极坐标方程为,曲线的极坐标方程为,
因为,所以
所以,.所以
23.(1),显然当时,取得最小值.
(2)∵,
∴.
