湘教版七年级上册1.1 具有相反意义的量课件+视频素材(25张ppt)
文档属性
| 名称 | 湘教版七年级上册1.1 具有相反意义的量课件+视频素材(25张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 10.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-14 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
湘教版·八年级数学上册
1.1
具有相反意义的量
其中阴与晴、圆与缺、悲与欢、离与合都是生活中具有相反意义的真实描绘。
在数学学科中,也有很多具有相反意义的量,为数学世界增添了无穷的魅力。
在日常生产和生活实践中,
由于记数、测量、分配等方面的需要产生了自然数、小数、分数.你还见过其他的数吗?
温度计上是如何区分零上的度数和零下的度数的?
如果仅用颜色来区分,就不便于运算.因此我们要想其他的办法.
点击播放
(1)在预报北京市某天的天气时,播音员说:“北京,晴,局部多云,零下
6
摄氏度到
5
摄氏度.”这时,
屏幕上是如何显示这天的温度的?
屏幕上显示“-6~5℃”
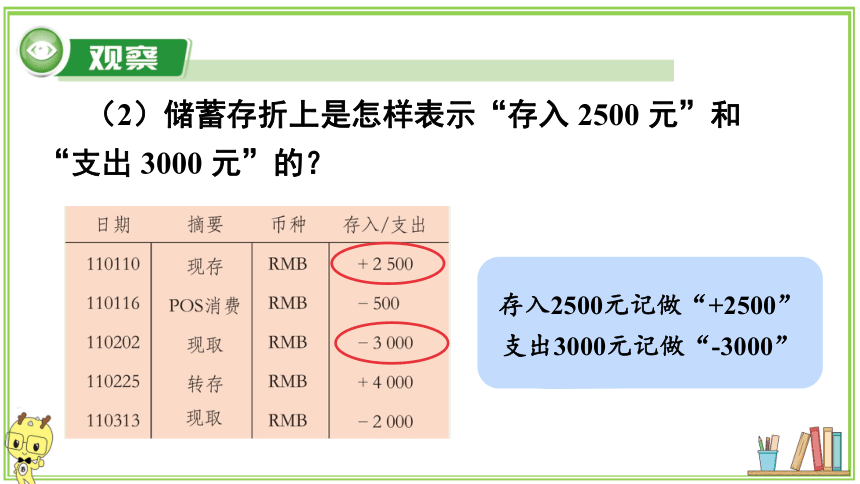
(2)储蓄存折上是怎样表示“存入
2500
元”和“支出
3000
元”的?
存入2500元记做“+2500”
支出3000元记做“-3000”
知识点一
正数、负数和
0
大于
0
的自然数和分数(或小数)就是正数,负数就是在正数前面加上“-”(读做负)号.
0
既不是正数,也不是负数.
我们把正数和
0
统称为非负数,负数和
0
统称为非正数.
选自《状元大课堂》
将下列各数填在相应的横线上:
+6
,
-21
,
54
,
0
,
,
0.11
,
-π,-35%
正数:____________________;
负数:____________________;
非负数:___________________.
-21
,
-π,-35%
在具有相反意义的一对量中,我们把其中的一种量用正数表示,而另一种量就用负数表示.
用正数和负数表示具有相反意义的量
知识点二
请举出一些具有相反意义的量的例子,并分别表示它们.
海平面以上与海平面以下表示的意义相反.海平面以上
1025
m
记做“1025
m”,海平面以下155
m记做“-155m”.
点击播放
请举出一些具有相反意义的量的例子,并分别表示它们.
点击播放
在东西向的马路上,把出发点记为
0,向东与向西意义相反.若把向东走
2
km
记做“2
km”,那么向西走2.6
km
应记做“-2.6
km”.
选自《状元大课堂》
用正负数表示下列具有相反意义的量:
(1)某地
12
月某天的最高温度是零上
10
℃,最低温度是零下
4
℃.若规定零上温度为正,则零上
10
℃
可记做_______,零下
4
℃
可记做_______;
(2)如果某蓄水池的水位比标准水位高
2
m
记做+2
m,那么比标准水位低
0.5
m
应记做______,恰好在标准水位应记做_________.
+10
℃
-4
℃
-5
m
0
请你举例说明从小学到现在,我们学过的数有哪些.
自然数:
0,1,2,3,…
小数:
分数:
负数:
分数可以化成有限小数或无限循环小数.
有限小数或无限循环小数也可以化为分数.
有理数的有关概念
知识点三
正整数、零和负整数统称为整数.
正分数和负分数统称为分数.
整数和分数统称为有理数.
1,3,167,…
正整数
-3,-1,-155,…
负整数
0
有理数
把下列各数分别填入相应的大括号中:
-6
,
5
,
10.5
,
,
0
,
-0.125
,
+5.33
,
-0.67,
(1)正数:{
···}
(2)负数:{
···}
(3)整数:{
···}
(4)正分数:{
···}
-6
,
-0.125
,
-0.67
-6
,
5
,
0
选自《状元大课堂》
把下列各数分别填入相应的大括号中:
-6
,
5
,
10.5
,
,
0
,
-0.125
,
+5.33
,
-0.67,
(5)负分数:{
···}
-0.125
,
-0.67
(6)非负数:{
···}
(7)有理数:{
···}
选自《状元大课堂》
有理数的分类
知识点四
(1)按概念分类:
(2)按性质分类:
下列说法中正确的是(
)
A.一个有理数不是正数就是负数
B.一个有理数不是整数就是分数
C.有理数是指整数、分数、正数、负数和零
D.正整数和负整数统称为整数
选自《状元大课堂》
B
1.
回答下列问题:
(1)
通常把水结冰时的温度规定为
0
℃,那么
比水结冰时的温度低
5
℃
应记做什么?
答:记作
-5
℃
练
习
练
习
(2)如果在东西向的马路上把出发点记为
0,
把向东走的路程记做正数,那么走
-50
m
是什么意思?
答:向西走了
50
m.
2.有下列数:3.6,
,-78,0,-0.37,9,-5.14,-1.其中
整数:
;
分数:
.
-78,0,9,-1
练
习
练
习
3.下列有理数中哪些是非负数,
哪些是负数?
湘教版·八年级数学上册
1.1
具有相反意义的量
其中阴与晴、圆与缺、悲与欢、离与合都是生活中具有相反意义的真实描绘。
在数学学科中,也有很多具有相反意义的量,为数学世界增添了无穷的魅力。
在日常生产和生活实践中,
由于记数、测量、分配等方面的需要产生了自然数、小数、分数.你还见过其他的数吗?
温度计上是如何区分零上的度数和零下的度数的?
如果仅用颜色来区分,就不便于运算.因此我们要想其他的办法.
点击播放
(1)在预报北京市某天的天气时,播音员说:“北京,晴,局部多云,零下
6
摄氏度到
5
摄氏度.”这时,
屏幕上是如何显示这天的温度的?
屏幕上显示“-6~5℃”
(2)储蓄存折上是怎样表示“存入
2500
元”和“支出
3000
元”的?
存入2500元记做“+2500”
支出3000元记做“-3000”
知识点一
正数、负数和
0
大于
0
的自然数和分数(或小数)就是正数,负数就是在正数前面加上“-”(读做负)号.
0
既不是正数,也不是负数.
我们把正数和
0
统称为非负数,负数和
0
统称为非正数.
选自《状元大课堂》
将下列各数填在相应的横线上:
+6
,
-21
,
54
,
0
,
,
0.11
,
-π,-35%
正数:____________________;
负数:____________________;
非负数:___________________.
-21
,
-π,-35%
在具有相反意义的一对量中,我们把其中的一种量用正数表示,而另一种量就用负数表示.
用正数和负数表示具有相反意义的量
知识点二
请举出一些具有相反意义的量的例子,并分别表示它们.
海平面以上与海平面以下表示的意义相反.海平面以上
1025
m
记做“1025
m”,海平面以下155
m记做“-155m”.
点击播放
请举出一些具有相反意义的量的例子,并分别表示它们.
点击播放
在东西向的马路上,把出发点记为
0,向东与向西意义相反.若把向东走
2
km
记做“2
km”,那么向西走2.6
km
应记做“-2.6
km”.
选自《状元大课堂》
用正负数表示下列具有相反意义的量:
(1)某地
12
月某天的最高温度是零上
10
℃,最低温度是零下
4
℃.若规定零上温度为正,则零上
10
℃
可记做_______,零下
4
℃
可记做_______;
(2)如果某蓄水池的水位比标准水位高
2
m
记做+2
m,那么比标准水位低
0.5
m
应记做______,恰好在标准水位应记做_________.
+10
℃
-4
℃
-5
m
0
请你举例说明从小学到现在,我们学过的数有哪些.
自然数:
0,1,2,3,…
小数:
分数:
负数:
分数可以化成有限小数或无限循环小数.
有限小数或无限循环小数也可以化为分数.
有理数的有关概念
知识点三
正整数、零和负整数统称为整数.
正分数和负分数统称为分数.
整数和分数统称为有理数.
1,3,167,…
正整数
-3,-1,-155,…
负整数
0
有理数
把下列各数分别填入相应的大括号中:
-6
,
5
,
10.5
,
,
0
,
-0.125
,
+5.33
,
-0.67,
(1)正数:{
···}
(2)负数:{
···}
(3)整数:{
···}
(4)正分数:{
···}
-6
,
-0.125
,
-0.67
-6
,
5
,
0
选自《状元大课堂》
把下列各数分别填入相应的大括号中:
-6
,
5
,
10.5
,
,
0
,
-0.125
,
+5.33
,
-0.67,
(5)负分数:{
···}
-0.125
,
-0.67
(6)非负数:{
···}
(7)有理数:{
···}
选自《状元大课堂》
有理数的分类
知识点四
(1)按概念分类:
(2)按性质分类:
下列说法中正确的是(
)
A.一个有理数不是正数就是负数
B.一个有理数不是整数就是分数
C.有理数是指整数、分数、正数、负数和零
D.正整数和负整数统称为整数
选自《状元大课堂》
B
1.
回答下列问题:
(1)
通常把水结冰时的温度规定为
0
℃,那么
比水结冰时的温度低
5
℃
应记做什么?
答:记作
-5
℃
练
习
练
习
(2)如果在东西向的马路上把出发点记为
0,
把向东走的路程记做正数,那么走
-50
m
是什么意思?
答:向西走了
50
m.
2.有下列数:3.6,
,-78,0,-0.37,9,-5.14,-1.其中
整数:
;
分数:
.
-78,0,9,-1
练
习
练
习
3.下列有理数中哪些是非负数,
哪些是负数?
同课章节目录
