北师大版数学九年级上册 1.3 正方形的性质与判定 同步练习题(Word版 含答案)
文档属性
| 名称 | 北师大版数学九年级上册 1.3 正方形的性质与判定 同步练习题(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 299.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-15 14:28:30 | ||
图片预览




文档简介
第一章 特殊平行四边形
1.3 正方形的性质与判定
1.
如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为(
)
A.
4
B.
5
C.
6
D.
8
2.
平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线互相垂直且相等
B.对角线相等
C.对角线互相垂直
D.对角线互相平分
3.
如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME等于( )
A.
25°
B.
35°
C.
45°
D.
50°
4.
如图所示,直线a经过正方形ABCD的顶点A,分别过顶点D,B作DE⊥a于点E,BF⊥a于点F,若DE=4,BF=3,则EF的长为( )
A.
7
B.
8
C.
9
D.
10
5.
如图,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
6.
如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.AC=BF
B.CF⊥BF
C.BD=DF
D.BC=AC
7.
如图,Rt△ABC中,∠ACB=90°,点D,E,F分别是AB,AC,BC的中点,连接DE,DF,CD,如果AC=BC,那么四边形DECF是( )
A.菱形
B.矩形
C.
正方形
D.
梯形
8.
下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相垂直平分的四边形是正方形
D.
对角线互相平分的四边形是平行四边形
9.
四边形ABCD的对角线AC和BD相交于点O,设有下列条件:①AB=AD;②∠DAB=90°;③AO=CO,BO=DO;④矩形ABCD;⑤菱形ABCD;⑥正方形ABCD,则下列推理不成立的是( )
A.①②?⑥
B.①③?⑤
C.①④?⑥
D.②③?④
10.
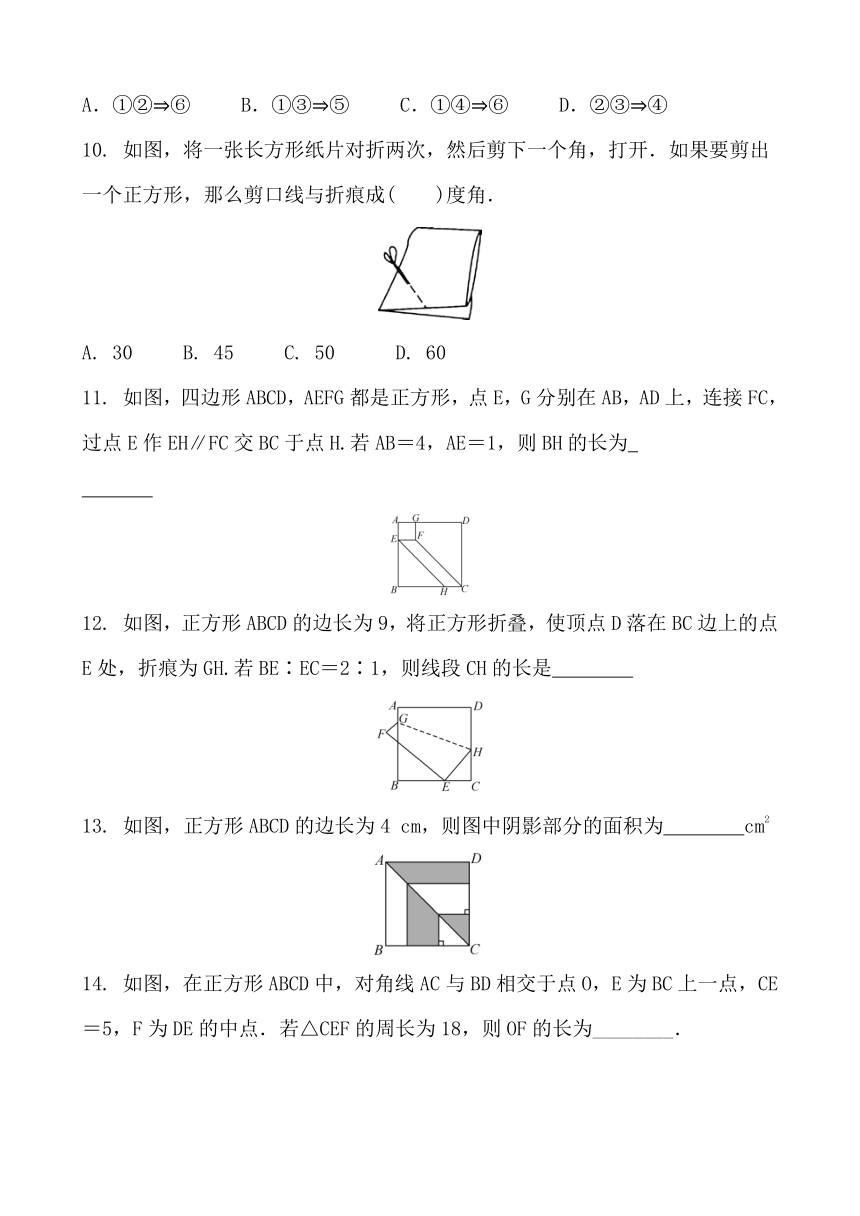
如图,将一张长方形纸片对折两次,然后剪下一个角,打开.如果要剪出一个正方形,那么剪口线与折痕成( )度角.
A.
30
B.
45
C.
50
D.
60
11.
如图,四边形ABCD,AEFG都是正方形,点E,G分别在AB,AD上,连接FC,过点E作EH∥FC交BC于点H.若AB=4,AE=1,则BH的长为
12.
如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE∶EC=2∶1,则线段CH的长是
13.
如图,正方形ABCD的边长为4
cm,则图中阴影部分的面积为
cm2
14.
如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为________.
15.
如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…,则正方形OB2
015B2
016C2
016的顶点B2
016的坐标是________.
16.
如图,在△ABC中,点D,E,F分别在边BC,AB,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②若∠BAC=90°,则四边形AEDF是矩形;③若AD平分∠BAC,则四边形AEDF是菱形;④若∠BAC=90°,AD平分∠BAC,则四边形AEDF是正方形,你认为正确的是
(填序号)
17.
?ABCD的对角线AC与BD相交于点O,且AC⊥BD,
请添加一个条件:____________,使得?ABCD为正方形.
18.
如图,在正方形ABCD中,△ABE和△CDF为直角三角形,
∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF=
19.
如图,以边长为1的正方形的四边中点为顶点作四边形,再以所得四边形的四边中点为顶点作四边形,…依次作下去,所作的第三个四边形的周长为________;第n个四边形的周长为________.
20.
如图,四边形ABCD是正方形,点E是BC的中点,∠AEF=90°,EF交正方形外角的平分线CF于点F.求证:AE=EF.
21.
如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8
cm,求线段BE的长.
22.
如图,点O是线段AB上一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.
(1)求证:四边形CDOF是矩形;
(2)当∠AOC为多少度时,四边形CDOF是正方形?请说明理由.
23.
如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其他条件不变(如图②),若∠ABC=58°,
则∠DPE=________度.
24.
如图①,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.
(1)如图②,连接EF,FG,GH,HE,试判断四边形EFGH的形状,并证明你的结论;
(2)将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图③的方式拼接成一个四边形.若正方形ABCD的边长为3
cm,HA=EB=FC=GD=1
cm,则图③中阴影部分的面积为________cm2.
25.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为点F,交直线MN于点E,连接CD,BE.
(1)求证:CE=AD;
(2)当点D是AB的中点时,四边形BECD是什么特殊四边形?请说明理由;
(3)若点D为AB的中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明理由.
答案:
1---10
BDCAB
ACDAB
11.
3
12.
4
13.
8
14.
15.
(21
008,0)
16.
①
②
③
④
17.
∠BAD=90°
18.
7
19.
4()n
20.
解:如图,取AB的中点H,连接EH,
∵∠AEF=90°,∴∠2+∠AEB=90°,∵四边形ABCD是正方形,
∴∠1+∠AEB=90°,∴∠1=∠2,∵点E是BC的中点,点H是AB的中点,∴BH=BE,AH=CE,∴∠BHE=45°,∵CF是∠DCG的角平分线,
∴∠FCG=45°,∴∠AHE=∠ECF=135°,
在△AHE和△ECF中,∴△AHE≌△ECF(ASA),∴AE=EF.
21.
解:.(1)四边形ACED是平行四边形.理由如下:∵四边形ABCD是正方形,∴AD∥BC,即AD∥CE,∵DE∥AC,∴四边形ACED是平行四边形.
(2)由(1)知,BC=AD=CE=CD,在Rt△BCD中,令BC=CD=x,
则x2+x2=82.解得x=4,∴BE=2x=8(cm).
22.
.(1)证明:∵OD平分∠AOC,OF平分∠COB,∴∠AOC=2∠COD,∠COB=2∠COF,∵∠AOC+∠BOC=180°,∴2∠COD+2∠COF=180°,∴∠COD+∠COF=90°,∴∠DOF=90°.
∵OA=OC,OD平分∠AOC,∴OD⊥AC,AD=DC,
∴∠CDO=90°,∵CF⊥OF,∴∠CFO=90°,∴四边形CDOF是矩形.
(2)当∠AOC=90°时,四边形CDOF是正方形.
理由如下:∵∠AOC=90°,AD=DC,∴OD=DC.
又由(1)知四边形CDOF是矩形,则矩形CDOF是正方形.
因此,当∠AOC=90°时,四边形CDOF是正方形.
23.
(1)证明:∵四边形ABCD是正方形,∴BC=DC,∠BCP=∠DCP=45°,
又∵CP=CP,∴△BCP≌△DCP(SAS).
(2)证明:由(1)知,△BCP≌△DCP,∴∠CBP=∠CDP,∵PE=PB,∴∠CBP=∠E,∴∠CDP=∠E,∵∠1=∠2(对顶角相等),
∴180°-∠1-∠CDP=180°-∠2-∠E,即∠DPE=∠DCE,∵AB∥CD,∴∠DCE=∠ABC,∴∠DPE=∠ABC.
(3)
58
24.
(1)四边形EFGH是正方形.
证明:∵四边形ABCD是正方形,∴∠A=∠B=∠C=∠D=90°,
AB=BC=CD=DA.∵HA=EB=FC=GD,∴AE=BF=CG=DH.∴△AEH≌△BFE≌△CGF≌△DHG.∴EH=EF=FG=GH.
∴四边形EFGH是菱形.由△DHG≌△AEH,知∠DHG=∠AEH.
∵∠AEH+∠AHE=90°,∴∠DHG+∠AHE=90°.∴∠GHE=90°.
∴菱形EFGH是正方形.
(2)
1
25.
(1)证明:∵DE⊥BC,∴∠DFB=90°,又∵∠ACB=90°,
∴∠ACB=∠DFB,∴AC∥DE,又∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,∴CE=AD.
(2)四边形BECD是菱形.理由如下:∵D为AB中点,∴AD=BD,又∵CE=AD,∴BD=CE,∵BD∥CE,∴四边形BECD是平行四边形,∵∠ACB=90°,D为AB中点,∴CD=BD,∴?BECD是菱形.
(3)当∠A=45°时,四边形BECD是正方形.理由如下:∵∠ACB=90°,∠A=45°,∴∠ABC=∠A=45°,∴AC=BC,∵D为BA的中点,∴CD⊥AB,∴∠CDB=90°,∵四边形BECD是菱形,∴四边形BECD是正方形,即当∠A=45°时,四边形BECD是正方形.
1.3 正方形的性质与判定
1.
如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为(
)
A.
4
B.
5
C.
6
D.
8
2.
平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线互相垂直且相等
B.对角线相等
C.对角线互相垂直
D.对角线互相平分
3.
如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME等于( )
A.
25°
B.
35°
C.
45°
D.
50°
4.
如图所示,直线a经过正方形ABCD的顶点A,分别过顶点D,B作DE⊥a于点E,BF⊥a于点F,若DE=4,BF=3,则EF的长为( )
A.
7
B.
8
C.
9
D.
10
5.
如图,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
6.
如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.AC=BF
B.CF⊥BF
C.BD=DF
D.BC=AC
7.
如图,Rt△ABC中,∠ACB=90°,点D,E,F分别是AB,AC,BC的中点,连接DE,DF,CD,如果AC=BC,那么四边形DECF是( )
A.菱形
B.矩形
C.
正方形
D.
梯形
8.
下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相垂直平分的四边形是正方形
D.
对角线互相平分的四边形是平行四边形
9.
四边形ABCD的对角线AC和BD相交于点O,设有下列条件:①AB=AD;②∠DAB=90°;③AO=CO,BO=DO;④矩形ABCD;⑤菱形ABCD;⑥正方形ABCD,则下列推理不成立的是( )
A.①②?⑥
B.①③?⑤
C.①④?⑥
D.②③?④
10.
如图,将一张长方形纸片对折两次,然后剪下一个角,打开.如果要剪出一个正方形,那么剪口线与折痕成( )度角.
A.
30
B.
45
C.
50
D.
60
11.
如图,四边形ABCD,AEFG都是正方形,点E,G分别在AB,AD上,连接FC,过点E作EH∥FC交BC于点H.若AB=4,AE=1,则BH的长为
12.
如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE∶EC=2∶1,则线段CH的长是
13.
如图,正方形ABCD的边长为4
cm,则图中阴影部分的面积为
cm2
14.
如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为________.
15.
如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…,则正方形OB2
015B2
016C2
016的顶点B2
016的坐标是________.
16.
如图,在△ABC中,点D,E,F分别在边BC,AB,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②若∠BAC=90°,则四边形AEDF是矩形;③若AD平分∠BAC,则四边形AEDF是菱形;④若∠BAC=90°,AD平分∠BAC,则四边形AEDF是正方形,你认为正确的是
(填序号)
17.
?ABCD的对角线AC与BD相交于点O,且AC⊥BD,
请添加一个条件:____________,使得?ABCD为正方形.
18.
如图,在正方形ABCD中,△ABE和△CDF为直角三角形,
∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF=
19.
如图,以边长为1的正方形的四边中点为顶点作四边形,再以所得四边形的四边中点为顶点作四边形,…依次作下去,所作的第三个四边形的周长为________;第n个四边形的周长为________.
20.
如图,四边形ABCD是正方形,点E是BC的中点,∠AEF=90°,EF交正方形外角的平分线CF于点F.求证:AE=EF.
21.
如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8
cm,求线段BE的长.
22.
如图,点O是线段AB上一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.
(1)求证:四边形CDOF是矩形;
(2)当∠AOC为多少度时,四边形CDOF是正方形?请说明理由.
23.
如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其他条件不变(如图②),若∠ABC=58°,
则∠DPE=________度.
24.
如图①,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.
(1)如图②,连接EF,FG,GH,HE,试判断四边形EFGH的形状,并证明你的结论;
(2)将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图③的方式拼接成一个四边形.若正方形ABCD的边长为3
cm,HA=EB=FC=GD=1
cm,则图③中阴影部分的面积为________cm2.
25.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为点F,交直线MN于点E,连接CD,BE.
(1)求证:CE=AD;
(2)当点D是AB的中点时,四边形BECD是什么特殊四边形?请说明理由;
(3)若点D为AB的中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明理由.
答案:
1---10
BDCAB
ACDAB
11.
3
12.
4
13.
8
14.
15.
(21
008,0)
16.
①
②
③
④
17.
∠BAD=90°
18.
7
19.
4()n
20.
解:如图,取AB的中点H,连接EH,
∵∠AEF=90°,∴∠2+∠AEB=90°,∵四边形ABCD是正方形,
∴∠1+∠AEB=90°,∴∠1=∠2,∵点E是BC的中点,点H是AB的中点,∴BH=BE,AH=CE,∴∠BHE=45°,∵CF是∠DCG的角平分线,
∴∠FCG=45°,∴∠AHE=∠ECF=135°,
在△AHE和△ECF中,∴△AHE≌△ECF(ASA),∴AE=EF.
21.
解:.(1)四边形ACED是平行四边形.理由如下:∵四边形ABCD是正方形,∴AD∥BC,即AD∥CE,∵DE∥AC,∴四边形ACED是平行四边形.
(2)由(1)知,BC=AD=CE=CD,在Rt△BCD中,令BC=CD=x,
则x2+x2=82.解得x=4,∴BE=2x=8(cm).
22.
.(1)证明:∵OD平分∠AOC,OF平分∠COB,∴∠AOC=2∠COD,∠COB=2∠COF,∵∠AOC+∠BOC=180°,∴2∠COD+2∠COF=180°,∴∠COD+∠COF=90°,∴∠DOF=90°.
∵OA=OC,OD平分∠AOC,∴OD⊥AC,AD=DC,
∴∠CDO=90°,∵CF⊥OF,∴∠CFO=90°,∴四边形CDOF是矩形.
(2)当∠AOC=90°时,四边形CDOF是正方形.
理由如下:∵∠AOC=90°,AD=DC,∴OD=DC.
又由(1)知四边形CDOF是矩形,则矩形CDOF是正方形.
因此,当∠AOC=90°时,四边形CDOF是正方形.
23.
(1)证明:∵四边形ABCD是正方形,∴BC=DC,∠BCP=∠DCP=45°,
又∵CP=CP,∴△BCP≌△DCP(SAS).
(2)证明:由(1)知,△BCP≌△DCP,∴∠CBP=∠CDP,∵PE=PB,∴∠CBP=∠E,∴∠CDP=∠E,∵∠1=∠2(对顶角相等),
∴180°-∠1-∠CDP=180°-∠2-∠E,即∠DPE=∠DCE,∵AB∥CD,∴∠DCE=∠ABC,∴∠DPE=∠ABC.
(3)
58
24.
(1)四边形EFGH是正方形.
证明:∵四边形ABCD是正方形,∴∠A=∠B=∠C=∠D=90°,
AB=BC=CD=DA.∵HA=EB=FC=GD,∴AE=BF=CG=DH.∴△AEH≌△BFE≌△CGF≌△DHG.∴EH=EF=FG=GH.
∴四边形EFGH是菱形.由△DHG≌△AEH,知∠DHG=∠AEH.
∵∠AEH+∠AHE=90°,∴∠DHG+∠AHE=90°.∴∠GHE=90°.
∴菱形EFGH是正方形.
(2)
1
25.
(1)证明:∵DE⊥BC,∴∠DFB=90°,又∵∠ACB=90°,
∴∠ACB=∠DFB,∴AC∥DE,又∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,∴CE=AD.
(2)四边形BECD是菱形.理由如下:∵D为AB中点,∴AD=BD,又∵CE=AD,∴BD=CE,∵BD∥CE,∴四边形BECD是平行四边形,∵∠ACB=90°,D为AB中点,∴CD=BD,∴?BECD是菱形.
(3)当∠A=45°时,四边形BECD是正方形.理由如下:∵∠ACB=90°,∠A=45°,∴∠ABC=∠A=45°,∴AC=BC,∵D为BA的中点,∴CD⊥AB,∴∠CDB=90°,∵四边形BECD是菱形,∴四边形BECD是正方形,即当∠A=45°时,四边形BECD是正方形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
