高一物理曲线运动重难点解析及典型例题
文档属性
| 名称 | 高一物理曲线运动重难点解析及典型例题 |  | |
| 格式 | zip | ||
| 文件大小 | 82.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2011-06-03 16:26:12 | ||
图片预览


文档简介
第五章 曲线运动
一. 知识要点:
1. 认识匀速圆周运动的概念,理解线速度的概念,知道它就是物体做匀速圆周运动的瞬时速度;理解角速度和周期的概念,会用它们的公式进行计算。理解线速度、角速度、周期之间的关系:v=rω=2πr/T。理解匀速圆周运动是变速运动。
2. 理解速度变化量和向心加速度的概念,知道向心加速度和线速度、角速度的关系式。能够运用向心加速度公式求解有关问题。
3. 运用极限法理解线速度的瞬时性。掌握运用圆周运动的特点如何去分析有关问题。体会有了线速度后。为什么还要引入角速度。运用数学知识推导角速度的单位。
二. 重难点解析:
1. 线速度
(1)定义:质点沿圆周运动通过的弧长Δl与所用时间Δt之比叫做线速度。它描述质点沿圆周运动的快慢。
(2)大小: 单位:m/s
(3)方向:质点在某点的线速度方向沿着圆周上该点的切线方向。
2. 匀速圆周运动
(1)定义:物体沿着圆周运动,并且线速度大小处处相等的运动叫匀速圆周运动。
(2)因线速度方向不断发生变化,故匀速圆周运动是变速运动,这里的“匀速”是指速率不变。
3. 角速度
(1)定义:在匀速圆周运动中,连接质点和圆心的半径转过的角度与所用时间的比值,就是指点的角速度。描述质点转过圆心角的快慢。匀速圆周运动是角速度不变的圆周运动。
(2)大小:,单位:rad/s
4. 周期T、频率f和转速n
定义:做圆周运动的物体运动一周所用的时间叫做周期,用T表示,单位为秒(s)。
做圆周运动的物体运动一秒,所转过圆周的次数叫做频率,用f表示,单位为赫兹(Hz)。1 Hz=1。
做圆周运动的物体在单位时间内沿圆周绕圆心转过的圈数叫做转速。用n表示,单位为转每秒(r/s),或转每分(r/min)。
周期频率和转速都是描述物体做圆周运动快慢的物理量。
5. 描述圆周运动各物理量的关系
(1)线速度和角速度间的关系。
v= rω。
(2)线速度与周期的关系。
。
(3)角速度与周期的关系。
。
(4)考虑频率f则有:,v=2πfr。
(5)而频率f与n的关系为f=n。
以上各物理量关系有:v=ωr=2πfr=2πnr。
6. 两个有用的结论
(1)在同一个转盘上的角速度相同。
(2)同一个轮子的边缘上,线速度相同,传动中线速度相同。
7. 匀速圆周运动向心加速度
(1)定义:做匀速圆周运动的物体,加速度指向圆心,称作向心加速度。描述线速度改变的快慢。
(2)公式:=ω2r==4π2n2r=4π2f2r=ωv。
(3)方向:总是沿着半径指向圆心。
(4)向心加速度公式也适用于非匀速圆周运动。
【典型例题】
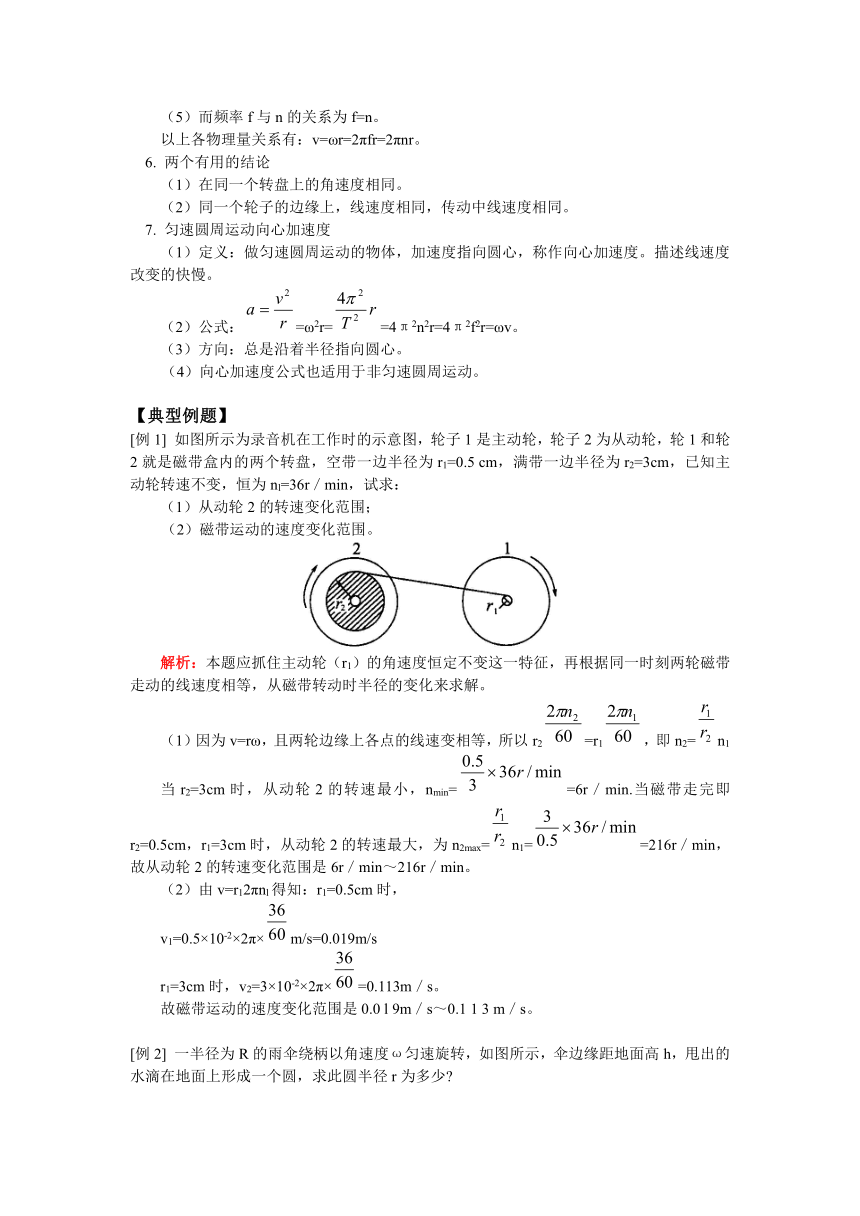
[例1] 如图所示为录音机在工作时的示意图,轮子1是主动轮,轮子2为从动轮,轮1和轮2就是磁带盒内的两个转盘,空带一边半径为r1=0.5 cm,满带一边半径为r2=3cm,已知主动轮转速不变,恒为nl=36r/min,试求:
(1)从动轮2的转速变化范围;
(2)磁带运动的速度变化范围。
解析:本题应抓住主动轮(r1)的角速度恒定不变这一特征,再根据同一时刻两轮磁带走动的线速度相等,从磁带转动时半径的变化来求解。
(1)因为v=rω,且两轮边缘上各点的线速变相等,所以r2=r1,即n2=n1
当r2=3cm时,从动轮2的转速最小,nmin==6r/min.当磁带走完即r2=0.5cm,r1=3cm时,从动轮2的转速最大,为n2max=n1==216r/min,故从动轮2的转速变化范围是6r/min~216r/min。
(2)由v=r12πnl得知:r1=0.5cm时,
v1=0.5×10-2×2π×m/s=0.019m/s
r1=3cm时,v2=3×10-2×2π×=0.113m/s。
故磁带运动的速度变化范围是0.0 l 9m/s~0.1 1 3 m/s。
[例2] 一半径为R的雨伞绕柄以角速度ω匀速旋转,如图所示,伞边缘距地面高h,甩出的水滴在地面上形成一个圆,求此圆半径r为多少
解析:雨滴飞出的速度大小为v=ωR, ①
雨滴做平抛运动。
在竖直方向上有 h= ②
在水平方向上有 S=vt ③
由几何关系知,雨滴半径 r= ④
解以上几式得 r=R
点评:雨滴离开伞边缘后沿切线方向水平抛出,做平抛运动,特别注意不是沿半径飞出,其间距关系见俯视图.。值得注意的是把立体图转化为平面图这个思想很重要,有助于我们弄清各物理量间的几何关系。
[例3] 一质点沿着半径r=1 m的圆周以n=2r/s的转速匀速转动,如图。试求:
(1)从A点开始计时,经过s的时间质点速度的变化;
(2)质点的向心加速度的大小。
解析:① 求出s的时间连接质点的半径转过的角度是多少
② 求出质点在A点和s末线速度的大小和方向。
③ 由矢量减法作出矢量三角形。
④ 明确边角关系,解三角形求得△v的大小和方向。
⑤ 根据或an=ω2r求出向心加速度的大小。
答案:(1)△v=2πm/s 方向与OA连线成45 角指向圆心O(2)a=l6π2
[例4] 如图所示,一个球绕中心轴线的角速度ω做匀速圆周转动,则( )
A. a、b两点线速度相同
B. a、b两点角速度相同
C. 若θ=30 ,则a、b两点的速度之比va:vb=:2
D. 若θ=30 ,则a、b两点的向心加速度之比aa:ab=:2
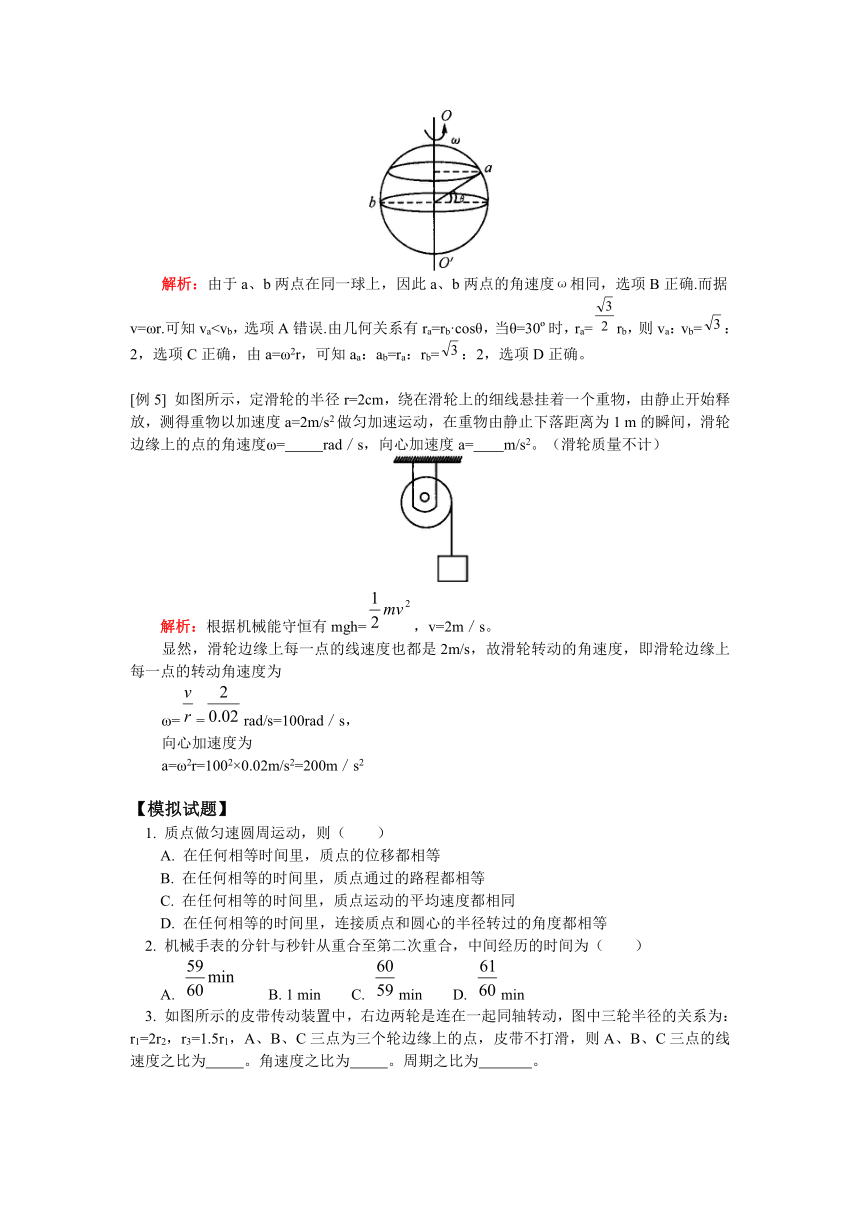
解析:由于a、b两点在同一球上,因此a、b两点的角速度ω相同,选项B正确.而据v=ωr.可知va[例5] 如图所示,定滑轮的半径r=2cm,绕在滑轮上的细线悬挂着一个重物,由静止开始释放,测得重物以加速度a=2m/s2做匀加速运动,在重物由静止下落距离为1 m的瞬间,滑轮边缘上的点的角速度ω= rad/s,向心加速度a= m/s2。(滑轮质量不计)
解析:根据机械能守恒有mgh=,v=2m/s。
显然,滑轮边缘上每一点的线速度也都是2m/s,故滑轮转动的角速度,即滑轮边缘上每一点的转动角速度为
ω==rad/s=100rad/s,
向心加速度为
a=ω2r=1002×0.02m/s2=200m/s2
【模拟试题】
1. 质点做匀速圆周运动,则( )
A. 在任何相等时间里,质点的位移都相等
B. 在任何相等的时间里,质点通过的路程都相等
C. 在任何相等的时间里,质点运动的平均速度都相同
D. 在任何相等的时间里,连接质点和圆心的半径转过的角度都相等
2. 机械手表的分针与秒针从重合至第二次重合,中间经历的时间为( )
A. B. 1 min C. min D. min
3. 如图所示的皮带传动装置中,右边两轮是连在一起同轴转动,图中三轮半径的关系为:r1=2r2,r3=1.5r1,A、B、C三点为三个轮边缘上的点,皮带不打滑,则A、B、C三点的线速度之比为 。角速度之比为 。周期之比为 。
4. 如图所示是生产流水线上的皮带传输装置,传输带上等间距地放着很多半成品产品。A轮处装有光电计数器,它可以记录通过A处的产品数目。已知测得轮A、B的半径分别为rA=20cm,rB=l0cm,相邻两产品距离为30cm,lmin内有41个产品通过A处,求:
(1)产品随传输带移动的速度大小;
(2)A、B轮轮缘上的两点P、Q及A轮半径中点M的线速度和角速度大小,并在图中画出线速度方向;
(3)如果A轮是通过摩擦带动C轮转动,且rC=5 cm,在图中描出C轮的转动方向,求出C轮的角速度(假设轮不打滑)。
5. 如图所示,直径为d的纸制圆筒以角速度ω绕垂直纸面的轴O匀速运动(图示为截面)。从枪口发射的子弹沿直径穿过圆筒。若子弹在圆筒旋转不到半周时,在圆周上留下a、b两个弹孔,已知aO与bO夹角为θ,求子弹的速度。
6. 如图所示,M、N是两个共轴圆筒横截面,外筒半径为R,内筒半径比R小得多,可以忽略不计,筒的两端是封闭的,两筒之间抽成真空,两筒以相同的角速度ω绕其中心轴线(图中垂直于纸面)作匀速转动。设从M筒内部可以通过狭缝s(与M筒的轴线平行)不断地向外射出两种不同速率v1和v2的微粒,从s处射出时的初速度的方向都是沿筒的半径方向,微粒到达N筒后就附着在N筒上.如果R、v1和v2都不变,而ω取某一合适的值,则( )
A. 有可能使微粒落在Ⅳ筒上的位置都在a处一条与s缝平行的窄条上
B. 有可能使微粒落在N筒上的位置都在某处,如b处一条与缝s平行的窄条上
C. 有可能使微粒落在N筒上的位置分别在某两处,如b处和c处与s缝平行的窄条上
D. 只要时间足够长,N筒上到处都落微粒
7. 关于向心加速度,下列说法正确的是( )
A. 它是描述角速度变化快慢的物理量
B. 它是描述线速度大小变化快慢的物理量
C. 它是描述线速度方向变化快慢的物理量
D. 它是描述角速度方向变化快慢的物理量
8. 一质点做匀速圆周运动的半径约为地球的半径,R=R地≈6400km,它的线速度大小是v=l00m/s,将这个匀速圆周运动看成是匀速直线运动你认为可以吗?试论证之。
9. 如图所示为质点P、Q做匀速圆周运动时向心加速度随半径变化的图线.表示质点P的图线是双曲线,表示质点Q的图线是过原点的一条直线。由图线可知( )
A. 质点P线速度大小不变 B. 质点P的角速度大小不变
C. 质点Q的角速度随半径变化 D. 质点Q的线速度大小不变
10. 如图所示,圆轨道AB是在竖直平面内的圆周,在B点轨道的切线是水平的,一质点自A点从静止开始下滑,不计摩擦和空气阻力,则在质点刚要到达B点时的加速度大小为 ,滑过B点时的加速度大小为 。
11. 如图所示,一质量为m的砂袋用长为l的绳子拴住悬挂在O点,被拳击运动员水平击中后,荡起的最大高度是h.求砂袋刚被击中后的瞬间,砂袋的向心加速度是多大
【试题答案】
1. 解析:质点做匀速圆周运动时,相等时间内通过的圆弧长度相等,即路程相等,B项正确,此时半径所转过的角度也相等,D项正确。但由于位移是矢量,在相等时间里,质点位移大小相等,方向却不一定相同,因此位移不一定相同,而平均速度也是矢量,虽然大小相等,但方向不尽相同,故A、C错误。本题选B、D。
2. 解析:先求出分针与秒针的角速度:
ω分=rad/s,ω秒=rad/s
设两次重合时间间隔为△t,则有
φ分=ω分△t,φ秒=ω秒△t,φ秒一φ分=2π,
即 Δt==(min)
故选项C正确
3. 解析:因为A、B两轮由不打滑的皮带相连,所以相等时间内A、B两点转过的弧长相等。即vA=vB.由v=ωr知==。又B、C是同轴转动,相等时间转过的角度相等,即ωB=ωA,由v=ωr知,
===
所以vA:vB:vC=1:1:3,ωA:ωB:ωC=l:2:2
再根据T=等得 TA:TB:TC=1::=2:1:1
4. 解析:首先明确产品与传送带保持相对静止的条件下,产品速度的大小就等于传送带上每一点速度的大小,在传送带不打滑的条件下,传送带上各点运动速度的大小都等于A、B轮缘上点的线速度的大小。由传送带相邻产品的间距及单位时间内通过A处的产品的个数可以确定出皮带上点的速度,进而知道A、B轮缘上的两点P、Q线速度的大小,然后由线速度与角速度的关系,求出A、B两轮的角速度及A轮半径中点M的线速度及C轮的角速度.由题意知,1分钟内有41个产品通过A处,说明1分钟内传输带上的每点运动的路程为两产品间距的40倍。设传输带运动速度大小为v,则
(1)v==m/s=0.2m/s
(2)vP=vQ=0.2m/s。A轮半径上的M点与P点的角速度相等,故
vM=vP=×0.2m/s=0.1m/s
ωP=ωM==rad/s=lrad/s,ωQ=2ωP=2rad/s
(3)C轮的转动方向如图所示,如果两轮间不打滑,则它们的接触处是相对静止的,即它们轮缘的线速度大小是相等的,所以ωCrC=ωArA。
C轮的角速度
ωC=ωA=·1rad/s=4rad/s
答案:(1)0.2m/s (2)vP=vQ=0.2m/s,vM=0.1m/s ωP=1 rad/s ωQ=2rad/s (3)ωC=4rad/s
5. 解析:设子弹速度为v,则子弹穿过筒的时间 t=
此时间内筒转过的角度 α=π—θ
据α=ωt,得 π一θ=ω,
则子弹速度 v=
本题中若无角度的限制,则在时间t内转过的角度 α=2nπ+π一θ=π(2n+1)一θ
α=2nπ十π一θ=π(2n+1)一θ
则子弹速度 v=(n=0,1,2,…)
6. 解析:因M、N的角速度ω相同,故在任意一段时间内,N筒与s缝在同一径向连线上的a点必定与s缝一起转过同样大小的角度,且粒子历时皆为,于是这些在不同时刻从s缝射出、速率为v的粒子一定落在N筒上比a点落后相同角度ωt=ω的位置上,即落在一条与s缝平行的窄条上,不会各处散落,故排除D。
题设中未限制ω的大小,而圆周上各点转过的角度又具有周期性(周期为2π)。只要ω满足ω=2πn,ω=2πm(m、n为任意整数),则两种粒子落在N筒上的位置都在a处的一条与s缝平行的窄条上,A正确。
若ω满足ω=2πn+ω,则均可以到达b,故B正确。
若速度为v1和v2的粒子到达N上的角度差不是2π的整数倍,则它们不能到达同一窄条上而分开,故C正确。
7. 解析:从匀速圆周运动的特点入手思考。匀速圆周运动其角速度大小不变,角速度的方向是不变的。线速度方向总是与半径垂直,半径转过多少度,线速度的方向就改变多少度。
答案:C
8. 解析:应从两个方面论述题中的看法:(1)求出质点的向心加速度,研究其大小是否可以忽略。(2)分析在不太大的空间内(如几百千米)速度方向变化的大小。
答案:在不太大的空间范围内可以看成匀速直线运动。
9. A
10. 解析:小球由A点到B点所做的运动是圆周运动的一部分,因而小球刚要到达B点时的运动为圆周运动,其加速度为向心加速度,大小为:a1=,从A到B,由机械能守恒定律有:
mgh=,
,
故 a1==2g
小球滑过B点后做平抛运动,只受重力,加速度大小为g
答案:2g;g
11. 解析:由机械能守恒得最低点速度
向心加速度
∴ a=
一. 知识要点:
1. 认识匀速圆周运动的概念,理解线速度的概念,知道它就是物体做匀速圆周运动的瞬时速度;理解角速度和周期的概念,会用它们的公式进行计算。理解线速度、角速度、周期之间的关系:v=rω=2πr/T。理解匀速圆周运动是变速运动。
2. 理解速度变化量和向心加速度的概念,知道向心加速度和线速度、角速度的关系式。能够运用向心加速度公式求解有关问题。
3. 运用极限法理解线速度的瞬时性。掌握运用圆周运动的特点如何去分析有关问题。体会有了线速度后。为什么还要引入角速度。运用数学知识推导角速度的单位。
二. 重难点解析:
1. 线速度
(1)定义:质点沿圆周运动通过的弧长Δl与所用时间Δt之比叫做线速度。它描述质点沿圆周运动的快慢。
(2)大小: 单位:m/s
(3)方向:质点在某点的线速度方向沿着圆周上该点的切线方向。
2. 匀速圆周运动
(1)定义:物体沿着圆周运动,并且线速度大小处处相等的运动叫匀速圆周运动。
(2)因线速度方向不断发生变化,故匀速圆周运动是变速运动,这里的“匀速”是指速率不变。
3. 角速度
(1)定义:在匀速圆周运动中,连接质点和圆心的半径转过的角度与所用时间的比值,就是指点的角速度。描述质点转过圆心角的快慢。匀速圆周运动是角速度不变的圆周运动。
(2)大小:,单位:rad/s
4. 周期T、频率f和转速n
定义:做圆周运动的物体运动一周所用的时间叫做周期,用T表示,单位为秒(s)。
做圆周运动的物体运动一秒,所转过圆周的次数叫做频率,用f表示,单位为赫兹(Hz)。1 Hz=1。
做圆周运动的物体在单位时间内沿圆周绕圆心转过的圈数叫做转速。用n表示,单位为转每秒(r/s),或转每分(r/min)。
周期频率和转速都是描述物体做圆周运动快慢的物理量。
5. 描述圆周运动各物理量的关系
(1)线速度和角速度间的关系。
v= rω。
(2)线速度与周期的关系。
。
(3)角速度与周期的关系。
。
(4)考虑频率f则有:,v=2πfr。
(5)而频率f与n的关系为f=n。
以上各物理量关系有:v=ωr=2πfr=2πnr。
6. 两个有用的结论
(1)在同一个转盘上的角速度相同。
(2)同一个轮子的边缘上,线速度相同,传动中线速度相同。
7. 匀速圆周运动向心加速度
(1)定义:做匀速圆周运动的物体,加速度指向圆心,称作向心加速度。描述线速度改变的快慢。
(2)公式:=ω2r==4π2n2r=4π2f2r=ωv。
(3)方向:总是沿着半径指向圆心。
(4)向心加速度公式也适用于非匀速圆周运动。
【典型例题】
[例1] 如图所示为录音机在工作时的示意图,轮子1是主动轮,轮子2为从动轮,轮1和轮2就是磁带盒内的两个转盘,空带一边半径为r1=0.5 cm,满带一边半径为r2=3cm,已知主动轮转速不变,恒为nl=36r/min,试求:
(1)从动轮2的转速变化范围;
(2)磁带运动的速度变化范围。
解析:本题应抓住主动轮(r1)的角速度恒定不变这一特征,再根据同一时刻两轮磁带走动的线速度相等,从磁带转动时半径的变化来求解。
(1)因为v=rω,且两轮边缘上各点的线速变相等,所以r2=r1,即n2=n1
当r2=3cm时,从动轮2的转速最小,nmin==6r/min.当磁带走完即r2=0.5cm,r1=3cm时,从动轮2的转速最大,为n2max=n1==216r/min,故从动轮2的转速变化范围是6r/min~216r/min。
(2)由v=r12πnl得知:r1=0.5cm时,
v1=0.5×10-2×2π×m/s=0.019m/s
r1=3cm时,v2=3×10-2×2π×=0.113m/s。
故磁带运动的速度变化范围是0.0 l 9m/s~0.1 1 3 m/s。
[例2] 一半径为R的雨伞绕柄以角速度ω匀速旋转,如图所示,伞边缘距地面高h,甩出的水滴在地面上形成一个圆,求此圆半径r为多少
解析:雨滴飞出的速度大小为v=ωR, ①
雨滴做平抛运动。
在竖直方向上有 h= ②
在水平方向上有 S=vt ③
由几何关系知,雨滴半径 r= ④
解以上几式得 r=R
点评:雨滴离开伞边缘后沿切线方向水平抛出,做平抛运动,特别注意不是沿半径飞出,其间距关系见俯视图.。值得注意的是把立体图转化为平面图这个思想很重要,有助于我们弄清各物理量间的几何关系。
[例3] 一质点沿着半径r=1 m的圆周以n=2r/s的转速匀速转动,如图。试求:
(1)从A点开始计时,经过s的时间质点速度的变化;
(2)质点的向心加速度的大小。
解析:① 求出s的时间连接质点的半径转过的角度是多少
② 求出质点在A点和s末线速度的大小和方向。
③ 由矢量减法作出矢量三角形。
④ 明确边角关系,解三角形求得△v的大小和方向。
⑤ 根据或an=ω2r求出向心加速度的大小。
答案:(1)△v=2πm/s 方向与OA连线成45 角指向圆心O(2)a=l6π2
[例4] 如图所示,一个球绕中心轴线的角速度ω做匀速圆周转动,则( )
A. a、b两点线速度相同
B. a、b两点角速度相同
C. 若θ=30 ,则a、b两点的速度之比va:vb=:2
D. 若θ=30 ,则a、b两点的向心加速度之比aa:ab=:2
解析:由于a、b两点在同一球上,因此a、b两点的角速度ω相同,选项B正确.而据v=ωr.可知va
解析:根据机械能守恒有mgh=,v=2m/s。
显然,滑轮边缘上每一点的线速度也都是2m/s,故滑轮转动的角速度,即滑轮边缘上每一点的转动角速度为
ω==rad/s=100rad/s,
向心加速度为
a=ω2r=1002×0.02m/s2=200m/s2
【模拟试题】
1. 质点做匀速圆周运动,则( )
A. 在任何相等时间里,质点的位移都相等
B. 在任何相等的时间里,质点通过的路程都相等
C. 在任何相等的时间里,质点运动的平均速度都相同
D. 在任何相等的时间里,连接质点和圆心的半径转过的角度都相等
2. 机械手表的分针与秒针从重合至第二次重合,中间经历的时间为( )
A. B. 1 min C. min D. min
3. 如图所示的皮带传动装置中,右边两轮是连在一起同轴转动,图中三轮半径的关系为:r1=2r2,r3=1.5r1,A、B、C三点为三个轮边缘上的点,皮带不打滑,则A、B、C三点的线速度之比为 。角速度之比为 。周期之比为 。
4. 如图所示是生产流水线上的皮带传输装置,传输带上等间距地放着很多半成品产品。A轮处装有光电计数器,它可以记录通过A处的产品数目。已知测得轮A、B的半径分别为rA=20cm,rB=l0cm,相邻两产品距离为30cm,lmin内有41个产品通过A处,求:
(1)产品随传输带移动的速度大小;
(2)A、B轮轮缘上的两点P、Q及A轮半径中点M的线速度和角速度大小,并在图中画出线速度方向;
(3)如果A轮是通过摩擦带动C轮转动,且rC=5 cm,在图中描出C轮的转动方向,求出C轮的角速度(假设轮不打滑)。
5. 如图所示,直径为d的纸制圆筒以角速度ω绕垂直纸面的轴O匀速运动(图示为截面)。从枪口发射的子弹沿直径穿过圆筒。若子弹在圆筒旋转不到半周时,在圆周上留下a、b两个弹孔,已知aO与bO夹角为θ,求子弹的速度。
6. 如图所示,M、N是两个共轴圆筒横截面,外筒半径为R,内筒半径比R小得多,可以忽略不计,筒的两端是封闭的,两筒之间抽成真空,两筒以相同的角速度ω绕其中心轴线(图中垂直于纸面)作匀速转动。设从M筒内部可以通过狭缝s(与M筒的轴线平行)不断地向外射出两种不同速率v1和v2的微粒,从s处射出时的初速度的方向都是沿筒的半径方向,微粒到达N筒后就附着在N筒上.如果R、v1和v2都不变,而ω取某一合适的值,则( )
A. 有可能使微粒落在Ⅳ筒上的位置都在a处一条与s缝平行的窄条上
B. 有可能使微粒落在N筒上的位置都在某处,如b处一条与缝s平行的窄条上
C. 有可能使微粒落在N筒上的位置分别在某两处,如b处和c处与s缝平行的窄条上
D. 只要时间足够长,N筒上到处都落微粒
7. 关于向心加速度,下列说法正确的是( )
A. 它是描述角速度变化快慢的物理量
B. 它是描述线速度大小变化快慢的物理量
C. 它是描述线速度方向变化快慢的物理量
D. 它是描述角速度方向变化快慢的物理量
8. 一质点做匀速圆周运动的半径约为地球的半径,R=R地≈6400km,它的线速度大小是v=l00m/s,将这个匀速圆周运动看成是匀速直线运动你认为可以吗?试论证之。
9. 如图所示为质点P、Q做匀速圆周运动时向心加速度随半径变化的图线.表示质点P的图线是双曲线,表示质点Q的图线是过原点的一条直线。由图线可知( )
A. 质点P线速度大小不变 B. 质点P的角速度大小不变
C. 质点Q的角速度随半径变化 D. 质点Q的线速度大小不变
10. 如图所示,圆轨道AB是在竖直平面内的圆周,在B点轨道的切线是水平的,一质点自A点从静止开始下滑,不计摩擦和空气阻力,则在质点刚要到达B点时的加速度大小为 ,滑过B点时的加速度大小为 。
11. 如图所示,一质量为m的砂袋用长为l的绳子拴住悬挂在O点,被拳击运动员水平击中后,荡起的最大高度是h.求砂袋刚被击中后的瞬间,砂袋的向心加速度是多大
【试题答案】
1. 解析:质点做匀速圆周运动时,相等时间内通过的圆弧长度相等,即路程相等,B项正确,此时半径所转过的角度也相等,D项正确。但由于位移是矢量,在相等时间里,质点位移大小相等,方向却不一定相同,因此位移不一定相同,而平均速度也是矢量,虽然大小相等,但方向不尽相同,故A、C错误。本题选B、D。
2. 解析:先求出分针与秒针的角速度:
ω分=rad/s,ω秒=rad/s
设两次重合时间间隔为△t,则有
φ分=ω分△t,φ秒=ω秒△t,φ秒一φ分=2π,
即 Δt==(min)
故选项C正确
3. 解析:因为A、B两轮由不打滑的皮带相连,所以相等时间内A、B两点转过的弧长相等。即vA=vB.由v=ωr知==。又B、C是同轴转动,相等时间转过的角度相等,即ωB=ωA,由v=ωr知,
===
所以vA:vB:vC=1:1:3,ωA:ωB:ωC=l:2:2
再根据T=等得 TA:TB:TC=1::=2:1:1
4. 解析:首先明确产品与传送带保持相对静止的条件下,产品速度的大小就等于传送带上每一点速度的大小,在传送带不打滑的条件下,传送带上各点运动速度的大小都等于A、B轮缘上点的线速度的大小。由传送带相邻产品的间距及单位时间内通过A处的产品的个数可以确定出皮带上点的速度,进而知道A、B轮缘上的两点P、Q线速度的大小,然后由线速度与角速度的关系,求出A、B两轮的角速度及A轮半径中点M的线速度及C轮的角速度.由题意知,1分钟内有41个产品通过A处,说明1分钟内传输带上的每点运动的路程为两产品间距的40倍。设传输带运动速度大小为v,则
(1)v==m/s=0.2m/s
(2)vP=vQ=0.2m/s。A轮半径上的M点与P点的角速度相等,故
vM=vP=×0.2m/s=0.1m/s
ωP=ωM==rad/s=lrad/s,ωQ=2ωP=2rad/s
(3)C轮的转动方向如图所示,如果两轮间不打滑,则它们的接触处是相对静止的,即它们轮缘的线速度大小是相等的,所以ωCrC=ωArA。
C轮的角速度
ωC=ωA=·1rad/s=4rad/s
答案:(1)0.2m/s (2)vP=vQ=0.2m/s,vM=0.1m/s ωP=1 rad/s ωQ=2rad/s (3)ωC=4rad/s
5. 解析:设子弹速度为v,则子弹穿过筒的时间 t=
此时间内筒转过的角度 α=π—θ
据α=ωt,得 π一θ=ω,
则子弹速度 v=
本题中若无角度的限制,则在时间t内转过的角度 α=2nπ+π一θ=π(2n+1)一θ
α=2nπ十π一θ=π(2n+1)一θ
则子弹速度 v=(n=0,1,2,…)
6. 解析:因M、N的角速度ω相同,故在任意一段时间内,N筒与s缝在同一径向连线上的a点必定与s缝一起转过同样大小的角度,且粒子历时皆为,于是这些在不同时刻从s缝射出、速率为v的粒子一定落在N筒上比a点落后相同角度ωt=ω的位置上,即落在一条与s缝平行的窄条上,不会各处散落,故排除D。
题设中未限制ω的大小,而圆周上各点转过的角度又具有周期性(周期为2π)。只要ω满足ω=2πn,ω=2πm(m、n为任意整数),则两种粒子落在N筒上的位置都在a处的一条与s缝平行的窄条上,A正确。
若ω满足ω=2πn+ω,则均可以到达b,故B正确。
若速度为v1和v2的粒子到达N上的角度差不是2π的整数倍,则它们不能到达同一窄条上而分开,故C正确。
7. 解析:从匀速圆周运动的特点入手思考。匀速圆周运动其角速度大小不变,角速度的方向是不变的。线速度方向总是与半径垂直,半径转过多少度,线速度的方向就改变多少度。
答案:C
8. 解析:应从两个方面论述题中的看法:(1)求出质点的向心加速度,研究其大小是否可以忽略。(2)分析在不太大的空间内(如几百千米)速度方向变化的大小。
答案:在不太大的空间范围内可以看成匀速直线运动。
9. A
10. 解析:小球由A点到B点所做的运动是圆周运动的一部分,因而小球刚要到达B点时的运动为圆周运动,其加速度为向心加速度,大小为:a1=,从A到B,由机械能守恒定律有:
mgh=,
,
故 a1==2g
小球滑过B点后做平抛运动,只受重力,加速度大小为g
答案:2g;g
11. 解析:由机械能守恒得最低点速度
向心加速度
∴ a=
