苏科版七年级下册10.1二元一次方程数学课件 (19张ppt)
文档属性
| 名称 | 苏科版七年级下册10.1二元一次方程数学课件 (19张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-14 09:35:08 | ||
图片预览






文档简介
定义解读:二元一次方程
①、是方程
②、两个未知数
③、含有未知数的项的次数是1
10.1 二一元一次方程
情景设置
根据篮球比赛规则:赢一场得2分,输一场得1分.在某次中学生篮球联赛中,一支球队,赢了若干场后积20分,问该球队赢了多少场?输了多少场?
10.1 二元一次方程
10.1 二一元一次方程
学习目标
1. 经历分析实际问题中数量关系的过程,进一步体会方程是刻画现实世界的有效数学模型。
2. 了解二元一次方程的概念,并会判断一组数据是否是某个二元一次方程的解。
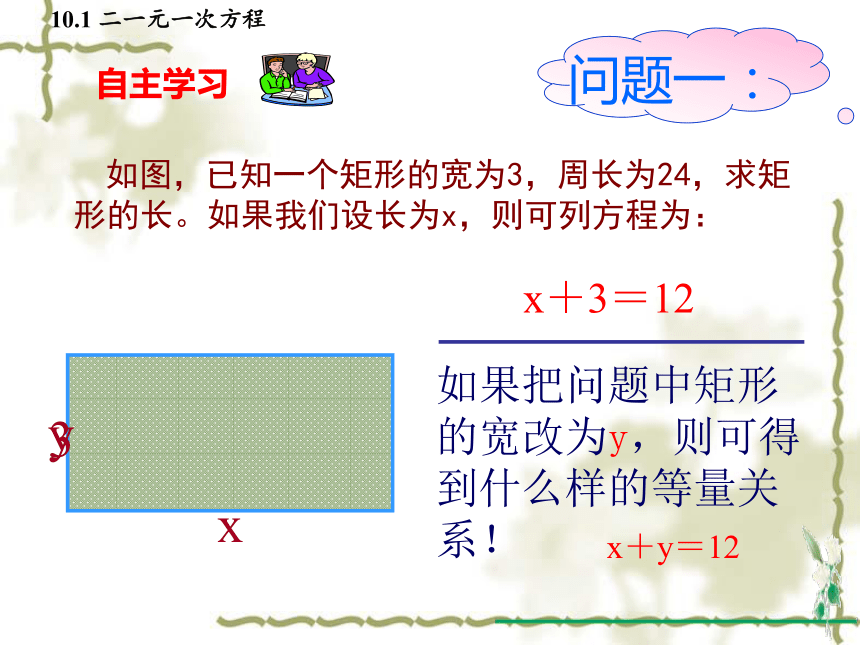
如图,已知一个矩形的宽为3,周长为24,求矩形的长。如果我们设长为x,则可列方程为:
如果把问题中矩形的宽改为y,则可得到什么样的等量关系!
3
x+3=12
x+y=12
x
y
问题一:
10.1 二一元一次方程
自主学习
根据篮球比赛规则:赢一场得2分,输一场得1分.在某次中学生篮球联赛中,一支球队,赢了若干场后积20分,问该球队赢了多少场?输了多少场?
如果设该队赢了x场,输了y场,那么请你填写下表:
场 数
得 分
积 分
赢
输
问题二:
10.1 二一元一次方程
x
y
2
1
2x
y
可以用式子表示为:
2x+y=20
自主学习
某球员在一场篮球比赛中共得35分(其中罚球得10分).问:他分别投中了多少个两分球和三分球?
解:设他投中了x个两分球、y个三分球,那么
2x+3y+10=35,
即 2x+3y=25.
10.1 二一元一次方程
自主学习
x+y=12,2x+y=20 ,2x+3y=25
你能否找出下列方程的共同特点?
含有两个未知数,且所含未知数的项的次数都是1的方程叫做二元一次方程。
二元一次方程
类比一元一次方程你能给这些方程取名吗?
根据上面的特点,你能试着用自己的语言来表述二元一次方程的定义吗?并与同桌交流.
10.1 二一元一次方程
归纳总结
判断下列式子是否为二元一次方程?
(1) 3x+1=x2
(5) xy+y=2
(3) x=y+1
(6) -2y=0
3
x
(2) x2+y=0
(4) y+ -x
2
1
不是
不是
是
不是
不是
是
10.1 二一元一次方程
互学互评
根据篮球比赛规则:赢一场得2分,输一场得1分.在某次中学生篮球联赛中,一支球队,赢了若干场后积20分,问该球队赢了多少场?输了多少场?
该队赢了x场,输了y场,那么
2x+y=20
哇!太简单了,赢5场,输十场.
10.1 二一元一次方程
精讲点拨
你同意小明的回答吗?为什么?
x
y
动动脑筋?你能列出输赢的所有可能情况吗?
2x+y=20
问题1:如果不是实际问题的限制,你能找出多少组解?
0
1
2
3
4
5
6
7
8
9
10
20
18
16
14
12
10
8
6
4
2
0
10.1 二一元一次方程
操作探究
无数组
问题2:用含有x的式子表示y为 。
y=20-2x
10.1 二一元一次方程
操作探究
某球员在一场篮球比赛中投篮共得25分.问:他分别投中了多少个两分球和三分球?
?用含有x的式子表示y为 .
根据你所列的表格,回答下列问题:
(1)这名球员最多投中了多少个三分球?
(2)这名球员最多投中了多少个球?
(3)如果这名球员投中了10个球,那么他投中了几个两分球?几个三分球?
解:设他投中了x个两分球、y个三分球,那么
2x+3y=25.
x
y
10.1 二一元一次方程
精讲点拨
③ 请根据②的结果列出这名球员投中的两分球和三分球的各种可能情况.
y=25-2x / 3
7
12
5
5
2
7
5
5
3
8
1
11
适合二元一次方程的一对未知数的值,叫做这个二元一次方程的一个解.
如x=8,y=3就是方程2x+3y=25的一个解,记作
1对数值必须用大括号合在一起,才是二元一次方程的一个解.
要注意呦!
10.1 二一元一次方程
归纳总结
10.1 二一元一次方程
活学活用
2、已知:5x3m+7-2y2n-1=4是二元一次方程,mn= .
考考你
3、已知 是方程2x+ay=5的解,则a= .
10.1 二一元一次方程
活学活用
—2
1
4、甲种铅笔每枝0.2元,乙种铅笔每枝0.5元,现在某人买了x枝甲种铅笔,y枝乙种铅笔,共花了7元.
(1)列出关于x, y的二元一次方程.
(2)用含x的式子表示y为
(3)如果x=5,那么y的值是多少?
(4)如果乙种铅笔买了10枝,那么甲种铅笔买了多少枝?
10.1 二一元一次方程
活学活用
0.2x+0.5y=7
y=70-2x / 5
y=12
x=10
小结与回顾
实际问题
数学问题
二元一次方程
求二元一次方程解的方法
二元一次方程解的概念
二元一次方程的概念
二元一次方程也是刻画现实世界数量关系的有效模型。
二元一次方程
10.1 二一元一次方程
课堂小结
①、是方程
②、两个未知数
③、含有未知数的项的次数是1
10.1 二一元一次方程
情景设置
根据篮球比赛规则:赢一场得2分,输一场得1分.在某次中学生篮球联赛中,一支球队,赢了若干场后积20分,问该球队赢了多少场?输了多少场?
10.1 二元一次方程
10.1 二一元一次方程
学习目标
1. 经历分析实际问题中数量关系的过程,进一步体会方程是刻画现实世界的有效数学模型。
2. 了解二元一次方程的概念,并会判断一组数据是否是某个二元一次方程的解。
如图,已知一个矩形的宽为3,周长为24,求矩形的长。如果我们设长为x,则可列方程为:
如果把问题中矩形的宽改为y,则可得到什么样的等量关系!
3
x+3=12
x+y=12
x
y
问题一:
10.1 二一元一次方程
自主学习
根据篮球比赛规则:赢一场得2分,输一场得1分.在某次中学生篮球联赛中,一支球队,赢了若干场后积20分,问该球队赢了多少场?输了多少场?
如果设该队赢了x场,输了y场,那么请你填写下表:
场 数
得 分
积 分
赢
输
问题二:
10.1 二一元一次方程
x
y
2
1
2x
y
可以用式子表示为:
2x+y=20
自主学习
某球员在一场篮球比赛中共得35分(其中罚球得10分).问:他分别投中了多少个两分球和三分球?
解:设他投中了x个两分球、y个三分球,那么
2x+3y+10=35,
即 2x+3y=25.
10.1 二一元一次方程
自主学习
x+y=12,2x+y=20 ,2x+3y=25
你能否找出下列方程的共同特点?
含有两个未知数,且所含未知数的项的次数都是1的方程叫做二元一次方程。
二元一次方程
类比一元一次方程你能给这些方程取名吗?
根据上面的特点,你能试着用自己的语言来表述二元一次方程的定义吗?并与同桌交流.
10.1 二一元一次方程
归纳总结
判断下列式子是否为二元一次方程?
(1) 3x+1=x2
(5) xy+y=2
(3) x=y+1
(6) -2y=0
3
x
(2) x2+y=0
(4) y+ -x
2
1
不是
不是
是
不是
不是
是
10.1 二一元一次方程
互学互评
根据篮球比赛规则:赢一场得2分,输一场得1分.在某次中学生篮球联赛中,一支球队,赢了若干场后积20分,问该球队赢了多少场?输了多少场?
该队赢了x场,输了y场,那么
2x+y=20
哇!太简单了,赢5场,输十场.
10.1 二一元一次方程
精讲点拨
你同意小明的回答吗?为什么?
x
y
动动脑筋?你能列出输赢的所有可能情况吗?
2x+y=20
问题1:如果不是实际问题的限制,你能找出多少组解?
0
1
2
3
4
5
6
7
8
9
10
20
18
16
14
12
10
8
6
4
2
0
10.1 二一元一次方程
操作探究
无数组
问题2:用含有x的式子表示y为 。
y=20-2x
10.1 二一元一次方程
操作探究
某球员在一场篮球比赛中投篮共得25分.问:他分别投中了多少个两分球和三分球?
?用含有x的式子表示y为 .
根据你所列的表格,回答下列问题:
(1)这名球员最多投中了多少个三分球?
(2)这名球员最多投中了多少个球?
(3)如果这名球员投中了10个球,那么他投中了几个两分球?几个三分球?
解:设他投中了x个两分球、y个三分球,那么
2x+3y=25.
x
y
10.1 二一元一次方程
精讲点拨
③ 请根据②的结果列出这名球员投中的两分球和三分球的各种可能情况.
y=25-2x / 3
7
12
5
5
2
7
5
5
3
8
1
11
适合二元一次方程的一对未知数的值,叫做这个二元一次方程的一个解.
如x=8,y=3就是方程2x+3y=25的一个解,记作
1对数值必须用大括号合在一起,才是二元一次方程的一个解.
要注意呦!
10.1 二一元一次方程
归纳总结
10.1 二一元一次方程
活学活用
2、已知:5x3m+7-2y2n-1=4是二元一次方程,mn= .
考考你
3、已知 是方程2x+ay=5的解,则a= .
10.1 二一元一次方程
活学活用
—2
1
4、甲种铅笔每枝0.2元,乙种铅笔每枝0.5元,现在某人买了x枝甲种铅笔,y枝乙种铅笔,共花了7元.
(1)列出关于x, y的二元一次方程.
(2)用含x的式子表示y为
(3)如果x=5,那么y的值是多少?
(4)如果乙种铅笔买了10枝,那么甲种铅笔买了多少枝?
10.1 二一元一次方程
活学活用
0.2x+0.5y=7
y=70-2x / 5
y=12
x=10
小结与回顾
实际问题
数学问题
二元一次方程
求二元一次方程解的方法
二元一次方程解的概念
二元一次方程的概念
二元一次方程也是刻画现实世界数量关系的有效模型。
二元一次方程
10.1 二一元一次方程
课堂小结
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
