沪科版八年级下册数学9.2 平行四边形性质(一)课件 (共16张PPT)
文档属性
| 名称 | 沪科版八年级下册数学9.2 平行四边形性质(一)课件 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-14 22:48:54 | ||
图片预览




文档简介
(共16张PPT)
19.2
平行四边形性质(一)
沪科版《数学》八年级(下)
活动
1
生活中的平行四边形
生活中的平行四边形
生活中的平行四边形
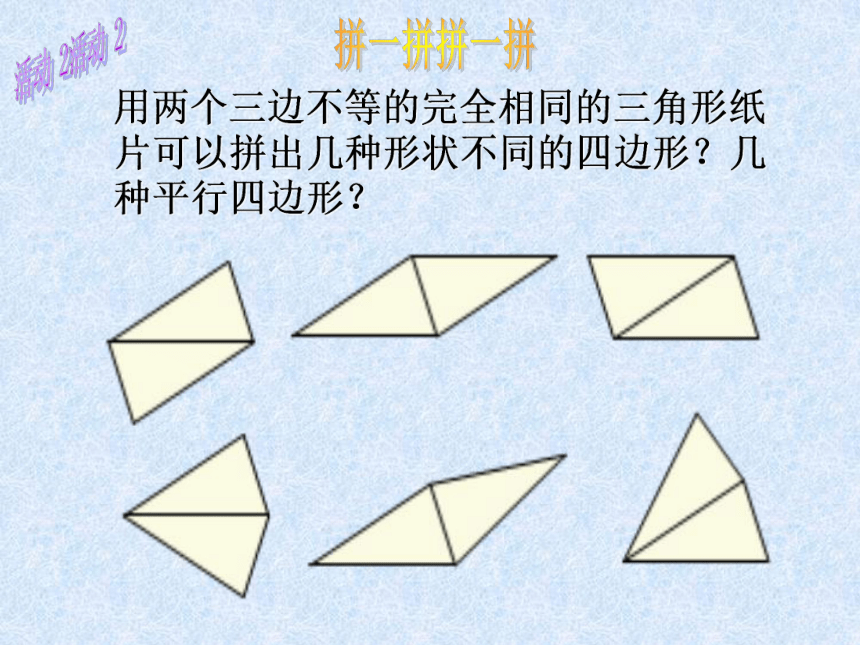
用两个三边不等的完全相同的三角形纸片可以拼出几种形状不同的四边形?几种平行四边形?
拼一拼
活动
2
A
B
C
D
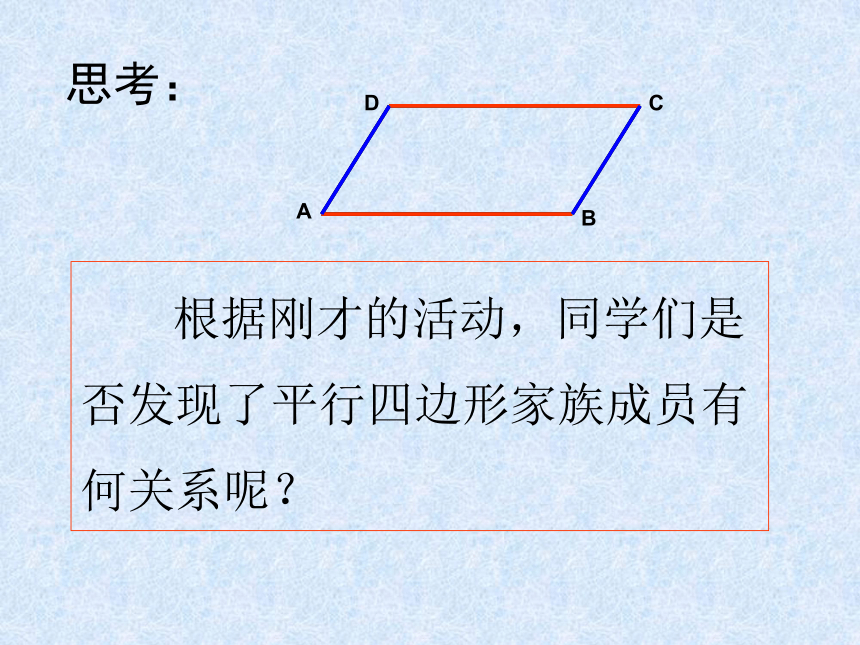
根据刚才的活动,同学们是否发现了平行四边形家族成员有何关系呢?
思考:
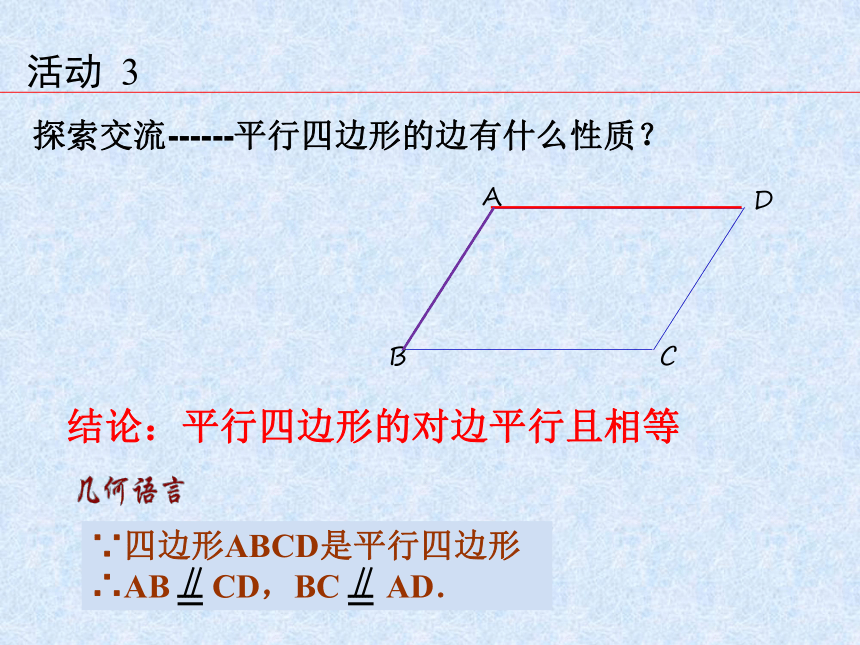
探索交流------平行四边形的边有什么性质?
C
B
A
D
结论:平行四边形的对边平行且相等
活动
3
∵四边形ABCD是平行四边形∴AB
CD,BC
AD.
探索交流------平行四边形的对角有什么性质?
A
B
C
D
结论:平行四边形的对角相等.
∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D.
性质1、平行四边形的对边相等.
性质2、平行四边形的对角相等.
平行四边形的性质
A
B
C
D
总结归纳:
性质1、平行四边形的对边相等.
性质2、平行四边形的对角相等.
平行四边形的性质
A
B
C
D
总结归纳:
解:
例题讲解
例2、如图,已知
ABCD中,AB=8,BC=4,其余各边长为多少?其周长等于多少?
例题讲解
例3:已知如图在
ABCD中,BE平分∠ABC交AD于点E。
(1)如果AE=2,求CD的长。
(2)如果∠AEB=400,求∠C的度数。
解(1)∵BE平分∠ABC,并且AD∥BC,
∴
∠ABE=
∠EBC=
∠AEB
∴
AB=AE=2
又∵CD=AB
∴
CD=2
(2)由(1)知
∠AEB=
∠
ABE=400
∴
∠A=1800-(400+400)=1000
又∵
∠C=
∠A,
∴
∠C=1000.
例题讲解
课堂小结
2、性质:
1、定义:
3、数学思想:转化思想
平行四边形的对边相等.
平行四边形的对角相等.
两组对边分别平行的四边形叫做平行四边形.
4、性质的运用
作业:
课本习题:19.2第1~3题
谢谢!
19.2
平行四边形性质(一)
沪科版《数学》八年级(下)
活动
1
生活中的平行四边形
生活中的平行四边形
生活中的平行四边形
用两个三边不等的完全相同的三角形纸片可以拼出几种形状不同的四边形?几种平行四边形?
拼一拼
活动
2
A
B
C
D
根据刚才的活动,同学们是否发现了平行四边形家族成员有何关系呢?
思考:
探索交流------平行四边形的边有什么性质?
C
B
A
D
结论:平行四边形的对边平行且相等
活动
3
∵四边形ABCD是平行四边形∴AB
CD,BC
AD.
探索交流------平行四边形的对角有什么性质?
A
B
C
D
结论:平行四边形的对角相等.
∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D.
性质1、平行四边形的对边相等.
性质2、平行四边形的对角相等.
平行四边形的性质
A
B
C
D
总结归纳:
性质1、平行四边形的对边相等.
性质2、平行四边形的对角相等.
平行四边形的性质
A
B
C
D
总结归纳:
解:
例题讲解
例2、如图,已知
ABCD中,AB=8,BC=4,其余各边长为多少?其周长等于多少?
例题讲解
例3:已知如图在
ABCD中,BE平分∠ABC交AD于点E。
(1)如果AE=2,求CD的长。
(2)如果∠AEB=400,求∠C的度数。
解(1)∵BE平分∠ABC,并且AD∥BC,
∴
∠ABE=
∠EBC=
∠AEB
∴
AB=AE=2
又∵CD=AB
∴
CD=2
(2)由(1)知
∠AEB=
∠
ABE=400
∴
∠A=1800-(400+400)=1000
又∵
∠C=
∠A,
∴
∠C=1000.
例题讲解
课堂小结
2、性质:
1、定义:
3、数学思想:转化思想
平行四边形的对边相等.
平行四边形的对角相等.
两组对边分别平行的四边形叫做平行四边形.
4、性质的运用
作业:
课本习题:19.2第1~3题
谢谢!
