基本不等式
图片预览










文档简介
(共33张PPT)
重要不等式
定理1:如果 ,那么
(当且仅当 时取“=”号).
我们可以用比较法证明.
探究
你能从几何的角度解释定理1吗?
几何解释1-课本第五页.
动画
几何解释2
a
a
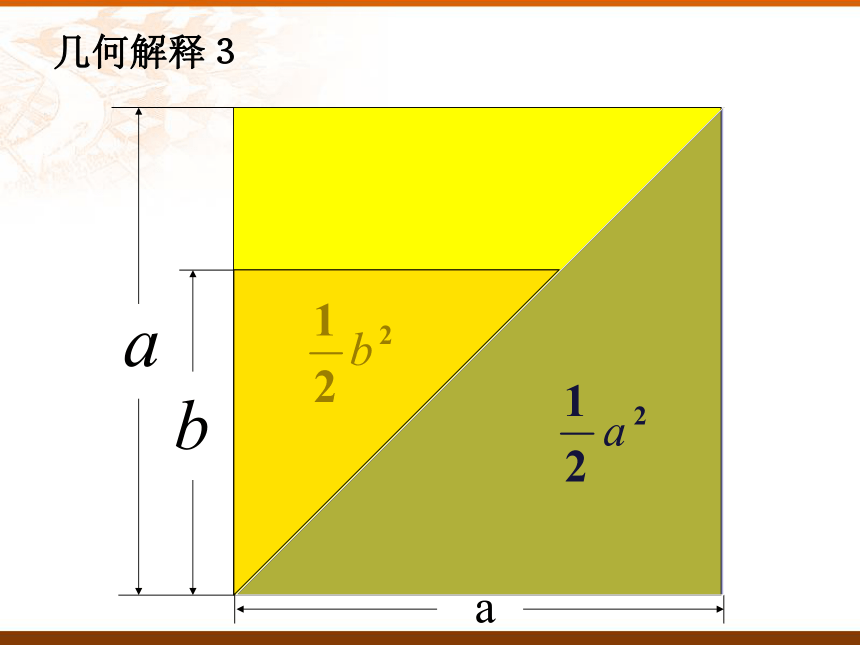
几何解释3
思考 1
(当且仅当
时取“ = ”号).
如果 是正数,那么
基本不等式
定理2(均值定理)
概念
如果a、b都是正数,我们就称 为a、b
的算术平均数, 称为a、b的几何平均数。
均值定理可以描述为:
两个正数的算术平均数不小于(即大于或等于)它们的几何平均数
.
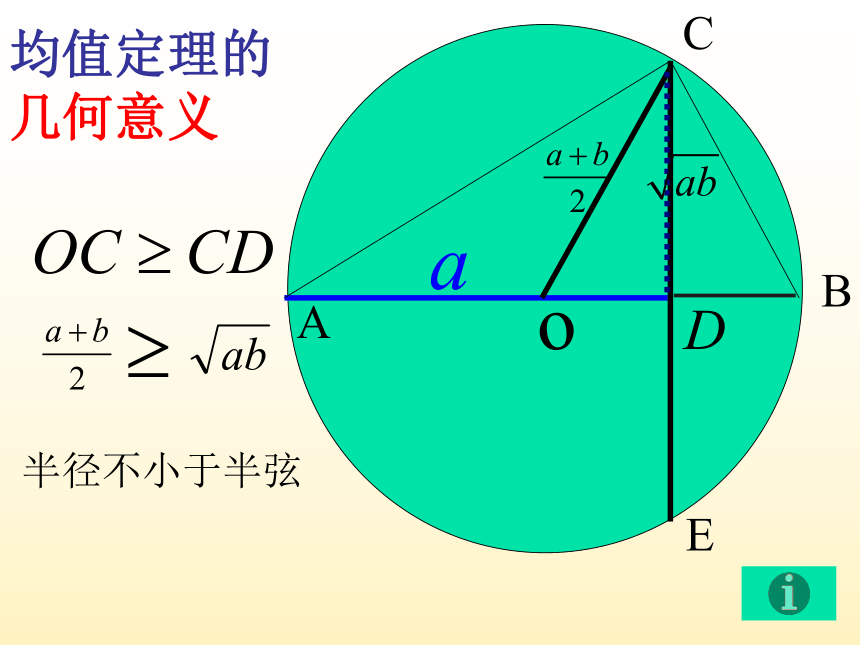
均值定理的几何意义
D
B
C
E
o
A
当且仅当
中的“ = ”号成立.
时
这句话的含义是:
思考 2
当
当
和
成立的条件相同吗?
如: 成立,而 不成立。
思考 3
成立的条件_______
成立的条件______
典例探讨
例1 求证:
(2)已知
都是正数,求证
证明:由
都是正数,得
练习1
例2 求证:(1)在所有周长相同的矩形中,正方形的面积最大;(2)在所有面积相同的矩形中,正方形的周长最短。
变形.
1 如果积
已知
都是正数,求证:
是定值
那么当
时,和
有最小值
2 如果和
是定值
那么当
时,积
有最大值
证:
∵
∴
1 当
(定值)时,
∵上式当
时取“=” ∴当
时,
有最小值
2 当
(定值)时,
∴
∵上式当
时取“=”
∴当
时,
∴
注意:
1、最值的含义(“≥”取最小
值,“≤”取最大值)
2、用极值定理求最值的三个必要条
件:一“正”、二“定”、三“相等”
练习2
1.巳知x>0,y>0且xy=100,则x+y的最小 值
是 _______,此时x=___,y= _____
4.证明
(1)
证:∵
∴
于是
(2)
解:∵
于是
从而
?
≤
解:
解:∵
∴
∴
=
当且仅当
即
时
有最小值1
例3.
若X>-1,则x为何值时
有最小值,最小值为几?
练习3
已知0<x<1,求x(1-x)的最大值.
例4
注意:利用算术平均数和集合平均
数定理时一定要注意定理的条件:
一正;二定;三相等.有一个条件达不
到就不能取得最值.
练习4
求f(x)=2+log2x+5/log2x的最值.
例5.
且
1、已知
,
求
的最小值
解:
当且仅当
即
时
证明:
注意:本题条件a,b,c为实数
练习5
作业
课本作业;P10 5、6
重要不等式
定理1:如果 ,那么
(当且仅当 时取“=”号).
我们可以用比较法证明.
探究
你能从几何的角度解释定理1吗?
几何解释1-课本第五页.
动画
几何解释2
a
a
几何解释3
思考 1
(当且仅当
时取“ = ”号).
如果 是正数,那么
基本不等式
定理2(均值定理)
概念
如果a、b都是正数,我们就称 为a、b
的算术平均数, 称为a、b的几何平均数。
均值定理可以描述为:
两个正数的算术平均数不小于(即大于或等于)它们的几何平均数
.
均值定理的几何意义
D
B
C
E
o
A
当且仅当
中的“ = ”号成立.
时
这句话的含义是:
思考 2
当
当
和
成立的条件相同吗?
如: 成立,而 不成立。
思考 3
成立的条件_______
成立的条件______
典例探讨
例1 求证:
(2)已知
都是正数,求证
证明:由
都是正数,得
练习1
例2 求证:(1)在所有周长相同的矩形中,正方形的面积最大;(2)在所有面积相同的矩形中,正方形的周长最短。
变形.
1 如果积
已知
都是正数,求证:
是定值
那么当
时,和
有最小值
2 如果和
是定值
那么当
时,积
有最大值
证:
∵
∴
1 当
(定值)时,
∵上式当
时取“=” ∴当
时,
有最小值
2 当
(定值)时,
∴
∵上式当
时取“=”
∴当
时,
∴
注意:
1、最值的含义(“≥”取最小
值,“≤”取最大值)
2、用极值定理求最值的三个必要条
件:一“正”、二“定”、三“相等”
练习2
1.巳知x>0,y>0且xy=100,则x+y的最小 值
是 _______,此时x=___,y= _____
4.证明
(1)
证:∵
∴
于是
(2)
解:∵
于是
从而
?
≤
解:
解:∵
∴
∴
=
当且仅当
即
时
有最小值1
例3.
若X>-1,则x为何值时
有最小值,最小值为几?
练习3
已知0<x<1,求x(1-x)的最大值.
例4
注意:利用算术平均数和集合平均
数定理时一定要注意定理的条件:
一正;二定;三相等.有一个条件达不
到就不能取得最值.
练习4
求f(x)=2+log2x+5/log2x的最值.
例5.
且
1、已知
,
求
的最小值
解:
当且仅当
即
时
证明:
注意:本题条件a,b,c为实数
练习5
作业
课本作业;P10 5、6
