绝对值三角不等式
图片预览




文档简介
(共17张PPT)
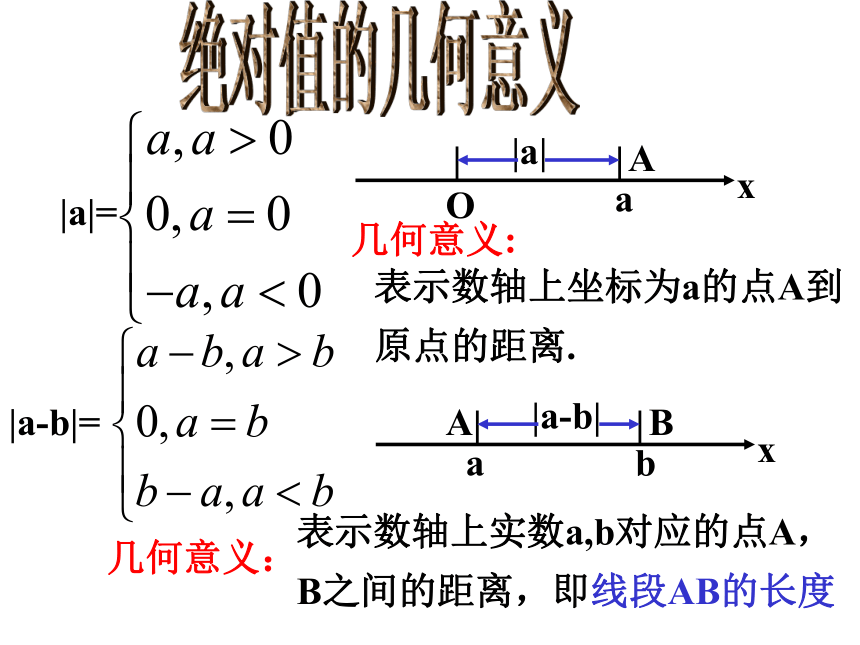
|a|=
|a|
A
a
O
x
|a-b|
A
a
B
x
b
几何意义:
表示数轴上坐标为a的点A到原点的距离.
|a-b|=
几何意义:
表示数轴上实数a,b对应的点A,B之间的距离,即线段AB的长度
类比不等式基本性质的得出过程,同学们认为可以怎样提出关于绝对值不等式性质的猜想?
从“运算”的角度考察绝对值不等式。
如:对于实数a,b,可以考察|a|, |b|, |a+b|, |a-b|, |a|+|b|, |a|-|b| 等之间的关系。
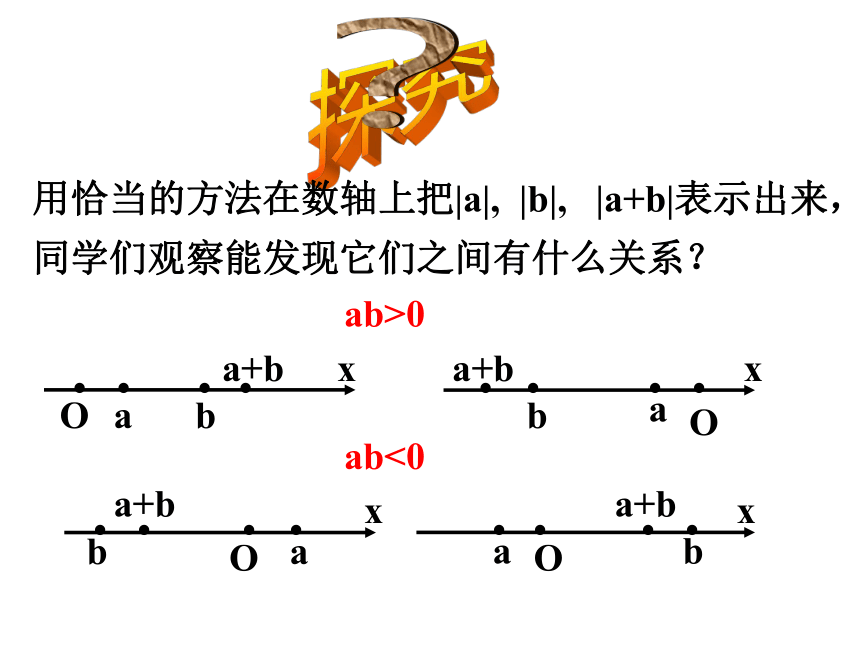
用恰当的方法在数轴上把|a|, |b|, |a+b|表示出来,同学们观察能发现它们之间有什么关系?
x
O
a
b
a+b
x
O
a
b
a+b
x
O
a
b
a+b
x
O
a
b
a+b
ab>0
ab<0
(1)当ab>0时,
x
O
a
b
a+b
x
O
a
b
a+b
a>0,b>0
a<0,b<0
由图可得: |a+b|=|a|+|b|
(2)当ab<0时
x
O
a
b
a+b
x
O
a
b
a+b
a>0,b<0
a<0,b>0
|a+b|<|a|+|b|
|a+b|<|a|+|b|
(3)如果ab=0,则a=0或b=0
易得: |a+b|=|a|+|b|
综上所述,可得:
定理1: 如果a,b是实数,则
|a+b| |a|+|b|
当且仅当ab 0时,等号成立.
如果把定理1中的实数a,b分别换为向量 ,能得出什么结果
当向量 共线呢
x
y
O
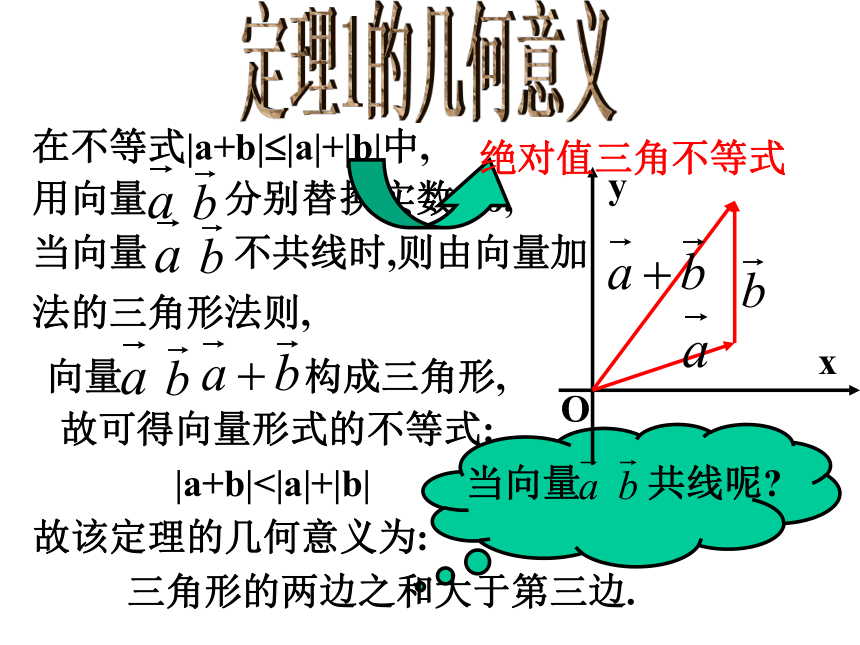
在不等式|a+b| |a|+|b|中,
当向量 不共线时,则由向量加法的三角形法则,
用向量 分别替换实数a,b,
向量 构成三角形,
故可得向量形式的不等式:
|a+b|<|a|+|b|
故该定理的几何意义为:
三角形的两边之和大于第三边.
绝对值三角不等式
绝对值三角不等式: |a+b| |a|+|b|
证明:
当ab 0时,ab=|ab|
|a+b|
当ab<0时, ab=-|ab|
|a+b|
故 |a+b| |a|+|b|
当且仅当ab 0时,等号成立.
同学们能再探究一下|a|-|b|与|a+b|, |a|+|b|与 |a-b|, |a|-|b|与|a-b|等之间的关系
如: 如果a,b是实数,则
|a|-|b| |a-b| |a|+|b|
再如: 如果a,b,c是实数,则
|a-c| |a-b|+|b-c|
当且仅当(a-b)(b-c) 0时,等号成立.
定理2: 如果a,b,c是实数,则
|a-c| |a-b|+|b-c|
当且仅当(a-b)(b-c) 0时,等号成立.
分析:由于a-c, a-b与b-c都是实数,且a-c=(a-b)+(b-c)
证明:根据定理1,有:
|a-c|=|(a-b)+(b-c)|
|a-b|+|b-c|
当且仅当(a-b)(b-c) 0时,等号成立.
则可使用定理1的结论进行证明.
x
a
b
c
A
B
C
x
b
c
a
A
B
C
x
a
c
b
A
B
C
在数轴上,a,b,c所对应的点分别为A,B,C,
(1)当点B在点A,C之间时,|a-c|=|a-b|+|b-c|
(2)当点B在点A,C之外时,|a-c|<|a-b|+|b-c|
例:已知 >0 |x-a|< |y-b|< , 求证:
|2x+3y-2a-3b|<5
证明:
|2x+3y-2a-3b|
=|(2x-2a)+(3y-3b)|
|2(x-a)|+|3(y- b)|
=2|x-a|+3|y-b|
<2 +3 =5
故 |2x+3y-2a-3b|<5
例:两个施工队分别被安排在公路沿线的两个地点
施工,这两个地点分别位于公路路牌的第10km和
第20km处.现要在公路沿线建两个施工队的共同
临时生活区,每个施工队每天在生活区和施工地点
之间往返一次,要使两个施工队每天往返的路程
之和最小,生活区应该建于何处
分析:如果生活区建于公路路碑的第x km处,两个施工队每天往返的路程之和为S(x) km.
那么S(x)=2(|x-10|+|x-20|)
故实际问题转化为数学问题:
当x取何值时,函数S(x)=2(|x-10|+|x-20|)取得最小值.
解:设生活区应该建于公路路碑的第x km处,两个施工队每天往返的路程之和为S(x) km,则:
S(x)=2(|x-10|+|x-20|)
S(x)=2(|x-10|+|x-20|)
我们先来考察它的图像:
S(x)=2(|x-10|+|x-20|)=
O
x
S
10
20
30
20
40
60
S(x)=2(|x-10|+|x-20|)
60-4x
020
104x-60
x>20
S(x)=2(|x-10|+|x-20|)
|x-10|+|x-20|=|x-10|+|20-x|
|(x-10)+(20-x)|=10
当且仅当(x-10)(20-x) 0时取等号.
又解不等式: (x-10)(20-x) 0 得: 10 x 20
故当10 x 20时, 函数S(x)=2(|x-10|+|x-20|)取最小值20.
O
x
S
10
20
30
20
40
60
S(x)=2(|x-10|+|x-20|)
|a|=
|a|
A
a
O
x
|a-b|
A
a
B
x
b
几何意义:
表示数轴上坐标为a的点A到原点的距离.
|a-b|=
几何意义:
表示数轴上实数a,b对应的点A,B之间的距离,即线段AB的长度
类比不等式基本性质的得出过程,同学们认为可以怎样提出关于绝对值不等式性质的猜想?
从“运算”的角度考察绝对值不等式。
如:对于实数a,b,可以考察|a|, |b|, |a+b|, |a-b|, |a|+|b|, |a|-|b| 等之间的关系。
用恰当的方法在数轴上把|a|, |b|, |a+b|表示出来,同学们观察能发现它们之间有什么关系?
x
O
a
b
a+b
x
O
a
b
a+b
x
O
a
b
a+b
x
O
a
b
a+b
ab>0
ab<0
(1)当ab>0时,
x
O
a
b
a+b
x
O
a
b
a+b
a>0,b>0
a<0,b<0
由图可得: |a+b|=|a|+|b|
(2)当ab<0时
x
O
a
b
a+b
x
O
a
b
a+b
a>0,b<0
a<0,b>0
|a+b|<|a|+|b|
|a+b|<|a|+|b|
(3)如果ab=0,则a=0或b=0
易得: |a+b|=|a|+|b|
综上所述,可得:
定理1: 如果a,b是实数,则
|a+b| |a|+|b|
当且仅当ab 0时,等号成立.
如果把定理1中的实数a,b分别换为向量 ,能得出什么结果
当向量 共线呢
x
y
O
在不等式|a+b| |a|+|b|中,
当向量 不共线时,则由向量加法的三角形法则,
用向量 分别替换实数a,b,
向量 构成三角形,
故可得向量形式的不等式:
|a+b|<|a|+|b|
故该定理的几何意义为:
三角形的两边之和大于第三边.
绝对值三角不等式
绝对值三角不等式: |a+b| |a|+|b|
证明:
当ab 0时,ab=|ab|
|a+b|
当ab<0时, ab=-|ab|
|a+b|
故 |a+b| |a|+|b|
当且仅当ab 0时,等号成立.
同学们能再探究一下|a|-|b|与|a+b|, |a|+|b|与 |a-b|, |a|-|b|与|a-b|等之间的关系
如: 如果a,b是实数,则
|a|-|b| |a-b| |a|+|b|
再如: 如果a,b,c是实数,则
|a-c| |a-b|+|b-c|
当且仅当(a-b)(b-c) 0时,等号成立.
定理2: 如果a,b,c是实数,则
|a-c| |a-b|+|b-c|
当且仅当(a-b)(b-c) 0时,等号成立.
分析:由于a-c, a-b与b-c都是实数,且a-c=(a-b)+(b-c)
证明:根据定理1,有:
|a-c|=|(a-b)+(b-c)|
|a-b|+|b-c|
当且仅当(a-b)(b-c) 0时,等号成立.
则可使用定理1的结论进行证明.
x
a
b
c
A
B
C
x
b
c
a
A
B
C
x
a
c
b
A
B
C
在数轴上,a,b,c所对应的点分别为A,B,C,
(1)当点B在点A,C之间时,|a-c|=|a-b|+|b-c|
(2)当点B在点A,C之外时,|a-c|<|a-b|+|b-c|
例:已知 >0 |x-a|< |y-b|< , 求证:
|2x+3y-2a-3b|<5
证明:
|2x+3y-2a-3b|
=|(2x-2a)+(3y-3b)|
|2(x-a)|+|3(y- b)|
=2|x-a|+3|y-b|
<2 +3 =5
故 |2x+3y-2a-3b|<5
例:两个施工队分别被安排在公路沿线的两个地点
施工,这两个地点分别位于公路路牌的第10km和
第20km处.现要在公路沿线建两个施工队的共同
临时生活区,每个施工队每天在生活区和施工地点
之间往返一次,要使两个施工队每天往返的路程
之和最小,生活区应该建于何处
分析:如果生活区建于公路路碑的第x km处,两个施工队每天往返的路程之和为S(x) km.
那么S(x)=2(|x-10|+|x-20|)
故实际问题转化为数学问题:
当x取何值时,函数S(x)=2(|x-10|+|x-20|)取得最小值.
解:设生活区应该建于公路路碑的第x km处,两个施工队每天往返的路程之和为S(x) km,则:
S(x)=2(|x-10|+|x-20|)
S(x)=2(|x-10|+|x-20|)
我们先来考察它的图像:
S(x)=2(|x-10|+|x-20|)=
O
x
S
10
20
30
20
40
60
S(x)=2(|x-10|+|x-20|)
60-4x
0
10
x>20
S(x)=2(|x-10|+|x-20|)
|x-10|+|x-20|=|x-10|+|20-x|
|(x-10)+(20-x)|=10
当且仅当(x-10)(20-x) 0时取等号.
又解不等式: (x-10)(20-x) 0 得: 10 x 20
故当10 x 20时, 函数S(x)=2(|x-10|+|x-20|)取最小值20.
O
x
S
10
20
30
20
40
60
S(x)=2(|x-10|+|x-20|)
