青岛版六年级数学下册 二 冰淇淋盒有多大——圆柱和圆锥 复习课件(16张ppt)
文档属性
| 名称 | 青岛版六年级数学下册 二 冰淇淋盒有多大——圆柱和圆锥 复习课件(16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 946.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-14 13:31:29 | ||
图片预览



文档简介
二 冰淇淋盒有多大——圆柱和圆锥
复习课件
整体回顾
综合运用
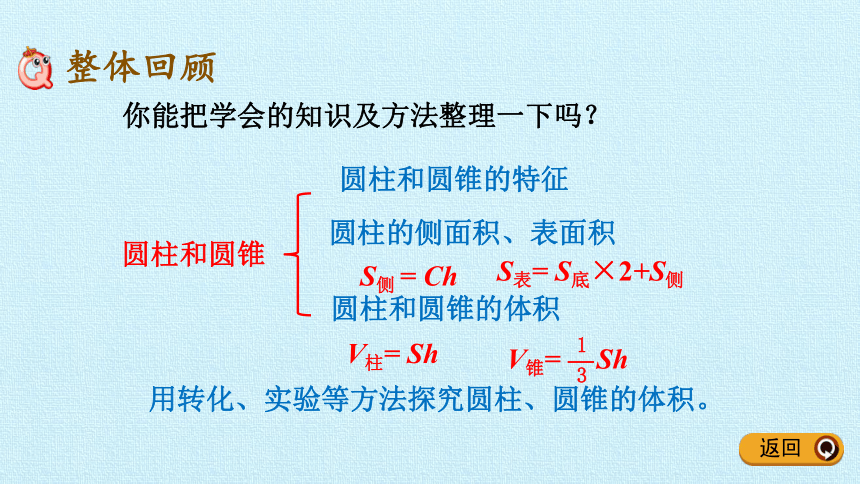
圆柱和圆锥
知识梳理
圆柱和圆锥
圆柱的侧面积、表面积
圆柱和圆锥的特征
圆柱和圆锥的体积
S侧 = Ch
V柱= Sh
S表= S底×2+S侧
1
3
V锥= Sh
你能把学会的知识及方法整理一下吗?
用转化、实验等方法探究圆柱、圆锥的体积。
整体回顾
返回
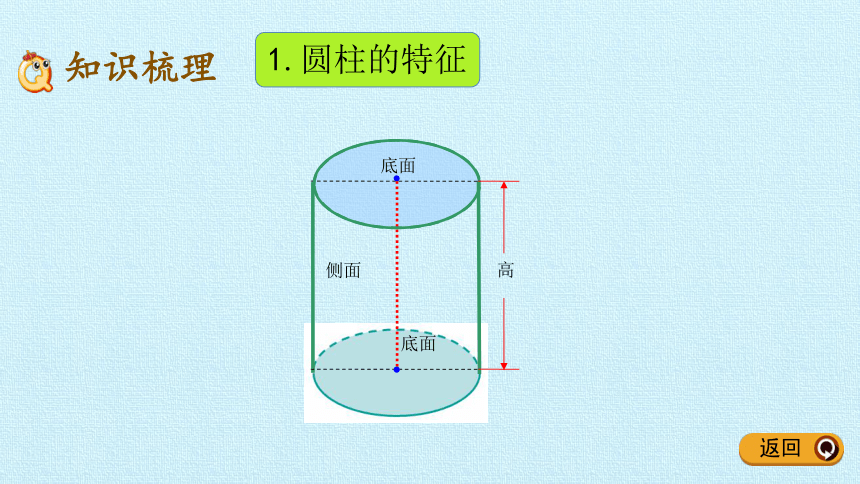
1.圆柱的特征
底面
底面
高
侧面
知识梳理
返回
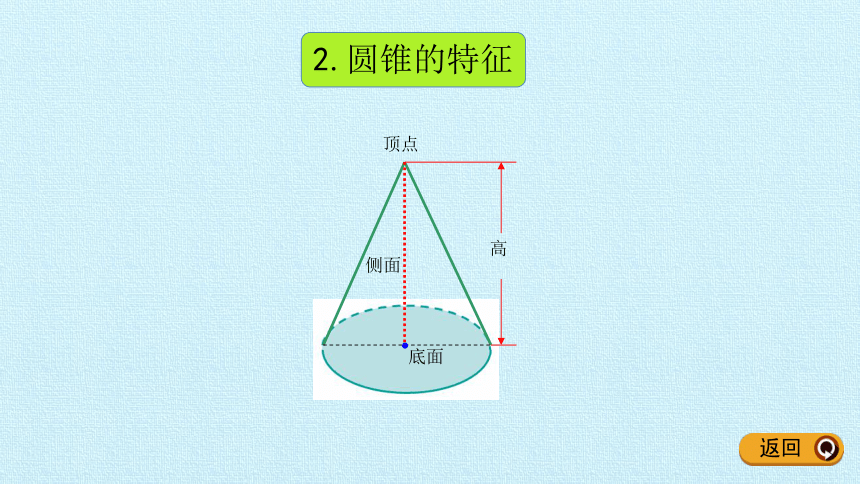
2.圆锥的特征
高
底面
侧面
顶点
返回
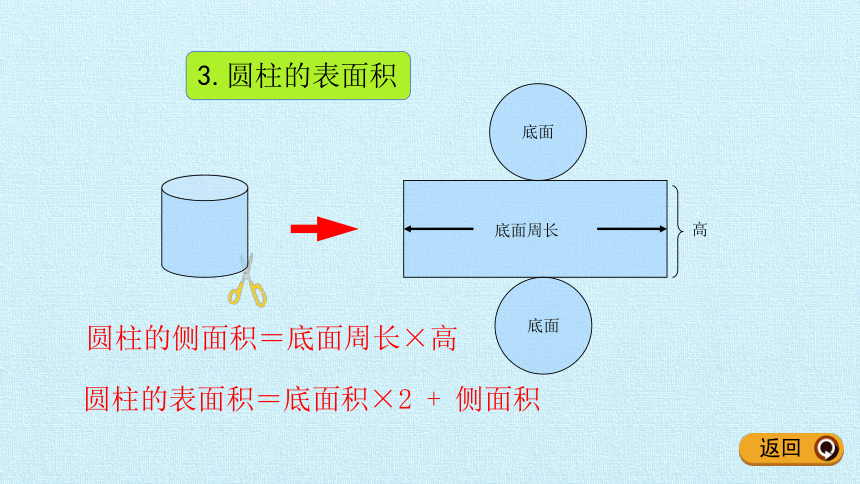
3.圆柱的表面积
圆柱的侧面积=底面周长×高
底面
底面
高
底面周长
圆柱的表面积=底面积×2 + 侧面积
返回
4.圆柱的体积
V = S h
圆柱底面周长的一半
圆柱的高
底面
半径
底面积
高
圆柱的体积
=
×
长方体的体积=底面积×高
返回
5.圆锥的体积
圆锥的体积等于和它等底等高的圆柱体积的三分之一。
圆锥的体积 = 底面积 × 高 × ????????
?
圆锥的体积与圆柱有怎样的关系呢?
Ⅴ=????????????h
?
返回
有一个圆圆的底面,一个侧面;只有一条高。
将下面图形分类,说说每类图形的名称和特征。
圆 柱
圆 锥
有两个圆圆的底面,一个侧面;有无数条高;侧面沿高展开是一个长方形(或正方形),长方形的一组邻边等于圆柱的底面周长和高。
综合运用
返回
判断。对的画“√”,错的画“×”。
1.一个三角形沿着一条边旋转一定可以形成一个圆锥。
( )
2.圆柱的侧面展开图不一定是个长方形。 ( )
3.圆柱体积是圆锥体积的3倍。 ( )
√
×
×
圆锥的体积是与它等底等高的圆柱体积的13。
?
返回
想一想:圆柱的侧面积、表面积怎样计算?圆柱、圆锥的体积公式是怎样导出的?再填写下表。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}体 积
半 径
直 径
高
表面积
体 积
圆 柱
5dm
4dm
2m
0.7m
20cm
5cm
S表= 2πrh+2πr2
V=πr2h
×2
10dm
1m
40cm
282.6dm2
10.676m2
3140cm2
314dm3
2.198m3
6280cm3
返回
如图,一个直角梯形绕轴旋转一周后形成的立体图形的体积是多少?
圆锥的体积
圆柱的体积
+
3.14×42×(8-5)× ????????
?
3.14×42×5
+
=301.44(cm3)
答:旋转一周后围成的立体图形的体积是301.44cm3。
=50.24 + 251.2
返回
30cm
2m
结合圆柱和圆锥的知识,联系实际,展开想象的翅膀,看看你能提出什么问题,你能列出算式吗?
(1)圆柱的表面积是多少平方厘米?
3.14×30×200+3.14×(30÷2)2×2
=18840+1413
=20253(平方厘米)
答:圆柱的表面积是20253平方厘米。
2m=200cm
返回
30cm
2m
结合圆柱和圆锥的知识,联系实际,展开想象的翅膀,看看你能提出什么问题,你能列出算式吗?
(2)圆柱的体积是多少立方厘米?
3.14×(30÷2)2 ×200
= 3.14×225×200
=141300 (立方厘米)
答:圆柱的体积是141300立方厘米。
返回
30cm
2m
结合圆柱和圆锥的知识,联系实际,展开想象的翅膀,看看你能提出什么问题,你能列出算式吗?
(3)如果把它削成一个最大圆锥体,
圆锥体的体积是多少立方厘米?
??13×3.14×(30÷2)2×200
=13×3.14×225×200
=47100(立方厘米)
?
答:圆锥体的体积是47100立方厘米。
返回
谢 谢
复习课件
整体回顾
综合运用
圆柱和圆锥
知识梳理
圆柱和圆锥
圆柱的侧面积、表面积
圆柱和圆锥的特征
圆柱和圆锥的体积
S侧 = Ch
V柱= Sh
S表= S底×2+S侧
1
3
V锥= Sh
你能把学会的知识及方法整理一下吗?
用转化、实验等方法探究圆柱、圆锥的体积。
整体回顾
返回
1.圆柱的特征
底面
底面
高
侧面
知识梳理
返回
2.圆锥的特征
高
底面
侧面
顶点
返回
3.圆柱的表面积
圆柱的侧面积=底面周长×高
底面
底面
高
底面周长
圆柱的表面积=底面积×2 + 侧面积
返回
4.圆柱的体积
V = S h
圆柱底面周长的一半
圆柱的高
底面
半径
底面积
高
圆柱的体积
=
×
长方体的体积=底面积×高
返回
5.圆锥的体积
圆锥的体积等于和它等底等高的圆柱体积的三分之一。
圆锥的体积 = 底面积 × 高 × ????????
?
圆锥的体积与圆柱有怎样的关系呢?
Ⅴ=????????????h
?
返回
有一个圆圆的底面,一个侧面;只有一条高。
将下面图形分类,说说每类图形的名称和特征。
圆 柱
圆 锥
有两个圆圆的底面,一个侧面;有无数条高;侧面沿高展开是一个长方形(或正方形),长方形的一组邻边等于圆柱的底面周长和高。
综合运用
返回
判断。对的画“√”,错的画“×”。
1.一个三角形沿着一条边旋转一定可以形成一个圆锥。
( )
2.圆柱的侧面展开图不一定是个长方形。 ( )
3.圆柱体积是圆锥体积的3倍。 ( )
√
×
×
圆锥的体积是与它等底等高的圆柱体积的13。
?
返回
想一想:圆柱的侧面积、表面积怎样计算?圆柱、圆锥的体积公式是怎样导出的?再填写下表。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}体 积
半 径
直 径
高
表面积
体 积
圆 柱
5dm
4dm
2m
0.7m
20cm
5cm
S表= 2πrh+2πr2
V=πr2h
×2
10dm
1m
40cm
282.6dm2
10.676m2
3140cm2
314dm3
2.198m3
6280cm3
返回
如图,一个直角梯形绕轴旋转一周后形成的立体图形的体积是多少?
圆锥的体积
圆柱的体积
+
3.14×42×(8-5)× ????????
?
3.14×42×5
+
=301.44(cm3)
答:旋转一周后围成的立体图形的体积是301.44cm3。
=50.24 + 251.2
返回
30cm
2m
结合圆柱和圆锥的知识,联系实际,展开想象的翅膀,看看你能提出什么问题,你能列出算式吗?
(1)圆柱的表面积是多少平方厘米?
3.14×30×200+3.14×(30÷2)2×2
=18840+1413
=20253(平方厘米)
答:圆柱的表面积是20253平方厘米。
2m=200cm
返回
30cm
2m
结合圆柱和圆锥的知识,联系实际,展开想象的翅膀,看看你能提出什么问题,你能列出算式吗?
(2)圆柱的体积是多少立方厘米?
3.14×(30÷2)2 ×200
= 3.14×225×200
=141300 (立方厘米)
答:圆柱的体积是141300立方厘米。
返回
30cm
2m
结合圆柱和圆锥的知识,联系实际,展开想象的翅膀,看看你能提出什么问题,你能列出算式吗?
(3)如果把它削成一个最大圆锥体,
圆锥体的体积是多少立方厘米?
??13×3.14×(30÷2)2×200
=13×3.14×225×200
=47100(立方厘米)
?
答:圆锥体的体积是47100立方厘米。
返回
谢 谢
