回归分析的基本思想及其初步应用
文档属性
| 名称 | 回归分析的基本思想及其初步应用 |

|
|
| 格式 | rar | ||
| 文件大小 | 389.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-06-04 00:00:00 | ||
图片预览











文档简介
(共76张PPT)
一、复习 数学3——统计内容
1. 画散点图
2. 了解最小二乘法的思想
3. 求回归直线方程
4. 用回归直线方程解决应用问题
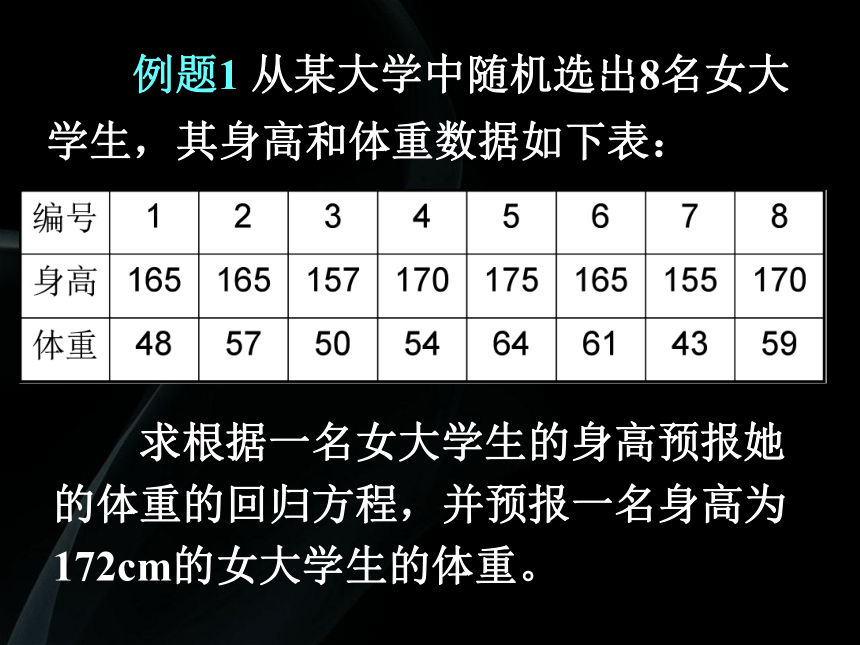
例题1 从某大学中随机选出8名女大学生,其身高和体重数据如下表:
求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重。
最小二乘法:
最小二乘法:
称为样本点的中心。
1. 回归直线方程
1. 回归直线方程
1) 所求直线方程叫做回归直线方程;相应的直线叫做回归直线。
1. 回归直线方程
1) 所求直线方程叫做回归直线方程;相应的直线叫做回归直线。 2) 对两个变量进行的线性分析叫做线性回归分析。
1. 回归直线方程
1) 所求直线方程叫做回归直线方程;相应的直线叫做回归直线。 2) 对两个变量进行的线性分析叫做线性回归分析。
2. 求回归直线方程的步骤:
2. 求回归直线方程的步骤:
2. 求回归直线方程的步骤:
2. 求回归直线方程的步骤:
2. 求回归直线方程的步骤:
二、新授: 1. 回归分析的定义 对具有相关关系的两个变量进行统计分析的方法叫回归分析。
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
1. 散点图;
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
1. 散点图;
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
1. 散点图;
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
1. 散点图; 2. 回归方程:
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
1. 散点图; 2. 回归方程:
探究? 身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,其原因是什么
探究:
身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,你能解析一下原因吗?
探究:
身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,你能解析一下原因吗?
答:身高为172cm的女大学生的体重不一定是60.316kg,但一般可以认为她的体重接近于60.316kg。
探究:
身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,你能解析一下原因吗?
答:身高为172cm的女大学生的体重不一定是60.316kg,但一般可以认为她的体重接近于60.316kg。 即,用这个回归方程不能给出每个身高为172cm的女大学生的体重的预测值,只能给出她们平均体重的值。
2. 如何描述两个变量之间线性相关关系的强弱? 在《数学3》中,我们学习了用相关系数r来衡量两个变量之间线性相关关系的方法。
2. 如何描述两个变量之间线性相关关系的强弱? 在《数学3》中,我们学习了用相关系数r来衡量两个变量之间线性相关关系的方法。
2. 如何描述两个变量之间线性相关关系的强弱? 在《数学3》中,我们学习了用相关系数r来衡量两个变量之间线性相关关系的方法。
相关系数
相关系数
r>0正相关;r<0负相关.通常,r>0.75,认为两个变量有很强的相关性.
相关系数
r>0正相关;r<0负相关.通常,r>0.75,认为两个变量有很强的相关性. 本例中,由上面公式r=0.798>0.75.
3. 线性回归模型 : y=bx+a+e, 其中a和b为模型的未知参数,e称为随机误差。
思考:
产生随机误差项e的原因是什么?
思考:
产生随机误差项e的原因是什么?
随机误差e的来源(可以推广到一般):
1. 忽略了其它因素的影响:影响身高y的因素不只是体重x,可能还包括遗传基因、饮食习惯、生长环境等因素;
2. 用线性回归模型近似真实模型所引起的误差;
3. 身高y的观测误差。 以上三项误差越小,说明我们的回归模型的拟合效果越好。
函数模型与回归模型之间的差别 函数模型:y=bx+a 回归模型:y=bx+a+e
函数模型与回归模型之间的差别 函数模型:y=bx+a 回归模型:y=bx+a+e 线性回归模型y=bx+a+e增加了随机误差项 e,因变量y的值由自变量x和随机误差项e共同确 定,即自变量x只能解析部分y的变化。
函数模型与回归模型之间的差别 函数模型:y=bx+a 回归模型:y=bx+a+e 线性回归模型y=bx+a+e增加了随机误差项 e,因变量y的值由自变量x和随机误差项e共同确 定,即自变量x只能解析部分y的变化。 在统计中,我们也把自变量x称为解析变 量, 因变量y称为预报变量。
函数模型与回归模型之间的差别 函数模型:y=bx+a 回归模型:y=bx+a+e 线性回归模型y=bx+a+e增加了随机误差项 e,因变量y的值由自变量x和随机误差项e共同确 定,即自变量x只能解析部分y的变化。 在统计中,我们也把自变量x称为解析变 量, 因变量y称为预报变量。
函数模型与回归模型之间的差别 函数模型:y=bx+a 回归模型:y=bx+a+e 线性回归模型y=bx+a+e增加了随机误差项 e,因变量y的值由自变量x和随机误差项e共同确 定,即自变量x只能解析部分y的变化。 在统计中,我们也把自变量x称为解析变 量, 因变量y称为预报变量。
4. 对回归模型进行统计检验
假设身高和随机误差的不同不会对体重产生任何影响,那么所有人的体重将相同。在体重不受任何变量影响的假设下,设8名女大学生的体重都是她们的平均值,即8个人的体重都为54.5kg。
假设身高和随机误差的不同不会对体重产生任何影响,那么所有人的体重将相同。在体重不受任何变量影响的假设下,设8名女大学生的体重都是她们的平均值,即8个人的体重都为54.5kg。
4. 对回归模型进行统计检验
在散点图中,所有的点应该落在同一条水平直线上,但是观测到的数据并非如此。这就意味着预报变量(体重)的值受解释变量(身高)或随机误差的影响。
在散点图中,所有的点应该落在同一条水平直线上,但是观测到的数据并非如此。这就意味着预报变量(体重)的值受解释变量(身高)或随机误差的影响。 思考:
如何刻画预报变量(体重)的变化?这个变化在多大程度上与解释变量(身高)有关?在多大程度上与随机误差有关?
例如,编号为6的女大学生的体重并没有落在水平直线上,她的体重为61kg。解释变量(身高)和随机误差共同把这名学生的体重从54.5kg“推”到了61kg,相差6.5kg,所以6.5kg是解析变量和随机误差的组合效应。 编号为3的女大学生的体重并也没有落在水平直线上,她的体重为50kg。解释变量(身高)和随机误差共同把这名学生的体重从50kg “推”到了54.5kg,相差-4.5kg,这时解释变量和随机误差的组合效应为-4.5kg。
用这种方法可以对所有预报变量计算组合效应。
用这种方法可以对所有预报变量计算组合效应。
用这种方法可以对所有预报变量计算组合效应。
在例1中,总偏差平方和为354。
那么,在这个总的效应(总偏差平方和)中,有多少来自于解释变量(身高)?有多少来自于随机误差?
那么,在这个总的效应(总偏差平方和)中, 有多少来自于解释变量(身高)?有多少来自于随机误差? 假设随机误差对体重没有影响,也就是说, 体重仅受身高的影响,那么散点图中所有的点将完全落在回归直线上。但是,在图中,数据点并没有完全落在回归直线上。这些点散布在回归直线附近,所以一定是随机误差把这些点从回归直线上 “推”开了。
例如,编号为6的女大学生,计算随机误差的效应(残差)为: 61-(0.849×165-85.712)=6.627
例如,编号为6的女大学生,计算随机误差的效应(残差)为: 61-(0.849×165-85.712)=6.627
例如,编号为6的女大学生,计算随机误差的效应(残差)为: 61-(0.849×165-85.712)=6.627
在例1中,残差平方和约为128.361。
由于解释变量和随机误差的总效应 (总偏差平方和)为354,而随机误差的效 应为128.361,所以解释变量的效应为 354-128.361=225.639
由于解释变量和随机误差的总效应 (总偏差平方和)为354,而随机误差的效 应为128.361,所以解释变量的效应为 354-128.361=225.639 这个值称为回归平方和.
由于解释变量和随机误差的总效应 (总偏差平方和)为354,而随机误差的效 应为128.361,所以解释变量的效应为 354-128.361=225.639 这个值称为回归平方和.
解释变量和随机误差的总效应(总偏差平方和)=解释变量的效应(回归平方和) +随机误差的效应(残差平方和)
样本决定系数(判定系数 R2) 1.回归平方和占总离差平方和的比例
2. 反映回归直线的拟合程度
3. 取值范围在[0, 1]之间
4. R2 1,说明回归方程拟合的越好; R2 0,说明回归方程拟合的越差
5. 判定系数等于相关系数的平方,即R2=(r)2
显然,R2的值越大,说明残差平方和越小, 也就是说模型拟合效果越好。
显然,R2的值越大,说明残差平方和越小, 也就是说模型拟合效果越好。 在线性回归模型中,R2表示解释变量对预 报变量变化的贡献率。
显然,R2的值越大,说明残差平方和越小, 也就是说模型拟合效果越好。 在线性回归模型中,R2表示解释变量对预 报变量变化的贡献率。 R2越接近1,表示回归的效果越好(因为R2 越接近1,表示解释变量和预报变量的线性相 关性越强)。
如果某组数据可能采取几种不同回归方程进行回归分析,则可以通过比较R2的值来做出选择,即选取R2较大的模型作为这组数据的模型。
如果某组数据可能采取几种不同回归方程进行回归分析,则可以通过比较R2的值来做出选择,即选取R2较大的模型作为这组数据的模型。 总的来说:
相关指数R2是度量模型拟合效果的一种指标。
在线性模型中,它代表自变量刻画预报变量的能力。
从表1-3中 可以看出,解 释变量对总效 应约贡献了64%, 即R2 0.64,可以叙述为“身高解析了64%的体重 变化”,而随机误差贡献了剩余的36%。所以, 身高对体重的效应比随机误差的效应大得多。
残差分析与残差图的定义:
在研究两个变量间的关系时,首先要根据散点图来粗略判断它们是否线性相关,是否可以用回归模型来拟合数据.
我们可以利用图形来分析残差特性,作图时纵坐标为残差,横坐标可以选为样本编号,或身高数据,或体重估计值等,这样作出的图形称为残差图。
残差图的制作及作用
1. 坐标纵轴为残差变量,横轴可以有不同的选择;
2. 若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;
3. 对于远离横轴的点,要特别注意.
残差图的制作及作用
1. 坐标纵轴为残差变量,横轴可以有不同的选择;
2. 若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;
3. 对于远离横轴的点,要特别注意.
残差图的制作及作用
1. 坐标纵轴为残差变量,横轴可以有不同的选择;
2. 若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;
3. 对于远离横轴的点,要特别注意.
异常点
·错误数据
·模型问题
残差图的制作及作用
1. 坐标纵轴为残差变量,横轴可以有不同的选择;
2. 若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;
3. 对于远离横轴的点,要特别注意.
异常点
·错误数据
·模型问题
1. 线性回归模型;
2. 变量间新的关系;
3. 刻画回归效果的方式;
4. 残差图
知识归纳
用身高预报体重时,需要注意下列问题:
1、回归方程只适用于我们所研究的样本的总体;
2、我们所建立的回归方程一般都有时间性;
3、样本采集的范围会影响回归方程的适用范围;
4、不能期望回归方程得到的预报值就是预报变量的精确值。
事实上,它是预报变量的可能取值的平均值。
——这些问题也使用于其他问题。
涉及到统计的一些思想:
模型适用的总体;
模型的时间性;
样本的取值范围对模型的影响;
模型预报结果的正确理解。
小结
一般地,建立回归模型的基本步骤为:
(1)确定研究对象,明确哪个变量是解析变量,哪个变量是预报变量。
(2)画出确定好的解析变量和预报变量的散点图,观察它们之间的关系
(如是否存在线性关系等)。
(3)由经验确定回归方程的类型(如我们观察到数据呈线性关系,则选用线性回归方程y=bx+a).
(4)按一定规则估计回归方程中的参数(如最小二乘法)。
(5)得出结果后分析残差图是否有异常(个别数据对应残差过大,或残差呈现不随机的规律性,等等),过存在异常,则检查数据是否有误,或模型是否合适等。
一、复习 数学3——统计内容
1. 画散点图
2. 了解最小二乘法的思想
3. 求回归直线方程
4. 用回归直线方程解决应用问题
例题1 从某大学中随机选出8名女大学生,其身高和体重数据如下表:
求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为172cm的女大学生的体重。
最小二乘法:
最小二乘法:
称为样本点的中心。
1. 回归直线方程
1. 回归直线方程
1) 所求直线方程叫做回归直线方程;相应的直线叫做回归直线。
1. 回归直线方程
1) 所求直线方程叫做回归直线方程;相应的直线叫做回归直线。 2) 对两个变量进行的线性分析叫做线性回归分析。
1. 回归直线方程
1) 所求直线方程叫做回归直线方程;相应的直线叫做回归直线。 2) 对两个变量进行的线性分析叫做线性回归分析。
2. 求回归直线方程的步骤:
2. 求回归直线方程的步骤:
2. 求回归直线方程的步骤:
2. 求回归直线方程的步骤:
2. 求回归直线方程的步骤:
二、新授: 1. 回归分析的定义 对具有相关关系的两个变量进行统计分析的方法叫回归分析。
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
1. 散点图;
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
1. 散点图;
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
1. 散点图;
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
1. 散点图; 2. 回归方程:
分析:由于问题中要求根据身高预报体重,因此选取身高为自变量,体重为因变量.
1. 散点图; 2. 回归方程:
探究? 身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,其原因是什么
探究:
身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,你能解析一下原因吗?
探究:
身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,你能解析一下原因吗?
答:身高为172cm的女大学生的体重不一定是60.316kg,但一般可以认为她的体重接近于60.316kg。
探究:
身高为172cm的女大学生的体重一定是60.316kg吗?如果不是,你能解析一下原因吗?
答:身高为172cm的女大学生的体重不一定是60.316kg,但一般可以认为她的体重接近于60.316kg。 即,用这个回归方程不能给出每个身高为172cm的女大学生的体重的预测值,只能给出她们平均体重的值。
2. 如何描述两个变量之间线性相关关系的强弱? 在《数学3》中,我们学习了用相关系数r来衡量两个变量之间线性相关关系的方法。
2. 如何描述两个变量之间线性相关关系的强弱? 在《数学3》中,我们学习了用相关系数r来衡量两个变量之间线性相关关系的方法。
2. 如何描述两个变量之间线性相关关系的强弱? 在《数学3》中,我们学习了用相关系数r来衡量两个变量之间线性相关关系的方法。
相关系数
相关系数
r>0正相关;r<0负相关.通常,r>0.75,认为两个变量有很强的相关性.
相关系数
r>0正相关;r<0负相关.通常,r>0.75,认为两个变量有很强的相关性. 本例中,由上面公式r=0.798>0.75.
3. 线性回归模型 : y=bx+a+e, 其中a和b为模型的未知参数,e称为随机误差。
思考:
产生随机误差项e的原因是什么?
思考:
产生随机误差项e的原因是什么?
随机误差e的来源(可以推广到一般):
1. 忽略了其它因素的影响:影响身高y的因素不只是体重x,可能还包括遗传基因、饮食习惯、生长环境等因素;
2. 用线性回归模型近似真实模型所引起的误差;
3. 身高y的观测误差。 以上三项误差越小,说明我们的回归模型的拟合效果越好。
函数模型与回归模型之间的差别 函数模型:y=bx+a 回归模型:y=bx+a+e
函数模型与回归模型之间的差别 函数模型:y=bx+a 回归模型:y=bx+a+e 线性回归模型y=bx+a+e增加了随机误差项 e,因变量y的值由自变量x和随机误差项e共同确 定,即自变量x只能解析部分y的变化。
函数模型与回归模型之间的差别 函数模型:y=bx+a 回归模型:y=bx+a+e 线性回归模型y=bx+a+e增加了随机误差项 e,因变量y的值由自变量x和随机误差项e共同确 定,即自变量x只能解析部分y的变化。 在统计中,我们也把自变量x称为解析变 量, 因变量y称为预报变量。
函数模型与回归模型之间的差别 函数模型:y=bx+a 回归模型:y=bx+a+e 线性回归模型y=bx+a+e增加了随机误差项 e,因变量y的值由自变量x和随机误差项e共同确 定,即自变量x只能解析部分y的变化。 在统计中,我们也把自变量x称为解析变 量, 因变量y称为预报变量。
函数模型与回归模型之间的差别 函数模型:y=bx+a 回归模型:y=bx+a+e 线性回归模型y=bx+a+e增加了随机误差项 e,因变量y的值由自变量x和随机误差项e共同确 定,即自变量x只能解析部分y的变化。 在统计中,我们也把自变量x称为解析变 量, 因变量y称为预报变量。
4. 对回归模型进行统计检验
假设身高和随机误差的不同不会对体重产生任何影响,那么所有人的体重将相同。在体重不受任何变量影响的假设下,设8名女大学生的体重都是她们的平均值,即8个人的体重都为54.5kg。
假设身高和随机误差的不同不会对体重产生任何影响,那么所有人的体重将相同。在体重不受任何变量影响的假设下,设8名女大学生的体重都是她们的平均值,即8个人的体重都为54.5kg。
4. 对回归模型进行统计检验
在散点图中,所有的点应该落在同一条水平直线上,但是观测到的数据并非如此。这就意味着预报变量(体重)的值受解释变量(身高)或随机误差的影响。
在散点图中,所有的点应该落在同一条水平直线上,但是观测到的数据并非如此。这就意味着预报变量(体重)的值受解释变量(身高)或随机误差的影响。 思考:
如何刻画预报变量(体重)的变化?这个变化在多大程度上与解释变量(身高)有关?在多大程度上与随机误差有关?
例如,编号为6的女大学生的体重并没有落在水平直线上,她的体重为61kg。解释变量(身高)和随机误差共同把这名学生的体重从54.5kg“推”到了61kg,相差6.5kg,所以6.5kg是解析变量和随机误差的组合效应。 编号为3的女大学生的体重并也没有落在水平直线上,她的体重为50kg。解释变量(身高)和随机误差共同把这名学生的体重从50kg “推”到了54.5kg,相差-4.5kg,这时解释变量和随机误差的组合效应为-4.5kg。
用这种方法可以对所有预报变量计算组合效应。
用这种方法可以对所有预报变量计算组合效应。
用这种方法可以对所有预报变量计算组合效应。
在例1中,总偏差平方和为354。
那么,在这个总的效应(总偏差平方和)中,有多少来自于解释变量(身高)?有多少来自于随机误差?
那么,在这个总的效应(总偏差平方和)中, 有多少来自于解释变量(身高)?有多少来自于随机误差? 假设随机误差对体重没有影响,也就是说, 体重仅受身高的影响,那么散点图中所有的点将完全落在回归直线上。但是,在图中,数据点并没有完全落在回归直线上。这些点散布在回归直线附近,所以一定是随机误差把这些点从回归直线上 “推”开了。
例如,编号为6的女大学生,计算随机误差的效应(残差)为: 61-(0.849×165-85.712)=6.627
例如,编号为6的女大学生,计算随机误差的效应(残差)为: 61-(0.849×165-85.712)=6.627
例如,编号为6的女大学生,计算随机误差的效应(残差)为: 61-(0.849×165-85.712)=6.627
在例1中,残差平方和约为128.361。
由于解释变量和随机误差的总效应 (总偏差平方和)为354,而随机误差的效 应为128.361,所以解释变量的效应为 354-128.361=225.639
由于解释变量和随机误差的总效应 (总偏差平方和)为354,而随机误差的效 应为128.361,所以解释变量的效应为 354-128.361=225.639 这个值称为回归平方和.
由于解释变量和随机误差的总效应 (总偏差平方和)为354,而随机误差的效 应为128.361,所以解释变量的效应为 354-128.361=225.639 这个值称为回归平方和.
解释变量和随机误差的总效应(总偏差平方和)=解释变量的效应(回归平方和) +随机误差的效应(残差平方和)
样本决定系数(判定系数 R2) 1.回归平方和占总离差平方和的比例
2. 反映回归直线的拟合程度
3. 取值范围在[0, 1]之间
4. R2 1,说明回归方程拟合的越好; R2 0,说明回归方程拟合的越差
5. 判定系数等于相关系数的平方,即R2=(r)2
显然,R2的值越大,说明残差平方和越小, 也就是说模型拟合效果越好。
显然,R2的值越大,说明残差平方和越小, 也就是说模型拟合效果越好。 在线性回归模型中,R2表示解释变量对预 报变量变化的贡献率。
显然,R2的值越大,说明残差平方和越小, 也就是说模型拟合效果越好。 在线性回归模型中,R2表示解释变量对预 报变量变化的贡献率。 R2越接近1,表示回归的效果越好(因为R2 越接近1,表示解释变量和预报变量的线性相 关性越强)。
如果某组数据可能采取几种不同回归方程进行回归分析,则可以通过比较R2的值来做出选择,即选取R2较大的模型作为这组数据的模型。
如果某组数据可能采取几种不同回归方程进行回归分析,则可以通过比较R2的值来做出选择,即选取R2较大的模型作为这组数据的模型。 总的来说:
相关指数R2是度量模型拟合效果的一种指标。
在线性模型中,它代表自变量刻画预报变量的能力。
从表1-3中 可以看出,解 释变量对总效 应约贡献了64%, 即R2 0.64,可以叙述为“身高解析了64%的体重 变化”,而随机误差贡献了剩余的36%。所以, 身高对体重的效应比随机误差的效应大得多。
残差分析与残差图的定义:
在研究两个变量间的关系时,首先要根据散点图来粗略判断它们是否线性相关,是否可以用回归模型来拟合数据.
我们可以利用图形来分析残差特性,作图时纵坐标为残差,横坐标可以选为样本编号,或身高数据,或体重估计值等,这样作出的图形称为残差图。
残差图的制作及作用
1. 坐标纵轴为残差变量,横轴可以有不同的选择;
2. 若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;
3. 对于远离横轴的点,要特别注意.
残差图的制作及作用
1. 坐标纵轴为残差变量,横轴可以有不同的选择;
2. 若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;
3. 对于远离横轴的点,要特别注意.
残差图的制作及作用
1. 坐标纵轴为残差变量,横轴可以有不同的选择;
2. 若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;
3. 对于远离横轴的点,要特别注意.
异常点
·错误数据
·模型问题
残差图的制作及作用
1. 坐标纵轴为残差变量,横轴可以有不同的选择;
2. 若模型选择的正确,残差图中的点应该分布在以横轴为心的带形区域;
3. 对于远离横轴的点,要特别注意.
异常点
·错误数据
·模型问题
1. 线性回归模型;
2. 变量间新的关系;
3. 刻画回归效果的方式;
4. 残差图
知识归纳
用身高预报体重时,需要注意下列问题:
1、回归方程只适用于我们所研究的样本的总体;
2、我们所建立的回归方程一般都有时间性;
3、样本采集的范围会影响回归方程的适用范围;
4、不能期望回归方程得到的预报值就是预报变量的精确值。
事实上,它是预报变量的可能取值的平均值。
——这些问题也使用于其他问题。
涉及到统计的一些思想:
模型适用的总体;
模型的时间性;
样本的取值范围对模型的影响;
模型预报结果的正确理解。
小结
一般地,建立回归模型的基本步骤为:
(1)确定研究对象,明确哪个变量是解析变量,哪个变量是预报变量。
(2)画出确定好的解析变量和预报变量的散点图,观察它们之间的关系
(如是否存在线性关系等)。
(3)由经验确定回归方程的类型(如我们观察到数据呈线性关系,则选用线性回归方程y=bx+a).
(4)按一定规则估计回归方程中的参数(如最小二乘法)。
(5)得出结果后分析残差图是否有异常(个别数据对应残差过大,或残差呈现不随机的规律性,等等),过存在异常,则检查数据是否有误,或模型是否合适等。
