平面直角坐标系
图片预览



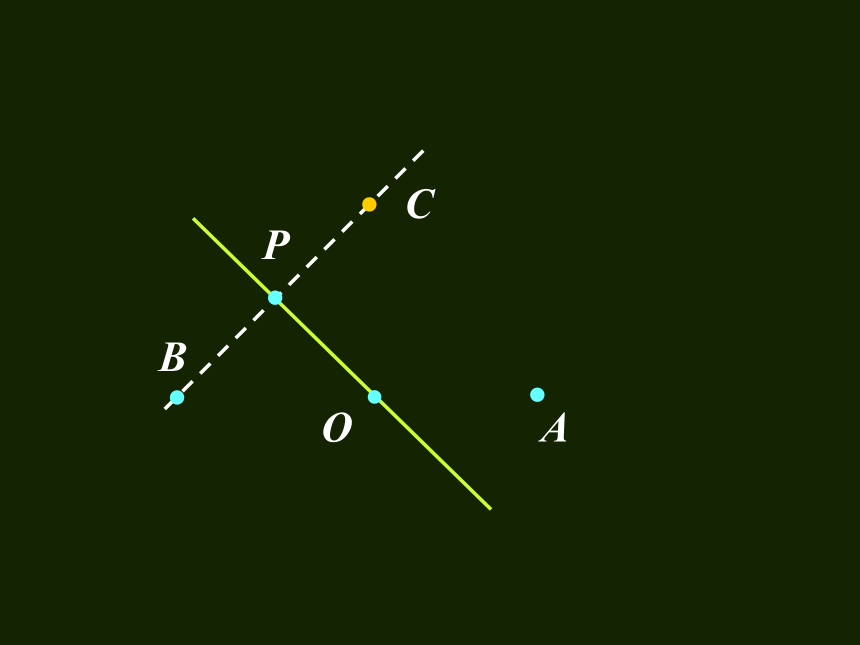
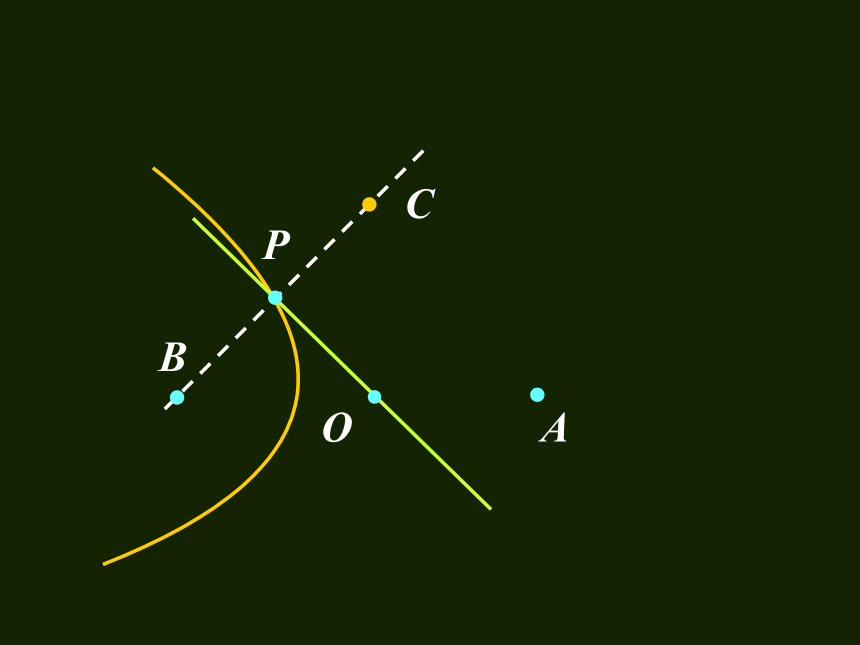
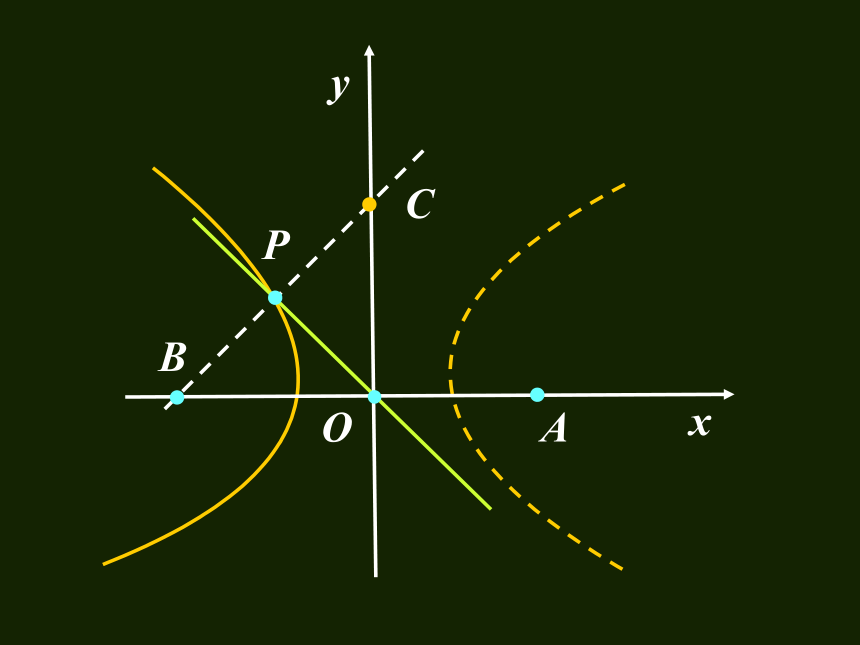




文档简介
(共50张PPT)
平面直角坐标系
一. 平面直角坐标系的建立
一. 平面直角坐标系的建立 思考:声响定位问题 某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到一声巨响,正东观测点听到巨响的时间比其他两个观测点晚4s,已知各观测点到中心的距离都是1020m,试确定该巨响的位置。(假定当时声音传播的速度为340m/s,各相关点均在同一平面上)
(2004年广东高考题)
A
O
B
P
C
A
O
B
P
C
A
O
B
P
C
A
O
B
P
C
x
A
O
B
P
C
y
以接报中心为原点O,以BA方向为x轴,建立直角坐标系.设A、B、C分别是西、东、北观测点,
x
A
O
B
P
C
y
以接报中心为原点O,以BA方向为x轴,建立直角坐标系.设A、B、C分别是西、东、北观测点,则A(1020,0), B(-1020,0),C(0,1020)
x
A
O
B
P
C
y
以接报中心为原点O,以BA方向为x轴,建立直角坐标系.设A、B、C分别是西、东、北观测点,则A(1020,0), B(-1020,0),C(0,1020) 设P(x,y)为巨响为生点,由B、C同时听到巨响声,得|PC|=|PB|, 故P在BC的垂直平分线 PO上,PO的方程为y= -x,因A点比B点晚4s 听到爆炸声,
x
A
O
B
P
C
y
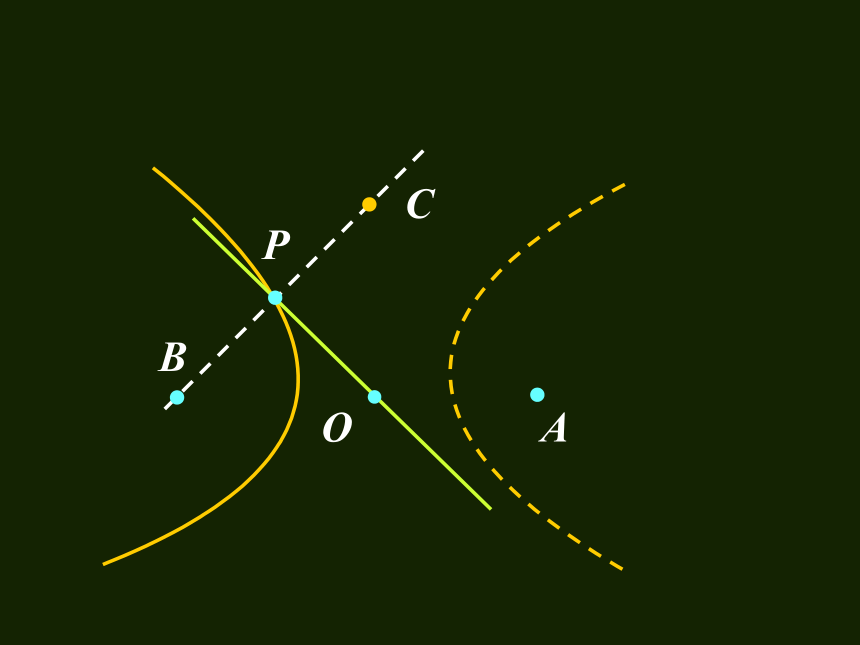
以接报中心为原点O,以BA方向为x轴,建立直角坐标系.设A、B、C分别是西、东、北观测点,则A(1020,0), B(-1020,0),C(0,1020) 设P(x,y)为巨响为生点,由B、C同时听到巨响声,得|PC|=|PB|, 故P在BC的垂直平分线 PO上,PO的方程为y= -x,因A点比B点晚4s 听到爆炸声, 故|PA|-|PB|=340×4=1360
x
A
O
B
P
C
y
由双曲线定义知P点在以A、B为焦点的
双曲线
解决此类应用题的关键:
1. 建立平面直角坐标系
2. 设点(点与坐标的对应)
3. 列式(方程与坐标的对应)
4. 化简
5. 说明
解决此类应用题的关键:坐标法
1. 建立平面直角坐标系
2. 设点(点与坐标的对应)
3. 列式(方程与坐标的对应)
4. 化简
5. 说明
[例1] 已知△ABC的三边a,b,c满足b2+c2=5a2,BE,CF分别为边AC,AB上的中线,建立适当的平面直角坐标系探究BE与CF的位置关系。
[例1] 已知△ABC的三边a,b,c满足b2+c2=5a2,BE,CF分别为边AC,AB上的中线,建立适当的平面直角坐标系探究BE与CF的位置关系。 解:以△ABC的 顶点A为原点O,边 AB所在的直线x轴, 建立直角坐标系,由 已知,点A、B、F的坐标分别为
O
(A)
F
B
x
E
C
y
[例1] 已知△ABC的三边a,b,c满足b2+c2=5a2,BE,CF分别为边AC,AB上的中线,建立适当的平面直角坐标系探究BE与CF的位置关系。 解:以△ABC的 顶点A为原点O,边 AB所在的直线x轴, 建立直角坐标系,由 已知,点A、B、F的坐标分别为
O
(A)
F
B
x
E
C
y
你能建立不同的直角坐标系解决这个问题吗?比较不同的直角坐标系下解决问题的过程,建立直角坐标系应注意什么问题?
建系时,根据几何特点选择适当的直角坐标系。
建系时,根据几何特点选择适当的直角坐标系。 (1) 如果图形有对称中心,可以选对称中心为坐标原点;
建系时,根据几何特点选择适当的直角坐标系。 (1) 如果图形有对称中心,可以选对称中心为坐标原点; (2) 如果图形有对称轴,可以选择对称轴为坐标轴;
建系时,根据几何特点选择适当的直角坐标系。 (1) 如果图形有对称中心,可以选对称中心为坐标原点; (2) 如果图形有对称轴,可以选择对称轴为坐标轴; (3) 使图形上的特殊点尽可能多的在坐标轴上。
[练习]1. 两个定点的距离为6,点M到这两个定点的距离的平方和为26,求点M的轨迹. 2. 已知点A为定点,线段BC在定直线l上滑动,已知|BC|=4,点A到直线l的距离为3,求 ABC的外心的轨迹方程. 3. 证明:三角形的三条高线交于一点.
平面直角坐标系2
二. 平面直角坐标系中的伸缩变换 思考: (1) 怎样由正弦曲线y=sinx得到曲 线y=sin2x
O
x
2
y=sinx
O
x
2
y=sinx
y=sin2x
O
x
2
(2) 怎样由正弦曲线y=sinx得到曲线 y=3sinx 写出其坐标变换。
在正弦曲线上任取一点P(x,y),保持横坐标x不变,将纵坐标伸长为原来的3倍,就得到曲线y=3sinx。 设点P(x,y)经变换得到点为P'(x',y')
(3) 怎样由正弦曲线y=sinx得到曲线 y=3sin2x 写出其坐标变换。
在正弦曲线y=sinx上任取一点P(x,y),保持纵坐标不变,将横坐标x缩为原来的1/2,在此基础上,将纵坐标变为原来的3倍,就得到正弦曲线y=3sin2x. 设点P(x,y)经变换得到点为P'(x',y')
定义:设P(x,y)是平面直角坐标系中任意一点,在变换
注:(1) >0, >0 (2) 把图形看成点的运动轨迹,平面图形的伸缩变换可以用坐标伸缩变换得到; (3) 在伸缩变换下,平面直角坐标系不变,在同一直角坐标系下进行伸缩变换。
[例2] 1. 在直角坐标系中,求下列方程所对应的图形经过伸缩变换
2. 在同一直角坐标系下,求满足下列图形的伸缩变换:曲线4x2+9y2=36变为曲线x'2+y'2=1
思考:在伸缩(4)下,椭圆是否可以 变成圆?抛物线,双曲线变成什么曲线
[练习]
发散思维
归纳小结
1. 伸缩变换的定义;
2. 求伸缩变换公式(直线、圆锥曲线)
3. 先平移变换和先伸缩变换平移单位 数的区别。
作业
考一本《配套练习》
平面直角坐标系
一. 平面直角坐标系的建立
一. 平面直角坐标系的建立 思考:声响定位问题 某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到一声巨响,正东观测点听到巨响的时间比其他两个观测点晚4s,已知各观测点到中心的距离都是1020m,试确定该巨响的位置。(假定当时声音传播的速度为340m/s,各相关点均在同一平面上)
(2004年广东高考题)
A
O
B
P
C
A
O
B
P
C
A
O
B
P
C
A
O
B
P
C
x
A
O
B
P
C
y
以接报中心为原点O,以BA方向为x轴,建立直角坐标系.设A、B、C分别是西、东、北观测点,
x
A
O
B
P
C
y
以接报中心为原点O,以BA方向为x轴,建立直角坐标系.设A、B、C分别是西、东、北观测点,则A(1020,0), B(-1020,0),C(0,1020)
x
A
O
B
P
C
y
以接报中心为原点O,以BA方向为x轴,建立直角坐标系.设A、B、C分别是西、东、北观测点,则A(1020,0), B(-1020,0),C(0,1020) 设P(x,y)为巨响为生点,由B、C同时听到巨响声,得|PC|=|PB|, 故P在BC的垂直平分线 PO上,PO的方程为y= -x,因A点比B点晚4s 听到爆炸声,
x
A
O
B
P
C
y
以接报中心为原点O,以BA方向为x轴,建立直角坐标系.设A、B、C分别是西、东、北观测点,则A(1020,0), B(-1020,0),C(0,1020) 设P(x,y)为巨响为生点,由B、C同时听到巨响声,得|PC|=|PB|, 故P在BC的垂直平分线 PO上,PO的方程为y= -x,因A点比B点晚4s 听到爆炸声, 故|PA|-|PB|=340×4=1360
x
A
O
B
P
C
y
由双曲线定义知P点在以A、B为焦点的
双曲线
解决此类应用题的关键:
1. 建立平面直角坐标系
2. 设点(点与坐标的对应)
3. 列式(方程与坐标的对应)
4. 化简
5. 说明
解决此类应用题的关键:坐标法
1. 建立平面直角坐标系
2. 设点(点与坐标的对应)
3. 列式(方程与坐标的对应)
4. 化简
5. 说明
[例1] 已知△ABC的三边a,b,c满足b2+c2=5a2,BE,CF分别为边AC,AB上的中线,建立适当的平面直角坐标系探究BE与CF的位置关系。
[例1] 已知△ABC的三边a,b,c满足b2+c2=5a2,BE,CF分别为边AC,AB上的中线,建立适当的平面直角坐标系探究BE与CF的位置关系。 解:以△ABC的 顶点A为原点O,边 AB所在的直线x轴, 建立直角坐标系,由 已知,点A、B、F的坐标分别为
O
(A)
F
B
x
E
C
y
[例1] 已知△ABC的三边a,b,c满足b2+c2=5a2,BE,CF分别为边AC,AB上的中线,建立适当的平面直角坐标系探究BE与CF的位置关系。 解:以△ABC的 顶点A为原点O,边 AB所在的直线x轴, 建立直角坐标系,由 已知,点A、B、F的坐标分别为
O
(A)
F
B
x
E
C
y
你能建立不同的直角坐标系解决这个问题吗?比较不同的直角坐标系下解决问题的过程,建立直角坐标系应注意什么问题?
建系时,根据几何特点选择适当的直角坐标系。
建系时,根据几何特点选择适当的直角坐标系。 (1) 如果图形有对称中心,可以选对称中心为坐标原点;
建系时,根据几何特点选择适当的直角坐标系。 (1) 如果图形有对称中心,可以选对称中心为坐标原点; (2) 如果图形有对称轴,可以选择对称轴为坐标轴;
建系时,根据几何特点选择适当的直角坐标系。 (1) 如果图形有对称中心,可以选对称中心为坐标原点; (2) 如果图形有对称轴,可以选择对称轴为坐标轴; (3) 使图形上的特殊点尽可能多的在坐标轴上。
[练习]1. 两个定点的距离为6,点M到这两个定点的距离的平方和为26,求点M的轨迹. 2. 已知点A为定点,线段BC在定直线l上滑动,已知|BC|=4,点A到直线l的距离为3,求 ABC的外心的轨迹方程. 3. 证明:三角形的三条高线交于一点.
平面直角坐标系2
二. 平面直角坐标系中的伸缩变换 思考: (1) 怎样由正弦曲线y=sinx得到曲 线y=sin2x
O
x
2
y=sinx
O
x
2
y=sinx
y=sin2x
O
x
2
(2) 怎样由正弦曲线y=sinx得到曲线 y=3sinx 写出其坐标变换。
在正弦曲线上任取一点P(x,y),保持横坐标x不变,将纵坐标伸长为原来的3倍,就得到曲线y=3sinx。 设点P(x,y)经变换得到点为P'(x',y')
(3) 怎样由正弦曲线y=sinx得到曲线 y=3sin2x 写出其坐标变换。
在正弦曲线y=sinx上任取一点P(x,y),保持纵坐标不变,将横坐标x缩为原来的1/2,在此基础上,将纵坐标变为原来的3倍,就得到正弦曲线y=3sin2x. 设点P(x,y)经变换得到点为P'(x',y')
定义:设P(x,y)是平面直角坐标系中任意一点,在变换
注:(1) >0, >0 (2) 把图形看成点的运动轨迹,平面图形的伸缩变换可以用坐标伸缩变换得到; (3) 在伸缩变换下,平面直角坐标系不变,在同一直角坐标系下进行伸缩变换。
[例2] 1. 在直角坐标系中,求下列方程所对应的图形经过伸缩变换
2. 在同一直角坐标系下,求满足下列图形的伸缩变换:曲线4x2+9y2=36变为曲线x'2+y'2=1
思考:在伸缩(4)下,椭圆是否可以 变成圆?抛物线,双曲线变成什么曲线
[练习]
发散思维
归纳小结
1. 伸缩变换的定义;
2. 求伸缩变换公式(直线、圆锥曲线)
3. 先平移变换和先伸缩变换平移单位 数的区别。
作业
考一本《配套练习》
