圆锥曲线的性质探讨
图片预览


文档简介
(共37张PPT)
第三讲 圆锥曲线性质的探讨
选修 4-1
几何证明选讲
阅读教材P43-44页,回答下列问题
一、什么是点在平面上的平行射影?什么是图形在平面上的平行射影?
二、用一个不平行于底面的平面截圆柱,截面是什么图形?
三、椭圆的定义是什么?
四、切线长定理是什么?推广到空间呢?
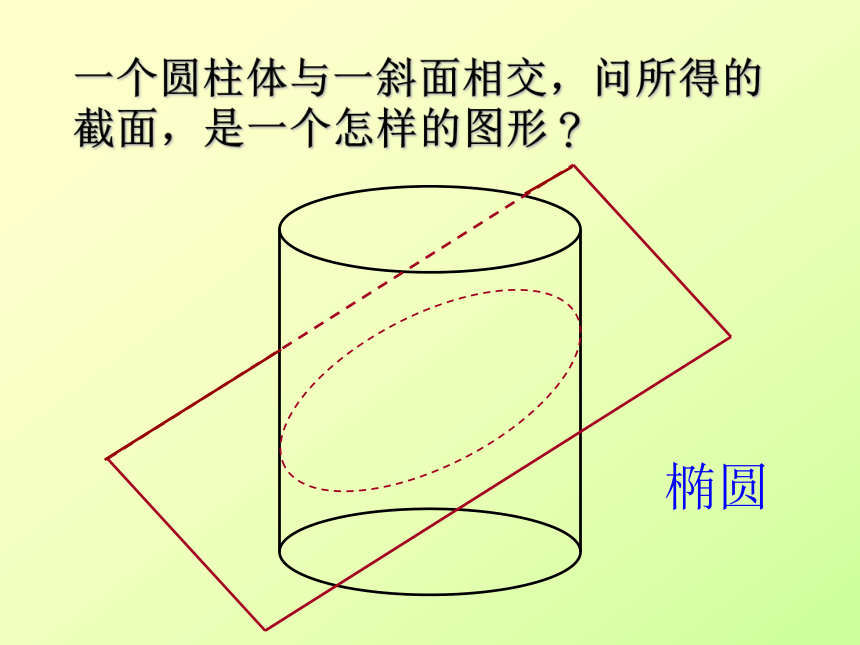
一个圆柱体与一斜面相交,问所得的截面,是一个怎样的图形?
椭圆
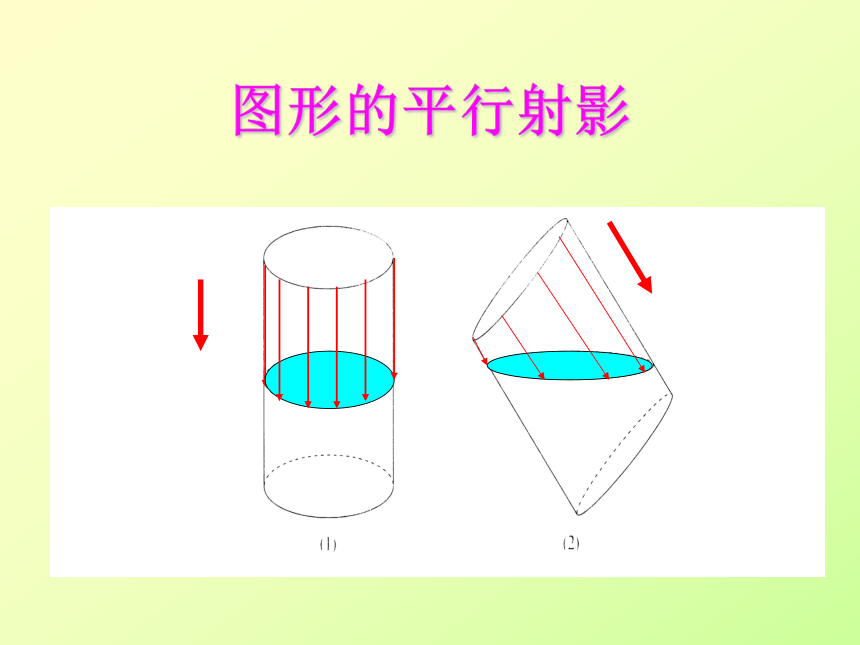
图形的平行射影
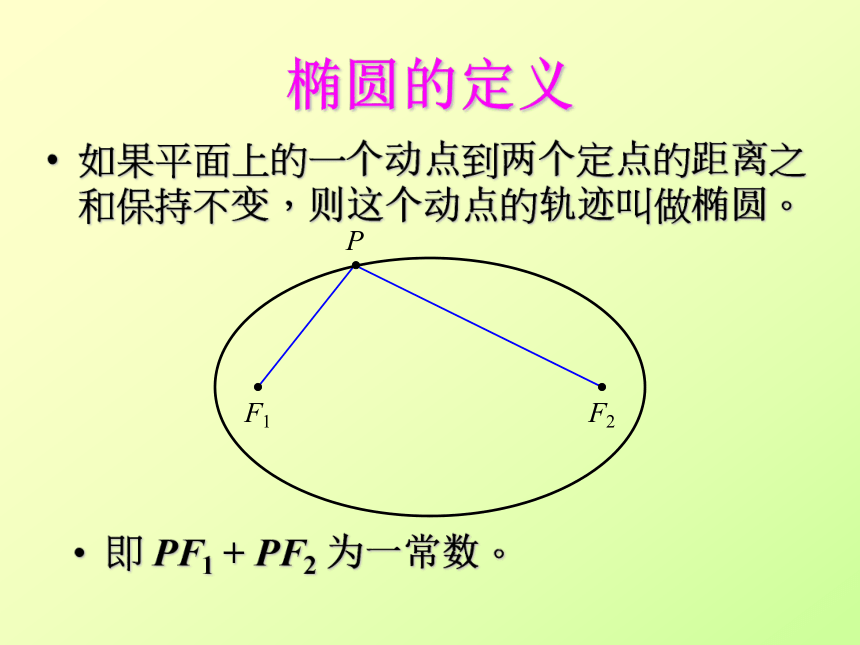
椭圆的定义
如果平面上的一个动点到两个定点的距离之和保持不变,则这个动点的轨迹叫做椭圆。
F1
F2
P
即 PF1 + PF2 为一常数。
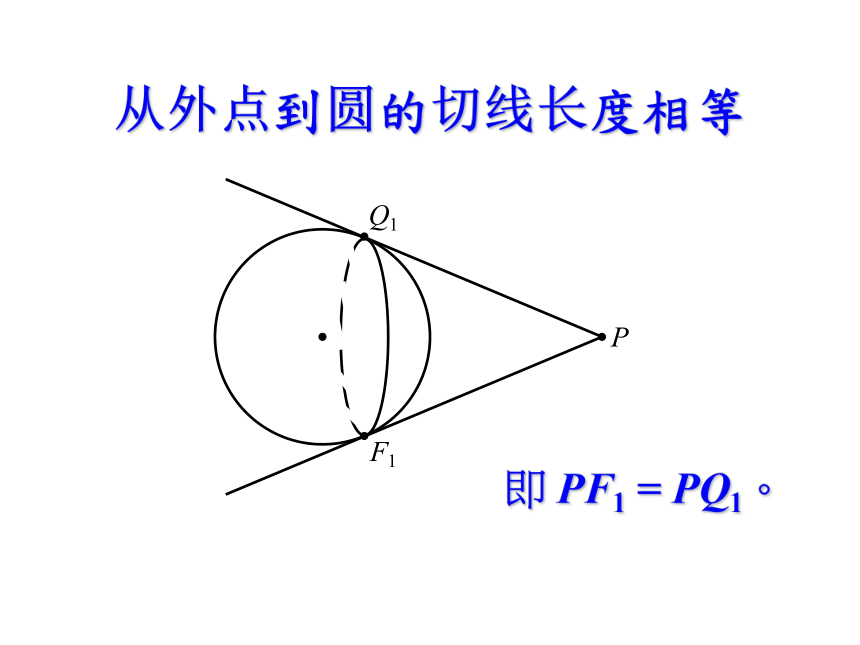
从外点到圆的切线长度相等
F1
Q1
P
即 PF1 = PQ1。
简单证明
F2
F1
Q1
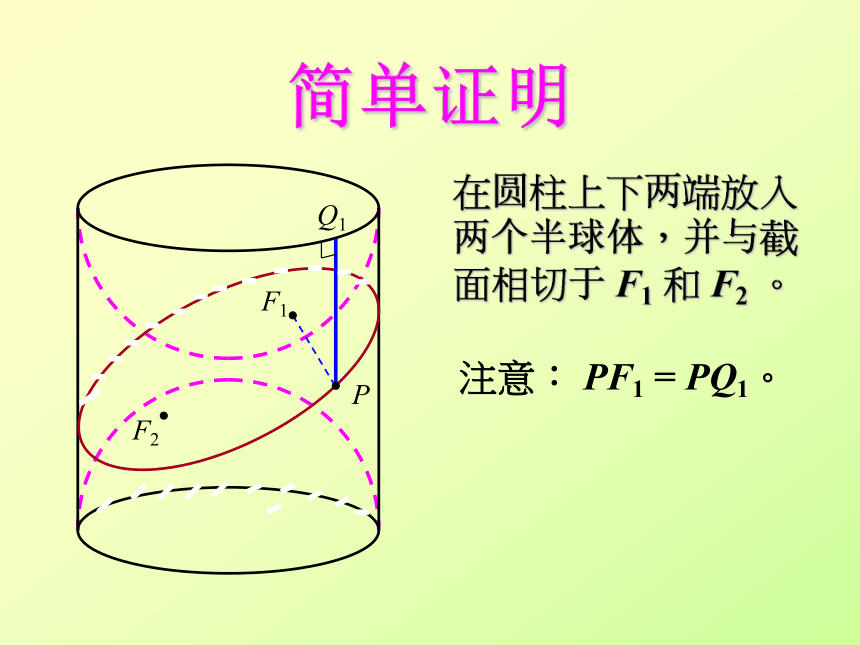
在圆柱上下两端放入两个半球体,并与截面相切于 F1 和 F2 。
P
注意: PF1 = PQ1。
简单证明
F2
F1
P
Q1
Q2
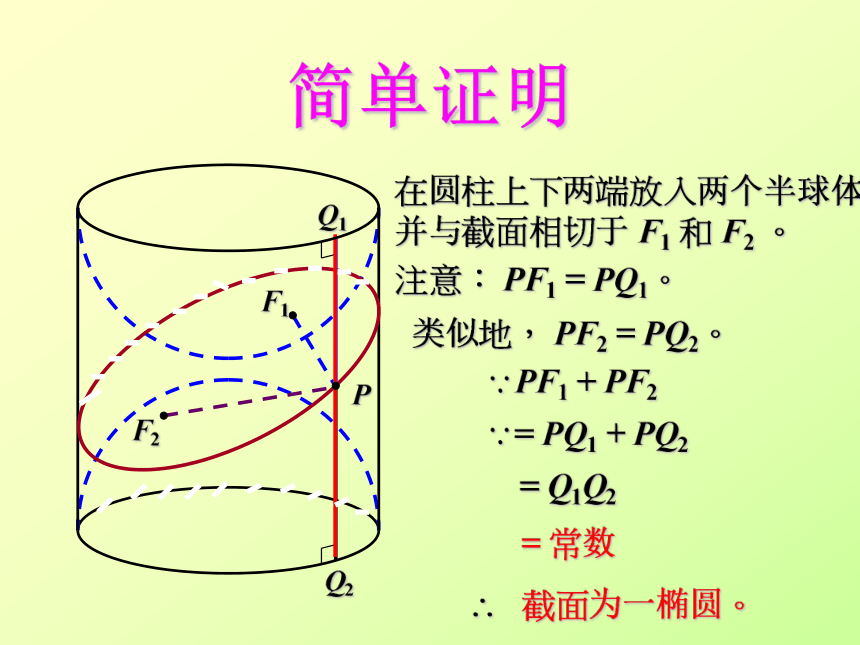
在圆柱上下两端放入两个半球体,并与截面相切于 F1 和 F2 。
注意: PF1 = PQ1。
类似地, PF2 = PQ2。
PF1 + PF2
= PQ1 + PQ2
= Q1Q2
= 常数
截面为一椭圆。
F2
F1
P
Q1
Q2
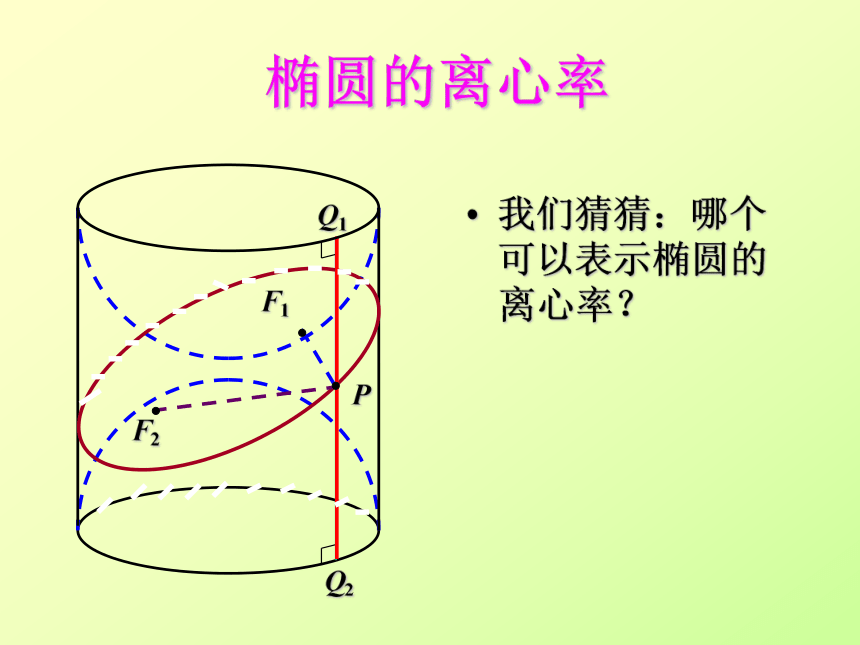
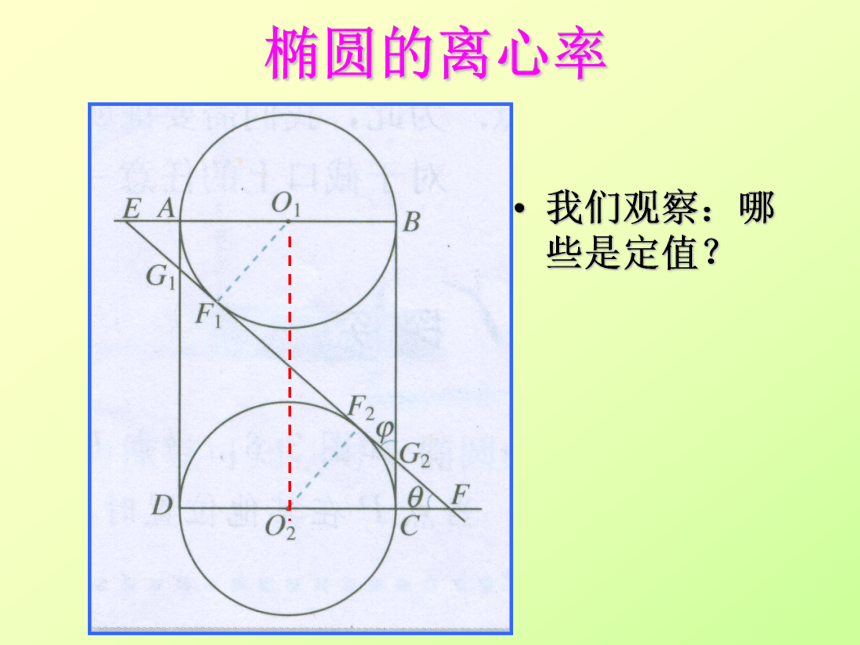
椭圆的离心率
我们猜猜:哪个可以表示椭圆的离心率?
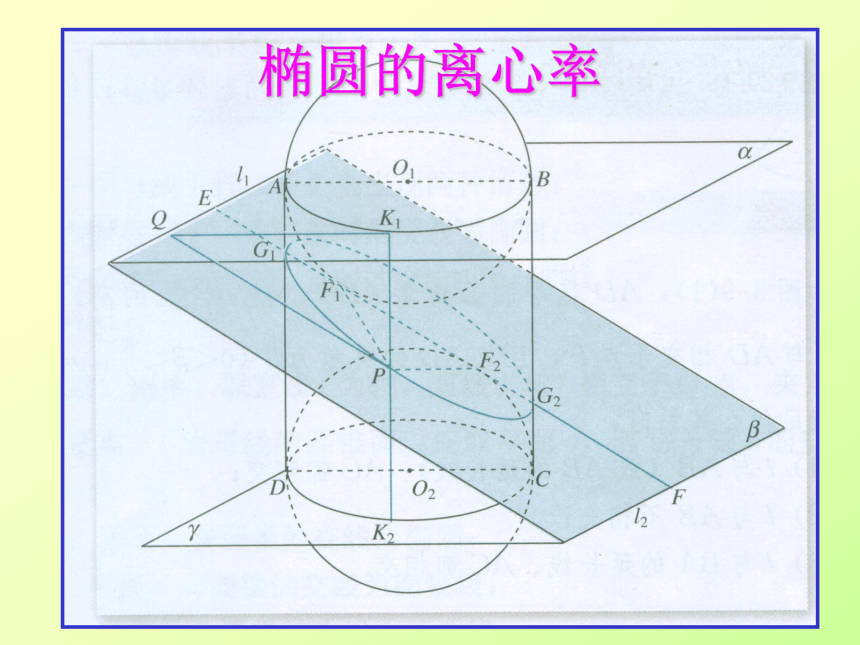
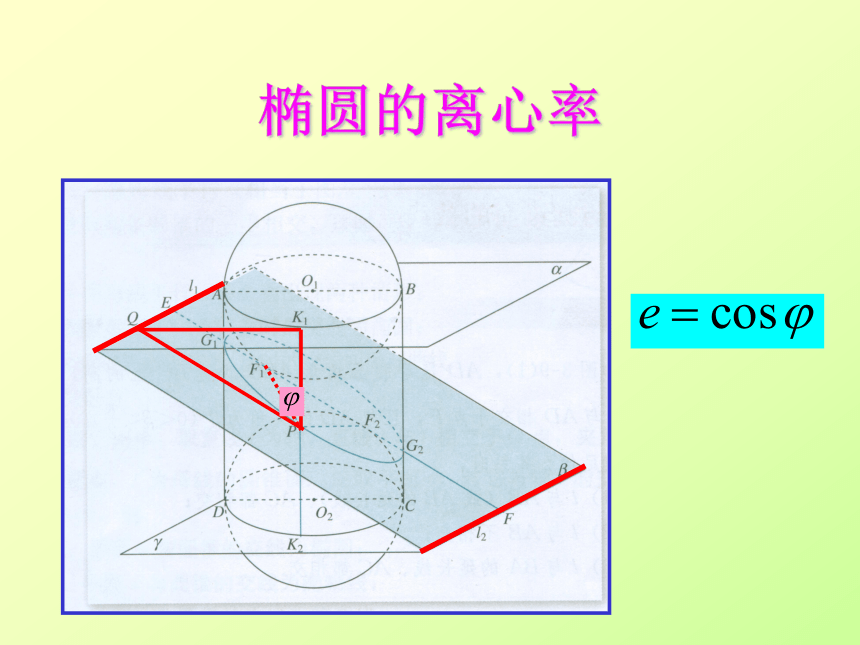
椭圆的离心率
椭圆的离心率
我们观察:哪些是定值?
椭圆的离心率
由圆柱到圆锥
由圆柱到圆锥
发现了什么?
探究:此时的椭圆的离心率
由圆锥到双锥
双曲线的定义
练习:P51习题
抛物线的定义
焦点?准线?
双曲线的准线
圆锥曲线的光学性质
因此,我们称 F1 和 F2 为椭圆的焦点。
F1
F2
抛物线
双曲线
圆锥曲线的光学性质
「抛物线」名称的由来
十七世紀意大利科学家伽利略指出:
物体自由下落的距离与运动时间的平方成正比。
即 s = gt 2 。
「抛物线」名称的由来
因此,当在地面上抛掷一件物件时,物件在空间所经过的轨迹,就会成「抛物线」的形状。
宇宙论的演变
十五世紀前后,欧洲人普遍认为地球是位于宇宙的中心的。
地球就被十一层「天球」所包围。
宇宙论的演变
在 1543 年,哥白尼提出了「日心说」的理论。
开普勒的行星定律
开普勒(1571 1630)
开普勒的行星定律
开普勒的行星定律是以布拉赫数十年对于行星运行的观察数据为基础,
再花十多年功夫才找到一個吻合布拉赫数据的数学模型。
他终于在 1609 年完成了火星运行的数学模型。
开普勒的行星定律
第一定律:恒星沿椭圆轨道绕太阳运行,太阳位于椭圆的一个焦点上。
第二定律:在相等时间内,连接每颗行星与太阳的向经所扫过的面积都相等。
第三定律:每颗行星绕太阳运行的公转周期的平方与它们到太阳的平均距离的立方成正比。
开普勒的行星定律
太阳
火星
开普勒的发现,为圆锥曲线的研究加添上一层实际的意义。
由圆锥到圆台
P
B
A
第三讲 圆锥曲线性质的探讨
选修 4-1
几何证明选讲
阅读教材P43-44页,回答下列问题
一、什么是点在平面上的平行射影?什么是图形在平面上的平行射影?
二、用一个不平行于底面的平面截圆柱,截面是什么图形?
三、椭圆的定义是什么?
四、切线长定理是什么?推广到空间呢?
一个圆柱体与一斜面相交,问所得的截面,是一个怎样的图形?
椭圆
图形的平行射影
椭圆的定义
如果平面上的一个动点到两个定点的距离之和保持不变,则这个动点的轨迹叫做椭圆。
F1
F2
P
即 PF1 + PF2 为一常数。
从外点到圆的切线长度相等
F1
Q1
P
即 PF1 = PQ1。
简单证明
F2
F1
Q1
在圆柱上下两端放入两个半球体,并与截面相切于 F1 和 F2 。
P
注意: PF1 = PQ1。
简单证明
F2
F1
P
Q1
Q2
在圆柱上下两端放入两个半球体,并与截面相切于 F1 和 F2 。
注意: PF1 = PQ1。
类似地, PF2 = PQ2。
PF1 + PF2
= PQ1 + PQ2
= Q1Q2
= 常数
截面为一椭圆。
F2
F1
P
Q1
Q2
椭圆的离心率
我们猜猜:哪个可以表示椭圆的离心率?
椭圆的离心率
椭圆的离心率
我们观察:哪些是定值?
椭圆的离心率
由圆柱到圆锥
由圆柱到圆锥
发现了什么?
探究:此时的椭圆的离心率
由圆锥到双锥
双曲线的定义
练习:P51习题
抛物线的定义
焦点?准线?
双曲线的准线
圆锥曲线的光学性质
因此,我们称 F1 和 F2 为椭圆的焦点。
F1
F2
抛物线
双曲线
圆锥曲线的光学性质
「抛物线」名称的由来
十七世紀意大利科学家伽利略指出:
物体自由下落的距离与运动时间的平方成正比。
即 s = gt 2 。
「抛物线」名称的由来
因此,当在地面上抛掷一件物件时,物件在空间所经过的轨迹,就会成「抛物线」的形状。
宇宙论的演变
十五世紀前后,欧洲人普遍认为地球是位于宇宙的中心的。
地球就被十一层「天球」所包围。
宇宙论的演变
在 1543 年,哥白尼提出了「日心说」的理论。
开普勒的行星定律
开普勒(1571 1630)
开普勒的行星定律
开普勒的行星定律是以布拉赫数十年对于行星运行的观察数据为基础,
再花十多年功夫才找到一個吻合布拉赫数据的数学模型。
他终于在 1609 年完成了火星运行的数学模型。
开普勒的行星定律
第一定律:恒星沿椭圆轨道绕太阳运行,太阳位于椭圆的一个焦点上。
第二定律:在相等时间内,连接每颗行星与太阳的向经所扫过的面积都相等。
第三定律:每颗行星绕太阳运行的公转周期的平方与它们到太阳的平均距离的立方成正比。
开普勒的行星定律
太阳
火星
开普勒的发现,为圆锥曲线的研究加添上一层实际的意义。
由圆锥到圆台
P
B
A
