直线与圆的位置关系2
图片预览










文档简介
(共37张PPT)
直线与圆的位置关系
典例精讲
题型一 圆内接四边形的判定与应用
典例精讲
题型一 圆内接四边形的判定与应用
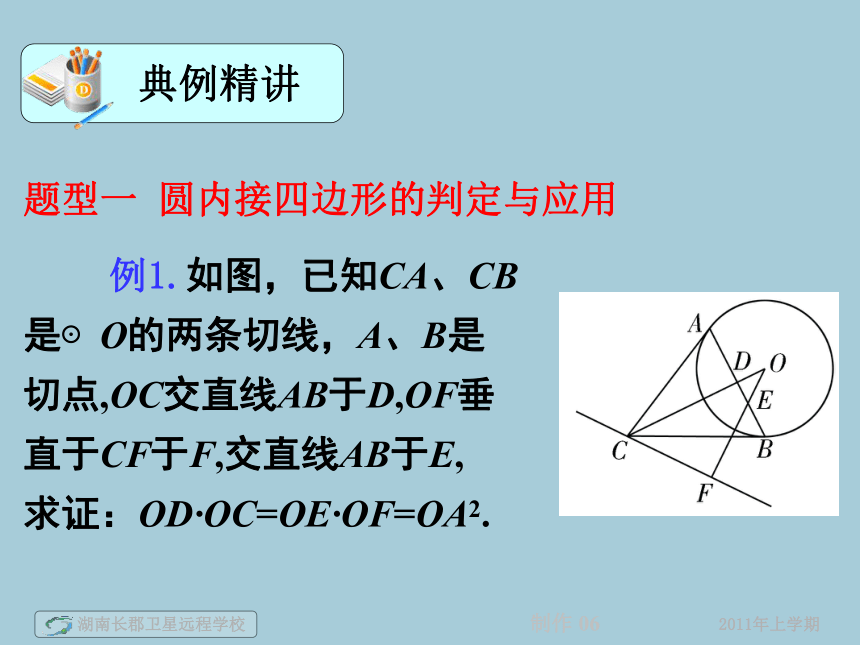
例1.如图,已知CA、CB
是⊙O的两条切线,A、B是
切点,OC交直线AB于D,OF垂
直于CF于F,交直线AB于E,
求证:OD·OC=OE·OF=OA2.
证明:
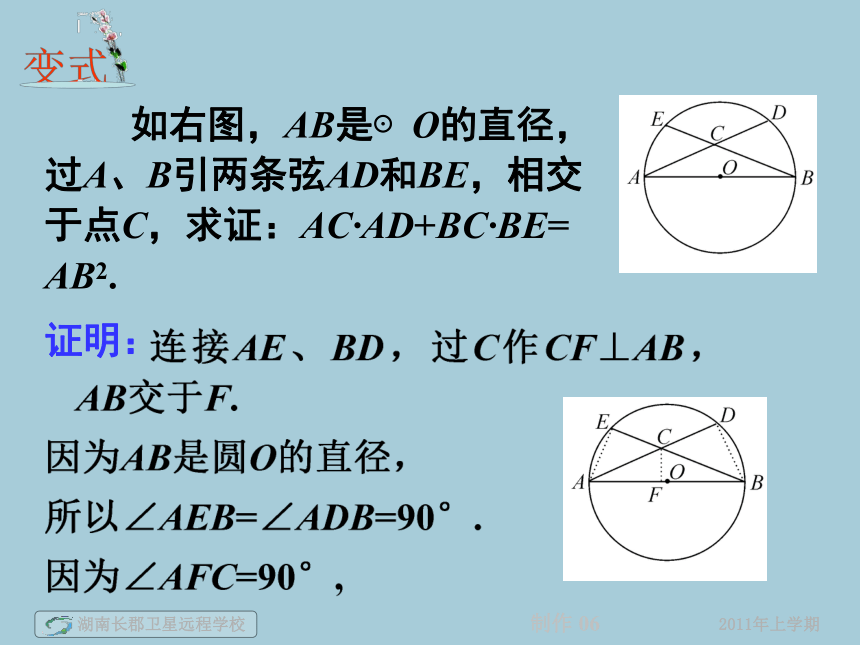
如右图,AB是⊙O的直径,
过A、B引两条弦AD和BE,相交
于点C,求证:AC·AD+BC·BE=
AB2.
如右图,AB是⊙O的直径,
过A、B引两条弦AD和BE,相交
于点C,求证:AC·AD+BC·BE=
AB2.
证明:
题型二 切割线定理及应用
题型二 切割线定理及应用
例2.例如右图,等边三角形
ABC中,边AB与⊙O相切于点H,
边BC、CA分别与⊙O交于点D、
E、F、G.已知AG=2,GF=6,FC=1,
求DE的长.
题型二 切割线定理及应用
例2.例如右图,等边三角形
ABC中,边AB与⊙O相切于点H,
边BC、CA分别与⊙O交于点D、
E、F、G.已知AG=2,GF=6,FC=1,
求DE的长.
分析:DE是CD与BE的公共部分,要求
DE,应与BE,BD,CD,CE建立联系,可利用切
割线定理转化为BH,CF,CG的关系从而得到
解决.
解析:
题型三 圆周角定理和圆的切线定理及应用
例3.如图,已知C是以AB为直径的半圆O
上一点,CH⊥AB于点H,直线AC与过B点的
圆的切线相交于点D,E为CH的中点,连接
AE并延长交BD于点F,直线CF交直线AB于
点G.
(1)求证:点F是BD的中点;
(2)求证:CG是⊙O的切线;
(3)若FB=FE=2,求⊙O
的半径.
题型三 圆周角定理和圆的切线定理及应用
解析
如图,PA、PB是⊙O的切线,A、B为切点,
∠OAB=30°.
(1)求∠APB的大小;
(2)当OA=3时,求AP的长.
如图,PA、PB是⊙O的切线,A、B为切点,
∠OAB=30°.
(1)求∠APB的大小;
(2)当OA=3时,求AP的长.
解析
点评:本题用到的知识点较多,主要知识
点有:①圆的切线的性质;②等腰三角形的性
质;③四边形内角和定理;④锐角三角函数等.
如右图,已知AB为半圆O的直径,直线
l切半圆于点C,AD⊥l于点D,BE⊥l于点E,
BE交半圆O于点F,AD=3cm,
BE=7 cm.
(1)求⊙O的半径;
(2)求线段DE的长.
分析:①连接OC,证C为DE的中点.
在解有关圆的切线问题时,常常要作出过
切点的半径.②对于(2)则连接AF,证四边
形ADEF为矩形,从而得到AD=EF,然后
在Rt△ABF中运用勾股定理,求AF的长.
解析
1.当题目中涉及圆的切线问题时,常常
需要作出过切点的半径,通过它可以构建有
用的垂直关系.
2.在梯形当中,最常见的辅助线是高
线,可以构造出直角三角形,然后在直角三
角形中进行相关的计算.
点评:
1.圆内接四边形的重要结论:内接于圆的平
行四边形是矩形;内接于圆的菱形是正方形;内
接于圆的梯形是等腰梯形.应用这些性质可以大大
简化证明有关几何题的推证过程.
2.圆的切线的性质定理及推论有如下结论:
如果一条直线具备以下三个条件中的任何两个,
就可推出第三个:①垂直于切线;②过切点;③
过圆心.于是利用切线性质时,过切点的半径是常
作的辅助线.
方法提炼
3.判定切线通常有三种方法:①和圆
有惟一一个公共点的直线是圆的切线;②
圆心到直线的距离等于半径的直线是圆的
切线;③过半径外端且和半径垂直的直线
是圆的切线.
4.圆心角、圆周角、弦切角是圆中三
类重要的角,准确理解它们的定义、定理
及所对、所夹弧的关系.
5.与圆有关的比例线段的证明要诀:
相交弦、切割线定理是法宝,相似三角形
中找诀窍,联想射影定理分角线,辅助线
来搭桥,第三比作介绍,代数方法不可少,
分析综合要记牢,十有八九能见效.
走进高考
学例1
解析
学例2 (2009·宁夏/海南卷)如图,已知
△ABC的两条角平分线AD和CE相交于H,
∠B=60°,F在AC上,且AE=AF.
(1)证明:B,D,H,E四点共圆;
(2)证明:CE平分∠DEF.
证明:(1)在△ABC中,因为∠B=60°,
所以∠BAC+∠BCA=120°.
因为AD,CE是角平分线,
所以∠HAC+∠HCA=60°,故∠AHC=120°.
于是∠EHD=∠AHC=120°.
因为∠EBD+∠EHD=180°,所以B,D,H,E四
点共圆.
(2)连接BH,则BH为∠ABC的平分线,
得∠HBD=30°.
由(1)知B,D,H,E四点共圆,
所以∠CED=∠HBD=30°.
又∠AHE=∠EBD=60°,
由已知可得EF⊥AD,
可得∠CEF=30°.
所以CE平分∠DEF.
作业布置
考一本《配套练习》
直线与圆的位置关系
典例精讲
题型一 圆内接四边形的判定与应用
典例精讲
题型一 圆内接四边形的判定与应用
例1.如图,已知CA、CB
是⊙O的两条切线,A、B是
切点,OC交直线AB于D,OF垂
直于CF于F,交直线AB于E,
求证:OD·OC=OE·OF=OA2.
证明:
如右图,AB是⊙O的直径,
过A、B引两条弦AD和BE,相交
于点C,求证:AC·AD+BC·BE=
AB2.
如右图,AB是⊙O的直径,
过A、B引两条弦AD和BE,相交
于点C,求证:AC·AD+BC·BE=
AB2.
证明:
题型二 切割线定理及应用
题型二 切割线定理及应用
例2.例如右图,等边三角形
ABC中,边AB与⊙O相切于点H,
边BC、CA分别与⊙O交于点D、
E、F、G.已知AG=2,GF=6,FC=1,
求DE的长.
题型二 切割线定理及应用
例2.例如右图,等边三角形
ABC中,边AB与⊙O相切于点H,
边BC、CA分别与⊙O交于点D、
E、F、G.已知AG=2,GF=6,FC=1,
求DE的长.
分析:DE是CD与BE的公共部分,要求
DE,应与BE,BD,CD,CE建立联系,可利用切
割线定理转化为BH,CF,CG的关系从而得到
解决.
解析:
题型三 圆周角定理和圆的切线定理及应用
例3.如图,已知C是以AB为直径的半圆O
上一点,CH⊥AB于点H,直线AC与过B点的
圆的切线相交于点D,E为CH的中点,连接
AE并延长交BD于点F,直线CF交直线AB于
点G.
(1)求证:点F是BD的中点;
(2)求证:CG是⊙O的切线;
(3)若FB=FE=2,求⊙O
的半径.
题型三 圆周角定理和圆的切线定理及应用
解析
如图,PA、PB是⊙O的切线,A、B为切点,
∠OAB=30°.
(1)求∠APB的大小;
(2)当OA=3时,求AP的长.
如图,PA、PB是⊙O的切线,A、B为切点,
∠OAB=30°.
(1)求∠APB的大小;
(2)当OA=3时,求AP的长.
解析
点评:本题用到的知识点较多,主要知识
点有:①圆的切线的性质;②等腰三角形的性
质;③四边形内角和定理;④锐角三角函数等.
如右图,已知AB为半圆O的直径,直线
l切半圆于点C,AD⊥l于点D,BE⊥l于点E,
BE交半圆O于点F,AD=3cm,
BE=7 cm.
(1)求⊙O的半径;
(2)求线段DE的长.
分析:①连接OC,证C为DE的中点.
在解有关圆的切线问题时,常常要作出过
切点的半径.②对于(2)则连接AF,证四边
形ADEF为矩形,从而得到AD=EF,然后
在Rt△ABF中运用勾股定理,求AF的长.
解析
1.当题目中涉及圆的切线问题时,常常
需要作出过切点的半径,通过它可以构建有
用的垂直关系.
2.在梯形当中,最常见的辅助线是高
线,可以构造出直角三角形,然后在直角三
角形中进行相关的计算.
点评:
1.圆内接四边形的重要结论:内接于圆的平
行四边形是矩形;内接于圆的菱形是正方形;内
接于圆的梯形是等腰梯形.应用这些性质可以大大
简化证明有关几何题的推证过程.
2.圆的切线的性质定理及推论有如下结论:
如果一条直线具备以下三个条件中的任何两个,
就可推出第三个:①垂直于切线;②过切点;③
过圆心.于是利用切线性质时,过切点的半径是常
作的辅助线.
方法提炼
3.判定切线通常有三种方法:①和圆
有惟一一个公共点的直线是圆的切线;②
圆心到直线的距离等于半径的直线是圆的
切线;③过半径外端且和半径垂直的直线
是圆的切线.
4.圆心角、圆周角、弦切角是圆中三
类重要的角,准确理解它们的定义、定理
及所对、所夹弧的关系.
5.与圆有关的比例线段的证明要诀:
相交弦、切割线定理是法宝,相似三角形
中找诀窍,联想射影定理分角线,辅助线
来搭桥,第三比作介绍,代数方法不可少,
分析综合要记牢,十有八九能见效.
走进高考
学例1
解析
学例2 (2009·宁夏/海南卷)如图,已知
△ABC的两条角平分线AD和CE相交于H,
∠B=60°,F在AC上,且AE=AF.
(1)证明:B,D,H,E四点共圆;
(2)证明:CE平分∠DEF.
证明:(1)在△ABC中,因为∠B=60°,
所以∠BAC+∠BCA=120°.
因为AD,CE是角平分线,
所以∠HAC+∠HCA=60°,故∠AHC=120°.
于是∠EHD=∠AHC=120°.
因为∠EBD+∠EHD=180°,所以B,D,H,E四
点共圆.
(2)连接BH,则BH为∠ABC的平分线,
得∠HBD=30°.
由(1)知B,D,H,E四点共圆,
所以∠CED=∠HBD=30°.
又∠AHE=∠EBD=60°,
由已知可得EF⊥AD,
可得∠CEF=30°.
所以CE平分∠DEF.
作业布置
考一本《配套练习》
