柱坐标系与球坐标系

(共33张PPT)
柱坐标系与球坐标系
一、柱坐标系
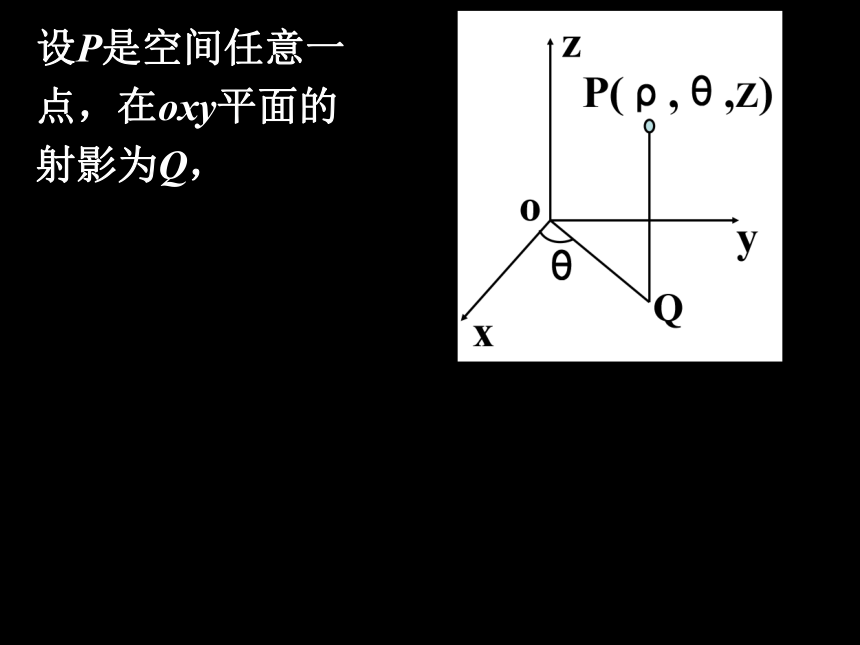
设P是空间任意一 点，在oxy平面的 射影为Q，
设P是空间任意一 点，在oxy平面的 射影为Q，用(ρ,θ) (ρ≥0, 0≤θ<2π) 表示点Q在平面oxy 上的极坐标，
设P是空间任意一 点，在oxy平面的 射影为Q，用(ρ,θ) (ρ≥0, 0≤θ<2π) 表示点Q在平面oxy 上的极坐标，点P 的位置可用有序数组(ρ,θ,Z)表示. 把建立上述对应关系的坐标系叫做柱坐标
系.
设P是空间任意一 点，在oxy平面的 射影为Q，用(ρ,θ) (ρ≥0, 0≤θ<2π) 表示点Q在平面oxy 上的极坐标，点P 的位置可用有序数组(ρ,θ,Z)表示. 把建立上述对应关系的坐标系叫做柱坐标
系.有序数组(ρ,θ,Z)叫点P的柱坐标，记作
(ρ,θ,Z). 其中ρ≥0, 0≤θ<2π, －∞柱坐标系又称半极坐标系，它是由
平面极坐标系及空间直角坐标系中的一
部分建立起来的.
柱坐标系又称半极坐标系，它是由
平面极坐标系及空间直角坐标系中的一
部分建立起来的. 空间点P的直角坐标(x, y, z)与柱坐
标(ρ,θ,Z)之间的变换公式为
柱坐标系又称半极坐标系，它是由
平面极坐标系及空间直角坐标系中的一
部分建立起来的. 空间点P的直角坐标(x, y, z)与柱坐
标(ρ,θ,Z)之间的变换公式为
***试一试*** 设点的直角坐标为(1，1，1)，求它在柱坐标系中的坐标.
***试一试*** 设点的直角坐标为(1，1，1)，求它在柱坐标系中的坐标.
***试一试*** 设点的直角坐标为(1，1，1)，求它在柱坐标系中的坐标.
***试一试*** 设点的直角坐标为(1，1，1)，求它在柱坐标系中的坐标.
注：求θ 时要注意角的终边与点的射影所在位置一致
二、球坐标系
设P是空间任意 一点，
设P是空间任意 一点，在oxy平面的 射影为Q，
设P是空间任意 一点，在oxy平面的 射影为Q，连接OP， 记|OP|=r，OP与OZ 轴正向所夹的角为φ.
设P是空间任意 一点，在oxy平面的 射影为Q，连接OP， 记|OP|=r，OP与OZ 轴正向所夹的角为φ. 设P在oxy平面上的射影为Q，Ox轴按逆时针方向旋转到OQ时所转过的最小正角为θ.这样点P的位置就可以用有序数组(r,φ,θ)表示.
空间的点与 有序数组(r,φ,θ) 之间建立了一种 对应关系.
空间的点与 有序数组(r,φ,θ) 之间建立了一种 对应关系. 我们把建立 上述对应关系的 坐标系叫做球坐标系(或空间极坐标系).
空间的点与 有序数组(r,φ,θ) 之间建立了一种 对应关系. 我们把建立 上述对应关系的 坐标系叫做球坐标系(或空间极坐标系).有序数组(r,φ,θ)叫做点P的球坐标，
空间点P的直角坐标(x, y, z)与球坐标(r,φ,θ)之间的变换关系为
空间点P的直角坐标(x, y, z)与球坐标(r,φ,θ)之间的变换关系为
空间点P的直角坐标(x, y, z)与球坐标(r,φ,θ)之间的变换关系为
***试一试***
[例1]
***例题讲解***
***练习***
[例2]
***练习***
***小结***
坐标系
数轴 平面直角坐标系 平面极坐标系 空间直角坐标系 柱坐标系 球坐标系
坐标系是联系形与数的桥梁，利用坐标系可以实现几何问题与代数问题的相互转化，从而产生了坐标法.
***作业***
《考一本》第6课时