青岛版五年级数学下册 七 包装盒——长方体和正方体 复习课件(19张ppt)
文档属性
| 名称 | 青岛版五年级数学下册 七 包装盒——长方体和正方体 复习课件(19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 557.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-14 00:00:00 | ||
图片预览




文档简介
七 包装盒——长方体和正方体
复习课件
整体回顾
正方体是特殊的长方体
棱
长方体和正方体的特点
面
顶点
表面积
长方体的表面积
正方体的表面积
体积和容积
长方体的体积
体积单位及换算
正方体的体积
容 积
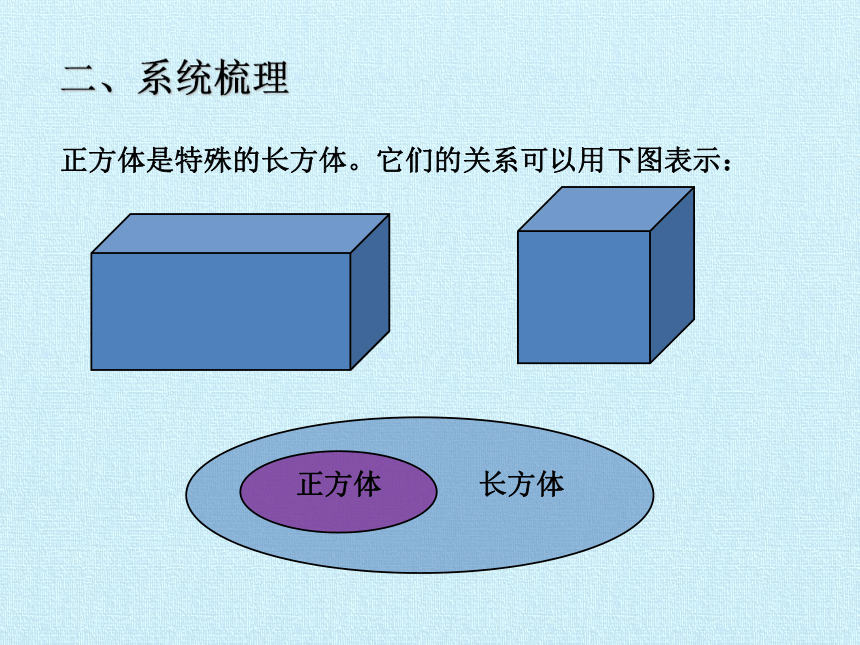
正方体是特殊的长方体。它们的关系可以用下图表示:
二、系统梳理
长方体
正方体
二、系统梳理
长方体和正方体的特征
名称
长方体
正方体
面
个数
形状
棱
条数
长度
顶点
个数
6个
6个面都是长方形(可能有两个相对的面是正方形),相对的面完全相同。
12条
相对的4条棱长度相等(可能有8条棱长度相等)
8个
6个
6个面都是正方形,6个面完全相同。
12条
12条棱长度相等
8个
二、系统梳理
长方体和正方体的表面积
意义
展开图
计算方法
长方体
上
下
前
后
左
右
正方体
后
前
左
右
下
上
长×宽×2
长×高×2
宽×高×2
+
+
(长×宽+长×高+宽×高)×2
棱长×棱长×6
或棱长2×6
长方体或正方体6个面的总面积,叫作它的表面积。
二、系统梳理
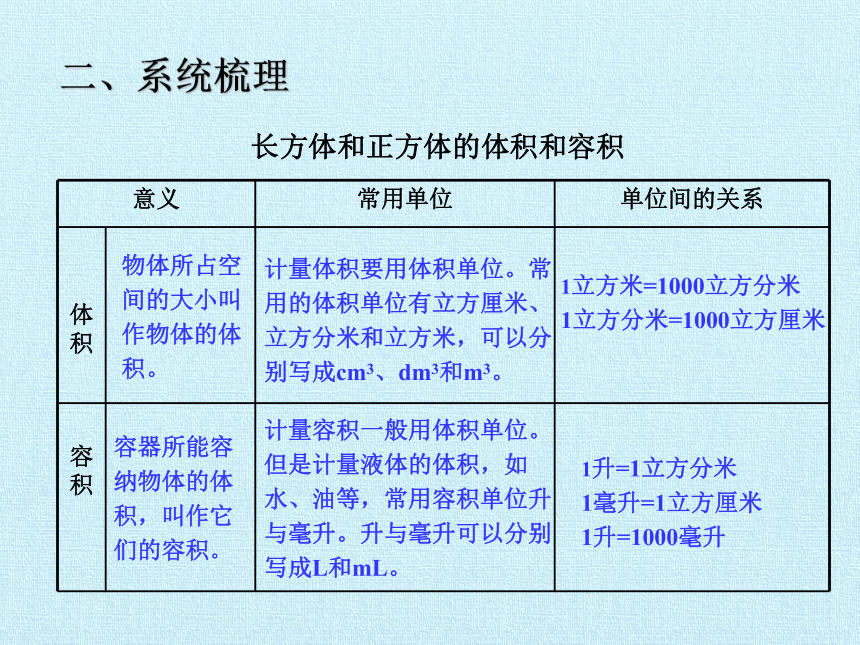
长方体和正方体的体积和容积
意义
常用单位
单位间的关系
体积
容积
1立方米=1000立方分米
1立方分米=1000立方厘米
1升=1立方分米
1毫升=1立方厘米
1升=1000毫升
物体所占空间的大小叫作物体的体积。
容器所能容纳物体的体积,叫作它们的容积。
计量容积一般用体积单位。但是计量液体的体积,如
水、油等,常用容积单位升与毫升。升与毫升可以分别写成L和mL。
计量体积要用体积单位。常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm3、dm3和m3。
二、系统梳理
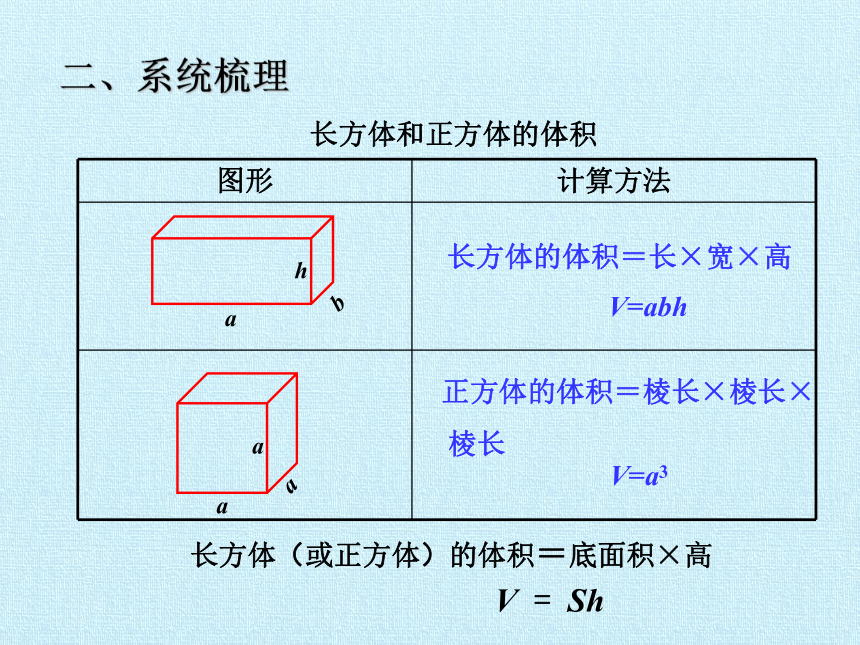
长方体和正方体的体积
图形
计算方法
b
a
h
a
a
a
长方体的体积=长×宽×高
V=abh
正方体的体积=棱长×棱长×
棱长
V=a3
长方体(或正方体)的体积=底面积×高
V = Sh
回顾长方体、正方体体积公式的推导过程:
现实问题
数学问题
联想已有
知识经验
二、系统梳理
二、系统梳理
寻找方法
算一算
可以先把长方体切成1立方厘米的小正方体,再
数一数有多少个,就知道体积是多少了。
一共36个小正方体,所以长方体的体积是36立方厘米。
也可以用1立方厘米的小正方体木块摆一摆。
长6厘米,一行可以摆6个。
宽2厘米,一层可以摆2行。
高3厘米,可以摆3层。
木块总数:
6×2×3=36(个)
体积:
6×2×3=36(立方厘米)
二、系统梳理
归纳结论
回顾刚才的活动过程,想一想,物体的体积与它所含“体积单位”的个数有着怎样的关系?
长方体(或正方体)所含“体积单位”的数量,就是它们的体积。
长方体(或正方体)所含“体积单位”的数量等于长、宽、高的乘积。
2cm
6cm
3cm
木块总数:
6×2×3 = 36(个)
体积:
6×2×3 = 36(立方厘米)
体积:
5×4×2 = 40(立方厘米)
木块总数:
5×4×2 = 40(个)
4cm
5cm
2cm
3×3×3 = 27(立方厘米)
3cm
3cm
3cm
木块总数:
3×3×3 = 27(个)
体积:
b
ɑ
h
长方体的体积 = 长×宽×高
V = ɑbh
正方体的体积=棱长×棱长×棱长
V = ɑ·ɑ·ɑ
ɑ
ɑ
ɑ
二、合作探索
根据以上探索过程,如果V表示长方体、正方体的体积,用你能总结出长方体和正方体的体积计算公式吗?
长
宽
高
棱长
棱长
棱长
ɑ·ɑ·ɑ也可以写作“ɑ3”,读作“ɑ的立方”,表示3个ɑ相乘。正方体的体积公式一般写成:
V = ɑ3
二、系统整理
解决问题、
解释应用
产生新问题
可乐箱的体积:
7×3×2 = 42(dm3)
啤酒箱的体积:
3×3×3 = 27(dm3)
你会求可乐箱的体积了吗?
答:可乐箱的体积是42 dm3。
答:啤酒箱的体积是27 dm3 。
是不是所有立体图形的体积都等于底面积乘高呢?
二、系统梳理
方法整理:
现实问题
怎样求可乐箱的体积?
数学问题
联想已有知识经验
归纳结论
解决问题、解释应用
产生新问题
怎样求长方体的体积?
体积的大小也就是含有 “体积单位” 数量的多少。
猜想、验证、总结体积公式:V=abh
运用公式求出长方体的体积,解决求饮料箱体积的问题。
是不是所有立方体的体积都等于底面积乘高。
寻找方法
切一切、摆一摆、数一数、算一算。
方法整理:
现实问题
怎样求饮料箱的体积?
数学问题
联想已有知识经验
归纳结论
解决问题、解释应用
产生新问题
怎样求长方体的体积?
面积的大小等于含有面积单位数的多少,体积的大小是否等于是含有体积单位数的多少。
猜想、验证、总结体积公式:v=abh
运用公式求出长方体的体积,解决求饮料箱体积的问题。
是不是所有立方体的体积都等于底面积乘高。
寻找方法
切一切、摆一摆、数一数、算一算。
三、综合应用
1.填一填。
3m2=( )dm2
300
5000cm2=( )dm2
0.05m3=( )dm3=( )cm3
3560mL=( )L=( )dm3
0.32m3=( )L
50
50
50000
3.56
3.56
320
三、综合应用
2.填一填。
长方体
长
宽
高
表面积
体积
1
8cm
5cm
4cm
2
18m
12m
7.5m
3
8.1dm
5dm
162dm3
184cm2
160cm3
882m2
1620m3
4dm
185.8dm2
3.计算下面图形的表面积和体积。
三、自主练习
(8×4+4×6+6×8)×2
=(32+24+48)×2
=104×2
=208(cm2)
表面积:
8×6×4=192(cm3)
体积:
(5×5)×6
=25×6
=150(cm2)
表面积:
5×5×5=125(cm3)
体积:
4×4×2+4×12×4
=32+192
=224(cm2)
表面积:
4×4×12=192(cm3)
体积:
8cm
6cm
4cm
5dm
5dm
5dm
4cm
4cm
12cm
4.
240÷12=20(厘米)
答:至少需用2400平方厘米纸板。
20×20×20=8000(立方厘米)
答:这个纸盒的体积是8000立方厘米。
20×20×6=2400(平方厘米)
三、综合应用
用240厘米长的铁丝做一个最大的正方体框架,然后用纸板将6个面包起来做一个正方体纸盒,至少需用多少平方厘米纸板?这个纸盒的体积是多少立方厘米?
谢 谢
复习课件
整体回顾
正方体是特殊的长方体
棱
长方体和正方体的特点
面
顶点
表面积
长方体的表面积
正方体的表面积
体积和容积
长方体的体积
体积单位及换算
正方体的体积
容 积
正方体是特殊的长方体。它们的关系可以用下图表示:
二、系统梳理
长方体
正方体
二、系统梳理
长方体和正方体的特征
名称
长方体
正方体
面
个数
形状
棱
条数
长度
顶点
个数
6个
6个面都是长方形(可能有两个相对的面是正方形),相对的面完全相同。
12条
相对的4条棱长度相等(可能有8条棱长度相等)
8个
6个
6个面都是正方形,6个面完全相同。
12条
12条棱长度相等
8个
二、系统梳理
长方体和正方体的表面积
意义
展开图
计算方法
长方体
上
下
前
后
左
右
正方体
后
前
左
右
下
上
长×宽×2
长×高×2
宽×高×2
+
+
(长×宽+长×高+宽×高)×2
棱长×棱长×6
或棱长2×6
长方体或正方体6个面的总面积,叫作它的表面积。
二、系统梳理
长方体和正方体的体积和容积
意义
常用单位
单位间的关系
体积
容积
1立方米=1000立方分米
1立方分米=1000立方厘米
1升=1立方分米
1毫升=1立方厘米
1升=1000毫升
物体所占空间的大小叫作物体的体积。
容器所能容纳物体的体积,叫作它们的容积。
计量容积一般用体积单位。但是计量液体的体积,如
水、油等,常用容积单位升与毫升。升与毫升可以分别写成L和mL。
计量体积要用体积单位。常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm3、dm3和m3。
二、系统梳理
长方体和正方体的体积
图形
计算方法
b
a
h
a
a
a
长方体的体积=长×宽×高
V=abh
正方体的体积=棱长×棱长×
棱长
V=a3
长方体(或正方体)的体积=底面积×高
V = Sh
回顾长方体、正方体体积公式的推导过程:
现实问题
数学问题
联想已有
知识经验
二、系统梳理
二、系统梳理
寻找方法
算一算
可以先把长方体切成1立方厘米的小正方体,再
数一数有多少个,就知道体积是多少了。
一共36个小正方体,所以长方体的体积是36立方厘米。
也可以用1立方厘米的小正方体木块摆一摆。
长6厘米,一行可以摆6个。
宽2厘米,一层可以摆2行。
高3厘米,可以摆3层。
木块总数:
6×2×3=36(个)
体积:
6×2×3=36(立方厘米)
二、系统梳理
归纳结论
回顾刚才的活动过程,想一想,物体的体积与它所含“体积单位”的个数有着怎样的关系?
长方体(或正方体)所含“体积单位”的数量,就是它们的体积。
长方体(或正方体)所含“体积单位”的数量等于长、宽、高的乘积。
2cm
6cm
3cm
木块总数:
6×2×3 = 36(个)
体积:
6×2×3 = 36(立方厘米)
体积:
5×4×2 = 40(立方厘米)
木块总数:
5×4×2 = 40(个)
4cm
5cm
2cm
3×3×3 = 27(立方厘米)
3cm
3cm
3cm
木块总数:
3×3×3 = 27(个)
体积:
b
ɑ
h
长方体的体积 = 长×宽×高
V = ɑbh
正方体的体积=棱长×棱长×棱长
V = ɑ·ɑ·ɑ
ɑ
ɑ
ɑ
二、合作探索
根据以上探索过程,如果V表示长方体、正方体的体积,用你能总结出长方体和正方体的体积计算公式吗?
长
宽
高
棱长
棱长
棱长
ɑ·ɑ·ɑ也可以写作“ɑ3”,读作“ɑ的立方”,表示3个ɑ相乘。正方体的体积公式一般写成:
V = ɑ3
二、系统整理
解决问题、
解释应用
产生新问题
可乐箱的体积:
7×3×2 = 42(dm3)
啤酒箱的体积:
3×3×3 = 27(dm3)
你会求可乐箱的体积了吗?
答:可乐箱的体积是42 dm3。
答:啤酒箱的体积是27 dm3 。
是不是所有立体图形的体积都等于底面积乘高呢?
二、系统梳理
方法整理:
现实问题
怎样求可乐箱的体积?
数学问题
联想已有知识经验
归纳结论
解决问题、解释应用
产生新问题
怎样求长方体的体积?
体积的大小也就是含有 “体积单位” 数量的多少。
猜想、验证、总结体积公式:V=abh
运用公式求出长方体的体积,解决求饮料箱体积的问题。
是不是所有立方体的体积都等于底面积乘高。
寻找方法
切一切、摆一摆、数一数、算一算。
方法整理:
现实问题
怎样求饮料箱的体积?
数学问题
联想已有知识经验
归纳结论
解决问题、解释应用
产生新问题
怎样求长方体的体积?
面积的大小等于含有面积单位数的多少,体积的大小是否等于是含有体积单位数的多少。
猜想、验证、总结体积公式:v=abh
运用公式求出长方体的体积,解决求饮料箱体积的问题。
是不是所有立方体的体积都等于底面积乘高。
寻找方法
切一切、摆一摆、数一数、算一算。
三、综合应用
1.填一填。
3m2=( )dm2
300
5000cm2=( )dm2
0.05m3=( )dm3=( )cm3
3560mL=( )L=( )dm3
0.32m3=( )L
50
50
50000
3.56
3.56
320
三、综合应用
2.填一填。
长方体
长
宽
高
表面积
体积
1
8cm
5cm
4cm
2
18m
12m
7.5m
3
8.1dm
5dm
162dm3
184cm2
160cm3
882m2
1620m3
4dm
185.8dm2
3.计算下面图形的表面积和体积。
三、自主练习
(8×4+4×6+6×8)×2
=(32+24+48)×2
=104×2
=208(cm2)
表面积:
8×6×4=192(cm3)
体积:
(5×5)×6
=25×6
=150(cm2)
表面积:
5×5×5=125(cm3)
体积:
4×4×2+4×12×4
=32+192
=224(cm2)
表面积:
4×4×12=192(cm3)
体积:
8cm
6cm
4cm
5dm
5dm
5dm
4cm
4cm
12cm
4.
240÷12=20(厘米)
答:至少需用2400平方厘米纸板。
20×20×20=8000(立方厘米)
答:这个纸盒的体积是8000立方厘米。
20×20×6=2400(平方厘米)
三、综合应用
用240厘米长的铁丝做一个最大的正方体框架,然后用纸板将6个面包起来做一个正方体纸盒,至少需用多少平方厘米纸板?这个纸盒的体积是多少立方厘米?
谢 谢
