人教版九年级下册数学 28.1 锐角三角函数——余弦和正切课件(共25张PPT)
文档属性
| 名称 | 人教版九年级下册数学 28.1 锐角三角函数——余弦和正切课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 10.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-15 08:57:31 | ||
图片预览




文档简介
(共25张PPT)
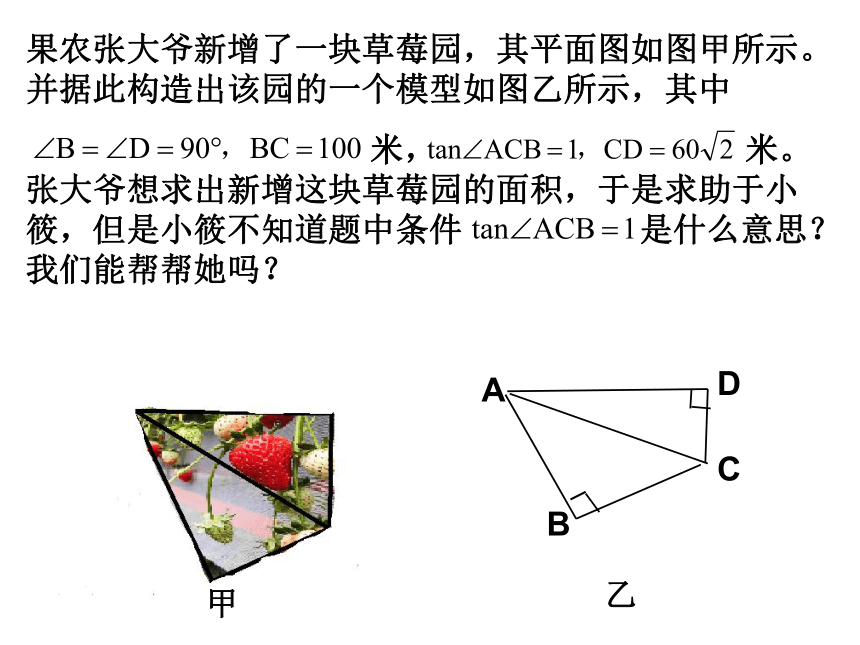
果农张大爷新增了一块草莓园,其平面图如图甲所示。并据此构造出该园的一个模型如图乙所示,其中
米,
米。张大爷想求出新增这块草莓园的面积,于是求助于小筱,但是小筱不知道题中条件
是什么意思?我们能帮帮她吗?
A
D
C
B
乙
甲
新人教版九年级数学(下册)第二十八章
§28.1
锐角三角函数
——余弦、正切
小筱热身练
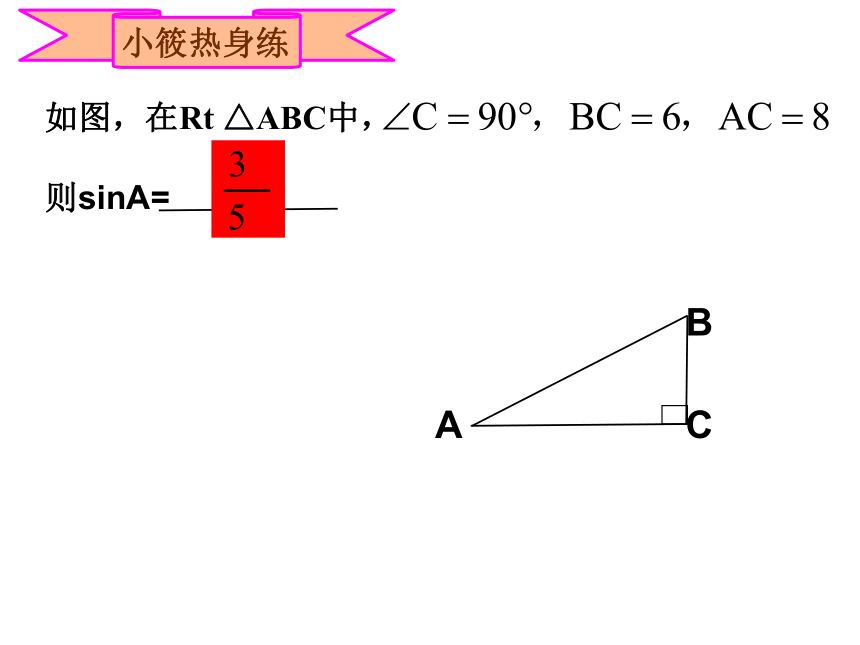
如图,在Rt
△ABC中,
则sinA=
A
B
C
小筱探新知
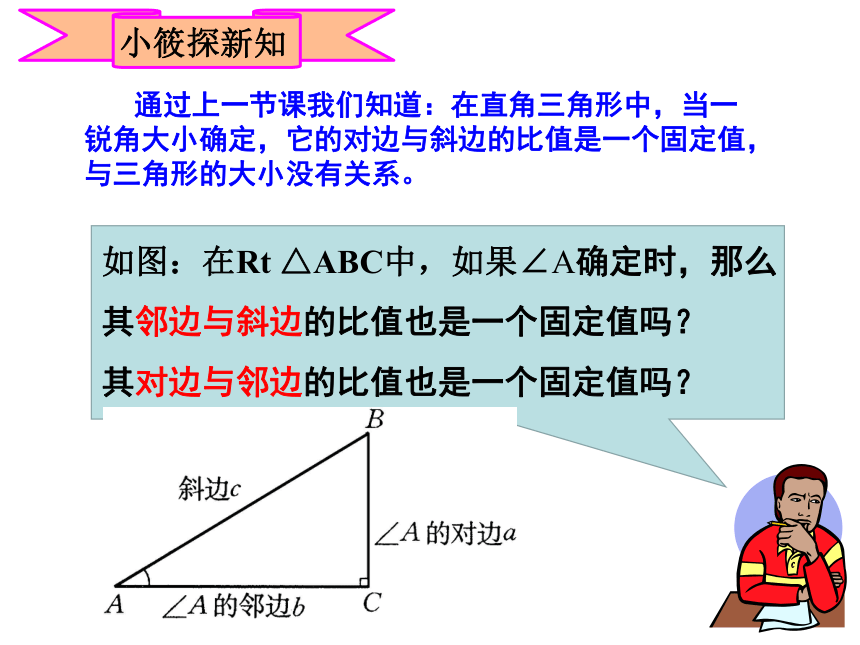
如图:在Rt
△ABC中,如果∠A确定时,那么
其邻边与斜边的比值也是一个固定值吗?
其对边与邻边的比值也是一个固定值吗?
通过上一节课我们知道:在直角三角形中,当一锐角大小确定,它的对边与斜边的比值是一个固定值,与三角形的大小没有关系。
如图:在Rt
△ABC中,∠C=90°,我们把
∠A的邻边与斜边的比叫做∠A的
余弦,记作
cosA。
余弦定义:
正切定义:
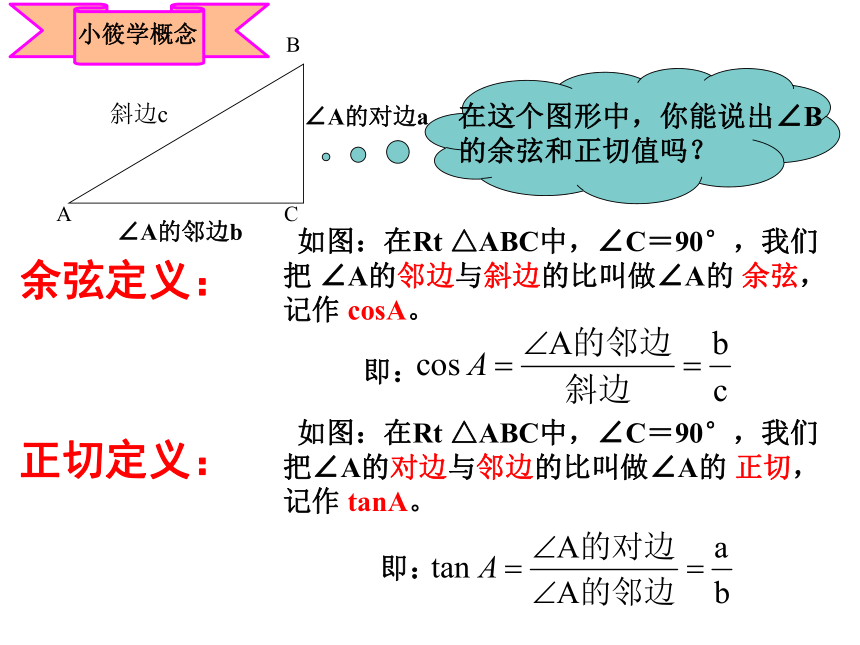
如图:在Rt
△ABC中,∠C=90°,我们把∠A的对边与邻边的比叫做∠A的
正切,记作
tanA。
在这个图形中,你能说出∠B的余弦和正切值吗?
小筱学概念
即:
即:
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
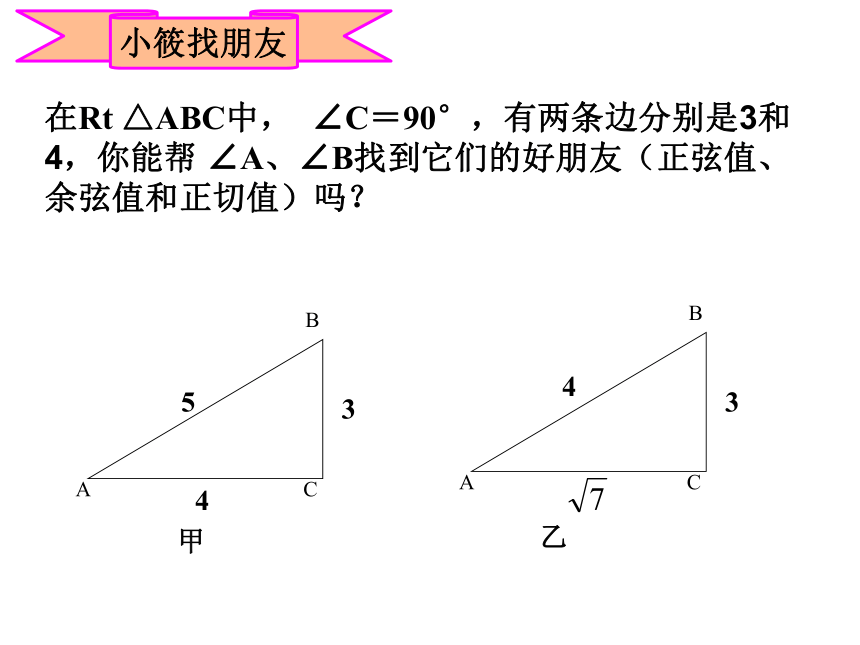
小筱找朋友
在Rt
△ABC中,
∠C=90°,有两条边分别是3和4,你能帮
∠A、∠B找到它们的好朋友(正弦值、余弦值和正切值)吗?
5
4
3
3
4
甲
乙
小筱学例题
如图,在Rt
△ABC中,
。BC=6.
求cosA和tanB的值
3x
6
解:∵BC=6,
∴AB=10
根据勾股定理可知:
AC=8
∴
方法感悟:当已知锐角三角函数值和线段值时,我们通常紧扣定义来解决问题
当不知线段长,已知线段比时,我们通常设每份为x,从而引入参数x来解决问题。
小筱大闯关
Are
you
ready
小组必答题
小组风险题
小组必答题
答题时间60秒,答对得相应的分值,答错不得分。
1
2
3
6
5
4
★
如图:在Rt
△ABC中,锐角A的对边和邻边同时扩大20倍,则cosA的值(
)
1
A.扩大20倍
D.不能确定
C.不变
B.缩小20倍
C
2
★
★
★
如图:在
△ABC中,以AB为直径作
⊙O
,
⊙O恰好经过点C。已知AB=5,AC=4
则cosB=
﹒
O
C
B
A
变式:若点D为⊙O上另一
点,如图,则tanD=
D
3
★
★
如图:在Rt
△ABC中,∠C=90°,
AD是BC边上的中线。AC=2,BC=4.
则
A
B
C
D
★
★
4
如图:在
Rt△ABC中,以点B为圆心,
BC长为半径作⊙B
,⊙B与AB交于点D,过
点D作DE⊥BC于点E,且BC=1,则cosB的
值等于下列哪条线段的长。(
)
A.DE
B.AC
C.BE
D.BC
﹒
D
A
E
C
B
C
★
★
5
在正方形网格中,∠AOB如图放置,则
tan∠AOB的值为(
)
A
B
O
D
★
★
6
如图:在
△ABC中,AB=AC=13,
BC=24.则cosB=
,
tanB=
.
A
C
B
答题时间3分钟,答对得相应的分,答错扣相应的分。
小组风险题
小组风险题1
小组风险题2
★
★
★
如图,已知AB是半圆O的直径,设AD、BC相交于点P。若AB=10,CD=6。sin∠BPD
﹒
C
A
D
B
P
O
解:连接BD
∴∠ADC=
∠ABC
∠BCD=
∠BAD
∴△CPD∽△APB
∴
又
∵AB是半圆O的直径
∴
∠ADB=90°
设PD=3k,PB=5k
∴BD=4k
∴
★
★
★
★
果农张大爷新增了一块草莓园,其平面图如图甲所示。并据此构造出该园的一个模型如图乙所示,其中
米,
米。求新增这块草莓园的面积?
甲
乙
A
D
C
B
解:∵∠B=90°,BC=100且tan∠ACB=1
∴AB=100,
又∵∠D=90°,
∴
∴
小筱谈收获
1、这节课,我们学习了什么知识?
我们学习了余弦和正切的函数的概念,学会了如何正确利用余弦、正切的概念来进行计算。了解了锐角三角函数的概念。
2、这节课,我们运用了哪些数学思想方法?
建立模型,由一般到特殊,分类讨论,借助参数,构造直角,等角转化等。
中考语录
一场、两场、三场、四场考试,
最终为了一场中考;
一次、两次、三次、四次痛苦,
最终为了一次微笑。
结束寄语
业精于勤而荒于嬉
阳光计划
小筱课后练
独立完成作业的良好习惯,是成长过程中的良师益友。
同学们,再见
收获
各小组收获
组别
一组
二组
三组
四组
五组
六组
果农张大爷新增了一块草莓园,其平面图如图甲所示。并据此构造出该园的一个模型如图乙所示,其中
米,
米。张大爷想求出新增这块草莓园的面积,于是求助于小筱,但是小筱不知道题中条件
是什么意思?我们能帮帮她吗?
A
D
C
B
乙
甲
新人教版九年级数学(下册)第二十八章
§28.1
锐角三角函数
——余弦、正切
小筱热身练
如图,在Rt
△ABC中,
则sinA=
A
B
C
小筱探新知
如图:在Rt
△ABC中,如果∠A确定时,那么
其邻边与斜边的比值也是一个固定值吗?
其对边与邻边的比值也是一个固定值吗?
通过上一节课我们知道:在直角三角形中,当一锐角大小确定,它的对边与斜边的比值是一个固定值,与三角形的大小没有关系。
如图:在Rt
△ABC中,∠C=90°,我们把
∠A的邻边与斜边的比叫做∠A的
余弦,记作
cosA。
余弦定义:
正切定义:
如图:在Rt
△ABC中,∠C=90°,我们把∠A的对边与邻边的比叫做∠A的
正切,记作
tanA。
在这个图形中,你能说出∠B的余弦和正切值吗?
小筱学概念
即:
即:
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
小筱找朋友
在Rt
△ABC中,
∠C=90°,有两条边分别是3和4,你能帮
∠A、∠B找到它们的好朋友(正弦值、余弦值和正切值)吗?
5
4
3
3
4
甲
乙
小筱学例题
如图,在Rt
△ABC中,
。BC=6.
求cosA和tanB的值
3x
6
解:∵BC=6,
∴AB=10
根据勾股定理可知:
AC=8
∴
方法感悟:当已知锐角三角函数值和线段值时,我们通常紧扣定义来解决问题
当不知线段长,已知线段比时,我们通常设每份为x,从而引入参数x来解决问题。
小筱大闯关
Are
you
ready
小组必答题
小组风险题
小组必答题
答题时间60秒,答对得相应的分值,答错不得分。
1
2
3
6
5
4
★
如图:在Rt
△ABC中,锐角A的对边和邻边同时扩大20倍,则cosA的值(
)
1
A.扩大20倍
D.不能确定
C.不变
B.缩小20倍
C
2
★
★
★
如图:在
△ABC中,以AB为直径作
⊙O
,
⊙O恰好经过点C。已知AB=5,AC=4
则cosB=
﹒
O
C
B
A
变式:若点D为⊙O上另一
点,如图,则tanD=
D
3
★
★
如图:在Rt
△ABC中,∠C=90°,
AD是BC边上的中线。AC=2,BC=4.
则
A
B
C
D
★
★
4
如图:在
Rt△ABC中,以点B为圆心,
BC长为半径作⊙B
,⊙B与AB交于点D,过
点D作DE⊥BC于点E,且BC=1,则cosB的
值等于下列哪条线段的长。(
)
A.DE
B.AC
C.BE
D.BC
﹒
D
A
E
C
B
C
★
★
5
在正方形网格中,∠AOB如图放置,则
tan∠AOB的值为(
)
A
B
O
D
★
★
6
如图:在
△ABC中,AB=AC=13,
BC=24.则cosB=
,
tanB=
.
A
C
B
答题时间3分钟,答对得相应的分,答错扣相应的分。
小组风险题
小组风险题1
小组风险题2
★
★
★
如图,已知AB是半圆O的直径,设AD、BC相交于点P。若AB=10,CD=6。sin∠BPD
﹒
C
A
D
B
P
O
解:连接BD
∴∠ADC=
∠ABC
∠BCD=
∠BAD
∴△CPD∽△APB
∴
又
∵AB是半圆O的直径
∴
∠ADB=90°
设PD=3k,PB=5k
∴BD=4k
∴
★
★
★
★
果农张大爷新增了一块草莓园,其平面图如图甲所示。并据此构造出该园的一个模型如图乙所示,其中
米,
米。求新增这块草莓园的面积?
甲
乙
A
D
C
B
解:∵∠B=90°,BC=100且tan∠ACB=1
∴AB=100,
又∵∠D=90°,
∴
∴
小筱谈收获
1、这节课,我们学习了什么知识?
我们学习了余弦和正切的函数的概念,学会了如何正确利用余弦、正切的概念来进行计算。了解了锐角三角函数的概念。
2、这节课,我们运用了哪些数学思想方法?
建立模型,由一般到特殊,分类讨论,借助参数,构造直角,等角转化等。
中考语录
一场、两场、三场、四场考试,
最终为了一场中考;
一次、两次、三次、四次痛苦,
最终为了一次微笑。
结束寄语
业精于勤而荒于嬉
阳光计划
小筱课后练
独立完成作业的良好习惯,是成长过程中的良师益友。
同学们,再见
收获
各小组收获
组别
一组
二组
三组
四组
五组
六组
