人教版九年级下册数学27.2.1 相似三角形的判定第一课时课件 (共27张PPT)
文档属性
| 名称 | 人教版九年级下册数学27.2.1 相似三角形的判定第一课时课件 (共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-15 09:14:44 | ||
图片预览




文档简介
(共27张PPT)
27.2.1相似三角形的判定
(第1课时)
人教版九年级数学下册
第二十七章
相似
27.2
相似三角形
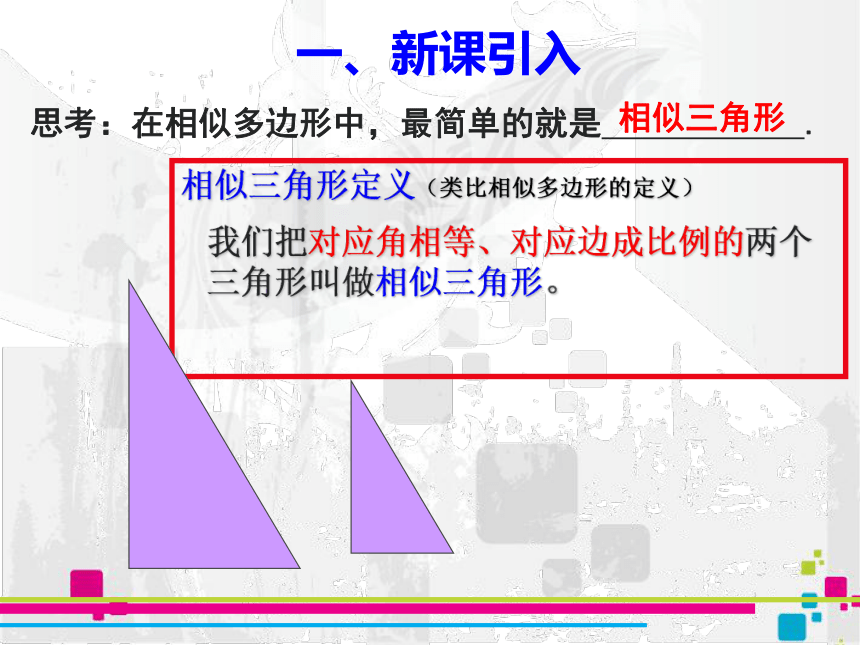
相似三角形定义(类比相似多边形的定义)
思考:在相似多边形中,最简单的就是
.
一、新课引入
相似三角形
我们把对应角相等、对应边成比例的两个三角形叫做相似三角形。
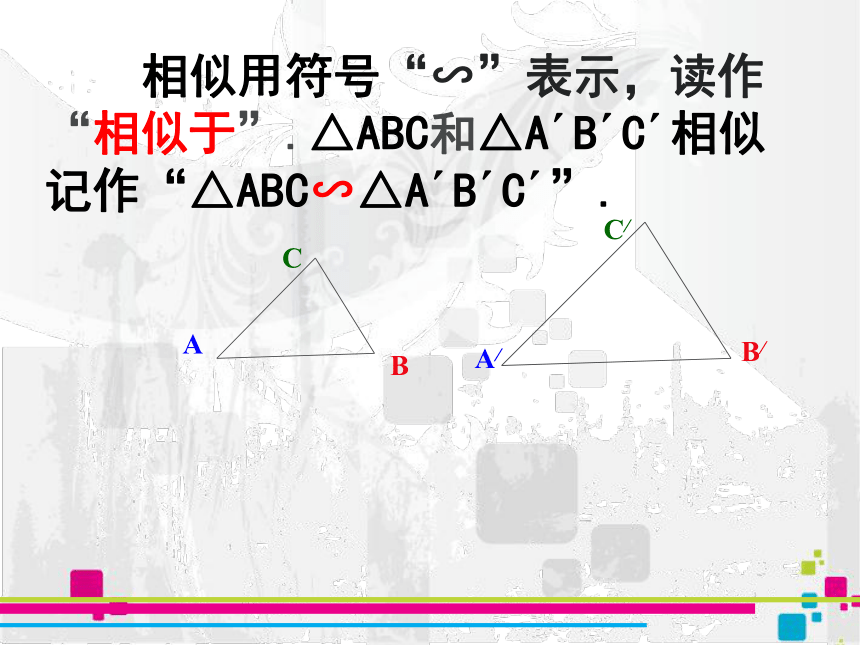
相似用符号“∽”表示,读作“相似于”.△ABC和△A?B?C?相似记作“△ABC∽△A?B?C?”.
用符号语言表示:
∴
△ABC∽△A'B'C'
(相似三角形的定义可以作为三角形相似的一种判定方法)
反过来,如△ABC∽△A'B'C’
即相似三角形对应角相等,对应边成比例。
A
B
C
D
E
F
2cm
3cm
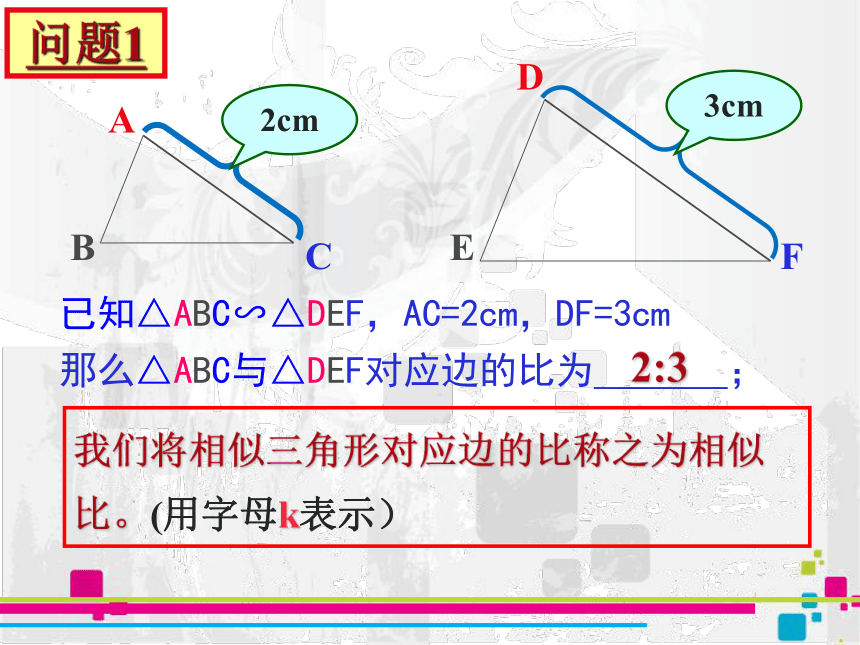
那么△ABC与△DEF对应边的比为
;
已知△ABC∽△DEF,AC=2cm,DF=3cm
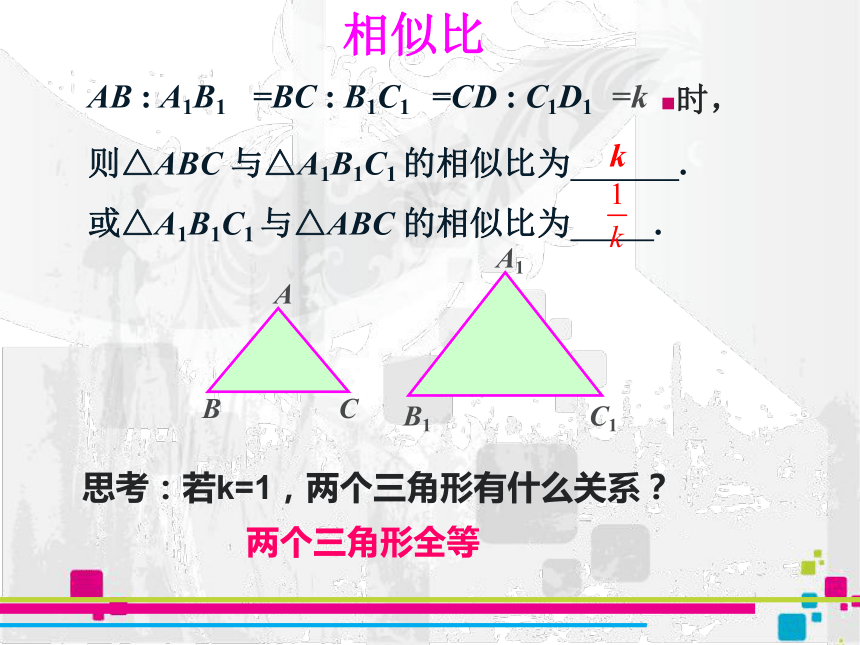
我们将相似三角形对应边的比称之为相似比。(用字母k表示)
2:3
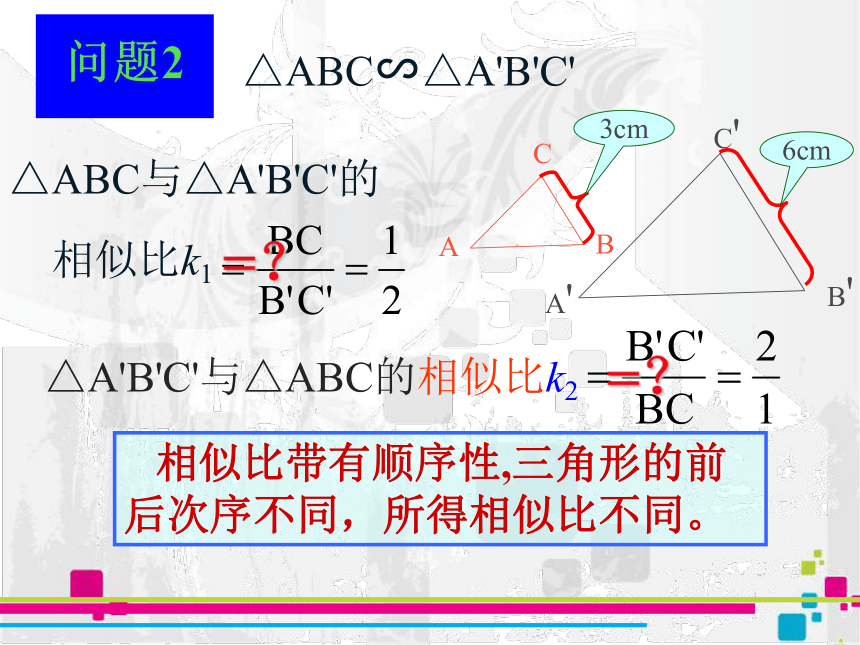
问题1
△ABC与△A'B'C'的
相似比k1
△A'B'C'与△ABC的相似比k2
=?
=?
△ABC∽△A'B'C'
相似比带有顺序性,三角形的前后次序不同,所得相似比不同。
相似比
AB
:
A1B1
=BC
:
B1C1
=CD
:
C1D1
=k
时,
则△ABC
与△A1B1C1
的相似比为
.
或△A1B1C1
与△ABC
的相似比为
.
k
思考:若k=1,两个三角形有什么关系?
两个三角形全等
判定两个三角形全等时,除了可以验证它们所有的角和边分别相等外,还可以使用简便的判定方(SSS,SAS,ASA,AAS).
【创设情境
引入新课】
判定两个三角形相似目前有什么方法?
类比全等三角形的判定,两个三角形相似的判定是不是也存在简便的判定方法呢?
学习目标
探究相似三角形的判定方法.
探究活动1:
已知如图,直线l3∥l4
∥
l5,添加直线l1和l2分别和三条平行线相交于,交点如图所示度量线段AB、BC、DE、EF、AC、DF,
A
B
C
D
E
F
l1
l2
l3
l4
l5
(2)你发现了什么?
(1)求出下列线段比值:
∵l3∥l4
∥
l5
∴
.
当l3∥l4
∥
l5时,
等.
,
,
,
平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
重点关注:等式两边的线段是共线.
探究活动2:把平行线分线段成比例基本事实如何应用于三角形中,会出现什么样的情况?
小组合作,看看如何应用到三角形中.
探究活动2:把平行线分线段成比例基本事实如何应用于三角形中,会出现什么样的情况?
,
,
下列比值还成立吗?
成立
(D)
E
F
平移直线l2,使得D点和A点重合
探究活动2:把平行线分线段成比例基本事实如何应用于三角形中,会出现什么样的情况?
,
,
下列比值还成立吗?
成立
平移直线l2,使得E点和B点重合
D
(E)
F
探究活动2:把平行线分线段成比例基本事实如何应用于三角形中,会出现什么样的情况?
重点研究
两种情况:
方法总结:利用平移,构造成目标图形“三角形”。
结论:平行于三角形一边的直线截其他两边(或两边的延长线),所得对应线段成比例.
简化为简单的数学模型
A字型
X字型
三角形中平行
对应线段比值相等
巩固练习
3
如图,在△ABC
中,DE//BC,
DE分别交AB,AC
于点D,E,
探究△ADE与△ABC有什么关系?并加以证明。
思
考
?
解:猜想
△ADE与△ABC相似,
证明:
在△ADE与△ABC中,
∠A=∠A,
∵DE//BC,
∴∠ADE=∠B,
∠AED=∠C.
唯一缺的是DE:BC,怎么办?
过E作EF//AB,EF交BC于F点.
∴四边形BFED为平行四边形,∴DE=BF,DB=EF.
F
即:△ADE与△ABC中,
∠A=∠A,∠ADE=∠B,
∠AED=∠C.
∴△ADE∽△ABC
F
判定三角形相似的预备定理
在△ABC中,
A型
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
∵DE∥BC
∴△ADE∽△ABC
练习.如图,已知DE
∥
BC,AE=50,EC=30,BC=70,
∠BAC=45°,∠ACB=40°.
(1)求∠AED和∠ADE的大小;
(2)求DE的长.
1、平行线分线段成比例的定理.
2、相似三角形判定方法:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
课堂小结:
3、重点运用的数学知识:平移
4、数学思想方法总结:
类比、数学模型、转化.
谢谢!
27.2.1相似三角形的判定
(第1课时)
人教版九年级数学下册
第二十七章
相似
27.2
相似三角形
相似三角形定义(类比相似多边形的定义)
思考:在相似多边形中,最简单的就是
.
一、新课引入
相似三角形
我们把对应角相等、对应边成比例的两个三角形叫做相似三角形。
相似用符号“∽”表示,读作“相似于”.△ABC和△A?B?C?相似记作“△ABC∽△A?B?C?”.
用符号语言表示:
∴
△ABC∽△A'B'C'
(相似三角形的定义可以作为三角形相似的一种判定方法)
反过来,如△ABC∽△A'B'C’
即相似三角形对应角相等,对应边成比例。
A
B
C
D
E
F
2cm
3cm
那么△ABC与△DEF对应边的比为
;
已知△ABC∽△DEF,AC=2cm,DF=3cm
我们将相似三角形对应边的比称之为相似比。(用字母k表示)
2:3
问题1
△ABC与△A'B'C'的
相似比k1
△A'B'C'与△ABC的相似比k2
=?
=?
△ABC∽△A'B'C'
相似比带有顺序性,三角形的前后次序不同,所得相似比不同。
相似比
AB
:
A1B1
=BC
:
B1C1
=CD
:
C1D1
=k
时,
则△ABC
与△A1B1C1
的相似比为
.
或△A1B1C1
与△ABC
的相似比为
.
k
思考:若k=1,两个三角形有什么关系?
两个三角形全等
判定两个三角形全等时,除了可以验证它们所有的角和边分别相等外,还可以使用简便的判定方(SSS,SAS,ASA,AAS).
【创设情境
引入新课】
判定两个三角形相似目前有什么方法?
类比全等三角形的判定,两个三角形相似的判定是不是也存在简便的判定方法呢?
学习目标
探究相似三角形的判定方法.
探究活动1:
已知如图,直线l3∥l4
∥
l5,添加直线l1和l2分别和三条平行线相交于,交点如图所示度量线段AB、BC、DE、EF、AC、DF,
A
B
C
D
E
F
l1
l2
l3
l4
l5
(2)你发现了什么?
(1)求出下列线段比值:
∵l3∥l4
∥
l5
∴
.
当l3∥l4
∥
l5时,
等.
,
,
,
平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
重点关注:等式两边的线段是共线.
探究活动2:把平行线分线段成比例基本事实如何应用于三角形中,会出现什么样的情况?
小组合作,看看如何应用到三角形中.
探究活动2:把平行线分线段成比例基本事实如何应用于三角形中,会出现什么样的情况?
,
,
下列比值还成立吗?
成立
(D)
E
F
平移直线l2,使得D点和A点重合
探究活动2:把平行线分线段成比例基本事实如何应用于三角形中,会出现什么样的情况?
,
,
下列比值还成立吗?
成立
平移直线l2,使得E点和B点重合
D
(E)
F
探究活动2:把平行线分线段成比例基本事实如何应用于三角形中,会出现什么样的情况?
重点研究
两种情况:
方法总结:利用平移,构造成目标图形“三角形”。
结论:平行于三角形一边的直线截其他两边(或两边的延长线),所得对应线段成比例.
简化为简单的数学模型
A字型
X字型
三角形中平行
对应线段比值相等
巩固练习
3
如图,在△ABC
中,DE//BC,
DE分别交AB,AC
于点D,E,
探究△ADE与△ABC有什么关系?并加以证明。
思
考
?
解:猜想
△ADE与△ABC相似,
证明:
在△ADE与△ABC中,
∠A=∠A,
∵DE//BC,
∴∠ADE=∠B,
∠AED=∠C.
唯一缺的是DE:BC,怎么办?
过E作EF//AB,EF交BC于F点.
∴四边形BFED为平行四边形,∴DE=BF,DB=EF.
F
即:△ADE与△ABC中,
∠A=∠A,∠ADE=∠B,
∠AED=∠C.
∴△ADE∽△ABC
F
判定三角形相似的预备定理
在△ABC中,
A型
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
∵DE∥BC
∴△ADE∽△ABC
练习.如图,已知DE
∥
BC,AE=50,EC=30,BC=70,
∠BAC=45°,∠ACB=40°.
(1)求∠AED和∠ADE的大小;
(2)求DE的长.
1、平行线分线段成比例的定理.
2、相似三角形判定方法:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
课堂小结:
3、重点运用的数学知识:平移
4、数学思想方法总结:
类比、数学模型、转化.
谢谢!
