人教版高中物理 必修二 第七章 7.1—7.2 功(共58张ppt)
文档属性
| 名称 | 人教版高中物理 必修二 第七章 7.1—7.2 功(共58张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 15.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-07-17 06:14:44 | ||
图片预览











文档简介
(共58张PPT)
第七章
机械能守恒定律
追寻守恒量—能量
1
1
化学能
太阳能
核能
动能
秦山核电站是中国自行设计、建造和运营管理的第一座30万千瓦压水堆核电站,总装机容量达到656.4万千瓦,年发电量约500亿千瓦时,成为目前国内核电机组数量最多、堆型最丰富、装机最大的核电基地。
风能
势能
三峡大坝,位于中国湖北省宜昌市三斗坪镇境内,是当今世界最大的水利发电工程.
大坝高185米,正常蓄水位175米,水库长2335米,总装机容量2250万千瓦,年发电量达1000亿度,是世界最大水电站。
弹性势能
能量具有不同的形式
动能、势能、电能、化学能、热能、
核能、光能……
不同形式的能量可以互相转化
太阳能转化为化学能(例如植物光合作用)
化学能转化为电能(例如电池供电)
电能转化为光能(例如灯泡)
动能转化为热能(例如摩擦生热)
……
“有一个事实,如果你愿意,也可以说一条定律,支配着至今所知的一切自然现象……这条定律称做能量守恒定律。它指出某一个量,我们把它称为能量,在自然界经历的多种多样的变化中它不变化。那是一个最抽象的概念……”
——诺贝尔物理学奖获得者费恩曼
“能量”是牛顿没有留给我们的少数力学概念之一。
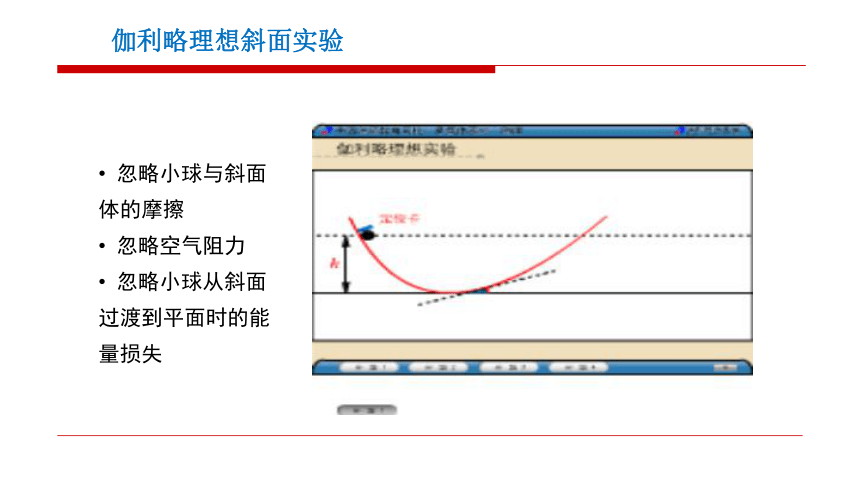
伽利略理想斜面实验
伽利略理想斜面实验
忽略小球与斜面
体的摩擦
忽略空气阻力
忽略小球从斜面过渡到平面时的能量损失
A
B
h
h
用所学知识证明:
α
β
v
v
好像小球能“记住”自己原来的初始高度
伽利略斜面实验表明,小球在运动过程中,“有某一量是守恒的”,这个量叫做能量或能。
说明:能量与物体的运动相对应,是对物体不同运动形式的统一的量度,不同的运动形式对应不同的能量。
能量
相互作用的物体凭借其位置而具有的能,叫做势能。
又叫位能。
弹性势能
重力势能
它们具有重力势能
球
杠铃
被弹高的人
它们具有弹性势能
起跳时的跳板
物体由于运动而具有的能,叫做动能。
它们都具有动能
足球
汽车
火箭
能量的转化
O→P:重力势能EP减少,动能Ek增加
P→Q:动能Ek减少,重力势能Ep增加
Ek+Ep=常数
O
Q
P
A
B
hB
hA
追寻守恒量——能量
机械能
弹簧
轻质弹簧原长为L0,一端固定于墙壁,另一端连接质量为m的小球.现将弹簧拉长至L(L>L0),由静止释放.忽略摩擦和空气阻力.
L0
L
弹性势能EP弹=1/2·kx2
x为弹簧形变量
A→O:
Ek增加,EP弹减少
O→B:
Ek减少,EP弹增加
Ek+EP弹=常数
lOA=lOB
·
·
·
A
O
B
L
L0
1.
下列实例中,动能转化为势能的是
(
)
A.
竖直上抛的正在上升的小球.
B.
上紧发条的玩具汽车正在行驶.
C.
从高处下落的石块.
D.
从斜槽上滚下的小球.
A
课堂练习
解析:B、C、D中均为势能转化为动能.
A中为重力势能转化为小球的动能.
2.苹果从树上掉下时,速度越来越大,忽略空气阻力,正确的是(
)
A.高度转变成了速度
B.苹果的能量增加
C.势能转变成了动能
D.苹果的机械能增加
C
长度可以用尺子——多少米来量度;
质量可以天平——多少千克来来量度;
势能和动能的转化又是怎么进行量度的呢?
课后探究
功
功
2
2
功是能量转化的量度
重力势能增大
动能增大
弹性势能增大
如果物体在力的作用下能量发生了变化,那么这个力一定对物体做了功。
一、功
笔记时间
1.定义:一个物体受到力的作用,并在力的方向上发生一段距离,这个力就对物体做了功。
2.做功的两要素:力和物体在力的方向上发生的位移。
劳而无功
(有力无距)
徒劳无功
(有力有距,但力⊥距)
力与位移方向相同,力做功
F
l
纹丝不动
真辛苦!!
l
笔记时间
3.公式:
F
l
(1)力和位移在同一方向上:
(2)力和位移不在同一方向上:
F
F1=Fcosα
F2=Fsinα
α
l
笔记时间
F
α
物体相对于地面的位移
力与位移的夹角
仅适用于恒力
4.单位:焦耳,简称”焦”,符号是”J”
(1J等于1N的力在力方向上移动1m位移时所做的功
)
D
笔记时间
5.标量:只有大小没有方向,但有正负之分。
正负既不表示大小也不表示方向,正负表示的是动力还是阻力。
l
力不做功。
l
力做正功。
动力
向物体提供能量
l
力做负功。
阻力
物体向外输出能量
F
α
α
例:
平移到同一个点
BC
FN
fBA
fAB
F压
lA=0
α=900
l
笔记时间
6.理解:
(1)功只与力的大小、位移的大小以及力与位移的夹角有关,与物体的质量、运动状态无关。
(2)功是过程量,反映了力在空间上的积累效果,对应着一段位移或一个过程。
F
α
(3)比较功的大小时,只需比较绝对值即可。
例如:
笔记时间
(4)力对物体做负功,也可以说成物体克服这个力做功(取绝对值)。
(5)功的表达式还可以理解成:
例如:重力对物体做功-10J,也可以说成物体克服重力做功10J.
l
F
F1
F2
α
功等于位移方向上的分力与位移的乘积。
功等于力与力方向分位移的乘积。
笔记时间
(6)重力做功公式:
注:重力做的功等于重力与下落(或上升)高度的乘积。
7.总功的计算方法:
方法一:先求出这几个力的合力
F合
的大小和方向,再求合力
F合
所做的功,即为总功。
方法二:先求出各个力所做的功,再求其代数和。
W总
=
F合
l
cos
α
W总
=
W1+W2+……+Wn
仅适用于合力为恒力的情况
功是标量,遵循算术法则
解:对雪橇受力分析,有牛二得
x
F
α
mg
FN
f
F2
F1
各个力的功为
由运动学公式得位移为
总功为
另一种方法
笔记时间
1.动摩擦力和静摩擦力都可以做正功、做负功、不做功,即可以是动力也可以是阻力。
二、几个特殊力的功
v
A
B
f动
f动
B固定不动
l
1800
f动不做功
f动做负功
F
地面光滑
f动
lA
1800
lB
f动做负功
f动做正功
f动
f1
f2
l
l
f静不做功
f静做正功
l
l
f静做负功
笔记时间
2.一对相互作用的动摩擦力做功的代数和为负值;
一对相互作用的静摩擦力做功的代数和为0。
v0
x1
x2
L
f
f
f1
f2
l
l
α
180-α
v0
x
l
L
μmg
μmg
解:(1)
(2)
(3)
笔记时间
3.作用力与反作用力可以做正功、负功或不做功,彼此之间无关联。
S
N
S
N
F
F
做功情况
作用力
反作用力
相向运动
正功
正功
反向运动
负功
负功
一个靠近,一个静止
正功
不做功
一个远离,一个静止
负功
不做功
例.关于两个物体间的一对作用力和反作用力的做功情况,下列说法正确的是(
)A.作用力做功,反作用力一定做功B.作用力做正功,反作用力一定做负功C.作用力和反作用力可能都做负功D.作用力和反作用力做的功一定大小相等
C
笔记时间
1.平均值法
若变力大小随位移均匀变化,且方向不变时,可用变力初、末状态的平均值计算功
三、变力做功的几种方法
满足F=kx的关系
解:水平力等于弹簧的弹力,则
拉力F=kx,拉力与位移成正比(拉力随位移均匀变化),则拉力的平均值为
则
笔记时间
2.图像法
F-x图像的面积表示力做的功.
第一象限面积取正值,代表力做正功;
第四象限面积为负值,代表力做负功.
O
x
F
f
F
O
x
F
O
x
F
解:力F对物体做的功等于l轴上方的正功(梯形“面积”)与l轴下方的负功(三角形“面积”)的代数和
所以力F对物体做的功为:
笔记时间
3.微元法
适应对象:当力的大小不变,力的方向时刻与速度同向或反向时.
解题方法:可用微元法将曲线分成无限个小元段,每一小元段可认为恒力做功,总功即为各个小元段做功的代数和.
解:(1)将圆弧AB分成很多小段l1、l2、…、ln,拉力在每小段上做的功为W1、W2、…、Wn,因拉力F大小不变,方向始终与物体所在位置的切线方向成37°,所以:W1=Fl1cos
37°,W2=Fl2cos
37°,…,Wn=Flncos
37°,所以
(2)
h
Rcos600
(3)
物体受的支持力FN始终与物体的运动方向垂直,所以WN=0
FN
v
BD
笔记时间
4.转换研究对象法
①分段转换法:力在全程是变力,但在每一个阶段是恒力,这样就可以先计算每个阶段的功,再利用求和的方法计算整个过程中变力做的功.
②等效替换法:若某一变力的功和某一恒力的功相等,则可以用求得的恒力的功来作为变力的功.
解:由几何关系得,绳子右端运动的位移为
h
x2
x1
在物体从A移到B的过程中,恒力F做的功为
故绳的拉力对物体所做的功为50
J
课堂小结
谢谢聆听
第七章
机械能守恒定律
追寻守恒量—能量
1
1
化学能
太阳能
核能
动能
秦山核电站是中国自行设计、建造和运营管理的第一座30万千瓦压水堆核电站,总装机容量达到656.4万千瓦,年发电量约500亿千瓦时,成为目前国内核电机组数量最多、堆型最丰富、装机最大的核电基地。
风能
势能
三峡大坝,位于中国湖北省宜昌市三斗坪镇境内,是当今世界最大的水利发电工程.
大坝高185米,正常蓄水位175米,水库长2335米,总装机容量2250万千瓦,年发电量达1000亿度,是世界最大水电站。
弹性势能
能量具有不同的形式
动能、势能、电能、化学能、热能、
核能、光能……
不同形式的能量可以互相转化
太阳能转化为化学能(例如植物光合作用)
化学能转化为电能(例如电池供电)
电能转化为光能(例如灯泡)
动能转化为热能(例如摩擦生热)
……
“有一个事实,如果你愿意,也可以说一条定律,支配着至今所知的一切自然现象……这条定律称做能量守恒定律。它指出某一个量,我们把它称为能量,在自然界经历的多种多样的变化中它不变化。那是一个最抽象的概念……”
——诺贝尔物理学奖获得者费恩曼
“能量”是牛顿没有留给我们的少数力学概念之一。
伽利略理想斜面实验
伽利略理想斜面实验
忽略小球与斜面
体的摩擦
忽略空气阻力
忽略小球从斜面过渡到平面时的能量损失
A
B
h
h
用所学知识证明:
α
β
v
v
好像小球能“记住”自己原来的初始高度
伽利略斜面实验表明,小球在运动过程中,“有某一量是守恒的”,这个量叫做能量或能。
说明:能量与物体的运动相对应,是对物体不同运动形式的统一的量度,不同的运动形式对应不同的能量。
能量
相互作用的物体凭借其位置而具有的能,叫做势能。
又叫位能。
弹性势能
重力势能
它们具有重力势能
球
杠铃
被弹高的人
它们具有弹性势能
起跳时的跳板
物体由于运动而具有的能,叫做动能。
它们都具有动能
足球
汽车
火箭
能量的转化
O→P:重力势能EP减少,动能Ek增加
P→Q:动能Ek减少,重力势能Ep增加
Ek+Ep=常数
O
Q
P
A
B
hB
hA
追寻守恒量——能量
机械能
弹簧
轻质弹簧原长为L0,一端固定于墙壁,另一端连接质量为m的小球.现将弹簧拉长至L(L>L0),由静止释放.忽略摩擦和空气阻力.
L0
L
弹性势能EP弹=1/2·kx2
x为弹簧形变量
A→O:
Ek增加,EP弹减少
O→B:
Ek减少,EP弹增加
Ek+EP弹=常数
lOA=lOB
·
·
·
A
O
B
L
L0
1.
下列实例中,动能转化为势能的是
(
)
A.
竖直上抛的正在上升的小球.
B.
上紧发条的玩具汽车正在行驶.
C.
从高处下落的石块.
D.
从斜槽上滚下的小球.
A
课堂练习
解析:B、C、D中均为势能转化为动能.
A中为重力势能转化为小球的动能.
2.苹果从树上掉下时,速度越来越大,忽略空气阻力,正确的是(
)
A.高度转变成了速度
B.苹果的能量增加
C.势能转变成了动能
D.苹果的机械能增加
C
长度可以用尺子——多少米来量度;
质量可以天平——多少千克来来量度;
势能和动能的转化又是怎么进行量度的呢?
课后探究
功
功
2
2
功是能量转化的量度
重力势能增大
动能增大
弹性势能增大
如果物体在力的作用下能量发生了变化,那么这个力一定对物体做了功。
一、功
笔记时间
1.定义:一个物体受到力的作用,并在力的方向上发生一段距离,这个力就对物体做了功。
2.做功的两要素:力和物体在力的方向上发生的位移。
劳而无功
(有力无距)
徒劳无功
(有力有距,但力⊥距)
力与位移方向相同,力做功
F
l
纹丝不动
真辛苦!!
l
笔记时间
3.公式:
F
l
(1)力和位移在同一方向上:
(2)力和位移不在同一方向上:
F
F1=Fcosα
F2=Fsinα
α
l
笔记时间
F
α
物体相对于地面的位移
力与位移的夹角
仅适用于恒力
4.单位:焦耳,简称”焦”,符号是”J”
(1J等于1N的力在力方向上移动1m位移时所做的功
)
D
笔记时间
5.标量:只有大小没有方向,但有正负之分。
正负既不表示大小也不表示方向,正负表示的是动力还是阻力。
l
力不做功。
l
力做正功。
动力
向物体提供能量
l
力做负功。
阻力
物体向外输出能量
F
α
α
例:
平移到同一个点
BC
FN
fBA
fAB
F压
lA=0
α=900
l
笔记时间
6.理解:
(1)功只与力的大小、位移的大小以及力与位移的夹角有关,与物体的质量、运动状态无关。
(2)功是过程量,反映了力在空间上的积累效果,对应着一段位移或一个过程。
F
α
(3)比较功的大小时,只需比较绝对值即可。
例如:
笔记时间
(4)力对物体做负功,也可以说成物体克服这个力做功(取绝对值)。
(5)功的表达式还可以理解成:
例如:重力对物体做功-10J,也可以说成物体克服重力做功10J.
l
F
F1
F2
α
功等于位移方向上的分力与位移的乘积。
功等于力与力方向分位移的乘积。
笔记时间
(6)重力做功公式:
注:重力做的功等于重力与下落(或上升)高度的乘积。
7.总功的计算方法:
方法一:先求出这几个力的合力
F合
的大小和方向,再求合力
F合
所做的功,即为总功。
方法二:先求出各个力所做的功,再求其代数和。
W总
=
F合
l
cos
α
W总
=
W1+W2+……+Wn
仅适用于合力为恒力的情况
功是标量,遵循算术法则
解:对雪橇受力分析,有牛二得
x
F
α
mg
FN
f
F2
F1
各个力的功为
由运动学公式得位移为
总功为
另一种方法
笔记时间
1.动摩擦力和静摩擦力都可以做正功、做负功、不做功,即可以是动力也可以是阻力。
二、几个特殊力的功
v
A
B
f动
f动
B固定不动
l
1800
f动不做功
f动做负功
F
地面光滑
f动
lA
1800
lB
f动做负功
f动做正功
f动
f1
f2
l
l
f静不做功
f静做正功
l
l
f静做负功
笔记时间
2.一对相互作用的动摩擦力做功的代数和为负值;
一对相互作用的静摩擦力做功的代数和为0。
v0
x1
x2
L
f
f
f1
f2
l
l
α
180-α
v0
x
l
L
μmg
μmg
解:(1)
(2)
(3)
笔记时间
3.作用力与反作用力可以做正功、负功或不做功,彼此之间无关联。
S
N
S
N
F
F
做功情况
作用力
反作用力
相向运动
正功
正功
反向运动
负功
负功
一个靠近,一个静止
正功
不做功
一个远离,一个静止
负功
不做功
例.关于两个物体间的一对作用力和反作用力的做功情况,下列说法正确的是(
)A.作用力做功,反作用力一定做功B.作用力做正功,反作用力一定做负功C.作用力和反作用力可能都做负功D.作用力和反作用力做的功一定大小相等
C
笔记时间
1.平均值法
若变力大小随位移均匀变化,且方向不变时,可用变力初、末状态的平均值计算功
三、变力做功的几种方法
满足F=kx的关系
解:水平力等于弹簧的弹力,则
拉力F=kx,拉力与位移成正比(拉力随位移均匀变化),则拉力的平均值为
则
笔记时间
2.图像法
F-x图像的面积表示力做的功.
第一象限面积取正值,代表力做正功;
第四象限面积为负值,代表力做负功.
O
x
F
f
F
O
x
F
O
x
F
解:力F对物体做的功等于l轴上方的正功(梯形“面积”)与l轴下方的负功(三角形“面积”)的代数和
所以力F对物体做的功为:
笔记时间
3.微元法
适应对象:当力的大小不变,力的方向时刻与速度同向或反向时.
解题方法:可用微元法将曲线分成无限个小元段,每一小元段可认为恒力做功,总功即为各个小元段做功的代数和.
解:(1)将圆弧AB分成很多小段l1、l2、…、ln,拉力在每小段上做的功为W1、W2、…、Wn,因拉力F大小不变,方向始终与物体所在位置的切线方向成37°,所以:W1=Fl1cos
37°,W2=Fl2cos
37°,…,Wn=Flncos
37°,所以
(2)
h
Rcos600
(3)
物体受的支持力FN始终与物体的运动方向垂直,所以WN=0
FN
v
BD
笔记时间
4.转换研究对象法
①分段转换法:力在全程是变力,但在每一个阶段是恒力,这样就可以先计算每个阶段的功,再利用求和的方法计算整个过程中变力做的功.
②等效替换法:若某一变力的功和某一恒力的功相等,则可以用求得的恒力的功来作为变力的功.
解:由几何关系得,绳子右端运动的位移为
h
x2
x1
在物体从A移到B的过程中,恒力F做的功为
故绳的拉力对物体所做的功为50
J
课堂小结
谢谢聆听
