人教版高中物理 选修3-5 第十六章 16.3 动量守恒定律(共25张PPT)
文档属性
| 名称 | 人教版高中物理 选修3-5 第十六章 16.3 动量守恒定律(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-07-17 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
动量守恒定律
3
3
为什么贝拉扔手臂能回到空间站?
1.系统:存在相互作用的几个物体所组成的整体称为系统,系统可按解决问题的需要灵活选取。
2.内力:系统内各个物体间相互用力称为内力。
3.外力:系统外其他物体作用在系统内任何一个物体上的力称为外力。
内力和外力的区分依赖于系统的选取,只有在确定了系统后,才能确定内力和外力。
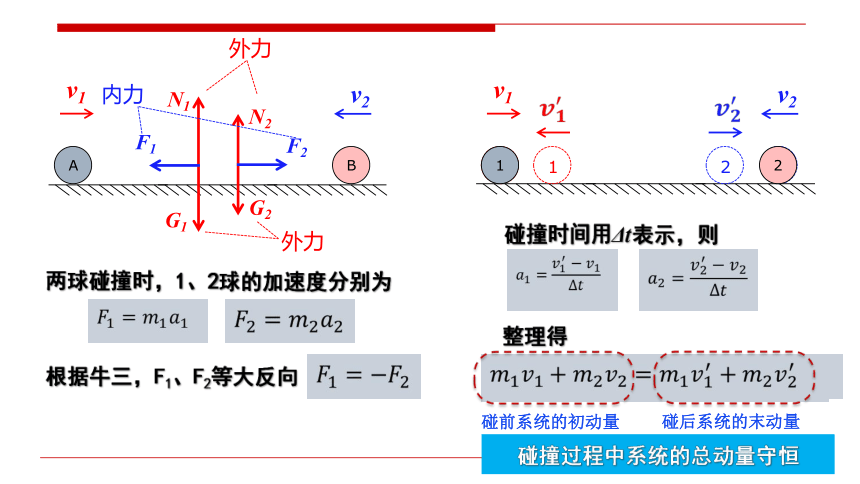
v1
v2
1
2
1
2
v1
v2
A
B
G1
N1
G2
N2
F1
F2
外力
外力
内力
两球碰撞时,1、2球的加速度分别为
根据牛三,F1、F2等大反向
碰撞时间用Δt表示,则
整理得
碰前系统的初动量
碰后系统的末动量
碰撞过程中系统的总动量守恒
笔记时间
1.内容:如果一个系统不受外力,或者所受外力的矢量和为零,
这个系统的总动量保持不变。
一、动量守恒定律
2.表达式:
3.守恒条件及实例
①系统不受外力;
①解题时选取正方向后用正、负来表示方向,将矢量运算变为代数运算。
理想化模型,实际不存在。
②守恒是指系统总动量的大小、方向时时刻刻保持不变,而单个物体的动量可以变化;
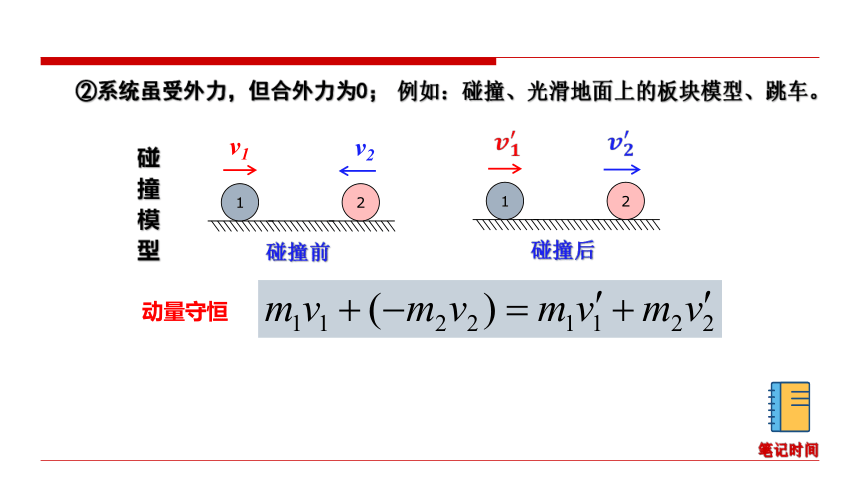
碰撞模型
v1
v2
1
2
碰撞前
②系统虽受外力,但合外力为0;
例如:碰撞、光滑地面上的板块模型、跳车。
1
2
碰撞后
笔记时间
动量守恒
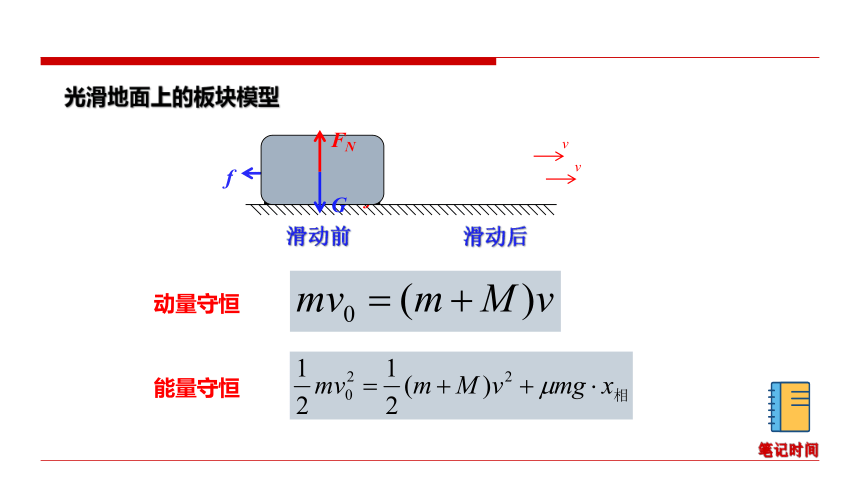
光滑地面上的板块模型
笔记时间
M
m
v0
f
f
G
FN
v
v
滑动前
滑动后
动量守恒
能量守恒
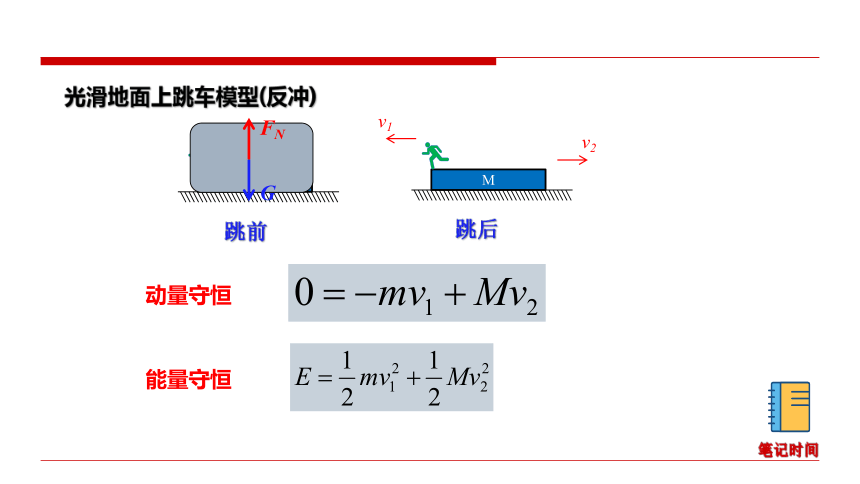
光滑地面上跳车模型(反冲)
笔记时间
M
动量守恒
能量守恒
G
FN
跳前
M
跳后
v1
v2
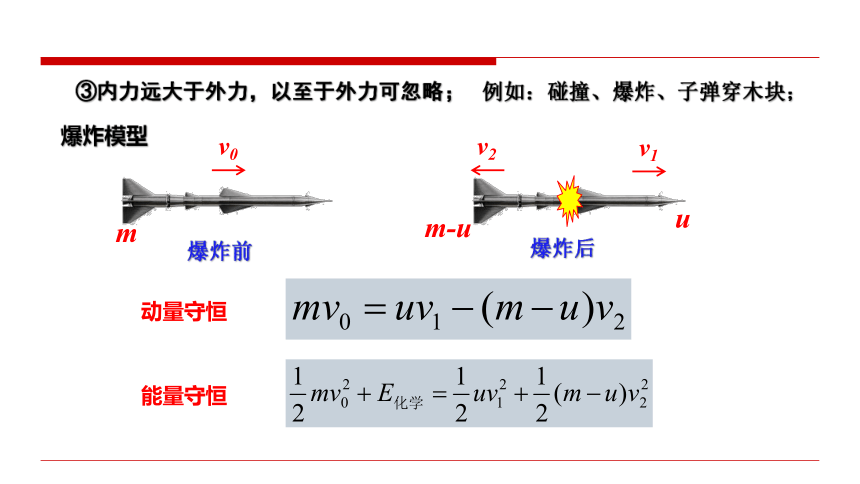
③内力远大于外力,以至于外力可忽略;
例如:碰撞、爆炸、子弹穿木块;
爆炸模型
v0
爆炸前
v1
v2
爆炸后
动量守恒
能量守恒
m
u
m-u
子弹穿木块模型
穿前
穿后
动量守恒
能量守恒
v0
m
M
v
v
x相
④系统虽合外力不为0,但在某一方向上合外力为0,则在这个方向上动量守恒;
初状态
G
FN
末状态
m
M
v2
v1
水平方向上动量守恒
能量守恒
地面光滑
4.动量守恒定律解题的一般步骤:
(1)明确题意,明确研究对象;
(2)受力分析,判断是否守恒;
(3)确定动量守恒系统的作用前总动量和作用后总动量;
(4)选定正方向根据动量守恒定律列出方程;
(5)解方程,得出结论。
5.动量守恒定律的普适性
①动量守恒定律是由牛顿第二、第三定律导出的,两者关系密切,在经典力学中都占有及其重要的地位。牛顿运动定律从“力”的角度反映物体间的相互作用;动量守恒定律从“动量”的角度描述物体间的相互作用。
②动量守恒定律是一个独立的实验定律,它的结论完全由实验决定。虽然它可有牛顿运动定律推导出来,但它并不依赖牛顿运动定律。
③用牛顿运动定律解决问题要涉及总个过程的力,有时候解决起来比较复杂,而动量守恒定律只涉及过程始末两个状态,与过程力的细节无关,能是问题大大简化。
④动量守恒定律比牛顿定律更普遍,它适用目前为止的物理学研究的一切领域,即不仅适用于宏观、低速领域,而且也适用于微观、高速领域。
1.内容:不受外力或者合外力为零,
这个系统的总动量保持不变。
一、动量守恒定律
2.表达式:
3.守恒条件及实例
①系统不受外力;
?
理想化模型,实际不存在。
②系统虽受外力,但合外力为0;
例如:碰撞、光滑地面上的板块模型、跳车。
③内力远大于外力,以至于外力可忽略;
例如:碰撞、爆炸、子弹穿木块;
④系统虽合外力不为0,但在某一方向上合外力为0,则在这个方向上动量守恒;
4.动量守恒定律解题的一般步骤:
5.动量守恒定律的普适性
初状态
v1
v2
末状态
动量守恒
动量守恒定律
3
3
为什么贝拉扔手臂能回到空间站?
1.系统:存在相互作用的几个物体所组成的整体称为系统,系统可按解决问题的需要灵活选取。
2.内力:系统内各个物体间相互用力称为内力。
3.外力:系统外其他物体作用在系统内任何一个物体上的力称为外力。
内力和外力的区分依赖于系统的选取,只有在确定了系统后,才能确定内力和外力。
v1
v2
1
2
1
2
v1
v2
A
B
G1
N1
G2
N2
F1
F2
外力
外力
内力
两球碰撞时,1、2球的加速度分别为
根据牛三,F1、F2等大反向
碰撞时间用Δt表示,则
整理得
碰前系统的初动量
碰后系统的末动量
碰撞过程中系统的总动量守恒
笔记时间
1.内容:如果一个系统不受外力,或者所受外力的矢量和为零,
这个系统的总动量保持不变。
一、动量守恒定律
2.表达式:
3.守恒条件及实例
①系统不受外力;
①解题时选取正方向后用正、负来表示方向,将矢量运算变为代数运算。
理想化模型,实际不存在。
②守恒是指系统总动量的大小、方向时时刻刻保持不变,而单个物体的动量可以变化;
碰撞模型
v1
v2
1
2
碰撞前
②系统虽受外力,但合外力为0;
例如:碰撞、光滑地面上的板块模型、跳车。
1
2
碰撞后
笔记时间
动量守恒
光滑地面上的板块模型
笔记时间
M
m
v0
f
f
G
FN
v
v
滑动前
滑动后
动量守恒
能量守恒
光滑地面上跳车模型(反冲)
笔记时间
M
动量守恒
能量守恒
G
FN
跳前
M
跳后
v1
v2
③内力远大于外力,以至于外力可忽略;
例如:碰撞、爆炸、子弹穿木块;
爆炸模型
v0
爆炸前
v1
v2
爆炸后
动量守恒
能量守恒
m
u
m-u
子弹穿木块模型
穿前
穿后
动量守恒
能量守恒
v0
m
M
v
v
x相
④系统虽合外力不为0,但在某一方向上合外力为0,则在这个方向上动量守恒;
初状态
G
FN
末状态
m
M
v2
v1
水平方向上动量守恒
能量守恒
地面光滑
4.动量守恒定律解题的一般步骤:
(1)明确题意,明确研究对象;
(2)受力分析,判断是否守恒;
(3)确定动量守恒系统的作用前总动量和作用后总动量;
(4)选定正方向根据动量守恒定律列出方程;
(5)解方程,得出结论。
5.动量守恒定律的普适性
①动量守恒定律是由牛顿第二、第三定律导出的,两者关系密切,在经典力学中都占有及其重要的地位。牛顿运动定律从“力”的角度反映物体间的相互作用;动量守恒定律从“动量”的角度描述物体间的相互作用。
②动量守恒定律是一个独立的实验定律,它的结论完全由实验决定。虽然它可有牛顿运动定律推导出来,但它并不依赖牛顿运动定律。
③用牛顿运动定律解决问题要涉及总个过程的力,有时候解决起来比较复杂,而动量守恒定律只涉及过程始末两个状态,与过程力的细节无关,能是问题大大简化。
④动量守恒定律比牛顿定律更普遍,它适用目前为止的物理学研究的一切领域,即不仅适用于宏观、低速领域,而且也适用于微观、高速领域。
1.内容:不受外力或者合外力为零,
这个系统的总动量保持不变。
一、动量守恒定律
2.表达式:
3.守恒条件及实例
①系统不受外力;
?
理想化模型,实际不存在。
②系统虽受外力,但合外力为0;
例如:碰撞、光滑地面上的板块模型、跳车。
③内力远大于外力,以至于外力可忽略;
例如:碰撞、爆炸、子弹穿木块;
④系统虽合外力不为0,但在某一方向上合外力为0,则在这个方向上动量守恒;
4.动量守恒定律解题的一般步骤:
5.动量守恒定律的普适性
初状态
v1
v2
末状态
动量守恒
