三年级下册数学教案-7.5 整理与提高 数学广场(谁围出的面积更大) 沪教版
文档属性
| 名称 | 三年级下册数学教案-7.5 整理与提高 数学广场(谁围出的面积更大) 沪教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 17.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-14 00:00:00 | ||
图片预览

文档简介
学科:数学
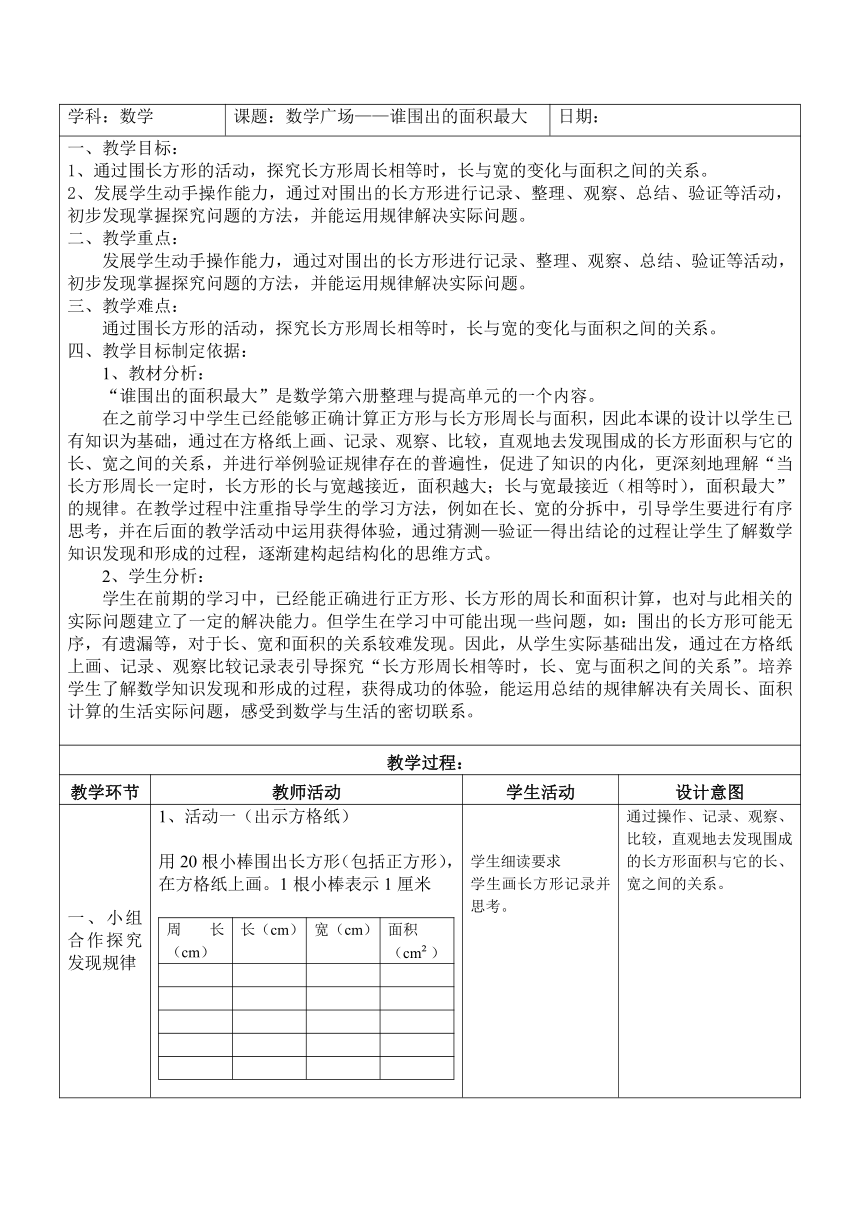
课题:数学广场——谁围出的面积最大
日期:
一、教学目标:
1、通过围长方形的活动,探究长方形周长相等时,长与宽的变化与面积之间的关系。
2、发展学生动手操作能力,通过对围出的长方形进行记录、整理、观察、总结、验证等活动,初步发现掌握探究问题的方法,并能运用规律解决实际问题。
二、教学重点:
发展学生动手操作能力,通过对围出的长方形进行记录、整理、观察、总结、验证等活动,初步发现掌握探究问题的方法,并能运用规律解决实际问题。
教学难点:
通过围长方形的活动,探究长方形周长相等时,长与宽的变化与面积之间的关系。
四、教学目标制定依据:
1、教材分析:
“谁围出的面积最大”是数学第六册整理与提高单元的一个内容。
在之前学习中学生已经能够正确计算正方形与长方形周长与面积,因此本课的设计以学生已有知识为基础,通过在方格纸上画、记录、观察、比较,直观地去发现围成的长方形面积与它的长、宽之间的关系,并进行举例验证规律存在的普遍性,促进了知识的内化,更深刻地理解“当长方形周长一定时,长方形的长与宽越接近,面积越大;长与宽最接近(相等时),面积最大”的规律。在教学过程中注重指导学生的学习方法,例如在长、宽的分拆中,引导学生要进行有序思考,并在后面的教学活动中运用获得体验,通过猜测—验证—得出结论的过程让学生了解数学知识发现和形成的过程,逐渐建构起结构化的思维方式。
2、学生分析:
学生在前期的学习中,已经能正确进行正方形、长方形的周长和面积计算,也对与此相关的实际问题建立了一定的解决能力。但学生在学习中可能出现一些问题,如:围出的长方形可能无序,有遗漏等,对于长、宽和面积的关系较难发现。因此,从学生实际基础出发,通过在方格纸上画、记录、观察比较记录表引导探究“长方形周长相等时,长、宽与面积之间的关系”。培养学生了解数学知识发现和形成的过程,获得成功的体验,能运用总结的规律解决有关周长、面积计算的生活实际问题,感受到数学与生活的密切联系。
教学过程:
教学环节
教师活动
学生活动
设计意图
一、小组合作探究发现规律
1、活动一(出示方格纸)
用20根小棒围出长方形(包括正方形),在方格纸上画。1根小棒表示1厘米
周长(cm)
长(cm)
宽(cm)
面积
(cm?)
2、呈现资源(投影出示记录表)
(1)围出了几个长方形(手势表示)?
(对比记录表)
你能看懂他是怎样围的吗?
(强调有序记录)
(2)观察记录表,小组讨论,发现了什么?
引导:怎么围,面积会大一些?
长和宽的相差数的变化与面积的大小有什么关系?
(相差数为0时,面积最大)
3、小结:
长方形周长相等,面积不一定相等。
长和宽越接近,面积越大。长和宽最接近(长=宽,正方形)时,面积最大。(板书)
4、今天我们探究的就是当长方形周长相等时,怎样围面积最大。(板书课题)
学生细读要求
学生画长方形记录并思考。
学生讨论交流
观察表1,小组讨论
发现:长方形周长相等,面积不一定相等。长和宽越接近,面积越大。长和宽最接近(长=宽,正方形)时,面积最大。
通过操作、记录、观察、比较,直观地去发现围成的长方形面积与它的长、宽之间的关系。
给予孩子充分的时间去观察、讨论、发现、交流、归纳。
二、验证规律
1、质疑:周长20厘米围出的长方形符合这句话,那其他周长的长方形是否符合呢?
2、活动二
任意确定周长,围出长方形,看看是否符合刚才得出的结论。
确定周长____ __cm
长(cm)
宽(cm)
面积(cm?)
小组交流讨论验证2句话。
4、资源呈现(投影学生记录表)
学生能围出正方形的:24cm,32cm……
学生不能围出正方形的:22cm,26cm……
(对于没有写完可帮助一起解决。)
5、(第二类)是否可以让长和宽最接近些,得到面积最大的正方形呢?
(相差数为0 ,长=宽)
6、小组讨论,动手操作:能不能用不同长度的铁丝围出面积最大的长方形。
7、总结规律(齐读)
学生进行举例验证
小组交流反馈
学生资源呈现,进行拓展学习
学生动手用铁丝围正方形。(对折再对折,折成正方形)
学生齐读规律
通过举例操作,验证规律存在的普遍性,促进了知识的内化,更深刻地理解“当长方形周长一定时,长方形的长与宽越接近,面积越大;长和宽相等时(正方形)时,面积最大。”的规律。培养学生初步探究问题的方法,获得成功的体验。
通过小组交流让学生从个别的结论通过小组活动得到规律的普遍性。
三、应用规律解决问题
解决实际问题
(1)公园里叔叔要用24米长的铁栏杆来围一个长方形花坛,怎样围面积最大?
(2)如果利用两面墙,叔叔仍用24米长的铁栏杆来围一个长方形花坛,怎样围面积最大?
学生练习巩固认识规律,全班交流
生:围正方形面积最大,所以24÷4=6米,6×6=36平方米
生:围正方形面积最大,所以24÷2=12米,12×12=144平方米
利用数学知识解决生活问题,学生感受数学在生活中的应用。
课题:数学广场——谁围出的面积最大
日期:
一、教学目标:
1、通过围长方形的活动,探究长方形周长相等时,长与宽的变化与面积之间的关系。
2、发展学生动手操作能力,通过对围出的长方形进行记录、整理、观察、总结、验证等活动,初步发现掌握探究问题的方法,并能运用规律解决实际问题。
二、教学重点:
发展学生动手操作能力,通过对围出的长方形进行记录、整理、观察、总结、验证等活动,初步发现掌握探究问题的方法,并能运用规律解决实际问题。
教学难点:
通过围长方形的活动,探究长方形周长相等时,长与宽的变化与面积之间的关系。
四、教学目标制定依据:
1、教材分析:
“谁围出的面积最大”是数学第六册整理与提高单元的一个内容。
在之前学习中学生已经能够正确计算正方形与长方形周长与面积,因此本课的设计以学生已有知识为基础,通过在方格纸上画、记录、观察、比较,直观地去发现围成的长方形面积与它的长、宽之间的关系,并进行举例验证规律存在的普遍性,促进了知识的内化,更深刻地理解“当长方形周长一定时,长方形的长与宽越接近,面积越大;长与宽最接近(相等时),面积最大”的规律。在教学过程中注重指导学生的学习方法,例如在长、宽的分拆中,引导学生要进行有序思考,并在后面的教学活动中运用获得体验,通过猜测—验证—得出结论的过程让学生了解数学知识发现和形成的过程,逐渐建构起结构化的思维方式。
2、学生分析:
学生在前期的学习中,已经能正确进行正方形、长方形的周长和面积计算,也对与此相关的实际问题建立了一定的解决能力。但学生在学习中可能出现一些问题,如:围出的长方形可能无序,有遗漏等,对于长、宽和面积的关系较难发现。因此,从学生实际基础出发,通过在方格纸上画、记录、观察比较记录表引导探究“长方形周长相等时,长、宽与面积之间的关系”。培养学生了解数学知识发现和形成的过程,获得成功的体验,能运用总结的规律解决有关周长、面积计算的生活实际问题,感受到数学与生活的密切联系。
教学过程:
教学环节
教师活动
学生活动
设计意图
一、小组合作探究发现规律
1、活动一(出示方格纸)
用20根小棒围出长方形(包括正方形),在方格纸上画。1根小棒表示1厘米
周长(cm)
长(cm)
宽(cm)
面积
(cm?)
2、呈现资源(投影出示记录表)
(1)围出了几个长方形(手势表示)?
(对比记录表)
你能看懂他是怎样围的吗?
(强调有序记录)
(2)观察记录表,小组讨论,发现了什么?
引导:怎么围,面积会大一些?
长和宽的相差数的变化与面积的大小有什么关系?
(相差数为0时,面积最大)
3、小结:
长方形周长相等,面积不一定相等。
长和宽越接近,面积越大。长和宽最接近(长=宽,正方形)时,面积最大。(板书)
4、今天我们探究的就是当长方形周长相等时,怎样围面积最大。(板书课题)
学生细读要求
学生画长方形记录并思考。
学生讨论交流
观察表1,小组讨论
发现:长方形周长相等,面积不一定相等。长和宽越接近,面积越大。长和宽最接近(长=宽,正方形)时,面积最大。
通过操作、记录、观察、比较,直观地去发现围成的长方形面积与它的长、宽之间的关系。
给予孩子充分的时间去观察、讨论、发现、交流、归纳。
二、验证规律
1、质疑:周长20厘米围出的长方形符合这句话,那其他周长的长方形是否符合呢?
2、活动二
任意确定周长,围出长方形,看看是否符合刚才得出的结论。
确定周长____ __cm
长(cm)
宽(cm)
面积(cm?)
小组交流讨论验证2句话。
4、资源呈现(投影学生记录表)
学生能围出正方形的:24cm,32cm……
学生不能围出正方形的:22cm,26cm……
(对于没有写完可帮助一起解决。)
5、(第二类)是否可以让长和宽最接近些,得到面积最大的正方形呢?
(相差数为0 ,长=宽)
6、小组讨论,动手操作:能不能用不同长度的铁丝围出面积最大的长方形。
7、总结规律(齐读)
学生进行举例验证
小组交流反馈
学生资源呈现,进行拓展学习
学生动手用铁丝围正方形。(对折再对折,折成正方形)
学生齐读规律
通过举例操作,验证规律存在的普遍性,促进了知识的内化,更深刻地理解“当长方形周长一定时,长方形的长与宽越接近,面积越大;长和宽相等时(正方形)时,面积最大。”的规律。培养学生初步探究问题的方法,获得成功的体验。
通过小组交流让学生从个别的结论通过小组活动得到规律的普遍性。
三、应用规律解决问题
解决实际问题
(1)公园里叔叔要用24米长的铁栏杆来围一个长方形花坛,怎样围面积最大?
(2)如果利用两面墙,叔叔仍用24米长的铁栏杆来围一个长方形花坛,怎样围面积最大?
学生练习巩固认识规律,全班交流
生:围正方形面积最大,所以24÷4=6米,6×6=36平方米
生:围正方形面积最大,所以24÷2=12米,12×12=144平方米
利用数学知识解决生活问题,学生感受数学在生活中的应用。
