五年级下册数学课件-5.4 解方程 西师大版 (共19张PPT)
文档属性
| 名称 | 五年级下册数学课件-5.4 解方程 西师大版 (共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-14 22:09:28 | ||
图片预览






文档简介
解 方 程
第1课时
学习目标
1、知道解方程的意义和基本思路。
2、会运用数量关系式或等式的性质对解方程的过程进行语言描述。
3、掌握解方程的方法,会检验方程的解是否正确。
复习
什么是等式?请举例说明。
什么是方程?请举例说明。
等式和方程有什么关系?
方程一定是等式,
但等式不一定是方程。
等式
方程
表示相等关系的式子都叫做等式。
含有未知数的等式叫做方程。
写出等式:
(1)25加上x等于35;
(2)8a等于2b减去21;
(3)15的4倍等于60;
(4)3y减去15等于15。
(1)25+x=35;
(2)8a=2b - 21;
(3)15 × 4=60;
(4)3y - 15=15。
这些等式里,哪些是方程?哪些不是方程?
课堂探索
x+50=200
X=?
平衡
课堂探索
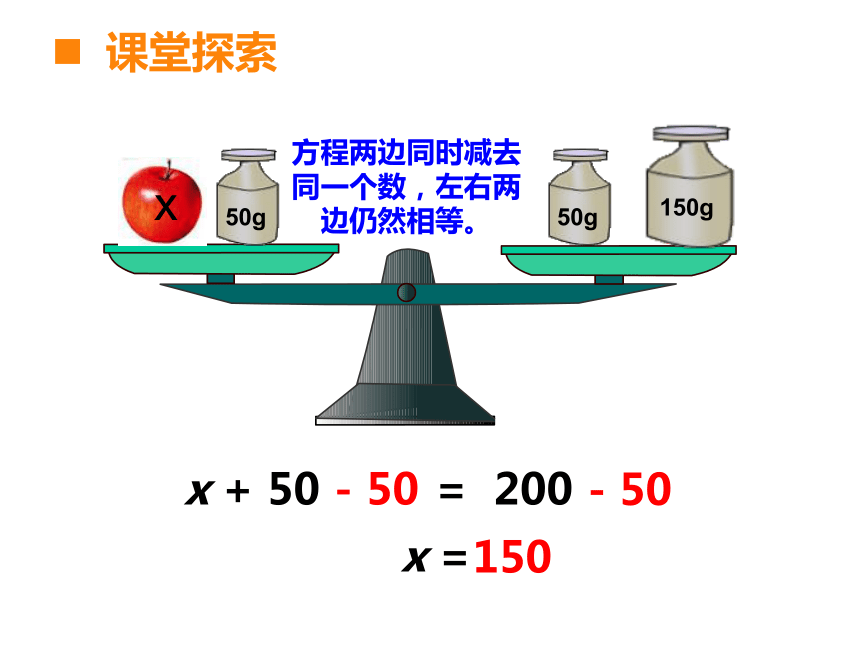
x + 50 = 200
x =
- 50
- 50
150
x
50g
50g
150g
方程两边同时减去同一个数,左右两边仍然相等。
课堂探索
x+50=200
x=150
方程左边=x+50
=150+50
=200
=方程右边
所以,x=150是方程的解。
x=150是不是正确答
案呢?验算一下。
当X=150时,X+50=200这个方程的左右两边会相等,像这样使方程相等的未知数的值,叫做方程的解。
总结:
求出方程中未知数的值,也就是求出方程的解,求方程的解的过程叫解方程。
课堂总结——思考
方程的解和解方程有
什么区别?
方程的解是使方程两边相等的未知数的值,它是一个数。
区别方程的解和解方程
解方程是指解未知数的值的计算过程,它是一个计算过程。
试一试 解方程x -25=60
X+a=b,通常两边同时减去a,求出x的值。
X - a=b,通常两边同时加上a,求出x的值。
课堂探索
解方程3x=150
想:3x÷( )=150÷( )
方程两边同时除以同一个不等于0的数,左右两边仍然相等。
课堂探索
x=50
解方程3x=150
想:3x÷(3 )=150÷(3 )
检验一下吧!
3x=150
解:3x ÷ 3=150 ÷3
x=50
检验:
把x=50代入原方程,
左边=3 ×50
=150
=右边
所以x=50是方程的解
试一试 解方程x ÷4=10
aX=b,通常两边同时除以a,求出x的值。
X ÷ a=b,通常两边同时乘a,求出x的值。
课堂练习
填空。
(1)使方程左右两边相等的( )
叫做方程的解。
(2)求方程的解的过程叫做( )。
(3)比x 多5的数是10。列方程为( )。
(4)8与x 的和是56。列方程为( )。
未知数的值
解方程
x+5=10
8+x=56
判断:
(1)等式就是方程。 ( )
(2)含有未知数的式子叫做方程。 ( )
(3)方程一定是等式,等式不一定是方程。( )
(4)x=0是方程8x=0的解。 ( )
(5)方程的解和解方程的意义相同。 ( )
√
√
╳
╳
╳
(1)8X=16.8
(2)(Y+4)X2=18
解:8X÷8=16.8÷8
解:(Y+4)X2÷2=18÷2
X=2.1
(Y+4)=9
Y+4-4=9-4
Y=5
解方程
通过这节课的学习,你学到了什么?
课堂总结
第1课时
学习目标
1、知道解方程的意义和基本思路。
2、会运用数量关系式或等式的性质对解方程的过程进行语言描述。
3、掌握解方程的方法,会检验方程的解是否正确。
复习
什么是等式?请举例说明。
什么是方程?请举例说明。
等式和方程有什么关系?
方程一定是等式,
但等式不一定是方程。
等式
方程
表示相等关系的式子都叫做等式。
含有未知数的等式叫做方程。
写出等式:
(1)25加上x等于35;
(2)8a等于2b减去21;
(3)15的4倍等于60;
(4)3y减去15等于15。
(1)25+x=35;
(2)8a=2b - 21;
(3)15 × 4=60;
(4)3y - 15=15。
这些等式里,哪些是方程?哪些不是方程?
课堂探索
x+50=200
X=?
平衡
课堂探索
x + 50 = 200
x =
- 50
- 50
150
x
50g
50g
150g
方程两边同时减去同一个数,左右两边仍然相等。
课堂探索
x+50=200
x=150
方程左边=x+50
=150+50
=200
=方程右边
所以,x=150是方程的解。
x=150是不是正确答
案呢?验算一下。
当X=150时,X+50=200这个方程的左右两边会相等,像这样使方程相等的未知数的值,叫做方程的解。
总结:
求出方程中未知数的值,也就是求出方程的解,求方程的解的过程叫解方程。
课堂总结——思考
方程的解和解方程有
什么区别?
方程的解是使方程两边相等的未知数的值,它是一个数。
区别方程的解和解方程
解方程是指解未知数的值的计算过程,它是一个计算过程。
试一试 解方程x -25=60
X+a=b,通常两边同时减去a,求出x的值。
X - a=b,通常两边同时加上a,求出x的值。
课堂探索
解方程3x=150
想:3x÷( )=150÷( )
方程两边同时除以同一个不等于0的数,左右两边仍然相等。
课堂探索
x=50
解方程3x=150
想:3x÷(3 )=150÷(3 )
检验一下吧!
3x=150
解:3x ÷ 3=150 ÷3
x=50
检验:
把x=50代入原方程,
左边=3 ×50
=150
=右边
所以x=50是方程的解
试一试 解方程x ÷4=10
aX=b,通常两边同时除以a,求出x的值。
X ÷ a=b,通常两边同时乘a,求出x的值。
课堂练习
填空。
(1)使方程左右两边相等的( )
叫做方程的解。
(2)求方程的解的过程叫做( )。
(3)比x 多5的数是10。列方程为( )。
(4)8与x 的和是56。列方程为( )。
未知数的值
解方程
x+5=10
8+x=56
判断:
(1)等式就是方程。 ( )
(2)含有未知数的式子叫做方程。 ( )
(3)方程一定是等式,等式不一定是方程。( )
(4)x=0是方程8x=0的解。 ( )
(5)方程的解和解方程的意义相同。 ( )
√
√
╳
╳
╳
(1)8X=16.8
(2)(Y+4)X2=18
解:8X÷8=16.8÷8
解:(Y+4)X2÷2=18÷2
X=2.1
(Y+4)=9
Y+4-4=9-4
Y=5
解方程
通过这节课的学习,你学到了什么?
课堂总结
