四年级下册数学课件 加、减法的意义和各部分间的关系( 58页ppt) 人教版
文档属性
| 名称 | 四年级下册数学课件 加、减法的意义和各部分间的关系( 58页ppt) 人教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-14 22:01:19 | ||
图片预览








文档简介
加、减法的意义和各部分关系
在已学过的加、减法知识的基础上,概括出加、减法的意义,并对加、减法的认识从感性上升到理性。
引导学生运用已有经验,通过知识迁移,理解新知,逐步培养学生的逻辑推理能力及运用知识解决问题的能力。
深刻理解加法、减法之间的关系,感悟到数学知识内在联系的逻辑之美。
教学目标
理解加、减法的意义,掌握加法、减法各部分之间的关系及其应用。
从实例中探究加、减法的互逆关系。
教学重点
教学难点
小猴子特别喜欢吃樱桃,第一次吃了 30 个,但是小猴子吃完了还想吃,就又吃了 20 个。
小猴子一共吃了多少个樱桃呢?
第一次比第二次多吃了几个樱桃呢?
复习加法、减法
四(1)班有男生 21 人,女生 17 人,一共有几名学生?
男生 21 人
女生 17 人
一共(? ? )人
21 + 17?
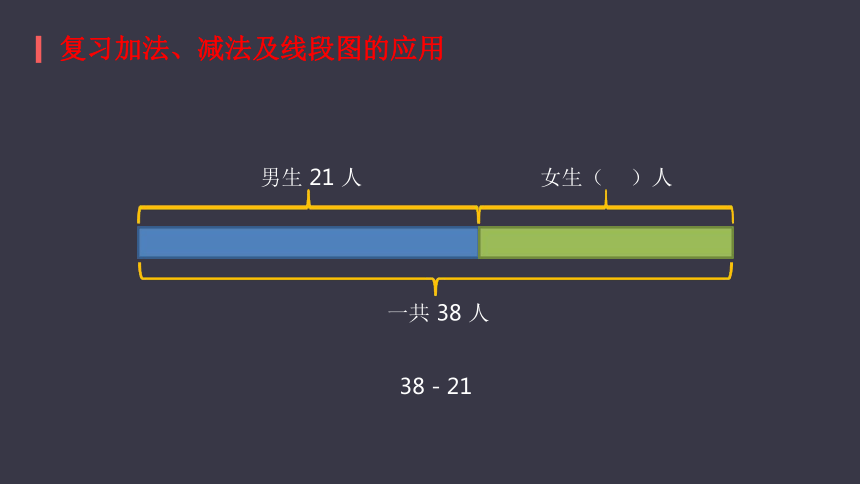
复习加法、减法及线段图的应用
男生 21 人
女生(? ? )人
一共 38 人
38 - 21?
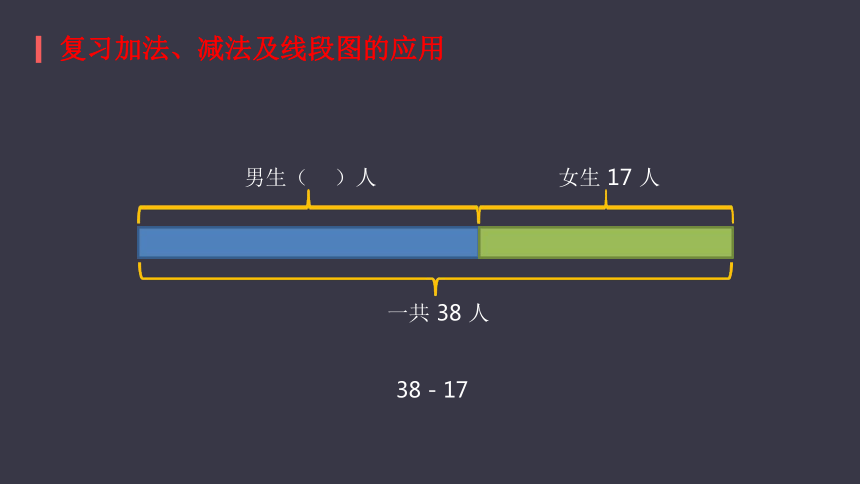
复习加法、减法及线段图的应用
男生(? ? )人
女生 17 人
一共 38 人
38 - 17?
复习加法、减法及线段图的应用
口算
300 + 700 =
1500 - 800 =
2000 + 499 =
1259 - 1000 =
1000
700
2499
259
复习加法、减法口算笔算
笔算
1945 + 367 =
3406 - 2789 =
1945
+
367
2
2312
3406
2789
-
6
1
7
617
2
3
1
1
1
1
复习加法、减法口算笔算
一列火车从西宁经过格尔木开往拉萨。西宁到格尔木的铁路长 814km,格尔木到拉萨的铁路长 1142km。西宁到拉萨的铁路长多少千米?
加法解决问题
一列火车从西宁经过格尔木开往拉萨。西宁到格尔木的铁路长 814km,格尔木到拉萨的铁路长 1142km。西宁到拉萨的铁路长多少千米?
问题:
1. 读题,你知道了什么??
2. 用线段图表示题目中的数量关系。
已知西宁到格尔木的路程和格尔木到拉萨的路程,要求西宁到拉萨的路程。
加法解决问题
一列火车从西宁经过格尔木开往拉萨。西宁到格尔木的铁路长 814km,格尔木到拉萨的铁路长 1142km。西宁到拉萨的铁路长多少千米?
西宁到拉萨的铁路长多少km?
问题:
1. 说一说你是怎样画线段图的。
2. “ 西宁到拉萨的铁路长 ” 在图上怎样表示?
3. 求西宁到拉萨的铁路长多少千米,用什么方法?你是怎么想的?
加法解决问题
一列火车从西宁经过格尔木开往拉萨。西宁到格尔木的铁路长 814km,格尔木到拉萨的铁路长 1142km。西宁到拉萨的铁路长多少千米?
814 + 1142
加数+
加数
= 和
把两个数合并成一个数的运算,叫做? ? ? ? 。
加法
相加的两个数叫做? ? ? ? 。
加数
加得的数叫做? ? 。
和
= 1956(千米)
加法解决问题
西宁到格尔木的距离+格尔木到拉萨的距离=西宁到拉萨的距离
814 + 1142
加数+
加数
= 和
= 1956?
问题:
如果知道和与一个加数,能求出另一个加数吗?
一个加数 = 和 - 另一个加数
加法各部分关系
填空并观察三个算式中各部分之间的关系:
加数 + 加数 = 和
58? ?+? ?61? ?=(? ? )?
(? ? )=? 119? -? 58
(? ? )=? 119? -? 61
和 = 加数 + 加数
一个加数 = 和 - 另一个加数
?
?
?
119
61
58
加法各部分关系
一个数同0相加结果怎样?
一个数同0相加还得(这个数)。
线段图哪里变了?哪里没变?
西宁到拉萨的铁路全长 1956km,其中格尔木到拉萨长 1142km。
西宁到格尔木的铁路长多少千米?
减法解决问题
西宁到拉萨的铁路全长 1956km,其中西宁到格尔木长 814km。
格尔木到拉萨的铁路长多少千米?
西宁到拉萨的铁路长 1956km
问题:
① 读题,你知道了什么??
② 求格尔木到拉萨的铁路长多少千米,用什么方法?你是怎么想的?
1956 - 814=1142(千米)
已知西宁到拉萨的路程和西宁到格尔木的路程,要求格尔木到拉萨的路程。
减法解决问题
西宁到拉萨的距离-西宁到格尔木的距离=格尔木到拉萨的距离
西宁到拉萨的铁路全长 1956km,其中格尔木到拉萨长1142km。
西宁到格尔木的铁路长多少千米?
西宁到拉萨的铁路长 1956km
问题:
求西宁到格尔木的铁路长多少千米,用什么方法?
你是怎么想的?
1956 - 1142 = 814(千米)
减法解决问题
西宁到拉萨的距离-格尔木到拉萨的距离=西宁到格尔木的距离
(1)一列火车从西宁经过格尔木开往拉萨。西宁到格尔木的铁路长 814km,格尔木到拉萨的铁路长 1142km。西宁到拉萨的铁路长多少千米?
814+1142=1956(千米)
(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木814km。
格尔木到拉萨的铁路长多少千米?
1956-814=1142(千米)
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长1142km。
西宁到格尔木的铁路长多少千米?
1956-1142=814(千米)
问题:
与第(1)题相比,第(2)、(3)题分别是已知什么?
求什么?怎样算?
减法解决问题
问题:
已知两个数的和与其中的一个加数,求另一个加数的运算,
叫做? ? ? ?。在减法中,已知的和叫做? ? ? ? ? ?。
减法
被减数
(1)
814 + 1142 = 1956
(2)
(3)
1956 - 1142 = 814
1956 - 814 = 1142
用你自己的话说一说,你认为什么是减法?
减法解决问题
减法各部分间的关系
被减数 - 减数 = 差
问题:
如果知道被减数和差,能求出减数吗?
减数 = 被减数- 差
问题:
如果知道减数和差,能求出被减数吗?
被减数 = 减数 + 差
减法解决问题
填空并观察三个算式中各部分之间的关系:
?
?
?
被减数 - 减数 =? ?差
169? ?-? ? 54? ?=(? ? )??
(? ? )= 169 - 115
(? ? )= 54 + 115
115
54
169
差 = 被减数 - 减数
减数 = 被减数 - 差
被减数 = 差 + 减数
减法解决问题
僧人? ? ? ? ? ? ?在莱茵德纸草书(大约公元前五千多年)上把加号、减号分别用记号 “? ? ? ?”“? ? ? ” 来表示。加号像一个人向右走的两条腿,减号像一个人向左走的两条腿。
两数相减,有用三条平行的箭头 “? ? ? ? ?” 表示。
阿默斯
加减号的历史
蹉跎一千多年过去了,数学估计上仍没有发现其他加、减号的印记,数学家们习惯的用文辞方式书写。?
各国加减一词的字母不少,写多了挺麻烦的。
如 3 + 2 写成 3 加 2;3 - 2 写成 3 减 2
加减号的历史
又经过一千多年即在公元 4 世纪左右,古希腊代数学的鼻祖? ? ? ? ? ? (约 246 ~ 330 年)创用了一套简洁漂亮的数学符号。他创用加减号,他写加法时把相加的各项并列在一起。丢番图采 “ 省略加号式 ”。
丢番图偶尔用一斜线 “ / ” 表示加号,用一曲线 “)” 表示减号,但无人采用。
丢番图
加减号的历史
古印度人一般不用加号,但是公元 3 世纪的巴赫沙里残简中用 “ yu ” 表示加号,用 “ + ” 表示减号。
加减号的历史
印度数学的始祖? ? ? ? ? ? ? ? ? ? (公元 598 ~ 665年以后)独树一帜,第一次创用缩写文字来表示运算,把许多有字母组成的词只用开始的音节表示,如加法 “? ? yTa ” 一词,只写成 “? ? y ”,表示加法。?
婆罗摩笈多
Й
Й
加减号的历史
500 年后的印度数学家婆什迦罗(1114 ~ 1185?),没有承袭始祖创用的加号。
他效仿丢番图的 “ 省略式 ” 表示加法,如
写成
到今天还可以见其踪迹。
,这种表达式的痕迹直
他采用留空的方法表示减法,即把数与数之间离开远一点。
加减号的历史
15 世纪阿拉伯人? ? ? ? ? ? ? ? ?用两个数并列表示加,而用一个特殊符号 “? ? ?” 作减号。
盖拉萨迪
加减号的历史
公元 15 世纪伊始,德国有一位天才数学家原名叫? ? ? ? (1436 ~ 1476),笔名叫雷格蒙塔努斯。他在 1456 年的一本数学手稿中使用 “ et ” 表示加号,如 3 + 4 写成 3 et 4。?
缪勒
加减号的历史
法国巴黎数学、医学学士? ? ? ? (约 1445 ~ 约 1500 年) ,他在论文中用缩写的代数符号体系,如他用 D 表示加号,用 M表示减号,这是一个前进的缩写符号。
许凯
加减号的历史
意大利修道士? ? ? ? ? ? (约 1445 ~ 约 1517年),一生热爱数学,后来被聘为米兰大学数学教授。他用意大利文 Piu(加)的第一个字母 “P ” 表示加号;又用意大利文meno (减)的第一个字母 “ m ” 表示减号。
帕乔利
加减号的历史
1489 年,出生在捷克的德国数学家? ?
维德曼
(1460 ~ 16 世纪前半叶)是最早在印刷图书中用 “ + ” 作加,用 “ - ” 作减。维德曼创用的加、减号,并不是作为运算符号使用的,而只表示剩余和不足。
加减号的历史
1514 年,荷兰数学家? ? ? ? 采用 “ + ” 表示加法,用 “ - ” 表示减法作为代数运算符号。
赫克
加减号的历史
30 年过去了,德国数学家? ? ? ? ? ? ? ? (1486 ~ 1567 年)终于冲破数坛沉闷的气氛,在 1544 年在《算术大全》一书里大量使用加、减号 “ + ”、“ - ”,且运用自如。
斯蒂菲尔
加减号的历史
英国数学家? ? ? ? ? ? (1510 ~ 1558 年)在 1557 写了一篇著名论文《励智石》,其中系统的采用了运算符号 “ + ”、“ - ”。
雷科德
加减号的历史
1608 年德国人? ? ? ? ? ? ? ?(1537 ~ 1612年)在罗马出版的《代数》 一书中也使用了 “ + ”、“ - ”。
克拉维斯
加减号的历史
英国数学家? ? ? ? ? ? ? ? (1560 ~ 1621年)还用 “ - ” 同时表示减号和负号等。
哈里奥特
加减号的历史
英国的? ? ? ? ? ? ? ? (1574 ~ 1660 年)单独用 “ ± ” 表示现代加减的意义。
奥特雷德
加减号的历史
我国第一次把西洋加减号介绍来的是清代著名翻译与数学家李善兰(1811 ~ 1852年),但他为了避免与中国数字 “ 十 ”(拾)和 “ 一 ”(壹),取篆文的上下二字,即用分别表示加减号。直到清末新学堂开办起来以后,外来数学书籍增多,才广泛使用加号 “ + ”、减号 “ - ”,并沿用至今。
加减号的历史
根据 2468 + 575 = 3043,不计算直接写出后面算式的结果。
3043 - 2468 =(? ? ? ?)
3043- 575 =(? ? ? ?)?
575
2468
做一做(数学书第3页)
下面各题应用什么方法计算?为什么?
86 + 59 = 145(张)
答:滑雪场全天一共卖出 145 张门票。
练习(数学书第4页第1题)
① 滑雪场上午卖出 86 张门票,下午卖出 59 张门票。
? ? ?滑雪场全天一共卖出多少张门票?
下面各题应用什么方法计算?为什么?
② 滑雪场全天卖出 145 张门票,其中上午卖出 86 张,
? ? ?下午卖出多少张?
145 - 86 = 59(张)
答:滑雪场下午卖出 59 张门票。
练习(数学书第4页第1题)
下面各题应用什么方法计算?为什么?
③ 华光文具店运来一批练习本,卖出 370 包,剩下 630 包。
? ? ?运来多少包练习本?
370 + 630 = 1000(包)
答:运来 1000 包练习本。
练习(数学书第4页第1题)
下面各题应用什么方法计算?为什么?
④ 兴华小学一共有学生 843 人,其中男生 418 人,
? ? ?女生有多少人?
843 - 418 = 425(人)
答:兴华小学女生有 425 人。
练习(数学书第4页第1题)
根据加、减法各部分间的关系,写出另外两个算式。
203 + 147 = 350
28 + 19 = 47
47 - 19 = 28
47 - 28 = 19
350- 203 = 147
350 - 147 = 203
67 - 55 = 12
850 - 239 = 611
67 - 12 = 55
55 + 12 = 67
850 - 611 = 239
239 + 611 = 850
练习(数学书第4页第2题)
猜猜我是几?
120 + 56 = 176
792 - 483 = 309
练习(数学书第4页第3题)
200 +
=?
654-
=?
300
200
128
651
500
400
328
851
154
297
511
381
500
357
143
273
练习(数学书第4页第4题)
计算下面各题,并利用加、减法各部分间的关系进行验算。
340 + 190 =
254 + 297 =
586 - 98 =
712 - 455 =
530
551
488
257
练习(数学书第4页第5题)
计算下面各题,并用加、减法各部分间的关系进行验算。
325 + 187 =
325
187
512
+
验算:
512
325
-
187
492 - 345 =
492
345
-
147
验算:
147
345
+
492
512
147
1
1
1
提高练习
一件衬衫 148 元,一条裙子比一件衬衫便宜 19 元,一件西服外套比一条裙子贵 316 元。一件西服外套多少钱?
衬衫:
裙子:
西服:
148 元
129 元
316 元
裙子:148 -19 = 129(元)
西服:129 + 316 = 445(元)
答:一件西服外套 445 元。
19元
?元?
提高练习
猪妈妈重多少千克?
200 - 21 = 179(kg)
提高练习
在一道整数减法算式中,减数与差相等,那么被减数可能是(? ? ? )
A.? 41? ? ? ? ? ? ? ? ? B.? 42? ? ? ? ? ? ? ? ? C.? 71? ? ? ? ? ? ? ? ? D.? 97
因为:被减数 = 差 + 减数
减数与差相等,说明被减数是减数或差的 2 倍,那么被减数一定是一个偶数
B
拓展练习
一道减法算式中,被减数、减数和差存在下面的关系,算一算,
写出这道减法算式。
被减数 + 减数 + 差 = 660
减数 - 差 = 70
拓展练习
被减数 + 减数 + 差 = 660
减数 - 差 = 70
330
330
减数:
差:
70
330
130
被减数:660 ÷ 2 = 330
330 - 70 = 260
差:260 ÷ 2 = 130
减数:130 + 70 = 200
减法算式:330 - 200 = 130
=
拓展练习
在一道减法算式中,被减数、减数、差三个数的和等于 134,且减数比差小 31,
请写出这道减法算式。
被减数 + 减数 + 差 = 134
被减数 = 减数 + 差
被减数 + 被减数 = 134
被减数 = 67
减数 + 差 = 67
减数 + 差 = 67
差 - 减数 = 31
差 = 减数 + 31
减数 + 减数 + 31 = 67
减数 = 18
差 = 49
67 - 18 = 49
拓展练习
5
+
-
3
8
4
6
8
1
0
0
6
1
0
9
0
9
9
9
9
1
拓展练习
在已学过的加、减法知识的基础上,概括出加、减法的意义,并对加、减法的认识从感性上升到理性。
引导学生运用已有经验,通过知识迁移,理解新知,逐步培养学生的逻辑推理能力及运用知识解决问题的能力。
深刻理解加法、减法之间的关系,感悟到数学知识内在联系的逻辑之美。
教学目标
理解加、减法的意义,掌握加法、减法各部分之间的关系及其应用。
从实例中探究加、减法的互逆关系。
教学重点
教学难点
小猴子特别喜欢吃樱桃,第一次吃了 30 个,但是小猴子吃完了还想吃,就又吃了 20 个。
小猴子一共吃了多少个樱桃呢?
第一次比第二次多吃了几个樱桃呢?
复习加法、减法
四(1)班有男生 21 人,女生 17 人,一共有几名学生?
男生 21 人
女生 17 人
一共(? ? )人
21 + 17?
复习加法、减法及线段图的应用
男生 21 人
女生(? ? )人
一共 38 人
38 - 21?
复习加法、减法及线段图的应用
男生(? ? )人
女生 17 人
一共 38 人
38 - 17?
复习加法、减法及线段图的应用
口算
300 + 700 =
1500 - 800 =
2000 + 499 =
1259 - 1000 =
1000
700
2499
259
复习加法、减法口算笔算
笔算
1945 + 367 =
3406 - 2789 =
1945
+
367
2
2312
3406
2789
-
6
1
7
617
2
3
1
1
1
1
复习加法、减法口算笔算
一列火车从西宁经过格尔木开往拉萨。西宁到格尔木的铁路长 814km,格尔木到拉萨的铁路长 1142km。西宁到拉萨的铁路长多少千米?
加法解决问题
一列火车从西宁经过格尔木开往拉萨。西宁到格尔木的铁路长 814km,格尔木到拉萨的铁路长 1142km。西宁到拉萨的铁路长多少千米?
问题:
1. 读题,你知道了什么??
2. 用线段图表示题目中的数量关系。
已知西宁到格尔木的路程和格尔木到拉萨的路程,要求西宁到拉萨的路程。
加法解决问题
一列火车从西宁经过格尔木开往拉萨。西宁到格尔木的铁路长 814km,格尔木到拉萨的铁路长 1142km。西宁到拉萨的铁路长多少千米?
西宁到拉萨的铁路长多少km?
问题:
1. 说一说你是怎样画线段图的。
2. “ 西宁到拉萨的铁路长 ” 在图上怎样表示?
3. 求西宁到拉萨的铁路长多少千米,用什么方法?你是怎么想的?
加法解决问题
一列火车从西宁经过格尔木开往拉萨。西宁到格尔木的铁路长 814km,格尔木到拉萨的铁路长 1142km。西宁到拉萨的铁路长多少千米?
814 + 1142
加数+
加数
= 和
把两个数合并成一个数的运算,叫做? ? ? ? 。
加法
相加的两个数叫做? ? ? ? 。
加数
加得的数叫做? ? 。
和
= 1956(千米)
加法解决问题
西宁到格尔木的距离+格尔木到拉萨的距离=西宁到拉萨的距离
814 + 1142
加数+
加数
= 和
= 1956?
问题:
如果知道和与一个加数,能求出另一个加数吗?
一个加数 = 和 - 另一个加数
加法各部分关系
填空并观察三个算式中各部分之间的关系:
加数 + 加数 = 和
58? ?+? ?61? ?=(? ? )?
(? ? )=? 119? -? 58
(? ? )=? 119? -? 61
和 = 加数 + 加数
一个加数 = 和 - 另一个加数
?
?
?
119
61
58
加法各部分关系
一个数同0相加结果怎样?
一个数同0相加还得(这个数)。
线段图哪里变了?哪里没变?
西宁到拉萨的铁路全长 1956km,其中格尔木到拉萨长 1142km。
西宁到格尔木的铁路长多少千米?
减法解决问题
西宁到拉萨的铁路全长 1956km,其中西宁到格尔木长 814km。
格尔木到拉萨的铁路长多少千米?
西宁到拉萨的铁路长 1956km
问题:
① 读题,你知道了什么??
② 求格尔木到拉萨的铁路长多少千米,用什么方法?你是怎么想的?
1956 - 814=1142(千米)
已知西宁到拉萨的路程和西宁到格尔木的路程,要求格尔木到拉萨的路程。
减法解决问题
西宁到拉萨的距离-西宁到格尔木的距离=格尔木到拉萨的距离
西宁到拉萨的铁路全长 1956km,其中格尔木到拉萨长1142km。
西宁到格尔木的铁路长多少千米?
西宁到拉萨的铁路长 1956km
问题:
求西宁到格尔木的铁路长多少千米,用什么方法?
你是怎么想的?
1956 - 1142 = 814(千米)
减法解决问题
西宁到拉萨的距离-格尔木到拉萨的距离=西宁到格尔木的距离
(1)一列火车从西宁经过格尔木开往拉萨。西宁到格尔木的铁路长 814km,格尔木到拉萨的铁路长 1142km。西宁到拉萨的铁路长多少千米?
814+1142=1956(千米)
(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木814km。
格尔木到拉萨的铁路长多少千米?
1956-814=1142(千米)
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长1142km。
西宁到格尔木的铁路长多少千米?
1956-1142=814(千米)
问题:
与第(1)题相比,第(2)、(3)题分别是已知什么?
求什么?怎样算?
减法解决问题
问题:
已知两个数的和与其中的一个加数,求另一个加数的运算,
叫做? ? ? ?。在减法中,已知的和叫做? ? ? ? ? ?。
减法
被减数
(1)
814 + 1142 = 1956
(2)
(3)
1956 - 1142 = 814
1956 - 814 = 1142
用你自己的话说一说,你认为什么是减法?
减法解决问题
减法各部分间的关系
被减数 - 减数 = 差
问题:
如果知道被减数和差,能求出减数吗?
减数 = 被减数- 差
问题:
如果知道减数和差,能求出被减数吗?
被减数 = 减数 + 差
减法解决问题
填空并观察三个算式中各部分之间的关系:
?
?
?
被减数 - 减数 =? ?差
169? ?-? ? 54? ?=(? ? )??
(? ? )= 169 - 115
(? ? )= 54 + 115
115
54
169
差 = 被减数 - 减数
减数 = 被减数 - 差
被减数 = 差 + 减数
减法解决问题
僧人? ? ? ? ? ? ?在莱茵德纸草书(大约公元前五千多年)上把加号、减号分别用记号 “? ? ? ?”“? ? ? ” 来表示。加号像一个人向右走的两条腿,减号像一个人向左走的两条腿。
两数相减,有用三条平行的箭头 “? ? ? ? ?” 表示。
阿默斯
加减号的历史
蹉跎一千多年过去了,数学估计上仍没有发现其他加、减号的印记,数学家们习惯的用文辞方式书写。?
各国加减一词的字母不少,写多了挺麻烦的。
如 3 + 2 写成 3 加 2;3 - 2 写成 3 减 2
加减号的历史
又经过一千多年即在公元 4 世纪左右,古希腊代数学的鼻祖? ? ? ? ? ? (约 246 ~ 330 年)创用了一套简洁漂亮的数学符号。他创用加减号,他写加法时把相加的各项并列在一起。丢番图采 “ 省略加号式 ”。
丢番图偶尔用一斜线 “ / ” 表示加号,用一曲线 “)” 表示减号,但无人采用。
丢番图
加减号的历史
古印度人一般不用加号,但是公元 3 世纪的巴赫沙里残简中用 “ yu ” 表示加号,用 “ + ” 表示减号。
加减号的历史
印度数学的始祖? ? ? ? ? ? ? ? ? ? (公元 598 ~ 665年以后)独树一帜,第一次创用缩写文字来表示运算,把许多有字母组成的词只用开始的音节表示,如加法 “? ? yTa ” 一词,只写成 “? ? y ”,表示加法。?
婆罗摩笈多
Й
Й
加减号的历史
500 年后的印度数学家婆什迦罗(1114 ~ 1185?),没有承袭始祖创用的加号。
他效仿丢番图的 “ 省略式 ” 表示加法,如
写成
到今天还可以见其踪迹。
,这种表达式的痕迹直
他采用留空的方法表示减法,即把数与数之间离开远一点。
加减号的历史
15 世纪阿拉伯人? ? ? ? ? ? ? ? ?用两个数并列表示加,而用一个特殊符号 “? ? ?” 作减号。
盖拉萨迪
加减号的历史
公元 15 世纪伊始,德国有一位天才数学家原名叫? ? ? ? (1436 ~ 1476),笔名叫雷格蒙塔努斯。他在 1456 年的一本数学手稿中使用 “ et ” 表示加号,如 3 + 4 写成 3 et 4。?
缪勒
加减号的历史
法国巴黎数学、医学学士? ? ? ? (约 1445 ~ 约 1500 年) ,他在论文中用缩写的代数符号体系,如他用 D 表示加号,用 M表示减号,这是一个前进的缩写符号。
许凯
加减号的历史
意大利修道士? ? ? ? ? ? (约 1445 ~ 约 1517年),一生热爱数学,后来被聘为米兰大学数学教授。他用意大利文 Piu(加)的第一个字母 “P ” 表示加号;又用意大利文meno (减)的第一个字母 “ m ” 表示减号。
帕乔利
加减号的历史
1489 年,出生在捷克的德国数学家? ?
维德曼
(1460 ~ 16 世纪前半叶)是最早在印刷图书中用 “ + ” 作加,用 “ - ” 作减。维德曼创用的加、减号,并不是作为运算符号使用的,而只表示剩余和不足。
加减号的历史
1514 年,荷兰数学家? ? ? ? 采用 “ + ” 表示加法,用 “ - ” 表示减法作为代数运算符号。
赫克
加减号的历史
30 年过去了,德国数学家? ? ? ? ? ? ? ? (1486 ~ 1567 年)终于冲破数坛沉闷的气氛,在 1544 年在《算术大全》一书里大量使用加、减号 “ + ”、“ - ”,且运用自如。
斯蒂菲尔
加减号的历史
英国数学家? ? ? ? ? ? (1510 ~ 1558 年)在 1557 写了一篇著名论文《励智石》,其中系统的采用了运算符号 “ + ”、“ - ”。
雷科德
加减号的历史
1608 年德国人? ? ? ? ? ? ? ?(1537 ~ 1612年)在罗马出版的《代数》 一书中也使用了 “ + ”、“ - ”。
克拉维斯
加减号的历史
英国数学家? ? ? ? ? ? ? ? (1560 ~ 1621年)还用 “ - ” 同时表示减号和负号等。
哈里奥特
加减号的历史
英国的? ? ? ? ? ? ? ? (1574 ~ 1660 年)单独用 “ ± ” 表示现代加减的意义。
奥特雷德
加减号的历史
我国第一次把西洋加减号介绍来的是清代著名翻译与数学家李善兰(1811 ~ 1852年),但他为了避免与中国数字 “ 十 ”(拾)和 “ 一 ”(壹),取篆文的上下二字,即用分别表示加减号。直到清末新学堂开办起来以后,外来数学书籍增多,才广泛使用加号 “ + ”、减号 “ - ”,并沿用至今。
加减号的历史
根据 2468 + 575 = 3043,不计算直接写出后面算式的结果。
3043 - 2468 =(? ? ? ?)
3043- 575 =(? ? ? ?)?
575
2468
做一做(数学书第3页)
下面各题应用什么方法计算?为什么?
86 + 59 = 145(张)
答:滑雪场全天一共卖出 145 张门票。
练习(数学书第4页第1题)
① 滑雪场上午卖出 86 张门票,下午卖出 59 张门票。
? ? ?滑雪场全天一共卖出多少张门票?
下面各题应用什么方法计算?为什么?
② 滑雪场全天卖出 145 张门票,其中上午卖出 86 张,
? ? ?下午卖出多少张?
145 - 86 = 59(张)
答:滑雪场下午卖出 59 张门票。
练习(数学书第4页第1题)
下面各题应用什么方法计算?为什么?
③ 华光文具店运来一批练习本,卖出 370 包,剩下 630 包。
? ? ?运来多少包练习本?
370 + 630 = 1000(包)
答:运来 1000 包练习本。
练习(数学书第4页第1题)
下面各题应用什么方法计算?为什么?
④ 兴华小学一共有学生 843 人,其中男生 418 人,
? ? ?女生有多少人?
843 - 418 = 425(人)
答:兴华小学女生有 425 人。
练习(数学书第4页第1题)
根据加、减法各部分间的关系,写出另外两个算式。
203 + 147 = 350
28 + 19 = 47
47 - 19 = 28
47 - 28 = 19
350- 203 = 147
350 - 147 = 203
67 - 55 = 12
850 - 239 = 611
67 - 12 = 55
55 + 12 = 67
850 - 611 = 239
239 + 611 = 850
练习(数学书第4页第2题)
猜猜我是几?
120 + 56 = 176
792 - 483 = 309
练习(数学书第4页第3题)
200 +
=?
654-
=?
300
200
128
651
500
400
328
851
154
297
511
381
500
357
143
273
练习(数学书第4页第4题)
计算下面各题,并利用加、减法各部分间的关系进行验算。
340 + 190 =
254 + 297 =
586 - 98 =
712 - 455 =
530
551
488
257
练习(数学书第4页第5题)
计算下面各题,并用加、减法各部分间的关系进行验算。
325 + 187 =
325
187
512
+
验算:
512
325
-
187
492 - 345 =
492
345
-
147
验算:
147
345
+
492
512
147
1
1
1
提高练习
一件衬衫 148 元,一条裙子比一件衬衫便宜 19 元,一件西服外套比一条裙子贵 316 元。一件西服外套多少钱?
衬衫:
裙子:
西服:
148 元
129 元
316 元
裙子:148 -19 = 129(元)
西服:129 + 316 = 445(元)
答:一件西服外套 445 元。
19元
?元?
提高练习
猪妈妈重多少千克?
200 - 21 = 179(kg)
提高练习
在一道整数减法算式中,减数与差相等,那么被减数可能是(? ? ? )
A.? 41? ? ? ? ? ? ? ? ? B.? 42? ? ? ? ? ? ? ? ? C.? 71? ? ? ? ? ? ? ? ? D.? 97
因为:被减数 = 差 + 减数
减数与差相等,说明被减数是减数或差的 2 倍,那么被减数一定是一个偶数
B
拓展练习
一道减法算式中,被减数、减数和差存在下面的关系,算一算,
写出这道减法算式。
被减数 + 减数 + 差 = 660
减数 - 差 = 70
拓展练习
被减数 + 减数 + 差 = 660
减数 - 差 = 70
330
330
减数:
差:
70
330
130
被减数:660 ÷ 2 = 330
330 - 70 = 260
差:260 ÷ 2 = 130
减数:130 + 70 = 200
减法算式:330 - 200 = 130
=
拓展练习
在一道减法算式中,被减数、减数、差三个数的和等于 134,且减数比差小 31,
请写出这道减法算式。
被减数 + 减数 + 差 = 134
被减数 = 减数 + 差
被减数 + 被减数 = 134
被减数 = 67
减数 + 差 = 67
减数 + 差 = 67
差 - 减数 = 31
差 = 减数 + 31
减数 + 减数 + 31 = 67
减数 = 18
差 = 49
67 - 18 = 49
拓展练习
5
+
-
3
8
4
6
8
1
0
0
6
1
0
9
0
9
9
9
9
1
拓展练习
