北师大版七年级上册数学第一章·丰富的图形世界素养拓展+中考真题课件(41张PPT)
文档属性
| 名称 | 北师大版七年级上册数学第一章·丰富的图形世界素养拓展+中考真题课件(41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 642.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-15 00:00:00 | ||
图片预览





文档简介
第一章·丰富的图形世界
数学·七年级上册·北师
专题1 立体图形的展开与折叠
专项素养拓训
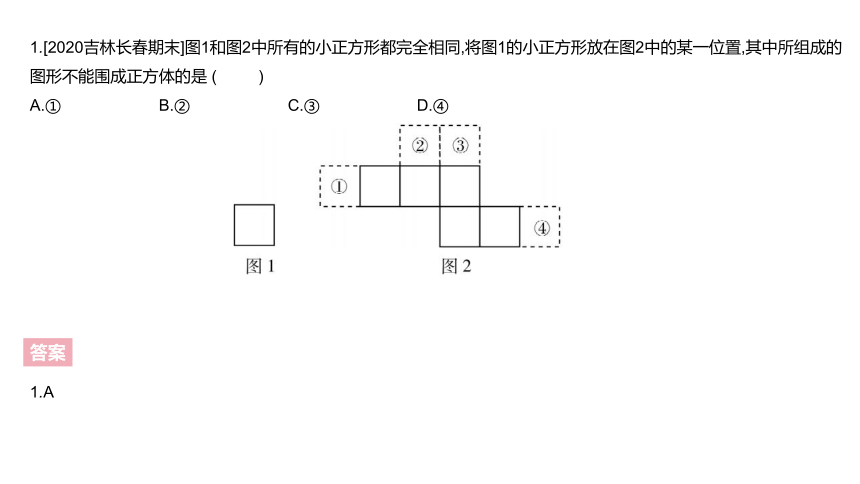
1.[2020吉林长春期末]图1和图2中所有的小正方形都完全相同,将图1的小正方形放在图2中的某一位置,其中所组成的图形不能围成正方体的是 ( )
A.① B.② C.③ D.④
答案
1.A
2.[2019吉林长春期末]如图是一个正方体的表面展开图,把展开图折叠成正方体后,有“我”字的一面的相对面上的字是 ( )
A.国 B.厉 C.害 D.了
答案
2.A 【解析】 根据题中正方体的表面展开图,可知“厉”字相对的是“了”字,“害”字相对的是“的”字,“我”字相对的是“国”字.故选A.
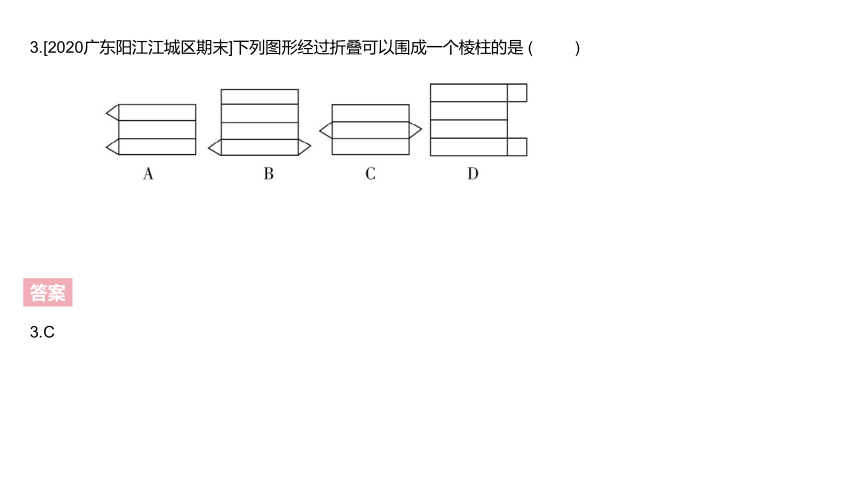
3.[2020广东阳江江城区期末]下列图形经过折叠可以围成一个棱柱的是 ( )
答案
3.C
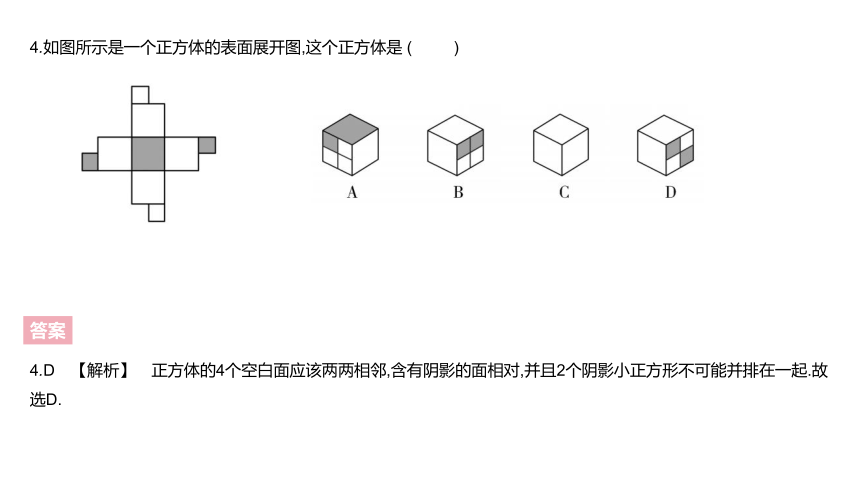
4.如图所示是一个正方体的表面展开图,这个正方体是 ( )
答案
4.D 【解析】 正方体的4个空白面应该两两相邻,含有阴影的面相对,并且2个阴影小正方形不可能并排在一起.故
选D.
专题2 从不同的方向看几何体
专项素养拓训
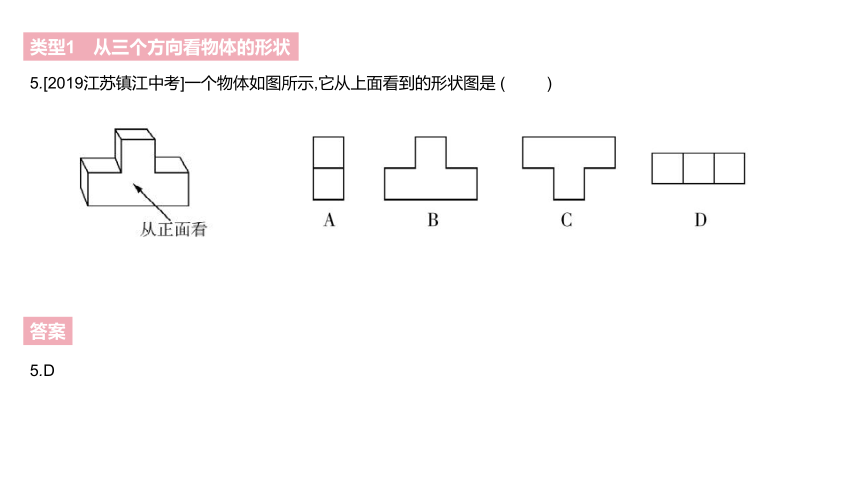
5.[2019江苏镇江中考]一个物体如图所示,它从上面看到的形状图是 ( )
答案
5.D
类型1 从三个方向看物体的形状
6.如图,一个几何体由5个棱长均为1的小立方块搭成,下列关于这个几何体的说法正确的是 ( )
A.从正面看到的形状图的面积为5
B.从左面看到的形状图的面积为3
C.从上面看到的形状图的面积为3
D.从三个方向看到的形状图的面积都是4
答案
6.B 【解析】 从正面看到的是4个小正方形,故面积为4;从左面看到的是3个小正方形,故面积为3;从上面看到的是4个小正方形,故面积为4.故选B.
类型1 从三个方向看物体的形状
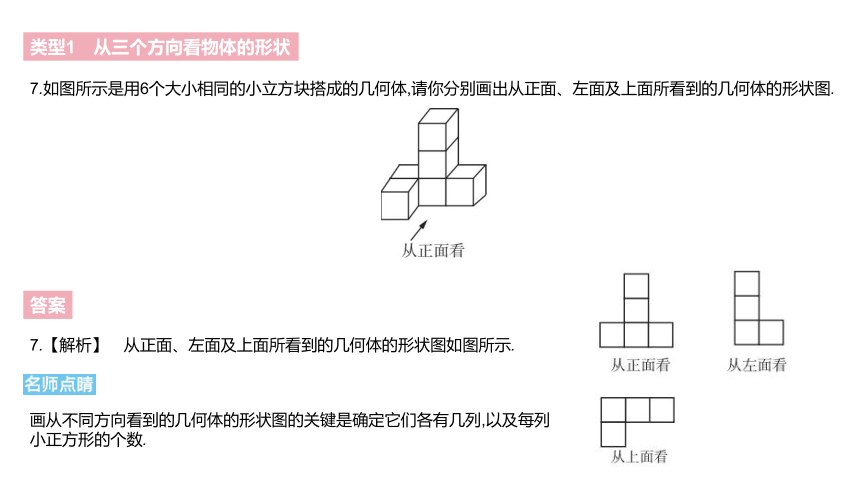
7.如图所示是用6个大小相同的小立方块搭成的几何体,请你分别画出从正面、左面及上面所看到的几何体的形状图.
答案
7.【解析】 从正面、左面及上面所看到的几何体的形状图如图所示.
类型1 从三个方向看物体的形状
画从不同方向看到的几何体的形状图的关键是确定它们各有几列,以及每列小正方形的个数.
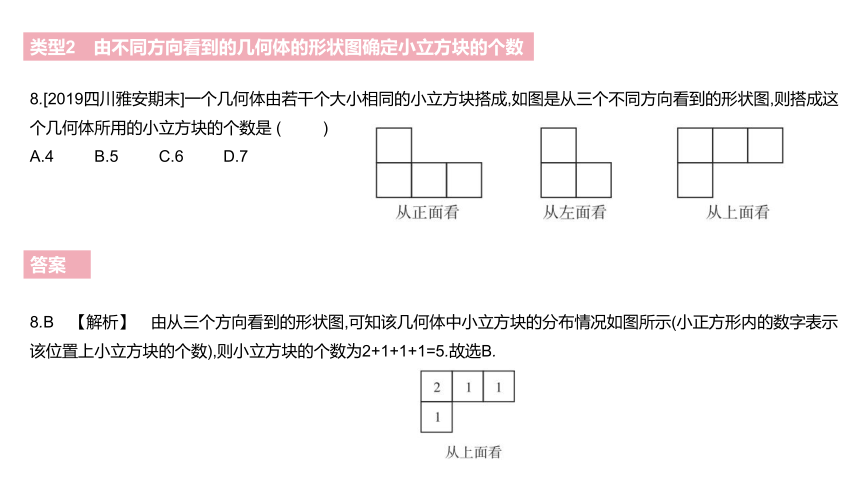
8.[2019四川雅安期末]一个几何体由若干个大小相同的小立方块搭成,如图是从三个不同方向看到的形状图,则搭成这个几何体所用的小立方块的个数是 ( )?
A.4 B.5 C.6 D.7
答案
8.B 【解析】 由从三个方向看到的形状图,可知该几何体中小立方块的分布情况如图所示(小正方形内的数字表示该位置上小立方块的个数),则小立方块的个数为2+1+1+1=5.故选B.
类型2 由不同方向看到的几何体的形状图确定小立方块的个数
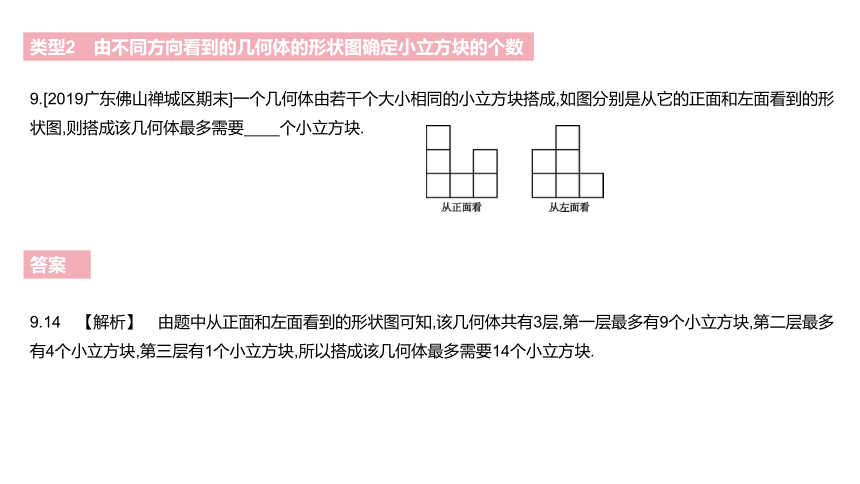
9.[2019广东佛山禅城区期末]一个几何体由若干个大小相同的小立方块搭成,如图分别是从它的正面和左面看到的形状图,则搭成该几何体最多需要 个小立方块.?
答案
9.14 【解析】 由题中从正面和左面看到的形状图可知,该几何体共有3层,第一层最多有9个小立方块,第二层最多有4个小立方块,第三层有1个小立方块,所以搭成该几何体最多需要14个小立方块.
类型2 由不同方向看到的几何体的形状图确定小立方块的个数
综合素养拓训
直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.培养直观想象,首先要培养空间观念.空间观念是指对相关物体和几何图形的形状、大小、位置关系及其变化的直觉,探究有关图形内在关系、结构关系的一种想象能力,在本章主要表现在“能够由实物的形状想象出几何图形,由几何图形想象出实物的形状,进行几何体与其三个方向看到的形状图、表面展开图之间的转化”.例如第3题,借助正方体的表面展开图寻找蚂蚁所爬行的最短路线,实现立体图形与平面图形之间的转化.
1.[探究被截几何体的顶点数、棱数、面数之间的关系]
(1)图1是正方体木块,把它切去一块,可能得到形如图2、3、4、5的木块.我们知道,图1的正方体木块有8个顶点,12条棱,6个面,请你将图2、3、4、5中木块的顶点数、棱数、面数填入下表.
(2)观察上表,请你归纳上述各个木块的顶点数、棱数、面数之间的数量关系: .?
(3)图6是用虚线画出的正方体木块,请你想象一种与图2~5不同的切法,把切去一块后得到的那一块的每条棱都改画成实线,则该木块的顶点数为 ,棱数为 ,面数为 .(答案不唯一,合理即可)?
图
顶点数
棱数
面数
1
8
12
6
2
3
4
5
答案
1.【解析】 (1)填表如下:
(2)顶点数+面数-棱数=2
(3)8 12 6(答案不唯一,合理即可)
如切过之后为一长方体,所画图形如图所示.
该木块的顶点数为8,棱数为12,面数为6.
图
顶点数
棱数
面数
1
8
12
6
2
6
9
5
3
8
12
6
4
8
13
7
5
10
15
7
2.[与正方体有关的涂色问题]做一个正方体,并把正方体表面涂上颜色.
(1)把正方体的棱二等分,然后沿等分线把正方体切开,得到8个小正方体,如图1所示,观察其中三面被涂色的有a个,那么a= ;?
(2)把正方体的棱三等分,然后沿等分线把正方体切开,得到27个小正方体,如图2所示,观察其中三面被涂色的有b个,各面都没有被涂色的有c个,那么b+c= ;?
(3)把正方体的棱四等分,然后沿等分线把正方体切开,得到64个小正方体,如图3所示,观察其中两面被涂色的有d个,各面都没有被涂色的有e个,那么d+e= .?
答案
2.(1)8;(2)9;(3)32 【解析】 顶点处的小正方体三面被涂色,除顶点处外位于棱上的小正方体两面被涂色,位于表面中心的一面被涂色,处于内部的没有面被涂色.
(1)三面被涂色的有8个,故a=8.(2)三面被涂色的有8个,各面都没有被涂色的有1个,故b+c=8+1=9.(3)两面被涂色的有
24个,各面都没有被涂色的有8个,故d+e=24+8=32.
3.[利用表面展开图寻找最短路线]地上有一个正方体物块,一只蚂蚁在正方体的顶点A处,一块食物在正方体的顶点
B处,如图所示,现在蚂蚁想尽快吃到这块食物,那么它所爬行的最短路线是怎样的?在图上画出来.这样的最短路线有几条?
答案
3.【分析】 欲求从点A到点B的最短路线,在立体图形中难以解决,可以考虑把正方体展开成平面图形.如图1,连接AB,沿着从点A到点B的虚线爬行,路程最短,然后把展开图折叠起来即可.
【解析】 所爬行的最短路线是正方体表面展开图中点A与点B之间的连线(如图1).在正方体上,像这样的最短路线一共有6条,但通过地面的有2条,这2条不符合实际意义,故符合题意的只有4条,如图2所示.
答案
1.D
一、选择题
1.下列图形中,不是柱体的是 ( )
答案
2.C
2.一把直角三角尺绕它的最长边旋转1周,所形成的几何体可能为 ( )
答案
3.B 【解析】 由题图可知该几何体从正面看到的形状图有3列,从左至右每列小正方形的数目分别为1,2,1,所以①不正确;从左面看
到的形状图有3列,从左至右每列小正方形的数目分别为2,2,1,所以②正确;从上面看到的形状图有3列,从左至右每列小正方形的数目分别为1,3,1,且成“十”字形,所以③正确.故选B.
3.如图所示的几何体是由7个相同的小立方块堆积而成,某同学画出了从三个方向看到的形状图,在这三个形状图中正确的是 ( )
A.①② B.②③ C.①③ D.①②③
答案
4.B 【解析】 A项,2与3是相对的,12与4是相对的,8与6是相对的,乘积都不是24,A项不满足题意;B项,3与8是相对的,6与4是相对的,2与12是相对的,乘积都是24,B项满足题意;C项,2与3是相对的,12与8是相对的,4与6是相对的,乘积不都是24,C项不满足题意;D项,2与12是相对的,3与6是相对的,4与8是相对的,乘积不都是24,D项不满足题意.故选B.
4.一个正方体模型,六个面上写着六个数,若相对的两个面上的数的乘积都等于24,则下列展开图中,正确的是 ( )
答案
5.A 【解析】 由从上面看到的形状图可知,最底层有5个小立方块,再结合从左面看到的形状图可知,第二层最多有3个小立方块,最少有1个小立方块,即小立方块的个数为6,7或8,不可能为5.故选A.
5.由若干个完全相同的小立方块搭成的一个几何体,从左面和上面看到的形状图如图所示,则搭成这个几何体的小立方块的个数不可能是 ( )
A.5 B.6
C.7 D.8
答案
6.②③④ ①④ 【解析】 用平面去截长方体,所得的截面可以为长方形、梯形、三角形等,不可能为圆;用平面去截圆锥,所得的截面可以为三角形和圆,不可能为四边形.
二、填空题
6.在如图所示的四个图形中,图形 可以用平面截长方体得到;图形 可以用平面截圆锥得到.(填序号)?
答案
7.4 【解析】 题图第二行的四个小正方形的下方的四个位置上随意添加1个小正方形都可以使拼接后的整个图形折叠成正方体,所以这种拼接的方式有4种.
7.如图所示的图形是由5个小正方形组成,若再添加1个小正方形,拼接后就能使得整个图形折叠成正方体,则这种拼接的方式有 种.?
答案
8.【解析】 (1)甲、丙
(2)如图,任选其一即可.
(3)该包装盒的表面积为2×6×12+2×4×12+2×6×4=144+96+48=288.
三、解答题
8.一种长方体牛奶包装盒的长、宽、高分别为6,4,12.为了生产这种包装盒,需要先画出展开图纸样.
(1)如图,给出甲、乙、丙三种纸样,其中正确的是 ;?
(2)从已知正确的纸样中选出一种,在图中标注上尺寸;
(3)利用你所选的一种纸样,求出包装盒的表面积.
9.[2020福建宁德期末]如图,用10个大小相同的小立方块搭成一个组合体.
(1)请在指定位置画出该组合体从左面、上面看到的形状图;
(2)在不改变该组合体中小立方块个数的前提下,从中移动一个小立方块,使所得新组合体与原组合体相比,从左面、上面看到的形状图保持不变,但从正面看到的形状图改变了,请画出新组合体从正面看到的所有可能的形状图.(所给的方格图不一定全用,不够可添)
答案
9.【解析】 (1)如图所示.
(2)如图所示.
第一章·丰富的图形世界(中考真题)
数学·七年级上册·北师
答案
1.C
1.[2019江苏盐城中考]如图是由6个相同的小正方体搭成的物体,该物体从正面看到的形状图是 ( )
答案
2.D
2.[2019湖北襄阳中考]某正方体的平面展开图如图所示,则原正方体中与“春”字所在的面相对的面上的字是 ( )
A.青 B.来 C.斗 D.奋
答案
3.B 【解析】 由题意可知,该几何体为四棱锥,所以它的底面是四边形.故选B.
3.[2019江苏连云港中考]一个几何体的侧面展开图如图所示,则该几何体的底面是 ( )
答案
4.C
4.[2019四川达州中考]如图是由7个相同的小立方块所搭成的几何体从上面看到的形状图,小正方形中的数字表示该位置小立方块的个数,这个几何体从左面看到的形状图是 ( )
答案
5.D
5.[2019广西南宁中考]如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是 ( )
答案
6.C 【解析】 C项中的图形不能围成正方体,不符合题意.故选C.
6.[2018四川巴中中考]毕业前夕,同学们准备了一份礼物送给自己的母校.现用一个正方体盒子进行包装,六个面上分别写上“祝、母、校、更、美、丽”,其中“祝”与“更”,“母”与“美”在相对的面上.则此包装盒的展开图(不考虑文字方向)不可能是( )
答案
7.B 【解析】 根据涂有颜色一面的位置,排除A,C项;D中的图形不是这个几何体的表面展开图,排除D.故选B.
7.[2019山东济宁中考]如图,一个几何体上半部为正四棱锥,下半部为正方体,且有一个面涂有颜色,该几何体的表面展开图是 ( )
答案
8.B 【解析】 由从上面看到的形状图可得该组合体的最底层有5个小立方块,由从正面看到的形状图可得第二层有2个,3个或4个小立方块,则组成这个组合体的小立方块的个数是7个,8个或9个,所以组成这个组合体的小立方块的个数最多是9个.故选B.
8.[2019四川宜宾中考]已知一个组合体是由几个相同的小立方块叠合在一起组成,该组合体从正面看到的形状图与从上面看到的形状图如图所示,则该组合体中小立方块的个数最多是 ( )
A.10 B.9
C.8 D.7
答案
9.B 【解析】 由题图可知,涂色部分的面积是从上、前、右三个方向所涂面积的和,即涂色部分面积为4+4+3=11.故选B.
9.[2018山东烟台中考]由5个棱长为1的小立方块组成的几何体如图放置,一面着地,两面靠墙.若要将露出来的部分涂色,则涂色部分的面积为 ( )
A.9 B.11 C.14 D.18
数学·七年级上册·北师
专题1 立体图形的展开与折叠
专项素养拓训
1.[2020吉林长春期末]图1和图2中所有的小正方形都完全相同,将图1的小正方形放在图2中的某一位置,其中所组成的图形不能围成正方体的是 ( )
A.① B.② C.③ D.④
答案
1.A
2.[2019吉林长春期末]如图是一个正方体的表面展开图,把展开图折叠成正方体后,有“我”字的一面的相对面上的字是 ( )
A.国 B.厉 C.害 D.了
答案
2.A 【解析】 根据题中正方体的表面展开图,可知“厉”字相对的是“了”字,“害”字相对的是“的”字,“我”字相对的是“国”字.故选A.
3.[2020广东阳江江城区期末]下列图形经过折叠可以围成一个棱柱的是 ( )
答案
3.C
4.如图所示是一个正方体的表面展开图,这个正方体是 ( )
答案
4.D 【解析】 正方体的4个空白面应该两两相邻,含有阴影的面相对,并且2个阴影小正方形不可能并排在一起.故
选D.
专题2 从不同的方向看几何体
专项素养拓训
5.[2019江苏镇江中考]一个物体如图所示,它从上面看到的形状图是 ( )
答案
5.D
类型1 从三个方向看物体的形状
6.如图,一个几何体由5个棱长均为1的小立方块搭成,下列关于这个几何体的说法正确的是 ( )
A.从正面看到的形状图的面积为5
B.从左面看到的形状图的面积为3
C.从上面看到的形状图的面积为3
D.从三个方向看到的形状图的面积都是4
答案
6.B 【解析】 从正面看到的是4个小正方形,故面积为4;从左面看到的是3个小正方形,故面积为3;从上面看到的是4个小正方形,故面积为4.故选B.
类型1 从三个方向看物体的形状
7.如图所示是用6个大小相同的小立方块搭成的几何体,请你分别画出从正面、左面及上面所看到的几何体的形状图.
答案
7.【解析】 从正面、左面及上面所看到的几何体的形状图如图所示.
类型1 从三个方向看物体的形状
画从不同方向看到的几何体的形状图的关键是确定它们各有几列,以及每列小正方形的个数.
8.[2019四川雅安期末]一个几何体由若干个大小相同的小立方块搭成,如图是从三个不同方向看到的形状图,则搭成这个几何体所用的小立方块的个数是 ( )?
A.4 B.5 C.6 D.7
答案
8.B 【解析】 由从三个方向看到的形状图,可知该几何体中小立方块的分布情况如图所示(小正方形内的数字表示该位置上小立方块的个数),则小立方块的个数为2+1+1+1=5.故选B.
类型2 由不同方向看到的几何体的形状图确定小立方块的个数
9.[2019广东佛山禅城区期末]一个几何体由若干个大小相同的小立方块搭成,如图分别是从它的正面和左面看到的形状图,则搭成该几何体最多需要 个小立方块.?
答案
9.14 【解析】 由题中从正面和左面看到的形状图可知,该几何体共有3层,第一层最多有9个小立方块,第二层最多有4个小立方块,第三层有1个小立方块,所以搭成该几何体最多需要14个小立方块.
类型2 由不同方向看到的几何体的形状图确定小立方块的个数
综合素养拓训
直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.培养直观想象,首先要培养空间观念.空间观念是指对相关物体和几何图形的形状、大小、位置关系及其变化的直觉,探究有关图形内在关系、结构关系的一种想象能力,在本章主要表现在“能够由实物的形状想象出几何图形,由几何图形想象出实物的形状,进行几何体与其三个方向看到的形状图、表面展开图之间的转化”.例如第3题,借助正方体的表面展开图寻找蚂蚁所爬行的最短路线,实现立体图形与平面图形之间的转化.
1.[探究被截几何体的顶点数、棱数、面数之间的关系]
(1)图1是正方体木块,把它切去一块,可能得到形如图2、3、4、5的木块.我们知道,图1的正方体木块有8个顶点,12条棱,6个面,请你将图2、3、4、5中木块的顶点数、棱数、面数填入下表.
(2)观察上表,请你归纳上述各个木块的顶点数、棱数、面数之间的数量关系: .?
(3)图6是用虚线画出的正方体木块,请你想象一种与图2~5不同的切法,把切去一块后得到的那一块的每条棱都改画成实线,则该木块的顶点数为 ,棱数为 ,面数为 .(答案不唯一,合理即可)?
图
顶点数
棱数
面数
1
8
12
6
2
3
4
5
答案
1.【解析】 (1)填表如下:
(2)顶点数+面数-棱数=2
(3)8 12 6(答案不唯一,合理即可)
如切过之后为一长方体,所画图形如图所示.
该木块的顶点数为8,棱数为12,面数为6.
图
顶点数
棱数
面数
1
8
12
6
2
6
9
5
3
8
12
6
4
8
13
7
5
10
15
7
2.[与正方体有关的涂色问题]做一个正方体,并把正方体表面涂上颜色.
(1)把正方体的棱二等分,然后沿等分线把正方体切开,得到8个小正方体,如图1所示,观察其中三面被涂色的有a个,那么a= ;?
(2)把正方体的棱三等分,然后沿等分线把正方体切开,得到27个小正方体,如图2所示,观察其中三面被涂色的有b个,各面都没有被涂色的有c个,那么b+c= ;?
(3)把正方体的棱四等分,然后沿等分线把正方体切开,得到64个小正方体,如图3所示,观察其中两面被涂色的有d个,各面都没有被涂色的有e个,那么d+e= .?
答案
2.(1)8;(2)9;(3)32 【解析】 顶点处的小正方体三面被涂色,除顶点处外位于棱上的小正方体两面被涂色,位于表面中心的一面被涂色,处于内部的没有面被涂色.
(1)三面被涂色的有8个,故a=8.(2)三面被涂色的有8个,各面都没有被涂色的有1个,故b+c=8+1=9.(3)两面被涂色的有
24个,各面都没有被涂色的有8个,故d+e=24+8=32.
3.[利用表面展开图寻找最短路线]地上有一个正方体物块,一只蚂蚁在正方体的顶点A处,一块食物在正方体的顶点
B处,如图所示,现在蚂蚁想尽快吃到这块食物,那么它所爬行的最短路线是怎样的?在图上画出来.这样的最短路线有几条?
答案
3.【分析】 欲求从点A到点B的最短路线,在立体图形中难以解决,可以考虑把正方体展开成平面图形.如图1,连接AB,沿着从点A到点B的虚线爬行,路程最短,然后把展开图折叠起来即可.
【解析】 所爬行的最短路线是正方体表面展开图中点A与点B之间的连线(如图1).在正方体上,像这样的最短路线一共有6条,但通过地面的有2条,这2条不符合实际意义,故符合题意的只有4条,如图2所示.
答案
1.D
一、选择题
1.下列图形中,不是柱体的是 ( )
答案
2.C
2.一把直角三角尺绕它的最长边旋转1周,所形成的几何体可能为 ( )
答案
3.B 【解析】 由题图可知该几何体从正面看到的形状图有3列,从左至右每列小正方形的数目分别为1,2,1,所以①不正确;从左面看
到的形状图有3列,从左至右每列小正方形的数目分别为2,2,1,所以②正确;从上面看到的形状图有3列,从左至右每列小正方形的数目分别为1,3,1,且成“十”字形,所以③正确.故选B.
3.如图所示的几何体是由7个相同的小立方块堆积而成,某同学画出了从三个方向看到的形状图,在这三个形状图中正确的是 ( )
A.①② B.②③ C.①③ D.①②③
答案
4.B 【解析】 A项,2与3是相对的,12与4是相对的,8与6是相对的,乘积都不是24,A项不满足题意;B项,3与8是相对的,6与4是相对的,2与12是相对的,乘积都是24,B项满足题意;C项,2与3是相对的,12与8是相对的,4与6是相对的,乘积不都是24,C项不满足题意;D项,2与12是相对的,3与6是相对的,4与8是相对的,乘积不都是24,D项不满足题意.故选B.
4.一个正方体模型,六个面上写着六个数,若相对的两个面上的数的乘积都等于24,则下列展开图中,正确的是 ( )
答案
5.A 【解析】 由从上面看到的形状图可知,最底层有5个小立方块,再结合从左面看到的形状图可知,第二层最多有3个小立方块,最少有1个小立方块,即小立方块的个数为6,7或8,不可能为5.故选A.
5.由若干个完全相同的小立方块搭成的一个几何体,从左面和上面看到的形状图如图所示,则搭成这个几何体的小立方块的个数不可能是 ( )
A.5 B.6
C.7 D.8
答案
6.②③④ ①④ 【解析】 用平面去截长方体,所得的截面可以为长方形、梯形、三角形等,不可能为圆;用平面去截圆锥,所得的截面可以为三角形和圆,不可能为四边形.
二、填空题
6.在如图所示的四个图形中,图形 可以用平面截长方体得到;图形 可以用平面截圆锥得到.(填序号)?
答案
7.4 【解析】 题图第二行的四个小正方形的下方的四个位置上随意添加1个小正方形都可以使拼接后的整个图形折叠成正方体,所以这种拼接的方式有4种.
7.如图所示的图形是由5个小正方形组成,若再添加1个小正方形,拼接后就能使得整个图形折叠成正方体,则这种拼接的方式有 种.?
答案
8.【解析】 (1)甲、丙
(2)如图,任选其一即可.
(3)该包装盒的表面积为2×6×12+2×4×12+2×6×4=144+96+48=288.
三、解答题
8.一种长方体牛奶包装盒的长、宽、高分别为6,4,12.为了生产这种包装盒,需要先画出展开图纸样.
(1)如图,给出甲、乙、丙三种纸样,其中正确的是 ;?
(2)从已知正确的纸样中选出一种,在图中标注上尺寸;
(3)利用你所选的一种纸样,求出包装盒的表面积.
9.[2020福建宁德期末]如图,用10个大小相同的小立方块搭成一个组合体.
(1)请在指定位置画出该组合体从左面、上面看到的形状图;
(2)在不改变该组合体中小立方块个数的前提下,从中移动一个小立方块,使所得新组合体与原组合体相比,从左面、上面看到的形状图保持不变,但从正面看到的形状图改变了,请画出新组合体从正面看到的所有可能的形状图.(所给的方格图不一定全用,不够可添)
答案
9.【解析】 (1)如图所示.
(2)如图所示.
第一章·丰富的图形世界(中考真题)
数学·七年级上册·北师
答案
1.C
1.[2019江苏盐城中考]如图是由6个相同的小正方体搭成的物体,该物体从正面看到的形状图是 ( )
答案
2.D
2.[2019湖北襄阳中考]某正方体的平面展开图如图所示,则原正方体中与“春”字所在的面相对的面上的字是 ( )
A.青 B.来 C.斗 D.奋
答案
3.B 【解析】 由题意可知,该几何体为四棱锥,所以它的底面是四边形.故选B.
3.[2019江苏连云港中考]一个几何体的侧面展开图如图所示,则该几何体的底面是 ( )
答案
4.C
4.[2019四川达州中考]如图是由7个相同的小立方块所搭成的几何体从上面看到的形状图,小正方形中的数字表示该位置小立方块的个数,这个几何体从左面看到的形状图是 ( )
答案
5.D
5.[2019广西南宁中考]如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是 ( )
答案
6.C 【解析】 C项中的图形不能围成正方体,不符合题意.故选C.
6.[2018四川巴中中考]毕业前夕,同学们准备了一份礼物送给自己的母校.现用一个正方体盒子进行包装,六个面上分别写上“祝、母、校、更、美、丽”,其中“祝”与“更”,“母”与“美”在相对的面上.则此包装盒的展开图(不考虑文字方向)不可能是( )
答案
7.B 【解析】 根据涂有颜色一面的位置,排除A,C项;D中的图形不是这个几何体的表面展开图,排除D.故选B.
7.[2019山东济宁中考]如图,一个几何体上半部为正四棱锥,下半部为正方体,且有一个面涂有颜色,该几何体的表面展开图是 ( )
答案
8.B 【解析】 由从上面看到的形状图可得该组合体的最底层有5个小立方块,由从正面看到的形状图可得第二层有2个,3个或4个小立方块,则组成这个组合体的小立方块的个数是7个,8个或9个,所以组成这个组合体的小立方块的个数最多是9个.故选B.
8.[2019四川宜宾中考]已知一个组合体是由几个相同的小立方块叠合在一起组成,该组合体从正面看到的形状图与从上面看到的形状图如图所示,则该组合体中小立方块的个数最多是 ( )
A.10 B.9
C.8 D.7
答案
9.B 【解析】 由题图可知,涂色部分的面积是从上、前、右三个方向所涂面积的和,即涂色部分面积为4+4+3=11.故选B.
9.[2018山东烟台中考]由5个棱长为1的小立方块组成的几何体如图放置,一面着地,两面靠墙.若要将露出来的部分涂色,则涂色部分的面积为 ( )
A.9 B.11 C.14 D.18
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
