二项式定理1
图片预览











文档简介
(共36张PPT)
主讲:高 李
二项式定理(一)
提出问题:
提出问题:
1. 在n=1,2,3时,写出并研究(a+b)n的展开式. (a+b)1=____________________, (a+b)2=____________________, (a+b)3=____________________.
提出问题:
1. 在n=1,2,3时,写出并研究(a+b)n的展开式. (a+b)1=____________________, (a+b)2=____________________, (a+b)3=____________________.
a+b
提出问题:
1. 在n=1,2,3时,写出并研究(a+b)n的展开式. (a+b)1=____________________, (a+b)2=____________________, (a+b)3=____________________.
a+b
a2+2ab+b2
提出问题:
1. 在n=1,2,3时,写出并研究(a+b)n的展开式. (a+b)1=____________________, (a+b)2=____________________, (a+b)3=____________________.
a+b
a2+2ab+b2
a3+3a2b+3ab2+b3
提出问题:
1. 在n=1,2,3时,写出并研究(a+b)n的展开式. (a+b)1=____________________, (a+b)2=____________________, (a+b)3=____________________.
a+b
a2+2ab+b2
a3+3a2b+3ab2+b3
结合左边的次数分析: 展开式中的项数、次数(a、b各自次数)每一项的系数规律.
2. 在n=4时,猜测(a+b)4的展开式. (a+b)4=_________________________.
2. 在n=4时,猜测(a+b)4的展开式. (a+b)4=_________________________.
a4+4a3b+6a2b2+4ab3+b4
复习引入
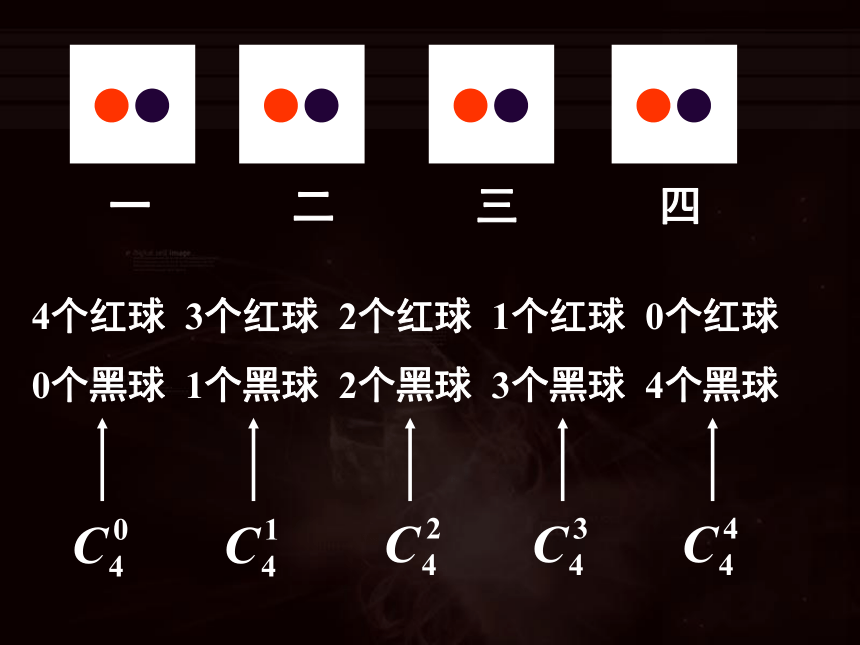
一
二
三
四
问题1:4个容器中有相同的红、黑玻璃球各一个,从每个容器中取一个球,有多少不同的结果?
一
二
三
四
4个红球 3个红球 2个红球 1个红球 0个红球 0个黑球 1个黑球 2个黑球 3个黑球 4个黑球
问题2:(a+b)4展开后有哪些项?各项的系数分别是什么?
问题2:(a+b)4展开后有哪些项?各项的系数分别是什么?
(a+b)4= (a+b) (a+b) (a+b) (a+b)
项
系数
都
不
取
b
取
一
个
b
取
两
个
b
取
三
个
b
取
四
个
b
a4
a3b
a2b2
ab3
b4
都
不
取
b
取
一
个
b
取
两
个
b
取
三
个
b
取
四
个
b
项
系数
a4
a3b
a2b2
ab3
b4
(a+b)的n次方展开式的系数的规律:
1
1
1
1
1
1
1
1
1
1
1
1
1
2
3
3
4
4
6
5
5
10
10
6
6
15
20
15
归纳提升
将(a+b)n展开的结果又是怎样呢?
将(a+b)n展开的结果又是怎样呢?
n个
引出定理,总结特征
二项式定理:
二项式定理:
该公式所表示的定理叫做二项式定理. 公式右边的多项式叫做(a+b)n的展开式,其中的系数Cnr(r=0,1,2,……,n)叫做二项式系数,式中的Cnran-rbr叫做二项展开式的通项,用Tr+1表示,即通项为展开式的第r+1项.
二项式定理:
例题分析
1. 求二项式的展开式:
[例1]
1. 求二项式的展开式:
[例1]
[例2]
2. 展开式的指定项:
[例3]
[例4]
3. 求指定项的系数:
课堂练习
课本P31
课堂小结
① 项数:共n+1项,是关于a与b的齐次多项式; ② 指数:a的指数从n逐项递减到0,是降幂排列;b的指数从0逐项递增到n,是升幂排列.
[ 杨辉简介 ] 南宋末年钱塘人,是当时有名的数学家和教育家,杨辉一生编写的数学书很多,但散佚严重.
杨辉生活在浙江杭州一带,曾当过地方官,到过苏州、台州等地,他每到一处都会有人慕名前来请教数学问题.
作业布置
《考一本》配套练习
主讲:高 李
二项式定理(一)
提出问题:
提出问题:
1. 在n=1,2,3时,写出并研究(a+b)n的展开式. (a+b)1=____________________, (a+b)2=____________________, (a+b)3=____________________.
提出问题:
1. 在n=1,2,3时,写出并研究(a+b)n的展开式. (a+b)1=____________________, (a+b)2=____________________, (a+b)3=____________________.
a+b
提出问题:
1. 在n=1,2,3时,写出并研究(a+b)n的展开式. (a+b)1=____________________, (a+b)2=____________________, (a+b)3=____________________.
a+b
a2+2ab+b2
提出问题:
1. 在n=1,2,3时,写出并研究(a+b)n的展开式. (a+b)1=____________________, (a+b)2=____________________, (a+b)3=____________________.
a+b
a2+2ab+b2
a3+3a2b+3ab2+b3
提出问题:
1. 在n=1,2,3时,写出并研究(a+b)n的展开式. (a+b)1=____________________, (a+b)2=____________________, (a+b)3=____________________.
a+b
a2+2ab+b2
a3+3a2b+3ab2+b3
结合左边的次数分析: 展开式中的项数、次数(a、b各自次数)每一项的系数规律.
2. 在n=4时,猜测(a+b)4的展开式. (a+b)4=_________________________.
2. 在n=4时,猜测(a+b)4的展开式. (a+b)4=_________________________.
a4+4a3b+6a2b2+4ab3+b4
复习引入
一
二
三
四
问题1:4个容器中有相同的红、黑玻璃球各一个,从每个容器中取一个球,有多少不同的结果?
一
二
三
四
4个红球 3个红球 2个红球 1个红球 0个红球 0个黑球 1个黑球 2个黑球 3个黑球 4个黑球
问题2:(a+b)4展开后有哪些项?各项的系数分别是什么?
问题2:(a+b)4展开后有哪些项?各项的系数分别是什么?
(a+b)4= (a+b) (a+b) (a+b) (a+b)
项
系数
都
不
取
b
取
一
个
b
取
两
个
b
取
三
个
b
取
四
个
b
a4
a3b
a2b2
ab3
b4
都
不
取
b
取
一
个
b
取
两
个
b
取
三
个
b
取
四
个
b
项
系数
a4
a3b
a2b2
ab3
b4
(a+b)的n次方展开式的系数的规律:
1
1
1
1
1
1
1
1
1
1
1
1
1
2
3
3
4
4
6
5
5
10
10
6
6
15
20
15
归纳提升
将(a+b)n展开的结果又是怎样呢?
将(a+b)n展开的结果又是怎样呢?
n个
引出定理,总结特征
二项式定理:
二项式定理:
该公式所表示的定理叫做二项式定理. 公式右边的多项式叫做(a+b)n的展开式,其中的系数Cnr(r=0,1,2,……,n)叫做二项式系数,式中的Cnran-rbr叫做二项展开式的通项,用Tr+1表示,即通项为展开式的第r+1项.
二项式定理:
例题分析
1. 求二项式的展开式:
[例1]
1. 求二项式的展开式:
[例1]
[例2]
2. 展开式的指定项:
[例3]
[例4]
3. 求指定项的系数:
课堂练习
课本P31
课堂小结
① 项数:共n+1项,是关于a与b的齐次多项式; ② 指数:a的指数从n逐项递减到0,是降幂排列;b的指数从0逐项递增到n,是升幂排列.
[ 杨辉简介 ] 南宋末年钱塘人,是当时有名的数学家和教育家,杨辉一生编写的数学书很多,但散佚严重.
杨辉生活在浙江杭州一带,曾当过地方官,到过苏州、台州等地,他每到一处都会有人慕名前来请教数学问题.
作业布置
《考一本》配套练习
