二项式定理2
图片预览


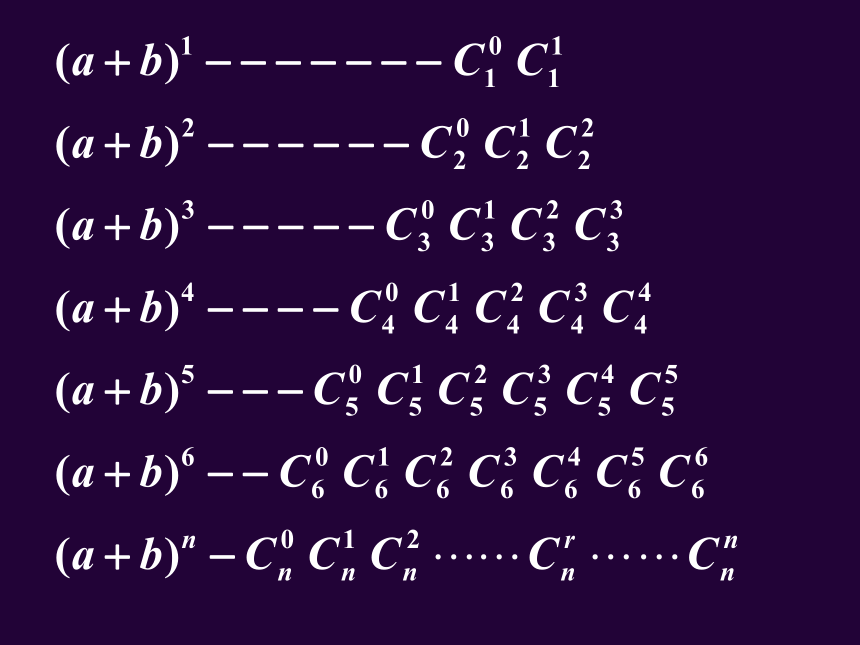
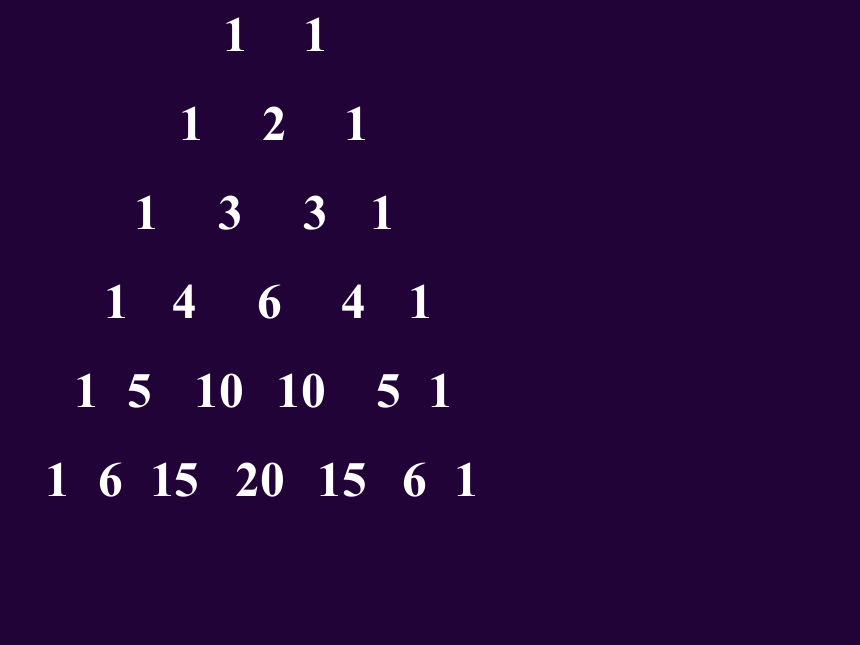
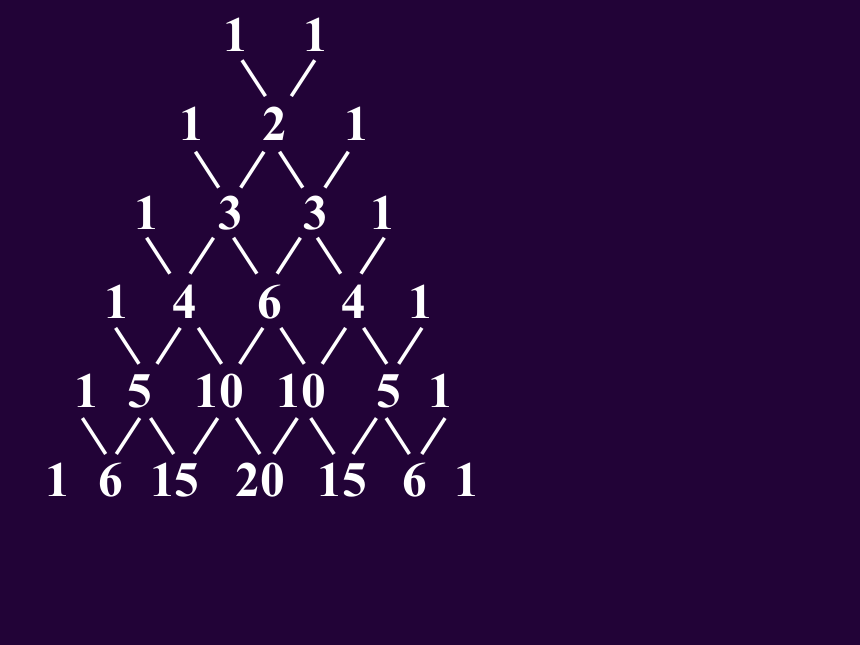




文档简介
(共33张PPT)
二项式定理
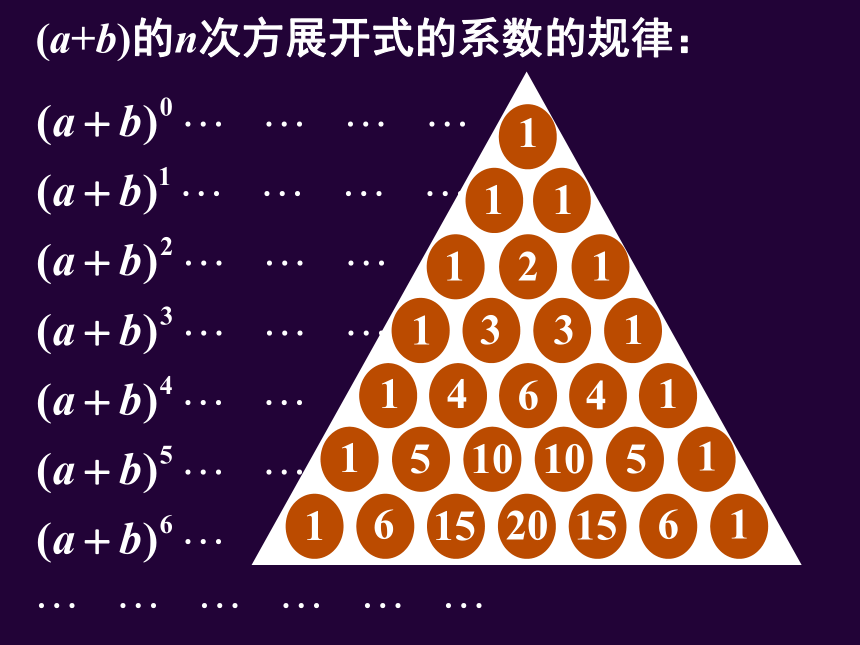
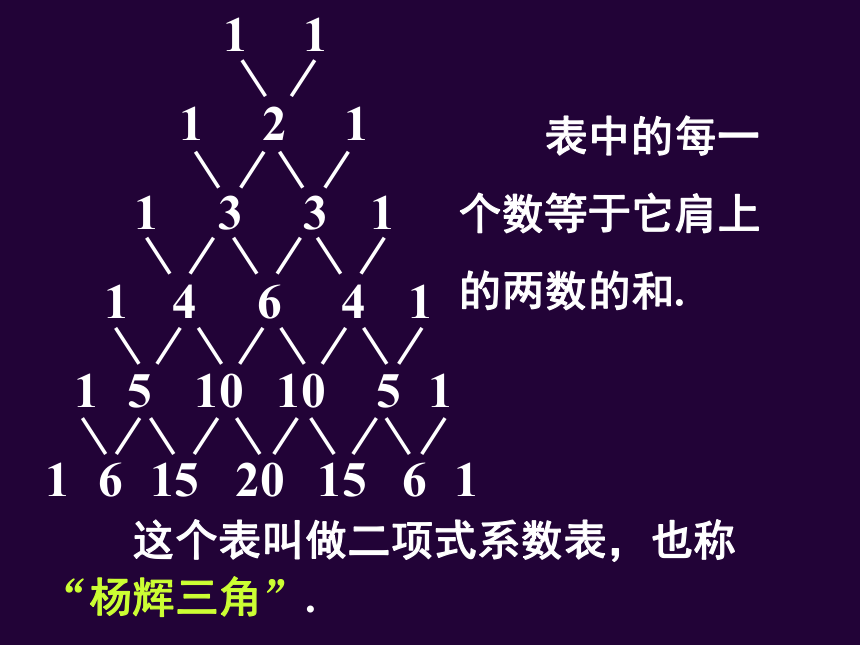
(a+b)的n次方展开式的系数的规律:
1
1
1
1
1
1
1
1
1
1
1
1
1
2
3
3
4
4
6
5
5
10
10
6
6
15
20
15
表中的每一个数等于它肩上的两数的和.
这个表叫做二项式系数表,也称
“杨辉三角”.
表中的每一个数等于它肩上的两数的和.
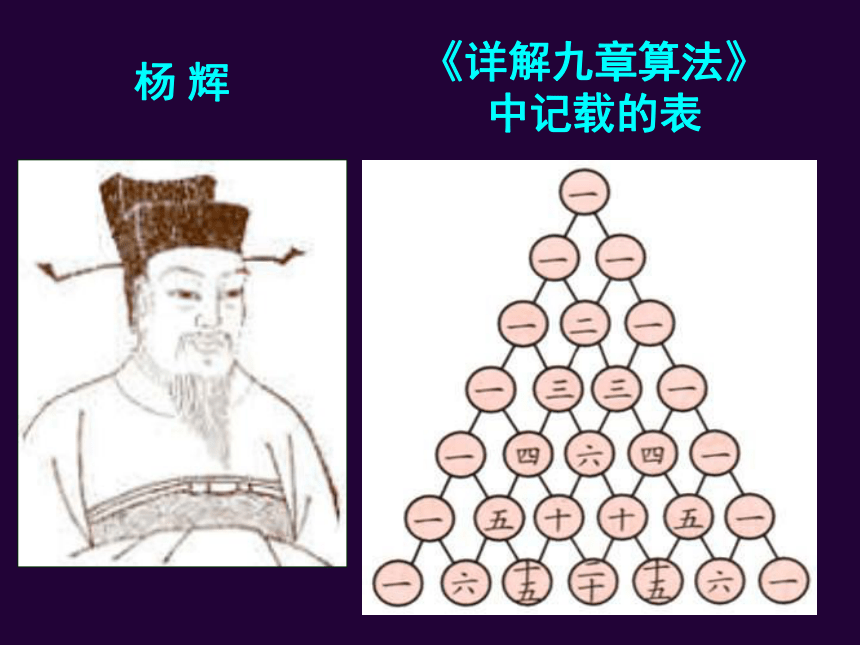
类似上面的表,早在我 国南宋数
学家杨辉1261年所著的《详解九章算
法》一书里就已经出现了,这个表称
为杨辉三角. 在书中,还说明了表里
“一”以外的每一个数都等于它肩上
两个数的和,杨辉指出这个方法出于
《释锁》算书,且我国北宋数学家贾
宪(约公元11世纪)已经用过它.
这表明我国发现这个表不晚于11
世纪. 在欧洲,这个表被认为是法国数
学家帕斯卡(1623-1662)首先发现的,
他们把这个表叫做帕斯卡三角. 这就是
说,杨辉三角的发现要比欧洲早五百
年左右,由此可见我国古代数学的成
就是非常值得中华民族自豪的.
[ 杨辉简介 ] 南宋末年钱塘人,是当时有名的数学家和教育家,杨辉一生编写的数学书很多,但散佚严重.
杨辉生活在浙江杭州一带,曾当过地方官,到过苏州、台州等地,他每到一处都会有人慕名前来请教数学问题.
《详解九章算法》
中记载的表
杨 辉
性质1:对称性 与首末两端
“等距离”的两
个二项式系数相
等.
性质1:对称性 与首末两端
“等距离”的两
个二项式系数相
等.
练习:
练习:
B
B
6
练习:
当n为偶数如
2、4、6时,中间
一项最大;
当n为偶数如
2、4、6时,中间
一项最大;
当n为奇数如
1、3、5时,中间
两项最大.
性质2: 增减性与最大值 先增后减
[例1]
[例2]
课本P35
课 堂 练 习
课本1.3 A组第1-8题
B组第1、2题(书上);
2.《考一本》配套练习
作 业 布 置
二项式定理
(a+b)的n次方展开式的系数的规律:
1
1
1
1
1
1
1
1
1
1
1
1
1
2
3
3
4
4
6
5
5
10
10
6
6
15
20
15
表中的每一个数等于它肩上的两数的和.
这个表叫做二项式系数表,也称
“杨辉三角”.
表中的每一个数等于它肩上的两数的和.
类似上面的表,早在我 国南宋数
学家杨辉1261年所著的《详解九章算
法》一书里就已经出现了,这个表称
为杨辉三角. 在书中,还说明了表里
“一”以外的每一个数都等于它肩上
两个数的和,杨辉指出这个方法出于
《释锁》算书,且我国北宋数学家贾
宪(约公元11世纪)已经用过它.
这表明我国发现这个表不晚于11
世纪. 在欧洲,这个表被认为是法国数
学家帕斯卡(1623-1662)首先发现的,
他们把这个表叫做帕斯卡三角. 这就是
说,杨辉三角的发现要比欧洲早五百
年左右,由此可见我国古代数学的成
就是非常值得中华民族自豪的.
[ 杨辉简介 ] 南宋末年钱塘人,是当时有名的数学家和教育家,杨辉一生编写的数学书很多,但散佚严重.
杨辉生活在浙江杭州一带,曾当过地方官,到过苏州、台州等地,他每到一处都会有人慕名前来请教数学问题.
《详解九章算法》
中记载的表
杨 辉
性质1:对称性 与首末两端
“等距离”的两
个二项式系数相
等.
性质1:对称性 与首末两端
“等距离”的两
个二项式系数相
等.
练习:
练习:
B
B
6
练习:
当n为偶数如
2、4、6时,中间
一项最大;
当n为偶数如
2、4、6时,中间
一项最大;
当n为奇数如
1、3、5时,中间
两项最大.
性质2: 增减性与最大值 先增后减
[例1]
[例2]
课本P35
课 堂 练 习
课本1.3 A组第1-8题
B组第1、2题(书上);
2.《考一本》配套练习
作 业 布 置
