单摆
图片预览









文档简介
(共78张PPT)
一、单摆
1.在细线的一端拴一小球,另一端固定在悬点上,如果悬挂小球的细线的伸缩和质量可以忽略,线长又比球的直径大得多,这样的装置就叫做单摆。
单摆的概念:
1.在细线的一端拴一小球,另一端固定在悬点上,如果悬挂小球的细线的伸缩和质量可以忽略,线长又比球的直径大得多,这样的装置就叫做单摆。
单摆的概念:
1.在细线的一端拴一小球,另一端固定在悬点上,如果悬挂小球的细线的伸缩和质量可以忽略,线长又比球的直径大得多,这样的装置就叫做单摆。
2. 实际摆能看成单摆 的条件:L线》R球 ,m球》 m线,摆线不可伸长。
单摆的概念:
1.在细线的一端拴一小球,另一端固定在悬点上,如果悬挂小球的细线的伸缩和质量可以忽略,线长又比球的直径大得多,这样的装置就叫做单摆。
2. 实际摆能看成单摆 的条件:L线》R球 ,m球》 m线,摆线不可伸长。
3. 单摆是实际摆的理 想化的物理模型。
课堂训练
用下列哪些材料能做成单摆( )
A.长为1米的细线
B.长为1米的细铁丝
C.长为0.2米的细丝线
D.长为1米的麻绳
E.直径为5厘米的泡沫塑料球
F.直径为1厘米的钢球
G.直径为1厘米的塑料球
H.直径为5厘米的钢球
课堂训练
悬线:细、长、伸缩可以忽略
用下列哪些材料能做成单摆( )
A.长为1米的细线
B.长为1米的细铁丝
C.长为0.2米的细丝线
D.长为1米的麻绳
E.直径为5厘米的泡沫塑料球
F.直径为1厘米的钢球
G.直径为1厘米的塑料球
H.直径为5厘米的钢球
课堂训练
悬线:细、长、伸缩可以忽略
摆球:小而重(即密度大)
用下列哪些材料能做成单摆( )
A.长为1米的细线
B.长为1米的细铁丝
C.长为0.2米的细丝线
D.长为1米的麻绳
E.直径为5厘米的泡沫塑料球
F.直径为1厘米的钢球
G.直径为1厘米的塑料球
H.直径为5厘米的钢球
课堂训练
悬线:细、长、伸缩可以忽略
摆球:小而重(即密度大)
用下列哪些材料能做成单摆( )
A.长为1米的细线
B.长为1米的细铁丝
C.长为0.2米的细丝线
D.长为1米的麻绳
E.直径为5厘米的泡沫塑料球
F.直径为1厘米的钢球
G.直径为1厘米的塑料球
H.直径为5厘米的钢球
A、F
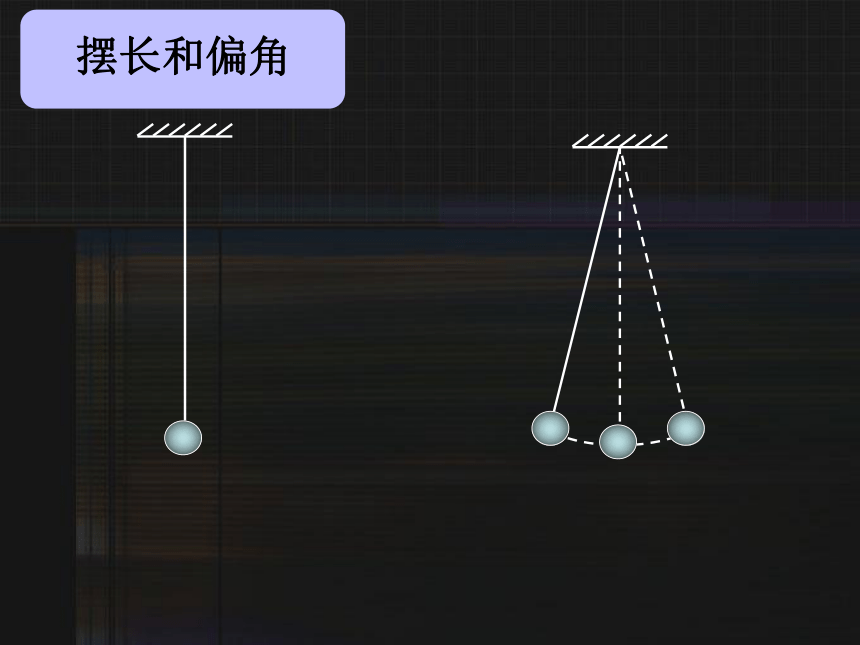
摆长和偏角
摆长:摆球重心到摆动圆弧圆心的距离
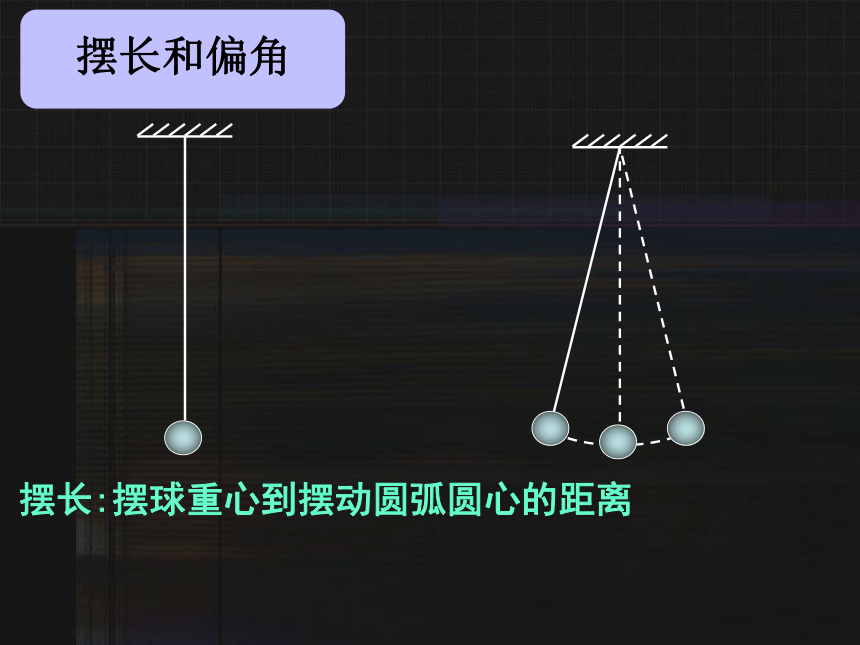
摆长和偏角
摆长:摆球重心到摆动圆弧圆心的距离
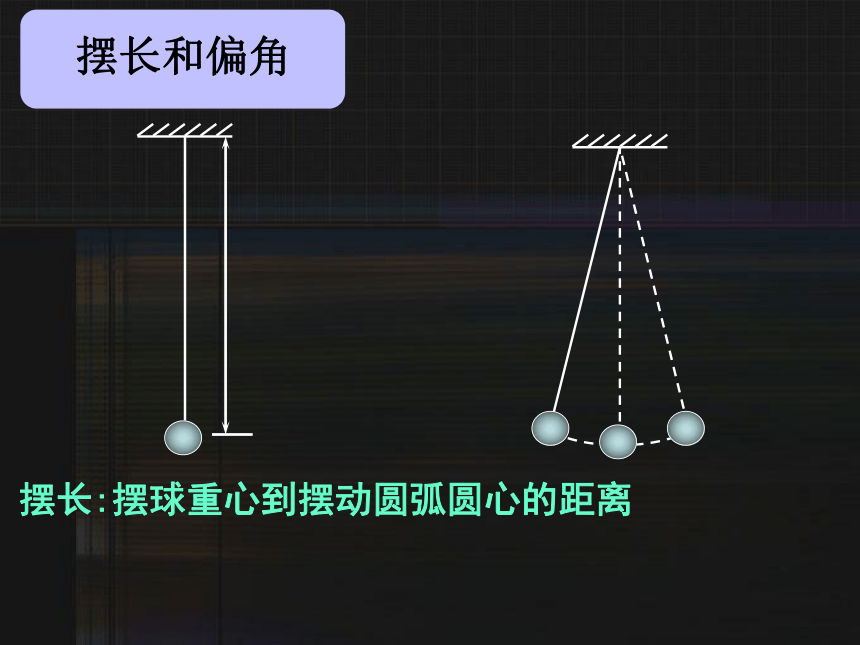
摆长和偏角
摆长 L=L0+R
摆长:摆球重心到摆动圆弧圆心的距离
摆长和偏角
摆长 L=L0+R
摆长:摆球重心到摆动圆弧圆心的距离
摆长和偏角
偏角:摆球摆到最高点时,细线与竖直方向的夹角
摆长 L=L0+R
摆长:摆球重心到摆动圆弧圆心的距离
摆长和偏角
θ
偏角
偏角:摆球摆到最高点时,细线与竖直方向的夹角
思考与讨论
单摆振动是不是简谐运动?
思考与讨论
单摆振动是不是简谐运动?
判断物体是否做简谐运动的方法:
思考与讨论
单摆振动是不是简谐运动?
判断物体是否做简谐运动的方法:
(1)根据物体的振动图像去判断
思考与讨论
单摆振动是不是简谐运动?
判断物体是否做简谐运动的方法:
(2)根据回复力的规律F=-kx去判断
(1)根据物体的振动图像去判断
C
B
A
O
二、单摆的回复力
θ
C
B
A
O
1.平衡位置:
二、单摆的回复力
θ
C
B
A
O
1.平衡位置:
二、单摆的回复力
θ
最低点O
C
B
A
O
1.平衡位置:
二、单摆的回复力
θ
最低点O
2.受力分析:
C
2.受力分析:
B
A
O
1.平衡位置:
二、单摆的回复力
θ
T
G
最低点O
C
2.受力分析:
B
A
O
1.平衡位置:
二、单摆的回复力
θ
T
G
最低点O
3.回复力来源:
C
2.受力分析:
B
A
O
3.回复力来源:
1.平衡位置:
二、单摆的回复力
θ
T
G
G2
G1
最低点O
C
2.受力分析:
B
A
O
3.回复力来源:
重力沿切线方向的分力G2
1.平衡位置:
二、单摆的回复力
θ
T
G
G2
G1
最低点O
C
2.受力分析:
B
A
O
3.回复力来源:
重力沿切线方向的分力G2
1.平衡位置:
二、单摆的回复力
大小:
θ
T
G
G2
G1
最低点O
C
2.受力分析:
B
A
O
3.回复力来源:
重力沿切线方向的分力G2
1.平衡位置:
二、单摆的回复力
大小:
G2=Gsinθ=mgsinθ
θ
T
G
G2
G1
最低点O
C
2.受力分析:
B
A
O
3.回复力来源:
重力沿切线方向的分力G2
1.平衡位置:
二、单摆的回复力
大小:
G2=Gsinθ=mgsinθ
方向:
θ
T
G
G2
G1
最低点O
C
2.受力分析:
B
A
O
3.回复力来源:
重力沿切线方向的分力G2
1.平衡位置:
二、单摆的回复力
大小:
G2=Gsinθ=mgsinθ
方向:
沿切线指向平衡位置
θ
T
G
G2
G1
最低点O
x
x
x
x
x
x
当θ很小时,x≈弧长
x
sinθ≈θ
=Lθ
当θ很小时,x≈弧长
x
当θ很小时,x≈弧长
F=G2=Gsinθ=mgsinθ
sinθ≈θ
=Lθ
x
F=G2=Gsinθ=mgsinθ
sinθ≈θ
=Lθ
当θ很小时,x≈弧长
x
F=G2=Gsinθ=mgsinθ
sinθ≈θ
=Lθ
当θ很小时,x≈弧长
x
F=G2=Gsinθ=mgsinθ
位移方向与回复力方向相反
sinθ≈θ
=Lθ
当θ很小时,x≈弧长
x
F=G2=Gsinθ=mgsinθ
位移方向与回复力方向相反
sinθ≈θ
=Lθ
当θ很小时,x≈弧长
x
F=G2=Gsinθ=mgsinθ
位移方向与回复力方向相反
sinθ≈θ
=Lθ
当θ很小时,x≈弧长
x
F=G2=Gsinθ=mgsinθ
位移方向与回复力方向相反
sinθ≈θ
=Lθ
当θ很小时,x≈弧长
结 论
在摆角很小的情况下,摆球所受的回复力跟位移大小成正比,方向始终指向平衡位置(即与位移方向相反),因此单摆做简谐运动
结 论
在摆角很小的情况下,摆球所受的回复力跟位移大小成正比,方向始终指向平衡位置(即与位移方向相反),因此单摆做简谐运动
结 论
在摆角很小的情况下,摆球所受的回复力跟位移大小成正比,方向始终指向平衡位置(即与位移方向相反),因此单摆做简谐运动
一般偏角θ< 5°
结 论
在摆角很小的情况下,摆球所受的回复力跟位移大小成正比,方向始终指向平衡位置(即与位移方向相反),因此单摆做简谐运动
三、单摆的周期
单摆振动的周期可能与哪些因素有关呢?
三、单摆的周期
单摆振动的周期可能与哪些因素有关呢?
1.周期与振幅是否有关
三、单摆的周期
单摆振动的周期可能与哪些因素有关呢?
1.周期与振幅是否有关
2.周期与摆球的质量是否有关
三、单摆的周期
单摆振动的周期可能与哪些因素有关呢?
1.周期与振幅是否有关
2.周期与摆球的质量是否有关
3.周期与摆长是否有关
三、单摆的周期
单摆振动的周期可能与哪些因素有关呢?
1.周期与振幅是否有关
2.周期与摆球的质量是否有关
3.周期与摆长是否有关
4.周期与重力加速度是否有关
三、单摆的周期
单摆振动的周期可能与哪些因素有关呢?
1.周期与振幅是否有关
2.周期与摆球的质量是否有关
3.周期与摆长是否有关
4.周期与重力加速度是否有关
探究方法:控制变量法
三、单摆的周期
4.与当地的重力加速度有关——重力加速 度越大,周期越小
单摆振动的周期
1.与振幅无关——单摆的等时性
伽利略首先发现的
2.与摆球的质量无关
3.与摆长有关——摆长越长,周期越大
结 论
单摆振动的周期公式:
单摆振动的周期公式:
单摆振动的周期公式:
荷兰物理学家惠更斯首先发现
单摆振动的周期公式:
单摆做简谐运动的振动周期跟摆长的平方根成正比,跟重力加速度的平方根成反比。
荷兰物理学家惠更斯首先发现
四、单摆周期公式的应用
1.惠更斯利用摆的等时性发明了带摆的计时器.
四、单摆周期公式的应用
1.惠更斯利用摆的等时性发明了带摆的计时器.
2.用单摆测定重力加速度。
四、单摆周期公式的应用
1.惠更斯利用摆的等时性发明了带摆的计时器.
2.用单摆测定重力加速度。
四、单摆周期公式的应用
1.惠更斯利用摆的等时性发明了带摆的计时器.
2.用单摆测定重力加速度。
四、单摆周期公式的应用
1.单摆作简谐运动时的回复力是( )
A.摆球的重力
B.摆球重力沿圆弧切线的分力
C.摆线的拉力
D.摆球重力与摆线拉力的合力
课堂训练
1.单摆作简谐运动时的回复力是( )
A.摆球的重力
B.摆球重力沿圆弧切线的分力
C.摆线的拉力
D.摆球重力与摆线拉力的合力
B
课堂训练
2.一个单摆,周期是T。
a. 如果摆球质量增到2倍,周期将 ;
b. 如果摆的振幅增到2倍,周期将 ;
c. 如果摆长增到2倍,周期将 ;
d. 如果将单摆从赤道移到北京,周期将 ;
e. 如果将单摆从海面移到高山,周期将 ;
课堂训练
2.一个单摆,周期是T。
a. 如果摆球质量增到2倍,周期将 ;
b. 如果摆的振幅增到2倍,周期将 ;
c. 如果摆长增到2倍,周期将 ;
d. 如果将单摆从赤道移到北京,周期将 ;
e. 如果将单摆从海面移到高山,周期将 ;
不变
课堂训练
2.一个单摆,周期是T。
a. 如果摆球质量增到2倍,周期将 ;
b. 如果摆的振幅增到2倍,周期将 ;
c. 如果摆长增到2倍,周期将 ;
d. 如果将单摆从赤道移到北京,周期将 ;
e. 如果将单摆从海面移到高山,周期将 ;
不变
不变
课堂训练
2.一个单摆,周期是T。
a. 如果摆球质量增到2倍,周期将 ;
b. 如果摆的振幅增到2倍,周期将 ;
c. 如果摆长增到2倍,周期将 ;
d. 如果将单摆从赤道移到北京,周期将 ;
e. 如果将单摆从海面移到高山,周期将 ;
变大
不变
不变
课堂训练
2.一个单摆,周期是T。
a. 如果摆球质量增到2倍,周期将 ;
b. 如果摆的振幅增到2倍,周期将 ;
c. 如果摆长增到2倍,周期将 ;
d. 如果将单摆从赤道移到北京,周期将 ;
e. 如果将单摆从海面移到高山,周期将 ;
变小
变大
不变
不变
课堂训练
2.一个单摆,周期是T。
a. 如果摆球质量增到2倍,周期将 ;
b. 如果摆的振幅增到2倍,周期将 ;
c. 如果摆长增到2倍,周期将 ;
d. 如果将单摆从赤道移到北京,周期将 ;
e. 如果将单摆从海面移到高山,周期将 ;
变小
变大
变大
不变
不变
课堂训练
小明家从广州搬到北京去,搬家时把家中的大摆钟也带到北京去了。 问:1.这个摆钟到 北京后是否还准时 2.若不准,是偏慢还是偏快 3.如须调整应该怎样调节
课堂训练
3.一摆长为L的单摆,在悬点正下方5L/9处有一钉子,则这个单摆的周期是多少?
课堂训练
3.一摆长为L的单摆,在悬点正下方5L/9处有一钉子,则这个单摆的周期是多少?
课堂训练
一、单摆
1.在细线的一端拴一小球,另一端固定在悬点上,如果悬挂小球的细线的伸缩和质量可以忽略,线长又比球的直径大得多,这样的装置就叫做单摆。
单摆的概念:
1.在细线的一端拴一小球,另一端固定在悬点上,如果悬挂小球的细线的伸缩和质量可以忽略,线长又比球的直径大得多,这样的装置就叫做单摆。
单摆的概念:
1.在细线的一端拴一小球,另一端固定在悬点上,如果悬挂小球的细线的伸缩和质量可以忽略,线长又比球的直径大得多,这样的装置就叫做单摆。
2. 实际摆能看成单摆 的条件:L线》R球 ,m球》 m线,摆线不可伸长。
单摆的概念:
1.在细线的一端拴一小球,另一端固定在悬点上,如果悬挂小球的细线的伸缩和质量可以忽略,线长又比球的直径大得多,这样的装置就叫做单摆。
2. 实际摆能看成单摆 的条件:L线》R球 ,m球》 m线,摆线不可伸长。
3. 单摆是实际摆的理 想化的物理模型。
课堂训练
用下列哪些材料能做成单摆( )
A.长为1米的细线
B.长为1米的细铁丝
C.长为0.2米的细丝线
D.长为1米的麻绳
E.直径为5厘米的泡沫塑料球
F.直径为1厘米的钢球
G.直径为1厘米的塑料球
H.直径为5厘米的钢球
课堂训练
悬线:细、长、伸缩可以忽略
用下列哪些材料能做成单摆( )
A.长为1米的细线
B.长为1米的细铁丝
C.长为0.2米的细丝线
D.长为1米的麻绳
E.直径为5厘米的泡沫塑料球
F.直径为1厘米的钢球
G.直径为1厘米的塑料球
H.直径为5厘米的钢球
课堂训练
悬线:细、长、伸缩可以忽略
摆球:小而重(即密度大)
用下列哪些材料能做成单摆( )
A.长为1米的细线
B.长为1米的细铁丝
C.长为0.2米的细丝线
D.长为1米的麻绳
E.直径为5厘米的泡沫塑料球
F.直径为1厘米的钢球
G.直径为1厘米的塑料球
H.直径为5厘米的钢球
课堂训练
悬线:细、长、伸缩可以忽略
摆球:小而重(即密度大)
用下列哪些材料能做成单摆( )
A.长为1米的细线
B.长为1米的细铁丝
C.长为0.2米的细丝线
D.长为1米的麻绳
E.直径为5厘米的泡沫塑料球
F.直径为1厘米的钢球
G.直径为1厘米的塑料球
H.直径为5厘米的钢球
A、F
摆长和偏角
摆长:摆球重心到摆动圆弧圆心的距离
摆长和偏角
摆长:摆球重心到摆动圆弧圆心的距离
摆长和偏角
摆长 L=L0+R
摆长:摆球重心到摆动圆弧圆心的距离
摆长和偏角
摆长 L=L0+R
摆长:摆球重心到摆动圆弧圆心的距离
摆长和偏角
偏角:摆球摆到最高点时,细线与竖直方向的夹角
摆长 L=L0+R
摆长:摆球重心到摆动圆弧圆心的距离
摆长和偏角
θ
偏角
偏角:摆球摆到最高点时,细线与竖直方向的夹角
思考与讨论
单摆振动是不是简谐运动?
思考与讨论
单摆振动是不是简谐运动?
判断物体是否做简谐运动的方法:
思考与讨论
单摆振动是不是简谐运动?
判断物体是否做简谐运动的方法:
(1)根据物体的振动图像去判断
思考与讨论
单摆振动是不是简谐运动?
判断物体是否做简谐运动的方法:
(2)根据回复力的规律F=-kx去判断
(1)根据物体的振动图像去判断
C
B
A
O
二、单摆的回复力
θ
C
B
A
O
1.平衡位置:
二、单摆的回复力
θ
C
B
A
O
1.平衡位置:
二、单摆的回复力
θ
最低点O
C
B
A
O
1.平衡位置:
二、单摆的回复力
θ
最低点O
2.受力分析:
C
2.受力分析:
B
A
O
1.平衡位置:
二、单摆的回复力
θ
T
G
最低点O
C
2.受力分析:
B
A
O
1.平衡位置:
二、单摆的回复力
θ
T
G
最低点O
3.回复力来源:
C
2.受力分析:
B
A
O
3.回复力来源:
1.平衡位置:
二、单摆的回复力
θ
T
G
G2
G1
最低点O
C
2.受力分析:
B
A
O
3.回复力来源:
重力沿切线方向的分力G2
1.平衡位置:
二、单摆的回复力
θ
T
G
G2
G1
最低点O
C
2.受力分析:
B
A
O
3.回复力来源:
重力沿切线方向的分力G2
1.平衡位置:
二、单摆的回复力
大小:
θ
T
G
G2
G1
最低点O
C
2.受力分析:
B
A
O
3.回复力来源:
重力沿切线方向的分力G2
1.平衡位置:
二、单摆的回复力
大小:
G2=Gsinθ=mgsinθ
θ
T
G
G2
G1
最低点O
C
2.受力分析:
B
A
O
3.回复力来源:
重力沿切线方向的分力G2
1.平衡位置:
二、单摆的回复力
大小:
G2=Gsinθ=mgsinθ
方向:
θ
T
G
G2
G1
最低点O
C
2.受力分析:
B
A
O
3.回复力来源:
重力沿切线方向的分力G2
1.平衡位置:
二、单摆的回复力
大小:
G2=Gsinθ=mgsinθ
方向:
沿切线指向平衡位置
θ
T
G
G2
G1
最低点O
x
x
x
x
x
x
当θ很小时,x≈弧长
x
sinθ≈θ
=Lθ
当θ很小时,x≈弧长
x
当θ很小时,x≈弧长
F=G2=Gsinθ=mgsinθ
sinθ≈θ
=Lθ
x
F=G2=Gsinθ=mgsinθ
sinθ≈θ
=Lθ
当θ很小时,x≈弧长
x
F=G2=Gsinθ=mgsinθ
sinθ≈θ
=Lθ
当θ很小时,x≈弧长
x
F=G2=Gsinθ=mgsinθ
位移方向与回复力方向相反
sinθ≈θ
=Lθ
当θ很小时,x≈弧长
x
F=G2=Gsinθ=mgsinθ
位移方向与回复力方向相反
sinθ≈θ
=Lθ
当θ很小时,x≈弧长
x
F=G2=Gsinθ=mgsinθ
位移方向与回复力方向相反
sinθ≈θ
=Lθ
当θ很小时,x≈弧长
x
F=G2=Gsinθ=mgsinθ
位移方向与回复力方向相反
sinθ≈θ
=Lθ
当θ很小时,x≈弧长
结 论
在摆角很小的情况下,摆球所受的回复力跟位移大小成正比,方向始终指向平衡位置(即与位移方向相反),因此单摆做简谐运动
结 论
在摆角很小的情况下,摆球所受的回复力跟位移大小成正比,方向始终指向平衡位置(即与位移方向相反),因此单摆做简谐运动
结 论
在摆角很小的情况下,摆球所受的回复力跟位移大小成正比,方向始终指向平衡位置(即与位移方向相反),因此单摆做简谐运动
一般偏角θ< 5°
结 论
在摆角很小的情况下,摆球所受的回复力跟位移大小成正比,方向始终指向平衡位置(即与位移方向相反),因此单摆做简谐运动
三、单摆的周期
单摆振动的周期可能与哪些因素有关呢?
三、单摆的周期
单摆振动的周期可能与哪些因素有关呢?
1.周期与振幅是否有关
三、单摆的周期
单摆振动的周期可能与哪些因素有关呢?
1.周期与振幅是否有关
2.周期与摆球的质量是否有关
三、单摆的周期
单摆振动的周期可能与哪些因素有关呢?
1.周期与振幅是否有关
2.周期与摆球的质量是否有关
3.周期与摆长是否有关
三、单摆的周期
单摆振动的周期可能与哪些因素有关呢?
1.周期与振幅是否有关
2.周期与摆球的质量是否有关
3.周期与摆长是否有关
4.周期与重力加速度是否有关
三、单摆的周期
单摆振动的周期可能与哪些因素有关呢?
1.周期与振幅是否有关
2.周期与摆球的质量是否有关
3.周期与摆长是否有关
4.周期与重力加速度是否有关
探究方法:控制变量法
三、单摆的周期
4.与当地的重力加速度有关——重力加速 度越大,周期越小
单摆振动的周期
1.与振幅无关——单摆的等时性
伽利略首先发现的
2.与摆球的质量无关
3.与摆长有关——摆长越长,周期越大
结 论
单摆振动的周期公式:
单摆振动的周期公式:
单摆振动的周期公式:
荷兰物理学家惠更斯首先发现
单摆振动的周期公式:
单摆做简谐运动的振动周期跟摆长的平方根成正比,跟重力加速度的平方根成反比。
荷兰物理学家惠更斯首先发现
四、单摆周期公式的应用
1.惠更斯利用摆的等时性发明了带摆的计时器.
四、单摆周期公式的应用
1.惠更斯利用摆的等时性发明了带摆的计时器.
2.用单摆测定重力加速度。
四、单摆周期公式的应用
1.惠更斯利用摆的等时性发明了带摆的计时器.
2.用单摆测定重力加速度。
四、单摆周期公式的应用
1.惠更斯利用摆的等时性发明了带摆的计时器.
2.用单摆测定重力加速度。
四、单摆周期公式的应用
1.单摆作简谐运动时的回复力是( )
A.摆球的重力
B.摆球重力沿圆弧切线的分力
C.摆线的拉力
D.摆球重力与摆线拉力的合力
课堂训练
1.单摆作简谐运动时的回复力是( )
A.摆球的重力
B.摆球重力沿圆弧切线的分力
C.摆线的拉力
D.摆球重力与摆线拉力的合力
B
课堂训练
2.一个单摆,周期是T。
a. 如果摆球质量增到2倍,周期将 ;
b. 如果摆的振幅增到2倍,周期将 ;
c. 如果摆长增到2倍,周期将 ;
d. 如果将单摆从赤道移到北京,周期将 ;
e. 如果将单摆从海面移到高山,周期将 ;
课堂训练
2.一个单摆,周期是T。
a. 如果摆球质量增到2倍,周期将 ;
b. 如果摆的振幅增到2倍,周期将 ;
c. 如果摆长增到2倍,周期将 ;
d. 如果将单摆从赤道移到北京,周期将 ;
e. 如果将单摆从海面移到高山,周期将 ;
不变
课堂训练
2.一个单摆,周期是T。
a. 如果摆球质量增到2倍,周期将 ;
b. 如果摆的振幅增到2倍,周期将 ;
c. 如果摆长增到2倍,周期将 ;
d. 如果将单摆从赤道移到北京,周期将 ;
e. 如果将单摆从海面移到高山,周期将 ;
不变
不变
课堂训练
2.一个单摆,周期是T。
a. 如果摆球质量增到2倍,周期将 ;
b. 如果摆的振幅增到2倍,周期将 ;
c. 如果摆长增到2倍,周期将 ;
d. 如果将单摆从赤道移到北京,周期将 ;
e. 如果将单摆从海面移到高山,周期将 ;
变大
不变
不变
课堂训练
2.一个单摆,周期是T。
a. 如果摆球质量增到2倍,周期将 ;
b. 如果摆的振幅增到2倍,周期将 ;
c. 如果摆长增到2倍,周期将 ;
d. 如果将单摆从赤道移到北京,周期将 ;
e. 如果将单摆从海面移到高山,周期将 ;
变小
变大
不变
不变
课堂训练
2.一个单摆,周期是T。
a. 如果摆球质量增到2倍,周期将 ;
b. 如果摆的振幅增到2倍,周期将 ;
c. 如果摆长增到2倍,周期将 ;
d. 如果将单摆从赤道移到北京,周期将 ;
e. 如果将单摆从海面移到高山,周期将 ;
变小
变大
变大
不变
不变
课堂训练
小明家从广州搬到北京去,搬家时把家中的大摆钟也带到北京去了。 问:1.这个摆钟到 北京后是否还准时 2.若不准,是偏慢还是偏快 3.如须调整应该怎样调节
课堂训练
3.一摆长为L的单摆,在悬点正下方5L/9处有一钉子,则这个单摆的周期是多少?
课堂训练
3.一摆长为L的单摆,在悬点正下方5L/9处有一钉子,则这个单摆的周期是多少?
课堂训练
