人教七下数学10.1统计调查(2)课件(共31张PPT)
文档属性
| 名称 | 人教七下数学10.1统计调查(2)课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-15 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
10.1
统计调查(2)
——抽样调查
一天,爸爸叫儿子小华去买一盒火柴。临出门前,爸爸嘱咐儿子要买能划燃的火柴。小华拿着钱出门了,过了好一会儿,小华才回到家。
“火柴能划燃吗?”爸爸问。
“都能划燃。”
“你这么肯定?”
小华递过一盒划过的火柴,兴奋地说:“我每根都试过啦。”
思考:得到火柴能否划燃的信息准确吗?
这样做好吗?
生活小片段
说一说:
在这则笑话中,儿子采用的是什
么调查方式?
这种调查方式好不好?你能帮他想出什么好方法来调查吗?
你知道其中蕴涵的道理吗?
品尝一勺汤
如何知道一锅汤的味道?
根据这个道理,小华买火柴时怎么做才合理?
探究一、问题
某校有2000名学生,要想了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,怎样进行调查?
可以采用全面调查的方法对全校学生逐个进行调查,然后整理收集到的数据,统计出全校学生对五类电视节目的喜爱情况。但是,由于学生比较多,全面调查不仅花费的时间长,而且消耗的人力物力也非常大,因此,需要寻找一种不作全面调查就能了解全校学生喜爱各类电视节目的情况的方法,达到既省时又省力又能解决问题的目的。这就是我们要讨论的——抽样调查
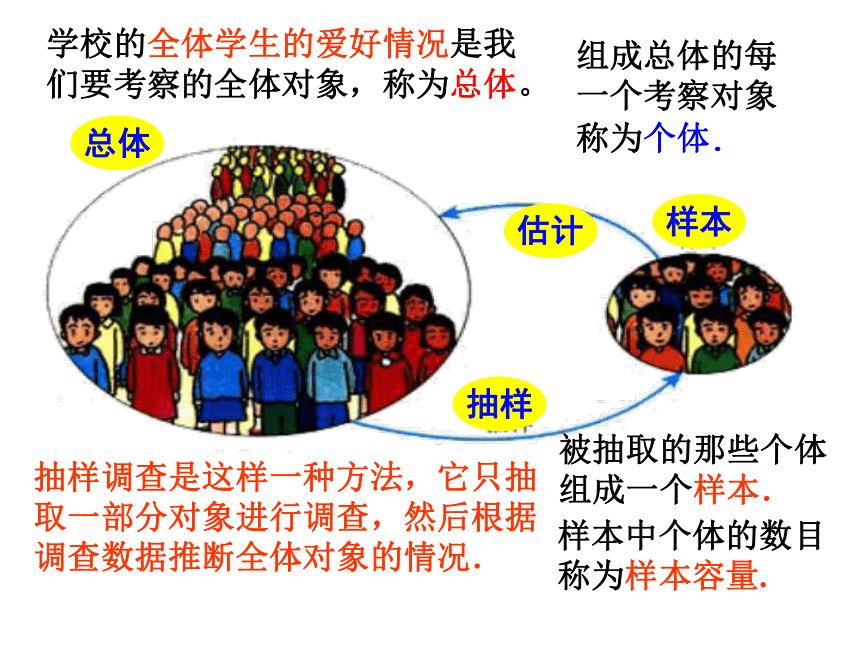
抽样调查是这样一种方法,它只抽
取一部分对象进行调查,然后根据
调查数据推断全体对象的情况.
学校的全体学生的爱好情况是我们要考察的全体对象,称为总体。
被抽取的那些个体组成一个样本.
组成总体的每一个考察对象称为个体.
样本中个体的数目称为样本容量.
采用调查部分对象的方式来收集数据,
根据部分来估计整体的情况,
叫做抽样调查.
所要考察对象的全体叫做总体.
从总体中所抽取的一部分个体叫做总体的一个样本.
总体中每一个考察对象叫做个体.
1.抽样调查:
2.总体:
3.个体:
4.样本:
5.样本容量:
样本中的个体的数目(没有单位).
形成概念
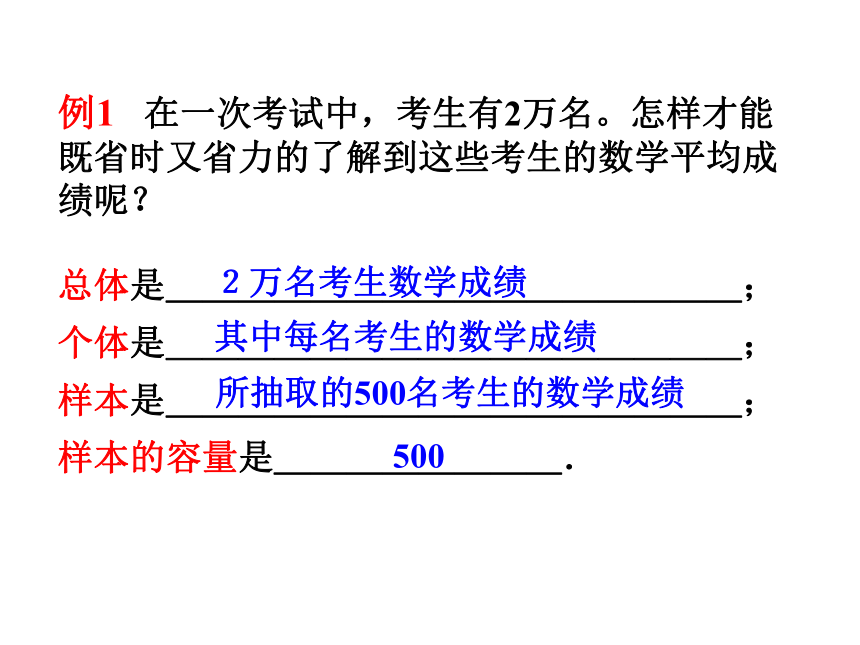
例1
在一次考试中,考生有2万名。怎样才能既省时又省力的了解到这些考生的数学平均成绩呢?
总体是________________;
个体是________________;
样本是________________;
样本的容量是________.
2万名考生数学成绩
其中每名考生的数学成绩
所抽取的500名考生的数学成绩
500
练一练:
1.某中学有520名学生参加升学考试从中随机抽取60名考生的数学成绩进行分析,在这个问题中:
总体是:
;
个体是:
;
样本是:
;
样本容量是:
。
520名考生的升学考试数学成绩
每一个考生的升学考试数学成绩
抽取60名考生的升学考试数学成绩
60
2.
下列说法正确的是(
)
A、样本中个体的数目叫总体;
B、考察对象的全体叫样本容量;
C、总体中的部分叫个体;
D、总体中抽出的一部分个体叫总体的一个样本.
D
3.说明在以下问题中,总体、个体、样本、样本的容量各指什么.
(1)为了考察我校的学生参加课外体育活动的情况,调查了其中20名学生每天参加课外体育活动的时间.
(2)为了了解一批灯泡的寿命,从中抽取10只进行试验.
(3)为了考察某公园一年中每天进园的人数,在其中的30天里对进园的人数进行了统计.
4.要调查下面几个问题,你认为应该作全面调查还是
抽样调查?
(1)要调查市场上某种食品含量是否符号国家标准
(2)检测某城市的空气质量
(3)调查一个村子所有家庭的收入
(4)调查人们对保护环境的意识
(5)调查一个班级中的学生对建立班级英语角的看法
(6)了解一批灯泡的使用寿命
抽样调查
全面调查
抽样调查
抽样调查
抽样调查
全面调查
小结
全面调查与抽样调查的比较
调查方式
适宜情境
调查对象
优点
缺点
全面调查
?个数较少?结果有特殊要求和特殊意义
全体
非常准确的得出总体情况
有时费时费力
抽样调查
?个数较多?结果具有破坏性或危害性
样本
(总体中一部分)
省时省力.范围小
只能估计出总体的情况
前面问题中
,我们只抽取一部分学生进行调查,然后通过分析被调查学生的数据来推断全校学生喜爱电视节目的情况。
探究二、简单随机抽样
某校有2000名学生,要想了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,你打算怎样进行调查?
抽样调查
样本容量?
样本?
抽取多少名学生进行调查比较合适?被调查的学生又如何抽取呢?
如果抽取调查的学生很少,样本就不容易具有代表性,也就不能客观地反映总体的情况;如果抽取调查的学生很多,虽然样本容易具有代表性,但花费的时间,精力也很多,达不到省时省力的目的。因此抽取调查的学生数目要适当。
例如,这个问题中可以抽取100名学生作为样本进行调查。(样本容量为100)
为了使样本能较好地反映总体情况,除了有合适的样本容量外,抽取样本时,不能偏向某些学生,应使学校中的每一个学生都有相等的机会被抽到.
归纳:
上面抽取样本的过程中,总体中每一个个体都有相等的机会被抽到,像这样的抽样方法叫简单随机抽样.
例如,上学时在校门口随意调查100名学生;可以在2
000名学生的注册学号中,随意抽取100个学号,调查这些学号对应的100名学生.
抽取100名学生最喜爱节目的人数统计表
节目类型
划
计
人数
百分比
A新闻
正
6
6%
B体育
正正正正
22
22%
C动画
正正正正正
29
29%
D娱乐
正正正正正
正正
38
38%
E戏曲
正
5
5%
合计
100
100
100%
节目类型
10
20
30
40
全校的2000名学生,
最喜欢哪类节目?
全校2000名学生,
对体育的最爱约占几人?
抽样调查是一种方法,它只抽取了一部分对象进行调查,然后根据样本数据推断全体对象的情况。
如上面的例题,如果在抽取样本的过程中,总体的每一个个体都有相等的机会被抽到,这样的抽样方法就叫简单的随机抽样。
抽样调查是实际中经常采用的调查方式,如果抽取的样本得当,就能很好地反应总体情况,否则,抽样调查的结果会偏离总体情况。
注意:在抽样调查中抽取的样本要具有代表。
深化概念
全面调查
是通过调查总体的方式来收集数据,因而得到的调查结果比较精确;但可能要投入数十倍甚至更多的人力、物力和时间.
抽样调查
是通过调查样本的方式来收集数据,因而调查结果与总体的结果可能的一些误差,但投入少、操作方便,而且有时只能用抽样的方式去调查,比如要研究一批炮弹的杀伤半径,不可能把所有的炮弹都发射出去,可见合理的抽样调查不失为一种很好的选择.
比较概念
(1)当调查的对象个数较少,调查容易进行时,我们一般采用全面调查的方式进行。
(2)当调查的结果对调查对象具有破坏性时,或者会产生一定的危害性时,我们通常采用抽样调查的方式进行调查。
(3)当调查对象的个数较多,调查不易进行时,我们常采用抽样调查的方式进行调查。
(4)当调查的结果有特别要求时,或调查的结果有特殊意义时,如国家的人口普查,我们仍须采用全面调查的方式进行。
活用概念
1.下面几个问题,应该做全面调查还是抽样调查?
(1)要调查市场上某种食品添加剂是否符合国家标准;
(2)检测某城市的空气质量;
(3)调查一个村子所有家庭的收入;
(4)调查人们对保护环境的意识;
(5)调查一个班级中的学生对建立班级英语角的看法;
(6)调查人们对电影院放映的电影的热衷程度。
抽样调查
抽样调查
抽样调查
抽样调查
全面调查
全面调查
活用概念
2、想知道一批灯泡的寿命采用什么调查方法?
4、想了解一个铁矿的含铁量,采用什么调查方法?为什么?
3、想知道一批导弹的杀伤半径,采用什么调查方法?为什么?
1、宜采用全面调查
①.
总体中个体数目较少且研究问题要求情况真实、准确性较高时.
②.
调查工作较方便、没有破坏性.
③.
当调查的结果有特别要求时,或调查的结果有特殊意义时,如国家的人口普查,我们仍须的方式进行.
经验总结
注意:在抽样调查中抽取的样本要具有代表性。
2、宜采用抽样调查
①.
总体中个体数目较多,全面调查的工作量大,受
到客观条件限制,无法对所有个体进行调查.
②
.
调查具有破坏性时,方式较好.
1、你能举一个抽样调查的例子并能说出总体和样本分别是什么吗?
2、利用抽样调查进行调查的好处是什么?
3、用样本的特征来估计总体的特征。
你能谈谈这堂课的收获吗?
好处:节省调查的人力和物力,
不足之处:与实际可能存在误差.
答:⑴是抽样调查。
⑵总体是全校学生,个体是每一名同学,样本是座位在自己旁边的3名同学,样本容量为3。
1、为了解全校学生的平均身高,小明调查了座位在自己身边的3名同学,把他们身高的平均值作为全校学生平均身高的估计.
⑴小明的调查是抽样调查吗?
⑵如果是抽样调查,指出调查的总体、个体、样本和样本容量。
⑶这个调查结果能较好地反映总体的情况吗?
如果不能,请说明理由。
1、为了解全校学生的平均身高,小明调查了座位在自己身边的3名同学,把他们身高的平均值作为全校学生平均身高的估计.
⑴小明的调查是抽样调查吗?
⑵如果是抽样调查,指出调查的总体、个体、样本和样本容量。
⑶这个调查结果能较好地反映总体的情况吗?
如果不能,请说明理由。
⑶一般不能反映总体,一是样本容量太小,二是坐在一起的同学一般身高都比较接近,所以这样的选择的样本缺乏代表性。
2.请指出下列调查中的样本是否具有代表性。
(1)在大学生中调查我国青年业余时间娱乐的主要方式。
(2)在公园里调查老年人的健康状况。
(3)调查一个班级里学号为3的倍数的学生,以了解学生们对班主任老师某一新举措的意见和建议。
10.1
统计调查(2)
——抽样调查
一天,爸爸叫儿子小华去买一盒火柴。临出门前,爸爸嘱咐儿子要买能划燃的火柴。小华拿着钱出门了,过了好一会儿,小华才回到家。
“火柴能划燃吗?”爸爸问。
“都能划燃。”
“你这么肯定?”
小华递过一盒划过的火柴,兴奋地说:“我每根都试过啦。”
思考:得到火柴能否划燃的信息准确吗?
这样做好吗?
生活小片段
说一说:
在这则笑话中,儿子采用的是什
么调查方式?
这种调查方式好不好?你能帮他想出什么好方法来调查吗?
你知道其中蕴涵的道理吗?
品尝一勺汤
如何知道一锅汤的味道?
根据这个道理,小华买火柴时怎么做才合理?
探究一、问题
某校有2000名学生,要想了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,怎样进行调查?
可以采用全面调查的方法对全校学生逐个进行调查,然后整理收集到的数据,统计出全校学生对五类电视节目的喜爱情况。但是,由于学生比较多,全面调查不仅花费的时间长,而且消耗的人力物力也非常大,因此,需要寻找一种不作全面调查就能了解全校学生喜爱各类电视节目的情况的方法,达到既省时又省力又能解决问题的目的。这就是我们要讨论的——抽样调查
抽样调查是这样一种方法,它只抽
取一部分对象进行调查,然后根据
调查数据推断全体对象的情况.
学校的全体学生的爱好情况是我们要考察的全体对象,称为总体。
被抽取的那些个体组成一个样本.
组成总体的每一个考察对象称为个体.
样本中个体的数目称为样本容量.
采用调查部分对象的方式来收集数据,
根据部分来估计整体的情况,
叫做抽样调查.
所要考察对象的全体叫做总体.
从总体中所抽取的一部分个体叫做总体的一个样本.
总体中每一个考察对象叫做个体.
1.抽样调查:
2.总体:
3.个体:
4.样本:
5.样本容量:
样本中的个体的数目(没有单位).
形成概念
例1
在一次考试中,考生有2万名。怎样才能既省时又省力的了解到这些考生的数学平均成绩呢?
总体是________________;
个体是________________;
样本是________________;
样本的容量是________.
2万名考生数学成绩
其中每名考生的数学成绩
所抽取的500名考生的数学成绩
500
练一练:
1.某中学有520名学生参加升学考试从中随机抽取60名考生的数学成绩进行分析,在这个问题中:
总体是:
;
个体是:
;
样本是:
;
样本容量是:
。
520名考生的升学考试数学成绩
每一个考生的升学考试数学成绩
抽取60名考生的升学考试数学成绩
60
2.
下列说法正确的是(
)
A、样本中个体的数目叫总体;
B、考察对象的全体叫样本容量;
C、总体中的部分叫个体;
D、总体中抽出的一部分个体叫总体的一个样本.
D
3.说明在以下问题中,总体、个体、样本、样本的容量各指什么.
(1)为了考察我校的学生参加课外体育活动的情况,调查了其中20名学生每天参加课外体育活动的时间.
(2)为了了解一批灯泡的寿命,从中抽取10只进行试验.
(3)为了考察某公园一年中每天进园的人数,在其中的30天里对进园的人数进行了统计.
4.要调查下面几个问题,你认为应该作全面调查还是
抽样调查?
(1)要调查市场上某种食品含量是否符号国家标准
(2)检测某城市的空气质量
(3)调查一个村子所有家庭的收入
(4)调查人们对保护环境的意识
(5)调查一个班级中的学生对建立班级英语角的看法
(6)了解一批灯泡的使用寿命
抽样调查
全面调查
抽样调查
抽样调查
抽样调查
全面调查
小结
全面调查与抽样调查的比较
调查方式
适宜情境
调查对象
优点
缺点
全面调查
?个数较少?结果有特殊要求和特殊意义
全体
非常准确的得出总体情况
有时费时费力
抽样调查
?个数较多?结果具有破坏性或危害性
样本
(总体中一部分)
省时省力.范围小
只能估计出总体的情况
前面问题中
,我们只抽取一部分学生进行调查,然后通过分析被调查学生的数据来推断全校学生喜爱电视节目的情况。
探究二、简单随机抽样
某校有2000名学生,要想了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,你打算怎样进行调查?
抽样调查
样本容量?
样本?
抽取多少名学生进行调查比较合适?被调查的学生又如何抽取呢?
如果抽取调查的学生很少,样本就不容易具有代表性,也就不能客观地反映总体的情况;如果抽取调查的学生很多,虽然样本容易具有代表性,但花费的时间,精力也很多,达不到省时省力的目的。因此抽取调查的学生数目要适当。
例如,这个问题中可以抽取100名学生作为样本进行调查。(样本容量为100)
为了使样本能较好地反映总体情况,除了有合适的样本容量外,抽取样本时,不能偏向某些学生,应使学校中的每一个学生都有相等的机会被抽到.
归纳:
上面抽取样本的过程中,总体中每一个个体都有相等的机会被抽到,像这样的抽样方法叫简单随机抽样.
例如,上学时在校门口随意调查100名学生;可以在2
000名学生的注册学号中,随意抽取100个学号,调查这些学号对应的100名学生.
抽取100名学生最喜爱节目的人数统计表
节目类型
划
计
人数
百分比
A新闻
正
6
6%
B体育
正正正正
22
22%
C动画
正正正正正
29
29%
D娱乐
正正正正正
正正
38
38%
E戏曲
正
5
5%
合计
100
100
100%
节目类型
10
20
30
40
全校的2000名学生,
最喜欢哪类节目?
全校2000名学生,
对体育的最爱约占几人?
抽样调查是一种方法,它只抽取了一部分对象进行调查,然后根据样本数据推断全体对象的情况。
如上面的例题,如果在抽取样本的过程中,总体的每一个个体都有相等的机会被抽到,这样的抽样方法就叫简单的随机抽样。
抽样调查是实际中经常采用的调查方式,如果抽取的样本得当,就能很好地反应总体情况,否则,抽样调查的结果会偏离总体情况。
注意:在抽样调查中抽取的样本要具有代表。
深化概念
全面调查
是通过调查总体的方式来收集数据,因而得到的调查结果比较精确;但可能要投入数十倍甚至更多的人力、物力和时间.
抽样调查
是通过调查样本的方式来收集数据,因而调查结果与总体的结果可能的一些误差,但投入少、操作方便,而且有时只能用抽样的方式去调查,比如要研究一批炮弹的杀伤半径,不可能把所有的炮弹都发射出去,可见合理的抽样调查不失为一种很好的选择.
比较概念
(1)当调查的对象个数较少,调查容易进行时,我们一般采用全面调查的方式进行。
(2)当调查的结果对调查对象具有破坏性时,或者会产生一定的危害性时,我们通常采用抽样调查的方式进行调查。
(3)当调查对象的个数较多,调查不易进行时,我们常采用抽样调查的方式进行调查。
(4)当调查的结果有特别要求时,或调查的结果有特殊意义时,如国家的人口普查,我们仍须采用全面调查的方式进行。
活用概念
1.下面几个问题,应该做全面调查还是抽样调查?
(1)要调查市场上某种食品添加剂是否符合国家标准;
(2)检测某城市的空气质量;
(3)调查一个村子所有家庭的收入;
(4)调查人们对保护环境的意识;
(5)调查一个班级中的学生对建立班级英语角的看法;
(6)调查人们对电影院放映的电影的热衷程度。
抽样调查
抽样调查
抽样调查
抽样调查
全面调查
全面调查
活用概念
2、想知道一批灯泡的寿命采用什么调查方法?
4、想了解一个铁矿的含铁量,采用什么调查方法?为什么?
3、想知道一批导弹的杀伤半径,采用什么调查方法?为什么?
1、宜采用全面调查
①.
总体中个体数目较少且研究问题要求情况真实、准确性较高时.
②.
调查工作较方便、没有破坏性.
③.
当调查的结果有特别要求时,或调查的结果有特殊意义时,如国家的人口普查,我们仍须的方式进行.
经验总结
注意:在抽样调查中抽取的样本要具有代表性。
2、宜采用抽样调查
①.
总体中个体数目较多,全面调查的工作量大,受
到客观条件限制,无法对所有个体进行调查.
②
.
调查具有破坏性时,方式较好.
1、你能举一个抽样调查的例子并能说出总体和样本分别是什么吗?
2、利用抽样调查进行调查的好处是什么?
3、用样本的特征来估计总体的特征。
你能谈谈这堂课的收获吗?
好处:节省调查的人力和物力,
不足之处:与实际可能存在误差.
答:⑴是抽样调查。
⑵总体是全校学生,个体是每一名同学,样本是座位在自己旁边的3名同学,样本容量为3。
1、为了解全校学生的平均身高,小明调查了座位在自己身边的3名同学,把他们身高的平均值作为全校学生平均身高的估计.
⑴小明的调查是抽样调查吗?
⑵如果是抽样调查,指出调查的总体、个体、样本和样本容量。
⑶这个调查结果能较好地反映总体的情况吗?
如果不能,请说明理由。
1、为了解全校学生的平均身高,小明调查了座位在自己身边的3名同学,把他们身高的平均值作为全校学生平均身高的估计.
⑴小明的调查是抽样调查吗?
⑵如果是抽样调查,指出调查的总体、个体、样本和样本容量。
⑶这个调查结果能较好地反映总体的情况吗?
如果不能,请说明理由。
⑶一般不能反映总体,一是样本容量太小,二是坐在一起的同学一般身高都比较接近,所以这样的选择的样本缺乏代表性。
2.请指出下列调查中的样本是否具有代表性。
(1)在大学生中调查我国青年业余时间娱乐的主要方式。
(2)在公园里调查老年人的健康状况。
(3)调查一个班级里学号为3的倍数的学生,以了解学生们对班主任老师某一新举措的意见和建议。
