四川省仁寿县文宫中学2019-2020学年高二7月月考(期末模拟)数学(文)试题(图片版含答案)
文档属性
| 名称 | 四川省仁寿县文宫中学2019-2020学年高二7月月考(期末模拟)数学(文)试题(图片版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-15 00:00:00 | ||
图片预览



文档简介
6若10件产品中有7件正品,3件次品,从中任取2件,则恰好取到1件次品的
概率是()
7.已知函数f(x)在R上可导,且f(x)=x2+2xf(),则f()=(-)
A.-2
B.2
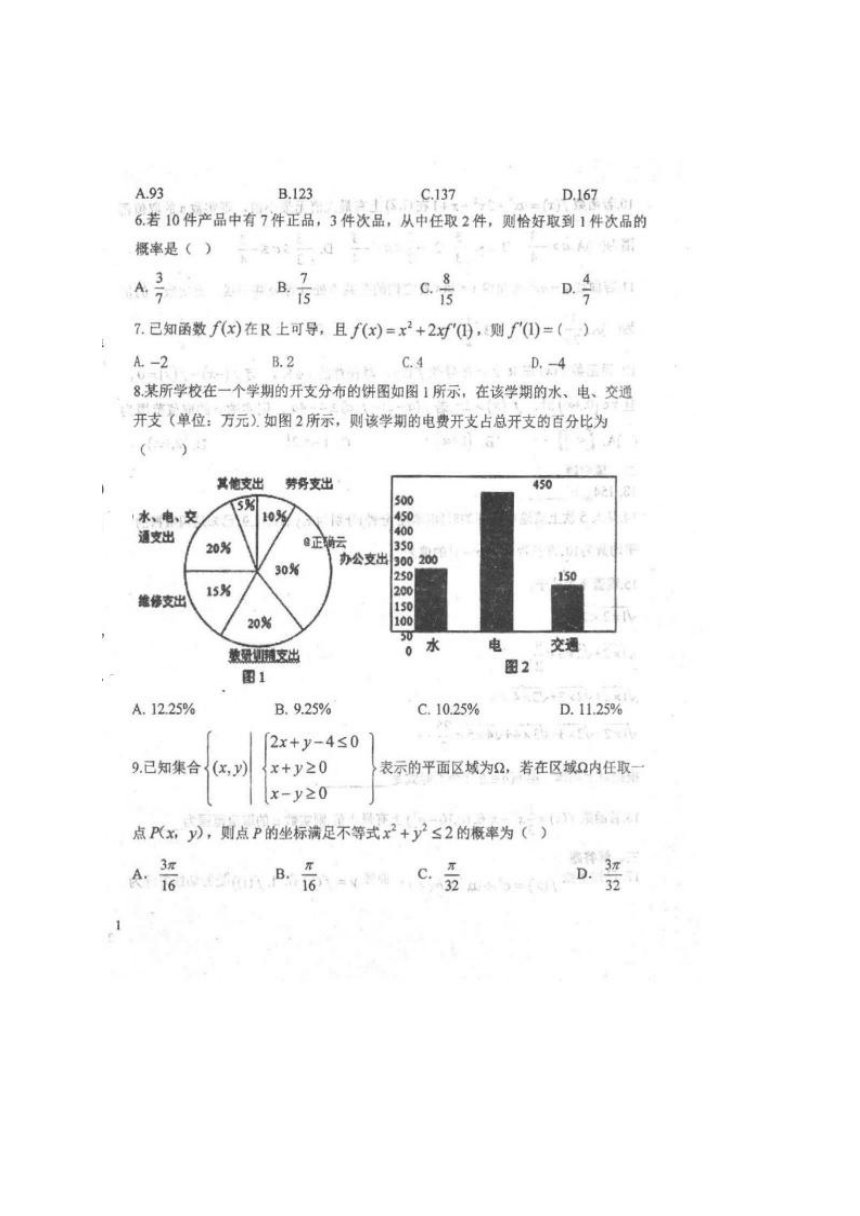
8某所学校在一个学期的开支分布的饼图如图1所示,在该学期的水、电、交通
开支(单位:万元)如图2所示,则该学期的电费开支占总开支的百分比为
其他支出劳务支出
水、电交
30x办公出A
能修出、15
20%
教出
交通
图2
A.1225%
B.9.25%
C.10.25%
D.1
2x+y-4≤0
9已知集合{(x,y){x+y≥0
表示的平面区域为92,若在区域Q内任取
x-y≥0
点P(x,y),则点P的坐标满足不等式x2+y2≤2的概率为()
10.若函数f(x)=ax3+2x2+x+1在(1,2)上有最大值无最小值,则实数a的取值范
围为(Ma>04C-3<04443s、3
5
3
11若曲线y=ax2与曲线y=nx在它们的公共点处具有公共切线,则实数a的值
为()A
B
D
12.设函数f(x)在R上存在导数f(x),对任意的x∈R,有f(-x)-f(x)=0,
且x∈[0,+∞)时,f(x)>2x若f(a-2)-f(a)24-4a,则实数a的取值范围为
()A.C∞]B.[+∞)
C
D.2+a
二、填空题
13.154
14某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的
平均数为10,方差为2则x-y的值为
15观查下列式子:
2<2
1×2+√2×3<
2
√1×2+√2×3+√3×4<8
√1×2+√2×3+3×4+4×5≤25…
根据以上规律,第n(n∈N)个不等式是
16.若函数f(七在(10-a2)上有最小值,则实数a的取值范围为
三、解答题
17已知函数()=c2+ax2+bx+1,曲线y=f(x)在(1,()处的切线方程为
(e-1)x+1
(1).求实数a、b的值;
(2).求函数y=f(x)在[-1,2]的最值
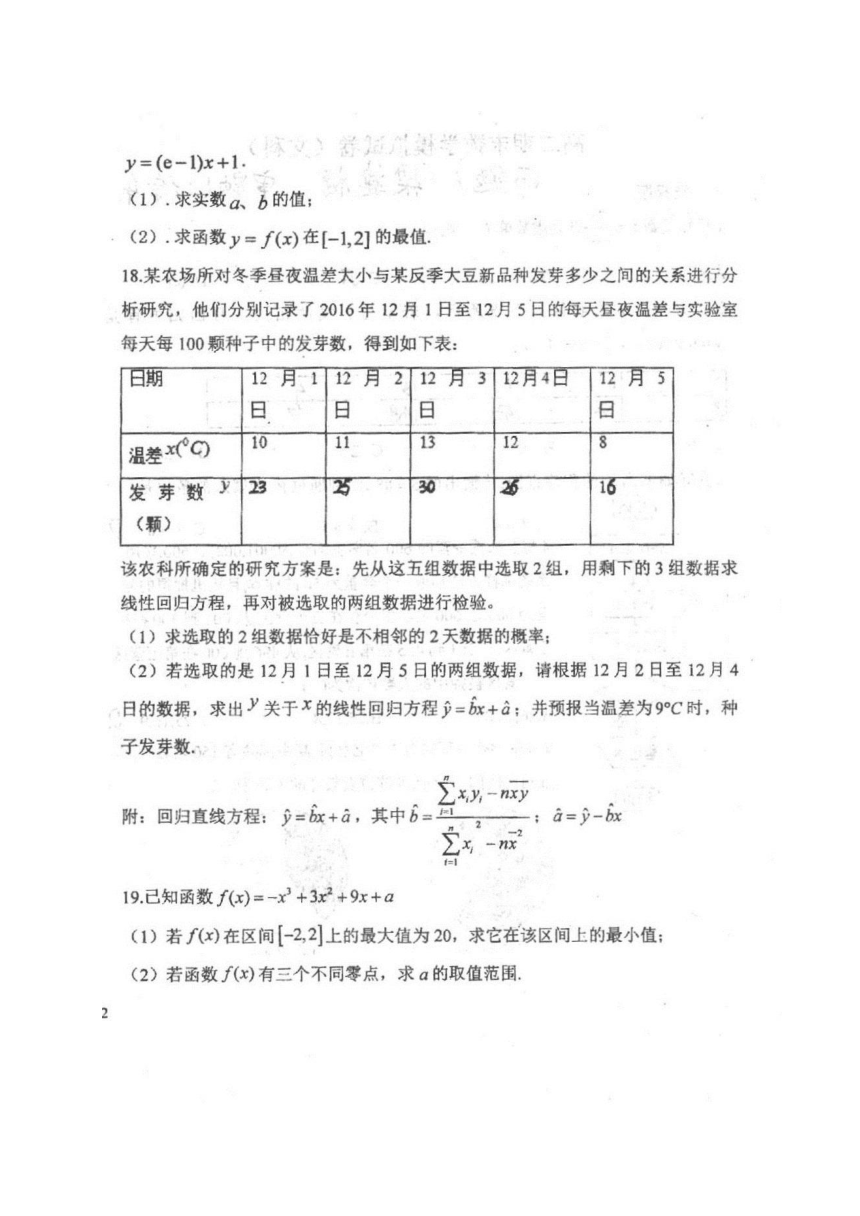
18某农场所对冬季昼夜温差大小与某反季大豆新品种发芽多少之间的关系进行分
析研究,他们分别记录了2016年12月1日至12月5日的每天昼夜温差与实验室
每天每100颗种子中的发芽数,得到如下表:
日期
12月11月212月32月4日2月5
日
日
日
日
温差x(C10
1
12
发芽数川2323
6
(颗)
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求
线性回归方程,再对被选取的两组数据进行检验。
(1)求选取的2组数据恰好是不相邻的2天数据的概率;
(2)若选取的是12月1日至12月5日的两组数据,请根据12月2日至12月4
日的数据,求出y关于x的线性回归方程j=bx+a;并预报当温差为9C时,种
子发芽数
附:回归直线方程:j=bx+a,其中b=-nxy
∑
i
a=y-bx
x
-nX
19已知函数f(x)=-x2+3x2+9x+a
(1)若f(x)在区间[-22]上的最大值为20,求它在该区间上的最小值;
(2)若函数f(x)有三个不同零点,求a的取值范围
概率是()
7.已知函数f(x)在R上可导,且f(x)=x2+2xf(),则f()=(-)
A.-2
B.2
8某所学校在一个学期的开支分布的饼图如图1所示,在该学期的水、电、交通
开支(单位:万元)如图2所示,则该学期的电费开支占总开支的百分比为
其他支出劳务支出
水、电交
30x办公出A
能修出、15
20%
教出
交通
图2
A.1225%
B.9.25%
C.10.25%
D.1
2x+y-4≤0
9已知集合{(x,y){x+y≥0
表示的平面区域为92,若在区域Q内任取
x-y≥0
点P(x,y),则点P的坐标满足不等式x2+y2≤2的概率为()
10.若函数f(x)=ax3+2x2+x+1在(1,2)上有最大值无最小值,则实数a的取值范
围为(Ma>04C-3<04443s、3
5
3
11若曲线y=ax2与曲线y=nx在它们的公共点处具有公共切线,则实数a的值
为()A
B
D
12.设函数f(x)在R上存在导数f(x),对任意的x∈R,有f(-x)-f(x)=0,
且x∈[0,+∞)时,f(x)>2x若f(a-2)-f(a)24-4a,则实数a的取值范围为
()A.C∞]B.[+∞)
C
D.2+a
二、填空题
13.154
14某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的
平均数为10,方差为2则x-y的值为
15观查下列式子:
2<2
1×2+√2×3<
2
√1×2+√2×3+√3×4<8
√1×2+√2×3+3×4+4×5≤25…
根据以上规律,第n(n∈N)个不等式是
16.若函数f(七在(10-a2)上有最小值,则实数a的取值范围为
三、解答题
17已知函数()=c2+ax2+bx+1,曲线y=f(x)在(1,()处的切线方程为
(e-1)x+1
(1).求实数a、b的值;
(2).求函数y=f(x)在[-1,2]的最值
18某农场所对冬季昼夜温差大小与某反季大豆新品种发芽多少之间的关系进行分
析研究,他们分别记录了2016年12月1日至12月5日的每天昼夜温差与实验室
每天每100颗种子中的发芽数,得到如下表:
日期
12月11月212月32月4日2月5
日
日
日
日
温差x(C10
1
12
发芽数川2323
6
(颗)
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求
线性回归方程,再对被选取的两组数据进行检验。
(1)求选取的2组数据恰好是不相邻的2天数据的概率;
(2)若选取的是12月1日至12月5日的两组数据,请根据12月2日至12月4
日的数据,求出y关于x的线性回归方程j=bx+a;并预报当温差为9C时,种
子发芽数
附:回归直线方程:j=bx+a,其中b=-nxy
∑
i
a=y-bx
x
-nX
19已知函数f(x)=-x2+3x2+9x+a
(1)若f(x)在区间[-22]上的最大值为20,求它在该区间上的最小值;
(2)若函数f(x)有三个不同零点,求a的取值范围
同课章节目录
