北师大版九年级上册数学第一章 特殊平行四边形 素养拓展+中考真题课件(63张)
文档属性
| 名称 | 北师大版九年级上册数学第一章 特殊平行四边形 素养拓展+中考真题课件(63张) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-15 15:14:28 | ||
图片预览






文档简介
第一章 特殊平行四边形
数学·九年级上册·北师
专题 特殊平行四边形与图形变换
专项素养拓训
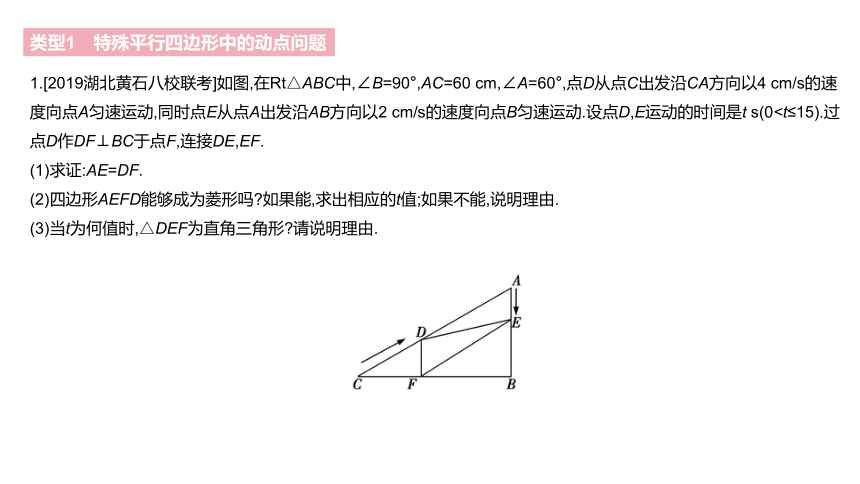
1.[2019湖北黄石八校联考]如图,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/s的速度向点B匀速运动.设点D,E运动的时间是t s(0(1)求证:AE=DF.
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
类型1 特殊平行四边形中的动点问题
答案
1.【解析】 (1)依题意,得CD=4t,AE=2t.
在Rt△ABC中,∠C=90°-∠A=30°.
在Rt△CDF中,∠C=30°,∴DF=12CD=2t,∴AE=DF.
(2)能.理由如下:
∵DF⊥BC,∠B=90°,∴DF∥AB,
由(1)知DF=AE,∴四边形AEFD是平行四边形.
当AD=AE时,四边形AEFD是菱形,
则60-4t=2t,解得t=10,
∴当t=10时,四边形AEFD是菱形.
?
类型1 特殊平行四边形中的动点问题
答案
(3)当t=152时,△DEF是直角三角形(∠EDF=90°);当t=12时,△DEF是直角三角形(∠DEF=90°).理由如下:
当∠EDF=90°时,DE∥BC,
∴∠ADE=∠C=30°,∴AD=2AE,
∴60-4t=2·2t,解得t=152(符合题意).
当∠DEF=90°时,DE⊥EF,
∵四边形AEFD是平行四边形,∴AD∥EF,∴DE⊥AD,
∴△ADE是直角三角形,∠ADE=90°.
∵∠A=60°,∴∠DEA=30°,
∴AD=12AE,∴60-4t=12·2t,解得t=12(符合题意).
综上,当t=152时,△DEF是直角三角形(∠EDF=90°);当t=12时,△DEF是直角三角形(∠DEF=90°).
?
类型1 特殊平行四边形中的动点问题
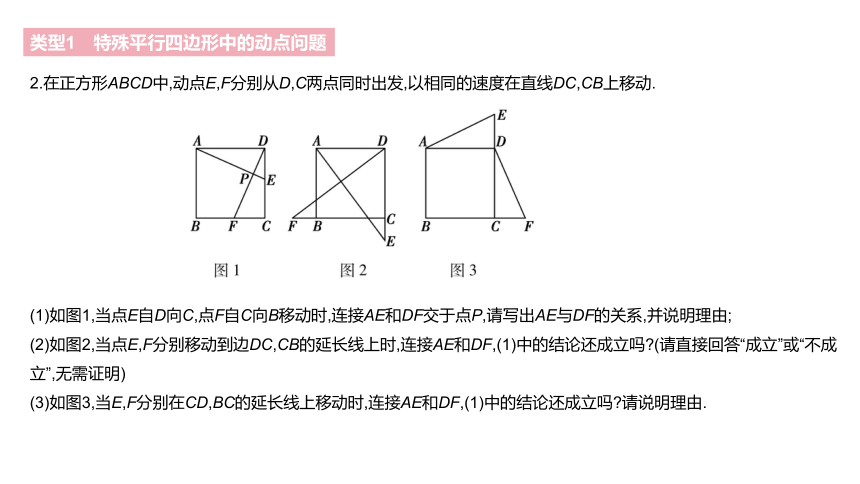
2.在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图1,当点E自D向C,点F自C向B移动时,连接AE和DF交于点P,请写出AE与DF的关系,并说明理由;
(2)如图2,当点E,F分别移动到边DC,CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请直接回答“成立”或“不成立”,无需证明)
(3)如图3,当E,F分别在CD,BC的延长线上移动时,连接AE和DF,(1)中的结论还成立吗?请说明理由.
类型1 特殊平行四边形中的动点问题
答案
2.【解析】 (1)AE=DF,AE⊥DF.理由如下:
∵四边形ABCD是正方形,∴AD=DC,∠ADC=∠C=90°.
∵DE=CF,∴△ADE≌△DCF,∴AE=DF,∠DAE=∠CDF.
∵∠CDF+∠ADF=90°,∴∠DAE+∠ADF=90°.
∴∠APD=90°,∴AE⊥DF.
(2)成立.
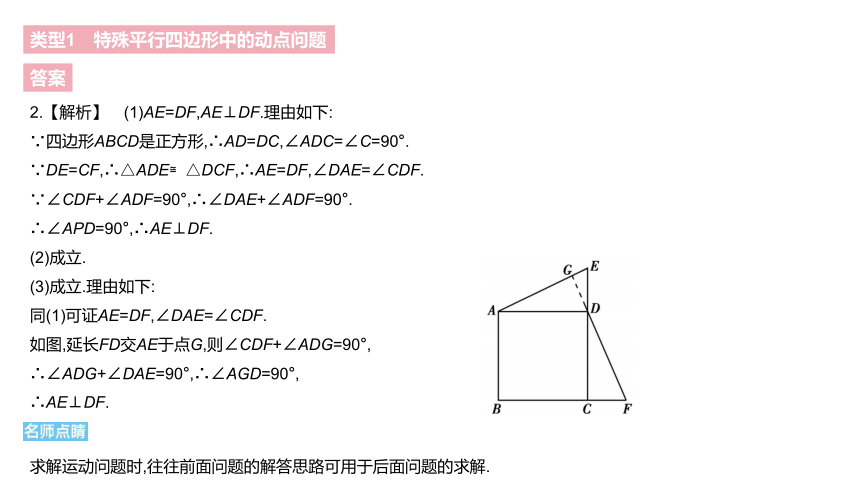
(3)成立.理由如下:
同(1)可证AE=DF,∠DAE=∠CDF.
如图,延长FD交AE于点G,则∠CDF+∠ADG=90°,
∴∠ADG+∠DAE=90°,∴∠AGD=90°,
∴AE⊥DF.
类型1 特殊平行四边形中的动点问题
求解运动问题时,往往前面问题的解答思路可用于后面问题的求解.
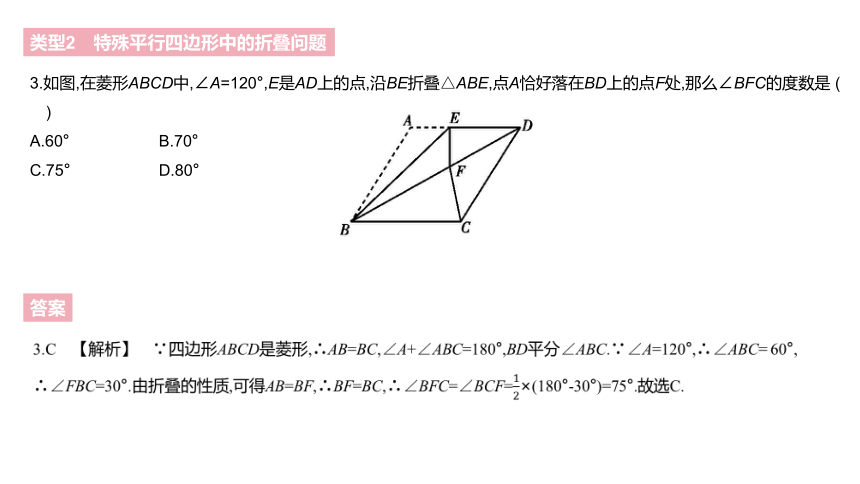
3.如图,在菱形ABCD中,∠A=120°,E是AD上的点,沿BE折叠△ABE,点A恰好落在BD上的点F处,那么∠BFC的度数是 ( )
A.60° B.70°
C.75° D.80°
答案
3.C 【解析】 ∵四边形ABCD是菱形,∴AB=BC,∠A+∠ABC=180°,BD平分∠ABC.∵∠A=120°,∴∠ABC= 60°, ∴∠FBC=30°.由折叠的性质,可得AB=BF,∴BF=BC,∴∠BFC=∠BCF=12×(180°-30°)=75°.故选C.
?
类型2 特殊平行四边形中的折叠问题
4.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D'的位置,则重叠部分△AFC的面积为 ( )
A.12 B.10
C.8 D.6
答案
4.B 【解析】 由折叠及矩形的性质可知,AD'=AD=BC=4,∠ACD=∠ACD'.∵AB∥CD,∴∠ACD= ∠CAF,∴∠ACF= ∠CAF,∴AF=CF,设AF=CF=x,则BF=8-x.在Rt△BCF中,BC2+BF2=CF2,∴42+(8-x)2=x2,解得x=5,∴AF=5,∴S△AFC= 12AF·BC= 10.故选B.
?
类型2 特殊平行四边形中的折叠问题
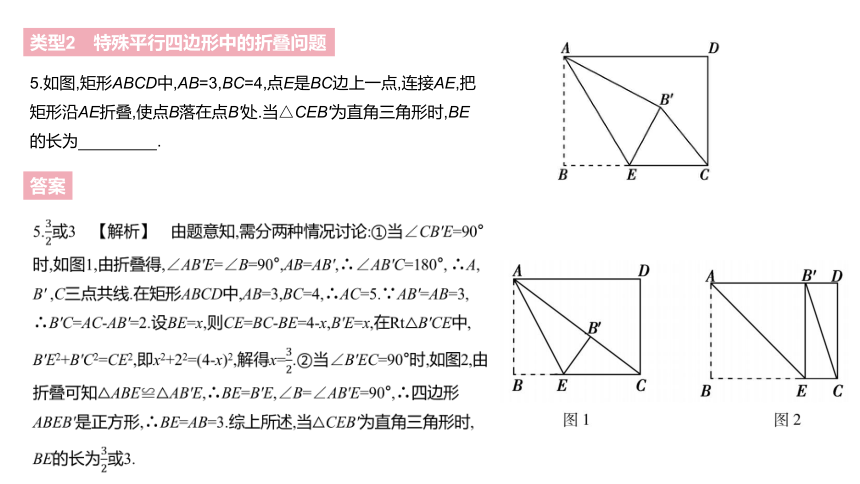
5.如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把矩形沿AE折叠,使点B落在点B'处.当△CEB'为直角三角形时,BE的长为? .?
答案
5.32或3 【解析】 由题意知,需分两种情况讨论:①当∠CB'E=90°时,如图1,由折叠得,∠AB'E=∠B=90°,AB=AB',∴∠AB'C=180°, ∴A, B' ,C三点共线.在矩形ABCD中,AB=3,BC=4,∴AC=5.∵AB'=AB=3, ∴B'C=AC-AB'=2.设BE=x,则CE=BC-BE=4-x,B'E=x,在Rt△B'CE中, B'E2+B'C2=CE2,即x2+22=(4-x)2,解得x=32.②当∠B'EC=90°时,如图2,由折叠可知△ABE≌△AB'E,∴BE=B'E,∠B=∠AB'E=90°,∴四边形ABEB'是正方形,∴BE=AB=3.综上所述,当△CEB'为直角三角形时, BE的长为32或3.
?
类型2 特殊平行四边形中的折叠问题
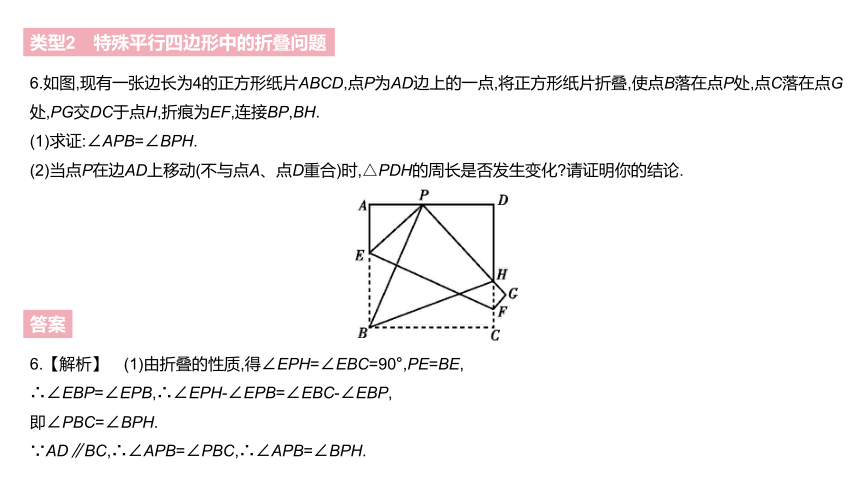
6.如图,现有一张边长为4的正方形纸片ABCD,点P为AD边上的一点,将正方形纸片折叠,使点B落在点P处,点C落在点G处,PG交DC于点H,折痕为EF,连接BP,BH.
(1)求证:∠APB=∠BPH.
(2)当点P在边AD上移动(不与点A、点D重合)时,△PDH的周长是否发生变化?请证明你的结论.
答案
6.【解析】 (1)由折叠的性质,得∠EPH=∠EBC=90°,PE=BE,
∴∠EBP=∠EPB,∴∠EPH-∠EPB=∠EBC-∠EBP,
即∠PBC=∠BPH.
∵AD∥BC,∴∠APB=∠PBC,∴∠APB=∠BPH.
类型2 特殊平行四边形中的折叠问题
答案
(2)△PDH的周长不变.证明如下:
过点B作BQ⊥PH,垂足为Q.
由(1)知∠APB=∠BPH.
在△ABP和△QBP中,∠????????????=∠????????????,∠????=∠????????????,????????????????=????????,????????????
∴△ABP≌△QBP,∴AP=QP,AB=QB.
∵AB=BC,∴BC=BQ.
在Rt△BCH和Rt△BQH中,????????=????????,????????=????????,
∴Rt△BCH≌Rt△BQH,∴CH=QH.
∴△PDH的周长为PD+DH+PH=PD+DH+AP+HC=AD+CD=8.
故△PDH的周长不发生变化.
?
类型2 特殊平行四边形中的折叠问题
7.小明参加数学兴趣小组的探究活动,将边长为2的正方形ABCD与边长为22的正方形AEFG按图1的位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
(1)小明发现DG⊥BE,请你帮他说明理由;
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.
?
类型3 特殊平行四边形中的旋转问题
答案
7.【解析】 (1)∵四边形ABCD与四边形AEFG是正方形,
∴AD=AB,∠DAG=∠BAE=90°,AG=AE,
∴△ADG≌△ABE,∴∠AGD=∠AEB.
如图1,延长EB交DG于点H.
在△ADG中,∠AGD+∠ADG=90°,∴∠AEB+∠ADG=90°,
∴∠DHE=180°-(∠AEB+∠ADG)=90°,∴DG⊥BE.
(2)∵四边形ABCD与四边形AEFG是正方形,
∴AD=AB,∠DAB=∠GAE=90°,AG=AE,
∴∠DAB+∠BAG=∠GAE+∠BAG,∴∠DAG=∠BAE,
又∵AD=AB,AG=AE,∴△ADG≌△ABE,∴DG=BE.
类型3 特殊平行四边形中的旋转问题
答案
如图2,过点A作AM⊥DG于点M,则∠AMD=∠AMG=90°,
∵BD是正方形ABCD的对角线,∴∠MDA=45°.
在Rt△AMD中,∠MDA=45°,AD=2,
可得DM=AM=2,
在Rt△AMG中,GM=????????2?????????2=6,
∴DG=DM+GM=2+6,∴BE=DG=2+6.
?
类型3 特殊平行四边形中的旋转问题
8.已知:正方形ABCD中,∠MAN=45°,将∠MAN绕点A接顺时针方向旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.
(1)当∠MAN绕点A旋转到BM=DN时(如图1),求证:BM+DN=MN.
(2)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间的数量关系是 .
(3)当∠MAN绕点A旋转到如图3的位置时,猜想线段BM,DN和MN之间又有怎样的数量关系,并对你的猜想加以说明.
类型3 特殊平行四边形中的旋转问题
答案
8.【解析】 (1)如图1,延长CB至点E,使得BE=DN,连接AE.
易证△ABE≌△ADN,
∴∠BAE=∠DAN,AE=AN,
∴∠EAN=∠BAE+∠BAN=∠DAN+∠BAN=90°,
∵∠MAN=45°,∴∠EAM=∠MAN,
又∵AM=AM,∴△AEM≌△ANM,
∴ME=MN,即BM+BE=MN,∴BM+DN=MN.
(2)BM+DN=MN
类型3 特殊平行四边形中的旋转问题
答案
(3)DN-BM=MN.理由如下:
如图2,在DC上截取DE=BM,连接AE.易证△ADE≌△ABM,
∴∠DAE=∠BAM,AE=AM,
∴∠EAM=∠BAM+∠BAE=∠DAE+∠BAE=90°,
∵∠MAN=45°,∴∠EAN=∠MAN,
又∵AN=AN,∴△MAN≌△EAN,
∴EN=MN,即DN-DE=MN,
∴DN-BM=MN.
类型3 特殊平行四边形中的旋转问题
综合素养拓训
发展核心素养,有助于学会用数学的眼光观察现实世界,所谓数学的眼光,就是数学抽象,而数学抽象中就包括几何直观.第1题在探究线段之间的数量关系时,注重对比训练,研究正方形中的解题思路在菱形中是否仍然适用,关注核心素养中的逻辑推理;第2题研究运动过程中的恒等关系,在直观想象中蕴含着抽象、推理,表明核心素养不是相互独立的,而是相互“渗透”的.
1.[与正方形有关的探究性问题]如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,连接PA,PC,PE,且PA=PE,PE交CD于点F.
(1)证明:PC=PE.
(2)求∠CPF的度数.
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
答案
1.【解析】 (1)在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,
在△ABP和△CBP中,AB=CB,∠ABP=∠CBP,PB=PB,
∴△ABP≌△CBP,∴PA=PC.
∵PA=PE,∴PC=PE.
(2)由(1)知△ABP≌△CBP,∴∠BAP=∠BCP,
∴∠DAP=∠DCP.
∵PA=PE,∴∠DAP=∠E,∴∠DCP=∠E.
∵∠CFP=∠EFD,
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,
∴∠CPF=∠EDF=90°.
答案
(3)AP=CE.理由如下:
在菱形ABCD中,AB=CB,∠ABP=∠CBP=60°,∠BAD=∠BCD.
在△ABP和△CBP中,AB=CB,∠ABP=∠CBP,PB=PB,
∴△ABP≌△CBP,∴AP=CP,∠BAP=∠BCP,
∴∠DAP=∠DCP.
∵AP=EP,∴CP=EP,∠DAP=∠AEP,∴∠DCP=∠AEP.
∵∠CFP=∠EFD,
∴180°-∠CFP-∠DCP=180°-∠EFD-∠AEP,
∴∠CPF=∠EDF=180°-∠ADC=180°-120°=60°,
∴△EPC是等边三角形,
∴CP=CE,∴AP=CE.
2.[正方形与图形旋转]已知正方形ABCD中,E为对角线BD上一点,过点E作EF⊥BD交BC于点F,连接DF,G为DF的中点,连接EG,CG.
(1)如图1,求证:EG=CG.
(2)将图1中的△BEF绕点B按逆时针方向旋转45°,如图2,取DF的中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
(3)将图1中的△BEF绕点B逆时针旋转任意角度,如图3,取DF的中点G,连接EG,CG.问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)
答案
2.【解析】 (1)在Rt△FCD中,G为DF的中点,∴CG=12FD.
同理,在Rt△DEF中,EG=12FD,∴EG=CG.
(2)(1)中的结论仍然成立.证明如下:
连接AG,过点G作GM⊥AD于点M,与EF的延长线交于点N,则∠AMN=∠ENM=∠EAM=90°,∴四边形AENM为矩形.
在△DAG和△DCG中,AD=CD,∠ADG=∠CDG,DG=DG,
∴△DAG≌△DCG,∴AG=CG.
在△DMG和△FNG中,∠DGM=∠FGN,DG=FG,∠MGD=∠NGF,
∴△DMG≌△FNG,∴MG=NG.
在矩形AENM中,AM=EN.
在Rt△AMG和Rt△ENG中,AM=EN,MG=NG,
∴Rt△AMG≌Rt△ENG,∴AG=EG.
∴EG=CG.
(3)(1)中的结论仍然成立.
其他的结论还有EG⊥CG.(答案不唯一)
?
答案
1.B 【解析】 如图,∵A(-3,0),B(0,2),C(3,0),D(0,-2),∴OA=OC,OB=OD,∴四边形ABCD为平行四边形,又∵BD⊥AC, ∴四边形ABCD为菱形.故选B.
一、选择题
1.[2019广西北海期末]平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-3,0),B(0,2),C(3,0),D(0,-2),则四边形ABCD是 ( )
A.矩形 B.菱形
C.正方形 D.以上都不对
答案
2.C 【解析】 ∵四边形ABCD是矩形,∴AD=BC=4,∠BAD=90°,又∵AB=3,∴BD=5.∵????△????????????=12BD×AF=12AB×AD, ∴AF=2.4.故选C.
?
2.[2019江苏常州金坛区期中]如图,在矩形ABCD中,AB=3,BC=4,AE⊥BD于点F,则线段AF的长是 ( )
A.3 B.2.5
C.2.4 D.2
答案
3.A 【解析】 ∵四边形AEFG是正方形,∴∠AEF=90°.∵四边形ABCD是平行四边形,∴AD∥BC,∠C=∠BAD, ∴∠EAD=180°-∠AEC=180°-90°-15°=75°,∴∠BAD=40°+75°=115°,∴∠C=115°.故选A.
3.如图,在平行四边形ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=40°,∠CEF=15°,则∠C的度数是 ( )
A.115° B.105°
C.75° D.65°
答案
4.A 【解析】 如图,连接AC,∵四边形ABCD是菱形,∴BC=AB=3.∵∠B=60°, ∴△ABC是等边三角形,∴AC=AB=3,∵点F,G分别是AE,CE的中点,∴FG是△ACE的中位线,∴FG=12AC=32.故选A.
?
4.如图,在菱形ABCD中,∠B=60°,AB=3,点E是BC边上的一个动点(点E与点C不重合),点F,G分别是AE,CE的中点,则线段FG的长为 ( )
A.32 B.3
C.2 2 D.2 3
?
答案
5.C 【解析】 顺次连接平行四边形ABCD各边中点,利用三角形中位线性质可得,新的四边形是平行四边形.①若AC⊥BD,则利用“有一个角是直角的平行四边形是矩形”判定新的四边形是矩形;②∵四边形ABCD是平行四边形, ∴AO=OC,BO=DO,∵△ABO的周长等于△CBO的周长,∴AB=BC,根据等腰三角形的性质可知BO⊥AC,∴BD⊥AC,同①可判定新的四边形是矩形;③∵四边形ABCD是平行四边形,∴∠CBO=∠ADO,∵∠DAO=∠CBO,∴∠ADO= ∠DAO, ∴AO=OD,∴AC=BD,可利用“有一组邻边相等的平行四边形是菱形”判定新的四边形是菱形,不符合题意;④在平行四边形ABCD中,∠DAO=∠BAO,易得平行四边形ABCD是菱形,∴AC⊥BD,同①可判定新的四边形是矩形.∴①②④符合题意.故选C.
5.[2019上海普陀区二模]如图,平行四边形ABCD的对角线AC,BD交于点O,顺次连接平行四边形ABCD各边中点得到一个新的四边形,给出下列四个条件:①AC⊥BD;②△ABO的周长等于△CBO的周长;③∠DAO=∠CBO;④∠DAO= ∠BAO. 如果从中选择一个条件可以使这个新的四边形成为矩形,那么这样的条件个数是 ( )
A.1 B.2
C.3 D.4
答案
6.D 【解析】 ∵四边形ABCD是矩形,∴∠DCB=∠ABC=90°,∵BF与CF分别平分∠ABC和∠BCD,∴∠FCB= ∠FBC=12∠DCB=45°,∴CF=BF,∠F=180°-45°-45°=90°.①∵EB∥CF,CE∥BF,∴四边形BFCE是平行四边形,又∵CF= BF, ∴四边形BFCE是菱形,又∵∠F=90°,∴四边形BFCE是正方形;②∵BE=CE,BE=BF,CF=BF,∴BF=CF=CE=BE,∴四边形BFCE是菱形,又∵∠F=90°,∴四边形BFCE是正方形;③∵BE∥CF,CE⊥BE,∠F=90°,∴∠FBE=∠E=∠F=90°, ∴四边形BFCE是矩形,又∵BF=CF,∴四边形BFCE是正方形;④∵CE∥BF,∠FBC=45°,∴∠ECB=∠FBC=45°,又∵BE=CE,∴∠EBC=∠ECB=45°,∴∠FCE=∠FBE=90°,又∵∠F=90°,∴四边形BFCE是矩形,又∵BF=CF,∴四边形BFCE是正方形.∴能判定四边形BFCE是正方形的条件共有4个.故选D.
?
6.如图,在矩形ABCD内有一点F,BF与CF分别平分∠ABC和∠BCD,点E为矩形ABCD外一点,连接BE,CE.给出下列四个条件:①BE∥CF,CE∥BF;②BE=CE,BE=BF;③BE∥CF,CE⊥BE;④BE=CE,CE∥BF.其中能判定四边形BFCE是正方形的共有 ( )
A.1个 B.2个 C.3个 D.4个
答案
7.30° 【解析】 ∵四边形ABCD为菱形,∴BC=CD,∠BCA=∠DCA,又∵CE=CE,∴△BEC≌△DEC,∴∠EDC= ∠1. ∵∠1+∠2=75°,∴∠EDC+∠2=75°,∴∠AED=∠EDC+∠2=75°,∴∠BED=2∠AED=150°,∴∠3=30°.
二、填空题
7.[2019天津和平区一模]如图,菱形ABCD中,点E是对角线AC上一点,BE的延长线交边CD于点F.若∠1+∠2=75°,则∠3的度数为 .?
答案
8.①④
8.小明在探究“四边形的不稳定性”活动中,将四根木条用钉子钉成一个矩形框架ABCD,如图所示.扭动矩形框架,观察矩形ABCD的变化,有下列判断:
①四边形ABCD由矩形变为平行四边形;
②A,C两点之间的距离不变;
③四边形ABCD的面积不变;
④四边形ABCD的周长不变.
其中正确的是 .(填序号)?
答案
9.12 【解析】 如图,取CD的中点E,连接OE,AE,OA.∵AB=9,BC=6,四边形ABCD是矩形,∴CD=9,AD=6,又∵∠MON=90°,∴OE=DE=12CD=92,∴AE=
????????2+????????2=152,∵OA≤OE+AE,∴当O,A,E三点共线时,点A到点O的距离最大,∴点A到点O的最大距离为92+152=12.
?
9.如图,∠MON=90°,矩形ABCD的顶点C,D分别在射线ON,OM上滑动,AB=9, BC=6,在滑动过程中,点A到点O的最大距离为 .?
答案
10.①②③ 【解析】 在矩形ABCD中,对角线AC,BD相交于点O,连接PM,QN,若PM与QN均经过点O,则四边形MNPQ为平行四边形,此时若PM=QN,则四边形MNPQ为矩形;若PM⊥QN,则四边形MNPQ为菱形.有的矩形不存在以点M,N,P,Q为顶点的正方形.故正确的结论是①②③.
10.[2019北京中考]在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合).对于任意矩形ABCD,下面四个结论中,
①存在无数个四边形MNPQ是平行四边形;
②存在无数个四边形MNPQ是矩形;
③存在无数个四边形MNPQ是菱形;
④至少存在一个四边形MNPQ是正方形.
所有正确结论的序号是 .?
三、解答题
11.[2018新疆乌鲁木齐中考]如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.
(1)求证:四边形AECD是菱形.
(2)若AB=6,BC=10,求EF的长.
答案
11.【解析】 (1)∵AD∥BC,AE∥DC,
∴四边形AECD是平行四边形.
在△ABC中,∠BAC=90°,E是BC的中点,
∴AE=12BC,CE=12BC,
∴AE=CE,∴四边形AECD是菱形.
(2)如图,过点A作AH⊥BC于点H.
在△ABC中,∠BAC=90°,AB=6,BC=10,
∴AC=????????2?????????2=102?62=8.
由(1)知四边形AECD是菱形,∴DC=CE.
∵ S △ABC =12AB·AC=12BC·AH,∴AH=245.
∵S菱形AECD =CE·AH=CD·EF,CD=CE,
∴EF=AH=245.
?
答案
12.【解析】 (1)∵ME⊥AO,MF⊥BO,
∴∠MEO=∠MFO=90°.
∵正方形ABCD的对角线AC,BD交于点O,
∴∠EOF=90°,
∴四边形OEMF为矩形.
(2)连接MO,∵边长为8的正方形ABCD的对角线AC,BD交于点O,
∴OA=OB=4 2,
由(1)知EF=MO,易知当M在AB的中点时,MO有最小值,即EF有最小值,此时MO=12AB=4,∴EF的最小值为4.
?
12.[2019江苏无锡期中]如图,边长为8的正方形ABCD的对角线AC,BD交于点O,M是AB边上一动点,ME⊥AO,MF⊥BO.
(1)求证:四边形OEMF为矩形.
(2)连接EF,求EF的最小值.
13.如图1,在正方形ABCD中,点E为AB上的点(不与A,B重合),△ADE与△FDE关于DE对称,作射线CF,与DE的延长线相交于点G,连接AG.
(1)当∠ADE=15°时,求∠DGC的度数;
(2)若点E在AB上移动,请你判断∠DGC的度数是否发生变化,若不变化,请证明你的结论;若会发生变化,请说明理由;
(3)如图2,点F在对角线BD上,点M为DE的中点,连接AM,FM,请判断四边形AGFM的形状,并证明结论.
答案
13.【解析】 (1)∵∠ADE=15°,∴∠FDE=15°,∴∠CDF=60°.
由对称可知AD=DF,∴DF=DC,∴△DFC是等边三角形,∴∠CFD=60°.
∵∠CFD=∠DGC+∠FDE=15°+∠DGC,
∴∠DGC=45°.
(2)∠DGC的度数不变化.证明如下:
∵△ADE与△FDE关于DE对称,∴AD=DF,∠ADE=∠FDE.
设∠ADE=x,可得∠FDE=x,∠CDF=90°-2x,
∵DC=AD=DF,∴∠CFD=12[180°-(90°-2x)]=45°+x.
∵∠CFD=∠DGC+∠FDE=x+∠DGC,
∴x+∠DGC=45°+x,
∴∠DGC=45°.
(3)四边形AGFM是正方形.证明如下:
∵∠DAE=∠DFE=90°,点M为DE的中点,
?
答案
∴AM=FM=DM=12DE,
∴∠ADM=∠DAM,∠MDF=∠DFM,
又∵∠ADM=∠MDF=22.5°,
∴∠AME=∠FME=2∠ADM=2∠MDF=45°,
∴∠AMF=90°.
由(2)可知,∠DGC=45°,∴FM=FG.
在△ADG与△FDG中,????????=????????,????????????∠????????????=∠????????????,????????=????????,?????????
∴△ADG≌△FDG,∴AG=FG,
∴AM=MF=FG=AG,∴四边形AGFM是菱形,
又∵∠AMF=90°,
∴四边形AGFM是正方形.
?
14.[2019江苏南京秦淮区期末]已知:如图,在?ABCD中,G,H分别是AD,BC的中点,E,O,F均是对角线BD上的四等分点,顺次连接G,E,H,F.
(1)求证:四边形GEHF是平行四边形.
(2)当?ABCD满足 条件时,四边形GEHF是菱形.?
(3)若BD=2AB,
①探究四边形GEHF的形状,并说明理由.
②当AB=2,∠ABD=120°时,直接写出四边形GEHF的面积.
答案
14.【解析】 (1)如图1,连接AC,易知AC与BD交于点O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E,O,F分别是对角线BD上的四等分点,
∴E,F分别为OB,OD的中点,
又∵G是AD的中点,∴GF为△AOD的中位线,
∴GF∥OA,GF=12OA.
同理,EH∥OC,EH=12OC,
∴EH=GF,EH∥GF,
∴四边形GEHF是平行四边形.
?
答案
(2)AB⊥BD
连接GH,则AG=BH,AG∥BH,
∴四边形ABHG是平行四边形,∴AB∥GH.
∵AB⊥BD,∴GH⊥BD,∴GH⊥EF.
由(1)得,四边形GEHF是平行四边形,
∴四边形GEHF是菱形.
(3)①四边形GEHF是矩形.理由如下:
在?ABCD中,由G,H分别是AD,BC的中点,易得GH=AB.
∵BD=2AB,∴AB=12BD=EF,∴GH=EF,
由(1)得,四边形GEHF是平行四边形,
∴四边形GEHF是矩形.
?
答案
②3.
如图2,作AM⊥BD交DB的延长线于M,GN⊥BD于N,则AM∥GN.
∵G是AD的中点,∴GN是△ADM的中位线,∴GN=12AM.
∵∠ABD=120°,∴∠ABM=60°,∴∠BAM=30°,
∴BM=12AB=1,AM=3,∴GN=32.
∵BD=2AB=4,∴EF=12BD=2,
∴ S△EFG =12EF×GN=12×2×32=32,
∴ S四边形????????????????= 2S△EFG =3.
?
第一章 特殊平行四边形(中考真题)
数学·九年级上册·北师
答案
1.C 【解析】 ∵点A,B的坐标分别为(2,0)和(0,1),∴OA=2,OB=1.在Rt△AOB中,由勾股定理,得AB=22+12=5,故菱形ABCD的周长为4 5.
?
1.[2019天津中考]如图,四边形ABCD为菱形,A,B两点的坐标分别是(2,0),(0,1),点C,D在坐标轴上,则菱形ABCD的周长等于 ( )
A.5 B.4 3
C.4 5 D.20
?
答案
2.C 【解析】 由菱形的性质可知OB=8,OA=2,AC⊥BD.由平移的性质,得O'B'=OB=8,O'A=3OA= 6,∠AO'B'= ∠AOB= 90°, ∴AB'=????′????′2+????′????2=82+62=10.
?
2.[2019江苏苏州中考]如图,菱形ABCD的对角线AC,BD交于点O,AC=4,BD=16,将△ABO沿点A到点C的方向平移,得到△A'B'O'.当点A'与点C重合时,点A与点B'之间的距离为 ( )
A.6 B.8
C.10 D.12
答案
3.A 【解析】 如图,连接AE,设AC,EF交于点O,∵四边形ABCD是矩形,∴AD∥BC,∴∠DAC=∠ACB.∵直线EF垂直平分AC,∴OA=OC,AE=EC,又∵∠AOF=∠COE,∴△AOF≌△COE,∴AE=CE=AF=5,∴BC=BE+EC=8.在Rt△ABE中, AB= ????????2?????????2=52?32=4.在Rt△ABC中,AC=????????2+????????2=42+82=45.故选A.
?
3.[2019广东广州中考]如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为 ( )
A.4 5 B.4 3
C.10 D.8
?
答案
4.A 【解析】 ∵点E,F分别是AD,BC的中点,点M,N分别是AC,BD的中点,∴EN,NF,FM,ME分别是△ABD,△BCD, △ABC,△ACD的中位线,∴EN∥AB∥FM,ME∥CD∥NF,EN=12AB=FM,ME=12CD=NF.当AB=CD时,EN=FM=ME=NF,∴平行四边形EMFN是菱形.当AB⊥CD时,EN⊥ME,则∠MEN=90°,∴菱形EMFN是正方形.故选A.
?
4.[2019辽宁抚顺中考]如图,AC,BD是四边形ABCD的对角线,点E,F分别是AD,BC的中点,点M,N分别是AC,BD的中点,连接EM,MF,FN,NE,要使四边形EMFN为正方形,则需添加的条件是 ( )
A.AB=CD,AB⊥CD
B.AB=CD,AD=BC
C.AB=CD,AC⊥BD
D.AB=CD,AD∥BC
答案
5.D 【解析】 连接PC,CE.易知点A,C关于直线BD对称,∴AP=CP,∴AP+EP=CP+EP,∴AP+EP的最小值等于CP+EP的最小值.根据“两点之间,线段最短”可知,当C,P,E三点在同一条直线上时,CP+EP的值最小,最小值为CE的长.易证△ABF≌△CDE,∴AF=CE,即AP+EP的最小值等于AF的长.故选D.
5.[2018天津中考]如图,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于AP+EP最小值的是 ( )
A.AB B.DE
C.BD D.AF
解决这类问题是利用轴对称的性质将“同侧折线”转化为“异侧折线”,再根据“两点之间,线段最短”确定出折线长度的最小值.
答案
6.85 【解析】 如图,连接BD,交AC于点O,∵四边形ABCD为正方形,∴BD⊥AC, OA=OB=OC=OD.∵AC=8,AE=CF=2,∴OE=OF=2,∴四边形BEDF为菱形,∴DE=DF= BE=BF.∵BD=AC=8,∴OB=OD=4,在Rt△DOE中,由勾股定理,得DE=????????2+????????2=42+22=25,∴四边形BEDF的周长为4DE=85.
?
6.[2019山东菏泽中考]如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是 . ?
答案
7.12 【解析】 设每个直角三角形中较长的直角边的长为a,较短的直角边的长为b,则????+????=5,?????????=1,解得????=3,????=2,∴菱形的面积为12×ab×4=2ab=2×3×2=12.
?
7.[2019北京中考]如图,把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2、图3所示的正方形,则图1中菱形的面积为 .?
答案
8.15+3 【解析】 ∵阴影部分的面积与正方形ABCD的面积之比为2∶3,AB=3,∴阴影部分的面积为23×32=6,∴空白部分的面积为9-6=3.∵四边形ABCD为正方形,∴BC=CD,∠BCE=∠CDF=90°,又∵CE=DF,∴△BCE≌△CDF, ∴△BCG 的面积与四边形DEGF的面积相等,均为12×3=32.∵△BCE≌△CDF,∴∠CBE=∠DCF,又∵∠DCF+∠GCB= 90°, ∴∠GCB+∠CBE=90°,∴∠BGC=90°.设BG=a,CG=b,则12ab=32,∵a2+b2=32,∴a2+2ab+b2=9+6=15,即(a+b)2=15,∴a+ b= 15,即BG+CG=15,∴△BCG的周长为15+3.
?
8.[2018浙江台州中考]如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2∶3,则△BCG的周长为? .?
答案
9.【分析】 (1)先根据对边平行且相等的四边形是平行四边形,得到四边形ABCD是平行四边形,再根据邻边相等的平行四边形是菱形,即可证明结论.(2)先根据菱形的性质及勾股定理得到AO的长,再在Rt△AEC中根据斜边上的中线等于斜边的一半计算即可.
【解析】 (1)∵AB∥DC,∴∠BAC=∠DCA.
∵AC平分∠BAD,∴∠BAC=∠DAC,
∴∠DAC=∠DCA,∴AD=DC.
9.[2018北京中考]如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形.
(2)若AB=5,BD=2,求OE的长.
?
答案
∵AB=AD,∴AB=DC,
∴四边形ABCD是平行四边形.
又∵AB=AD,
∴四边形ABCD是菱形.
(2)∵四边形ABCD是菱形,BD=2,
∴AO=12AC,BO=12BD=1,∠AOB=90°,
∴AO=????????2?????????2=2.
∵CE⊥AB,∴∠AEC=90°,
∴OE=12AC=AO=2.
?
10.[2019云南中考]如图,四边形ABCD中,对角线AC,BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形.
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
答案
10.【解析】 (1)∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形.
∵∠AOB=∠OAD+∠ODA=2∠OAD,
∴∠OAD=∠ODA,∴AO=DO,∴AC=BD,
∴四边形ABCD是矩形.
(2)由(1)知四边形ABCD是矩形,
∴AB∥CD,∴∠ABO=∠CDO.
∵∠AOB∶∠ODC=4∶3,∴∠AOB∶∠ABO=4∶3,
∴∠BAO∶∠AOB∶∠ABO=3∶4∶3.
∵∠BAO+∠AOB+∠ABO=180°,
∴∠ABO=54°.
∵∠BAD=90°,∴∠ADO=90°-54°=36°.
11.[2019浙江宁波中考]如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)求证:BG=DE.
(2)若E为AD的中点,FH=2,求菱形ABCD的周长.
答案
11.【解析】 (1)在矩形EFGH中,EH=FG,EH∥FG,
∴∠GFH=∠EHF.
∵∠BFG=180°-∠GFH,∠DHE=180°-∠EHF,
∴∠BFG=∠DHE.
在菱形ABCD中,AD∥BC,
∴∠GBF=∠EDH,
∴△BGF≌△DEH,
∴BG=DE.
答案
(2)如图,连接EG.
在菱形ABCD中,AD∥BC,AD=BC.
∵E为AD的中点,∴AE=ED.
∵BG=DE,∴AE=BG,
∴四边形ABGE为平行四边形,
∴AB=EG.
在矩形EFGH中,EG=FH=2,
∴AB=2,
∴菱形ABCD的周长为2×4=8.
12.[2018吉林长春中考]在正方形ABCD中,E是边CD上一点(点E不与点C,D重合),连接BE.
【感知】 如图1,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)
【探究】 如图2,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连接CM.若CM=1,则FG的长为 .?
【应用】 如图3,取BE的中点M,连接CM.过点C作CG⊥BE交AD于点G,连接EG,MG.若CM=3,则四边形GMCE的面积为 .?
答案
12.【解析】 【探究】(1)如图,将GF平移到AH处,
则AH∥GF,AH=GF.
∵GF⊥BE,∴AH⊥BE,∴∠ABE+∠BAH=90°.
∵四边形ABCD是正方形,
∴AB=BC,∠ABH=∠BCE=90°,
∴∠ABE+∠CBE=90°,
∴∠BAH=∠CBE.
在△ABH和△BCE中,∠????????????=∠????????????,????????=????????,?????????????∠????????????=∠????????????,?
∴△ABH≌△BCE,∴BE=AH,
∴BE=FG.
?
答案
(2)2
【应用】9
在Rt△BCE中,∠BCE=90°,CM是BE边上的中线,
∴BE=2CM=6.
易证△BCE≌△CDG,∴BE=CG=6.
又∵ME=12BE=3,且BE⊥CG,
∴????四边形????????????????=12×3×6=9.
数学·九年级上册·北师
专题 特殊平行四边形与图形变换
专项素养拓训
1.[2019湖北黄石八校联考]如图,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/s的速度向点B匀速运动.设点D,E运动的时间是t s(0
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
类型1 特殊平行四边形中的动点问题
答案
1.【解析】 (1)依题意,得CD=4t,AE=2t.
在Rt△ABC中,∠C=90°-∠A=30°.
在Rt△CDF中,∠C=30°,∴DF=12CD=2t,∴AE=DF.
(2)能.理由如下:
∵DF⊥BC,∠B=90°,∴DF∥AB,
由(1)知DF=AE,∴四边形AEFD是平行四边形.
当AD=AE时,四边形AEFD是菱形,
则60-4t=2t,解得t=10,
∴当t=10时,四边形AEFD是菱形.
?
类型1 特殊平行四边形中的动点问题
答案
(3)当t=152时,△DEF是直角三角形(∠EDF=90°);当t=12时,△DEF是直角三角形(∠DEF=90°).理由如下:
当∠EDF=90°时,DE∥BC,
∴∠ADE=∠C=30°,∴AD=2AE,
∴60-4t=2·2t,解得t=152(符合题意).
当∠DEF=90°时,DE⊥EF,
∵四边形AEFD是平行四边形,∴AD∥EF,∴DE⊥AD,
∴△ADE是直角三角形,∠ADE=90°.
∵∠A=60°,∴∠DEA=30°,
∴AD=12AE,∴60-4t=12·2t,解得t=12(符合题意).
综上,当t=152时,△DEF是直角三角形(∠EDF=90°);当t=12时,△DEF是直角三角形(∠DEF=90°).
?
类型1 特殊平行四边形中的动点问题
2.在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图1,当点E自D向C,点F自C向B移动时,连接AE和DF交于点P,请写出AE与DF的关系,并说明理由;
(2)如图2,当点E,F分别移动到边DC,CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请直接回答“成立”或“不成立”,无需证明)
(3)如图3,当E,F分别在CD,BC的延长线上移动时,连接AE和DF,(1)中的结论还成立吗?请说明理由.
类型1 特殊平行四边形中的动点问题
答案
2.【解析】 (1)AE=DF,AE⊥DF.理由如下:
∵四边形ABCD是正方形,∴AD=DC,∠ADC=∠C=90°.
∵DE=CF,∴△ADE≌△DCF,∴AE=DF,∠DAE=∠CDF.
∵∠CDF+∠ADF=90°,∴∠DAE+∠ADF=90°.
∴∠APD=90°,∴AE⊥DF.
(2)成立.
(3)成立.理由如下:
同(1)可证AE=DF,∠DAE=∠CDF.
如图,延长FD交AE于点G,则∠CDF+∠ADG=90°,
∴∠ADG+∠DAE=90°,∴∠AGD=90°,
∴AE⊥DF.
类型1 特殊平行四边形中的动点问题
求解运动问题时,往往前面问题的解答思路可用于后面问题的求解.
3.如图,在菱形ABCD中,∠A=120°,E是AD上的点,沿BE折叠△ABE,点A恰好落在BD上的点F处,那么∠BFC的度数是 ( )
A.60° B.70°
C.75° D.80°
答案
3.C 【解析】 ∵四边形ABCD是菱形,∴AB=BC,∠A+∠ABC=180°,BD平分∠ABC.∵∠A=120°,∴∠ABC= 60°, ∴∠FBC=30°.由折叠的性质,可得AB=BF,∴BF=BC,∴∠BFC=∠BCF=12×(180°-30°)=75°.故选C.
?
类型2 特殊平行四边形中的折叠问题
4.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D'的位置,则重叠部分△AFC的面积为 ( )
A.12 B.10
C.8 D.6
答案
4.B 【解析】 由折叠及矩形的性质可知,AD'=AD=BC=4,∠ACD=∠ACD'.∵AB∥CD,∴∠ACD= ∠CAF,∴∠ACF= ∠CAF,∴AF=CF,设AF=CF=x,则BF=8-x.在Rt△BCF中,BC2+BF2=CF2,∴42+(8-x)2=x2,解得x=5,∴AF=5,∴S△AFC= 12AF·BC= 10.故选B.
?
类型2 特殊平行四边形中的折叠问题
5.如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把矩形沿AE折叠,使点B落在点B'处.当△CEB'为直角三角形时,BE的长为? .?
答案
5.32或3 【解析】 由题意知,需分两种情况讨论:①当∠CB'E=90°时,如图1,由折叠得,∠AB'E=∠B=90°,AB=AB',∴∠AB'C=180°, ∴A, B' ,C三点共线.在矩形ABCD中,AB=3,BC=4,∴AC=5.∵AB'=AB=3, ∴B'C=AC-AB'=2.设BE=x,则CE=BC-BE=4-x,B'E=x,在Rt△B'CE中, B'E2+B'C2=CE2,即x2+22=(4-x)2,解得x=32.②当∠B'EC=90°时,如图2,由折叠可知△ABE≌△AB'E,∴BE=B'E,∠B=∠AB'E=90°,∴四边形ABEB'是正方形,∴BE=AB=3.综上所述,当△CEB'为直角三角形时, BE的长为32或3.
?
类型2 特殊平行四边形中的折叠问题
6.如图,现有一张边长为4的正方形纸片ABCD,点P为AD边上的一点,将正方形纸片折叠,使点B落在点P处,点C落在点G处,PG交DC于点H,折痕为EF,连接BP,BH.
(1)求证:∠APB=∠BPH.
(2)当点P在边AD上移动(不与点A、点D重合)时,△PDH的周长是否发生变化?请证明你的结论.
答案
6.【解析】 (1)由折叠的性质,得∠EPH=∠EBC=90°,PE=BE,
∴∠EBP=∠EPB,∴∠EPH-∠EPB=∠EBC-∠EBP,
即∠PBC=∠BPH.
∵AD∥BC,∴∠APB=∠PBC,∴∠APB=∠BPH.
类型2 特殊平行四边形中的折叠问题
答案
(2)△PDH的周长不变.证明如下:
过点B作BQ⊥PH,垂足为Q.
由(1)知∠APB=∠BPH.
在△ABP和△QBP中,∠????????????=∠????????????,∠????=∠????????????,????????????????=????????,????????????
∴△ABP≌△QBP,∴AP=QP,AB=QB.
∵AB=BC,∴BC=BQ.
在Rt△BCH和Rt△BQH中,????????=????????,????????=????????,
∴Rt△BCH≌Rt△BQH,∴CH=QH.
∴△PDH的周长为PD+DH+PH=PD+DH+AP+HC=AD+CD=8.
故△PDH的周长不发生变化.
?
类型2 特殊平行四边形中的折叠问题
7.小明参加数学兴趣小组的探究活动,将边长为2的正方形ABCD与边长为22的正方形AEFG按图1的位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
(1)小明发现DG⊥BE,请你帮他说明理由;
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.
?
类型3 特殊平行四边形中的旋转问题
答案
7.【解析】 (1)∵四边形ABCD与四边形AEFG是正方形,
∴AD=AB,∠DAG=∠BAE=90°,AG=AE,
∴△ADG≌△ABE,∴∠AGD=∠AEB.
如图1,延长EB交DG于点H.
在△ADG中,∠AGD+∠ADG=90°,∴∠AEB+∠ADG=90°,
∴∠DHE=180°-(∠AEB+∠ADG)=90°,∴DG⊥BE.
(2)∵四边形ABCD与四边形AEFG是正方形,
∴AD=AB,∠DAB=∠GAE=90°,AG=AE,
∴∠DAB+∠BAG=∠GAE+∠BAG,∴∠DAG=∠BAE,
又∵AD=AB,AG=AE,∴△ADG≌△ABE,∴DG=BE.
类型3 特殊平行四边形中的旋转问题
答案
如图2,过点A作AM⊥DG于点M,则∠AMD=∠AMG=90°,
∵BD是正方形ABCD的对角线,∴∠MDA=45°.
在Rt△AMD中,∠MDA=45°,AD=2,
可得DM=AM=2,
在Rt△AMG中,GM=????????2?????????2=6,
∴DG=DM+GM=2+6,∴BE=DG=2+6.
?
类型3 特殊平行四边形中的旋转问题
8.已知:正方形ABCD中,∠MAN=45°,将∠MAN绕点A接顺时针方向旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.
(1)当∠MAN绕点A旋转到BM=DN时(如图1),求证:BM+DN=MN.
(2)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间的数量关系是 .
(3)当∠MAN绕点A旋转到如图3的位置时,猜想线段BM,DN和MN之间又有怎样的数量关系,并对你的猜想加以说明.
类型3 特殊平行四边形中的旋转问题
答案
8.【解析】 (1)如图1,延长CB至点E,使得BE=DN,连接AE.
易证△ABE≌△ADN,
∴∠BAE=∠DAN,AE=AN,
∴∠EAN=∠BAE+∠BAN=∠DAN+∠BAN=90°,
∵∠MAN=45°,∴∠EAM=∠MAN,
又∵AM=AM,∴△AEM≌△ANM,
∴ME=MN,即BM+BE=MN,∴BM+DN=MN.
(2)BM+DN=MN
类型3 特殊平行四边形中的旋转问题
答案
(3)DN-BM=MN.理由如下:
如图2,在DC上截取DE=BM,连接AE.易证△ADE≌△ABM,
∴∠DAE=∠BAM,AE=AM,
∴∠EAM=∠BAM+∠BAE=∠DAE+∠BAE=90°,
∵∠MAN=45°,∴∠EAN=∠MAN,
又∵AN=AN,∴△MAN≌△EAN,
∴EN=MN,即DN-DE=MN,
∴DN-BM=MN.
类型3 特殊平行四边形中的旋转问题
综合素养拓训
发展核心素养,有助于学会用数学的眼光观察现实世界,所谓数学的眼光,就是数学抽象,而数学抽象中就包括几何直观.第1题在探究线段之间的数量关系时,注重对比训练,研究正方形中的解题思路在菱形中是否仍然适用,关注核心素养中的逻辑推理;第2题研究运动过程中的恒等关系,在直观想象中蕴含着抽象、推理,表明核心素养不是相互独立的,而是相互“渗透”的.
1.[与正方形有关的探究性问题]如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,连接PA,PC,PE,且PA=PE,PE交CD于点F.
(1)证明:PC=PE.
(2)求∠CPF的度数.
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
答案
1.【解析】 (1)在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,
在△ABP和△CBP中,AB=CB,∠ABP=∠CBP,PB=PB,
∴△ABP≌△CBP,∴PA=PC.
∵PA=PE,∴PC=PE.
(2)由(1)知△ABP≌△CBP,∴∠BAP=∠BCP,
∴∠DAP=∠DCP.
∵PA=PE,∴∠DAP=∠E,∴∠DCP=∠E.
∵∠CFP=∠EFD,
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,
∴∠CPF=∠EDF=90°.
答案
(3)AP=CE.理由如下:
在菱形ABCD中,AB=CB,∠ABP=∠CBP=60°,∠BAD=∠BCD.
在△ABP和△CBP中,AB=CB,∠ABP=∠CBP,PB=PB,
∴△ABP≌△CBP,∴AP=CP,∠BAP=∠BCP,
∴∠DAP=∠DCP.
∵AP=EP,∴CP=EP,∠DAP=∠AEP,∴∠DCP=∠AEP.
∵∠CFP=∠EFD,
∴180°-∠CFP-∠DCP=180°-∠EFD-∠AEP,
∴∠CPF=∠EDF=180°-∠ADC=180°-120°=60°,
∴△EPC是等边三角形,
∴CP=CE,∴AP=CE.
2.[正方形与图形旋转]已知正方形ABCD中,E为对角线BD上一点,过点E作EF⊥BD交BC于点F,连接DF,G为DF的中点,连接EG,CG.
(1)如图1,求证:EG=CG.
(2)将图1中的△BEF绕点B按逆时针方向旋转45°,如图2,取DF的中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
(3)将图1中的△BEF绕点B逆时针旋转任意角度,如图3,取DF的中点G,连接EG,CG.问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)
答案
2.【解析】 (1)在Rt△FCD中,G为DF的中点,∴CG=12FD.
同理,在Rt△DEF中,EG=12FD,∴EG=CG.
(2)(1)中的结论仍然成立.证明如下:
连接AG,过点G作GM⊥AD于点M,与EF的延长线交于点N,则∠AMN=∠ENM=∠EAM=90°,∴四边形AENM为矩形.
在△DAG和△DCG中,AD=CD,∠ADG=∠CDG,DG=DG,
∴△DAG≌△DCG,∴AG=CG.
在△DMG和△FNG中,∠DGM=∠FGN,DG=FG,∠MGD=∠NGF,
∴△DMG≌△FNG,∴MG=NG.
在矩形AENM中,AM=EN.
在Rt△AMG和Rt△ENG中,AM=EN,MG=NG,
∴Rt△AMG≌Rt△ENG,∴AG=EG.
∴EG=CG.
(3)(1)中的结论仍然成立.
其他的结论还有EG⊥CG.(答案不唯一)
?
答案
1.B 【解析】 如图,∵A(-3,0),B(0,2),C(3,0),D(0,-2),∴OA=OC,OB=OD,∴四边形ABCD为平行四边形,又∵BD⊥AC, ∴四边形ABCD为菱形.故选B.
一、选择题
1.[2019广西北海期末]平面直角坐标系中,四边形ABCD的顶点坐标分别是A(-3,0),B(0,2),C(3,0),D(0,-2),则四边形ABCD是 ( )
A.矩形 B.菱形
C.正方形 D.以上都不对
答案
2.C 【解析】 ∵四边形ABCD是矩形,∴AD=BC=4,∠BAD=90°,又∵AB=3,∴BD=5.∵????△????????????=12BD×AF=12AB×AD, ∴AF=2.4.故选C.
?
2.[2019江苏常州金坛区期中]如图,在矩形ABCD中,AB=3,BC=4,AE⊥BD于点F,则线段AF的长是 ( )
A.3 B.2.5
C.2.4 D.2
答案
3.A 【解析】 ∵四边形AEFG是正方形,∴∠AEF=90°.∵四边形ABCD是平行四边形,∴AD∥BC,∠C=∠BAD, ∴∠EAD=180°-∠AEC=180°-90°-15°=75°,∴∠BAD=40°+75°=115°,∴∠C=115°.故选A.
3.如图,在平行四边形ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=40°,∠CEF=15°,则∠C的度数是 ( )
A.115° B.105°
C.75° D.65°
答案
4.A 【解析】 如图,连接AC,∵四边形ABCD是菱形,∴BC=AB=3.∵∠B=60°, ∴△ABC是等边三角形,∴AC=AB=3,∵点F,G分别是AE,CE的中点,∴FG是△ACE的中位线,∴FG=12AC=32.故选A.
?
4.如图,在菱形ABCD中,∠B=60°,AB=3,点E是BC边上的一个动点(点E与点C不重合),点F,G分别是AE,CE的中点,则线段FG的长为 ( )
A.32 B.3
C.2 2 D.2 3
?
答案
5.C 【解析】 顺次连接平行四边形ABCD各边中点,利用三角形中位线性质可得,新的四边形是平行四边形.①若AC⊥BD,则利用“有一个角是直角的平行四边形是矩形”判定新的四边形是矩形;②∵四边形ABCD是平行四边形, ∴AO=OC,BO=DO,∵△ABO的周长等于△CBO的周长,∴AB=BC,根据等腰三角形的性质可知BO⊥AC,∴BD⊥AC,同①可判定新的四边形是矩形;③∵四边形ABCD是平行四边形,∴∠CBO=∠ADO,∵∠DAO=∠CBO,∴∠ADO= ∠DAO, ∴AO=OD,∴AC=BD,可利用“有一组邻边相等的平行四边形是菱形”判定新的四边形是菱形,不符合题意;④在平行四边形ABCD中,∠DAO=∠BAO,易得平行四边形ABCD是菱形,∴AC⊥BD,同①可判定新的四边形是矩形.∴①②④符合题意.故选C.
5.[2019上海普陀区二模]如图,平行四边形ABCD的对角线AC,BD交于点O,顺次连接平行四边形ABCD各边中点得到一个新的四边形,给出下列四个条件:①AC⊥BD;②△ABO的周长等于△CBO的周长;③∠DAO=∠CBO;④∠DAO= ∠BAO. 如果从中选择一个条件可以使这个新的四边形成为矩形,那么这样的条件个数是 ( )
A.1 B.2
C.3 D.4
答案
6.D 【解析】 ∵四边形ABCD是矩形,∴∠DCB=∠ABC=90°,∵BF与CF分别平分∠ABC和∠BCD,∴∠FCB= ∠FBC=12∠DCB=45°,∴CF=BF,∠F=180°-45°-45°=90°.①∵EB∥CF,CE∥BF,∴四边形BFCE是平行四边形,又∵CF= BF, ∴四边形BFCE是菱形,又∵∠F=90°,∴四边形BFCE是正方形;②∵BE=CE,BE=BF,CF=BF,∴BF=CF=CE=BE,∴四边形BFCE是菱形,又∵∠F=90°,∴四边形BFCE是正方形;③∵BE∥CF,CE⊥BE,∠F=90°,∴∠FBE=∠E=∠F=90°, ∴四边形BFCE是矩形,又∵BF=CF,∴四边形BFCE是正方形;④∵CE∥BF,∠FBC=45°,∴∠ECB=∠FBC=45°,又∵BE=CE,∴∠EBC=∠ECB=45°,∴∠FCE=∠FBE=90°,又∵∠F=90°,∴四边形BFCE是矩形,又∵BF=CF,∴四边形BFCE是正方形.∴能判定四边形BFCE是正方形的条件共有4个.故选D.
?
6.如图,在矩形ABCD内有一点F,BF与CF分别平分∠ABC和∠BCD,点E为矩形ABCD外一点,连接BE,CE.给出下列四个条件:①BE∥CF,CE∥BF;②BE=CE,BE=BF;③BE∥CF,CE⊥BE;④BE=CE,CE∥BF.其中能判定四边形BFCE是正方形的共有 ( )
A.1个 B.2个 C.3个 D.4个
答案
7.30° 【解析】 ∵四边形ABCD为菱形,∴BC=CD,∠BCA=∠DCA,又∵CE=CE,∴△BEC≌△DEC,∴∠EDC= ∠1. ∵∠1+∠2=75°,∴∠EDC+∠2=75°,∴∠AED=∠EDC+∠2=75°,∴∠BED=2∠AED=150°,∴∠3=30°.
二、填空题
7.[2019天津和平区一模]如图,菱形ABCD中,点E是对角线AC上一点,BE的延长线交边CD于点F.若∠1+∠2=75°,则∠3的度数为 .?
答案
8.①④
8.小明在探究“四边形的不稳定性”活动中,将四根木条用钉子钉成一个矩形框架ABCD,如图所示.扭动矩形框架,观察矩形ABCD的变化,有下列判断:
①四边形ABCD由矩形变为平行四边形;
②A,C两点之间的距离不变;
③四边形ABCD的面积不变;
④四边形ABCD的周长不变.
其中正确的是 .(填序号)?
答案
9.12 【解析】 如图,取CD的中点E,连接OE,AE,OA.∵AB=9,BC=6,四边形ABCD是矩形,∴CD=9,AD=6,又∵∠MON=90°,∴OE=DE=12CD=92,∴AE=
????????2+????????2=152,∵OA≤OE+AE,∴当O,A,E三点共线时,点A到点O的距离最大,∴点A到点O的最大距离为92+152=12.
?
9.如图,∠MON=90°,矩形ABCD的顶点C,D分别在射线ON,OM上滑动,AB=9, BC=6,在滑动过程中,点A到点O的最大距离为 .?
答案
10.①②③ 【解析】 在矩形ABCD中,对角线AC,BD相交于点O,连接PM,QN,若PM与QN均经过点O,则四边形MNPQ为平行四边形,此时若PM=QN,则四边形MNPQ为矩形;若PM⊥QN,则四边形MNPQ为菱形.有的矩形不存在以点M,N,P,Q为顶点的正方形.故正确的结论是①②③.
10.[2019北京中考]在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合).对于任意矩形ABCD,下面四个结论中,
①存在无数个四边形MNPQ是平行四边形;
②存在无数个四边形MNPQ是矩形;
③存在无数个四边形MNPQ是菱形;
④至少存在一个四边形MNPQ是正方形.
所有正确结论的序号是 .?
三、解答题
11.[2018新疆乌鲁木齐中考]如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.
(1)求证:四边形AECD是菱形.
(2)若AB=6,BC=10,求EF的长.
答案
11.【解析】 (1)∵AD∥BC,AE∥DC,
∴四边形AECD是平行四边形.
在△ABC中,∠BAC=90°,E是BC的中点,
∴AE=12BC,CE=12BC,
∴AE=CE,∴四边形AECD是菱形.
(2)如图,过点A作AH⊥BC于点H.
在△ABC中,∠BAC=90°,AB=6,BC=10,
∴AC=????????2?????????2=102?62=8.
由(1)知四边形AECD是菱形,∴DC=CE.
∵ S △ABC =12AB·AC=12BC·AH,∴AH=245.
∵S菱形AECD =CE·AH=CD·EF,CD=CE,
∴EF=AH=245.
?
答案
12.【解析】 (1)∵ME⊥AO,MF⊥BO,
∴∠MEO=∠MFO=90°.
∵正方形ABCD的对角线AC,BD交于点O,
∴∠EOF=90°,
∴四边形OEMF为矩形.
(2)连接MO,∵边长为8的正方形ABCD的对角线AC,BD交于点O,
∴OA=OB=4 2,
由(1)知EF=MO,易知当M在AB的中点时,MO有最小值,即EF有最小值,此时MO=12AB=4,∴EF的最小值为4.
?
12.[2019江苏无锡期中]如图,边长为8的正方形ABCD的对角线AC,BD交于点O,M是AB边上一动点,ME⊥AO,MF⊥BO.
(1)求证:四边形OEMF为矩形.
(2)连接EF,求EF的最小值.
13.如图1,在正方形ABCD中,点E为AB上的点(不与A,B重合),△ADE与△FDE关于DE对称,作射线CF,与DE的延长线相交于点G,连接AG.
(1)当∠ADE=15°时,求∠DGC的度数;
(2)若点E在AB上移动,请你判断∠DGC的度数是否发生变化,若不变化,请证明你的结论;若会发生变化,请说明理由;
(3)如图2,点F在对角线BD上,点M为DE的中点,连接AM,FM,请判断四边形AGFM的形状,并证明结论.
答案
13.【解析】 (1)∵∠ADE=15°,∴∠FDE=15°,∴∠CDF=60°.
由对称可知AD=DF,∴DF=DC,∴△DFC是等边三角形,∴∠CFD=60°.
∵∠CFD=∠DGC+∠FDE=15°+∠DGC,
∴∠DGC=45°.
(2)∠DGC的度数不变化.证明如下:
∵△ADE与△FDE关于DE对称,∴AD=DF,∠ADE=∠FDE.
设∠ADE=x,可得∠FDE=x,∠CDF=90°-2x,
∵DC=AD=DF,∴∠CFD=12[180°-(90°-2x)]=45°+x.
∵∠CFD=∠DGC+∠FDE=x+∠DGC,
∴x+∠DGC=45°+x,
∴∠DGC=45°.
(3)四边形AGFM是正方形.证明如下:
∵∠DAE=∠DFE=90°,点M为DE的中点,
?
答案
∴AM=FM=DM=12DE,
∴∠ADM=∠DAM,∠MDF=∠DFM,
又∵∠ADM=∠MDF=22.5°,
∴∠AME=∠FME=2∠ADM=2∠MDF=45°,
∴∠AMF=90°.
由(2)可知,∠DGC=45°,∴FM=FG.
在△ADG与△FDG中,????????=????????,????????????∠????????????=∠????????????,????????=????????,?????????
∴△ADG≌△FDG,∴AG=FG,
∴AM=MF=FG=AG,∴四边形AGFM是菱形,
又∵∠AMF=90°,
∴四边形AGFM是正方形.
?
14.[2019江苏南京秦淮区期末]已知:如图,在?ABCD中,G,H分别是AD,BC的中点,E,O,F均是对角线BD上的四等分点,顺次连接G,E,H,F.
(1)求证:四边形GEHF是平行四边形.
(2)当?ABCD满足 条件时,四边形GEHF是菱形.?
(3)若BD=2AB,
①探究四边形GEHF的形状,并说明理由.
②当AB=2,∠ABD=120°时,直接写出四边形GEHF的面积.
答案
14.【解析】 (1)如图1,连接AC,易知AC与BD交于点O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E,O,F分别是对角线BD上的四等分点,
∴E,F分别为OB,OD的中点,
又∵G是AD的中点,∴GF为△AOD的中位线,
∴GF∥OA,GF=12OA.
同理,EH∥OC,EH=12OC,
∴EH=GF,EH∥GF,
∴四边形GEHF是平行四边形.
?
答案
(2)AB⊥BD
连接GH,则AG=BH,AG∥BH,
∴四边形ABHG是平行四边形,∴AB∥GH.
∵AB⊥BD,∴GH⊥BD,∴GH⊥EF.
由(1)得,四边形GEHF是平行四边形,
∴四边形GEHF是菱形.
(3)①四边形GEHF是矩形.理由如下:
在?ABCD中,由G,H分别是AD,BC的中点,易得GH=AB.
∵BD=2AB,∴AB=12BD=EF,∴GH=EF,
由(1)得,四边形GEHF是平行四边形,
∴四边形GEHF是矩形.
?
答案
②3.
如图2,作AM⊥BD交DB的延长线于M,GN⊥BD于N,则AM∥GN.
∵G是AD的中点,∴GN是△ADM的中位线,∴GN=12AM.
∵∠ABD=120°,∴∠ABM=60°,∴∠BAM=30°,
∴BM=12AB=1,AM=3,∴GN=32.
∵BD=2AB=4,∴EF=12BD=2,
∴ S△EFG =12EF×GN=12×2×32=32,
∴ S四边形????????????????= 2S△EFG =3.
?
第一章 特殊平行四边形(中考真题)
数学·九年级上册·北师
答案
1.C 【解析】 ∵点A,B的坐标分别为(2,0)和(0,1),∴OA=2,OB=1.在Rt△AOB中,由勾股定理,得AB=22+12=5,故菱形ABCD的周长为4 5.
?
1.[2019天津中考]如图,四边形ABCD为菱形,A,B两点的坐标分别是(2,0),(0,1),点C,D在坐标轴上,则菱形ABCD的周长等于 ( )
A.5 B.4 3
C.4 5 D.20
?
答案
2.C 【解析】 由菱形的性质可知OB=8,OA=2,AC⊥BD.由平移的性质,得O'B'=OB=8,O'A=3OA= 6,∠AO'B'= ∠AOB= 90°, ∴AB'=????′????′2+????′????2=82+62=10.
?
2.[2019江苏苏州中考]如图,菱形ABCD的对角线AC,BD交于点O,AC=4,BD=16,将△ABO沿点A到点C的方向平移,得到△A'B'O'.当点A'与点C重合时,点A与点B'之间的距离为 ( )
A.6 B.8
C.10 D.12
答案
3.A 【解析】 如图,连接AE,设AC,EF交于点O,∵四边形ABCD是矩形,∴AD∥BC,∴∠DAC=∠ACB.∵直线EF垂直平分AC,∴OA=OC,AE=EC,又∵∠AOF=∠COE,∴△AOF≌△COE,∴AE=CE=AF=5,∴BC=BE+EC=8.在Rt△ABE中, AB= ????????2?????????2=52?32=4.在Rt△ABC中,AC=????????2+????????2=42+82=45.故选A.
?
3.[2019广东广州中考]如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为 ( )
A.4 5 B.4 3
C.10 D.8
?
答案
4.A 【解析】 ∵点E,F分别是AD,BC的中点,点M,N分别是AC,BD的中点,∴EN,NF,FM,ME分别是△ABD,△BCD, △ABC,△ACD的中位线,∴EN∥AB∥FM,ME∥CD∥NF,EN=12AB=FM,ME=12CD=NF.当AB=CD时,EN=FM=ME=NF,∴平行四边形EMFN是菱形.当AB⊥CD时,EN⊥ME,则∠MEN=90°,∴菱形EMFN是正方形.故选A.
?
4.[2019辽宁抚顺中考]如图,AC,BD是四边形ABCD的对角线,点E,F分别是AD,BC的中点,点M,N分别是AC,BD的中点,连接EM,MF,FN,NE,要使四边形EMFN为正方形,则需添加的条件是 ( )
A.AB=CD,AB⊥CD
B.AB=CD,AD=BC
C.AB=CD,AC⊥BD
D.AB=CD,AD∥BC
答案
5.D 【解析】 连接PC,CE.易知点A,C关于直线BD对称,∴AP=CP,∴AP+EP=CP+EP,∴AP+EP的最小值等于CP+EP的最小值.根据“两点之间,线段最短”可知,当C,P,E三点在同一条直线上时,CP+EP的值最小,最小值为CE的长.易证△ABF≌△CDE,∴AF=CE,即AP+EP的最小值等于AF的长.故选D.
5.[2018天津中考]如图,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于AP+EP最小值的是 ( )
A.AB B.DE
C.BD D.AF
解决这类问题是利用轴对称的性质将“同侧折线”转化为“异侧折线”,再根据“两点之间,线段最短”确定出折线长度的最小值.
答案
6.85 【解析】 如图,连接BD,交AC于点O,∵四边形ABCD为正方形,∴BD⊥AC, OA=OB=OC=OD.∵AC=8,AE=CF=2,∴OE=OF=2,∴四边形BEDF为菱形,∴DE=DF= BE=BF.∵BD=AC=8,∴OB=OD=4,在Rt△DOE中,由勾股定理,得DE=????????2+????????2=42+22=25,∴四边形BEDF的周长为4DE=85.
?
6.[2019山东菏泽中考]如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是 . ?
答案
7.12 【解析】 设每个直角三角形中较长的直角边的长为a,较短的直角边的长为b,则????+????=5,?????????=1,解得????=3,????=2,∴菱形的面积为12×ab×4=2ab=2×3×2=12.
?
7.[2019北京中考]如图,把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2、图3所示的正方形,则图1中菱形的面积为 .?
答案
8.15+3 【解析】 ∵阴影部分的面积与正方形ABCD的面积之比为2∶3,AB=3,∴阴影部分的面积为23×32=6,∴空白部分的面积为9-6=3.∵四边形ABCD为正方形,∴BC=CD,∠BCE=∠CDF=90°,又∵CE=DF,∴△BCE≌△CDF, ∴△BCG 的面积与四边形DEGF的面积相等,均为12×3=32.∵△BCE≌△CDF,∴∠CBE=∠DCF,又∵∠DCF+∠GCB= 90°, ∴∠GCB+∠CBE=90°,∴∠BGC=90°.设BG=a,CG=b,则12ab=32,∵a2+b2=32,∴a2+2ab+b2=9+6=15,即(a+b)2=15,∴a+ b= 15,即BG+CG=15,∴△BCG的周长为15+3.
?
8.[2018浙江台州中考]如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2∶3,则△BCG的周长为? .?
答案
9.【分析】 (1)先根据对边平行且相等的四边形是平行四边形,得到四边形ABCD是平行四边形,再根据邻边相等的平行四边形是菱形,即可证明结论.(2)先根据菱形的性质及勾股定理得到AO的长,再在Rt△AEC中根据斜边上的中线等于斜边的一半计算即可.
【解析】 (1)∵AB∥DC,∴∠BAC=∠DCA.
∵AC平分∠BAD,∴∠BAC=∠DAC,
∴∠DAC=∠DCA,∴AD=DC.
9.[2018北京中考]如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形.
(2)若AB=5,BD=2,求OE的长.
?
答案
∵AB=AD,∴AB=DC,
∴四边形ABCD是平行四边形.
又∵AB=AD,
∴四边形ABCD是菱形.
(2)∵四边形ABCD是菱形,BD=2,
∴AO=12AC,BO=12BD=1,∠AOB=90°,
∴AO=????????2?????????2=2.
∵CE⊥AB,∴∠AEC=90°,
∴OE=12AC=AO=2.
?
10.[2019云南中考]如图,四边形ABCD中,对角线AC,BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形.
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
答案
10.【解析】 (1)∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形.
∵∠AOB=∠OAD+∠ODA=2∠OAD,
∴∠OAD=∠ODA,∴AO=DO,∴AC=BD,
∴四边形ABCD是矩形.
(2)由(1)知四边形ABCD是矩形,
∴AB∥CD,∴∠ABO=∠CDO.
∵∠AOB∶∠ODC=4∶3,∴∠AOB∶∠ABO=4∶3,
∴∠BAO∶∠AOB∶∠ABO=3∶4∶3.
∵∠BAO+∠AOB+∠ABO=180°,
∴∠ABO=54°.
∵∠BAD=90°,∴∠ADO=90°-54°=36°.
11.[2019浙江宁波中考]如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)求证:BG=DE.
(2)若E为AD的中点,FH=2,求菱形ABCD的周长.
答案
11.【解析】 (1)在矩形EFGH中,EH=FG,EH∥FG,
∴∠GFH=∠EHF.
∵∠BFG=180°-∠GFH,∠DHE=180°-∠EHF,
∴∠BFG=∠DHE.
在菱形ABCD中,AD∥BC,
∴∠GBF=∠EDH,
∴△BGF≌△DEH,
∴BG=DE.
答案
(2)如图,连接EG.
在菱形ABCD中,AD∥BC,AD=BC.
∵E为AD的中点,∴AE=ED.
∵BG=DE,∴AE=BG,
∴四边形ABGE为平行四边形,
∴AB=EG.
在矩形EFGH中,EG=FH=2,
∴AB=2,
∴菱形ABCD的周长为2×4=8.
12.[2018吉林长春中考]在正方形ABCD中,E是边CD上一点(点E不与点C,D重合),连接BE.
【感知】 如图1,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)
【探究】 如图2,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连接CM.若CM=1,则FG的长为 .?
【应用】 如图3,取BE的中点M,连接CM.过点C作CG⊥BE交AD于点G,连接EG,MG.若CM=3,则四边形GMCE的面积为 .?
答案
12.【解析】 【探究】(1)如图,将GF平移到AH处,
则AH∥GF,AH=GF.
∵GF⊥BE,∴AH⊥BE,∴∠ABE+∠BAH=90°.
∵四边形ABCD是正方形,
∴AB=BC,∠ABH=∠BCE=90°,
∴∠ABE+∠CBE=90°,
∴∠BAH=∠CBE.
在△ABH和△BCE中,∠????????????=∠????????????,????????=????????,?????????????∠????????????=∠????????????,?
∴△ABH≌△BCE,∴BE=AH,
∴BE=FG.
?
答案
(2)2
【应用】9
在Rt△BCE中,∠BCE=90°,CM是BE边上的中线,
∴BE=2CM=6.
易证△BCE≌△CDG,∴BE=CG=6.
又∵ME=12BE=3,且BE⊥CG,
∴????四边形????????????????=12×3×6=9.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
