北师大版九年级上册数学第一章 特殊平行四边形整章同步教学课件(176张PPT)
文档属性
| 名称 | 北师大版九年级上册数学第一章 特殊平行四边形整章同步教学课件(176张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-15 15:16:08 | ||
图片预览




文档简介
第一章 特殊平行四边形
数学·九年级上册·北师
1 菱形的性质与判定
课时1 菱形的性质
课时1
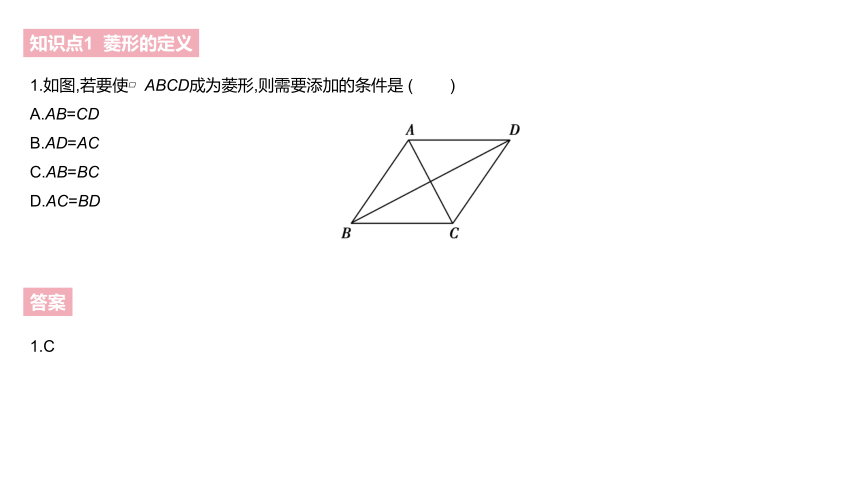
1.如图,若要使?ABCD成为菱形,则需要添加的条件是 ( )
A.AB=CD
B.AD=AC
C.AB=BC
D.AC=BD
答案
1.C
知识点1 菱形的定义
2.[2019广西玉林中考]菱形不具备的性质是 ( )
A.是轴对称图形
B.是中心对称图形
C.对角线互相垂直
D.对角线一定相等
答案
2.D
知识点2 菱形的性质
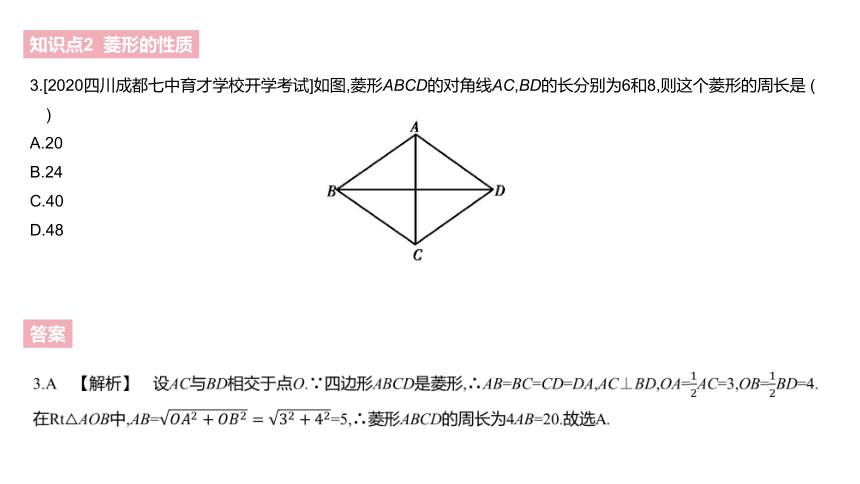
3.[2020四川成都七中育才学校开学考试]如图,菱形ABCD的对角线AC,BD的长分别为6和8,则这个菱形的周长是 ( )
A.20
B.24
C.40
D.48
答案
3.A 【解析】 设AC与BD相交于点O.∵四边形ABCD是菱形,∴AB=BC=CD=DA,AC⊥BD,OA=12AC=3,OB=12BD=4.在Rt△AOB中,AB=????????2+????????2=32+42=5,∴菱形ABCD的周长为4AB=20.故选A.
?
知识点2 菱形的性质
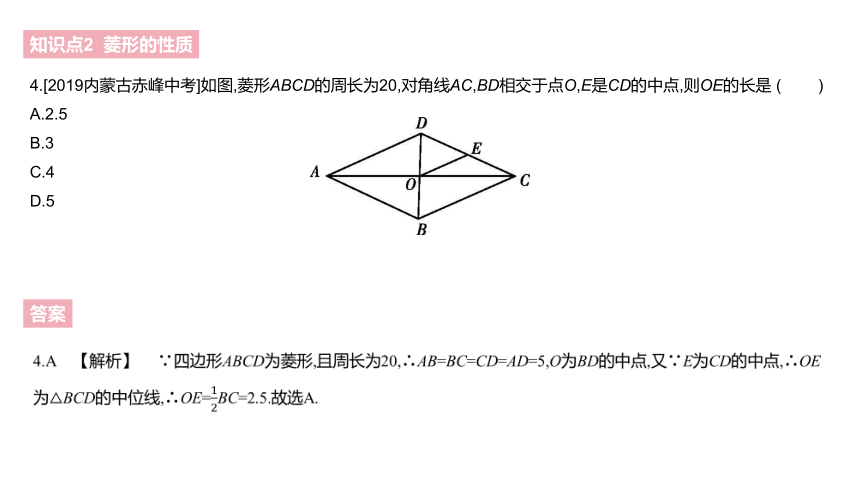
4.[2019内蒙古赤峰中考]如图,菱形ABCD的周长为20,对角线AC,BD相交于点O,E是CD的中点,则OE的长是 ( )
A.2.5
B.3
C.4
D.5
答案
4.A 【解析】 ∵四边形ABCD为菱形,且周长为20,∴AB=BC=CD=AD=5,O为BD的中点,又∵E为CD的中点,∴OE为△BCD的中位线,∴OE=12BC=2.5.故选A.
?
知识点2 菱形的性质
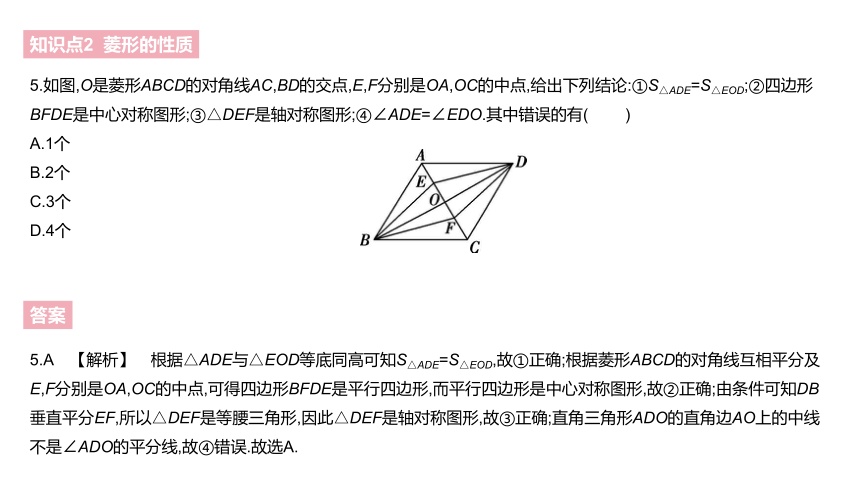
5.如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点,给出下列结论:①S△ADE=S△EOD;②四边形BFDE是中心对称图形;③△DEF是轴对称图形;④∠ADE=∠EDO.其中错误的有( )
A.1个
B.2个
C.3个
D.4个
答案
5.A 【解析】 根据△ADE与△EOD等底同高可知S△ADE=S△EOD,故①正确;根据菱形ABCD的对角线互相平分及E,F分别是OA,OC的中点,可得四边形BFDE是平行四边形,而平行四边形是中心对称图形,故②正确;由条件可知DB垂直平分EF,所以△DEF是等腰三角形,因此△DEF是轴对称图形,故③正确;直角三角形ADO的直角边AO上的中线不是∠ADO的平分线,故④错误.故选A.
知识点2 菱形的性质
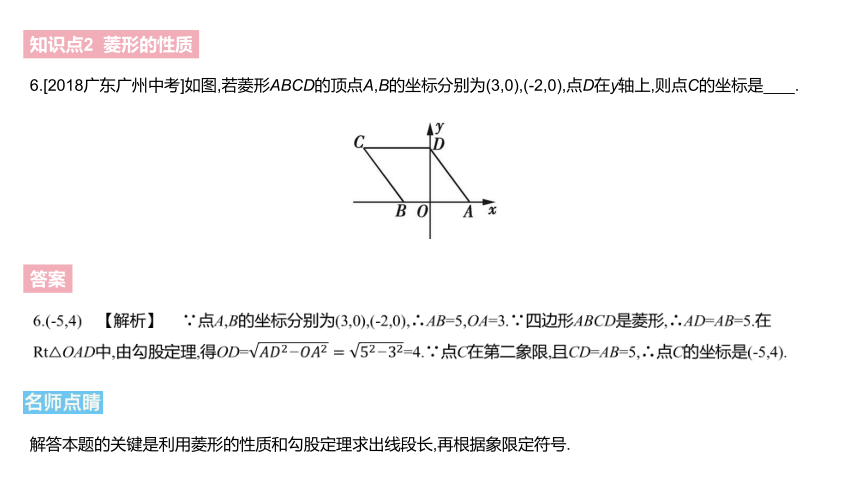
6.[2018广东广州中考]如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0),点D在y轴上,则点C的坐标是 .?
答案
6.(-5,4) 【解析】 ∵点A,B的坐标分别为(3,0),(-2,0),∴AB=5,OA=3.∵四边形ABCD是菱形,∴AD=AB=5.在Rt△OAD中,由勾股定理,得OD=????????2?????????2=52?32=4.∵点C在第二象限,且CD=AB=5,∴点C的坐标是(-5,4).
?
知识点2 菱形的性质
解答本题的关键是利用菱形的性质和勾股定理求出线段长,再根据象限定符号.
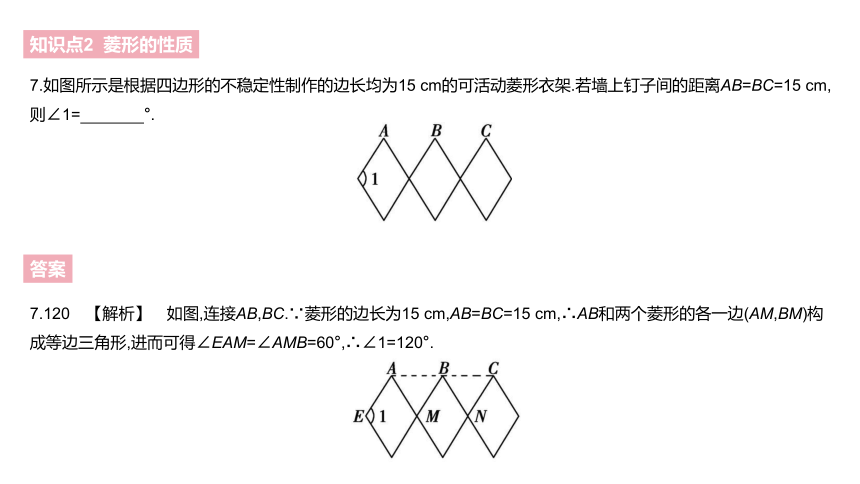
7.如图所示是根据四边形的不稳定性制作的边长均为15 cm的可活动菱形衣架.若墙上钉子间的距离AB=BC=15 cm,则∠1= °.?
答案
7.120 【解析】 如图,连接AB,BC.∵菱形的边长为15 cm,AB=BC=15 cm,∴AB和两个菱形的各一边(AM,BM)构成等边三角形,进而可得∠EAM=∠AMB=60°,∴∠1=120°.
知识点2 菱形的性质
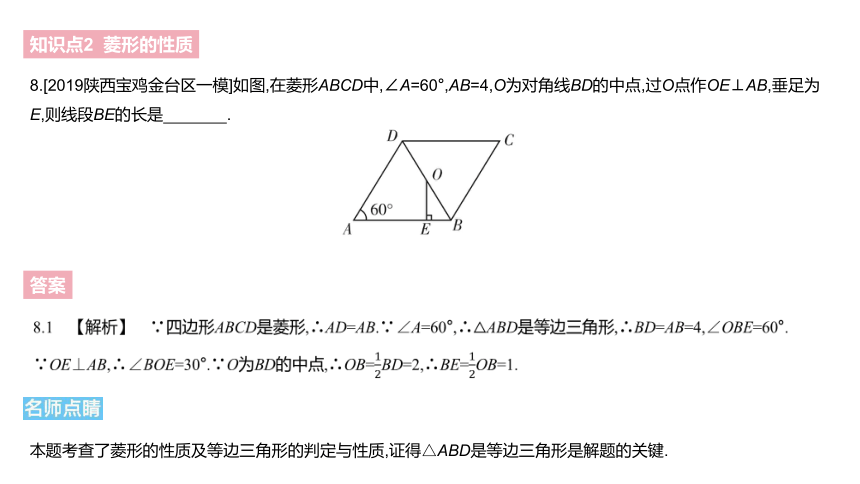
8.[2019陕西宝鸡金台区一模]如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E,则线段BE的长是 .?
答案
8.1 【解析】 ∵四边形ABCD是菱形,∴AD=AB.∵∠A=60°,∴△ABD是等边三角形,∴BD=AB=4,∠OBE=60°. ∵OE⊥AB,∴∠BOE=30°.∵O为BD的中点,∴OB=12BD=2,∴BE=12OB=1.
?
知识点2 菱形的性质
本题考查了菱形的性质及等边三角形的判定与性质,证得△ABD是等边三角形是解题的关键.
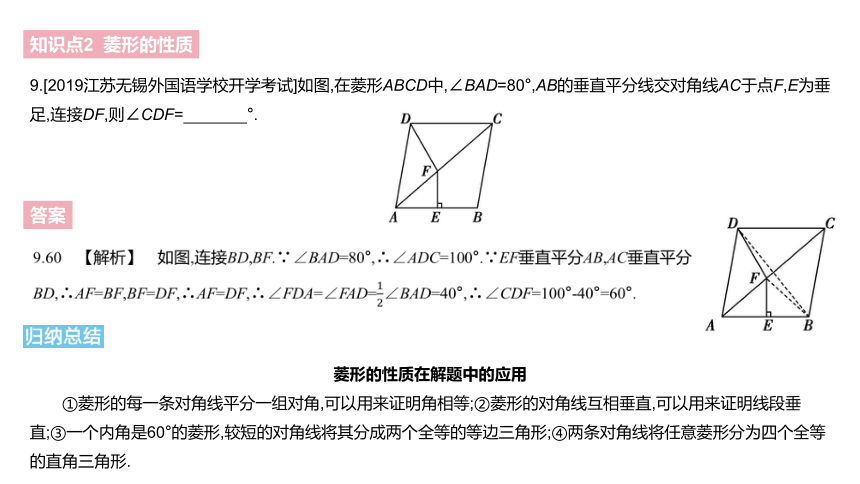
9.[2019江苏无锡外国语学校开学考试]如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF= °.?
答案
9.60 【解析】 如图,连接BD,BF.∵∠BAD=80°,∴∠ADC=100°.∵EF垂直平分AB,AC垂直平分BD,∴AF=BF,BF=DF,∴AF=DF,∴∠FDA=∠FAD=12∠BAD=40°,∴∠CDF=100°-40°=60°.
?
知识点2 菱形的性质
菱形的性质在解题中的应用
①菱形的每一条对角线平分一组对角,可以用来证明角相等;②菱形的对角线互相垂直,可以用来证明线段垂直;③一个内角是60°的菱形,较短的对角线将其分成两个全等的等边三角形;④两条对角线将任意菱形分为四个全等的直角三角形.
10.[2020福建三明期中]如图,在菱形ABCD中,AB=2,∠ABC=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是??? .?
?
答案
10.3 【解析】 有关直线同侧的折线段相加值最小问题,常转化为直线两侧两点之间线段最短问题,即将点B借助菱形的对称性转移到点D,如图,连接DE交AC于点P,易知PB=PD,此时PE+PB的最小值为DE的长.因为四边形ABCD是菱形,E是AB的中点,所以AD=AB=2,AE=12AB=1.易知DE垂直平分AB,在Rt△ADE中,DE=????????2?????????2=3,即PE+PB的最小值为3.
?
知识点2 菱形的性质
11.[2019天津和平区期末]在菱形ABCD中,AC是对角线.
(1)如图1,若AB=6,则菱形ABCD的周长为 ,若∠DAB=70°,则∠D的度数是 ,∠DCA的度数是 .?
(2)如图2,P是AB上一点,连接DP交对角线AC于点E,连接EB,求证:∠APD=∠EBC.
知识点2 菱形的性质
答案
11.【解析】 (1)24 110° 35°
∵四边形ABCD是菱形,∴AB=BC=CD=AD=6,∴菱形ABCD的周长为4×6=24.∵四边形ABCD是菱形,∠DAB=70°,∴∠D=110°,∠DCA=12∠DCB=12∠DAB=35°.
(2)∵四边形ABCD是菱形,
∴DC=BC,∠DCE=∠BCE,
又∵CE=CE,∴△DCE≌△BCE,
∴∠CDP=∠EBC.
∵DC∥AB,∴∠CDP=∠APD,
∴∠APD=∠EBC.
?
知识点2 菱形的性质
1.[2020广东珠海北大附属实验学校段考]如图,在菱形ABCD中,AE,AF分别垂直平分BC,CD,垂足分别为E,F,则∠EAF的度数是 ( )
A.90°
B.60°
C.45°
D.30°
答案
1.B 【解析】 连接AC,根据垂直平分线的性质和菱形的邻边相等,可得△ABC,△ACD都是等边三角形,∴∠B=60°, ∴∠BCD=120°.在四边形AECF中,由四边形的内角和为360°,可得∠EAF=360°-90°-90°-120°=60°.故选B.
2.[2019重庆巴蜀中学开学考试]如图,在菱形ABCD中,∠BCD=50°,BC的垂直平分线交对角线AC于点F,垂足为E,连接BF,DF,则∠DFC的度数是 ( )
A.100°
B.110°
C.120°
D.130°
答案
2.D 【解析】 ∵四边形ABCD是菱形,∴∠ACD=∠ACB=12∠BCD=25°.∵EF垂直平分线段BC,∴FB=FC,∴∠FBC= ∠FCB=25°,∴∠CFB=180°-25°-25°=130°,根据菱形的对称性,可知∠CFD=∠CFB=130°.故选D.
?
3.[2019天津北辰区模拟]如图,在菱形ABCD中,∠ABC=60°,E为BC边的中点,M为对角线BD上的一个动点,则下列线段的长等于AM+12BM的最小值的是 ( )
A.AD B.AE
C.BD D.BE
?
答案
3.B 【解析】 如图,过点M作MF⊥BC于点F,∵四边形ABCD是菱形,∠ABC=60°,点E为BC的中点,∴∠DBC= 12∠ABC=30°,AE⊥BC,∴MF=12BM,∴AM+12BM=AM+MF,∴当A,M,F三点共线时,AM+MF取得最小值,∴AM+12BM的最小值为线段AE的长.故选B.
?
4.[2019广东广州华南师大附中段测]如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为 ( )
A.(1,-1)
B.(-1,-1)
C.(2,0)
D.(0,-2)
?
答案
4.B 【解析】 由菱形OABC的顶点O(0,0),B(2,2),得点D的坐标为(1,1).每秒旋转45°,则第60秒时,旋转了45°×60=
2 700°,2 700÷360=7.5(周), 即OD旋转了7周半,故第60秒时,菱形的对角线交点D的坐标为(-1,-1).故选B.
5.[2019江苏镇江外国语学校段测]如图,菱形纸片ABCD中,∠A=60°,P为AB的中点,折叠菱形纸片ABCD,使点C落在DP所在直线上的C'处,折痕为DE,则∠DEC= °.?
答案
5.75 【解析】 如图,连接BD,∵四边形ABCD是菱形,∠A=60°,∴AB=AD,∠ADC=120°,∠C=60°,△ABD是等边三角形.∵P为AB的中点,∴DP平分∠ADB,∴∠ADP=30°,∴∠PDC=∠ADC-∠ADP=90°,由折叠可知∠CDE=∠PDE, ∴∠CDE=45°,在△DEC中,∠DEC=180°-∠C-∠CDE=75°.
6.如图,在菱形ABCD中,AB=4 cm,∠ADC=120°,点E,F同时从A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1 cm/s,点F的速度为2 cm/s,经过t秒△DEF为等边三角形,则t的值为? .?
答案
6.43 【解析】 如图,连接BD.∵四边形ABCD是菱形,∴AB=AD,∠ADB=12∠ADC=60°,∴△ABD是等边三角形, ∴AD= BD,∵△DEF是等边三角形,∴DE=DF,∠EDF=60°,又∵∠ADB=60°,∴∠ADE=∠BDF.在△ADE和△BDF中,
????????=????????,????????????∠????????????=∠????????????,????????=????????,????????????∴△ADE≌△BDF(SAS),∴AE=BF.∵AE=t cm,CF=2t cm,∴BF=BC-CF=(4-2t)cm,∴t=4-2t,∴t=43.
?
7.[2018内蒙古呼和浩特中考]如图,已知A,F,C,D四点在同一条直线上,AF=CD,AB∥DE,且AB=DE.
(1)求证:△ABC≌△DEF.
(2)若EF=3,DE=4,∠DEF=90°,请直接写出使四边形EFBC为菱形时AF的长度.
答案
7.【解析】 (1)∵AB∥DE,∴∠A=∠D.
∵AF=CD,∴AF+CF=CD+CF,即AC=DF.
在△ABC和△DEF中,????????=????????,∠????=∠????,????????=????????,
∴△ABC≌△DEF.
?
答案
(2)四边形EFBC为菱形时,AF=75.
如图,连接BE,交CF于点O.
∵EF=3,DE=4,∠DEF=90°,
∴DF=????????2+????????2=32+42=5.
当四边形EFBC是菱形时,BE⊥CF,CF=2OF,∴∠EOF=90°.
∵12DF×OE=12DE×EF=????△????????????,∴5OE=3×4,∴OE=125.
在Rt△EFO中,OF=????????2?????????2=32?(125)2=95,
∴CF=2OF=185,∴CD=DF-CF=5-185=75,
∴AF=CD=75.
?
8.[2020山东泰安模拟]在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC的延长线上一点,且CF=AE,连接BE,EF.如图1,当点E是线段AC的中点时,易证BE=EF.
(1)如图2,当点E不是线段AC的中点,其他条件不变时,请你判断结论:BE=EF .(填“成立”或“不成立”)?
(2)如图3,当点E是线段AC的延长线上任意一点,其他条件不变时,结论BE=EF是否成立?若成立,请给予证明;若不成立,请说明理由.
答案
8.【解析】 (1)成立
过点E作EG∥BC交AB于点G,
∵四边形ABCD为菱形,∴AB=BC,
又∵∠ABC=60°,∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°.
∵EG∥BC,∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,∴△AGE是等边三角形,
∴AG=AE=GE,∴BG=EC.
∵CF=AE,∴GE=CF,
又∵∠BGE=∠ECF=120°,
∴△BGE≌△ECF,∴BE=EF.
答案
(2)结论BE=EF成立.证明如下:
过点E作EG∥BC交AB的延长线于点G,
∵四边形ABCD为菱形,∴AB=BC,
又∵∠ABC=60°,∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°.
∵EG∥BC,∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,∴△AGE是等边三角形,
∴AG=AE=GE,∴BG=EC.
∵CF=AE,∴GE=CF,
又∵∠BGE=∠ECF=60°,
∴△BGE≌△ECF,∴BE=EF.
课时2 菱形的判定
课时2
1.在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是 ( )
A.∠ABC=90° B.AC⊥BD
C.AB=CD D.∠A=∠C
答案
1.B 【解析】 在四边形ABCD中,对角线AC,BD互相平分,∴四边形ABCD是平行四边形,∴当AC⊥BD时,四边形ABCD是菱形.故选B.
知识点1 菱形的判定
2.如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连接EB,EC,DB,下列条件中,不能使四边形DBCE成为菱形的是 ( )
A.AB=BE
B.BE⊥DC
C.AD=BD
D.BE平分∠DBC
答案
2.A 【解析】 ∵四边形ABCD为平行四边形,∴AD∥BC,AD=BC,又∵DE=AD,∴DE∥BC,DE=BC,∴四边形DBCE为平行四边形.B项,BE⊥DC,根据“对角线互相垂直的平行四边形是菱形”,可知能使四边形DBCE成为菱形;C项,AD= BD, 则BD=DE,根据“有一组邻边相等的平行四边形是菱形”,可知能使四边形DBCE成为菱形;D项,BE平分∠DBC,则∠DBE=∠EBC=∠DEB,可得BD=DE,根据“有一组邻边相等的平行四边形是菱形”,可知能使四边形DBCE成为菱形.故选A.
知识点1 菱形的判定
3.[2020陕西西安莲湖区期中]如图,四边形ABCD是一张平行四边形纸片,要求利用所学知识作出一个菱形,甲、乙两位同学的作法如下,则关于甲、乙两人的作法,下列判断正确的为 ( )
A.仅甲正确
B.仅乙正确
C.甲、乙均正确
D.甲、乙均错误
知识点1 菱形的判定
答案
3.C 【解析】 甲的作法正确,理由如下:设EF交AC于点O,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAC=
∠ACB,∵EF是AC的垂直平分线,∴AO=CO,在△AOE和△COF中, ∠????????????=∠????????????,????????=????????,???????????∠????????????=∠????????????,∴△AOE≌△COF,∴AE=CF,
∵AE∥ CF, ∴四边形AECF是平行四边形,又∵EF⊥AC,∴四边形AECF是菱形.乙的作法正确,理由如下:如图, ∵AD∥BC, ∴∠1=∠2,∠5=∠6,∵BF平分∠ABC,AE平分∠BAD,∴∠2=∠3,∠4=∠5,∴∠1=∠3,∠4=∠6, ∴AB= AF,AB=BE, ∴AF=BE,∵AF∥BE,∴四边形ABEF是平行四边形,又∵AB=AF,∴四边形ABEF是菱形.故选C.
?
知识点1 菱形的判定
4.[2019甘肃兰州中考A卷]如图,AC=8,分别以点A,C为圆心,以长度5为半径作弧,两条弧分别相交于点B和D,依次连接A,B,C,D,连接BD交AC于点O.
(1)判断四边形ABCD的形状并说明理由;
(2)求BD的长.
答案
4.【解析】 (1)四边形ABCD是菱形.理由如下:
由题意可知,AB=BC=CD=DA=5,
∴四边形ABCD是菱形.
(2)∵四边形ABCD是菱形,AC=8,
∴OA=OC=12AC=4,OB=OD=12BD,AC⊥BD.
在Rt△AOD中,∠AOD=90°,OA=4,AD=5,
∴OD=52?42=3,∴BD=2OD=6.
?
知识点1 菱形的判定
5.易错题 如图,四边形ABCD的对角线AC,BD相交于点O,且AO=OC=8,BO=OD=6,AB=10,则四边形ABCD是菱形吗?请说明理由.
答案
5.【解析】 四边形ABCD是菱形.理由如下:
∵AO=OC=8,BO=OD=6,
∴四边形ABCD是平行四边形.
∵AO=8,BO=6,AB=10,
∴AO2+BO2=AB2,∴∠AOB=90°,
∴四边形ABCD是菱形.
知识点1 菱形的判定
本题借助勾股定理的逆定理判定直角(垂直),注意:运用一组邻边相等或对角线互相垂直证明四边形是菱形的前提条件是该四边形为平行四边形.
6.[2019江西南昌期中]如图,在?ABCD中,AB=2,AD=1,∠ADC=60°,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D'处,折痕交CD边于点E.求证:四边形BCED'是菱形.
答案
6.【解析】 ∵四边形ABCD是平行四边形,
∴BC=AD,DC=AB,DC∥AB,∴∠DEA=∠D'AE.
由折叠可知∠DAE=∠D'AE,AD'=AD=1,ED'=ED,
∴∠DAE=∠DEA,∴AD=ED=AD'=ED'=1,
又∵DC=AB=2,
∴BD'=AB-AD'=2-1=1,EC=DC-ED=2-1=1,
又∵BC=AD=1,
∴EC=BC=BD'=ED',∴四边形BCED'是菱形.
知识点1 菱形的判定
7.[2020河南省实验中学模拟]如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点,当四边形EFGH满足条件
时,四边形EFGH是菱形.(只需写出一个即可,图中不能再添加别的“点”或“线”)?
答案
7.HG=GF(答案不唯一) 【解析】 连接AC,BD,在四边形ABCD中,∵点E,F,G,H分别为四边形ABCD的边AB,BC,CD, DA的中点,∴HG∥AC∥EF,GF∥BD∥HE,∴四边形EFGH是平行四边形.要判定平行四边形EFGH是菱形,只要HG= GF (或FE=EH等)即可,答案不唯一.
知识点2 与菱形的判定有关的开放探究
8.[2019山东青岛市北区期中]如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:①BE=EC;②BF∥EC;③AB=AC.其中能证明四边形BECF是菱形的是 .(只填写序号)?
答案
8.①③ 【解析】 由点D是BC的中点及DE=DF可得,四边形BECF是平行四边形.①当BE=EC时,由有一组邻边相等的平行四边形是菱形,可知①能证明四边形BECF是菱形;③由AB=AC,点D为BC的中点可得,AD⊥BC,由对角线互相垂直的平行四边形是菱形,可知③能证明四边形BECF是菱形.故填①③.
知识点2 与菱形的判定有关的开放探究
1.如图,将△ABC沿BC方向平移得到△DCE,连接AD.下列条件中,能够判定四边形ACED为菱形的是 ( )
A.AB=BC
B.AC=BC
C.∠ABC=60°
D.∠ACB=60°
答案
1.B 【解析】 由平移的性质,得AC=DE,AD=BC=CE,当AC=BC时,有AC=AD=DE=CE,∴四边形ACED是菱形.故选B.
2.如图,已知四边形ABCD的四条边都相等,等边三角形AEF的顶点E,F分别在BC,CD上,且AE=AB,则∠C=( )
A.100°
B.105°
C.110°
D.120°
答案
2.A 【解析】 ∵四边形ABCD的四条边都相等,∴四边形ABCD是菱形,∴∠B=∠D,∠BAD=∠C,AB∥CD, ∴∠BAD+ ∠D=180°.∵△AEF是等边三角形,AE=AB,∴∠AEF=∠AFE=60°,∠B=∠AEB,AF=AD, ∴∠D= ∠AFD, ∴∠BAE=∠FAD.设∠BAE=∠FAD=x,则∠D=∠AFD=180°-60°-2x,∵∠FAD+∠D+∠AFD=180°,∴x+2(180°-60°-2x)=180°,解得x=20°,∴∠C=∠BAD=2×20°+60°=100°.故选A.
3.如图,在△ABC中,AD,CD分别平分∠BAC和∠ACB,AE∥CD,CE∥AD.若从三个条件:①AB=AC;②AB=BC;③AC=BC中,选择一个作为已知条件,则能使四边形ADCE为菱形的是 .(填序号)?
答案
3.② 【解析】 当AB=BC时,∵AE∥CD,CE∥AD,∴四边形ADCE是平行四边形.∵AB=BC,∴∠BAC=∠ACB.∵AD, CD分别平分∠BAC和∠ACB,∴∠DAC=∠DCA,∴DA=DC,∴四边形ADCE是菱形.
4.已知四边形的四条边长分别为a,b,c,d,且满足条件a2+b2+c2+d2=ab+bc+cd+da,则此四边形一定是 .?
答案
4.菱形 【解析】 ∵a2+b2+c2+d2=ab+bc+cd+da,∴2(a2+b2+c2+d2)-2ab-2bc-2cd-2da=0,∴(a-b)2+(b-c)2+(c-d)2+(d-a)2=0,由平方的非负性,可知a-b=0,b-c=0,c-d=0,d-a=0,∴a=b=c=d,∴此四边形一定是菱形.
5.[2019湖南长沙明德教育集团期中]如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD.
(1)求∠AOD的度数.
(2)求证:四边形ABCD是菱形.
答案
5.【解析】 (1)∵AC,BD分别是∠BAE,∠ABF的平分线,
∴∠DAC=∠BAC,∠ABD=∠DBC.
∵AE∥BF,∴∠DAB+∠CBA=180°,
∴∠BAC+∠ABD=12(∠DAB+∠CBA)=12×180°=90°,
∴∠AOD=90°.
(2)∵AE∥BF,∴∠ADB=∠DBC,∠DAC=∠BCA,
由(1)知∠DAC=∠BAC,∠ABD=∠DBC,
∴∠BAC=∠BCA,∠ABD=∠ADB,
∴AB=BC,AB=AD,∴AD=BC,
又∵AD∥BC,∴四边形ABCD是平行四边形,
又∵AD=AB,∴四边形ABCD是菱形.
?
6.[2018贵州毕节中考]如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ∥DB,且CQ=DP,连接AP,BQ,PQ.
(1)求证:△APD≌△BQC.
(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.
答案
6.【解析】 (1)如图,∵CQ∥BD,∴∠2=∠3.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠1=∠2,∴∠1=∠3.
在△APD和△BQC中,????????=????????,∠1=∠3,????????=????????,
∴△APD≌△BQC.
(2)∵△APD≌△BQC,∴AP=BQ,∠APD=∠BQC,
又∵∠ABP+∠BQC=180°,∴∠ABP+∠APD=180°.
∵∠APB+∠APD=180°,∴∠ABP=∠APB,∴AB=AP.
∵CQ∥DB,CQ=DP,∴四边形CDPQ是平行四边形,∴CD=PQ.
在平行四边形ABCD中,AB=CD,∴AB=AP=PQ=BQ,
∴四边形ABQP为菱形.
?
7.[2020河南郑州外国语中学月考]如图1,△ABC为等腰三角形,AB=AC=a,P点是底边BC上的一个动点,PD∥AC, PE∥AB.
(1)用a表示四边形ADPE的周长为 .?
(2)点P运动到什么位置时,四边形ADPE是菱形?请说明理由.
(3)如果△ABC不是等腰三角形,如图2,其他条件不变,点P运动到什么位置时,四边形ADPE是菱形?(不必说明理由)
答案
7.【解析】 (1)2a
∵PD∥AC,PE∥AB,∴四边形ADPE为平行四边形,∴AD=PE,DP=AE.∵AB=AC,∴∠B=∠C,又∵DP∥AC,∴∠DPB=∠C,∴∠B=∠DPB,∴BD=DP,∴四边形ADPE的周长为2(AD+DP)=2(AD+BD)=2AB=2a.
(2)当点P运动到BC的中点时,四边形ADPE是菱形.理由如下:
如图1,连接AP.
∵PD∥AC,PE∥AB,
∴四边形ADPE为平行四边形.
∵AB=AC,P为BC的中点,
∴∠PAD=∠PAE.
∵PE∥AB,∴∠PAD=∠APE,
∴∠PAE=∠APE,∴EA=EP,
∴四边形ADPE是菱形.
答案
(3)点P运动到∠BAC的平分线上时,四边形ADPE是菱形.
如图2,∵PD∥AC,PE∥AB,
∴四边形ADPE是平行四边形.
∵AP平分∠BAC,∴∠1=∠2,
∵AB∥EP,∴∠1=∠3,
∴∠2=∠3,∴AE=EP,
∴四边形ADPE是菱形.
课时3 菱形的性质与判定的综合应用
课时3
1.[2020湖南长沙长郡梅溪湖中学开学考试]如图,四边形ABCD是菱形,DH⊥AB于点H,若AC=8 cm,BD=6 cm,则DH的长是 ( )
A.5 3 cm B.2 5 cm
C.245 cm D.485 cm
?
答案
1.C 【解析】 ∵四边形ABCD是菱形,AC=8 cm,BD=6 cm,∴∠AOB=90°,AO=4 cm,BO=3 cm,∴AB=42+32=5(cm).由菱形的面积可知,12AC·BD=AB·DH,∴5DH=24,∴DH=245 cm.故选C.
?
知识点1 菱形的面积
2.[2019四川泸州中考]一个菱形的边长为6,面积为28,则该菱形的两条对角线的长度之和为 ( )
A.8 B.12 C.16 D.32
答案
2.C 【解析】 如图,在菱形ABCD中,OA=OC=12AC,OB=OD=12BD,AC⊥BD.根据题意,得12AC·BD=28,∴12×2OA× 2OB=28,∴OA·OB=14,∴(OA+OB)2=OA2+OB2+2OA·OB=AB2+2OA·OB=62+2×14=64,∴OA+OB=8(-8舍去),∴AC+ BD=16.故选C.
?
知识点1 菱形的面积
3.如图,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四边形ABCD,若AD=6 cm,∠ABC=60°,则四边形ABCD的面积为 cm2.?
答案
3.183 【解析】 如图,∵AD∥BC,AB∥CD,∴四边形ABCD是平行四边形.过点A作AE⊥BC于点E,AF⊥CD于点F,∵∠ABC=60°,∴∠ADF=60°.∵纸条等宽,∴AE=AF.由∠AEB=∠AFD=90°,∠ABE=∠ADF,AE=AF,得△ABE≌△ADF, ∴AB=AD,∴四边形ABCD是菱形.∵AD=6 cm,∴BE=3 cm,∴AE=33 cm,∴四边形ABCD的面积为6×33=183(cm2).
?
知识点2 菱形的性质与判定的综合应用
4.[2018广西北部湾经济区中考]如图,在?ABCD中,AE⊥BC,AF⊥CD,垂足分别为点E,F,且BE=DF.
(1)求证:?ABCD是菱形.
(2)若AB=5,AC=6,求?ABCD的面积.
答案
4.【解析】 (1)∵四边形ABCD是平行四边形,
∴∠B=∠D.
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
又∵BE=DF,∴△AEB≌△AFD,
∴AB=AD,∴?ABCD是菱形.
知识点2 菱形的性质与判定的综合应用
答案
(2)连接BD,交AC于点O.
由(1)知四边形ABCD是菱形,
∴AC⊥BD,AO=OC=12AC=12×6=3.
∵AB=5,AO=3,
∴BO=????????2?????????2=52?32=4,
∴BD=2BO=8,
∴S?ABCD=12AC·BD=12×6×8=24.
?
知识点2 菱形的性质与判定的综合应用
1.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,连接BE交AC于点F,连接DF.
(1)求证:∠BAC=∠DAC,∠AFD=∠CFE.
(2)若AB∥CD,试证明四边形ABCD是菱形.
(3)在(2)的条件下,试确定点E的位置,使∠EFD=∠BCD,并说明理由.
答案
1.【解析】 (1)在△ABC和△ADC中,????????=????????,????????=????????,????????=????????,
∴△ABC≌△ADC,∴∠BAC=∠DAC.
在△ABF和△ADF中,????????=????????,????????????∠????????????=∠????????????,????????=????????,???????????
∴△ABF≌△ADF,∴∠AFB=∠AFD.
∵∠AFB=∠CFE,∴∠AFD=∠CFE.
(2)∵AB∥CD,∴∠BAC=∠ACD,
又∵∠BAC=∠DAC,
∴∠CAD=∠ACD,∴AD=CD,
又∵AB=AD,CB=CD,
∴AB=CB=CD=AD,
∴四边形ABCD是菱形.
?
答案
(3)当EB⊥CD时,∠EFD=∠BCD.理由如下:
∵四边形ABCD为菱形,∴∠BCF=∠DCF,
在△BCF和△DCF中,????????=????????,∠????????????=∠????????????,????????=????????,
∴△BCF≌△DCF,∴∠CBF=∠CDF.
∵BE⊥CD,∴∠BEC=∠DEF=90°,
∴∠EFD=90°-∠EDF=90°-∠CBF=∠BCD.
?
2.如图,在等腰三角形ABC中,AB=AC,AD平分∠BAC,交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC,BC于点E,F,作PM∥AC,交AB于点M,连接ME.
(1)求证:四边形AEPM为菱形.
(2)当点P在何处时,菱形AEPM的面积为四边形EFBM面积的一半?请说明理由.
答案
2.【解析】 (1)∵EF∥AB,PM∥AC,
∴四边形AEPM为平行四边形.
∵AD平分∠BAC,∴∠CAD=∠BAD.
∵EP∥AB,∴∠BAD=∠EPA,
∴∠CAD=∠EPA,∴EA=EP,
∴四边形AEPM为菱形.
答案
(2)当点P为EF的中点时,S菱形AEPM=12S四边形EFBM.理由如下:
∵四边形AEPM为菱形,∴AP⊥EM.
∵AB=AC,∠CAD=∠BAD,
∴AD⊥BC,∴EM∥BC,
又∵EF∥AB,
∴四边形EFBM为平行四边形.
如图,过点E作EN⊥AB于点N.
∵EP=12EF,
∴S菱形AEPM=EP·EN=12EF·EN=12S四边形EFBM.
?
2 矩形的性质与判定
课时1 矩形的性质
课时1
1.[2020四川成都石室联合中学开学考试]如图,四边形ABCD的对角线互相平分,要使它成为矩形,需要添加的条件是 ( )
A.AB∥CD
B.AD=BC
C.∠AOB=45°
D.∠ABC=90°
答案
1.D 【解析】 因为四边形ABCD的对角线互相平分,所以四边形ABCD为平行四边形.根据矩形的定义知添加D项后四边形ABCD是矩形.故选D.
知识点1 矩形的定义
2.[2019河南省实验中学月考]矩形具有而一般平行四边形不具有的性质是( )
A.对边平行且相等 B.对角线相等
C.对角线互相平分 D.对角相等
3.[2018湖南株洲中考]如图,矩形ABCD的对角线AC与BD相交于点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长度为 .?
答案
2.B
3.2.5 【解析】 ∵四边形ABCD是矩形,∴AC=BD=10,BO=DO=12BD,∴DO=12BD=5.∵点P,Q分别是AO,AD的中点, ∴PQ是△AOD的中位线,∴PQ=12DO=2.5.
?
知识点2 矩形的性质
4.如图,将矩形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C'处,点B落在点B'处,其中AB=9,BC=6,则FC'的长为 .?
答案
4.5 【解析】 由题意可知,C'D=12AD=12BC=3.设CF=x,则FC'=x,DF=9-x.在Rt△C'DF中,DF2+C'D2=FC'2,即(9-x)2+32= x2, 解得x=5,所以FC'=5.
?
知识点2 矩形的性质
5.如图,在矩形ABCD中,已知对角线AC与BD相交于点O,△OBC的周长为16,且BC=7,求矩形对角线的长.
答案
5.【解析】 ∵四边形ABCD为矩形,
∴AC=BD=2BO=2CO.
∵BO+CO+BC=16,BC=7,
∴BO+CO=9,∴AC=BD=9,
即矩形对角线的长为9.
知识点2 矩形的性质
6.如图,在矩形ABCD中,E,F是BC边上的两点,且BE=CF.求证:AF=DE.
答案
6.【解析】 ∵四边形ABCD是矩形,
∴AB=CD,∠B=∠C=90°.
∵BE=CF,∴BF=CE.
在△ABF和△DCE中,????????=????????,∠????=∠????,????????=????????,
∴△ABF≌△DCE,∴AF=DE.
?
知识点2 矩形的性质
要证明线段相等,可以借助三角形全等.要判定两个三角形全等,可先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法进行判定.
7.[2018甘肃天水中考]如图,点O是矩形ABCD对角线AC的中点,OE∥AB交AD于点E.若OE=3,BC=8,则OB的长为 ( )
A.4 B.5
C.342 D.34
?
答案
7.B 【解析】 ∵四边形ABCD是矩形,∴∠ABC=90°,AB∥CD,AB=CD.∵OE∥AB,∴OE∥CD,又∵点O是AC的中点,∴OE是△ACD的中位线,∴CD=2OE=6,∴AB=6.在Rt△ABC中,AB=6,BC=8,∴AC=10.∵OB是Rt△ABC斜边上的中线, ∴OB=12AC=5.故选B.
?
知识点3 直角三角形斜边上的中线的性质
8.[2019广西来宾期中]如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,若∠A=26°,则∠BDC的度数是 ( )
A.26° B.38°
C.42° D.52°
答案
8.D 【解析】 ∵∠ACB=90°,CD是斜边AB上的中线,∴BD=CD=AD,∴∠DCA=∠A=26°, ∴∠BDC=∠A+ ∠DCA= 26°+26°=52°.故选D.
知识点3 直角三角形斜边上的中线的性质
9.[2019江苏扬州江都区月考]如图,在四边形ABCD中,∠BAD=90°,∠DCB=90°,E,F分别是BD,AC的中点.
(1)请你猜测EF与AC的位置关系,并给予证明;
(2)当AC=8,BD=10时,求EF的长.
知识点3 直角三角形斜边上的中线的性质
答案
9.【解析】 (1)EF⊥AC.证明如下:
如图,连接AE,CE.
∵∠BAD=90°,∠DCB=90°,E为BD的中点,
∴AE=12BD,CE=12BD,∴AE=CE.
∵F是AC的中点,∴EF⊥AC.
(2)由(1)知AE=CE=12BD,
∵BD=10,∴AE=CE=5.
∵F是AC的中点,AC=8,
∴CF=12AC=4.
由(1)知EF⊥AC,
∴EF=????????2?????????2=52?42=3.
?
知识点3 直角三角形斜边上的中线的性质
1.[2020江苏宿迁湖滨新区模拟]如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上的点G处,并使折痕经过点A,展平纸片后,∠DAG的度数为 ( )
A.30° B.45°
C.60° D.75°
答案
1.C 【解析】 如图,设AM与EF交于点N,由题意得∠1=∠2,AN=MN, ∠MGA=90°,∴NG=12AM,∴AN=NG,∴∠2=∠4.∵EF∥AB,∴∠4=∠3, ∴∠1=∠2=∠3=13×90°=30°,∴∠DAG=60°.故选C.
?
2.如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为 ( )
A.8 B.9
C.10 D.241
?
答案
2.B 【解析】 如图,取BC的中点为O,连接OE,OF.∵四边形ABCD是矩形, ∴AB=CD=6,AD=BC=8,∠BCD=90°,∵点F是CD的中点,点O是BC的中点, ∴CF=3,CO=4,∴OF=5.∵点O是Rt△BCE的斜边BC的中点,∴OE=OC=4.根据三角形三边关系可得OE+OF≥EF,∴当点O、点E、点F共线时,EF取得最大值,最大值为OE+OF=4+5=9.故选B.
3.[2020河南郑州金水区模拟]如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(8,6),以A为圆心,任意长为半径画弧,分别交AC,AO于点M,N,再分别以M,N为圆心,大于12MN长为半径画弧,两弧交于点Q,作射线AQ交y轴于点D,则点D的坐标为 ( )
A.(0,1) B.(0,83)
C.(0,53) D.(0,2)
?
答案
3.B 【解析】 如图,过点D作DE⊥AC于点E.∵四边形OABC为矩形,点B的坐标为(8,6),∴OA=8,OC=6,∴AC=10.由题意可得AD平分∠OAC,∴∠DAE=∠DAO, ∵AD=AD,∠AOD=∠AED=90°,∴△ADO≌△ADE,∴AE=AO=8,OD=DE,∴CE=2. ∵CD2=DE2+CE2,∴(6-OD)2=4+OD2,∴OD=83,∴点D(0,83).故选B.
?
4.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE的度数为 .?
答案
4.22.5° 【解析】 ∵四边形ABCD是矩形,∴∠BAD=90°,AC=BD,OA=OC=OB=OD,∴∠OAD=∠ODA. ∵∠EAC= 2∠CAD,∴∠EAD=3∠ODA.在Rt△ADE中,∠EAD+∠ODA=90°,∴∠ODA=22.5°,∴∠BAE=90°-∠EAD=90°-3∠ODA= 22.5°.
5.[2019四川南充期末]如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ADB=30°,E为BC边上一点,∠AEB=45°, CF⊥ BD 于点F.给出下列结论:①BE=CD;②BF=3DF;③AE=2AO;④CE=CF.其中正确的是 .(填序号)?
?
答案
5.①②③ 【解析】 ∵四边形ABCD是矩形,∴AB=CD,AO=CO=BO=DO,∠ABC=∠BAD=90°.∵∠AEB=45°, ∴∠BAE= ∠AEB=45°,∴AB=BE,∴BE=CD,故①正确.∵∠ADB=30°,∴∠ABO=60°,又∵AO=BO,∴△ABO是等边三角形,∴AB=AO.在Rt△ABE中,AE=2AB,∴AE=2AO,故③正确.∵△OCD是等边三角形,CF⊥BD,∴DF=FO= 12OD= 14BD, ∴BF=3DF,故②正确.∵△OCD是等边三角形,∴CF=32CD.∵∠ACB=30°,∴AC=2AB,∴BC=3AB,又∵BE=AB,∴CE= (3-1)AB,∵AB=CD,∴CE≠CF,故④错误.综上,正确的结论是①②③.
?
6.[2020重庆涪陵十九中月考]如图,在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.
(1)求证:DF=AB.
(2)若∠FDC=30°,且AB=4,求AD的长.
答案
6.【解析】 (1)∵四边形ABCD为矩形,
∴∠B=90°,AD∥BC,∴∠DAE=∠AEB.
∵DF⊥AE,∴∠DFA=90°,∴∠DFA=∠B.
在△ADF和△EAB中,∠????????????=∠????????????,∠????????????=∠????????????,????????=????????,????????????
∴△ADF≌△EAB,∴DF=AB.
(2)∵∠AFD=90°,∠ADC=90°,
∴∠DAF+∠ADF=90°,∠ADF+∠FDC=90°,
∴∠DAF=∠FDC=30°,∴AD=2DF,
又∵DF=AB,∴AD=2AB=8.
?
7.易错题[2019黑龙江大庆中考]如图,在矩形ABCD中,AB=3,BC=4,M,N在对角线AC上,且AM=CN,E,F分别是AD,BC的中点.
(1)求证:△ABM≌△CDN.
(2)点G是对角线AC上的点,∠EGF=90°,求AG的长.
答案
7.【解析】 (1)∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,∴∠MAB=∠NCD.
在△ABM和△CDN中,????????=????????,∠????????????=∠????????????,????????=????????,
∴△ABM≌△CDN.
(2)连接EF,交AC于点O.
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,∴∠EAO=∠FCO,
?
答案
∵E,F分别是AD,BC的中点,∴AE=CF.
在△AEO和△CFO中,∠????????????=∠????????????,∠????????????=∠????????????,????????=????????,
∴△AEO≌△CFO,∴EO=FO,AO=CO,
∴O为EF,AC的中点.
∵∠EGF=90°,∴OG=12EF=12AB=32,
∵AB=3,BC=4,∠ABC=90°,
∴AC=5,∴AO=52.
当点G在OA上时,AG=OA-OG=1;
当点G在OC上时,AG=OA+OG=4.
∴AG的长为1或4.
?
8.[2019山东东营胜利一中期中]如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B'的位置,AB'与CD交于点E.
(1)试找出一个与△AED全等的三角形,并加以证明;
(2)若AB=8,DE=3,P为线段AC上的任意一点,PG⊥AB'于点G,PH⊥DC于点H,试求PG+PH的值.
答案
8.【解析】 (1)△AED≌△CEB'.证明如下:
∵四边形ABCD为矩形,
∴AD=BC=B'C,∠D=∠B=∠B'=90°,
又∵∠DEA=∠B'EC,∴△AED≌△CEB'.
(2)由已知得∠EAC=∠CAB,且∠CAB=∠ECA,
∴∠EAC=∠ECA,∴AE=EC=8-3=5.
在Rt△ADE中,AD=????????2?????????2=4.
延长HP交AB于点M,则PM⊥AB,
∵∠CAB'=∠CAB,PG⊥AB',PM⊥AB,∴PG=PM,
∴PG+PH=PM+PH=HM=AD=4.
?
课时2 矩形的判定
课时2
1.[2019吉林长春南关区月考]如图,给出下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④∠ADC=∠BAD.从中选取一个作为补充条件,使?ABCD为矩形,其中错误的是 ( )
A.① B.②
C.③ D.④
答案
1.A 【解析】 当AB=BC时,根据“有一组邻边相等的平行四边形是菱形”,可以判定?ABCD为菱形,但不能判定?ABCD为矩形;当∠ABC=90°时,根据“有一个角是直角的平行四边形是矩形”,可以判定?ABCD为矩形;当AC=BD时,根据“对角线相等的平行四边形是矩形”,可以判定?ABCD为矩形;当∠ADC=∠BAD时,可得∠ADC=∠BAD=90°,根据“有一个角是直角的平行四边形是矩形”,可以判定?ABCD为矩形.故选A.
知识点1 矩形的判定
2.[2020福建三明期中]在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的几位同学拟订的方案,其中正确的是 ( )
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量一组对角是否都为直角
D.测量其中三个内角是否都为直角
答案
2.D 【解析】 A项,对角线互相平分的四边形是平行四边形;B项,两组对边分别相等的四边形是平行四边形;C项,无法判断一组对角为直角的四边形的形状.故选D.
知识点1 矩形的判定
3.[2019湖北荆门沙洋期中节选]如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE,BF.当∠ACB=
°时,四边形ABFE为矩形.?
答案
3.60 【解析】 当∠ACB=60°时,∵AB=AC,∴△ABC是等边三角形,∴AC=BC,又∵BC=CE,AC=CF,∴AF=BE.易知四边形ABFE是平行四边形,∴四边形ABFE是矩形.
知识点1 矩形的判定
4.如图,已知直线AB∥CD,EF分别交AB,CD于点M,N,射线MP,MQ,NP,NQ分别是∠AMN,∠BMN,∠MNC,∠MND的平分线,MP,NP相交于点P,MQ,NQ相交于点Q.求证:四边形MPNQ是矩形.
答案
4.【解析】 ∵MP平分∠AMN,∴∠PMN=12∠AMN,
同理∠MNQ=12∠MND,∠NMQ=12∠BMN,∠PNM=12∠MNC.
∵AB∥CD,∴∠AMN=∠MND,
∴∠PMN=∠MNQ,∴PM∥NQ,
同理NP∥MQ,∴四边形MPNQ是平行四边形,
又∵∠PMN+∠NMQ=12(∠AMN+∠BMN)=90°,
∴四边形MPNQ是矩形.
?
知识点1 矩形的判定
5.[2019山东青岛期中]如图,四边形ABCD的对角线AC,BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF.
(2)若OD=12AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
?
答案
5.【解析】 (1)∵O是AC的中点,∴AO=CO,
又∵AE=CF,∴OE=OF.
∵DF∥BE,∴∠OEB=∠OFD,
又∵∠EOB=∠FOD,∴△BOE≌△DOF.
(2)四边形ABCD是矩形.证明如下:
由(1)知△BOE≌△DOF,∴OB=OD,
又∵AO=CO,∴四边形ABCD是平行四边形,∴OD=12BD,
又∵OD=12AC,∴AC=BD,
∴四边形ABCD是矩形.
?
知识点1 矩形的判定
6.如图,连接四边形ABCD各边中点得到四边形EFGH,还要添加 才能使四边形EFGH是矩形.(只需写出一个条件即可,图中不能再添加别的点或线)?
答案
6.AC⊥BD(答案不唯一) 【解析】 由E,F,G,H分别是AD,AB,BC,CD的中点,可得EF∥GH∥BD,FG∥EH∥AC,所以四边形EFGH是平行四边形,要使四边形EFGH是矩形,则EF⊥FG,从而得到AC⊥BD.
知识点2 与矩形的判定有关的开放探究
7.[2019江苏连云港中考]如图,在△ABC中,AB=AC.将△ABC沿着BC方向平移得到△DEF,其中点E在边BC上,DE与AC相交于点O.
(1)求证:△OEC为等腰三角形.
(2)连接AE,DC,AD,当点E在什么位置时,四边形AECD为矩形,并说明理由.
答案
7.【解析】 (1)∵AB=AC,∴∠B=∠ACB.
∵△ABC平移得到△DEF,
∴∠B=∠DEC,
∴∠ACB=∠DEC,∴OE=OC,
∴△OEC为等腰三角形.
知识点2 与矩形的判定有关的开放探究
答案
(2)当E为BC的中点时,四边形AECD是矩形.理由如下:
∵AB=AC,E为BC的中点,
∴AE⊥BC,BE=EC.
∵△ABC平移得到△DEF,
∴BE∥AD,BE=AD,
∴AD∥EC,AD=EC,
∴四边形AECD是平行四边形,
又∵AE⊥BC,
∴四边形AECD是矩形.
知识点2 与矩形的判定有关的开放探究
8.一张矩形纸片经过折叠得到一个三角形(如图所示),则该矩形纸片的长与宽的比为 .?
答案
8.2∶3 【解析】 根据折叠的性质,得BC'=BC,∠ABC'=∠C'BE=∠EBC.∵四边形ABCD是矩形,∴∠ABC=∠A= 90°,∴∠ABC'=13∠ABC=30°,∴在Rt△ABC'中,AC'∶AB∶BC'=1∶3∶2,∴BC∶AB=2∶3,∴该矩形纸片的长与宽的比为2∶3.
?
知识点3 矩形的折叠
9.[2019山东济南育华中学月考]如图,将矩形ABCD沿AE折叠,使点D落在BC边的点F处,已知AB=DC=8,AD=BC=10.求EC的长.
答案
9.【解析】 设EC的长为x,则DE=8-x.
∵△ADE折叠后的图形是△AFE,
∴AD=AF,DE=EF.
∵AD=BC=10,∴AF=10.
∵四边形ABCD是矩形,∴∠B=∠C=90°.
在Rt△ABF中,BF=????????2?????????2=6,
∴FC=BC-BF=10-6=4.
在Rt△EFC中,FC2+EC2=EF2,
∴42+x2=(8-x)2,解得x=3,
∴EC的长为3.
?
知识点3 矩形的折叠
1.[2019山东临沂中考]如图,在?ABCD中,M,N是BD上两点,BM=DN,连接AM,MC,CN,NA.添加一个条件,使四边形AMCN是矩形,这个条件是 ( )
A.OM=12AC
B.MB=MO
C.BD⊥AC
D.∠AMB=∠CND
?
答案
1.A 【解析】 ∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.∵BM=DN,∴OB-BM=OD-DN,即OM=ON,∴四边形AMCN是平行四边形.当OM=12AC时,MN=AC,∴四边形AMCN是矩形.故选A.
?
2.如图,在四边形ABCD中,∠A=60°,∠ABC=∠ADC=90°,BC=2,CD=11,过点D作DH⊥AB于点H,则DH的长是 ( )
A.7.5 B.7
C.6.5 D.5.5
答案
2.A 【解析】 如图,过点C作CE⊥DH于点E.∵DH⊥AB,∠ABC=90°,CE⊥DH,∴四边形BCEH是矩形,∴HE=BC=2.在Rt△AHD中,∠A=60°,∴∠ADH=30°,又∵∠ADC= 90°, ∴∠CDE=60°,∴∠DCE=30°,∴在Rt△CED中,DE=12CD=5.5,∴DH=HE+ DE= 2+ 5.5=7.5.故选A.
?
3.[2019江西南昌期中]如图,在四边形ABCD中,对角线AC⊥BD,E,F,G,H分别是AB,BC,CD,DA的中点,若AC=8,BD=6,则四边形EFGH的面积是 .?
答案
3.12 【解析】 ∵E,F,G,H分别是AB,BC,CD,DA的中点,∴HG∥AC且HG=12AC,EH∥BD且EH=12BD,FG∥BD且FG=12BD,∴EH∥FG且EH=FG,∴四边形EFGH是平行四边形,又∵AC⊥BD,∴EH⊥HG,∴平行四边形EFGH是矩形,∴四边形EFGH的面积为HG·EH=12AC·12BD=12×8×12×6=12.
?
4.如图,沿DE折叠矩形ABCD,使点C落在AB边上的点F处,若AD=8,且△AFD的面积为60,则△DEC的面积为? .?
答案
4.2898 【解析】 ∵四边形ABCD是矩形,∴∠A=∠B=90°,BC=AD=8,CD=AB.在Rt△AFD中,△AFD的面积为60, ∴12 AD·AF=60,解得AF=15,∴DF=????????2+????????2=17.由折叠的性质,得CD=DF=17,∴AB=17,∴BF=AB-AF=17-15=2.设CE=x,则EF=CE=x,BE=BC-CE=8-x.在Rt△BEF中,EF2=BF2+BE2,即x2=22+(8-x)2,解得x=174,即CE=174,∴△DEC的面积为12 CD·CE=2898.
?
5.易错题 矩形ABCD中,对角线AC,BD交于点O,AE⊥BD于点E,若OE∶ED=1∶3,AE=3,则BD= .?
?
答案
5.4或855 【解析】 由于不能确定AB为矩形ABCD的长边还是短边,故需分两种情况讨论:①如图1,若AB是矩形ABCD的较短边,设OE=x,则ED=3x,AO=OD=2x,在Rt△OEA中,AO2=AE2+OE2,即(2x)2=3+x2,所以x=1,所以OD=2,所以BD=2OD=4;②如图2,若AB是矩形ABCD的较长边,设OE=y,则ED=3y,AO=OD=4y,在Rt△OEA中,AO2=AE2+OE2,即(4y)2=3+y2,所以y=55,所以OD=455,所以BD=2OD=855.综上,BD的长为4或855.
?
6.[2019河南省实验中学月考改编]如图,在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形.
(2)若AF平分∠DAB,CF=3,BF=4,求DF的长.
答案
6.【解析】 (1)∵四边形ABCD是平行四边形,∴AB∥DC,
又∵DF=BE,∴四边形BFDE是平行四边形.
∵DE⊥AB,∴∠DEB=90°,
∴四边形BFDE是矩形.
(2)∵四边形BFDE是矩形,
∴∠BFD=90°,∴∠BFC=90°,
在Rt△BCF中,CF=3,BF=4,∴BC=5.
∵AF平分∠DAB,∴∠DAF=∠BAF,
∵AB∥DC,∴∠DFA=∠BAF,
∴∠DAF=∠DFA,∴AD=DF.
∵AD=BC,∴DF=BC,
∴DF=5.
7.[2019浙江杭州西湖区月考]在矩形ABCD中,AB=3 cm,BC=4 cm,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1 cm/s,运动时间为t s,0≤t≤5.
(1)AE= cm,EF= cm.(用含t的式子表示)?
(2)若G,H分别是AB,DC的中点,求证:四边形EGFH是平行四边形.
(3)在(2)条件下,当t为何值时,四边形EGFH为矩形.
答案
7.【解析】 (1)t (5-2t)(0≤t≤2.5)或(2t-5)(2.5∵四边形ABCD是矩形,∴∠B=90°,∴AC=????????2+????????2=32+42=5(cm),由题意得,AE=CF=t cm,当0≤t≤2.5时,EF= AC-AE-CF=(5-2t)cm,当2.5(2)∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,∴∠GAF=∠HCE.
∵G,H分别是AB,DC的中点,
∴AG=CH,
∵AE=CF,∴AF=CE.
在△AFG与△CEH中,????????=????????,???????????∠????????????=∠????????????,????????=????????,?????????
∴△AFG≌△CEH,∴GF=HE,
同理,GE=HF,
∴四边形EGFH是平行四边形.
?
答案
(3)如图,连接GH.
由(2)知四边形EGFH是平行四边形.
∵点G,H分别是矩形ABCD的边AB,DC的中点,
∴GH=BC=4 cm,
∴当EF=GH=4 cm时,四边形EGFH是矩形,分两种情况:
①EF=(5-2t)cm,
即5-2t=4,解得t=0.5.
②EF=5-2(5-t)=(2t-5)cm,
即2t-5=4,解得t=4.5.
∴当t=0.5或4.5时,四边形EGFH为矩形.
课时3 矩形的性质与判定的综合应用
课时3
1.如图,在△ABC中,AC的垂直平分线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是 ( )
A.23 B.33
C.4 D.4 3
?
答案
1.A 【解析】 ∵DE是AC的垂直平分线,AF=BF,∴∠FDC=∠FDA=90°,DF∥BC,∴∠C=∠FDA=90°,又∵BE⊥DF, ∴四边形BCDE是矩形.∵∠A=30°,∠C=90°,BC=2,∴AB=4,∴AC=42?22=23,∴BE=CD=3,∴四边形BCDE的面积为2×3=23.故选A.
?
2.[2020山东枣庄期中]如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,M为EF的中点,则AM的最小值为 ( )
A.54 B.52
C.53 D.65
?
答案
2.D 【解析】 连接AP.在△ABC中,AB=3,AC=4,BC=5,∴AB2+AC2=BC2,∴∠BAC=90°,又∵PE⊥AB,PF⊥AC,∴四边形AEPF是矩形,∴EF=AP.∵M是EF的中点,∴AM=12EF=12AP.由题意知,AP的最小值即Rt△ABC斜边上的高,易得AP的最小值为125,∴AM 的最小值是12×125=65.故选D.
?
3.[2020辽宁辽阳九中二检]如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3 cm,EF=4 cm,则边AD的长是 cm.?
答案
3.5 【解析】 由折叠的性质,知∠HEM=∠AEH,∠BEF=∠FEM,∴∠HEF=∠HEM+∠FEM=12(∠AEM+∠BEM)= 12×180°=90°.同理可得∠EHG=∠HGF=90°,∴四边形EFGH为矩形.易证△HNG≌△FME,∴HN=MF, ∴AD=AH+ HD= HM+HN=HM+MF=HF,在Rt△HEF中,HF=????????2+????????2=32+42=5(cm),∴AD=5 cm.
?
4.如图,在平行四边形ABCD中,点M,N是AD边上的点,BM,CN交于点O,AN=DM,BM=CN.
(1)求证:平行四边形ABCD是矩形.
(2)若∠BOC=90°,MN=1,AM·MD=12,求四边形ABCD的面积.
答案
4.【解析】 (1)∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠A+∠D=180°.
∵AN=DM,∴AM=DN,
在△ABM和△DCN中,????????=????????,????????=????????,????????=????????,
∴△ABM≌△DCN,∴∠A=∠D.
∵∠A+∠D=180°,∴∠A=∠D=90°,
∴平行四边形ABCD是矩形.
?
答案
(2)∵△ABM≌△DCN,∴∠AMB=∠DNC,
∵∠BOC=90°,∴∠AMB+∠DNC=180°-90°=90°,
∴∠AMB=45°,
又∵∠A=90°,∴∠ABM=∠AMB=45°,∴AB=AM.
∵AM·MD=12,AN=DM,
∴AM(AM-1)=12,
解得AM=4(-3舍去),
∴AB=AM=4,MD=3,
∴AD=AM+MD=7,
∴四边形ABCD的面积为AD×AB=7×4=28.
5.如图,在△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交△ACB的外角∠ACD的平分线于点F.
(1)求证:OE=OF.
(2)若CE=12,CF=5,求OC的长.
(3)连接AE,AF.点O在边AC上运动到什么位置时,四边形AECF是矩形?请说明理由.
答案
5.【解析】 (1)如图,∵MN交∠ACB的平分线于点E,交△ACB的外角∠ACD的平分线于点F,
∴∠2=∠5,∠4=∠6.
∵MN∥BC,∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴OE=CO,OF=CO,∴OE=OF.
(2)∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°.
∵∠ECF=∠2+∠4=90°,CE=12,CF=5,
∴EF=122+52=13,
∴OC=12EF=6.5.
(3)点O在边AC上运动到AC的中点时,四边形AECF是矩形.理由如下:
当O为AC的中点时,AO=CO,
∵OE=OF,∴四边形AECF是平行四边形,
又∵∠ECF=90°,∴四边形AECF是矩形.
?
6.[2020天津南开翔宇学校期初考试]如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD,△BCE, △ACF,请探究:
(1)四边形ADEF是什么四边形?
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
(3)当△ABC满足什么条件时,以A,D,E,F为顶点的四边形不存在?
答案
6.【解析】 (1)四边形ADEF是平行四边形.理由如下:
∵△ABD,△BCE都是等边三角形,
∴AD=BD=AB,BC=BE=EC,∠DBA=∠EBC=60°,
∴∠DBE+∠EBA=∠ABC+∠EBA,∴∠DBE=∠ABC.
在△DBE和△ABC中,????????=????????,∠????????????=∠????????????,????????=????????,
∴△DBE≌△ABC,∴DE=AC.
∵△ACF是等边三角形,∴AC=AF,∴DE=AF.
同理可证AD=EF,
∴四边形ADEF是平行四边形.
(2)若四边形ADEF是矩形,则∠FAD=90°,
∴∠BAC=360°-∠FAD-∠DAB-∠FAC=360°-90°-60°-60°=150°.
∴当△ABC满足∠BAC=150°时,四边形ADEF是矩形.
(3)当A与E重合,即∠BAC=60°时,以A,D,E,F为顶点的四边形不存在.
?
3 正方形的性质与判定
课时1 正方形的性质
课时1
1.下列条件可以利用定义说明平行四边形ABCD是正方形的是 ( )
A.AB=CD,∠A=90°
B.AB=AD,∠A=90°
C.AB∥CD,∠A=90°
D.以上都对
答案
1.B 【解析】 正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形是正方形.由此可知选B.
知识点1 正方形的定义
2.[2019广东广铁一中开学考试]正方形具有而菱形不一定具有的性质是 ( )
A.四边相等 B.对角线相等
C.对角相等 D.对角线互相垂直
3.[2019山西太原期中]矩形、菱形、正方形都具有的性质是 ( )
A.对角线相等 B.对角线平分一组对角
C.对角线互相平分 D.对角线互相垂直
答案
2.B
3.C
知识点2 正方形的性质
4.如图,正方形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=8 2 cm,则EF的长度为 ( )
A.1 cm B.2 cm
C.2 2 cm D.4 cm
?
答案
4.B 【解析】 ∵四边形ABCD是正方形,∴AC=BD,∵AC+BD=8 2 cm,∴AC=BD=4 2 cm.∵AB2=12AC·BD,∴AB= 4 cm.∵点E,F分别是线段AO,BO的中点,∴EF=12AB=2 cm.故选B.
?
知识点2 正方形的性质
5.如图,正方形ABCD的边长为4 cm,则阴影部分的面积为 ( )
A.4 cm2 B.8 cm2
C.12 cm2 D.16 cm2
答案
5.B 【解析】 根据正方形的轴对称性可得,S阴影=12S正方形ABCD,∵正方形ABCD的边长为4 cm,∴S阴影=12×42=8(cm2).故选B.
?
知识点2 正方形的性质
根据正方形的轴对称性,得出阴影部分的面积等于正方形面积的一半是解题的关键.
6.如图,正方形纸片ABCD的边长为8,将其沿EF折叠,则图中①②③④四个三角形的周长之和为 .?
答案
6.32 【解析】 如图,C'B'与AB交于点G',与AD交于点H',FC'与AD交于点W',由折叠可知,点G',H',W'关于EF对称的点分别为G,H,W.由题意知,EB'=BE,B'G'=BG,G'H'=GH,H'C'=HC,C'W'=CW,FW'=FW,故①②③④四个三角形的周长之和等于正方形ABCD的周长,即4×8=32.
知识点2 正方形的性质
7.如图,在正方形ABCD中,E,F分别为边AD和CD上的点,且AE=CF,连接AF,CE交于点G.
求证:AG=CG.
答案
7.【分析】 先证明△ADF≌△CDE,得出∠DAF=∠DCE,然后证明△AGE≌△CGF,即可得出结论.
【解析】 ∵四边形ABCD是正方形,
∴∠ADF=∠CDE=90°,AD=CD.
∵AE=CF,∴DE=DF,
∴△ADF≌△CDE,∴∠DAF=∠DCE.
又∵∠AGE=∠CGF,AE=CF,∴△AGE≌△CGF,∴AG=CG.
知识点2 正方形的性质
知识点2 正方形的性质
利用正方形的性质求解证明题的关键
充分利用正方形的四条边相等、四个角为直角、对角线互相垂直平分且相等是求解此类证明题的关键,注意在解题时要与三角形全等、等腰直角三角形等知识相结合.
8.如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为? .?
答案
8.17 【解析】 在AD上取一点M,使得AM=2,连接EM,交AC于点P,易知此时PF+PE取最小值,即EM的长.过点M作MN⊥BC于点N,由题意可知EN=BN-BE=AM-BE=2-1=1,MN=AB=4,所以EM=????????2+????????2=12+42=17.
?
知识点3 与正方形有关的动态探究
9.[2019广东惠州一中期中]如图,正方形ABCD的对角线AC,BD相交于点O,正方形A'B'C'D'的顶点A'与点O重合,A'B'交BC于点E,A'D'交CD于点F.
(1)求证:OE=OF.
(2)若正方形ABCD的边长为1,求两个正方形重叠部分的面积.
(3)在(2)的条件下,若正方形A'B'C'D'绕着点O旋转,EF的长度何时最小?最小值是多少?
知识点3 与正方形有关的动态探究
答案
9.【解析】 (1)∵正方形ABCD的对角线AC,BD交于点O,
∴∠BOC=90°,∠OBC=∠OCF=45°,OB=OC.
∵四边形A'B'C'D'是正方形,∴∠EOF=90°.
∵∠BOE=∠BOC-∠EOC=90°-∠EOC,∠COF=∠EOF-∠EOC=90°-∠EOC,
∴∠BOE=∠COF.
在△BOE和△COF中,∠????????????=∠????????????,????????=????????,∠????????????=∠????????????,
∴△BOE≌△COF,
∴OE=OF.
(2)∵△BOE≌△COF,∴????△????????????=????△????????????,
∴????△????????????+????△????????????=????△????????????+????△????????????,
?
知识点3 与正方形有关的动态探究
答案
即????四边形OECF?=????△?????????????.
∵????△????????????=14S正方形ABCD=14×1×1=14,
∴两个正方形重叠部分的面积为14.
(3)当OE垂直于BC时,EF的长度最小,最小值为22.
连接EF,∵∠EOF=90°,∴EF2=OE2+OF2.
∵OE=OF,∴EF2=2OE2,
∴要使EF的长度最小,则OE的长度最小,
当OE垂直于BC时,OE最小,此时OE=12,则EF=22.
∴当OE垂直于BC时,EF的长度最小,最小值为22.
?
知识点3 与正方形有关的动态探究
1.如图,将甲、乙两张不同的纸片分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则 ( )
A.甲、乙都可以
B.甲、乙都不可以
C.甲不可以,乙可以
D.甲可以,乙不可以
答案
1.A 【解析】 对剪开后的纸片进行旋转平移操作,可得如图所示的图形,可见甲、乙都可以拼成和原来面积相等的正方形.故选A.
2.[2018湖北仙桃中考]如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是 ( )
A.1 B.1.5
C.2 D.2.5
答案
2.C 【解析】 连接AE.∵四边形ABCD是正方形,∴AB=AD,∠B=∠D=90°.∵△ABG沿AG对折至△AFG,G是BC的中点,∴AB=AF,GB=GF=3,∠B=∠AFG=90°,∴∠AFE=∠D=90°,AF=AD,又∵AE=AE,∴Rt△AFE≌Rt△ADE(HL),∴DE= EF.设DE=x,则EF=DE=x,GE=x+3,CE=6-x.在Rt△CGE中,由勾股定理得CG2+CE2=GE2,∴32+(6-x)2=(x+3)2,解得x=2.故选C.
利用正方形的性质求解线段的长的思路
利用正方形的性质求解线段长度时,通常将涉及的线段转化到直角三角形(特别是等腰直角三角形)中,结合勾股定理或三角形全等求解.
3.如图,在正方形ABCD中,点E在边BC上,点F在线段DE上,若AB=AF,则∠BFE= ( )
A.45° B.30°
C.60° D.55°
答案
3.A 【解析】 如图,∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,∵AB=AF,∴AF=AD,∴∠1=∠2, ∠3=∠4. ∵∠BAD+∠1+∠2+∠3+∠4=360°,∴2∠2+2∠3=270°,∴∠2+∠3=135°,∴∠BFE=180°-135°=45°.故选A.
4.如图,正方形ABCD中,AB=4 cm,点E,F分别在边AD和边BC上,且BF=ED=3 cm,动点P,Q分别从A,C两点同时出发,点P沿A→F→B方向运动,点Q沿C→D→E→C方向运动,点P,Q的运动速度分别为1 cm/s,3 cm/s.设运动时间为t(0答案
4.3或6 【解析】 ∵四边形ABCD是正方形,∴AD=BC,AD∥BC,∵BF=ED,∴四边形AFCE是平行四边形,∴AF∥EC, AF=EC.在Rt△ABF中,AB=4 cm,BF=3 cm,∴AF=5 cm.由P,Q的运动速度和运动方向可知,当Q 在EC上运动,P在AF上运动时,若EQ=FP,则以A,C,P,Q四点为顶点的四边形是平行四边形,∴3t-7=5-t,∴t=3.当P,Q分别在BC,AD上运动时,若QD=BP,则以A,C,P,Q四点为顶点的四边形是平行四边形,此时Q点已经运动一周,∴3t-12-4=8-t,∴t=6.综上所述,t的值为3或6.
5.如图,过正方形ABCD的顶点B作直线l,分别过点A,C作l的垂线,垂足分别为E,F.若AE=1,CF=3,则AB的长度为? .?
答案
5.10 【解析】 ∵四边形ABCD是正方形,∴∠CBF+∠FBA=90°,∵CF⊥l,∴∠CBF+∠BCF=90°,∴∠ABE=∠BCF,又∵∠AEB=∠BFC=90°,AB=BC,∴△ABE≌△BCF,∴BE=CF=3,∴在Rt△ABE中,AB=????????2+????????2=12+32=10.
?
6.若以正方形ABCD的边CD为边作等边三角形CDE,则∠AED的度数是 .?
答案
6.15°或75° 【解析】 有两种情况:(1)当点E在正方形ABCD内时,如图1,在正方形ABCD中,AD=CD,∠ADC=90°,在等边三角形CDE中,CD=DE,∠CDE=60°,∴∠ADE=90°-60°=30°,AD=DE,∴∠AED=∠DAE=12(180°-∠ADE)=75°;(2)当点E在正方形ABCD外时,如图2,在等边三角形CDE中,∠EDC=60°,∴∠ADE=90°+60°=150°,∴∠AED=∠DAE=12(180°-∠ADE)=15°.综上,∠AED的度数是15°或75°.
?
7.[2018江苏盐城中考]在正方形 ABCD中,对角线 BD所在的直线上有两点E,F满足 BE=DF,连接 AE,AF,CE,CF,如图所示.
(1)求证:△ABE≌△ADF.
(2)试判断四边形 AECF的形状,并说明理由.
答案
7.【解析】 (1)∵四边形ABCD为正方形,
∴AB=AD,∠ABD=∠ADB=45°,∴∠ABE=∠ADF=135°,
又∵BE=DF,∴△ABE≌△ADF.
(2)四边形AECF是菱形.理由如下:
由(1)得△ABE≌△ADF,∴AE=AF.
∵四边形ABCD是正方形,
∴CB=CD,∠CBD=∠CDB=45°,∴∠CBE=∠CDF=135°,
又∵BE=DF,∴△CBE≌△CDF,∴CE=CF.
∵BE=BE,∠CBE=∠ABE=135°,CB=AB,∴△CBE≌△ABE,
∴CE=AE,∴CE=AE=AF=CF,∴四边形AECF是菱形.
8.如图,四边形ABCD和四边形CEFG都是正方形.
求证:(1)△BCG≌△DCE;
(2)BG⊥DE.
答案
8.【解析】 (1)∵四边形ABCD和四边形CEFG都是正方形,
∴BC=DC,CE=CG,∠BCD=∠GCE=90°,
∴∠BCG=∠DCE.
在△BCG和△DCE中,BC=DC,∠BCG=∠DCE,CG=CE,
∴△BCG≌△DCE.
(2)设BG分别与DC,DE交于点H,O.
∵△BCG≌△DCE,∴∠HBC=∠ODH,
∵∠BHC=∠DHO,∠HBC+∠BHC=90°,
∴∠ODH+∠DHO=90°,∴∠DOH=90°,
∴BG⊥DE.
9.如图,在正方形ABCD中,点E,F分别在BC,CD上移动,且A到EF的距离AH始终保持与AB的长相等,问在点E,F移动的过程中:
(1)∠EAF的大小是否有变化?请说明理由.
(2)△ECF的周长是否有变化?请说明理由.
答案
9.【解析】 (1)∠EAF的大小没有变化.理由如下:
根据题意,知AB=AH,∠B=90°,
∵AH⊥EF,∴∠AHE=90°,
又∵AE=AE,∴Rt△BAE≌Rt△HAE,
∴∠BAE=∠EAH.
同理,Rt△HAF≌Rt△DAF,∴∠HAF=∠DAF,
∴∠EAF=∠EAH+∠HAF=12∠BAH+12∠HAD=12∠BAD=45°,
∴∠EAF的大小没有变化.
(2)△ECF的周长没有变化.理由如下:
由(1)得Rt△BAE≌Rt△HAE,Rt△HAF≌Rt△DAF,
∴BE=EH,HF=DF,
∴△ECF的周长为EF+EC+FC=BE+DF+EC+FC=2BC,
∴△ECF的周长没有变化.
?
课时2 正方形的判定
课时2
1.[2019北京顺义区期末]学习了正方形之后,王老师提出问题:要判断一个四边形是正方形,有哪些思路?甲同学说:先判定四边形是菱形,再确定这个菱形有一个角是直角.乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等.丙同学说:判定四边形的对角线相等,并且互相垂直平分.丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.上述四名同学的说法中,正确的是 ( )
A.甲、乙 B.甲、丙
C.乙、丙、丁 D.甲、乙、丙、丁
答案
1.D
知识点 正方形的判定
正方形是特殊的平行四边形,也是邻边相等的特殊矩形,也是有一个角是直角的特殊菱形,所以在判定一个四边形是正方形时,要从它的特殊性逐步突破
2.已知四边形ABCD的对角线AC与BD相交于点O,有下列条件:①AB=AD;②∠DAB=90°;③AO=CO,BO=DO;④四边形ABCD为矩形;⑤四边形ABCD为菱形;⑥四边形ABCD为正方形.则下列推理不成立的是 ( )
A.①④?⑥ B.①③?⑤
C.①②?⑥ D.②③?④
答案
2.C 【解析】 A项,有一组邻边相等的矩形是正方形,成立;B项,由③得四边形ABCD是平行四边形,再由①知平行四边形ABCD有一组邻边相等,故四边形ABCD为菱形,成立;C项,由①②不能判定四边形ABCD是正方形,不成立;D项,由③得四边形ABCD是平行四边形,再由②知平行四边形ABCD有一个角是直角,故四边形ABCD是矩形,成立.故选C.
知识点 正方形的判定
3.如图,四边形ABCD中,对角线AC与BD相交于点O,且OA=OB=OC=OD,不添加任何字母与辅助线,若要使四边形ABCD是正方形,则还需要添加的一个条件是 .?
答案
3.AC⊥BD(或AB=AD等) 【解析】 由OA=OB=OC=OD可得四边形ABCD是矩形,因此再添加一组邻边相等或对角线互相垂直即可.
知识点 正方形的判定
4.如图,在Rt△ABC中,∠C=90°,∠BAC,∠ABC的平分线交于点D,DE⊥BC于点E,DF⊥AC于点F.求证:四边形CEDF为正方形.
答案
4.【解析】 过点D作DG⊥AB交AB于点G.
∵∠C=∠CFD=∠CED=90°,
∴四边形CEDF是矩形.
∵AD是∠BAC的平分线,DF⊥AC,DG⊥AB,∴DF=DG,
同理可得DE=DG,∴DE=DF,
∴四边形CEDF是正方形.
知识点 正方形的判定
5.[2020陕西西安电子科大附中月考] 如图,等边三角形AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
答案
5.【解析】 ∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°.
∵△AEF是等边三角形,
∴AE=AF,∠AEF=∠AFE=60°.
∵∠CEF=45°,∴∠CFE=∠CEF=45°,
∴∠AFD=∠AEB=180°-45°-60°=75°,
∴△ABE≌△ADF,∴AB=AD,
∴矩形ABCD是正方形.
知识点 正方形的判定
6.如图,在平行四边形ABCD中,AD=9 cm,CD=3 2 cm,∠B=45°,点M,N分别以A,C为起点,1 cm/s的速度沿AD,CB方向运动,设点M,N运动的时间为t(0≤t≤6)s.
(1)求BC边上的高AE的长.
(2)连接AN,CM,当t为何值时,四边形AMCN为菱形?
(3)过点M作MP⊥BC于点P,过点N作NQ⊥AD于点Q,当t为何值时,四边形MPNQ为正方形?
?
知识点 正方形的判定
答案
6.【解析】 (1)∵四边形ABCD是平行四边形,
∴AB=CD=32cm.
在Rt△ABE中,∠AEB=90°,∠B=45°,
∴AE=3 cm.
(2)如图1,连接AN,CM.由题意可知AM=CN=t cm,
∵AM∥CN,∴四边形AMCN为平行四边形,
∴当AN=AM时,四边形AMCN为菱形.
易知BE=AE=3 cm,∴EN=9-3-t=(6-t)cm,
∴AN2=32+(6-t)2,∴32+(6-t)2=t2,
解得t=154.
∴当t为154时,四边形AMCN为菱形.
?
知识点 正方形的判定
答案
?(3)∵MP⊥BC于点P,NQ⊥AD于点Q,QM∥NP,
∴四边形MPNQ为矩形,
∴当QM=QN时,四边形MPNQ为正方形.
分两种情况,
①当点Q在点M的右侧时,如图2.
易知AM=CN=EP=t cm,
∴QM=PN=BC-BE-EP-CN=9-3-t-t=(6-2t)cm,
∴6-2t=3,解得t=1.5.
②当点Q在点M的左侧时,如图3.
易知AM=CN=t cm,
∴AQ=EN=BC-BE-CN=9-3-t=(6-t)cm,
∴QM=AM-AQ=t-(6-t)=(2t-6)cm,
∴2t-6=3,解得t=4.5.
故当t为4.5或1.5时,四边形MPNQ为正方形.
知识点 正方形的判定
1.[2019四川成都金牛区月考]下列说法正确的是 ( )
A.对角线相等且有一个角是直角的平行四边形是正方形
B.对角线互相垂直且一组邻边相等的平行四边形是正方形
C.四个角都相等的菱形是正方形
D.对角线互相垂直平分且有一组邻边相等的四边形是正方形
答案
1.C 【解析】 A项,对角线相等且有一个角是直角的平行四边形是矩形,不一定是正方形,不符合题意;B项,对角线互相垂直且有一组邻边相等的平行四边形是菱形,不一定是正方形,不符合题意;D项,对角线互相垂直平分且有一组邻边相等的四边形是菱形,不一定是正方形,不符合题意.故选C.
利用对角线证明正方形的方法
(1)证“四边形+对角线互相垂直、平分且相等”;(2)证“平行四边形+对角线互相垂直且相等”;(3)证“矩形+对角线互相垂直”;(4)证“菱形+对角线相等”.
2.若一个平行四边形绕着对角线的交点旋转90°,能够与它自身重合,则该平行四边形为 ( )
A.矩形 B.菱形
C.正方形 D.无法确定
答案
2.C 【解析】 该平行四边形绕着它的对角线的交点旋转90°,能够与它自身重合,说明对角线互相垂直平分且相等,所以该平行四边形是正方形.故选C.
3.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加下列一个条件,仍不能证明四边形BECF为正方形的是 ( )
A.BC=AC
B.CF⊥BF
C.BD=DF
D.AC=BF
答案
3.D 【解析】 ∵EF垂直平分BC,∴BE=CE,BF=CF.∵BE=BF,∴BE=EC=CF=BF,∴四边形BECF是菱形.A项,当BC= AC时,∵∠ACB=90°,∴∠EBC=45°,∴∠EBF=2∠EBC=90°,∴四边形BECF是正方形;B项,当CF⊥BF时,∠BFC=90°,根据“有一个角是直角的菱形是正方形”,可得四边形BECF是正方形;C项,当BD=DF时,根据“对角线相等的菱形是正方形”,可得四边形BECF是正方形;D项,当AC=BF时,无法得出四边形BECF是正方形.故选D.
4.[2019四川雅安中学月考]如图,菱形ABCD中,点E,O,F分别是AB,AC,AD的中点,连接CE,CF,OF,OE.
(1)求证:△BCE≌△DCF.
(2)猜测:当AB和BC满足条件 时,四边形AEOF是正方形,请说明理由.?
答案
4.【解析】 (1)∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=DC=AD.
∵点E,O,F分别为AB,AC,AD的中点,
∴AE=BE=DF=AF.
在△BCE和△DCF中,????????=????????,∠????=∠????,????????=????????,
∴△BCE≌△DCF.
?
答案
(2)AB⊥BC
当AB⊥BC时,四边形AEOF是正方形.理由如下:
在菱形ABCD中,∵点E,O,F分别为AB,AC,AD的中点,
∴AE=OE=OF=AF,
∴四边形AEOF是菱形.
∵AB⊥BC,OE∥BC,
∴OE⊥AB,∴∠AEO=90°,
∴四边形AEOF是正方形.
5.如图,E是矩形ABCD的边BC的中点,P是AD边上一动点,PF⊥AE,PH⊥DE,垂足分别为F,H.
(1)当矩形ABCD的边AD与AB满足什么条件时,四边形PHEF是矩形?请予以证明.
(2)在(1)中,动点P运动到什么位置时,矩形PHEF为正方形?为什么?
答案
5.【解析】 (1)当AD=2AB时,四边形PHEF是矩形.证明如下:
∵四边形ABCD是矩形,∴AD=BC,AB=CD.
∵E是BC的中点,AD=2AB,∴AB=BE=EC=CD,
∴△ABE,△DCE是等腰直角三角形,
∴∠AEB=∠DEC=45°,∴∠AED=90°.
在四边形PHEF中,∵∠PFE=∠FEH=∠EHP=90°,
∴四边形PHEF是矩形.
(2)点P运动到AD的中点时,矩形PHEF为正方形.理由如下:
由(1)可得∠BAE=∠CDE=45°,
∴∠FAP=∠HDP=45°,
又∵∠AFP=∠PHD=90°,AP=PD,
∴△AFP≌△DHP,∴PF=PH,
∴矩形PHEF是正方形.
6.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE的外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.
(1)求证:四边形ABCD是正方形.
(2)已知AB的长为6,求(BE+6)(DF+6)的值.
(3)借助上面问题的解题思路,解决下列问题:若△PQR中,∠QPR=45°,RQ上的高PH=6,HQ=2,则HR= .?
答案
6.【解析】 (1)如图1,过点A作AG⊥EF于点G.
∵AB⊥CE,AD⊥CF,∴∠B=∠D=90°,
∴∠B=∠C=∠D=90°,
∴四边形ABCD是矩形.
∵∠CEF,∠CFE的外角平分线交于点A,
∴AB=AG,AD=AG,∴AB=AD,
∴四边形ABCD是正方形.
(2)∵四边形ABCD是正方形,∴BC=CD=AB=6.
在Rt△ABE和Rt△AGE中,????????=????????,????????=????????,
∴Rt△ABE≌Rt△AGE,∴BE=GE,
同理,Rt△ADF≌Rt△AGF,
∴DF=GF,∴BE+DF=GE+GF=EF.
设BE=x,DF=y,则CE=BC-BE=6-x,CF=CD-DF=6-y,EF=x+y,
?
答案
在Rt△CEF中,由勾股定理得,(6-x)2+(6-y)2=(x+y)2,
∴xy+6(x+y)=36,
∴(BE+6)(DF+6)=(x+6)(y+6)=xy+6(x+y)+36=36+36=72.
(3)3
如图2,把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ,MR交于点G.
由(1)(2)得,四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ=2,
∴MG=DG=MP=PH=6,∴GQ=4,
设MR=HR=a,则GR=6-a,QR=a+2,
在Rt△GQR中,由勾股定理得,(6-a)2+42=(2+a)2,
解得a=3,即HR=3.
课时3 正方形的性质与判定的综合应用
课时3
1.如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是 ( )
A.7 B.8
C.72 D.73
?
答案
1.C 【解析】 如图,设AG交FD于点G,CH交BE于点H,由正方形的性质得, ∠BAD=∠ABC=∠BCD=∠ADC=90°,AB=BC=CD=AD,由“SSS”可证△ABE≌△CDF,所以∠ABE=∠CDF.易证∠ABE=∠DAG=∠CDF=∠BCH,所以∠BAE=∠ADG,由“ASA”可证△ABE≌△DAG,所以AE=DG,BE=AG,同理可得AE=DG=CF=BH= 5,BE= AG=DF=CH=12,所以EG=GF=FH=HE=7,又因为∠HEG=90°,所以四边形EGFH是正方形,所以EF=72.故选C.
?
2.如图1,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图2的方式拼接成一个四边形.若正方形ABCD的边长为3 cm,HA= EB=FC=GD=1 cm,则图2中阴影部分的面积为 cm2.?
答案
2.1 【解析】 在题图1中,连接GH,HE,EF,FG,由HA=EB=FC=GD=1 cm,AB=BC=CD=AD=3 cm,∠A=∠B=∠C= ∠D=90°,易得四边形GHEF是正方形,GF=EF=EH=GH=12+22=5(cm).根据已知条件,知重新拼成的四边形是正方形,且拼成的正方形的边长为正方形GHEF的对角线长,设其边长为a cm,根据勾股定理,得a=(5)2+(5)2=10,其面积为(10)2=10(cm2),∴S阴影=10-S正方形ABCD=10-9=1(cm2).
?
3.如图,在正方形ABCD中,动点E在AC上,AF⊥AC,垂足为A,AF=AE.
(1)求证:BF=DE.
(2)当点E运动到AC的中点时(其他条件都保持不变),四边形AFBE是什么特殊四边形?请说明理由.
答案
3.【解析】 (1)∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°.
∵AF⊥AC,∴∠EAF=90°,∴∠BAF=∠DAE,
又∵AF=AE,AB=AD,∴△ABF≌△ADE,
∴BF=DE.
(2)四边形AFBE是正方形.理由如下:
∵点E为AC的中点,AB=BC,
∴BE⊥AC,BE=AE=12AC.
∵AF=AE,∴BE=AF=AE.
∵BE⊥AC,AF⊥AC,∴BE∥AF,
∴四边形AFBE是平行四边形,
又∵∠FAE=90°,AF=AE,
∴四边形AFBE是正方形.
?
4.如图,已知四边形ABCD是正方形,AB=22,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形.
(2)探究:CE+CG是否为定值?若是,求出这个定值;若不是,请说明理由.
?
答案
4.【解析】 (1)如图,过点E作EM⊥BC于点M,EN⊥CD于点N.
∵四边形ABCD是正方形,点E在对角线AC上,
∴CE平分∠BCD,
∵EM⊥BC,EN⊥CD,∴EM=EN,∠EMF=∠END=90°,
又∵∠MCN=90°,
∴四边形EMCN是正方形,∴∠MEN=90°,
∵∠NED+∠NEF=90°,∠MEF+∠NEF=90°,
∴∠MEF=∠NED,∴△MEF≌△NED,
∴EF=DE,∴矩形DEFG是正方形.
答案
(2)CE+CG是定值,定值为4.
∵四边形ABCD和四边形DEFG均为正方形,
∴AD=CD,DE=DG,∠ADC=∠EDG=90°,
∴∠ADE+∠EDC=90°,∠CDG+∠EDC=90°,
∴∠ADE=∠CDG,
∴△ADE≌△CDG,∴AE=CG,
∴CE+CG=CE+AE=AC=2AB=4.
?
易错疑难集训
集训
1.已知四边形ABCD为菱形,该菱形的周长为16,面积为8,则∠ABC的度数为 .?
答案
1.30°或150° 【解析】 如图1,当∠ABC为锐角时,过点A作AE⊥BC于点E,∵菱形ABCD的周长为16,∴AB=4,又∵菱形ABCD的面积为8,∴AE=2,∴∠ABE=30°,即∠ABC=30°.如图2,当∠ABC为钝角时,过点D作DF⊥AB于点F,∵菱形ABCD的周长为16,∴AD=4,又∵菱形ABCD的面积为8,∴DF=2,∴∠DAF=30°,∴∠ABC=150°.故∠ABC的度数为30°或150°.
易错点1 忽略情况造成漏解
本题的易错之处是只考虑∠ABC为锐角或只考虑∠ABC为钝角,从而出现答案不全面的错误.当题目中的条件不确定时,应分类讨论求解,分类的原则是不重不漏.
2.如图,在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP,PC,△BPC是以PB为腰的等腰三角形,则PB的长为 .?
答案
2.5或6 【解析】 如图1,当BC为底边时,PB=PC.由“SAS”可证△ABP≌△DCP,所以AP=PD=12AD=12BC=3.在Rt△ABP中,由勾股定理,得PB=????????2+????????2=42+32=5.如图2,当CP为底边时,则BP=BC=6.综上所述,PB的长为5或6.
?
易错点1 忽略情况造成漏解
3.如图,矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D'落在∠ABC的平分线上时,求DE的长.
答案
3.【解析】 如图,过点D'作MN⊥AB,交CD于点N,交AB于点M,连接BD'.
∵点D的对应点D'落在∠ABC的平分线上,∴D'M=BM.
设BM=D'M=x,则AM=7-x.由折叠知,AD=AD'=5.
在Rt△D'AM中,D'M2=AD'2-AM2,
∴25-(7-x)2=x2,
∴x=3或x=4,即D'M=3或D'M=4.
易错点1 忽略情况造成漏解
答案
设DE=m,则D'E=m,分两种情况讨论:
(1)当D'M=3时,BM=NC=3,D'N=2,EN=CD-DE-NC=7-m-3=4-m.
在Rt△D'NE中,m2=(4-m)2+22,
∴m=52,即DE=52.
(2)当D'M=4时,BM=NC=4,D'N=1,EN=CD-DE-NC=7-m-4=3-m.
在Rt△D'NE中,m2=(3-m)2+12,
∴m=53,即DE=53.
综上,DE的长为52或53.
?
易错点1 忽略情况造成漏解
4.两个完全相同的矩形纸片ABCD,BFDE如图放置.求证:四边形BNDM是菱形.
答案
4.【解析】 ∵四边形ABCD,BFDE是矩形,
∴BM∥DN,DM∥BN,
∴四边形BNDM是平行四边形.
∵AB=ED,∠A=∠E=90°,∠AMB=∠EMD,
∴△ABM≌△EDM,∴BM=DM,
∴四边形BNDM是菱形.
易错点2 对特殊平行四边形的判定定理理解不透彻
错解:∵四边形ABCD,BFDE是两个完全相同的矩形,∴AB=ED,∠A=∠E=90°,又∵∠AMB=∠EMD,∴△ABM≌△EDM,∴BM=DM,∵四边形BNDM有一组邻边相等,∴四边形BNDM是菱形.
分析:这是由于概念模糊,误以为有一组邻边相等的四边形是菱形,根据菱形的判定定理,有一组邻边相等的平行四边形是菱形,因此还需先说明四边形BNDM是平行四边形.
5.如图,在四边形ABCD中,AB∥CD,AD∥BC,对角线AC,BD交于点O,∠OBC=∠OCB.求证:四边形ABCD是矩形.
答案
5.【解析】 ∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴OC=OA=12AC,OB=OD=12BD.
又∵∠OBC=∠OCB,∴OB=OC,
∴AC=BD,∴四边形ABCD是矩形.
?
易错点2 对特殊平行四边形的判定定理理解不透彻
易错点2 对特殊平行四边形的判定定理理解不透彻
解此题容易出现论证不严密的错误,即没有先证明四边形ABCD是平行四边形.即使平行四边形的判定很容易,在证明过程中也不能省略.
根据“对角线相等的平行四边形是矩形”判定四边形是矩形
分两步证明:第一步先证明四边形是平行四边形,第二步证明该平行四边形的对角线相等.也就是说,运用此方法判定一个四边形是矩形时,必须满足两个条件:一是平行四边形;二是对角线相等.
6.如图,将矩形ABCD沿直线EF对折,点D恰好与BC边上的点H重合,若∠GFP=62°,则∠EHF的度数为 °.?
答案
6.56 【解析】 由折叠可知∠CFP=∠GFP=62°,∴∠HFG=180°-∠CFP-∠GFP=56°,∵HE∥FG,∴∠EHF= ∠HFG= 56°.
易错点3 矩形折叠问题中的常见错误
7.如图,将矩形纸片ABCD沿着对角线BD折叠,使点C落在点C'处,BC'交AD于点E,AD=8,AB=4,求DE的长.
答案
7.【解析】 ∵四边形ABCD是矩形,
∴AD∥BC,∠CBD=∠ADB,
由折叠知∠CBD=∠DBE,
∴∠DBE=∠EDB,∴DE=BE.
设DE的长为x,则BE=x,AE=8-x,
在Rt△ABE中,AB2+AE2=BE2,即42+(8-x)2=x2,
解得x=5,∴DE=5.
易错点3 矩形折叠问题中的常见错误
1.矩形ABCD中,∠ABC的平分线与直线CD相交于点E,DE=2,CD=4,则这个矩形的面积是 .?
答案
1.8或24 【解析】 ①如图1,当点E在CD上时,∵DE=2,CD=4,∴CE=CD-DE=2.∵BE平分∠ABC,∠ABC= ∠C=90°, ∴∠CBE=45°,△BCE是等腰直角三角形,∴BC=CE=2,S矩形ABCD=BC·CD=8;②如图2,CE=CD+DE=6,易知△BCE是等腰直角三角形,∴BC=CE=6,S矩形ABCD=BC·CD=24.综上,这个矩形的面积为8或24.
疑难点1 应用特殊平行四边形的性质与判定解决问题
2.动手操作:在一张长12 cm、宽5 cm的矩形纸片内,折出一个菱形.小颖同学按照取两组对边中点的方法折出菱形EFGH(见方案一),小明同学沿矩形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB的方法得到菱形AECF(见方案二).
(1)你能说出小颖、小明折出菱形的理由吗?
(2)请你通过计算,比较小颖和小明折出的菱形,哪个菱形面积较大?
疑难点1 应用特殊平行四边形的性质与判定解决问题
答案
2.【解析】 (1)小颖的理由:依次连接矩形ABCD各边的中点及对角线,由于矩形的对角线相等,利用中位线的性质,得四边形EFGH的四条边相等,根据四边相等的四边形是菱形,得四边形EFGH是菱形.
小明的理由:∵四边形ABCD是矩形,∴AD∥BC,则∠DAC=∠ACB,又∵∠CAE=∠CAD,∠ACF=∠ACB,∴∠CAE=∠CAD=∠ACF=∠ACB,∴AE=EC=CF=FA,∴四边形AECF是菱形.
(2)方案一:S菱形EFGH=S矩形ABCD-4S△AEH=12×5-4×12×6×52=30(cm2).
方案二:设BE=x cm,则CE=(12-x)cm,
∴AE=????2+25 cm,
由四边形AECF是菱形,得AE2=CE2,即x2+25=(12-x)2,
∴x=11924,
S菱形AECF=S矩形ABCD-2S△ABE=12×5-2×12×5×11924=84524(cm2).
比较可知,小明所折的菱形面积较大.
?
疑难点1 应用特殊平行四边形的性质与判定解决问题
3.如图,在四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点,顺次连接E,F,G,H,得到的四边形EFGH叫中点四边形.
(1)求证:四边形EFGH是平行四边形.
(2)请你探究并填空:
当四边形ABCD变成平行四边形时,它的中点四边形是 ;?
当四边形ABCD变成矩形时,它的中点四边形是 ;?
当四边形ABCD变成菱形时,它的中点四边形是 ;?
当四边形ABCD变成正方形时,它的中点四边形是 .?
(3)根据以上探究,请你总结中点四边形的形状是由原四边形的什么决定的.
疑难点2 中点四边形与特殊平行四边形
答案
3.【解析】 (1)连接BD,∵E,H分别是AB,AD的中点,
∴EH是△ABD的中位线,
∴EH=12BD,EH∥BD,
同理可得FG=12BD,FG∥BD,
∴EH=FG,EH∥FG,
∴四边形EFGH是平行四边形.
(2)平行四边形 菱形 矩形 正方形
(3)中点四边形的形状是由原四边形的对角线的关系决定的.
?
疑难点2 中点四边形与特殊平行四边形
中点四边形的形状是由原四边形的两条对角线的数量关系和位置关系决定的.首先,不管原四边形的形状怎样改变,中点四边形始终是平行四边形;其次,具体的中点四边形形状的确定还需参考原四边形具备的其他条件.
4.在平行四边形ABCD中,AC,BD交于点O,过点O作直线EF,GH,分别交平行四边形的四条边于E,G,F,H四点,连接EG,GF,FH,HE.
(1)如图1,试判断四边形EGFH的形状,并说明理由;
(2)如图2,当EF⊥GH时,四边形EGFH的形状是 ;?
(3)如图3,在(2)的条件下,若AC=BD,则四边形EGFH的形状是 ;?
(4)如图4,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
疑难点2 中点四边形与特殊平行四边形
答案
4.【解析】 (1)四边形EGFH是平行四边形.理由如下:
∵平行四边形ABCD的对角线AC,BD交于点O,
∴点O是平行四边形ABCD的对称中心,
∴EO=FO,GO=HO,
∴四边形EGFH是平行四边形.
(2)菱形
(3)菱形
(4)四边形EGFH是正方形.理由如下:
∵AC=BD,∴平行四边形ABCD是矩形,∴OA=OB=OC,
又∵AC⊥BD,∴∠BOC=90°,∠GBO=∠FCO=45°.
∵EF⊥GH,∴∠GOF=90°,∴∠BOG=∠COF,
∴△BOG≌△COF,∴OG=OF,∴GH=EF.
由(3)知四边形EGFH是菱形,
又∵GH=EF,
∴四边形EGFH是正方形.
疑难点2 中点四边形与特殊平行四边形
数学·九年级上册·北师
1 菱形的性质与判定
课时1 菱形的性质
课时1
1.如图,若要使?ABCD成为菱形,则需要添加的条件是 ( )
A.AB=CD
B.AD=AC
C.AB=BC
D.AC=BD
答案
1.C
知识点1 菱形的定义
2.[2019广西玉林中考]菱形不具备的性质是 ( )
A.是轴对称图形
B.是中心对称图形
C.对角线互相垂直
D.对角线一定相等
答案
2.D
知识点2 菱形的性质
3.[2020四川成都七中育才学校开学考试]如图,菱形ABCD的对角线AC,BD的长分别为6和8,则这个菱形的周长是 ( )
A.20
B.24
C.40
D.48
答案
3.A 【解析】 设AC与BD相交于点O.∵四边形ABCD是菱形,∴AB=BC=CD=DA,AC⊥BD,OA=12AC=3,OB=12BD=4.在Rt△AOB中,AB=????????2+????????2=32+42=5,∴菱形ABCD的周长为4AB=20.故选A.
?
知识点2 菱形的性质
4.[2019内蒙古赤峰中考]如图,菱形ABCD的周长为20,对角线AC,BD相交于点O,E是CD的中点,则OE的长是 ( )
A.2.5
B.3
C.4
D.5
答案
4.A 【解析】 ∵四边形ABCD为菱形,且周长为20,∴AB=BC=CD=AD=5,O为BD的中点,又∵E为CD的中点,∴OE为△BCD的中位线,∴OE=12BC=2.5.故选A.
?
知识点2 菱形的性质
5.如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点,给出下列结论:①S△ADE=S△EOD;②四边形BFDE是中心对称图形;③△DEF是轴对称图形;④∠ADE=∠EDO.其中错误的有( )
A.1个
B.2个
C.3个
D.4个
答案
5.A 【解析】 根据△ADE与△EOD等底同高可知S△ADE=S△EOD,故①正确;根据菱形ABCD的对角线互相平分及E,F分别是OA,OC的中点,可得四边形BFDE是平行四边形,而平行四边形是中心对称图形,故②正确;由条件可知DB垂直平分EF,所以△DEF是等腰三角形,因此△DEF是轴对称图形,故③正确;直角三角形ADO的直角边AO上的中线不是∠ADO的平分线,故④错误.故选A.
知识点2 菱形的性质
6.[2018广东广州中考]如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0),点D在y轴上,则点C的坐标是 .?
答案
6.(-5,4) 【解析】 ∵点A,B的坐标分别为(3,0),(-2,0),∴AB=5,OA=3.∵四边形ABCD是菱形,∴AD=AB=5.在Rt△OAD中,由勾股定理,得OD=????????2?????????2=52?32=4.∵点C在第二象限,且CD=AB=5,∴点C的坐标是(-5,4).
?
知识点2 菱形的性质
解答本题的关键是利用菱形的性质和勾股定理求出线段长,再根据象限定符号.
7.如图所示是根据四边形的不稳定性制作的边长均为15 cm的可活动菱形衣架.若墙上钉子间的距离AB=BC=15 cm,则∠1= °.?
答案
7.120 【解析】 如图,连接AB,BC.∵菱形的边长为15 cm,AB=BC=15 cm,∴AB和两个菱形的各一边(AM,BM)构成等边三角形,进而可得∠EAM=∠AMB=60°,∴∠1=120°.
知识点2 菱形的性质
8.[2019陕西宝鸡金台区一模]如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E,则线段BE的长是 .?
答案
8.1 【解析】 ∵四边形ABCD是菱形,∴AD=AB.∵∠A=60°,∴△ABD是等边三角形,∴BD=AB=4,∠OBE=60°. ∵OE⊥AB,∴∠BOE=30°.∵O为BD的中点,∴OB=12BD=2,∴BE=12OB=1.
?
知识点2 菱形的性质
本题考查了菱形的性质及等边三角形的判定与性质,证得△ABD是等边三角形是解题的关键.
9.[2019江苏无锡外国语学校开学考试]如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF= °.?
答案
9.60 【解析】 如图,连接BD,BF.∵∠BAD=80°,∴∠ADC=100°.∵EF垂直平分AB,AC垂直平分BD,∴AF=BF,BF=DF,∴AF=DF,∴∠FDA=∠FAD=12∠BAD=40°,∴∠CDF=100°-40°=60°.
?
知识点2 菱形的性质
菱形的性质在解题中的应用
①菱形的每一条对角线平分一组对角,可以用来证明角相等;②菱形的对角线互相垂直,可以用来证明线段垂直;③一个内角是60°的菱形,较短的对角线将其分成两个全等的等边三角形;④两条对角线将任意菱形分为四个全等的直角三角形.
10.[2020福建三明期中]如图,在菱形ABCD中,AB=2,∠ABC=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是??? .?
?
答案
10.3 【解析】 有关直线同侧的折线段相加值最小问题,常转化为直线两侧两点之间线段最短问题,即将点B借助菱形的对称性转移到点D,如图,连接DE交AC于点P,易知PB=PD,此时PE+PB的最小值为DE的长.因为四边形ABCD是菱形,E是AB的中点,所以AD=AB=2,AE=12AB=1.易知DE垂直平分AB,在Rt△ADE中,DE=????????2?????????2=3,即PE+PB的最小值为3.
?
知识点2 菱形的性质
11.[2019天津和平区期末]在菱形ABCD中,AC是对角线.
(1)如图1,若AB=6,则菱形ABCD的周长为 ,若∠DAB=70°,则∠D的度数是 ,∠DCA的度数是 .?
(2)如图2,P是AB上一点,连接DP交对角线AC于点E,连接EB,求证:∠APD=∠EBC.
知识点2 菱形的性质
答案
11.【解析】 (1)24 110° 35°
∵四边形ABCD是菱形,∴AB=BC=CD=AD=6,∴菱形ABCD的周长为4×6=24.∵四边形ABCD是菱形,∠DAB=70°,∴∠D=110°,∠DCA=12∠DCB=12∠DAB=35°.
(2)∵四边形ABCD是菱形,
∴DC=BC,∠DCE=∠BCE,
又∵CE=CE,∴△DCE≌△BCE,
∴∠CDP=∠EBC.
∵DC∥AB,∴∠CDP=∠APD,
∴∠APD=∠EBC.
?
知识点2 菱形的性质
1.[2020广东珠海北大附属实验学校段考]如图,在菱形ABCD中,AE,AF分别垂直平分BC,CD,垂足分别为E,F,则∠EAF的度数是 ( )
A.90°
B.60°
C.45°
D.30°
答案
1.B 【解析】 连接AC,根据垂直平分线的性质和菱形的邻边相等,可得△ABC,△ACD都是等边三角形,∴∠B=60°, ∴∠BCD=120°.在四边形AECF中,由四边形的内角和为360°,可得∠EAF=360°-90°-90°-120°=60°.故选B.
2.[2019重庆巴蜀中学开学考试]如图,在菱形ABCD中,∠BCD=50°,BC的垂直平分线交对角线AC于点F,垂足为E,连接BF,DF,则∠DFC的度数是 ( )
A.100°
B.110°
C.120°
D.130°
答案
2.D 【解析】 ∵四边形ABCD是菱形,∴∠ACD=∠ACB=12∠BCD=25°.∵EF垂直平分线段BC,∴FB=FC,∴∠FBC= ∠FCB=25°,∴∠CFB=180°-25°-25°=130°,根据菱形的对称性,可知∠CFD=∠CFB=130°.故选D.
?
3.[2019天津北辰区模拟]如图,在菱形ABCD中,∠ABC=60°,E为BC边的中点,M为对角线BD上的一个动点,则下列线段的长等于AM+12BM的最小值的是 ( )
A.AD B.AE
C.BD D.BE
?
答案
3.B 【解析】 如图,过点M作MF⊥BC于点F,∵四边形ABCD是菱形,∠ABC=60°,点E为BC的中点,∴∠DBC= 12∠ABC=30°,AE⊥BC,∴MF=12BM,∴AM+12BM=AM+MF,∴当A,M,F三点共线时,AM+MF取得最小值,∴AM+12BM的最小值为线段AE的长.故选B.
?
4.[2019广东广州华南师大附中段测]如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为 ( )
A.(1,-1)
B.(-1,-1)
C.(2,0)
D.(0,-2)
?
答案
4.B 【解析】 由菱形OABC的顶点O(0,0),B(2,2),得点D的坐标为(1,1).每秒旋转45°,则第60秒时,旋转了45°×60=
2 700°,2 700÷360=7.5(周), 即OD旋转了7周半,故第60秒时,菱形的对角线交点D的坐标为(-1,-1).故选B.
5.[2019江苏镇江外国语学校段测]如图,菱形纸片ABCD中,∠A=60°,P为AB的中点,折叠菱形纸片ABCD,使点C落在DP所在直线上的C'处,折痕为DE,则∠DEC= °.?
答案
5.75 【解析】 如图,连接BD,∵四边形ABCD是菱形,∠A=60°,∴AB=AD,∠ADC=120°,∠C=60°,△ABD是等边三角形.∵P为AB的中点,∴DP平分∠ADB,∴∠ADP=30°,∴∠PDC=∠ADC-∠ADP=90°,由折叠可知∠CDE=∠PDE, ∴∠CDE=45°,在△DEC中,∠DEC=180°-∠C-∠CDE=75°.
6.如图,在菱形ABCD中,AB=4 cm,∠ADC=120°,点E,F同时从A,C两点出发,分别沿AB,CB方向向点B匀速移动(到点B为止),点E的速度为1 cm/s,点F的速度为2 cm/s,经过t秒△DEF为等边三角形,则t的值为? .?
答案
6.43 【解析】 如图,连接BD.∵四边形ABCD是菱形,∴AB=AD,∠ADB=12∠ADC=60°,∴△ABD是等边三角形, ∴AD= BD,∵△DEF是等边三角形,∴DE=DF,∠EDF=60°,又∵∠ADB=60°,∴∠ADE=∠BDF.在△ADE和△BDF中,
????????=????????,????????????∠????????????=∠????????????,????????=????????,????????????∴△ADE≌△BDF(SAS),∴AE=BF.∵AE=t cm,CF=2t cm,∴BF=BC-CF=(4-2t)cm,∴t=4-2t,∴t=43.
?
7.[2018内蒙古呼和浩特中考]如图,已知A,F,C,D四点在同一条直线上,AF=CD,AB∥DE,且AB=DE.
(1)求证:△ABC≌△DEF.
(2)若EF=3,DE=4,∠DEF=90°,请直接写出使四边形EFBC为菱形时AF的长度.
答案
7.【解析】 (1)∵AB∥DE,∴∠A=∠D.
∵AF=CD,∴AF+CF=CD+CF,即AC=DF.
在△ABC和△DEF中,????????=????????,∠????=∠????,????????=????????,
∴△ABC≌△DEF.
?
答案
(2)四边形EFBC为菱形时,AF=75.
如图,连接BE,交CF于点O.
∵EF=3,DE=4,∠DEF=90°,
∴DF=????????2+????????2=32+42=5.
当四边形EFBC是菱形时,BE⊥CF,CF=2OF,∴∠EOF=90°.
∵12DF×OE=12DE×EF=????△????????????,∴5OE=3×4,∴OE=125.
在Rt△EFO中,OF=????????2?????????2=32?(125)2=95,
∴CF=2OF=185,∴CD=DF-CF=5-185=75,
∴AF=CD=75.
?
8.[2020山东泰安模拟]在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC的延长线上一点,且CF=AE,连接BE,EF.如图1,当点E是线段AC的中点时,易证BE=EF.
(1)如图2,当点E不是线段AC的中点,其他条件不变时,请你判断结论:BE=EF .(填“成立”或“不成立”)?
(2)如图3,当点E是线段AC的延长线上任意一点,其他条件不变时,结论BE=EF是否成立?若成立,请给予证明;若不成立,请说明理由.
答案
8.【解析】 (1)成立
过点E作EG∥BC交AB于点G,
∵四边形ABCD为菱形,∴AB=BC,
又∵∠ABC=60°,∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°.
∵EG∥BC,∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,∴△AGE是等边三角形,
∴AG=AE=GE,∴BG=EC.
∵CF=AE,∴GE=CF,
又∵∠BGE=∠ECF=120°,
∴△BGE≌△ECF,∴BE=EF.
答案
(2)结论BE=EF成立.证明如下:
过点E作EG∥BC交AB的延长线于点G,
∵四边形ABCD为菱形,∴AB=BC,
又∵∠ABC=60°,∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°.
∵EG∥BC,∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,∴△AGE是等边三角形,
∴AG=AE=GE,∴BG=EC.
∵CF=AE,∴GE=CF,
又∵∠BGE=∠ECF=60°,
∴△BGE≌△ECF,∴BE=EF.
课时2 菱形的判定
课时2
1.在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是 ( )
A.∠ABC=90° B.AC⊥BD
C.AB=CD D.∠A=∠C
答案
1.B 【解析】 在四边形ABCD中,对角线AC,BD互相平分,∴四边形ABCD是平行四边形,∴当AC⊥BD时,四边形ABCD是菱形.故选B.
知识点1 菱形的判定
2.如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连接EB,EC,DB,下列条件中,不能使四边形DBCE成为菱形的是 ( )
A.AB=BE
B.BE⊥DC
C.AD=BD
D.BE平分∠DBC
答案
2.A 【解析】 ∵四边形ABCD为平行四边形,∴AD∥BC,AD=BC,又∵DE=AD,∴DE∥BC,DE=BC,∴四边形DBCE为平行四边形.B项,BE⊥DC,根据“对角线互相垂直的平行四边形是菱形”,可知能使四边形DBCE成为菱形;C项,AD= BD, 则BD=DE,根据“有一组邻边相等的平行四边形是菱形”,可知能使四边形DBCE成为菱形;D项,BE平分∠DBC,则∠DBE=∠EBC=∠DEB,可得BD=DE,根据“有一组邻边相等的平行四边形是菱形”,可知能使四边形DBCE成为菱形.故选A.
知识点1 菱形的判定
3.[2020陕西西安莲湖区期中]如图,四边形ABCD是一张平行四边形纸片,要求利用所学知识作出一个菱形,甲、乙两位同学的作法如下,则关于甲、乙两人的作法,下列判断正确的为 ( )
A.仅甲正确
B.仅乙正确
C.甲、乙均正确
D.甲、乙均错误
知识点1 菱形的判定
答案
3.C 【解析】 甲的作法正确,理由如下:设EF交AC于点O,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAC=
∠ACB,∵EF是AC的垂直平分线,∴AO=CO,在△AOE和△COF中, ∠????????????=∠????????????,????????=????????,???????????∠????????????=∠????????????,∴△AOE≌△COF,∴AE=CF,
∵AE∥ CF, ∴四边形AECF是平行四边形,又∵EF⊥AC,∴四边形AECF是菱形.乙的作法正确,理由如下:如图, ∵AD∥BC, ∴∠1=∠2,∠5=∠6,∵BF平分∠ABC,AE平分∠BAD,∴∠2=∠3,∠4=∠5,∴∠1=∠3,∠4=∠6, ∴AB= AF,AB=BE, ∴AF=BE,∵AF∥BE,∴四边形ABEF是平行四边形,又∵AB=AF,∴四边形ABEF是菱形.故选C.
?
知识点1 菱形的判定
4.[2019甘肃兰州中考A卷]如图,AC=8,分别以点A,C为圆心,以长度5为半径作弧,两条弧分别相交于点B和D,依次连接A,B,C,D,连接BD交AC于点O.
(1)判断四边形ABCD的形状并说明理由;
(2)求BD的长.
答案
4.【解析】 (1)四边形ABCD是菱形.理由如下:
由题意可知,AB=BC=CD=DA=5,
∴四边形ABCD是菱形.
(2)∵四边形ABCD是菱形,AC=8,
∴OA=OC=12AC=4,OB=OD=12BD,AC⊥BD.
在Rt△AOD中,∠AOD=90°,OA=4,AD=5,
∴OD=52?42=3,∴BD=2OD=6.
?
知识点1 菱形的判定
5.易错题 如图,四边形ABCD的对角线AC,BD相交于点O,且AO=OC=8,BO=OD=6,AB=10,则四边形ABCD是菱形吗?请说明理由.
答案
5.【解析】 四边形ABCD是菱形.理由如下:
∵AO=OC=8,BO=OD=6,
∴四边形ABCD是平行四边形.
∵AO=8,BO=6,AB=10,
∴AO2+BO2=AB2,∴∠AOB=90°,
∴四边形ABCD是菱形.
知识点1 菱形的判定
本题借助勾股定理的逆定理判定直角(垂直),注意:运用一组邻边相等或对角线互相垂直证明四边形是菱形的前提条件是该四边形为平行四边形.
6.[2019江西南昌期中]如图,在?ABCD中,AB=2,AD=1,∠ADC=60°,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D'处,折痕交CD边于点E.求证:四边形BCED'是菱形.
答案
6.【解析】 ∵四边形ABCD是平行四边形,
∴BC=AD,DC=AB,DC∥AB,∴∠DEA=∠D'AE.
由折叠可知∠DAE=∠D'AE,AD'=AD=1,ED'=ED,
∴∠DAE=∠DEA,∴AD=ED=AD'=ED'=1,
又∵DC=AB=2,
∴BD'=AB-AD'=2-1=1,EC=DC-ED=2-1=1,
又∵BC=AD=1,
∴EC=BC=BD'=ED',∴四边形BCED'是菱形.
知识点1 菱形的判定
7.[2020河南省实验中学模拟]如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点,当四边形EFGH满足条件
时,四边形EFGH是菱形.(只需写出一个即可,图中不能再添加别的“点”或“线”)?
答案
7.HG=GF(答案不唯一) 【解析】 连接AC,BD,在四边形ABCD中,∵点E,F,G,H分别为四边形ABCD的边AB,BC,CD, DA的中点,∴HG∥AC∥EF,GF∥BD∥HE,∴四边形EFGH是平行四边形.要判定平行四边形EFGH是菱形,只要HG= GF (或FE=EH等)即可,答案不唯一.
知识点2 与菱形的判定有关的开放探究
8.[2019山东青岛市北区期中]如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:①BE=EC;②BF∥EC;③AB=AC.其中能证明四边形BECF是菱形的是 .(只填写序号)?
答案
8.①③ 【解析】 由点D是BC的中点及DE=DF可得,四边形BECF是平行四边形.①当BE=EC时,由有一组邻边相等的平行四边形是菱形,可知①能证明四边形BECF是菱形;③由AB=AC,点D为BC的中点可得,AD⊥BC,由对角线互相垂直的平行四边形是菱形,可知③能证明四边形BECF是菱形.故填①③.
知识点2 与菱形的判定有关的开放探究
1.如图,将△ABC沿BC方向平移得到△DCE,连接AD.下列条件中,能够判定四边形ACED为菱形的是 ( )
A.AB=BC
B.AC=BC
C.∠ABC=60°
D.∠ACB=60°
答案
1.B 【解析】 由平移的性质,得AC=DE,AD=BC=CE,当AC=BC时,有AC=AD=DE=CE,∴四边形ACED是菱形.故选B.
2.如图,已知四边形ABCD的四条边都相等,等边三角形AEF的顶点E,F分别在BC,CD上,且AE=AB,则∠C=( )
A.100°
B.105°
C.110°
D.120°
答案
2.A 【解析】 ∵四边形ABCD的四条边都相等,∴四边形ABCD是菱形,∴∠B=∠D,∠BAD=∠C,AB∥CD, ∴∠BAD+ ∠D=180°.∵△AEF是等边三角形,AE=AB,∴∠AEF=∠AFE=60°,∠B=∠AEB,AF=AD, ∴∠D= ∠AFD, ∴∠BAE=∠FAD.设∠BAE=∠FAD=x,则∠D=∠AFD=180°-60°-2x,∵∠FAD+∠D+∠AFD=180°,∴x+2(180°-60°-2x)=180°,解得x=20°,∴∠C=∠BAD=2×20°+60°=100°.故选A.
3.如图,在△ABC中,AD,CD分别平分∠BAC和∠ACB,AE∥CD,CE∥AD.若从三个条件:①AB=AC;②AB=BC;③AC=BC中,选择一个作为已知条件,则能使四边形ADCE为菱形的是 .(填序号)?
答案
3.② 【解析】 当AB=BC时,∵AE∥CD,CE∥AD,∴四边形ADCE是平行四边形.∵AB=BC,∴∠BAC=∠ACB.∵AD, CD分别平分∠BAC和∠ACB,∴∠DAC=∠DCA,∴DA=DC,∴四边形ADCE是菱形.
4.已知四边形的四条边长分别为a,b,c,d,且满足条件a2+b2+c2+d2=ab+bc+cd+da,则此四边形一定是 .?
答案
4.菱形 【解析】 ∵a2+b2+c2+d2=ab+bc+cd+da,∴2(a2+b2+c2+d2)-2ab-2bc-2cd-2da=0,∴(a-b)2+(b-c)2+(c-d)2+(d-a)2=0,由平方的非负性,可知a-b=0,b-c=0,c-d=0,d-a=0,∴a=b=c=d,∴此四边形一定是菱形.
5.[2019湖南长沙明德教育集团期中]如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD.
(1)求∠AOD的度数.
(2)求证:四边形ABCD是菱形.
答案
5.【解析】 (1)∵AC,BD分别是∠BAE,∠ABF的平分线,
∴∠DAC=∠BAC,∠ABD=∠DBC.
∵AE∥BF,∴∠DAB+∠CBA=180°,
∴∠BAC+∠ABD=12(∠DAB+∠CBA)=12×180°=90°,
∴∠AOD=90°.
(2)∵AE∥BF,∴∠ADB=∠DBC,∠DAC=∠BCA,
由(1)知∠DAC=∠BAC,∠ABD=∠DBC,
∴∠BAC=∠BCA,∠ABD=∠ADB,
∴AB=BC,AB=AD,∴AD=BC,
又∵AD∥BC,∴四边形ABCD是平行四边形,
又∵AD=AB,∴四边形ABCD是菱形.
?
6.[2018贵州毕节中考]如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ∥DB,且CQ=DP,连接AP,BQ,PQ.
(1)求证:△APD≌△BQC.
(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.
答案
6.【解析】 (1)如图,∵CQ∥BD,∴∠2=∠3.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠1=∠2,∴∠1=∠3.
在△APD和△BQC中,????????=????????,∠1=∠3,????????=????????,
∴△APD≌△BQC.
(2)∵△APD≌△BQC,∴AP=BQ,∠APD=∠BQC,
又∵∠ABP+∠BQC=180°,∴∠ABP+∠APD=180°.
∵∠APB+∠APD=180°,∴∠ABP=∠APB,∴AB=AP.
∵CQ∥DB,CQ=DP,∴四边形CDPQ是平行四边形,∴CD=PQ.
在平行四边形ABCD中,AB=CD,∴AB=AP=PQ=BQ,
∴四边形ABQP为菱形.
?
7.[2020河南郑州外国语中学月考]如图1,△ABC为等腰三角形,AB=AC=a,P点是底边BC上的一个动点,PD∥AC, PE∥AB.
(1)用a表示四边形ADPE的周长为 .?
(2)点P运动到什么位置时,四边形ADPE是菱形?请说明理由.
(3)如果△ABC不是等腰三角形,如图2,其他条件不变,点P运动到什么位置时,四边形ADPE是菱形?(不必说明理由)
答案
7.【解析】 (1)2a
∵PD∥AC,PE∥AB,∴四边形ADPE为平行四边形,∴AD=PE,DP=AE.∵AB=AC,∴∠B=∠C,又∵DP∥AC,∴∠DPB=∠C,∴∠B=∠DPB,∴BD=DP,∴四边形ADPE的周长为2(AD+DP)=2(AD+BD)=2AB=2a.
(2)当点P运动到BC的中点时,四边形ADPE是菱形.理由如下:
如图1,连接AP.
∵PD∥AC,PE∥AB,
∴四边形ADPE为平行四边形.
∵AB=AC,P为BC的中点,
∴∠PAD=∠PAE.
∵PE∥AB,∴∠PAD=∠APE,
∴∠PAE=∠APE,∴EA=EP,
∴四边形ADPE是菱形.
答案
(3)点P运动到∠BAC的平分线上时,四边形ADPE是菱形.
如图2,∵PD∥AC,PE∥AB,
∴四边形ADPE是平行四边形.
∵AP平分∠BAC,∴∠1=∠2,
∵AB∥EP,∴∠1=∠3,
∴∠2=∠3,∴AE=EP,
∴四边形ADPE是菱形.
课时3 菱形的性质与判定的综合应用
课时3
1.[2020湖南长沙长郡梅溪湖中学开学考试]如图,四边形ABCD是菱形,DH⊥AB于点H,若AC=8 cm,BD=6 cm,则DH的长是 ( )
A.5 3 cm B.2 5 cm
C.245 cm D.485 cm
?
答案
1.C 【解析】 ∵四边形ABCD是菱形,AC=8 cm,BD=6 cm,∴∠AOB=90°,AO=4 cm,BO=3 cm,∴AB=42+32=5(cm).由菱形的面积可知,12AC·BD=AB·DH,∴5DH=24,∴DH=245 cm.故选C.
?
知识点1 菱形的面积
2.[2019四川泸州中考]一个菱形的边长为6,面积为28,则该菱形的两条对角线的长度之和为 ( )
A.8 B.12 C.16 D.32
答案
2.C 【解析】 如图,在菱形ABCD中,OA=OC=12AC,OB=OD=12BD,AC⊥BD.根据题意,得12AC·BD=28,∴12×2OA× 2OB=28,∴OA·OB=14,∴(OA+OB)2=OA2+OB2+2OA·OB=AB2+2OA·OB=62+2×14=64,∴OA+OB=8(-8舍去),∴AC+ BD=16.故选C.
?
知识点1 菱形的面积
3.如图,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四边形ABCD,若AD=6 cm,∠ABC=60°,则四边形ABCD的面积为 cm2.?
答案
3.183 【解析】 如图,∵AD∥BC,AB∥CD,∴四边形ABCD是平行四边形.过点A作AE⊥BC于点E,AF⊥CD于点F,∵∠ABC=60°,∴∠ADF=60°.∵纸条等宽,∴AE=AF.由∠AEB=∠AFD=90°,∠ABE=∠ADF,AE=AF,得△ABE≌△ADF, ∴AB=AD,∴四边形ABCD是菱形.∵AD=6 cm,∴BE=3 cm,∴AE=33 cm,∴四边形ABCD的面积为6×33=183(cm2).
?
知识点2 菱形的性质与判定的综合应用
4.[2018广西北部湾经济区中考]如图,在?ABCD中,AE⊥BC,AF⊥CD,垂足分别为点E,F,且BE=DF.
(1)求证:?ABCD是菱形.
(2)若AB=5,AC=6,求?ABCD的面积.
答案
4.【解析】 (1)∵四边形ABCD是平行四边形,
∴∠B=∠D.
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
又∵BE=DF,∴△AEB≌△AFD,
∴AB=AD,∴?ABCD是菱形.
知识点2 菱形的性质与判定的综合应用
答案
(2)连接BD,交AC于点O.
由(1)知四边形ABCD是菱形,
∴AC⊥BD,AO=OC=12AC=12×6=3.
∵AB=5,AO=3,
∴BO=????????2?????????2=52?32=4,
∴BD=2BO=8,
∴S?ABCD=12AC·BD=12×6×8=24.
?
知识点2 菱形的性质与判定的综合应用
1.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,连接BE交AC于点F,连接DF.
(1)求证:∠BAC=∠DAC,∠AFD=∠CFE.
(2)若AB∥CD,试证明四边形ABCD是菱形.
(3)在(2)的条件下,试确定点E的位置,使∠EFD=∠BCD,并说明理由.
答案
1.【解析】 (1)在△ABC和△ADC中,????????=????????,????????=????????,????????=????????,
∴△ABC≌△ADC,∴∠BAC=∠DAC.
在△ABF和△ADF中,????????=????????,????????????∠????????????=∠????????????,????????=????????,???????????
∴△ABF≌△ADF,∴∠AFB=∠AFD.
∵∠AFB=∠CFE,∴∠AFD=∠CFE.
(2)∵AB∥CD,∴∠BAC=∠ACD,
又∵∠BAC=∠DAC,
∴∠CAD=∠ACD,∴AD=CD,
又∵AB=AD,CB=CD,
∴AB=CB=CD=AD,
∴四边形ABCD是菱形.
?
答案
(3)当EB⊥CD时,∠EFD=∠BCD.理由如下:
∵四边形ABCD为菱形,∴∠BCF=∠DCF,
在△BCF和△DCF中,????????=????????,∠????????????=∠????????????,????????=????????,
∴△BCF≌△DCF,∴∠CBF=∠CDF.
∵BE⊥CD,∴∠BEC=∠DEF=90°,
∴∠EFD=90°-∠EDF=90°-∠CBF=∠BCD.
?
2.如图,在等腰三角形ABC中,AB=AC,AD平分∠BAC,交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC,BC于点E,F,作PM∥AC,交AB于点M,连接ME.
(1)求证:四边形AEPM为菱形.
(2)当点P在何处时,菱形AEPM的面积为四边形EFBM面积的一半?请说明理由.
答案
2.【解析】 (1)∵EF∥AB,PM∥AC,
∴四边形AEPM为平行四边形.
∵AD平分∠BAC,∴∠CAD=∠BAD.
∵EP∥AB,∴∠BAD=∠EPA,
∴∠CAD=∠EPA,∴EA=EP,
∴四边形AEPM为菱形.
答案
(2)当点P为EF的中点时,S菱形AEPM=12S四边形EFBM.理由如下:
∵四边形AEPM为菱形,∴AP⊥EM.
∵AB=AC,∠CAD=∠BAD,
∴AD⊥BC,∴EM∥BC,
又∵EF∥AB,
∴四边形EFBM为平行四边形.
如图,过点E作EN⊥AB于点N.
∵EP=12EF,
∴S菱形AEPM=EP·EN=12EF·EN=12S四边形EFBM.
?
2 矩形的性质与判定
课时1 矩形的性质
课时1
1.[2020四川成都石室联合中学开学考试]如图,四边形ABCD的对角线互相平分,要使它成为矩形,需要添加的条件是 ( )
A.AB∥CD
B.AD=BC
C.∠AOB=45°
D.∠ABC=90°
答案
1.D 【解析】 因为四边形ABCD的对角线互相平分,所以四边形ABCD为平行四边形.根据矩形的定义知添加D项后四边形ABCD是矩形.故选D.
知识点1 矩形的定义
2.[2019河南省实验中学月考]矩形具有而一般平行四边形不具有的性质是( )
A.对边平行且相等 B.对角线相等
C.对角线互相平分 D.对角相等
3.[2018湖南株洲中考]如图,矩形ABCD的对角线AC与BD相交于点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长度为 .?
答案
2.B
3.2.5 【解析】 ∵四边形ABCD是矩形,∴AC=BD=10,BO=DO=12BD,∴DO=12BD=5.∵点P,Q分别是AO,AD的中点, ∴PQ是△AOD的中位线,∴PQ=12DO=2.5.
?
知识点2 矩形的性质
4.如图,将矩形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C'处,点B落在点B'处,其中AB=9,BC=6,则FC'的长为 .?
答案
4.5 【解析】 由题意可知,C'D=12AD=12BC=3.设CF=x,则FC'=x,DF=9-x.在Rt△C'DF中,DF2+C'D2=FC'2,即(9-x)2+32= x2, 解得x=5,所以FC'=5.
?
知识点2 矩形的性质
5.如图,在矩形ABCD中,已知对角线AC与BD相交于点O,△OBC的周长为16,且BC=7,求矩形对角线的长.
答案
5.【解析】 ∵四边形ABCD为矩形,
∴AC=BD=2BO=2CO.
∵BO+CO+BC=16,BC=7,
∴BO+CO=9,∴AC=BD=9,
即矩形对角线的长为9.
知识点2 矩形的性质
6.如图,在矩形ABCD中,E,F是BC边上的两点,且BE=CF.求证:AF=DE.
答案
6.【解析】 ∵四边形ABCD是矩形,
∴AB=CD,∠B=∠C=90°.
∵BE=CF,∴BF=CE.
在△ABF和△DCE中,????????=????????,∠????=∠????,????????=????????,
∴△ABF≌△DCE,∴AF=DE.
?
知识点2 矩形的性质
要证明线段相等,可以借助三角形全等.要判定两个三角形全等,可先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法进行判定.
7.[2018甘肃天水中考]如图,点O是矩形ABCD对角线AC的中点,OE∥AB交AD于点E.若OE=3,BC=8,则OB的长为 ( )
A.4 B.5
C.342 D.34
?
答案
7.B 【解析】 ∵四边形ABCD是矩形,∴∠ABC=90°,AB∥CD,AB=CD.∵OE∥AB,∴OE∥CD,又∵点O是AC的中点,∴OE是△ACD的中位线,∴CD=2OE=6,∴AB=6.在Rt△ABC中,AB=6,BC=8,∴AC=10.∵OB是Rt△ABC斜边上的中线, ∴OB=12AC=5.故选B.
?
知识点3 直角三角形斜边上的中线的性质
8.[2019广西来宾期中]如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,若∠A=26°,则∠BDC的度数是 ( )
A.26° B.38°
C.42° D.52°
答案
8.D 【解析】 ∵∠ACB=90°,CD是斜边AB上的中线,∴BD=CD=AD,∴∠DCA=∠A=26°, ∴∠BDC=∠A+ ∠DCA= 26°+26°=52°.故选D.
知识点3 直角三角形斜边上的中线的性质
9.[2019江苏扬州江都区月考]如图,在四边形ABCD中,∠BAD=90°,∠DCB=90°,E,F分别是BD,AC的中点.
(1)请你猜测EF与AC的位置关系,并给予证明;
(2)当AC=8,BD=10时,求EF的长.
知识点3 直角三角形斜边上的中线的性质
答案
9.【解析】 (1)EF⊥AC.证明如下:
如图,连接AE,CE.
∵∠BAD=90°,∠DCB=90°,E为BD的中点,
∴AE=12BD,CE=12BD,∴AE=CE.
∵F是AC的中点,∴EF⊥AC.
(2)由(1)知AE=CE=12BD,
∵BD=10,∴AE=CE=5.
∵F是AC的中点,AC=8,
∴CF=12AC=4.
由(1)知EF⊥AC,
∴EF=????????2?????????2=52?42=3.
?
知识点3 直角三角形斜边上的中线的性质
1.[2020江苏宿迁湖滨新区模拟]如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上的点G处,并使折痕经过点A,展平纸片后,∠DAG的度数为 ( )
A.30° B.45°
C.60° D.75°
答案
1.C 【解析】 如图,设AM与EF交于点N,由题意得∠1=∠2,AN=MN, ∠MGA=90°,∴NG=12AM,∴AN=NG,∴∠2=∠4.∵EF∥AB,∴∠4=∠3, ∴∠1=∠2=∠3=13×90°=30°,∴∠DAG=60°.故选C.
?
2.如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为 ( )
A.8 B.9
C.10 D.241
?
答案
2.B 【解析】 如图,取BC的中点为O,连接OE,OF.∵四边形ABCD是矩形, ∴AB=CD=6,AD=BC=8,∠BCD=90°,∵点F是CD的中点,点O是BC的中点, ∴CF=3,CO=4,∴OF=5.∵点O是Rt△BCE的斜边BC的中点,∴OE=OC=4.根据三角形三边关系可得OE+OF≥EF,∴当点O、点E、点F共线时,EF取得最大值,最大值为OE+OF=4+5=9.故选B.
3.[2020河南郑州金水区模拟]如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(8,6),以A为圆心,任意长为半径画弧,分别交AC,AO于点M,N,再分别以M,N为圆心,大于12MN长为半径画弧,两弧交于点Q,作射线AQ交y轴于点D,则点D的坐标为 ( )
A.(0,1) B.(0,83)
C.(0,53) D.(0,2)
?
答案
3.B 【解析】 如图,过点D作DE⊥AC于点E.∵四边形OABC为矩形,点B的坐标为(8,6),∴OA=8,OC=6,∴AC=10.由题意可得AD平分∠OAC,∴∠DAE=∠DAO, ∵AD=AD,∠AOD=∠AED=90°,∴△ADO≌△ADE,∴AE=AO=8,OD=DE,∴CE=2. ∵CD2=DE2+CE2,∴(6-OD)2=4+OD2,∴OD=83,∴点D(0,83).故选B.
?
4.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE的度数为 .?
答案
4.22.5° 【解析】 ∵四边形ABCD是矩形,∴∠BAD=90°,AC=BD,OA=OC=OB=OD,∴∠OAD=∠ODA. ∵∠EAC= 2∠CAD,∴∠EAD=3∠ODA.在Rt△ADE中,∠EAD+∠ODA=90°,∴∠ODA=22.5°,∴∠BAE=90°-∠EAD=90°-3∠ODA= 22.5°.
5.[2019四川南充期末]如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ADB=30°,E为BC边上一点,∠AEB=45°, CF⊥ BD 于点F.给出下列结论:①BE=CD;②BF=3DF;③AE=2AO;④CE=CF.其中正确的是 .(填序号)?
?
答案
5.①②③ 【解析】 ∵四边形ABCD是矩形,∴AB=CD,AO=CO=BO=DO,∠ABC=∠BAD=90°.∵∠AEB=45°, ∴∠BAE= ∠AEB=45°,∴AB=BE,∴BE=CD,故①正确.∵∠ADB=30°,∴∠ABO=60°,又∵AO=BO,∴△ABO是等边三角形,∴AB=AO.在Rt△ABE中,AE=2AB,∴AE=2AO,故③正确.∵△OCD是等边三角形,CF⊥BD,∴DF=FO= 12OD= 14BD, ∴BF=3DF,故②正确.∵△OCD是等边三角形,∴CF=32CD.∵∠ACB=30°,∴AC=2AB,∴BC=3AB,又∵BE=AB,∴CE= (3-1)AB,∵AB=CD,∴CE≠CF,故④错误.综上,正确的结论是①②③.
?
6.[2020重庆涪陵十九中月考]如图,在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.
(1)求证:DF=AB.
(2)若∠FDC=30°,且AB=4,求AD的长.
答案
6.【解析】 (1)∵四边形ABCD为矩形,
∴∠B=90°,AD∥BC,∴∠DAE=∠AEB.
∵DF⊥AE,∴∠DFA=90°,∴∠DFA=∠B.
在△ADF和△EAB中,∠????????????=∠????????????,∠????????????=∠????????????,????????=????????,????????????
∴△ADF≌△EAB,∴DF=AB.
(2)∵∠AFD=90°,∠ADC=90°,
∴∠DAF+∠ADF=90°,∠ADF+∠FDC=90°,
∴∠DAF=∠FDC=30°,∴AD=2DF,
又∵DF=AB,∴AD=2AB=8.
?
7.易错题[2019黑龙江大庆中考]如图,在矩形ABCD中,AB=3,BC=4,M,N在对角线AC上,且AM=CN,E,F分别是AD,BC的中点.
(1)求证:△ABM≌△CDN.
(2)点G是对角线AC上的点,∠EGF=90°,求AG的长.
答案
7.【解析】 (1)∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,∴∠MAB=∠NCD.
在△ABM和△CDN中,????????=????????,∠????????????=∠????????????,????????=????????,
∴△ABM≌△CDN.
(2)连接EF,交AC于点O.
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,∴∠EAO=∠FCO,
?
答案
∵E,F分别是AD,BC的中点,∴AE=CF.
在△AEO和△CFO中,∠????????????=∠????????????,∠????????????=∠????????????,????????=????????,
∴△AEO≌△CFO,∴EO=FO,AO=CO,
∴O为EF,AC的中点.
∵∠EGF=90°,∴OG=12EF=12AB=32,
∵AB=3,BC=4,∠ABC=90°,
∴AC=5,∴AO=52.
当点G在OA上时,AG=OA-OG=1;
当点G在OC上时,AG=OA+OG=4.
∴AG的长为1或4.
?
8.[2019山东东营胜利一中期中]如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B'的位置,AB'与CD交于点E.
(1)试找出一个与△AED全等的三角形,并加以证明;
(2)若AB=8,DE=3,P为线段AC上的任意一点,PG⊥AB'于点G,PH⊥DC于点H,试求PG+PH的值.
答案
8.【解析】 (1)△AED≌△CEB'.证明如下:
∵四边形ABCD为矩形,
∴AD=BC=B'C,∠D=∠B=∠B'=90°,
又∵∠DEA=∠B'EC,∴△AED≌△CEB'.
(2)由已知得∠EAC=∠CAB,且∠CAB=∠ECA,
∴∠EAC=∠ECA,∴AE=EC=8-3=5.
在Rt△ADE中,AD=????????2?????????2=4.
延长HP交AB于点M,则PM⊥AB,
∵∠CAB'=∠CAB,PG⊥AB',PM⊥AB,∴PG=PM,
∴PG+PH=PM+PH=HM=AD=4.
?
课时2 矩形的判定
课时2
1.[2019吉林长春南关区月考]如图,给出下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④∠ADC=∠BAD.从中选取一个作为补充条件,使?ABCD为矩形,其中错误的是 ( )
A.① B.②
C.③ D.④
答案
1.A 【解析】 当AB=BC时,根据“有一组邻边相等的平行四边形是菱形”,可以判定?ABCD为菱形,但不能判定?ABCD为矩形;当∠ABC=90°时,根据“有一个角是直角的平行四边形是矩形”,可以判定?ABCD为矩形;当AC=BD时,根据“对角线相等的平行四边形是矩形”,可以判定?ABCD为矩形;当∠ADC=∠BAD时,可得∠ADC=∠BAD=90°,根据“有一个角是直角的平行四边形是矩形”,可以判定?ABCD为矩形.故选A.
知识点1 矩形的判定
2.[2020福建三明期中]在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的几位同学拟订的方案,其中正确的是 ( )
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量一组对角是否都为直角
D.测量其中三个内角是否都为直角
答案
2.D 【解析】 A项,对角线互相平分的四边形是平行四边形;B项,两组对边分别相等的四边形是平行四边形;C项,无法判断一组对角为直角的四边形的形状.故选D.
知识点1 矩形的判定
3.[2019湖北荆门沙洋期中节选]如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE,BF.当∠ACB=
°时,四边形ABFE为矩形.?
答案
3.60 【解析】 当∠ACB=60°时,∵AB=AC,∴△ABC是等边三角形,∴AC=BC,又∵BC=CE,AC=CF,∴AF=BE.易知四边形ABFE是平行四边形,∴四边形ABFE是矩形.
知识点1 矩形的判定
4.如图,已知直线AB∥CD,EF分别交AB,CD于点M,N,射线MP,MQ,NP,NQ分别是∠AMN,∠BMN,∠MNC,∠MND的平分线,MP,NP相交于点P,MQ,NQ相交于点Q.求证:四边形MPNQ是矩形.
答案
4.【解析】 ∵MP平分∠AMN,∴∠PMN=12∠AMN,
同理∠MNQ=12∠MND,∠NMQ=12∠BMN,∠PNM=12∠MNC.
∵AB∥CD,∴∠AMN=∠MND,
∴∠PMN=∠MNQ,∴PM∥NQ,
同理NP∥MQ,∴四边形MPNQ是平行四边形,
又∵∠PMN+∠NMQ=12(∠AMN+∠BMN)=90°,
∴四边形MPNQ是矩形.
?
知识点1 矩形的判定
5.[2019山东青岛期中]如图,四边形ABCD的对角线AC,BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF.
(2)若OD=12AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
?
答案
5.【解析】 (1)∵O是AC的中点,∴AO=CO,
又∵AE=CF,∴OE=OF.
∵DF∥BE,∴∠OEB=∠OFD,
又∵∠EOB=∠FOD,∴△BOE≌△DOF.
(2)四边形ABCD是矩形.证明如下:
由(1)知△BOE≌△DOF,∴OB=OD,
又∵AO=CO,∴四边形ABCD是平行四边形,∴OD=12BD,
又∵OD=12AC,∴AC=BD,
∴四边形ABCD是矩形.
?
知识点1 矩形的判定
6.如图,连接四边形ABCD各边中点得到四边形EFGH,还要添加 才能使四边形EFGH是矩形.(只需写出一个条件即可,图中不能再添加别的点或线)?
答案
6.AC⊥BD(答案不唯一) 【解析】 由E,F,G,H分别是AD,AB,BC,CD的中点,可得EF∥GH∥BD,FG∥EH∥AC,所以四边形EFGH是平行四边形,要使四边形EFGH是矩形,则EF⊥FG,从而得到AC⊥BD.
知识点2 与矩形的判定有关的开放探究
7.[2019江苏连云港中考]如图,在△ABC中,AB=AC.将△ABC沿着BC方向平移得到△DEF,其中点E在边BC上,DE与AC相交于点O.
(1)求证:△OEC为等腰三角形.
(2)连接AE,DC,AD,当点E在什么位置时,四边形AECD为矩形,并说明理由.
答案
7.【解析】 (1)∵AB=AC,∴∠B=∠ACB.
∵△ABC平移得到△DEF,
∴∠B=∠DEC,
∴∠ACB=∠DEC,∴OE=OC,
∴△OEC为等腰三角形.
知识点2 与矩形的判定有关的开放探究
答案
(2)当E为BC的中点时,四边形AECD是矩形.理由如下:
∵AB=AC,E为BC的中点,
∴AE⊥BC,BE=EC.
∵△ABC平移得到△DEF,
∴BE∥AD,BE=AD,
∴AD∥EC,AD=EC,
∴四边形AECD是平行四边形,
又∵AE⊥BC,
∴四边形AECD是矩形.
知识点2 与矩形的判定有关的开放探究
8.一张矩形纸片经过折叠得到一个三角形(如图所示),则该矩形纸片的长与宽的比为 .?
答案
8.2∶3 【解析】 根据折叠的性质,得BC'=BC,∠ABC'=∠C'BE=∠EBC.∵四边形ABCD是矩形,∴∠ABC=∠A= 90°,∴∠ABC'=13∠ABC=30°,∴在Rt△ABC'中,AC'∶AB∶BC'=1∶3∶2,∴BC∶AB=2∶3,∴该矩形纸片的长与宽的比为2∶3.
?
知识点3 矩形的折叠
9.[2019山东济南育华中学月考]如图,将矩形ABCD沿AE折叠,使点D落在BC边的点F处,已知AB=DC=8,AD=BC=10.求EC的长.
答案
9.【解析】 设EC的长为x,则DE=8-x.
∵△ADE折叠后的图形是△AFE,
∴AD=AF,DE=EF.
∵AD=BC=10,∴AF=10.
∵四边形ABCD是矩形,∴∠B=∠C=90°.
在Rt△ABF中,BF=????????2?????????2=6,
∴FC=BC-BF=10-6=4.
在Rt△EFC中,FC2+EC2=EF2,
∴42+x2=(8-x)2,解得x=3,
∴EC的长为3.
?
知识点3 矩形的折叠
1.[2019山东临沂中考]如图,在?ABCD中,M,N是BD上两点,BM=DN,连接AM,MC,CN,NA.添加一个条件,使四边形AMCN是矩形,这个条件是 ( )
A.OM=12AC
B.MB=MO
C.BD⊥AC
D.∠AMB=∠CND
?
答案
1.A 【解析】 ∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.∵BM=DN,∴OB-BM=OD-DN,即OM=ON,∴四边形AMCN是平行四边形.当OM=12AC时,MN=AC,∴四边形AMCN是矩形.故选A.
?
2.如图,在四边形ABCD中,∠A=60°,∠ABC=∠ADC=90°,BC=2,CD=11,过点D作DH⊥AB于点H,则DH的长是 ( )
A.7.5 B.7
C.6.5 D.5.5
答案
2.A 【解析】 如图,过点C作CE⊥DH于点E.∵DH⊥AB,∠ABC=90°,CE⊥DH,∴四边形BCEH是矩形,∴HE=BC=2.在Rt△AHD中,∠A=60°,∴∠ADH=30°,又∵∠ADC= 90°, ∴∠CDE=60°,∴∠DCE=30°,∴在Rt△CED中,DE=12CD=5.5,∴DH=HE+ DE= 2+ 5.5=7.5.故选A.
?
3.[2019江西南昌期中]如图,在四边形ABCD中,对角线AC⊥BD,E,F,G,H分别是AB,BC,CD,DA的中点,若AC=8,BD=6,则四边形EFGH的面积是 .?
答案
3.12 【解析】 ∵E,F,G,H分别是AB,BC,CD,DA的中点,∴HG∥AC且HG=12AC,EH∥BD且EH=12BD,FG∥BD且FG=12BD,∴EH∥FG且EH=FG,∴四边形EFGH是平行四边形,又∵AC⊥BD,∴EH⊥HG,∴平行四边形EFGH是矩形,∴四边形EFGH的面积为HG·EH=12AC·12BD=12×8×12×6=12.
?
4.如图,沿DE折叠矩形ABCD,使点C落在AB边上的点F处,若AD=8,且△AFD的面积为60,则△DEC的面积为? .?
答案
4.2898 【解析】 ∵四边形ABCD是矩形,∴∠A=∠B=90°,BC=AD=8,CD=AB.在Rt△AFD中,△AFD的面积为60, ∴12 AD·AF=60,解得AF=15,∴DF=????????2+????????2=17.由折叠的性质,得CD=DF=17,∴AB=17,∴BF=AB-AF=17-15=2.设CE=x,则EF=CE=x,BE=BC-CE=8-x.在Rt△BEF中,EF2=BF2+BE2,即x2=22+(8-x)2,解得x=174,即CE=174,∴△DEC的面积为12 CD·CE=2898.
?
5.易错题 矩形ABCD中,对角线AC,BD交于点O,AE⊥BD于点E,若OE∶ED=1∶3,AE=3,则BD= .?
?
答案
5.4或855 【解析】 由于不能确定AB为矩形ABCD的长边还是短边,故需分两种情况讨论:①如图1,若AB是矩形ABCD的较短边,设OE=x,则ED=3x,AO=OD=2x,在Rt△OEA中,AO2=AE2+OE2,即(2x)2=3+x2,所以x=1,所以OD=2,所以BD=2OD=4;②如图2,若AB是矩形ABCD的较长边,设OE=y,则ED=3y,AO=OD=4y,在Rt△OEA中,AO2=AE2+OE2,即(4y)2=3+y2,所以y=55,所以OD=455,所以BD=2OD=855.综上,BD的长为4或855.
?
6.[2019河南省实验中学月考改编]如图,在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形.
(2)若AF平分∠DAB,CF=3,BF=4,求DF的长.
答案
6.【解析】 (1)∵四边形ABCD是平行四边形,∴AB∥DC,
又∵DF=BE,∴四边形BFDE是平行四边形.
∵DE⊥AB,∴∠DEB=90°,
∴四边形BFDE是矩形.
(2)∵四边形BFDE是矩形,
∴∠BFD=90°,∴∠BFC=90°,
在Rt△BCF中,CF=3,BF=4,∴BC=5.
∵AF平分∠DAB,∴∠DAF=∠BAF,
∵AB∥DC,∴∠DFA=∠BAF,
∴∠DAF=∠DFA,∴AD=DF.
∵AD=BC,∴DF=BC,
∴DF=5.
7.[2019浙江杭州西湖区月考]在矩形ABCD中,AB=3 cm,BC=4 cm,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1 cm/s,运动时间为t s,0≤t≤5.
(1)AE= cm,EF= cm.(用含t的式子表示)?
(2)若G,H分别是AB,DC的中点,求证:四边形EGFH是平行四边形.
(3)在(2)条件下,当t为何值时,四边形EGFH为矩形.
答案
7.【解析】 (1)t (5-2t)(0≤t≤2.5)或(2t-5)(2.5
∴AB=CD,AB∥CD,∴∠GAF=∠HCE.
∵G,H分别是AB,DC的中点,
∴AG=CH,
∵AE=CF,∴AF=CE.
在△AFG与△CEH中,????????=????????,???????????∠????????????=∠????????????,????????=????????,?????????
∴△AFG≌△CEH,∴GF=HE,
同理,GE=HF,
∴四边形EGFH是平行四边形.
?
答案
(3)如图,连接GH.
由(2)知四边形EGFH是平行四边形.
∵点G,H分别是矩形ABCD的边AB,DC的中点,
∴GH=BC=4 cm,
∴当EF=GH=4 cm时,四边形EGFH是矩形,分两种情况:
①EF=(5-2t)cm,
即5-2t=4,解得t=0.5.
②EF=5-2(5-t)=(2t-5)cm,
即2t-5=4,解得t=4.5.
∴当t=0.5或4.5时,四边形EGFH为矩形.
课时3 矩形的性质与判定的综合应用
课时3
1.如图,在△ABC中,AC的垂直平分线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是 ( )
A.23 B.33
C.4 D.4 3
?
答案
1.A 【解析】 ∵DE是AC的垂直平分线,AF=BF,∴∠FDC=∠FDA=90°,DF∥BC,∴∠C=∠FDA=90°,又∵BE⊥DF, ∴四边形BCDE是矩形.∵∠A=30°,∠C=90°,BC=2,∴AB=4,∴AC=42?22=23,∴BE=CD=3,∴四边形BCDE的面积为2×3=23.故选A.
?
2.[2020山东枣庄期中]如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于点E,PF⊥AC于点F,M为EF的中点,则AM的最小值为 ( )
A.54 B.52
C.53 D.65
?
答案
2.D 【解析】 连接AP.在△ABC中,AB=3,AC=4,BC=5,∴AB2+AC2=BC2,∴∠BAC=90°,又∵PE⊥AB,PF⊥AC,∴四边形AEPF是矩形,∴EF=AP.∵M是EF的中点,∴AM=12EF=12AP.由题意知,AP的最小值即Rt△ABC斜边上的高,易得AP的最小值为125,∴AM 的最小值是12×125=65.故选D.
?
3.[2020辽宁辽阳九中二检]如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3 cm,EF=4 cm,则边AD的长是 cm.?
答案
3.5 【解析】 由折叠的性质,知∠HEM=∠AEH,∠BEF=∠FEM,∴∠HEF=∠HEM+∠FEM=12(∠AEM+∠BEM)= 12×180°=90°.同理可得∠EHG=∠HGF=90°,∴四边形EFGH为矩形.易证△HNG≌△FME,∴HN=MF, ∴AD=AH+ HD= HM+HN=HM+MF=HF,在Rt△HEF中,HF=????????2+????????2=32+42=5(cm),∴AD=5 cm.
?
4.如图,在平行四边形ABCD中,点M,N是AD边上的点,BM,CN交于点O,AN=DM,BM=CN.
(1)求证:平行四边形ABCD是矩形.
(2)若∠BOC=90°,MN=1,AM·MD=12,求四边形ABCD的面积.
答案
4.【解析】 (1)∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠A+∠D=180°.
∵AN=DM,∴AM=DN,
在△ABM和△DCN中,????????=????????,????????=????????,????????=????????,
∴△ABM≌△DCN,∴∠A=∠D.
∵∠A+∠D=180°,∴∠A=∠D=90°,
∴平行四边形ABCD是矩形.
?
答案
(2)∵△ABM≌△DCN,∴∠AMB=∠DNC,
∵∠BOC=90°,∴∠AMB+∠DNC=180°-90°=90°,
∴∠AMB=45°,
又∵∠A=90°,∴∠ABM=∠AMB=45°,∴AB=AM.
∵AM·MD=12,AN=DM,
∴AM(AM-1)=12,
解得AM=4(-3舍去),
∴AB=AM=4,MD=3,
∴AD=AM+MD=7,
∴四边形ABCD的面积为AD×AB=7×4=28.
5.如图,在△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交△ACB的外角∠ACD的平分线于点F.
(1)求证:OE=OF.
(2)若CE=12,CF=5,求OC的长.
(3)连接AE,AF.点O在边AC上运动到什么位置时,四边形AECF是矩形?请说明理由.
答案
5.【解析】 (1)如图,∵MN交∠ACB的平分线于点E,交△ACB的外角∠ACD的平分线于点F,
∴∠2=∠5,∠4=∠6.
∵MN∥BC,∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴OE=CO,OF=CO,∴OE=OF.
(2)∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°.
∵∠ECF=∠2+∠4=90°,CE=12,CF=5,
∴EF=122+52=13,
∴OC=12EF=6.5.
(3)点O在边AC上运动到AC的中点时,四边形AECF是矩形.理由如下:
当O为AC的中点时,AO=CO,
∵OE=OF,∴四边形AECF是平行四边形,
又∵∠ECF=90°,∴四边形AECF是矩形.
?
6.[2020天津南开翔宇学校期初考试]如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD,△BCE, △ACF,请探究:
(1)四边形ADEF是什么四边形?
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
(3)当△ABC满足什么条件时,以A,D,E,F为顶点的四边形不存在?
答案
6.【解析】 (1)四边形ADEF是平行四边形.理由如下:
∵△ABD,△BCE都是等边三角形,
∴AD=BD=AB,BC=BE=EC,∠DBA=∠EBC=60°,
∴∠DBE+∠EBA=∠ABC+∠EBA,∴∠DBE=∠ABC.
在△DBE和△ABC中,????????=????????,∠????????????=∠????????????,????????=????????,
∴△DBE≌△ABC,∴DE=AC.
∵△ACF是等边三角形,∴AC=AF,∴DE=AF.
同理可证AD=EF,
∴四边形ADEF是平行四边形.
(2)若四边形ADEF是矩形,则∠FAD=90°,
∴∠BAC=360°-∠FAD-∠DAB-∠FAC=360°-90°-60°-60°=150°.
∴当△ABC满足∠BAC=150°时,四边形ADEF是矩形.
(3)当A与E重合,即∠BAC=60°时,以A,D,E,F为顶点的四边形不存在.
?
3 正方形的性质与判定
课时1 正方形的性质
课时1
1.下列条件可以利用定义说明平行四边形ABCD是正方形的是 ( )
A.AB=CD,∠A=90°
B.AB=AD,∠A=90°
C.AB∥CD,∠A=90°
D.以上都对
答案
1.B 【解析】 正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形是正方形.由此可知选B.
知识点1 正方形的定义
2.[2019广东广铁一中开学考试]正方形具有而菱形不一定具有的性质是 ( )
A.四边相等 B.对角线相等
C.对角相等 D.对角线互相垂直
3.[2019山西太原期中]矩形、菱形、正方形都具有的性质是 ( )
A.对角线相等 B.对角线平分一组对角
C.对角线互相平分 D.对角线互相垂直
答案
2.B
3.C
知识点2 正方形的性质
4.如图,正方形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=8 2 cm,则EF的长度为 ( )
A.1 cm B.2 cm
C.2 2 cm D.4 cm
?
答案
4.B 【解析】 ∵四边形ABCD是正方形,∴AC=BD,∵AC+BD=8 2 cm,∴AC=BD=4 2 cm.∵AB2=12AC·BD,∴AB= 4 cm.∵点E,F分别是线段AO,BO的中点,∴EF=12AB=2 cm.故选B.
?
知识点2 正方形的性质
5.如图,正方形ABCD的边长为4 cm,则阴影部分的面积为 ( )
A.4 cm2 B.8 cm2
C.12 cm2 D.16 cm2
答案
5.B 【解析】 根据正方形的轴对称性可得,S阴影=12S正方形ABCD,∵正方形ABCD的边长为4 cm,∴S阴影=12×42=8(cm2).故选B.
?
知识点2 正方形的性质
根据正方形的轴对称性,得出阴影部分的面积等于正方形面积的一半是解题的关键.
6.如图,正方形纸片ABCD的边长为8,将其沿EF折叠,则图中①②③④四个三角形的周长之和为 .?
答案
6.32 【解析】 如图,C'B'与AB交于点G',与AD交于点H',FC'与AD交于点W',由折叠可知,点G',H',W'关于EF对称的点分别为G,H,W.由题意知,EB'=BE,B'G'=BG,G'H'=GH,H'C'=HC,C'W'=CW,FW'=FW,故①②③④四个三角形的周长之和等于正方形ABCD的周长,即4×8=32.
知识点2 正方形的性质
7.如图,在正方形ABCD中,E,F分别为边AD和CD上的点,且AE=CF,连接AF,CE交于点G.
求证:AG=CG.
答案
7.【分析】 先证明△ADF≌△CDE,得出∠DAF=∠DCE,然后证明△AGE≌△CGF,即可得出结论.
【解析】 ∵四边形ABCD是正方形,
∴∠ADF=∠CDE=90°,AD=CD.
∵AE=CF,∴DE=DF,
∴△ADF≌△CDE,∴∠DAF=∠DCE.
又∵∠AGE=∠CGF,AE=CF,∴△AGE≌△CGF,∴AG=CG.
知识点2 正方形的性质
知识点2 正方形的性质
利用正方形的性质求解证明题的关键
充分利用正方形的四条边相等、四个角为直角、对角线互相垂直平分且相等是求解此类证明题的关键,注意在解题时要与三角形全等、等腰直角三角形等知识相结合.
8.如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为? .?
答案
8.17 【解析】 在AD上取一点M,使得AM=2,连接EM,交AC于点P,易知此时PF+PE取最小值,即EM的长.过点M作MN⊥BC于点N,由题意可知EN=BN-BE=AM-BE=2-1=1,MN=AB=4,所以EM=????????2+????????2=12+42=17.
?
知识点3 与正方形有关的动态探究
9.[2019广东惠州一中期中]如图,正方形ABCD的对角线AC,BD相交于点O,正方形A'B'C'D'的顶点A'与点O重合,A'B'交BC于点E,A'D'交CD于点F.
(1)求证:OE=OF.
(2)若正方形ABCD的边长为1,求两个正方形重叠部分的面积.
(3)在(2)的条件下,若正方形A'B'C'D'绕着点O旋转,EF的长度何时最小?最小值是多少?
知识点3 与正方形有关的动态探究
答案
9.【解析】 (1)∵正方形ABCD的对角线AC,BD交于点O,
∴∠BOC=90°,∠OBC=∠OCF=45°,OB=OC.
∵四边形A'B'C'D'是正方形,∴∠EOF=90°.
∵∠BOE=∠BOC-∠EOC=90°-∠EOC,∠COF=∠EOF-∠EOC=90°-∠EOC,
∴∠BOE=∠COF.
在△BOE和△COF中,∠????????????=∠????????????,????????=????????,∠????????????=∠????????????,
∴△BOE≌△COF,
∴OE=OF.
(2)∵△BOE≌△COF,∴????△????????????=????△????????????,
∴????△????????????+????△????????????=????△????????????+????△????????????,
?
知识点3 与正方形有关的动态探究
答案
即????四边形OECF?=????△?????????????.
∵????△????????????=14S正方形ABCD=14×1×1=14,
∴两个正方形重叠部分的面积为14.
(3)当OE垂直于BC时,EF的长度最小,最小值为22.
连接EF,∵∠EOF=90°,∴EF2=OE2+OF2.
∵OE=OF,∴EF2=2OE2,
∴要使EF的长度最小,则OE的长度最小,
当OE垂直于BC时,OE最小,此时OE=12,则EF=22.
∴当OE垂直于BC时,EF的长度最小,最小值为22.
?
知识点3 与正方形有关的动态探究
1.如图,将甲、乙两张不同的纸片分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则 ( )
A.甲、乙都可以
B.甲、乙都不可以
C.甲不可以,乙可以
D.甲可以,乙不可以
答案
1.A 【解析】 对剪开后的纸片进行旋转平移操作,可得如图所示的图形,可见甲、乙都可以拼成和原来面积相等的正方形.故选A.
2.[2018湖北仙桃中考]如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是 ( )
A.1 B.1.5
C.2 D.2.5
答案
2.C 【解析】 连接AE.∵四边形ABCD是正方形,∴AB=AD,∠B=∠D=90°.∵△ABG沿AG对折至△AFG,G是BC的中点,∴AB=AF,GB=GF=3,∠B=∠AFG=90°,∴∠AFE=∠D=90°,AF=AD,又∵AE=AE,∴Rt△AFE≌Rt△ADE(HL),∴DE= EF.设DE=x,则EF=DE=x,GE=x+3,CE=6-x.在Rt△CGE中,由勾股定理得CG2+CE2=GE2,∴32+(6-x)2=(x+3)2,解得x=2.故选C.
利用正方形的性质求解线段的长的思路
利用正方形的性质求解线段长度时,通常将涉及的线段转化到直角三角形(特别是等腰直角三角形)中,结合勾股定理或三角形全等求解.
3.如图,在正方形ABCD中,点E在边BC上,点F在线段DE上,若AB=AF,则∠BFE= ( )
A.45° B.30°
C.60° D.55°
答案
3.A 【解析】 如图,∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,∵AB=AF,∴AF=AD,∴∠1=∠2, ∠3=∠4. ∵∠BAD+∠1+∠2+∠3+∠4=360°,∴2∠2+2∠3=270°,∴∠2+∠3=135°,∴∠BFE=180°-135°=45°.故选A.
4.如图,正方形ABCD中,AB=4 cm,点E,F分别在边AD和边BC上,且BF=ED=3 cm,动点P,Q分别从A,C两点同时出发,点P沿A→F→B方向运动,点Q沿C→D→E→C方向运动,点P,Q的运动速度分别为1 cm/s,3 cm/s.设运动时间为t(0
4.3或6 【解析】 ∵四边形ABCD是正方形,∴AD=BC,AD∥BC,∵BF=ED,∴四边形AFCE是平行四边形,∴AF∥EC, AF=EC.在Rt△ABF中,AB=4 cm,BF=3 cm,∴AF=5 cm.由P,Q的运动速度和运动方向可知,当Q 在EC上运动,P在AF上运动时,若EQ=FP,则以A,C,P,Q四点为顶点的四边形是平行四边形,∴3t-7=5-t,∴t=3.当P,Q分别在BC,AD上运动时,若QD=BP,则以A,C,P,Q四点为顶点的四边形是平行四边形,此时Q点已经运动一周,∴3t-12-4=8-t,∴t=6.综上所述,t的值为3或6.
5.如图,过正方形ABCD的顶点B作直线l,分别过点A,C作l的垂线,垂足分别为E,F.若AE=1,CF=3,则AB的长度为? .?
答案
5.10 【解析】 ∵四边形ABCD是正方形,∴∠CBF+∠FBA=90°,∵CF⊥l,∴∠CBF+∠BCF=90°,∴∠ABE=∠BCF,又∵∠AEB=∠BFC=90°,AB=BC,∴△ABE≌△BCF,∴BE=CF=3,∴在Rt△ABE中,AB=????????2+????????2=12+32=10.
?
6.若以正方形ABCD的边CD为边作等边三角形CDE,则∠AED的度数是 .?
答案
6.15°或75° 【解析】 有两种情况:(1)当点E在正方形ABCD内时,如图1,在正方形ABCD中,AD=CD,∠ADC=90°,在等边三角形CDE中,CD=DE,∠CDE=60°,∴∠ADE=90°-60°=30°,AD=DE,∴∠AED=∠DAE=12(180°-∠ADE)=75°;(2)当点E在正方形ABCD外时,如图2,在等边三角形CDE中,∠EDC=60°,∴∠ADE=90°+60°=150°,∴∠AED=∠DAE=12(180°-∠ADE)=15°.综上,∠AED的度数是15°或75°.
?
7.[2018江苏盐城中考]在正方形 ABCD中,对角线 BD所在的直线上有两点E,F满足 BE=DF,连接 AE,AF,CE,CF,如图所示.
(1)求证:△ABE≌△ADF.
(2)试判断四边形 AECF的形状,并说明理由.
答案
7.【解析】 (1)∵四边形ABCD为正方形,
∴AB=AD,∠ABD=∠ADB=45°,∴∠ABE=∠ADF=135°,
又∵BE=DF,∴△ABE≌△ADF.
(2)四边形AECF是菱形.理由如下:
由(1)得△ABE≌△ADF,∴AE=AF.
∵四边形ABCD是正方形,
∴CB=CD,∠CBD=∠CDB=45°,∴∠CBE=∠CDF=135°,
又∵BE=DF,∴△CBE≌△CDF,∴CE=CF.
∵BE=BE,∠CBE=∠ABE=135°,CB=AB,∴△CBE≌△ABE,
∴CE=AE,∴CE=AE=AF=CF,∴四边形AECF是菱形.
8.如图,四边形ABCD和四边形CEFG都是正方形.
求证:(1)△BCG≌△DCE;
(2)BG⊥DE.
答案
8.【解析】 (1)∵四边形ABCD和四边形CEFG都是正方形,
∴BC=DC,CE=CG,∠BCD=∠GCE=90°,
∴∠BCG=∠DCE.
在△BCG和△DCE中,BC=DC,∠BCG=∠DCE,CG=CE,
∴△BCG≌△DCE.
(2)设BG分别与DC,DE交于点H,O.
∵△BCG≌△DCE,∴∠HBC=∠ODH,
∵∠BHC=∠DHO,∠HBC+∠BHC=90°,
∴∠ODH+∠DHO=90°,∴∠DOH=90°,
∴BG⊥DE.
9.如图,在正方形ABCD中,点E,F分别在BC,CD上移动,且A到EF的距离AH始终保持与AB的长相等,问在点E,F移动的过程中:
(1)∠EAF的大小是否有变化?请说明理由.
(2)△ECF的周长是否有变化?请说明理由.
答案
9.【解析】 (1)∠EAF的大小没有变化.理由如下:
根据题意,知AB=AH,∠B=90°,
∵AH⊥EF,∴∠AHE=90°,
又∵AE=AE,∴Rt△BAE≌Rt△HAE,
∴∠BAE=∠EAH.
同理,Rt△HAF≌Rt△DAF,∴∠HAF=∠DAF,
∴∠EAF=∠EAH+∠HAF=12∠BAH+12∠HAD=12∠BAD=45°,
∴∠EAF的大小没有变化.
(2)△ECF的周长没有变化.理由如下:
由(1)得Rt△BAE≌Rt△HAE,Rt△HAF≌Rt△DAF,
∴BE=EH,HF=DF,
∴△ECF的周长为EF+EC+FC=BE+DF+EC+FC=2BC,
∴△ECF的周长没有变化.
?
课时2 正方形的判定
课时2
1.[2019北京顺义区期末]学习了正方形之后,王老师提出问题:要判断一个四边形是正方形,有哪些思路?甲同学说:先判定四边形是菱形,再确定这个菱形有一个角是直角.乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等.丙同学说:判定四边形的对角线相等,并且互相垂直平分.丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.上述四名同学的说法中,正确的是 ( )
A.甲、乙 B.甲、丙
C.乙、丙、丁 D.甲、乙、丙、丁
答案
1.D
知识点 正方形的判定
正方形是特殊的平行四边形,也是邻边相等的特殊矩形,也是有一个角是直角的特殊菱形,所以在判定一个四边形是正方形时,要从它的特殊性逐步突破
2.已知四边形ABCD的对角线AC与BD相交于点O,有下列条件:①AB=AD;②∠DAB=90°;③AO=CO,BO=DO;④四边形ABCD为矩形;⑤四边形ABCD为菱形;⑥四边形ABCD为正方形.则下列推理不成立的是 ( )
A.①④?⑥ B.①③?⑤
C.①②?⑥ D.②③?④
答案
2.C 【解析】 A项,有一组邻边相等的矩形是正方形,成立;B项,由③得四边形ABCD是平行四边形,再由①知平行四边形ABCD有一组邻边相等,故四边形ABCD为菱形,成立;C项,由①②不能判定四边形ABCD是正方形,不成立;D项,由③得四边形ABCD是平行四边形,再由②知平行四边形ABCD有一个角是直角,故四边形ABCD是矩形,成立.故选C.
知识点 正方形的判定
3.如图,四边形ABCD中,对角线AC与BD相交于点O,且OA=OB=OC=OD,不添加任何字母与辅助线,若要使四边形ABCD是正方形,则还需要添加的一个条件是 .?
答案
3.AC⊥BD(或AB=AD等) 【解析】 由OA=OB=OC=OD可得四边形ABCD是矩形,因此再添加一组邻边相等或对角线互相垂直即可.
知识点 正方形的判定
4.如图,在Rt△ABC中,∠C=90°,∠BAC,∠ABC的平分线交于点D,DE⊥BC于点E,DF⊥AC于点F.求证:四边形CEDF为正方形.
答案
4.【解析】 过点D作DG⊥AB交AB于点G.
∵∠C=∠CFD=∠CED=90°,
∴四边形CEDF是矩形.
∵AD是∠BAC的平分线,DF⊥AC,DG⊥AB,∴DF=DG,
同理可得DE=DG,∴DE=DF,
∴四边形CEDF是正方形.
知识点 正方形的判定
5.[2020陕西西安电子科大附中月考] 如图,等边三角形AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
答案
5.【解析】 ∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°.
∵△AEF是等边三角形,
∴AE=AF,∠AEF=∠AFE=60°.
∵∠CEF=45°,∴∠CFE=∠CEF=45°,
∴∠AFD=∠AEB=180°-45°-60°=75°,
∴△ABE≌△ADF,∴AB=AD,
∴矩形ABCD是正方形.
知识点 正方形的判定
6.如图,在平行四边形ABCD中,AD=9 cm,CD=3 2 cm,∠B=45°,点M,N分别以A,C为起点,1 cm/s的速度沿AD,CB方向运动,设点M,N运动的时间为t(0≤t≤6)s.
(1)求BC边上的高AE的长.
(2)连接AN,CM,当t为何值时,四边形AMCN为菱形?
(3)过点M作MP⊥BC于点P,过点N作NQ⊥AD于点Q,当t为何值时,四边形MPNQ为正方形?
?
知识点 正方形的判定
答案
6.【解析】 (1)∵四边形ABCD是平行四边形,
∴AB=CD=32cm.
在Rt△ABE中,∠AEB=90°,∠B=45°,
∴AE=3 cm.
(2)如图1,连接AN,CM.由题意可知AM=CN=t cm,
∵AM∥CN,∴四边形AMCN为平行四边形,
∴当AN=AM时,四边形AMCN为菱形.
易知BE=AE=3 cm,∴EN=9-3-t=(6-t)cm,
∴AN2=32+(6-t)2,∴32+(6-t)2=t2,
解得t=154.
∴当t为154时,四边形AMCN为菱形.
?
知识点 正方形的判定
答案
?(3)∵MP⊥BC于点P,NQ⊥AD于点Q,QM∥NP,
∴四边形MPNQ为矩形,
∴当QM=QN时,四边形MPNQ为正方形.
分两种情况,
①当点Q在点M的右侧时,如图2.
易知AM=CN=EP=t cm,
∴QM=PN=BC-BE-EP-CN=9-3-t-t=(6-2t)cm,
∴6-2t=3,解得t=1.5.
②当点Q在点M的左侧时,如图3.
易知AM=CN=t cm,
∴AQ=EN=BC-BE-CN=9-3-t=(6-t)cm,
∴QM=AM-AQ=t-(6-t)=(2t-6)cm,
∴2t-6=3,解得t=4.5.
故当t为4.5或1.5时,四边形MPNQ为正方形.
知识点 正方形的判定
1.[2019四川成都金牛区月考]下列说法正确的是 ( )
A.对角线相等且有一个角是直角的平行四边形是正方形
B.对角线互相垂直且一组邻边相等的平行四边形是正方形
C.四个角都相等的菱形是正方形
D.对角线互相垂直平分且有一组邻边相等的四边形是正方形
答案
1.C 【解析】 A项,对角线相等且有一个角是直角的平行四边形是矩形,不一定是正方形,不符合题意;B项,对角线互相垂直且有一组邻边相等的平行四边形是菱形,不一定是正方形,不符合题意;D项,对角线互相垂直平分且有一组邻边相等的四边形是菱形,不一定是正方形,不符合题意.故选C.
利用对角线证明正方形的方法
(1)证“四边形+对角线互相垂直、平分且相等”;(2)证“平行四边形+对角线互相垂直且相等”;(3)证“矩形+对角线互相垂直”;(4)证“菱形+对角线相等”.
2.若一个平行四边形绕着对角线的交点旋转90°,能够与它自身重合,则该平行四边形为 ( )
A.矩形 B.菱形
C.正方形 D.无法确定
答案
2.C 【解析】 该平行四边形绕着它的对角线的交点旋转90°,能够与它自身重合,说明对角线互相垂直平分且相等,所以该平行四边形是正方形.故选C.
3.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加下列一个条件,仍不能证明四边形BECF为正方形的是 ( )
A.BC=AC
B.CF⊥BF
C.BD=DF
D.AC=BF
答案
3.D 【解析】 ∵EF垂直平分BC,∴BE=CE,BF=CF.∵BE=BF,∴BE=EC=CF=BF,∴四边形BECF是菱形.A项,当BC= AC时,∵∠ACB=90°,∴∠EBC=45°,∴∠EBF=2∠EBC=90°,∴四边形BECF是正方形;B项,当CF⊥BF时,∠BFC=90°,根据“有一个角是直角的菱形是正方形”,可得四边形BECF是正方形;C项,当BD=DF时,根据“对角线相等的菱形是正方形”,可得四边形BECF是正方形;D项,当AC=BF时,无法得出四边形BECF是正方形.故选D.
4.[2019四川雅安中学月考]如图,菱形ABCD中,点E,O,F分别是AB,AC,AD的中点,连接CE,CF,OF,OE.
(1)求证:△BCE≌△DCF.
(2)猜测:当AB和BC满足条件 时,四边形AEOF是正方形,请说明理由.?
答案
4.【解析】 (1)∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=DC=AD.
∵点E,O,F分别为AB,AC,AD的中点,
∴AE=BE=DF=AF.
在△BCE和△DCF中,????????=????????,∠????=∠????,????????=????????,
∴△BCE≌△DCF.
?
答案
(2)AB⊥BC
当AB⊥BC时,四边形AEOF是正方形.理由如下:
在菱形ABCD中,∵点E,O,F分别为AB,AC,AD的中点,
∴AE=OE=OF=AF,
∴四边形AEOF是菱形.
∵AB⊥BC,OE∥BC,
∴OE⊥AB,∴∠AEO=90°,
∴四边形AEOF是正方形.
5.如图,E是矩形ABCD的边BC的中点,P是AD边上一动点,PF⊥AE,PH⊥DE,垂足分别为F,H.
(1)当矩形ABCD的边AD与AB满足什么条件时,四边形PHEF是矩形?请予以证明.
(2)在(1)中,动点P运动到什么位置时,矩形PHEF为正方形?为什么?
答案
5.【解析】 (1)当AD=2AB时,四边形PHEF是矩形.证明如下:
∵四边形ABCD是矩形,∴AD=BC,AB=CD.
∵E是BC的中点,AD=2AB,∴AB=BE=EC=CD,
∴△ABE,△DCE是等腰直角三角形,
∴∠AEB=∠DEC=45°,∴∠AED=90°.
在四边形PHEF中,∵∠PFE=∠FEH=∠EHP=90°,
∴四边形PHEF是矩形.
(2)点P运动到AD的中点时,矩形PHEF为正方形.理由如下:
由(1)可得∠BAE=∠CDE=45°,
∴∠FAP=∠HDP=45°,
又∵∠AFP=∠PHD=90°,AP=PD,
∴△AFP≌△DHP,∴PF=PH,
∴矩形PHEF是正方形.
6.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE的外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.
(1)求证:四边形ABCD是正方形.
(2)已知AB的长为6,求(BE+6)(DF+6)的值.
(3)借助上面问题的解题思路,解决下列问题:若△PQR中,∠QPR=45°,RQ上的高PH=6,HQ=2,则HR= .?
答案
6.【解析】 (1)如图1,过点A作AG⊥EF于点G.
∵AB⊥CE,AD⊥CF,∴∠B=∠D=90°,
∴∠B=∠C=∠D=90°,
∴四边形ABCD是矩形.
∵∠CEF,∠CFE的外角平分线交于点A,
∴AB=AG,AD=AG,∴AB=AD,
∴四边形ABCD是正方形.
(2)∵四边形ABCD是正方形,∴BC=CD=AB=6.
在Rt△ABE和Rt△AGE中,????????=????????,????????=????????,
∴Rt△ABE≌Rt△AGE,∴BE=GE,
同理,Rt△ADF≌Rt△AGF,
∴DF=GF,∴BE+DF=GE+GF=EF.
设BE=x,DF=y,则CE=BC-BE=6-x,CF=CD-DF=6-y,EF=x+y,
?
答案
在Rt△CEF中,由勾股定理得,(6-x)2+(6-y)2=(x+y)2,
∴xy+6(x+y)=36,
∴(BE+6)(DF+6)=(x+6)(y+6)=xy+6(x+y)+36=36+36=72.
(3)3
如图2,把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ,MR交于点G.
由(1)(2)得,四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ=2,
∴MG=DG=MP=PH=6,∴GQ=4,
设MR=HR=a,则GR=6-a,QR=a+2,
在Rt△GQR中,由勾股定理得,(6-a)2+42=(2+a)2,
解得a=3,即HR=3.
课时3 正方形的性质与判定的综合应用
课时3
1.如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是 ( )
A.7 B.8
C.72 D.73
?
答案
1.C 【解析】 如图,设AG交FD于点G,CH交BE于点H,由正方形的性质得, ∠BAD=∠ABC=∠BCD=∠ADC=90°,AB=BC=CD=AD,由“SSS”可证△ABE≌△CDF,所以∠ABE=∠CDF.易证∠ABE=∠DAG=∠CDF=∠BCH,所以∠BAE=∠ADG,由“ASA”可证△ABE≌△DAG,所以AE=DG,BE=AG,同理可得AE=DG=CF=BH= 5,BE= AG=DF=CH=12,所以EG=GF=FH=HE=7,又因为∠HEG=90°,所以四边形EGFH是正方形,所以EF=72.故选C.
?
2.如图1,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图2的方式拼接成一个四边形.若正方形ABCD的边长为3 cm,HA= EB=FC=GD=1 cm,则图2中阴影部分的面积为 cm2.?
答案
2.1 【解析】 在题图1中,连接GH,HE,EF,FG,由HA=EB=FC=GD=1 cm,AB=BC=CD=AD=3 cm,∠A=∠B=∠C= ∠D=90°,易得四边形GHEF是正方形,GF=EF=EH=GH=12+22=5(cm).根据已知条件,知重新拼成的四边形是正方形,且拼成的正方形的边长为正方形GHEF的对角线长,设其边长为a cm,根据勾股定理,得a=(5)2+(5)2=10,其面积为(10)2=10(cm2),∴S阴影=10-S正方形ABCD=10-9=1(cm2).
?
3.如图,在正方形ABCD中,动点E在AC上,AF⊥AC,垂足为A,AF=AE.
(1)求证:BF=DE.
(2)当点E运动到AC的中点时(其他条件都保持不变),四边形AFBE是什么特殊四边形?请说明理由.
答案
3.【解析】 (1)∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°.
∵AF⊥AC,∴∠EAF=90°,∴∠BAF=∠DAE,
又∵AF=AE,AB=AD,∴△ABF≌△ADE,
∴BF=DE.
(2)四边形AFBE是正方形.理由如下:
∵点E为AC的中点,AB=BC,
∴BE⊥AC,BE=AE=12AC.
∵AF=AE,∴BE=AF=AE.
∵BE⊥AC,AF⊥AC,∴BE∥AF,
∴四边形AFBE是平行四边形,
又∵∠FAE=90°,AF=AE,
∴四边形AFBE是正方形.
?
4.如图,已知四边形ABCD是正方形,AB=22,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形.
(2)探究:CE+CG是否为定值?若是,求出这个定值;若不是,请说明理由.
?
答案
4.【解析】 (1)如图,过点E作EM⊥BC于点M,EN⊥CD于点N.
∵四边形ABCD是正方形,点E在对角线AC上,
∴CE平分∠BCD,
∵EM⊥BC,EN⊥CD,∴EM=EN,∠EMF=∠END=90°,
又∵∠MCN=90°,
∴四边形EMCN是正方形,∴∠MEN=90°,
∵∠NED+∠NEF=90°,∠MEF+∠NEF=90°,
∴∠MEF=∠NED,∴△MEF≌△NED,
∴EF=DE,∴矩形DEFG是正方形.
答案
(2)CE+CG是定值,定值为4.
∵四边形ABCD和四边形DEFG均为正方形,
∴AD=CD,DE=DG,∠ADC=∠EDG=90°,
∴∠ADE+∠EDC=90°,∠CDG+∠EDC=90°,
∴∠ADE=∠CDG,
∴△ADE≌△CDG,∴AE=CG,
∴CE+CG=CE+AE=AC=2AB=4.
?
易错疑难集训
集训
1.已知四边形ABCD为菱形,该菱形的周长为16,面积为8,则∠ABC的度数为 .?
答案
1.30°或150° 【解析】 如图1,当∠ABC为锐角时,过点A作AE⊥BC于点E,∵菱形ABCD的周长为16,∴AB=4,又∵菱形ABCD的面积为8,∴AE=2,∴∠ABE=30°,即∠ABC=30°.如图2,当∠ABC为钝角时,过点D作DF⊥AB于点F,∵菱形ABCD的周长为16,∴AD=4,又∵菱形ABCD的面积为8,∴DF=2,∴∠DAF=30°,∴∠ABC=150°.故∠ABC的度数为30°或150°.
易错点1 忽略情况造成漏解
本题的易错之处是只考虑∠ABC为锐角或只考虑∠ABC为钝角,从而出现答案不全面的错误.当题目中的条件不确定时,应分类讨论求解,分类的原则是不重不漏.
2.如图,在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP,PC,△BPC是以PB为腰的等腰三角形,则PB的长为 .?
答案
2.5或6 【解析】 如图1,当BC为底边时,PB=PC.由“SAS”可证△ABP≌△DCP,所以AP=PD=12AD=12BC=3.在Rt△ABP中,由勾股定理,得PB=????????2+????????2=42+32=5.如图2,当CP为底边时,则BP=BC=6.综上所述,PB的长为5或6.
?
易错点1 忽略情况造成漏解
3.如图,矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D'落在∠ABC的平分线上时,求DE的长.
答案
3.【解析】 如图,过点D'作MN⊥AB,交CD于点N,交AB于点M,连接BD'.
∵点D的对应点D'落在∠ABC的平分线上,∴D'M=BM.
设BM=D'M=x,则AM=7-x.由折叠知,AD=AD'=5.
在Rt△D'AM中,D'M2=AD'2-AM2,
∴25-(7-x)2=x2,
∴x=3或x=4,即D'M=3或D'M=4.
易错点1 忽略情况造成漏解
答案
设DE=m,则D'E=m,分两种情况讨论:
(1)当D'M=3时,BM=NC=3,D'N=2,EN=CD-DE-NC=7-m-3=4-m.
在Rt△D'NE中,m2=(4-m)2+22,
∴m=52,即DE=52.
(2)当D'M=4时,BM=NC=4,D'N=1,EN=CD-DE-NC=7-m-4=3-m.
在Rt△D'NE中,m2=(3-m)2+12,
∴m=53,即DE=53.
综上,DE的长为52或53.
?
易错点1 忽略情况造成漏解
4.两个完全相同的矩形纸片ABCD,BFDE如图放置.求证:四边形BNDM是菱形.
答案
4.【解析】 ∵四边形ABCD,BFDE是矩形,
∴BM∥DN,DM∥BN,
∴四边形BNDM是平行四边形.
∵AB=ED,∠A=∠E=90°,∠AMB=∠EMD,
∴△ABM≌△EDM,∴BM=DM,
∴四边形BNDM是菱形.
易错点2 对特殊平行四边形的判定定理理解不透彻
错解:∵四边形ABCD,BFDE是两个完全相同的矩形,∴AB=ED,∠A=∠E=90°,又∵∠AMB=∠EMD,∴△ABM≌△EDM,∴BM=DM,∵四边形BNDM有一组邻边相等,∴四边形BNDM是菱形.
分析:这是由于概念模糊,误以为有一组邻边相等的四边形是菱形,根据菱形的判定定理,有一组邻边相等的平行四边形是菱形,因此还需先说明四边形BNDM是平行四边形.
5.如图,在四边形ABCD中,AB∥CD,AD∥BC,对角线AC,BD交于点O,∠OBC=∠OCB.求证:四边形ABCD是矩形.
答案
5.【解析】 ∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴OC=OA=12AC,OB=OD=12BD.
又∵∠OBC=∠OCB,∴OB=OC,
∴AC=BD,∴四边形ABCD是矩形.
?
易错点2 对特殊平行四边形的判定定理理解不透彻
易错点2 对特殊平行四边形的判定定理理解不透彻
解此题容易出现论证不严密的错误,即没有先证明四边形ABCD是平行四边形.即使平行四边形的判定很容易,在证明过程中也不能省略.
根据“对角线相等的平行四边形是矩形”判定四边形是矩形
分两步证明:第一步先证明四边形是平行四边形,第二步证明该平行四边形的对角线相等.也就是说,运用此方法判定一个四边形是矩形时,必须满足两个条件:一是平行四边形;二是对角线相等.
6.如图,将矩形ABCD沿直线EF对折,点D恰好与BC边上的点H重合,若∠GFP=62°,则∠EHF的度数为 °.?
答案
6.56 【解析】 由折叠可知∠CFP=∠GFP=62°,∴∠HFG=180°-∠CFP-∠GFP=56°,∵HE∥FG,∴∠EHF= ∠HFG= 56°.
易错点3 矩形折叠问题中的常见错误
7.如图,将矩形纸片ABCD沿着对角线BD折叠,使点C落在点C'处,BC'交AD于点E,AD=8,AB=4,求DE的长.
答案
7.【解析】 ∵四边形ABCD是矩形,
∴AD∥BC,∠CBD=∠ADB,
由折叠知∠CBD=∠DBE,
∴∠DBE=∠EDB,∴DE=BE.
设DE的长为x,则BE=x,AE=8-x,
在Rt△ABE中,AB2+AE2=BE2,即42+(8-x)2=x2,
解得x=5,∴DE=5.
易错点3 矩形折叠问题中的常见错误
1.矩形ABCD中,∠ABC的平分线与直线CD相交于点E,DE=2,CD=4,则这个矩形的面积是 .?
答案
1.8或24 【解析】 ①如图1,当点E在CD上时,∵DE=2,CD=4,∴CE=CD-DE=2.∵BE平分∠ABC,∠ABC= ∠C=90°, ∴∠CBE=45°,△BCE是等腰直角三角形,∴BC=CE=2,S矩形ABCD=BC·CD=8;②如图2,CE=CD+DE=6,易知△BCE是等腰直角三角形,∴BC=CE=6,S矩形ABCD=BC·CD=24.综上,这个矩形的面积为8或24.
疑难点1 应用特殊平行四边形的性质与判定解决问题
2.动手操作:在一张长12 cm、宽5 cm的矩形纸片内,折出一个菱形.小颖同学按照取两组对边中点的方法折出菱形EFGH(见方案一),小明同学沿矩形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB的方法得到菱形AECF(见方案二).
(1)你能说出小颖、小明折出菱形的理由吗?
(2)请你通过计算,比较小颖和小明折出的菱形,哪个菱形面积较大?
疑难点1 应用特殊平行四边形的性质与判定解决问题
答案
2.【解析】 (1)小颖的理由:依次连接矩形ABCD各边的中点及对角线,由于矩形的对角线相等,利用中位线的性质,得四边形EFGH的四条边相等,根据四边相等的四边形是菱形,得四边形EFGH是菱形.
小明的理由:∵四边形ABCD是矩形,∴AD∥BC,则∠DAC=∠ACB,又∵∠CAE=∠CAD,∠ACF=∠ACB,∴∠CAE=∠CAD=∠ACF=∠ACB,∴AE=EC=CF=FA,∴四边形AECF是菱形.
(2)方案一:S菱形EFGH=S矩形ABCD-4S△AEH=12×5-4×12×6×52=30(cm2).
方案二:设BE=x cm,则CE=(12-x)cm,
∴AE=????2+25 cm,
由四边形AECF是菱形,得AE2=CE2,即x2+25=(12-x)2,
∴x=11924,
S菱形AECF=S矩形ABCD-2S△ABE=12×5-2×12×5×11924=84524(cm2).
比较可知,小明所折的菱形面积较大.
?
疑难点1 应用特殊平行四边形的性质与判定解决问题
3.如图,在四边形ABCD中,点E,F,G,H分别是边AB,BC,CD,DA的中点,顺次连接E,F,G,H,得到的四边形EFGH叫中点四边形.
(1)求证:四边形EFGH是平行四边形.
(2)请你探究并填空:
当四边形ABCD变成平行四边形时,它的中点四边形是 ;?
当四边形ABCD变成矩形时,它的中点四边形是 ;?
当四边形ABCD变成菱形时,它的中点四边形是 ;?
当四边形ABCD变成正方形时,它的中点四边形是 .?
(3)根据以上探究,请你总结中点四边形的形状是由原四边形的什么决定的.
疑难点2 中点四边形与特殊平行四边形
答案
3.【解析】 (1)连接BD,∵E,H分别是AB,AD的中点,
∴EH是△ABD的中位线,
∴EH=12BD,EH∥BD,
同理可得FG=12BD,FG∥BD,
∴EH=FG,EH∥FG,
∴四边形EFGH是平行四边形.
(2)平行四边形 菱形 矩形 正方形
(3)中点四边形的形状是由原四边形的对角线的关系决定的.
?
疑难点2 中点四边形与特殊平行四边形
中点四边形的形状是由原四边形的两条对角线的数量关系和位置关系决定的.首先,不管原四边形的形状怎样改变,中点四边形始终是平行四边形;其次,具体的中点四边形形状的确定还需参考原四边形具备的其他条件.
4.在平行四边形ABCD中,AC,BD交于点O,过点O作直线EF,GH,分别交平行四边形的四条边于E,G,F,H四点,连接EG,GF,FH,HE.
(1)如图1,试判断四边形EGFH的形状,并说明理由;
(2)如图2,当EF⊥GH时,四边形EGFH的形状是 ;?
(3)如图3,在(2)的条件下,若AC=BD,则四边形EGFH的形状是 ;?
(4)如图4,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
疑难点2 中点四边形与特殊平行四边形
答案
4.【解析】 (1)四边形EGFH是平行四边形.理由如下:
∵平行四边形ABCD的对角线AC,BD交于点O,
∴点O是平行四边形ABCD的对称中心,
∴EO=FO,GO=HO,
∴四边形EGFH是平行四边形.
(2)菱形
(3)菱形
(4)四边形EGFH是正方形.理由如下:
∵AC=BD,∴平行四边形ABCD是矩形,∴OA=OB=OC,
又∵AC⊥BD,∴∠BOC=90°,∠GBO=∠FCO=45°.
∵EF⊥GH,∴∠GOF=90°,∴∠BOG=∠COF,
∴△BOG≌△COF,∴OG=OF,∴GH=EF.
由(3)知四边形EGFH是菱形,
又∵GH=EF,
∴四边形EGFH是正方形.
疑难点2 中点四边形与特殊平行四边形
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
