北师大版八年级上册数学第一章勾股定理 素养拓展+中考真题课件(43张PPT)
文档属性
| 名称 | 北师大版八年级上册数学第一章勾股定理 素养拓展+中考真题课件(43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-15 00:00:00 | ||
图片预览






文档简介
第一章·勾股定理
数学·八年级上册·北师
专项素养拓训
专题 勾股定理的应用
专项
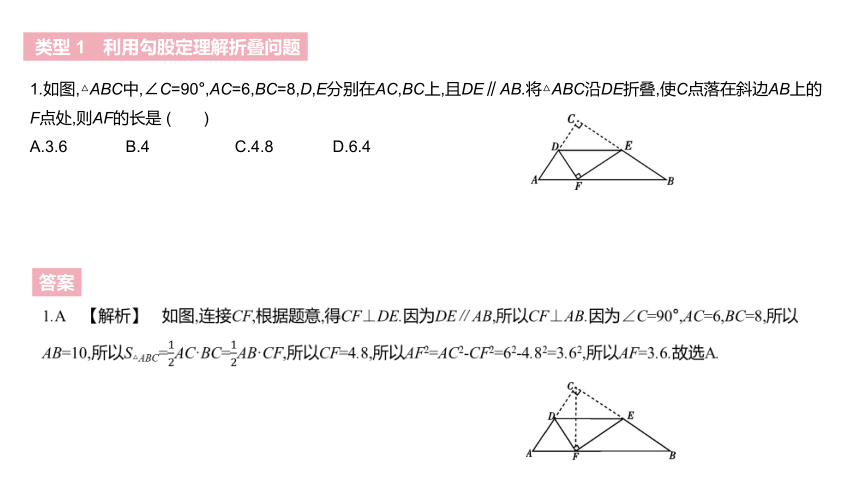
1.如图,△ABC中,∠C=90°,AC=6,BC=8,D,E分别在AC,BC上,且DE∥AB.将△ABC沿DE折叠,使C点落在斜边AB上的F点处,则AF的长是 ( )
A.3.6 B.4 C.4.8 D.6.4
答案
1.A 【解析】 如图,连接CF,根据题意,得CF⊥DE.因为DE∥AB,所以CF⊥AB.因为∠C=90°,AC=6,BC=8,所以AB=10,所以S△ABC=12AC·BC=12AB·CF,所以CF=4.8,所以AF2=AC2-CF2=62-4.82=3.62,所以AF=3.6.故选A.
?
类型 1 利用勾股定理解折叠问题
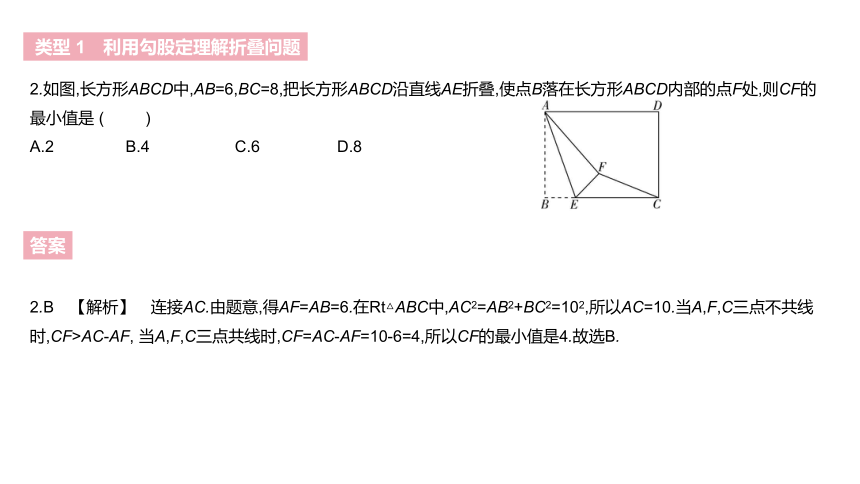
2.如图,长方形ABCD中,AB=6,BC=8,把长方形ABCD沿直线AE折叠,使点B落在长方形ABCD内部的点F处,则CF的最小值是 ( )
A.2 B.4 C.6 D.8
答案
2.B 【解析】 连接AC.由题意,得AF=AB=6.在Rt△ABC中,AC2=AB2+BC2=102,所以AC=10.当A,F,C三点不共线时,CF>AC-AF, 当A,F,C三点共线时,CF=AC-AF=10-6=4,所以CF的最小值是4.故选B.
类型 1 利用勾股定理解折叠问题
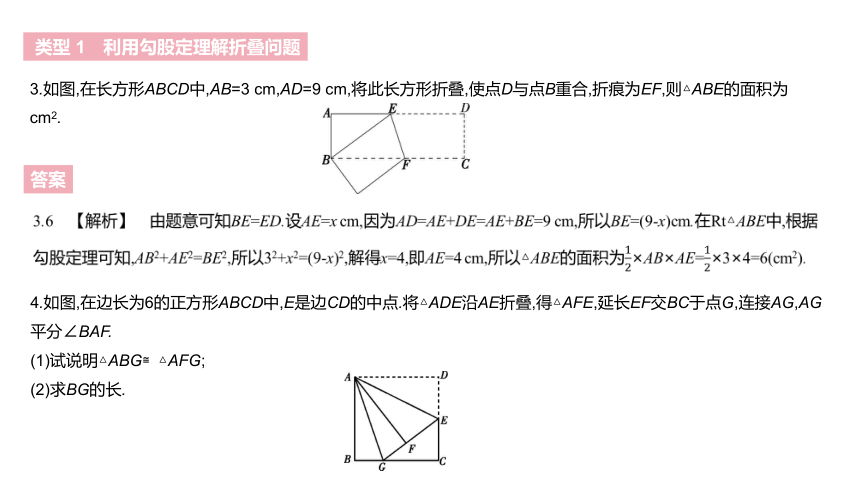
3.如图,在长方形ABCD中,AB=3 cm,AD=9 cm,将此长方形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为 cm2.?
答案
3.6 【解析】 由题意可知BE=ED.设AE=x cm,因为AD=AE+DE=AE+BE=9 cm,所以BE=(9-x)cm.在Rt△ABE中,根据勾股定理可知,AB2+AE2=BE2,所以32+x2=(9-x)2,解得x=4,即AE=4 cm,所以△ABE的面积为12×AB×AE=12×3×4=6(cm2).
?
类型 1 利用勾股定理解折叠问题
4.如图,在边长为6的正方形ABCD中,E是边CD的中点.将△ADE沿AE折叠,得△AFE,延长EF交BC于点G,连接AG,AG平分∠BAF.
(1)试说明△ABG≌△AFG;
(2)求BG的长.
答案
4.【解析】 (1)在正方形ABCD中,AD=AB=BC=CD=6.
由折叠的性质,可知AD=AF,所以AB=AF,
因为AG平分∠BAF,所以∠BAG=∠FAG.
在△ABG和△AFG中,????????=????????,∠????????????=∠????????????,????????=????????,
所以△ABG≌△AFG.
(2)因为△ABG≌△AFG,所以BG=FG.
设BG=FG=x,则GC=6-x.
因为E为CD的中点,
所以CE=EF=DE=12CD=3,所以EG=3+x,
在Rt△CEG中,由勾股定理,得CE2+CG2=EG2,即32+(6-x)2=(3+x)2,
解得x=2,所以BG=2.
?
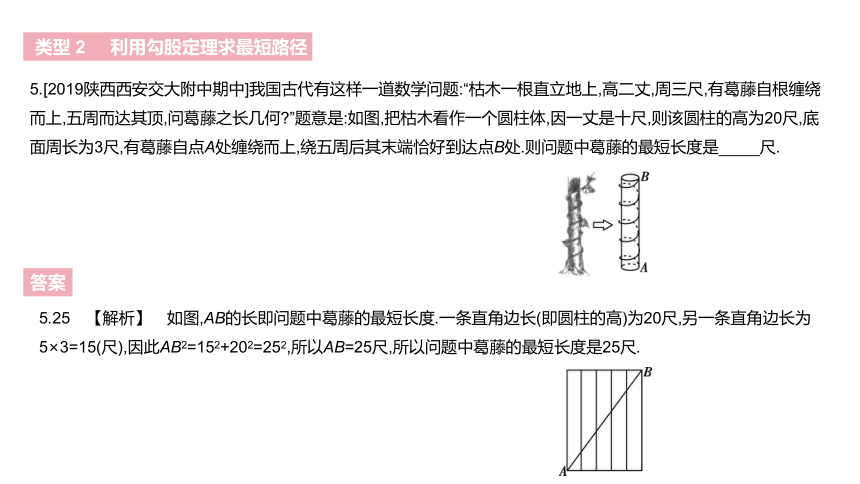
5.[2019陕西西安交大附中期中]我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处.则问题中葛藤的最短长度是 尺.?
答案
5.25 【解析】 如图,AB的长即问题中葛藤的最短长度.一条直角边长(即圆柱的高)为20尺,另一条直角边长为5×3=15(尺),因此AB2=152+202=252,所以AB=25尺,所以问题中葛藤的最短长度是25尺.
类型 2 利用勾股定理求最短路径
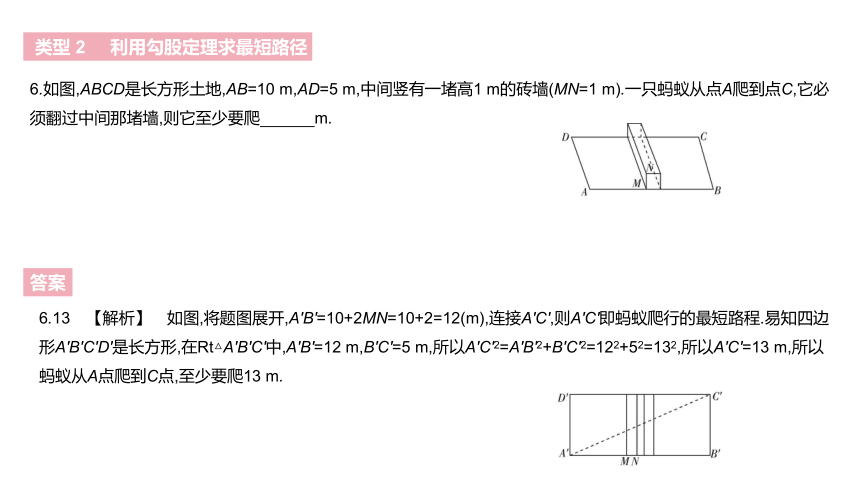
6.如图,ABCD是长方形土地,AB=10 m,AD=5 m,中间竖有一堵高1 m的砖墙(MN=1 m).一只蚂蚁从点A爬到点C,它必须翻过中间那堵墙,则它至少要爬 m.?
答案
6.13 【解析】 如图,将题图展开,A'B'=10+2MN=10+2=12(m),连接A'C',则A'C'即蚂蚁爬行的最短路程.易知四边形A'B'C'D'是长方形,在Rt△A'B'C'中,A'B'=12 m,B'C'=5 m,所以A'C'2=A'B'2+B'C'2=122+52=132,所以A'C'=13 m,所以蚂蚁从A点爬到C点,至少要爬13 m.
类型 2 利用勾股定理求最短路径
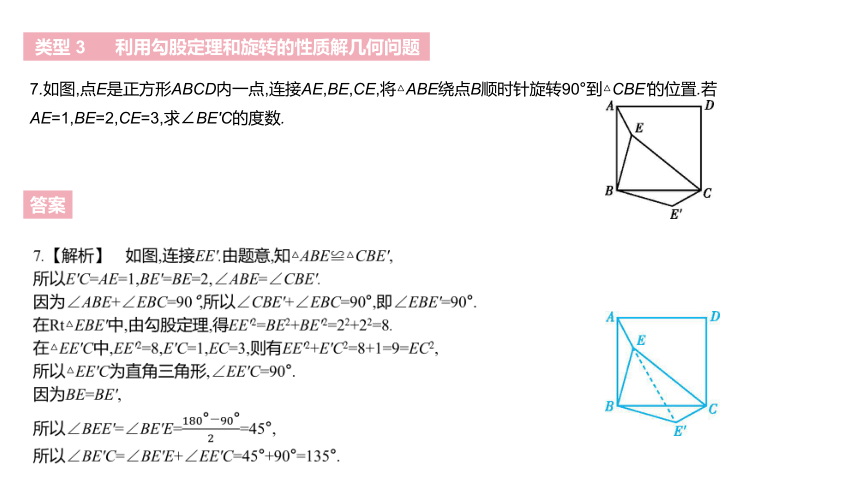
7.如图,点E是正方形ABCD内一点,连接AE,BE,CE,将△ABE绕点B顺时针旋转90°到△CBE'的位置.若AE=1,BE=2,CE=3,求∠BE'C的度数.
答案
7.【解析】 如图,连接EE'.由题意,知△ABE≌△CBE',
所以E'C=AE=1,BE'=BE=2,∠ABE=∠CBE'.
因为∠ABE+∠EBC=90°,所以∠CBE'+∠EBC=90°,即∠EBE'=90°.
在Rt△EBE'中,由勾股定理,得EE'2=BE2+BE'2=22+22=8.
在△EE'C中,EE'2=8,E'C=1,EC=3,则有EE'2+E'C2=8+1=9=EC2,
所以△EE'C为直角三角形,∠EE'C=90°.
因为BE=BE',
所以∠BEE'=∠BE'E=180°?90°2=45°,
所以∠BE'C=∠BE'E+∠EE'C=45°+90°=135°.
?
类型 3 利用勾股定理和旋转的性质解几何问题
综合素养拓训
素养解读
数学素养的形成离不开数学方法与思想的潜移默化.勾股定理是用代数思想解决几何问题的重要工具.在对勾股定理的研究中会逐渐体会到数形结合思想、方程思想,同时在用面积法验证勾股定理时会用到转化思想.第1题体现了转化思想,利用勾股定理将正方形的面积问题转化到直角三角形中解决;第2题通过用类比面积法来验证等式的方式,创设数学活动,体验图形组合、变换的过程;第3题以最短路径问题为背景,通过探究、对比,说明利用表面展开图得到的不一定是最短路径,对阅读理解能力、知识迁移能力及分析并解决问题的能力有一定的要求.
1.[利用转化思想求面积]在直线l上依次摆放着七个正方形(如图所示).已知斜放的三个正方形的面积分别是1,2,3,正放的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4= .?
答案
1.4 【解析】 如图,容易证明Rt△ACB≌Rt△BDE,所以BC=ED,所以AC2+ED2=AC2+BC2=AB2,所以S1+S2=1.同理可得S3+S4=3.所以S1+S2+S3+S4=1+3=4.
2.[勾股定理与图形组合]我们运用图1中大正方形的面积可表示为(a+b)2,也可表示为c2+4×12ab,即(a+b)2=c2+4×12ab,推导出一个重要的结论a2+b2=c2,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
请你用图2提供的图形(每种图形数量不限)进行组合,画出组合图形,用组合图形的面积表达式验证:(x+2y)2=x2+4xy+4y2.
?
答案
2.【解析】 画出组合图形如图所示.大正方形的面积为x2+4y2+4xy,也可以表示为(x+2y)2,
所以(x+2y)2=x2+4xy+4y2.
图1 图2
3.[探究最短路径]先阅读下面的材料,再解决问题.
【实际问题】 如图1,一圆柱的底面半径为5 cm,BC是底面直径,高AB为5 cm,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线.
【解决方案】 路线1:侧面展开图中的线段AC,如图2所示.
设路线1的长度为l1,则????12=AC2=AB2+BC2=52+(5π)2=25+25π2.
路线2:高线AB+底面直径BC.
设路线2的长度为l2,则????22=(AB+BC)2=(5+10)2=225.
为比较l1,l2的大小,采用“作差法”:
因为????12-????22=25(π2-8)>0,
所以????12>????22,所以l1>l2,
所以小明认为路线2较短.
(1)【问题类比】 小亮对上述结论有些疑惑,于是他把条件改成“圆柱的底面半径为1 cm,高AB为5 cm”.请你用上述方法帮小亮比较出l1与l2的大小.
(2)【问题拓展】 请你帮他们继续研究:在一般情况下,若圆柱的底面半径为r cm,高为h cm,蚂蚁从A点出发沿圆柱表面爬行到点C,当????h满足什么条件时,路线2较短?请说明理由.
(3)【问题解决】 图3是紧密排列在一起的2个相同的圆柱,高为5 cm.当蚂蚁从A点出发沿圆柱表面爬行到C点的两条路线长度相等时,求圆柱的底面半径r.
?
?
图1 图2 图3
答案
3.【解析】 (1)如题图2.
因为圆柱的底面半径为1 cm,高AB为5 cm,
所以路线1:????12=AC2=AB2+BC2=25+π2;
路线2:l2=AB+BC=5+2=7,则????22=49.
因为????12-????22=25+π2-49=π2-24<0,
所以????12所以路线1较短.
A出发沿圆柱表面爬行到C点的两条路线长度相等.
(2)如题图2.
因为圆柱的底面半径为r cm,高为h cm,
所以路线1:????12=AC2=AB2+BC2=h2+(πr)2,
路线2:????22=(AB+BC)2=(h+2r)2,
所以????12-????22=h2+(πr)2-(h+2r)2=r(π2r-4r-4h)=r[(π2-4)r-4h].
因为r恒大于0,所以当(π2-4)r-4h>0,即????h>4π2?4时,????12>????22,此时路线2较短.
?
答案
(3)如题图3,圆柱的高为5 cm.
路线1:????12=AC2=AB2+BC2=25+(2πr)2,
路线2:????22=(AB+BC)2=(5+4r)2,
由题意,得25+(2πr)2=(5+4r)2,
解得r=10π2?4.
即当圆柱的底面半径r为10π2?4 cm时,蚂蚁从点A出发沿圆柱表面爬行到C点的两条路线长度相等.
?
答案
1.A 【解析】 A项,因为62+82=102,所以此选项符合题意;B项,因为42+62≠82,所以此选项不符合题意;C项,因为不是三个正整数,所以此选项不符合题意;D项,因为3+6=9,不能构成三角形,所以此选项不符合题意.故选A.
一、选择题
1.[2020江苏盐城大丰区期中]下列各组数中,是勾股数的是 ( )
A.6,8,10
B.4,6,8
C.0.3,0.4,0.5
D.3,6,9
答案
2.D 【解析】 如图,延长AB,DC相交于点F,则△BFC是直角三角形,根据勾股定理,得BC2=(15-3)2+(20-4)2=122+162=400,所以BC=20.则剪去的直角三角形的斜边长为20 cm.故选D.
2.如图,小明将一张长为20 cm,宽为15 cm的长方形纸片(AE>DE)剪去了一角,量得AB=3 cm,CD=4 cm,则剪去的直角三角形的斜边长为 ( )
A.5 cm B.12 cm C.16 cm D.20 cm
答案
3.A 【解析】 因为a2+(b+c)2=2bc+2c2,所以a2+b2=c2,所以△ABC为直角三角形.故选A.
3.若a,b,c分别是△ABC的三边长,且a2+(b+c)2=2bc+2c2,则△ABC为 ( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等腰直角三角形
4.如图,在△ABC中,∠ACB=90°,AC=40,BC=9,点M,N在AB上,且AM=AC,BN=BC,则MN的长为 ( )
A.6 B.7 C.8 D.9
答案
4.C 【解析】 在△ABC中,∠ACB=90°,AC=40,BC=9,根据勾股定理,得AB2=AC2+CB2=412,所以AB=41.因为AM=AC=40,BN=BC=9,所以MN=AM+BN-AB=40+9-41=8.故选C.
答案
5.C 【解析】 在△ABC中,AB=7,BC=24,AC=25,所以AB2+BC2=72+242=252=AC2,所以∠ABC=90°.
如图,连接AP,BP,CP.由题意,知PE=PF=PG,设PE=PF=PG=x,因为S△ABC=12AB·CB=
12AB·x+12AC·x+12BC·x=12(AB+BC+AC)·x=12×56x=28x,所以28x=84,所以x=3.故选C.
?
5.[2020山东滨州一模]在△ABC中,AB=7,BC=24,AC=25,若△ABC内有一点P到各边的距离相等,则这个距离为 ( )
A.1 B.2 C.3 D.4
6.D 【解析】 在Rt△ABC中,AC2=AB2-BC2=42,所以AC=4米,所以地毯的长度为AC+BC=7米.故选D.
答案
6.[2020陕西宝鸡期中]如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度为 ( )
A.4米 B.5米 C.6米 D.7米
答案
7.D 【解析】 根据折叠的性质,得AB=AF,BE=FE=3,∠B=∠AFE=∠CFE=90°.因为BC=AD=8,所以CE=BC-BE=5.在Rt△CEF中,由勾股定理,得CF2=CE2-EF2=52-32=42,所以CF=4.设AB=x,则AC=4+x.在Rt△ABC中,由勾股定理,得AC2=AB2+BC2,即(4+x)2=x2+82,解得x=6.故选D.
7.[2019江苏无锡惠山区七校联考]如图,在长方形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为 ( )
A.3 B.4 C.5 D.6
答案
8.B 【解析】 如图,设旗杆的高度为x m,则AD=x m,AB=(x-1)m.在Rt△ADC中,AC2=AD2+CD2=x2+4.在Rt△ABC'中,AC'2=AB2+BC'2=(x-1)2+25,因为AC=AC',所以x2+4=(x-1)2+25,所以x=11.故选B.
8.[2020江苏常州新北区期中]2019年10月1日,中华人民共和国70年华诞之际,王梓涵和学校国旗护卫队的其他同学们赶到学校举行了简朴而隆重的升旗仪式.倾听着雄壮的国歌声,目送着五星红旗缓缓升起,不禁心潮澎湃,爱国之情油然而生.爱动脑筋的王梓涵设计了一个方案来测量学校旗杆的高度.将升旗的绳子拉直到末端刚好接触地面,测得此时绳子末端距旗杆底端2米,然后将绳子末端拉直到距离旗杆5 m处,测得此时绳子末端距离地面高度为1 m,最后根据学习的勾股定理算出旗杆的高度为 ( )
A.10 m B.11 m C.12 m D.13 m
图1 图2
答案
9.80 【解析】 如图,过点P作PG⊥BF于点G,连接BP.由题意,知AG=3,AP=AB=5,所以PG=4,BG=8,所以PB2=BG2+PG2=80,故这只蚂蚁的最短行程的平方是80.
二、填空题
9.如图,教室的墙面ADEF与地面ABCD垂直,点P在墙面上.已知PA=AB=5,点P到AD的距离是3,有一只蚂蚁要从点P爬到点B,它的最短行程的平方是 .?
答案
10.49 【解析】 如图,设正方形A的面积为a2,正方形B的面积为b2,正方形C的面积为c2,正方形D的面积为d2.因为a2+b2=x2,c2+d2=y2,所以正方形A,B,C,D的面积和为a2+b2+c2+d2=x2+y2=72=49(cm2).
10.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形A,B,C,D的面积之和为 cm2.?
答案
11.1 【解析】 由题图可知,a-b为小正方形的边长,因为小正方形的面积为1,所以(a-b)2=1.
11.[2019黑龙江大庆中考]我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a,b,那么(a-b)2的值是 .?
答案
12.40 【解析】 由题意知,∠CBD=90°,BC=8千米,BD=15千米,由勾股定理,得CD2=82+152=172,即CD=17千米,所以从C飞到D需要17分钟,所以沿B→C→D→B路线配送途中飞行的时间是8+15+17=40(分).
12.[2020河南平顶山期中]如图,幸福小区C位于快递站点B的北偏东35°方向,沁苑小区D位于B的南偏东55°方向,无人机以1千米/分的速度配送快递时,从B到C需飞行8分钟,从B到D需飞行15分钟.若无人机的配送路线是B→C→D→B,则配送途中飞行的时间为 分钟.?
答案
13.【解析】 在△ADE中,AD=3,AE=4,ED=5,
所以AD2+AE2=ED2,
所以△ADE是直角三角形,∠A=90°,
所以DA⊥AB.
因为∠C=90°,所以DC⊥BC,
又因为BD平分∠ABC,
所以CD=AD=3.
三、解答题
13.如图,在四边形ABCD中,∠C=90°,BD平分∠ABC,AD=3,E为AB上一点,AE=4,ED=5,求CD的长.
答案
14.【解析】 (1)第一类:(9,40,41).
第二类:(12,35,37).(答案不唯一)
(2)当a为奇数时,b=????2?12,c=????2+12;
当a为偶数时,b=????24-1,c=????24+1.
验证:当a为奇数时,a2+b2=a2+(????2?12)2=(????2+12)2=c2,
所以(a,b,c)是一组勾股数.
当a为偶数时,a2+b2=a2+(????24-1)2=(????24+1)2=c2,
所以(a,b,c)是一组勾股数.
(任选一种情形验证即可)
?
14.[2019安徽马鞍山二模]若正整数a,b,c(a观察下列两类勾股数:
第一类(a是奇数):(3,4,5);(5,12,13);(7,24,25)……
第二类(a是偶数):(6,8,10);(8,15,17);(10,24,26)……
(1)请再写出两组勾股数,每类各写一组;
(2)分别就a为奇数、偶数两种情形,用a表示b和c,并选择其中一种情形验证(a,b,c)是一组勾股数.
答案
15.【解析】 (1)村庄能听到广播宣传.理由如下:
因为村庄A到公路MN的距离AB=600米,600<1 000,
所以村庄能听到广播宣传.
(2)如图,假设当宣讲车行驶到C点时,村庄A开始听到宣传,行驶到D点时,刚好听不到宣传,
则AC=AD=1 000米,AB=600米,
所以BC2=BD2=1 0002-6002=8002,
所以BC=800米,所以CD=1 600米,
所以村庄总共能听到宣传的时间为1 600÷200=8(分).
15.[2020四川遂宁期末]为了积极响应国家新农村建设,遂宁市某镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路MN的一侧点A处有一村庄,村庄A到公路MN的距离AB=600米,宣讲车P周围1 000米以内能听到广播宣传,宣讲车P在公路MN上沿PN方向行驶.
(1)请问村庄能否听到广播宣传?说明理由;
(2)如果能听到,已知宣讲车的速度是200米/分,那么村庄总共能听到多长时间的宣传?
16.[2019四川成都外国语学校模拟]如图,已知△ABC中,∠B=90°,AB=8 cm,BC=6 cm,P,Q是△ABC边上的两个动点,点P从点A开始沿A→B方向运动,且速度为1 cm/s,点Q从点B开始沿B→C→A方向运动,且速度为2 cm/s,它们同时出发,设运动的时间为t s.
(1)求运动几秒时,△APC是等腰三角形?
(2)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
答案
16.【解析】 (1)当△APC是等腰三角形时,AP=CP=t cm,则BP=(8-t)cm.
在Rt△BPC中,由勾股定理,得BC2+BP2=CP2,
即62+(8-t)2=t2,解得t=254,
故当运动254 s时,△APC是等腰三角形.
?
答案
(2)由△ABC是直角三角形,AB=8 cm,BC=6 cm,可得AC=10 cm.
分三种情况:
①当CQ=BQ时,如图1,则∠C=∠CBQ.
因为∠ABC=90°,所以∠CBQ+∠ABQ=90°,∠A+∠C=90°,
所以∠A=∠ABQ,所以BQ=AQ,
所以CQ=AQ=12AC=5 cm,所以BC+CQ=11 cm,
所以t=11÷2=5.5.
②当CQ=BC时,如图2,则BC+CQ=12 cm.
所以t=12÷2=6.
③当BC=BQ时,如图3,
过点B作BE⊥AC交AC于点E,
则BE=????????·????????????????=6×810=4.8(cm).
在Rt△CEB中,由勾股定理,得CE2=CB2-BE2=62-4.82=3.62,所以CE=3.6 cm,所以CQ=2CE=7.2 cm,
所以BC+CQ=13.2 cm,
所以t=13.2÷2=6.6.
综上,当运动时间为5.5 s或6 s或6.6 s时,△BCQ为等腰三角形.
?
图3
图2
图1
第一章·勾股定理中考真题
数学·八年级上册 ·北师
答案
1.B 【解析】 如图,AC=AM+MN=4,BC=MN+NB=3,AB=AM+MN+NB=2+2+1=5,所以AC2+BC2=AB2,所以△ABC是直角三角形.故选B.
1.[2019湖南益阳中考]已知M,N是线段AB上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则△ABC一定是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
答案
2.B 【解析】 设题图中小正方形的边长为x,由勾股定理,得(x+3)2+(x+4)2=(3+4)2,化简,得x2+7x=12,故该长方形的面积为(x+3)(x+4)=x2+7x+12=12+12=24.故选B.
2. [2018浙江温州中考]我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的长方形由两个同样的图形拼成,若a=3,b=4,则该长方形的面积为( )
A.20 B.24 C.994 D.532
?
答案
3.C 【解析】 设直角三角形的斜边长为c,较长直角边为b,较短直角边为a,由勾股定理,得c2=a2+b2,所以阴影部分的面积为c2-b2-a(c-b)=a2-ac+ab=a(a+b-c),因为较小两个正方形重叠部分的宽为a-(c-b),长为a,所以较小两个正方形重叠部分的面积为a(a+b-c),所以知道图中阴影部分的面积,则一定能求出较小两个正方形重叠部分的面积.故选C.
3.[2019浙江宁波中考]勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出 ( )
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
答案
4.10 【解析】 由题意知,BG=AF=DE=8,FG=EF=2,所以BF=BG-FG=6.在Rt△ABF中,由勾股定理,得AB2=AF2+BF2=82+62=102,所以AB的长为10.
4.[2017吉林长春中考]如图1,这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图2,其中四边形ABCD和四边形EFGH都是正方形,△ABF,△BCG,△CDH,△DAE是四个全等的直角三角形.若EF=2,DE=8,则AB的长为 .?
答案
5.5 【解析】 由题意可得,122+92=152,所以木筷在杯子内的部分最长为15 cm,所以木筷露在杯子外面的部分至少有20-15=5(cm).
5.[2019江苏南京中考]无盖圆柱形杯子的展开图如图所示.将一根长为20 cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 cm.?
答案
6.45 【解析】 如图,延长AP到点D,连接BD,设小正方形的边长为1,则PD2=BD2=12+22=5,PB2=12+32=10,所以PD2+BD2=PB2,所以△PDB是等腰直角三角形,且∠PDB=90°,所以∠DPB=45°,所以∠PAB+∠PBA=∠DPB=45°.
6.[2019北京中考]如图所示的网格是正方形网格,则∠PAB+∠PBA= °(点A,B,P是网格线交点).?
答案
7.3.6,4.32或4.8 【解析】 在Rt△ABC中,∠ABC=90°,AB=3,BC=4,由勾股定理,得AC2=AB2+BC2=32+42=52,所以AC=5,过点B作BD⊥AC于点D,则S△ABC=12AB·BC=12AC·BD,所以BD=2.4.沿过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,如图,有三种情况:
①当AB=AP=3时,如图1,S等腰三角形ABP=12AP·BD=12×3×2.4=3.6;②当AB=BP=3时,如图2,在Rt△ABD中,由勾股定理,得AD2=AB2-BD2=1.82,所以AD=1.8,所以AP=2AD=3.6,所以S等腰三角形ABP=12AP·BD=12×3.6×2.4=4.32;③当CB=CP=4时,如图3,S等腰三角形BCP=12CP·BD=12×4×2.4=4.8.综上所述,等腰三角形的面积可能为3.6,4.32或4.8.
?
7.[2018黑龙江龙东地区中考]Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是 .?
图1 图2 图3
答案
8.【解析】 (1)因为四边形ABCD是长方形,
所以AB=CD,∠B=∠D=90°,
因为将长方形ABCD沿对角线AC翻折,点B落在点F处,
所以∠F=∠B,AB=AF,
所以AF=CD,∠F=∠D.
在△AFE与△CDE中,∠????=∠????,∠????????????=∠????????????,????????=????????,
所以△AFE≌△CDE.
?
8.[2017湖北鄂州中考]如图,将长方形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
(1)求证:△AFE≌△CDE.
(2)若AB=4,BC=8,求图中阴影部分的面积.
答案
(2)因为AB=4,BC=8,
所以CF=AD=BC=8,AF=CD=AB=4.
由(1)知△AFE≌△CDE,所以AE=CE,FE=DE,
在Rt△CDE中,由勾股定理,得DE2+CD2=CE2,
即DE2+42=CE2=AE2=(8-DE)2,
所以DE=3,所以FE=DE=3,
所以图中阴影部分的面积为????△????????????-????△????????????=12×4×8-12×4×3=10.
数学·八年级上册·北师
专项素养拓训
专题 勾股定理的应用
专项
1.如图,△ABC中,∠C=90°,AC=6,BC=8,D,E分别在AC,BC上,且DE∥AB.将△ABC沿DE折叠,使C点落在斜边AB上的F点处,则AF的长是 ( )
A.3.6 B.4 C.4.8 D.6.4
答案
1.A 【解析】 如图,连接CF,根据题意,得CF⊥DE.因为DE∥AB,所以CF⊥AB.因为∠C=90°,AC=6,BC=8,所以AB=10,所以S△ABC=12AC·BC=12AB·CF,所以CF=4.8,所以AF2=AC2-CF2=62-4.82=3.62,所以AF=3.6.故选A.
?
类型 1 利用勾股定理解折叠问题
2.如图,长方形ABCD中,AB=6,BC=8,把长方形ABCD沿直线AE折叠,使点B落在长方形ABCD内部的点F处,则CF的最小值是 ( )
A.2 B.4 C.6 D.8
答案
2.B 【解析】 连接AC.由题意,得AF=AB=6.在Rt△ABC中,AC2=AB2+BC2=102,所以AC=10.当A,F,C三点不共线时,CF>AC-AF, 当A,F,C三点共线时,CF=AC-AF=10-6=4,所以CF的最小值是4.故选B.
类型 1 利用勾股定理解折叠问题
3.如图,在长方形ABCD中,AB=3 cm,AD=9 cm,将此长方形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为 cm2.?
答案
3.6 【解析】 由题意可知BE=ED.设AE=x cm,因为AD=AE+DE=AE+BE=9 cm,所以BE=(9-x)cm.在Rt△ABE中,根据勾股定理可知,AB2+AE2=BE2,所以32+x2=(9-x)2,解得x=4,即AE=4 cm,所以△ABE的面积为12×AB×AE=12×3×4=6(cm2).
?
类型 1 利用勾股定理解折叠问题
4.如图,在边长为6的正方形ABCD中,E是边CD的中点.将△ADE沿AE折叠,得△AFE,延长EF交BC于点G,连接AG,AG平分∠BAF.
(1)试说明△ABG≌△AFG;
(2)求BG的长.
答案
4.【解析】 (1)在正方形ABCD中,AD=AB=BC=CD=6.
由折叠的性质,可知AD=AF,所以AB=AF,
因为AG平分∠BAF,所以∠BAG=∠FAG.
在△ABG和△AFG中,????????=????????,∠????????????=∠????????????,????????=????????,
所以△ABG≌△AFG.
(2)因为△ABG≌△AFG,所以BG=FG.
设BG=FG=x,则GC=6-x.
因为E为CD的中点,
所以CE=EF=DE=12CD=3,所以EG=3+x,
在Rt△CEG中,由勾股定理,得CE2+CG2=EG2,即32+(6-x)2=(3+x)2,
解得x=2,所以BG=2.
?
5.[2019陕西西安交大附中期中]我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处.则问题中葛藤的最短长度是 尺.?
答案
5.25 【解析】 如图,AB的长即问题中葛藤的最短长度.一条直角边长(即圆柱的高)为20尺,另一条直角边长为5×3=15(尺),因此AB2=152+202=252,所以AB=25尺,所以问题中葛藤的最短长度是25尺.
类型 2 利用勾股定理求最短路径
6.如图,ABCD是长方形土地,AB=10 m,AD=5 m,中间竖有一堵高1 m的砖墙(MN=1 m).一只蚂蚁从点A爬到点C,它必须翻过中间那堵墙,则它至少要爬 m.?
答案
6.13 【解析】 如图,将题图展开,A'B'=10+2MN=10+2=12(m),连接A'C',则A'C'即蚂蚁爬行的最短路程.易知四边形A'B'C'D'是长方形,在Rt△A'B'C'中,A'B'=12 m,B'C'=5 m,所以A'C'2=A'B'2+B'C'2=122+52=132,所以A'C'=13 m,所以蚂蚁从A点爬到C点,至少要爬13 m.
类型 2 利用勾股定理求最短路径
7.如图,点E是正方形ABCD内一点,连接AE,BE,CE,将△ABE绕点B顺时针旋转90°到△CBE'的位置.若AE=1,BE=2,CE=3,求∠BE'C的度数.
答案
7.【解析】 如图,连接EE'.由题意,知△ABE≌△CBE',
所以E'C=AE=1,BE'=BE=2,∠ABE=∠CBE'.
因为∠ABE+∠EBC=90°,所以∠CBE'+∠EBC=90°,即∠EBE'=90°.
在Rt△EBE'中,由勾股定理,得EE'2=BE2+BE'2=22+22=8.
在△EE'C中,EE'2=8,E'C=1,EC=3,则有EE'2+E'C2=8+1=9=EC2,
所以△EE'C为直角三角形,∠EE'C=90°.
因为BE=BE',
所以∠BEE'=∠BE'E=180°?90°2=45°,
所以∠BE'C=∠BE'E+∠EE'C=45°+90°=135°.
?
类型 3 利用勾股定理和旋转的性质解几何问题
综合素养拓训
素养解读
数学素养的形成离不开数学方法与思想的潜移默化.勾股定理是用代数思想解决几何问题的重要工具.在对勾股定理的研究中会逐渐体会到数形结合思想、方程思想,同时在用面积法验证勾股定理时会用到转化思想.第1题体现了转化思想,利用勾股定理将正方形的面积问题转化到直角三角形中解决;第2题通过用类比面积法来验证等式的方式,创设数学活动,体验图形组合、变换的过程;第3题以最短路径问题为背景,通过探究、对比,说明利用表面展开图得到的不一定是最短路径,对阅读理解能力、知识迁移能力及分析并解决问题的能力有一定的要求.
1.[利用转化思想求面积]在直线l上依次摆放着七个正方形(如图所示).已知斜放的三个正方形的面积分别是1,2,3,正放的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4= .?
答案
1.4 【解析】 如图,容易证明Rt△ACB≌Rt△BDE,所以BC=ED,所以AC2+ED2=AC2+BC2=AB2,所以S1+S2=1.同理可得S3+S4=3.所以S1+S2+S3+S4=1+3=4.
2.[勾股定理与图形组合]我们运用图1中大正方形的面积可表示为(a+b)2,也可表示为c2+4×12ab,即(a+b)2=c2+4×12ab,推导出一个重要的结论a2+b2=c2,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
请你用图2提供的图形(每种图形数量不限)进行组合,画出组合图形,用组合图形的面积表达式验证:(x+2y)2=x2+4xy+4y2.
?
答案
2.【解析】 画出组合图形如图所示.大正方形的面积为x2+4y2+4xy,也可以表示为(x+2y)2,
所以(x+2y)2=x2+4xy+4y2.
图1 图2
3.[探究最短路径]先阅读下面的材料,再解决问题.
【实际问题】 如图1,一圆柱的底面半径为5 cm,BC是底面直径,高AB为5 cm,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线.
【解决方案】 路线1:侧面展开图中的线段AC,如图2所示.
设路线1的长度为l1,则????12=AC2=AB2+BC2=52+(5π)2=25+25π2.
路线2:高线AB+底面直径BC.
设路线2的长度为l2,则????22=(AB+BC)2=(5+10)2=225.
为比较l1,l2的大小,采用“作差法”:
因为????12-????22=25(π2-8)>0,
所以????12>????22,所以l1>l2,
所以小明认为路线2较短.
(1)【问题类比】 小亮对上述结论有些疑惑,于是他把条件改成“圆柱的底面半径为1 cm,高AB为5 cm”.请你用上述方法帮小亮比较出l1与l2的大小.
(2)【问题拓展】 请你帮他们继续研究:在一般情况下,若圆柱的底面半径为r cm,高为h cm,蚂蚁从A点出发沿圆柱表面爬行到点C,当????h满足什么条件时,路线2较短?请说明理由.
(3)【问题解决】 图3是紧密排列在一起的2个相同的圆柱,高为5 cm.当蚂蚁从A点出发沿圆柱表面爬行到C点的两条路线长度相等时,求圆柱的底面半径r.
?
?
图1 图2 图3
答案
3.【解析】 (1)如题图2.
因为圆柱的底面半径为1 cm,高AB为5 cm,
所以路线1:????12=AC2=AB2+BC2=25+π2;
路线2:l2=AB+BC=5+2=7,则????22=49.
因为????12-????22=25+π2-49=π2-24<0,
所以????12所以路线1较短.
A出发沿圆柱表面爬行到C点的两条路线长度相等.
(2)如题图2.
因为圆柱的底面半径为r cm,高为h cm,
所以路线1:????12=AC2=AB2+BC2=h2+(πr)2,
路线2:????22=(AB+BC)2=(h+2r)2,
所以????12-????22=h2+(πr)2-(h+2r)2=r(π2r-4r-4h)=r[(π2-4)r-4h].
因为r恒大于0,所以当(π2-4)r-4h>0,即????h>4π2?4时,????12>????22,此时路线2较短.
?
答案
(3)如题图3,圆柱的高为5 cm.
路线1:????12=AC2=AB2+BC2=25+(2πr)2,
路线2:????22=(AB+BC)2=(5+4r)2,
由题意,得25+(2πr)2=(5+4r)2,
解得r=10π2?4.
即当圆柱的底面半径r为10π2?4 cm时,蚂蚁从点A出发沿圆柱表面爬行到C点的两条路线长度相等.
?
答案
1.A 【解析】 A项,因为62+82=102,所以此选项符合题意;B项,因为42+62≠82,所以此选项不符合题意;C项,因为不是三个正整数,所以此选项不符合题意;D项,因为3+6=9,不能构成三角形,所以此选项不符合题意.故选A.
一、选择题
1.[2020江苏盐城大丰区期中]下列各组数中,是勾股数的是 ( )
A.6,8,10
B.4,6,8
C.0.3,0.4,0.5
D.3,6,9
答案
2.D 【解析】 如图,延长AB,DC相交于点F,则△BFC是直角三角形,根据勾股定理,得BC2=(15-3)2+(20-4)2=122+162=400,所以BC=20.则剪去的直角三角形的斜边长为20 cm.故选D.
2.如图,小明将一张长为20 cm,宽为15 cm的长方形纸片(AE>DE)剪去了一角,量得AB=3 cm,CD=4 cm,则剪去的直角三角形的斜边长为 ( )
A.5 cm B.12 cm C.16 cm D.20 cm
答案
3.A 【解析】 因为a2+(b+c)2=2bc+2c2,所以a2+b2=c2,所以△ABC为直角三角形.故选A.
3.若a,b,c分别是△ABC的三边长,且a2+(b+c)2=2bc+2c2,则△ABC为 ( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等腰直角三角形
4.如图,在△ABC中,∠ACB=90°,AC=40,BC=9,点M,N在AB上,且AM=AC,BN=BC,则MN的长为 ( )
A.6 B.7 C.8 D.9
答案
4.C 【解析】 在△ABC中,∠ACB=90°,AC=40,BC=9,根据勾股定理,得AB2=AC2+CB2=412,所以AB=41.因为AM=AC=40,BN=BC=9,所以MN=AM+BN-AB=40+9-41=8.故选C.
答案
5.C 【解析】 在△ABC中,AB=7,BC=24,AC=25,所以AB2+BC2=72+242=252=AC2,所以∠ABC=90°.
如图,连接AP,BP,CP.由题意,知PE=PF=PG,设PE=PF=PG=x,因为S△ABC=12AB·CB=
12AB·x+12AC·x+12BC·x=12(AB+BC+AC)·x=12×56x=28x,所以28x=84,所以x=3.故选C.
?
5.[2020山东滨州一模]在△ABC中,AB=7,BC=24,AC=25,若△ABC内有一点P到各边的距离相等,则这个距离为 ( )
A.1 B.2 C.3 D.4
6.D 【解析】 在Rt△ABC中,AC2=AB2-BC2=42,所以AC=4米,所以地毯的长度为AC+BC=7米.故选D.
答案
6.[2020陕西宝鸡期中]如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度为 ( )
A.4米 B.5米 C.6米 D.7米
答案
7.D 【解析】 根据折叠的性质,得AB=AF,BE=FE=3,∠B=∠AFE=∠CFE=90°.因为BC=AD=8,所以CE=BC-BE=5.在Rt△CEF中,由勾股定理,得CF2=CE2-EF2=52-32=42,所以CF=4.设AB=x,则AC=4+x.在Rt△ABC中,由勾股定理,得AC2=AB2+BC2,即(4+x)2=x2+82,解得x=6.故选D.
7.[2019江苏无锡惠山区七校联考]如图,在长方形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为 ( )
A.3 B.4 C.5 D.6
答案
8.B 【解析】 如图,设旗杆的高度为x m,则AD=x m,AB=(x-1)m.在Rt△ADC中,AC2=AD2+CD2=x2+4.在Rt△ABC'中,AC'2=AB2+BC'2=(x-1)2+25,因为AC=AC',所以x2+4=(x-1)2+25,所以x=11.故选B.
8.[2020江苏常州新北区期中]2019年10月1日,中华人民共和国70年华诞之际,王梓涵和学校国旗护卫队的其他同学们赶到学校举行了简朴而隆重的升旗仪式.倾听着雄壮的国歌声,目送着五星红旗缓缓升起,不禁心潮澎湃,爱国之情油然而生.爱动脑筋的王梓涵设计了一个方案来测量学校旗杆的高度.将升旗的绳子拉直到末端刚好接触地面,测得此时绳子末端距旗杆底端2米,然后将绳子末端拉直到距离旗杆5 m处,测得此时绳子末端距离地面高度为1 m,最后根据学习的勾股定理算出旗杆的高度为 ( )
A.10 m B.11 m C.12 m D.13 m
图1 图2
答案
9.80 【解析】 如图,过点P作PG⊥BF于点G,连接BP.由题意,知AG=3,AP=AB=5,所以PG=4,BG=8,所以PB2=BG2+PG2=80,故这只蚂蚁的最短行程的平方是80.
二、填空题
9.如图,教室的墙面ADEF与地面ABCD垂直,点P在墙面上.已知PA=AB=5,点P到AD的距离是3,有一只蚂蚁要从点P爬到点B,它的最短行程的平方是 .?
答案
10.49 【解析】 如图,设正方形A的面积为a2,正方形B的面积为b2,正方形C的面积为c2,正方形D的面积为d2.因为a2+b2=x2,c2+d2=y2,所以正方形A,B,C,D的面积和为a2+b2+c2+d2=x2+y2=72=49(cm2).
10.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形A,B,C,D的面积之和为 cm2.?
答案
11.1 【解析】 由题图可知,a-b为小正方形的边长,因为小正方形的面积为1,所以(a-b)2=1.
11.[2019黑龙江大庆中考]我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a,b,那么(a-b)2的值是 .?
答案
12.40 【解析】 由题意知,∠CBD=90°,BC=8千米,BD=15千米,由勾股定理,得CD2=82+152=172,即CD=17千米,所以从C飞到D需要17分钟,所以沿B→C→D→B路线配送途中飞行的时间是8+15+17=40(分).
12.[2020河南平顶山期中]如图,幸福小区C位于快递站点B的北偏东35°方向,沁苑小区D位于B的南偏东55°方向,无人机以1千米/分的速度配送快递时,从B到C需飞行8分钟,从B到D需飞行15分钟.若无人机的配送路线是B→C→D→B,则配送途中飞行的时间为 分钟.?
答案
13.【解析】 在△ADE中,AD=3,AE=4,ED=5,
所以AD2+AE2=ED2,
所以△ADE是直角三角形,∠A=90°,
所以DA⊥AB.
因为∠C=90°,所以DC⊥BC,
又因为BD平分∠ABC,
所以CD=AD=3.
三、解答题
13.如图,在四边形ABCD中,∠C=90°,BD平分∠ABC,AD=3,E为AB上一点,AE=4,ED=5,求CD的长.
答案
14.【解析】 (1)第一类:(9,40,41).
第二类:(12,35,37).(答案不唯一)
(2)当a为奇数时,b=????2?12,c=????2+12;
当a为偶数时,b=????24-1,c=????24+1.
验证:当a为奇数时,a2+b2=a2+(????2?12)2=(????2+12)2=c2,
所以(a,b,c)是一组勾股数.
当a为偶数时,a2+b2=a2+(????24-1)2=(????24+1)2=c2,
所以(a,b,c)是一组勾股数.
(任选一种情形验证即可)
?
14.[2019安徽马鞍山二模]若正整数a,b,c(a
第一类(a是奇数):(3,4,5);(5,12,13);(7,24,25)……
第二类(a是偶数):(6,8,10);(8,15,17);(10,24,26)……
(1)请再写出两组勾股数,每类各写一组;
(2)分别就a为奇数、偶数两种情形,用a表示b和c,并选择其中一种情形验证(a,b,c)是一组勾股数.
答案
15.【解析】 (1)村庄能听到广播宣传.理由如下:
因为村庄A到公路MN的距离AB=600米,600<1 000,
所以村庄能听到广播宣传.
(2)如图,假设当宣讲车行驶到C点时,村庄A开始听到宣传,行驶到D点时,刚好听不到宣传,
则AC=AD=1 000米,AB=600米,
所以BC2=BD2=1 0002-6002=8002,
所以BC=800米,所以CD=1 600米,
所以村庄总共能听到宣传的时间为1 600÷200=8(分).
15.[2020四川遂宁期末]为了积极响应国家新农村建设,遂宁市某镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路MN的一侧点A处有一村庄,村庄A到公路MN的距离AB=600米,宣讲车P周围1 000米以内能听到广播宣传,宣讲车P在公路MN上沿PN方向行驶.
(1)请问村庄能否听到广播宣传?说明理由;
(2)如果能听到,已知宣讲车的速度是200米/分,那么村庄总共能听到多长时间的宣传?
16.[2019四川成都外国语学校模拟]如图,已知△ABC中,∠B=90°,AB=8 cm,BC=6 cm,P,Q是△ABC边上的两个动点,点P从点A开始沿A→B方向运动,且速度为1 cm/s,点Q从点B开始沿B→C→A方向运动,且速度为2 cm/s,它们同时出发,设运动的时间为t s.
(1)求运动几秒时,△APC是等腰三角形?
(2)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
答案
16.【解析】 (1)当△APC是等腰三角形时,AP=CP=t cm,则BP=(8-t)cm.
在Rt△BPC中,由勾股定理,得BC2+BP2=CP2,
即62+(8-t)2=t2,解得t=254,
故当运动254 s时,△APC是等腰三角形.
?
答案
(2)由△ABC是直角三角形,AB=8 cm,BC=6 cm,可得AC=10 cm.
分三种情况:
①当CQ=BQ时,如图1,则∠C=∠CBQ.
因为∠ABC=90°,所以∠CBQ+∠ABQ=90°,∠A+∠C=90°,
所以∠A=∠ABQ,所以BQ=AQ,
所以CQ=AQ=12AC=5 cm,所以BC+CQ=11 cm,
所以t=11÷2=5.5.
②当CQ=BC时,如图2,则BC+CQ=12 cm.
所以t=12÷2=6.
③当BC=BQ时,如图3,
过点B作BE⊥AC交AC于点E,
则BE=????????·????????????????=6×810=4.8(cm).
在Rt△CEB中,由勾股定理,得CE2=CB2-BE2=62-4.82=3.62,所以CE=3.6 cm,所以CQ=2CE=7.2 cm,
所以BC+CQ=13.2 cm,
所以t=13.2÷2=6.6.
综上,当运动时间为5.5 s或6 s或6.6 s时,△BCQ为等腰三角形.
?
图3
图2
图1
第一章·勾股定理中考真题
数学·八年级上册 ·北师
答案
1.B 【解析】 如图,AC=AM+MN=4,BC=MN+NB=3,AB=AM+MN+NB=2+2+1=5,所以AC2+BC2=AB2,所以△ABC是直角三角形.故选B.
1.[2019湖南益阳中考]已知M,N是线段AB上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则△ABC一定是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
答案
2.B 【解析】 设题图中小正方形的边长为x,由勾股定理,得(x+3)2+(x+4)2=(3+4)2,化简,得x2+7x=12,故该长方形的面积为(x+3)(x+4)=x2+7x+12=12+12=24.故选B.
2. [2018浙江温州中考]我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的长方形由两个同样的图形拼成,若a=3,b=4,则该长方形的面积为( )
A.20 B.24 C.994 D.532
?
答案
3.C 【解析】 设直角三角形的斜边长为c,较长直角边为b,较短直角边为a,由勾股定理,得c2=a2+b2,所以阴影部分的面积为c2-b2-a(c-b)=a2-ac+ab=a(a+b-c),因为较小两个正方形重叠部分的宽为a-(c-b),长为a,所以较小两个正方形重叠部分的面积为a(a+b-c),所以知道图中阴影部分的面积,则一定能求出较小两个正方形重叠部分的面积.故选C.
3.[2019浙江宁波中考]勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出 ( )
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
答案
4.10 【解析】 由题意知,BG=AF=DE=8,FG=EF=2,所以BF=BG-FG=6.在Rt△ABF中,由勾股定理,得AB2=AF2+BF2=82+62=102,所以AB的长为10.
4.[2017吉林长春中考]如图1,这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图2,其中四边形ABCD和四边形EFGH都是正方形,△ABF,△BCG,△CDH,△DAE是四个全等的直角三角形.若EF=2,DE=8,则AB的长为 .?
答案
5.5 【解析】 由题意可得,122+92=152,所以木筷在杯子内的部分最长为15 cm,所以木筷露在杯子外面的部分至少有20-15=5(cm).
5.[2019江苏南京中考]无盖圆柱形杯子的展开图如图所示.将一根长为20 cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 cm.?
答案
6.45 【解析】 如图,延长AP到点D,连接BD,设小正方形的边长为1,则PD2=BD2=12+22=5,PB2=12+32=10,所以PD2+BD2=PB2,所以△PDB是等腰直角三角形,且∠PDB=90°,所以∠DPB=45°,所以∠PAB+∠PBA=∠DPB=45°.
6.[2019北京中考]如图所示的网格是正方形网格,则∠PAB+∠PBA= °(点A,B,P是网格线交点).?
答案
7.3.6,4.32或4.8 【解析】 在Rt△ABC中,∠ABC=90°,AB=3,BC=4,由勾股定理,得AC2=AB2+BC2=32+42=52,所以AC=5,过点B作BD⊥AC于点D,则S△ABC=12AB·BC=12AC·BD,所以BD=2.4.沿过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,如图,有三种情况:
①当AB=AP=3时,如图1,S等腰三角形ABP=12AP·BD=12×3×2.4=3.6;②当AB=BP=3时,如图2,在Rt△ABD中,由勾股定理,得AD2=AB2-BD2=1.82,所以AD=1.8,所以AP=2AD=3.6,所以S等腰三角形ABP=12AP·BD=12×3.6×2.4=4.32;③当CB=CP=4时,如图3,S等腰三角形BCP=12CP·BD=12×4×2.4=4.8.综上所述,等腰三角形的面积可能为3.6,4.32或4.8.
?
7.[2018黑龙江龙东地区中考]Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是 .?
图1 图2 图3
答案
8.【解析】 (1)因为四边形ABCD是长方形,
所以AB=CD,∠B=∠D=90°,
因为将长方形ABCD沿对角线AC翻折,点B落在点F处,
所以∠F=∠B,AB=AF,
所以AF=CD,∠F=∠D.
在△AFE与△CDE中,∠????=∠????,∠????????????=∠????????????,????????=????????,
所以△AFE≌△CDE.
?
8.[2017湖北鄂州中考]如图,将长方形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
(1)求证:△AFE≌△CDE.
(2)若AB=4,BC=8,求图中阴影部分的面积.
答案
(2)因为AB=4,BC=8,
所以CF=AD=BC=8,AF=CD=AB=4.
由(1)知△AFE≌△CDE,所以AE=CE,FE=DE,
在Rt△CDE中,由勾股定理,得DE2+CD2=CE2,
即DE2+42=CE2=AE2=(8-DE)2,
所以DE=3,所以FE=DE=3,
所以图中阴影部分的面积为????△????????????-????△????????????=12×4×8-12×4×3=10.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
