北师大版八年级上册数学第一章勾股定理整章同步教学课件(69张PPT)
文档属性
| 名称 | 北师大版八年级上册数学第一章勾股定理整章同步教学课件(69张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-15 15:20:41 | ||
图片预览









文档简介
第一章·勾股定理
数学·八年级上册·北师
第一节 探索勾股定理
第一节
课时1 探索勾股定理
课时1
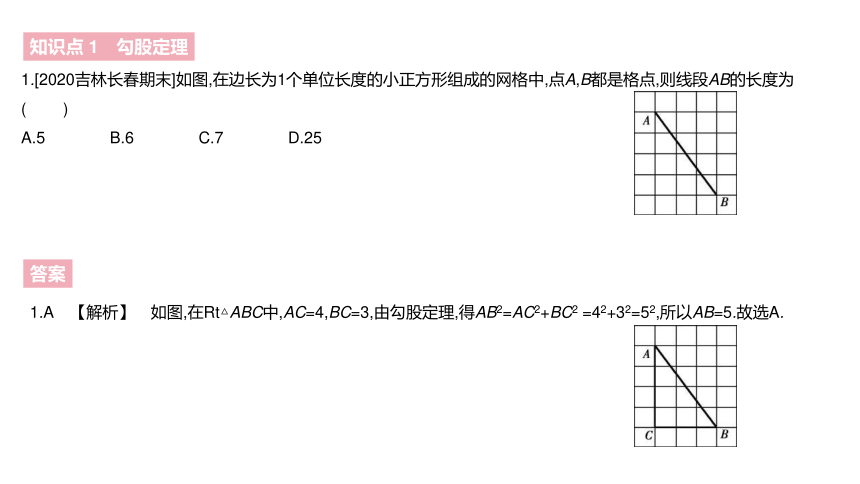
1.[2020吉林长春期末]如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则线段AB的长度为 ( )
A.5 B.6 C.7 D.25
答案
1.A 【解析】 如图,在Rt△ABC中,AC=4,BC=3,由勾股定理,得AB2=AC2+BC2 =42+32=52,所以AB=5.故选A.
知识点 1 勾股定理
2.易错题 下列说法中正确的是 ( )
A.已知a,b,c是三角形的三边长,则a2+b2=c2 B.在直角三角形中,两边的平方和等于第三边的平方
C.在Rt△ABC中,若∠C=90°,则BC2+AC2=AB2 D.在Rt△ABC中,若∠B=90°,则BC2+AC2=AB2
答案
2.C
知识点 1 勾股定理
3.[2019湖北鄂州模拟]如图是一张直角三角形纸片,∠C=90°,直角边AC=6 cm,BC=8 cm.现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为 ( )
A.4 cm B.5 cm C.6 cm D.10 cm
答案
3.B 【解析】 在Rt△ABC中,∠C=90°,所以AB2=AC2+BC2=62+82=100,所以AB=10 cm,又由折叠的性质可知BE=AE=12AB=5 cm.故选B.
?
4.易错题 [2019河北唐山路北区期中]在△ABC中,∠B=90°,a,b,c分别为∠A,∠B,∠C的对边.
(1)如果a=5,c=12,那么b= ;?
(2)如果b=61,a=60,那么c= .?
答案
4.(1)13;(2)11 【解析】 (1)在△ABC中,∠B=90°,a=5,c=12,所以b2=a2+c2=52+122=132,所以b=13.(2)在△ABC中,∠B=90°,b=61,a=60,所以c2=b2-a2=612-602=112,所以c=11.
知识点 1 勾股定理
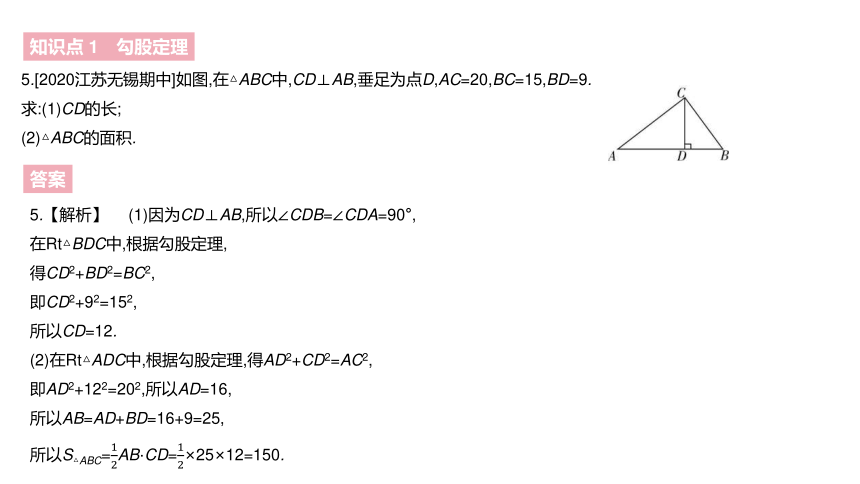
5.[2020江苏无锡期中]如图,在△ABC中,CD⊥AB,垂足为点D,AC=20,BC=15,BD=9.
求:(1)CD的长;
(2)△ABC的面积.
答案
5.【解析】 (1)因为CD⊥AB,所以∠CDB=∠CDA=90°,
在Rt△BDC中,根据勾股定理,
得CD2+BD2=BC2,
即CD2+92=152,
所以CD=12.
(2)在Rt△ADC中,根据勾股定理,得AD2+CD2=AC2,
即AD2+122=202,所以AD=16,
所以AB=AD+BD=16+9=25,
所以S△ABC=12AB·CD=12×25×12=150.
?
知识点 1 勾股定理
6.[2019山东济南育华中学月考]如图,25,169分别是相应正方形的面积,则字母B所代表的正方形的面积是 ( )
A.12 B.13 C.144 D.194
答案
6.C 【解析】 由题图可知,在直角三角形中,斜边的平方为169,一直角边的平方为25,根据勾股定理,知另一直角边的平方为169-25=144,所以字母B所代表的正方形的面积是144.故选C.
知识点 2 勾股定理与面积
7.[2020江苏宿迁期中]如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为 ( )
A.9 B.92 C.94 D.3
?
答案
7.B 【解析】 在Rt△AEC中,AE=EC,AC2=EC2+AE2,所以S△AEC=12AE·EC=12AE2=14AC2,同理可得,S△BCF=14BC2, S△ABD=14AB2.在Rt△ABC中,根据勾股定理,得AB2=AC2+BC2,因为AB=3,所以阴影部分的面积S=14(AC2+BC2+AB2)=12AB2=12×32=92.故选B.
?
知识点 2 勾股定理与面积
8.[2019贵州黔南州中考]如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,则正方形ABCD的面积为 .?
答案
8.3 【解析】 因为四边形ABCD是正方形,所以∠B=90°,所以BC2=EC2-EB2=22-12=3,所以正方形ABCD的面积为BC2=3.
知识点 2 勾股定理与面积
9.如图,在四边形ABCD中,∠BAD=90°,∠CBD=90°,AD=4,AB=3,BC=12,求以DC为边的正方形DCEF的面积.
答案
9.【解析】 在△ABD中,∠BAD=90°,
所以AD2+AB2=DB2,所以42+32=DB2,
所以DB=5.
在△BCD中,∠CBD=90°,
所以BD2+BC2=DC2,所以52+122=DC2,
所以DC=13,
所以S正方形DCEF=132=169.
知识点 2 勾股定理与面积
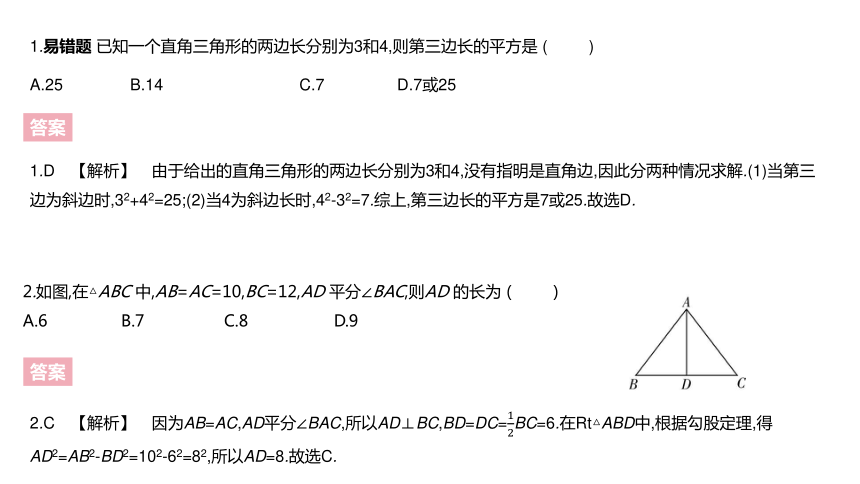
1.易错题 已知一个直角三角形的两边长分别为3和4,则第三边长的平方是 ( )
A.25 B.14 C.7 D.7或25
答案
1.D 【解析】 由于给出的直角三角形的两边长分别为3和4,没有指明是直角边,因此分两种情况求解.(1)当第三边为斜边时,32+42=25;(2)当4为斜边长时,42-32=7.综上,第三边长的平方是7或25.故选D.
2.C 【解析】 因为AB=AC,AD平分∠BAC,所以AD⊥BC,BD=DC=12BC=6.在Rt△ABD中,根据勾股定理,得AD2=AB2-BD2=102-62=82,所以AD=8.故选C.
?
2.如图,在△ABC 中,AB=AC=10,BC=12,AD 平分∠BAC,则AD 的长为 ( )
A.6 B.7 C.8 D.9
答案
3.如图所示的图形是由直角三角形和正方形组成的,其中正方形A的面积为40,四个正方形中的8,x,10,y分别表示该正方形的面积,则x+y= .?
答案
3.22 【解析】 根据题意,得x+8+(10+y)=S正方形A=40,所以x+y=40-18=22.
4.14或4 【解析】 ①当高AD在△ABC内部时,如图1,根据勾股定理,得BD2=152-122=81,CD2=132-122=25,所以BD=9,CD=5,所以BC=BD+CD=9+5=14;②当高AD在△ABC外部时,如图2,由①得BD=9,CD=5,所以BC=BD-CD=9-5=4.综合①②,得BC的长为14或4.
4.易错题 在△ABC中,AB=15,AC=13,BC边上的高AD=12,则BC的长为 .?
答案
图1 图2
5.如图,将长方形ABCD沿着AE折叠,点D落在BC边上的点F处,已知AB=8,BC=10,求EC的长.
答案
5.【解析】 依题意,得AD=AF=BC=10,DE=EF.
在△ABF中,∠ABF=90°,
所以BF2=AF2-AB2=102-82=62,
所以BF=6,所以FC=10-6=4.
设EC=x,则EF=DE=8-x.
因为∠C=90°,所以EC2+FC2=EF2,
所以x2+42=(8-x)2,解得x=3,
所以EC=3.
6.[2020江苏镇江期中]如图,在Rt△ABC中,AB=3,BC=4,动点P从点A出发沿AC向点C运动,同时动点Q从点B出发沿BA向点A运动,且到达A点后立刻以原来的速度沿AB返回.点P,Q的运动速度均为每秒1个单位长度,当点P到达点C时,点P,Q同时停止运动,连接PQ,CQ,设它们的运动时间为t(t>0)秒.
(1)设△CBQ的面积为S,请用含有t 的代数式来表示S;
(2)线段PQ的垂直平分线记为直线 l,当直线l 经过点C时,求AQ的长.
答案
6.【解析】 (1)在Rt△ABC中,AB=3,BC=4,
所以AC2=32+42=52,所以AC=5,
所以0当0当3所以S=12×4×(6-t)=12-2t.
综上,S=2????(0?
答案
(2)如图,因为PQ的垂直平分线过点C,所以CP=CQ=5-t.
在Rt△CBQ中,根据勾股定理,得BC2+BQ2=QC2,
当0当3所以AQ=3-910=2110.
?
7.在△ABC中,∠BAC=90°,分别以Rt△ABC的三边为直径作半圆.
(1)若这三个半圆在BC的两侧(如图1所示),半圆的面积分别为S1,S2,S3,则S1,S2,S3之间有什么数量关系?请说明理由.
(2)若这三个半圆在BC的同一侧(如图2所示),Rt△ABC的面积等于S3,两个“月牙”的面积分别为S1,S2,则S1,S2,S3之间有什么数量关系?请说明理由.
答案
7.【解析】 (1)S1+S2=S3.理由如下:
由题意,得S1=12π(????????2)2=18πAB2,S2=12π(????????2)2=18πAC2,S3=12π(????????2)2=18πBC2.
在Rt△ABC中,由勾股定理,得AB2+AC2=BC2,
所以18πAB2+18πAC2=18πBC2,所以S1+S2=S3.
?
答案
(2)S1+S2=S3.理由如下:
如图,由题意,得S1=12π(????????2)2-S4=18πAB2-S4,S2=12π(????????2)2-S5=18πAC2-S5,S3=12π(????????2)2-S4-S5=18πBC2-S4-S5.
在Rt△ABC中,由勾股定理,得AB2+AC2=BC2,
所以18πAB2-S4+18πAC2-S5=18πBC2-S4-S5,
所以S1+S2=S3.
?
课时2 验证并应用勾股定理
课时2
1.曾任美国总统的伽菲尔德曾经给出了一种勾股定理的证明方法.如图.
该图形整体上拼成了一个直角梯形,所以它的面积有两种表示方法,既可以表示为??????????????? ,
又可以表示为 .对比两种表示方法可得? ,化简,可得a2+b2=c2.?
?
答案
1.12(a+b)2 12ab+12c2+12ab 12(a+b)2=12ab+12c2+12ab
?
知识点 1 验证勾股定理
2.[2019安徽阜阳期末]用如图1所示的四个完全一样的直角三角形可以拼成如图2所示的大正方形.解答下列问题:
(1)请用含a,b,c的代数式表示大正方形的面积.
方法1: .方法2: .?
(2)根据图2及图形的面积关系,推导a,b,c之间满足的关系式.
(3)利用(2)的关系式解答:如果大正方形的面积是25,且(a+b)2=49,求小正方形的面积.
答案
2.【解析】 (1)(a-b)2+4×12ab c2
(2)由(1)可知,(a-b)2+4×12ab=c2,
即a2+b2=c2.
(3)由(2)知,a2+b2=c2.
因为(a+b)2=a2+b2+2ab=c2+4×12ab=大正方形的面积+四个直角三角形的面积和=49,
所以四个直角三角形的面积和为49-c2=49-25=24,
所以小正方形的面积为25-24=1.
?
知识点 1 验证勾股定理
图1 图2
3.如图,韩彬同学从家(记作A)出发向北偏东30°的方向行走了4 000 m到达超市(记作B),然后再从超市出发向南偏东60°的方向行走3 000 m到达卢飞同学家(记作C),则韩彬家到卢飞家的距离为 ( )
A.2 000 m B.3 000 m C.4 000 m D.5 000 m
答案
3.D 【解析】 如图,连接AC.依题意,得∠ABC=90°,AB=4 000 m,BC=3 000 m,则由勾股定理,得AC2=AB2+BC2=
4 0002+3 0002=5 0002,所以AC=5 000 m.故选D.
知识点 2 勾股定理的简单应用
4.[2020山东菏泽牡丹区期中]如图,有一架秋千,当它静止时,踏板离地的垂直高度DE=1 m,将它往前推送6 m(水平距离BC=6 m)时,秋千的踏板离地的垂直高度BF=4 m,秋千的绳索始终拉得很直,则绳索AD的长度为 m.?
答案
4.7.5 【解析】 设秋千的绳索长度为x m,则AB=AD=x m,AC=(x-3)m.在Rt△ACB中,根据勾股定理,得AC2+BC2=AB2,即(x-3)2+62=x2,解得x=7.5.所以绳索AD的长度是7.5 m.
知识点 2 勾股定理的简单应用
5.[2019山东济南育华中学月考]如图,一辆小汽车在一条限速为70 km/h的公路上直线行驶,某一时刻刚好行驶到路对面车速检测仪A正前方30 m的B处,过了2 s后,测得小汽车(位于C处)与车速检测仪A的距离为50 m,这辆小汽车超速了吗?
答案
5.【解析】在Rt△ABC中,由勾股定理,得BC2=AC2-AB2=502-302=402,
所以BC=40 m,
v=40÷2=20(m/s).
因为20 m/s=72 km/h,72>70,
所以这辆小汽车超速了.
知识点 2 勾股定理的简单应用
6.如图,有一只喜鹊在一棵3 m高的小树顶觅食,它的巢筑在距离该树24 m远的一棵大树上,大树高14 m,且巢离树顶部1 m,当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5 m/s,那么它至少需要多长时间才能赶回巢中?
答案
6.【解析】 如图,过点A作AE⊥CD于点E.
由题意知AB=3 m,CD=14-1=13(m),BD=24 m,
则CE=13-3=10(m),AE=24 m.
在Rt△AEC中,AC2=CE2+AE2=102+242,
故AC=26 m,则26÷5=5.2(s).
答:它至少需要5.2 s才能赶回巢中.
知识点 2 勾股定理的简单应用
1.如图,某学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,踩伤了花草,而他们仅仅少走路(假设2步为1米)( )
A.2步 B.4步 C.5步 D.10步
答案
1.B 【解析】 由题图可知,在Rt△ABC中,根据勾股定理,得AB2=AC2+BC2=32+42=52,所以AB=5 m,所以少走了2×(3+4-5)=4(步).故选B.
2.下列选项中(图中三角形都是直角三角形),不能用来验证勾股定理的是 ( )
答案
2.D
A B C D
3.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是 ( )
A.72 B.52 C.80 D.76
答案
3.D 【解析】 设“数学风车”中的四个直角三角形的斜边长为x,则x2=122+52=169,所以x=13,所以“数学风车”的外围周长是(13+6)×4=76.故选D.
图1 图2
4.铁路上A,B两站(视为直线上两点)相距25 km,C,D为两村庄(视为两个点),DA⊥AB于点A,CB⊥AB于点B,如图所示,已知AD=15 km,CB=10 km.现在要在铁路AB上建一个土特产收购站E,使得C,D两村庄到收购站E的距离相等,则收购站E应建在距A站 km处.?
答案
4.10 【解析】 因为C,D两村庄到收购站E的距离相等,所以CE=DE.在Rt△DAE和Rt△CBE中,DE2=AD2+AE2,
CE2=BE2+BC2,所以AD2+AE2=BE2+BC2.设 AE=x km,则BE=(25-x)km.将BC=10 km,AD=15 km代入关系式中,
得152+x2=(25-x)2+102,整理得50x=500,解得x=10,所以收购站E应建在距A站10 km处.
5.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明灵感,他惊喜地发现,当四个全等的直角三角形如图摆放时,可以用“面积法”来证明a2+b2=c2.请你写出证明过程.
答案
5.【解析】 如图,因为S五边形ABCDE=S梯形ABCF+S梯形AFDE=S正方形ABGE+2S△BCG,
即12(b+a+b)×b+12(a+a+b)×a=c2+2×12ab,
所以12ab+b2+a2+12ab=c2+ab,
所以a2+b2=c2.
?
6.[2019山东青岛期中]如图,教学楼走廊左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙底部的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,求教学楼走廊的宽度.
答案
6.【解析】 如图,在Rt△ABC中,∠ACB=90°,BC=0.7米,AC=2.4米,
所以AB2=0.72+2.42=6.25.
在Rt△A'BD中,∠A'DB=90°,A'D=2米,BD2+A'D2=A'B2,
所以BD2+22=6.25,所以BD2=2.25,
因为BD>0,所以BD=1.5米,
所以CD=BC+BD=0.7+1.5=2.2(米).
答:教学楼走廊的宽度是2.2米.
7.在△ABC中,BC=a,AC=b,AB=c.若∠ACB=90°,如图1所示,根据勾股定理,得a2+b2=c2.若△ABC不是直角三角形,如图2和图3所示.请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.
答案
7.【解析】 若△ABC是锐角三角形,则a2+b2>c2.
若△ABC是钝角三角形,∠C为钝角,则a2+b2当△ABC是锐角三角形时,证明如下:
在题图2中,过点A作AD⊥BC,垂足为D,设CD的长为x,则BD=a-x.
根据勾股定理,得b2-x2=AD2=c2-(a-x)2,
即b2-x2=c2-a2+2ax-x2,
所以a2+b2=c2+2ax.
图1 图2 图3
答案
因为a>0,x>0,所以2ax>0,所以a2+b2>c2.
当△ABC是钝角三角形,∠C为钝角时,证明如下:
在题图3中,过点B作BD⊥AC,交AC的延长线于点D,设CD的长为x,则有BD2=a2-x2.
在Rt△ABD中,
根据勾股定理,得(b+x)2+a2-x2=c2,
即a2+b2+2bx=c2,
因为b>0,x>0,所以2bx>0,
所以a2+b2第二节 一定是直角三角形吗
第二节
1.[2019江苏无锡期中]下列各组数,可以作为直角三角形的三边长的是 ( )
A.2,3,4 B.3,4,5 C.8,12,20 D.5,13,15
答案
1.B 【解析】 A项,22+32=13≠42,所以该三角形不是直角三角形,不合题意;B项,32+42=25=52,所以该三角形是直角三角形,符合题意;C项,8+12=20,所以不能构成三角形,不合题意;D项,52+132=194≠152,所以该三角形不是直角三角形,不合题意.故选B.
知识点 1 直角三角形的判别方法
2.C 【解析】 因为(a-b)2+|a2+b2-c2|=0,所以a-b=0,a2+b2-c2=0,解得a=b,a2+b2=c2,所以△ABC的形状为等腰直角三角形.故选C.
2.[2019河南新乡期末]若△ABC的三边长a,b,c满足(a-b)2+|a2+b2-c2|=0,则对△ABC的形状描述最准确的是 ( )
A.△ABC是等腰三角形 B.△ABC是直角三角形
C.△ABC是等腰直角三角形 D.△ABC是等腰三角形或直角三角形
答案
3.五根小木棒,其长度分别为7,15,20,24,25.现将它们摆成两个直角三角形,如图所示,其中正确的是 ( )
答案
3.C 【解析】 A项,152+202=252,72+202≠242,故A项不正确;B项,72+242=252,152+202≠242,故B项不正确;
C项,72+242=252,152+202=252,故C项正确;D项,72+202≠252,242+152≠252,故D项不正确.故选C.
知识点 1 直角三角形的判别方法
A B C D
4.[2020陕西宝鸡期中]如图,在△ABC中,AB=12,BC=13,AC=5,则BC边上的高AD为 ( )
A.12 B.13 C.6013 D.60
?
答案
4.C 【解析】 因为52+122=132,即AC2+AB2=BC2,所以△ABC是直角三角形,所以S△ABC=12AB·AC=12BC·AD,即12×12×5=12×13×AD,所以AD=6013.故选C.
?
知识点 1 直角三角形的判别方法
5.216 【解析】 根据题意,设这个三角形的三边长为9x cm,12x cm,15x cm.因为(9x)2+(12x)2=(15x)2,所以这个三角形是直角三角形.因为该三角形的周长为72 cm,所以9x+12x+15x=72,解得x=2,所以9x=18,12x=24,所以它的面积为12×18×24=216(cm 2).
?
答案
5.如果一个三角形的三边长之比为9∶12∶15,且其周长为72 cm,那么它的面积为 cm2.?
6.[2020云南昆明期末]如图,在锐角三角形ABC中,AB=13,AC=15,点D是BC边上一点,BD=5,AD=12,求BC的长度.
答案
6.【解析】 在△ABD中,AB=13,BD=5,AD=12,
所以BD2+AD2=52+122=169,AB2=132=169,
所以BD2+AD2=AB2,所以∠ADB=∠ADC=90°.
在Rt△ACD中,由勾股定理,得CD2=AC2-AD2=152-122=92,即CD=9.
所以BC=BD+CD=5+9=14.
知识点 1 直角三角形的判别方法
7.下列各组数据,是勾股数的是 ( )
A.13,14,15???????????????B.32,42,52 C.0.5,1.2,1.3 D.12,16,20
?
答案
7.D 【解析】 A项,13,14,15不是整数,故A项不符合题意;B项,92+162≠252,故B项不符合题意;C项,0.5,1.2,1.3不是整数,故C项不符合题意;D项,122+162=202,且是正整数,故D项符合题意.故选D.
?
知识点 2 勾股数
知识点 2 勾股数
8.[2019山东济南槐荫区期末]勾股定理a2+b2=c2本身就是一个关于a,b,c的方程,满足这个方程的正整数解(a,b,c)通常叫做勾股数组.根据该方程可以构造出如下勾股数组:(3,4,5),(5,12,13),(7,24,25),….分析上面勾股数组可以发现:4=1×(3+1),12=2×(5+1),24=3×(7+1),….分析上面规律,第5个勾股数组为 .?
8.(11,60,61) 【解析】 根据题意可得,第n个勾股数组中间的数为n×[(2n+1)+1],第一个数为2n+1,最后一个数为n×[(2n+1)+1]+1,所以第5个勾股数组为(11,60,61).
答案
9.已知一组勾股数中有一个数是5,另外两个数可以是 .?
答案
9.3,4或12,13
知识点 3 勾股定理的逆用
10.直角 【解析】 因为小方格边长均为1,所以BC2=42+62=52,AC2=22+32=13,AB2=12+82=65.在△ABC中,BC2+AC2=52+13=65,AB2=65,所以BC2+AC2=AB2,所以△ABC是直角三角形.
答案
10.正方形网格中的△ABC如图所示,若小方格边长均为1,则△ABC的形状是 三角形.?
11.如图所示的一块地,AD=12 m,CD=9 m,∠ADC=90°,AB=39 m,BC=36 m,求这块地的面积.
答案
11.【解析】 如图,连接AC.
在Rt△ADC中,由勾股定理,得AC2=CD2+AD2=92+122=225,所以AC=15 m.
在△ABC中,AB2=1 521,AC2+BC2=152+362=1 521,
所以AB2=AC2+BC2,所以∠ACB=90°,
所以这块地的面积为S△ABC-S△ACD=12AC·BC-12AD·CD= 12×15×36-12×12×9=270-54=216(m2).
答:这块地的面积是216 m2.
?
知识点3 勾股定理的逆用
1.△ABC的三边长分别为a,b,c,给出下列条件:①∠A=∠B-∠C;②∠A∶∠B∶∠C=3∶4∶5;③a2=(b+c)(b-c);
④a∶b∶c=5∶12∶13.其中能判断△ABC是直角三角形的个数为( )
A.1 B.2 C.3 D.4
答案
1.C 【解析】 ①∠A=∠B-∠C,∠A+∠B+∠C=180°,解得∠B=90°,故△ABC是直角三角形;②∠A∶∠B∶∠C=
3∶4∶5,∠A+∠B+∠C=180°,解得∠A=45°,∠B=60°,∠C=75°,故△ABC不是直角三角形;③因为a2=(b+c)(b-c),所以
a2+c2=b2,故△ABC是直角三角形;④因为a∶b∶c=5∶12∶13,所以a2+b2=c2,故△ABC是直角三角形.所以能判断
△ABC是直角三角形的个数为3.故选C.
2.[2019山东威海文登区期中]给出下列四个说法:
①由于0.3,0.4,0.5不是勾股数,所以以0.3,0.4,0.5为边长的三角形不是直角三角形;
②由于以0.5,1.2,1.3为边长的三角形是直角三角形,所以0.5,1.2,1.3是勾股数;
③若a,b,c是勾股数,且c最大,则一定有a2+b2=c2;
④若三个整数a,b,c(c最大)是直角三角形的三边长,则2a,2b,2c一定是勾股数.
其中正确的是( )
A.①② B.②③ C.③④ D.①④
答案
2.C 【解析】 ①由于0.32+0.42=0.52,所以以0.3,0.4,0.5为边长的三角形是直角三角形,但是0.3,0.4,0.5不是整数,所以0.3,0.4,0.5不是勾股数,故①说法错误;②虽然以0.5,1.2,1.3为边长的三角形是直角三角形,但是0.5,1.2,1.3不是整数,所以0.5,1.2,1.3不是勾股数,故②说法错误;③若a,b,c是勾股数,且c最大,则一定有a2+b2=c2,故③说法正确;④若三个整数a,b,c(c最大)是直角三角形的三边长,则a2+b2=c2,所以(2a)2+(2b)2=(2c)2,所以2a,2b,2c一定是勾股数,故④说法正确.故选C.
3.如图,正方形ABCD是由9个边长为1的小正方形组成,连接AE,AF,则∠EAF= ( )
A.30° B.45° C.60° D.75°
答案
3.B 【解析】 如图,连接EF.根据勾股定理,得AE2=EF2=5,AF2=10.因为5+5=10,所以AE2+EF2=AF2,所以△AEF是等腰直角三角形,所以∠EAF=45°.故选B.
4.如图,在△ABC中,∠ABC=90°,AB=6 cm,AD=24 cm,BC与CD的长度之和为34 cm,其中点C是直线l上的一个动点,则当点C离点B cm时,△ACD是以DC为斜边的直角三角形.?
答案
4.8 【解析】 设BC=x cm,因为BC与CD的长度之和为34 cm,所以CD=(34-x)cm.在△ABC中,∠ABC=90°,AB=6 cm,所以AC2=AB2+BC2=62+x2.因为△ACD是以DC为斜边的直角三角形,AD=24 cm,所以AC2=CD2-AD2=(34-x) 2-242,所以62+x2=(34-x)2-242,解得x=8,即BC=8 cm.
5.[2020江苏连云港期中]如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16.
(1)试说明BD⊥AC;
(2)若E是边AB上的动点,求线段DE的最小值.
答案
5.【解析】 (1)因为AC=21,AD=16,
所以CD=AC-AD=5.
因为BD2+CD2=122+52=169=BC2,
所以∠BDC=90°,即BD⊥AC.
(2)当DE⊥AB时,DE取得最小值,
因为AB2=AD2+BD2=162+122=202,所以AB=20.
因为12AD·DB=12AB·DE,所以DE=16×1220=9.6,
所以线段DE的最小值为9.6.
?
6.在B港口有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里的速度前进,乙船沿南偏东某个角度以每小时15海里的速度前进.2小时后,甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船是沿什么方向航行的吗?
答案
6.【解析】 如图,甲船航行的距离BM=8×2=16(海里),乙船航行的距离BP=15×2=30(海里).
因为162+302=1 156,342=1 156,
所以BM2+BP2=MP2,
所以△MBP为直角三角形,∠MBP=90°,
所以乙船是沿南偏东30°的方向航行的.
7.[2020吉林长春期末]张老师在一次“探究性学习”课中,设计了如下数表:
答案
7.【解析】 (1)n2-1 2n n2+1
(2)以a,b,c为边长的三角形是直角三角形.理由如下:
因为a2+b2=(n2-1)2+(2n)2=n4+2n2+1,c2=(n2+1)2=n4+2n2+1,
所以a2+b2=c2,
所以以a,b,c为边长的三角形是直角三角形.
{5940675A-B579-460E-94D1-54222C63F5DA}n
2
3
4
5
…
a
22-1
32-1
42-1
52-1
…
b
4
6
8
10
…
c
22+1
32+1
42+1
52+1
…
(1)请你分别观察a,b,c与n之间的关系,并用含n(n>1)的代数式表示:a= ;b= ;c= .?
(2)猜想:以a,b,c为边长的三角形是否是直角三角形?为什么?
第三节 勾股定理的应用
第三节
1.[2019河南省实验中学月考]如图,圆柱的底面直径为16π,高为12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S所经过的最短距离为( )
A.10 B.12 C.20 D.14
?
知识点 1 立体图形表面上两点间的最短距离
1.A 【解析】 如图是题中圆柱的侧面展开图的一半,则AS为动点P移动到点S的最短距离.由题意可得,AB=12×16π×π=8,BS=12BC=6,由勾股定理可得,AS=10.故选A.
?
答案
2.[2020吉林长春期末]如图是一个三级台阶,它的每一级的长、宽、高分别为20 dm,3 dm,2 dm.A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为 ( )
A.18 dm B.20 dm C.25 dm D.35 dm
知识点 1 立体图形表面上两点间的最短距离
2.C 【解析】 如图,三级台阶平面展开图为长方形,长为20 dm,宽为(2+3)×3 dm,则蚂蚁沿台阶面爬行到B点的最短路程是线段AB的长.AB2=202+[(2+3)×3]2=252,所以AB=25 dm.故选C.
答案
3. 如图所示是一棱长为3 cm的正方体,把其中两面(下底面和右面)分别均分成3×3个小正方形,其边长都为1 cm.假设一只蚂蚁每秒爬行2 cm,则它从下底面点A沿表面爬行至侧面的点B,最少要用 s.?
知识点 1 立体图形表面上两点间的最短距离
3.2.5 【解析】 因为爬行路径不唯一,所以分情况分别计算,再通过比较确定最短路径.(1)展开前面和右面,由勾股定理,得AB2=(2+3)2+22=29;(2)展开下底面和右面,由勾股定理,得AB2=32+(2+2)2=25;(3)展开下底面和后面,由勾股定理,得AB2=(3+2)2+22=29.因为25<29,所以最短路径为第(2)种情况,所以最短路径为5 cm,所以最少要用5÷2=2.5(s).
答案
4.如图,这是一个供滑板爱好者使用的U型池.该U型池可以看作是一个长方体去掉一个“半圆柱”,中间可供滑行部分的截面是半径为8 m的半圆,其边缘AB=CD=20 m,点E在CD上,CE=2 m.一滑板爱好者要从A点滑到E点,则他滑行的最短距离是多少?(边缘部分的厚度忽略不计,π取3)
知识点 1 立体图形表面上两点间的最短距离
4.【解析】 把“半圆柱”的侧面展开后,连接AE,如图所示.
由题意可知AD=8π=8×3=24(m),
DE=DC-CE=20-2=18(m).
在Rt△ADE中,由勾股定理,得AE2=DE2+AD2=182+242=900,
所以AE=30 m,
所以他滑行的最短距离是30 m.
答案
5.[2019河北保定期末]《九章算术》中的“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”意思是一根竹子,原高1丈(1丈=10尺),中间有一处折断,竹梢恰好抵地,抵地处离竹子底部3尺,则折断处离地面的高度是 ( )
A.3尺 B.4尺 C.3.2尺 D.4.55尺
知识点 2 运用勾股定理解决实际问题
5.D 【解析】 设竹子折断处离地面x尺,根据勾股定理,得x2+32=(10-x) 2,解得x=4.55,所以折断处离地面的高度是4.55尺.故选D.
答案
6.[2020浙江温州期中]如图,一高层住宅发生火灾,消防车立即赶到,升起云梯到火灾窗口.已知云梯伸长26米,云梯底部距地面1.5米(AE=1.5米),距住宅10米(AC=10米),则发生火灾的住户窗口(点B)距离地面 米.?
6.25.5 【解析】 因为AC⊥BC,所以∠ACB=90°,根据勾股定理,得BC2=AB2-AC2=262-102=242,所以BC=24米,所以BD=24+1.5=25.5(米).所以发生火灾的住户窗口距离地面25.5米.
答案
知识点 2 运用勾股定理解决实际问题
7.如图,如果只给你一把带有刻度的直尺,你能否检验∠P是不是直角?简述你的方法,并说明理由.
7.【解析】 能检验.
方法:①在射线PM上截取PA,使得PA为3 cm,确定点A的位置,在射线PN上截取PB,使得PB为4 cm,确定点B的位置;
②连接AB,得△PAB;
③用刻度尺测量AB的长度,如果AB恰为5 cm,则说明∠P是直角,否则,∠P不是直角.
理由如下:
PA=3 cm,PB=4 cm,PA2+PB2=32+42=52,
若AB=5 cm,则PA2+PB2=AB2,
根据上式可知△PAB是直角三角形,∠P是直角.
答案
8.[2019山东济南章丘区期末]公路旁有一块山地正在开发,现有C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围250米内不得进入,在进行爆破时,公路AB段是否需要暂时封锁?请通过计算进行说明.
知识点 2 运用勾股定理解决实际问题
8.【解析】 公路AB段需要暂时封锁.理由如下:
过点C作CD⊥AB于点D.
在Rt△ABC中,∠ACB=90°,BC=400米,AC=300米,
由勾股定理,得AB2=AC2+BC2=3002+4002=5002,所以AB=500米.
因为????△????????????=12AB·CD=12BC·AC,
所以CD=????????·????????????????=400×300500=240(米).
因为240<250,
所以公路AB段需要暂时封锁.
?
答案
1.[2019甘肃兰州外国语学校期末]如图,一架梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙脚C的距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.9米,则梯子顶端A下滑了 ( )
A.0.9米 B.1.3米 C.1.5米 D.2米
答案
1.B 【解析】 在Rt△ACB中,AC2=AB2-BC2=2.52-1.52=4,所以AC=2米.因为BD=0.9米,所以CD=2.4米.在Rt△ECD中,EC2=ED2-CD2=2.52-2.42=0.49,所以EC=0.7米,所以AE=AC-EC=2-0.7=1.3(米).故选B.
2.[2020江苏镇江期中]一根长18 cm的牙刷置于底面直径为5 cm、高为12 cm的圆柱形水杯中,牙刷露在杯子外面的长度为h cm,则h的取值范围是 ( )
A.5答案
2.C 【解析】 根据题意,易得杯子中牙刷长度的最小值等于杯子的高12 cm.设杯子中牙刷长度的最大值为x cm,由勾股定理可得,52+122=x2,所以x=13.因为牙刷的长为18 cm,所以h的取值范围是18-13≤h≤18-12,即5≤h≤6.故选C.
3.[2020山东济南期末]把一张长方形纸片ABCD按如图所示的方式折叠,使点B和点D重合,折痕为EF.若AB=3 cm,BC=
5 cm,则重叠部分△DEF的面积是 cm2.?
答案
3.5.1 【解析】 由折叠的性质可知,A'D=AB=3 cm,A'E=AE.在Rt△A'DE中,由勾股定理,得A'D2+A'E2=DE2.
设DE=x cm,因为AD=BC=5 cm,所以A'E=AE=AD-DE=(5-x)cm,所以32+(5-x)2=x2,解得x=3.4,即DE=3.4 cm,所以S△DEF=12DE·AB=12×3.4×3=5.1(cm2).
?
4.[2018湖北黄冈中考]如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为 cm(杯壁厚度不计).?
答案
4.20 【解析】 如图,将杯子侧面的一半展开,作点A关于EF的对称点A',连接A'B,则A'B即最短距离.在Rt△A'DB中,由勾股定理,得A'B2=A'D2+BD2=162+122=202,所以A'B=20 cm.
5.[2020辽宁朝阳一中期中]已知某开发区有一块四边形的空地ABCD,如图所示.现计划在空地上种植草皮,经测量,∠A=90°,AB=3 m,BC=12 m,CD=13 m,AD=4 m.若每平方米草皮需要200元,则总共需要投入多少钱?
答案
5.【解析】 如图,连接BD.在Rt△ABD中,由勾股定理,得BD2=AB2+AD2=32+42=52,所以BD=5 m.
在△CBD中,BC2+BD2=122+52=132,
因为CD2=132,所以BC2+BD2=CD2,所以∠DBC=90°,
所以????四边形????????????????=????△????????????+????△????????????=12AD·AB+12DB·BC=12×4×3+12×5×12=36(m2).
36×200=7 200(元),
所以总共需要投入7 200 元.
?
6.如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点H(A,H,B在一条直线上),并新修一条路CH,测得BC=3千米,CH=2.4千米,BH=1.8千米.
(1)问CH是否为从村庄C到河边的最近路线(即CH与AB是否垂直)?请通过计算加以说明.
(2)求原来的路线AC的长.
答案
6.【解析】 (1)CH是从村庄C到河边的最近路线.理由如下:
在△CHB中,CH2+BH2=(2.4)2+(1.8)2=9,BC2=9,
所以CH2+BH2=BC2,所以CH⊥AB,
所以CH是从村庄C到河边的最近路线.
(2)设AC=x千米,
在Rt△ACH中,AC=x千米,AH=(x-1.8)千米,CH=2.4千米,
由勾股定理,得AC 2=AH 2+CH 2,
所以x2=(x-1.8)2+(2.4)2,
解得x=2.5.
答:原来的路线AC的长为2.5千米.
7.一辆装满货物的卡车,其外形高2.5 m,宽1.6 m,某工厂的厂门形状及尺寸如图所示(上部是半圆形,下部是长方形).这辆卡车能否通过该工厂的厂门?
答案
7.【解析】 卡车能通过该工厂的厂门.理由如下:
如图,点D距厂门的中心线0.8 m,过点D作CH⊥AB,与地面交于点H,与厂门上方圆弧交于点C,连接OC.
易知OC=1 m,OD=0.8 m,
在Rt△OCD中,由勾股定理,得CD2=OC2-OD2=12-0.82=0.36,
所以CD=0.6 m,
所以CH=0.6+2.3=2.9(m),
因为2.9>2.5,
所以这辆卡车能通过该工厂的厂门.
易错疑难集训
集训
1.在Rt△ABC中,a,b,c分别是∠A,∠B,∠C的对边,若∠A=90°,则 ( )
A.a2+b2=c2 B.b2+c2=a2 C.c2+a2=b2 D.b+a=c
答案
1.B
易错点 1 思维定式或忽视分类讨论
2.在△ABC中,AB=AC=10,S△ABC=48,求BC边的长.
2.【解析】 根据题意,分两种情况:
(1)若∠A为锐角,如图1所示,
过点C作CD⊥AB于点D,
则∠ADC=∠BDC=90°.
因为AB=AC=10,S△ABC=????????·????????2=48,
所以CD=9.6.
?
答案
图1
在Rt△ADC中,由勾股定理,得AD2=AC2-CD2=102-9.62=2.82,
所以AD=2.8,
所以BD=AB-AD=10-2.8=7.2.
在Rt△BDC中,由勾股定理,得BC2=BD2+DC2=7.22+9.62=122,
所以BC=12.
(2)若∠BAC为钝角,如图2所示,
过点C作CD⊥AB交BA的延长线于点D,则∠D=90°.
按(1)中方法可得CD=9.6,AD=2.8,
所以BD=AB+AD=10+2.8=12.8.
在Rt△BDC中,BC2=BD2+CD2=12.82+9.62=162,
所以BC=16.
综上,BC边的长为12或16.
答案
图2
3.如图,A,B两个小镇在河岸CD的同侧,到河岸的距离分别为AC=10千米,BD=30千米,且CD=30千米.现在要在河边建一自来水厂,向A,B两镇供水,铺设水管的费用为每千米3万元,请你在河岸CD上找到水厂的位置M,使得铺设水管的总费用最少,并求出最少总费用.
答案
3.【解析】 如图,作点A关于CD的对称点A',连接A'B,与CD交于点M,点M即水厂的位置,连接AM,过点A'作A'K⊥BD交BD的延长线于点K,可得DK=A'C=AC=10千米,A'K=CD=30千米,
所以BK=BD+DK=40千米.
由作图可知∠A'KB=90°,
所以在Rt△A'KB中,由勾股定理,得A'B2=A'K2+BK2=302+402=502,
所以AM+BM=A'B=50 千米,
50×3=150(万元),
所以铺设水管的总费用最少为150万元.
易错点 2 确定符合要求的点时,忽视利用对称性
1.如图, 小方格都是边长为 1 的正方形, 则△ABC中BC边上的高为 ( B )
A.1.6 B.1.4 C.1.5 D.2
答案
1.B 【解析】 因为BC2=32+42=52,所以BC=5.因为S△ABC=4×4-12×1×1-12×3×4-12×3×4=72,所以△ABC中BC边上的高=
2×725=1.4.故选B.
?
疑难点 1 勾股定理与网格
2.如图,已知圆柱的底面直径为6π,高AB=3,小虫在圆柱侧面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程的平方为( )
A.18 B.48 C.120 D.72
?
答案
2.D 【解析】 把圆柱侧面展开,展开图如图所示,点A,C的最短距离为线段AC的长.在Rt△ABC中,∠ABC=90°,AB=3,BC=π·6π÷2=3,所以AC2=AB2+BC2=18,所以从C点爬到A点,然后再沿另一面爬回C点,
小虫爬行的最短路程的平方为(2AC)2=4AC2=72.故选D.
?
疑难点 2 最短路径问题
3.[2020山东枣庄山亭区期中]如图所示的长方体透明玻璃鱼缸,假设其长AD=80 cm,高AB=60 cm,水深AE=40 cm.在水面上紧贴内壁的G处有一块面包屑,G在水面线EF上,且EG=60 cm,一只蚂蚁想从鱼缸外的A点沿鱼缸壁爬到鱼缸内的G处吃面包屑,则蚂蚁爬行的最短路程为 cm.?
答案
3.100 【解析】 如图,作点A关于BC的对称点A',连接A'G交BC于点Q,则A'G即最短路程.在Rt△A'EG中,A'E=
80 cm,EG=60 cm,所以A'G2=A'E2+EG2=1002,所以A'G=100 cm,所以最短路程为100 cm.
疑难点 2 最短路径问题
数学·八年级上册·北师
第一节 探索勾股定理
第一节
课时1 探索勾股定理
课时1
1.[2020吉林长春期末]如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则线段AB的长度为 ( )
A.5 B.6 C.7 D.25
答案
1.A 【解析】 如图,在Rt△ABC中,AC=4,BC=3,由勾股定理,得AB2=AC2+BC2 =42+32=52,所以AB=5.故选A.
知识点 1 勾股定理
2.易错题 下列说法中正确的是 ( )
A.已知a,b,c是三角形的三边长,则a2+b2=c2 B.在直角三角形中,两边的平方和等于第三边的平方
C.在Rt△ABC中,若∠C=90°,则BC2+AC2=AB2 D.在Rt△ABC中,若∠B=90°,则BC2+AC2=AB2
答案
2.C
知识点 1 勾股定理
3.[2019湖北鄂州模拟]如图是一张直角三角形纸片,∠C=90°,直角边AC=6 cm,BC=8 cm.现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为 ( )
A.4 cm B.5 cm C.6 cm D.10 cm
答案
3.B 【解析】 在Rt△ABC中,∠C=90°,所以AB2=AC2+BC2=62+82=100,所以AB=10 cm,又由折叠的性质可知BE=AE=12AB=5 cm.故选B.
?
4.易错题 [2019河北唐山路北区期中]在△ABC中,∠B=90°,a,b,c分别为∠A,∠B,∠C的对边.
(1)如果a=5,c=12,那么b= ;?
(2)如果b=61,a=60,那么c= .?
答案
4.(1)13;(2)11 【解析】 (1)在△ABC中,∠B=90°,a=5,c=12,所以b2=a2+c2=52+122=132,所以b=13.(2)在△ABC中,∠B=90°,b=61,a=60,所以c2=b2-a2=612-602=112,所以c=11.
知识点 1 勾股定理
5.[2020江苏无锡期中]如图,在△ABC中,CD⊥AB,垂足为点D,AC=20,BC=15,BD=9.
求:(1)CD的长;
(2)△ABC的面积.
答案
5.【解析】 (1)因为CD⊥AB,所以∠CDB=∠CDA=90°,
在Rt△BDC中,根据勾股定理,
得CD2+BD2=BC2,
即CD2+92=152,
所以CD=12.
(2)在Rt△ADC中,根据勾股定理,得AD2+CD2=AC2,
即AD2+122=202,所以AD=16,
所以AB=AD+BD=16+9=25,
所以S△ABC=12AB·CD=12×25×12=150.
?
知识点 1 勾股定理
6.[2019山东济南育华中学月考]如图,25,169分别是相应正方形的面积,则字母B所代表的正方形的面积是 ( )
A.12 B.13 C.144 D.194
答案
6.C 【解析】 由题图可知,在直角三角形中,斜边的平方为169,一直角边的平方为25,根据勾股定理,知另一直角边的平方为169-25=144,所以字母B所代表的正方形的面积是144.故选C.
知识点 2 勾股定理与面积
7.[2020江苏宿迁期中]如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为 ( )
A.9 B.92 C.94 D.3
?
答案
7.B 【解析】 在Rt△AEC中,AE=EC,AC2=EC2+AE2,所以S△AEC=12AE·EC=12AE2=14AC2,同理可得,S△BCF=14BC2, S△ABD=14AB2.在Rt△ABC中,根据勾股定理,得AB2=AC2+BC2,因为AB=3,所以阴影部分的面积S=14(AC2+BC2+AB2)=12AB2=12×32=92.故选B.
?
知识点 2 勾股定理与面积
8.[2019贵州黔南州中考]如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,则正方形ABCD的面积为 .?
答案
8.3 【解析】 因为四边形ABCD是正方形,所以∠B=90°,所以BC2=EC2-EB2=22-12=3,所以正方形ABCD的面积为BC2=3.
知识点 2 勾股定理与面积
9.如图,在四边形ABCD中,∠BAD=90°,∠CBD=90°,AD=4,AB=3,BC=12,求以DC为边的正方形DCEF的面积.
答案
9.【解析】 在△ABD中,∠BAD=90°,
所以AD2+AB2=DB2,所以42+32=DB2,
所以DB=5.
在△BCD中,∠CBD=90°,
所以BD2+BC2=DC2,所以52+122=DC2,
所以DC=13,
所以S正方形DCEF=132=169.
知识点 2 勾股定理与面积
1.易错题 已知一个直角三角形的两边长分别为3和4,则第三边长的平方是 ( )
A.25 B.14 C.7 D.7或25
答案
1.D 【解析】 由于给出的直角三角形的两边长分别为3和4,没有指明是直角边,因此分两种情况求解.(1)当第三边为斜边时,32+42=25;(2)当4为斜边长时,42-32=7.综上,第三边长的平方是7或25.故选D.
2.C 【解析】 因为AB=AC,AD平分∠BAC,所以AD⊥BC,BD=DC=12BC=6.在Rt△ABD中,根据勾股定理,得AD2=AB2-BD2=102-62=82,所以AD=8.故选C.
?
2.如图,在△ABC 中,AB=AC=10,BC=12,AD 平分∠BAC,则AD 的长为 ( )
A.6 B.7 C.8 D.9
答案
3.如图所示的图形是由直角三角形和正方形组成的,其中正方形A的面积为40,四个正方形中的8,x,10,y分别表示该正方形的面积,则x+y= .?
答案
3.22 【解析】 根据题意,得x+8+(10+y)=S正方形A=40,所以x+y=40-18=22.
4.14或4 【解析】 ①当高AD在△ABC内部时,如图1,根据勾股定理,得BD2=152-122=81,CD2=132-122=25,所以BD=9,CD=5,所以BC=BD+CD=9+5=14;②当高AD在△ABC外部时,如图2,由①得BD=9,CD=5,所以BC=BD-CD=9-5=4.综合①②,得BC的长为14或4.
4.易错题 在△ABC中,AB=15,AC=13,BC边上的高AD=12,则BC的长为 .?
答案
图1 图2
5.如图,将长方形ABCD沿着AE折叠,点D落在BC边上的点F处,已知AB=8,BC=10,求EC的长.
答案
5.【解析】 依题意,得AD=AF=BC=10,DE=EF.
在△ABF中,∠ABF=90°,
所以BF2=AF2-AB2=102-82=62,
所以BF=6,所以FC=10-6=4.
设EC=x,则EF=DE=8-x.
因为∠C=90°,所以EC2+FC2=EF2,
所以x2+42=(8-x)2,解得x=3,
所以EC=3.
6.[2020江苏镇江期中]如图,在Rt△ABC中,AB=3,BC=4,动点P从点A出发沿AC向点C运动,同时动点Q从点B出发沿BA向点A运动,且到达A点后立刻以原来的速度沿AB返回.点P,Q的运动速度均为每秒1个单位长度,当点P到达点C时,点P,Q同时停止运动,连接PQ,CQ,设它们的运动时间为t(t>0)秒.
(1)设△CBQ的面积为S,请用含有t 的代数式来表示S;
(2)线段PQ的垂直平分线记为直线 l,当直线l 经过点C时,求AQ的长.
答案
6.【解析】 (1)在Rt△ABC中,AB=3,BC=4,
所以AC2=32+42=52,所以AC=5,
所以0
综上,S=2????(0?
答案
(2)如图,因为PQ的垂直平分线过点C,所以CP=CQ=5-t.
在Rt△CBQ中,根据勾股定理,得BC2+BQ2=QC2,
当0
?
7.在△ABC中,∠BAC=90°,分别以Rt△ABC的三边为直径作半圆.
(1)若这三个半圆在BC的两侧(如图1所示),半圆的面积分别为S1,S2,S3,则S1,S2,S3之间有什么数量关系?请说明理由.
(2)若这三个半圆在BC的同一侧(如图2所示),Rt△ABC的面积等于S3,两个“月牙”的面积分别为S1,S2,则S1,S2,S3之间有什么数量关系?请说明理由.
答案
7.【解析】 (1)S1+S2=S3.理由如下:
由题意,得S1=12π(????????2)2=18πAB2,S2=12π(????????2)2=18πAC2,S3=12π(????????2)2=18πBC2.
在Rt△ABC中,由勾股定理,得AB2+AC2=BC2,
所以18πAB2+18πAC2=18πBC2,所以S1+S2=S3.
?
答案
(2)S1+S2=S3.理由如下:
如图,由题意,得S1=12π(????????2)2-S4=18πAB2-S4,S2=12π(????????2)2-S5=18πAC2-S5,S3=12π(????????2)2-S4-S5=18πBC2-S4-S5.
在Rt△ABC中,由勾股定理,得AB2+AC2=BC2,
所以18πAB2-S4+18πAC2-S5=18πBC2-S4-S5,
所以S1+S2=S3.
?
课时2 验证并应用勾股定理
课时2
1.曾任美国总统的伽菲尔德曾经给出了一种勾股定理的证明方法.如图.
该图形整体上拼成了一个直角梯形,所以它的面积有两种表示方法,既可以表示为??????????????? ,
又可以表示为 .对比两种表示方法可得? ,化简,可得a2+b2=c2.?
?
答案
1.12(a+b)2 12ab+12c2+12ab 12(a+b)2=12ab+12c2+12ab
?
知识点 1 验证勾股定理
2.[2019安徽阜阳期末]用如图1所示的四个完全一样的直角三角形可以拼成如图2所示的大正方形.解答下列问题:
(1)请用含a,b,c的代数式表示大正方形的面积.
方法1: .方法2: .?
(2)根据图2及图形的面积关系,推导a,b,c之间满足的关系式.
(3)利用(2)的关系式解答:如果大正方形的面积是25,且(a+b)2=49,求小正方形的面积.
答案
2.【解析】 (1)(a-b)2+4×12ab c2
(2)由(1)可知,(a-b)2+4×12ab=c2,
即a2+b2=c2.
(3)由(2)知,a2+b2=c2.
因为(a+b)2=a2+b2+2ab=c2+4×12ab=大正方形的面积+四个直角三角形的面积和=49,
所以四个直角三角形的面积和为49-c2=49-25=24,
所以小正方形的面积为25-24=1.
?
知识点 1 验证勾股定理
图1 图2
3.如图,韩彬同学从家(记作A)出发向北偏东30°的方向行走了4 000 m到达超市(记作B),然后再从超市出发向南偏东60°的方向行走3 000 m到达卢飞同学家(记作C),则韩彬家到卢飞家的距离为 ( )
A.2 000 m B.3 000 m C.4 000 m D.5 000 m
答案
3.D 【解析】 如图,连接AC.依题意,得∠ABC=90°,AB=4 000 m,BC=3 000 m,则由勾股定理,得AC2=AB2+BC2=
4 0002+3 0002=5 0002,所以AC=5 000 m.故选D.
知识点 2 勾股定理的简单应用
4.[2020山东菏泽牡丹区期中]如图,有一架秋千,当它静止时,踏板离地的垂直高度DE=1 m,将它往前推送6 m(水平距离BC=6 m)时,秋千的踏板离地的垂直高度BF=4 m,秋千的绳索始终拉得很直,则绳索AD的长度为 m.?
答案
4.7.5 【解析】 设秋千的绳索长度为x m,则AB=AD=x m,AC=(x-3)m.在Rt△ACB中,根据勾股定理,得AC2+BC2=AB2,即(x-3)2+62=x2,解得x=7.5.所以绳索AD的长度是7.5 m.
知识点 2 勾股定理的简单应用
5.[2019山东济南育华中学月考]如图,一辆小汽车在一条限速为70 km/h的公路上直线行驶,某一时刻刚好行驶到路对面车速检测仪A正前方30 m的B处,过了2 s后,测得小汽车(位于C处)与车速检测仪A的距离为50 m,这辆小汽车超速了吗?
答案
5.【解析】在Rt△ABC中,由勾股定理,得BC2=AC2-AB2=502-302=402,
所以BC=40 m,
v=40÷2=20(m/s).
因为20 m/s=72 km/h,72>70,
所以这辆小汽车超速了.
知识点 2 勾股定理的简单应用
6.如图,有一只喜鹊在一棵3 m高的小树顶觅食,它的巢筑在距离该树24 m远的一棵大树上,大树高14 m,且巢离树顶部1 m,当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5 m/s,那么它至少需要多长时间才能赶回巢中?
答案
6.【解析】 如图,过点A作AE⊥CD于点E.
由题意知AB=3 m,CD=14-1=13(m),BD=24 m,
则CE=13-3=10(m),AE=24 m.
在Rt△AEC中,AC2=CE2+AE2=102+242,
故AC=26 m,则26÷5=5.2(s).
答:它至少需要5.2 s才能赶回巢中.
知识点 2 勾股定理的简单应用
1.如图,某学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,踩伤了花草,而他们仅仅少走路(假设2步为1米)( )
A.2步 B.4步 C.5步 D.10步
答案
1.B 【解析】 由题图可知,在Rt△ABC中,根据勾股定理,得AB2=AC2+BC2=32+42=52,所以AB=5 m,所以少走了2×(3+4-5)=4(步).故选B.
2.下列选项中(图中三角形都是直角三角形),不能用来验证勾股定理的是 ( )
答案
2.D
A B C D
3.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是 ( )
A.72 B.52 C.80 D.76
答案
3.D 【解析】 设“数学风车”中的四个直角三角形的斜边长为x,则x2=122+52=169,所以x=13,所以“数学风车”的外围周长是(13+6)×4=76.故选D.
图1 图2
4.铁路上A,B两站(视为直线上两点)相距25 km,C,D为两村庄(视为两个点),DA⊥AB于点A,CB⊥AB于点B,如图所示,已知AD=15 km,CB=10 km.现在要在铁路AB上建一个土特产收购站E,使得C,D两村庄到收购站E的距离相等,则收购站E应建在距A站 km处.?
答案
4.10 【解析】 因为C,D两村庄到收购站E的距离相等,所以CE=DE.在Rt△DAE和Rt△CBE中,DE2=AD2+AE2,
CE2=BE2+BC2,所以AD2+AE2=BE2+BC2.设 AE=x km,则BE=(25-x)km.将BC=10 km,AD=15 km代入关系式中,
得152+x2=(25-x)2+102,整理得50x=500,解得x=10,所以收购站E应建在距A站10 km处.
5.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明灵感,他惊喜地发现,当四个全等的直角三角形如图摆放时,可以用“面积法”来证明a2+b2=c2.请你写出证明过程.
答案
5.【解析】 如图,因为S五边形ABCDE=S梯形ABCF+S梯形AFDE=S正方形ABGE+2S△BCG,
即12(b+a+b)×b+12(a+a+b)×a=c2+2×12ab,
所以12ab+b2+a2+12ab=c2+ab,
所以a2+b2=c2.
?
6.[2019山东青岛期中]如图,教学楼走廊左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙底部的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,求教学楼走廊的宽度.
答案
6.【解析】 如图,在Rt△ABC中,∠ACB=90°,BC=0.7米,AC=2.4米,
所以AB2=0.72+2.42=6.25.
在Rt△A'BD中,∠A'DB=90°,A'D=2米,BD2+A'D2=A'B2,
所以BD2+22=6.25,所以BD2=2.25,
因为BD>0,所以BD=1.5米,
所以CD=BC+BD=0.7+1.5=2.2(米).
答:教学楼走廊的宽度是2.2米.
7.在△ABC中,BC=a,AC=b,AB=c.若∠ACB=90°,如图1所示,根据勾股定理,得a2+b2=c2.若△ABC不是直角三角形,如图2和图3所示.请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.
答案
7.【解析】 若△ABC是锐角三角形,则a2+b2>c2.
若△ABC是钝角三角形,∠C为钝角,则a2+b2
在题图2中,过点A作AD⊥BC,垂足为D,设CD的长为x,则BD=a-x.
根据勾股定理,得b2-x2=AD2=c2-(a-x)2,
即b2-x2=c2-a2+2ax-x2,
所以a2+b2=c2+2ax.
图1 图2 图3
答案
因为a>0,x>0,所以2ax>0,所以a2+b2>c2.
当△ABC是钝角三角形,∠C为钝角时,证明如下:
在题图3中,过点B作BD⊥AC,交AC的延长线于点D,设CD的长为x,则有BD2=a2-x2.
在Rt△ABD中,
根据勾股定理,得(b+x)2+a2-x2=c2,
即a2+b2+2bx=c2,
因为b>0,x>0,所以2bx>0,
所以a2+b2
第二节
1.[2019江苏无锡期中]下列各组数,可以作为直角三角形的三边长的是 ( )
A.2,3,4 B.3,4,5 C.8,12,20 D.5,13,15
答案
1.B 【解析】 A项,22+32=13≠42,所以该三角形不是直角三角形,不合题意;B项,32+42=25=52,所以该三角形是直角三角形,符合题意;C项,8+12=20,所以不能构成三角形,不合题意;D项,52+132=194≠152,所以该三角形不是直角三角形,不合题意.故选B.
知识点 1 直角三角形的判别方法
2.C 【解析】 因为(a-b)2+|a2+b2-c2|=0,所以a-b=0,a2+b2-c2=0,解得a=b,a2+b2=c2,所以△ABC的形状为等腰直角三角形.故选C.
2.[2019河南新乡期末]若△ABC的三边长a,b,c满足(a-b)2+|a2+b2-c2|=0,则对△ABC的形状描述最准确的是 ( )
A.△ABC是等腰三角形 B.△ABC是直角三角形
C.△ABC是等腰直角三角形 D.△ABC是等腰三角形或直角三角形
答案
3.五根小木棒,其长度分别为7,15,20,24,25.现将它们摆成两个直角三角形,如图所示,其中正确的是 ( )
答案
3.C 【解析】 A项,152+202=252,72+202≠242,故A项不正确;B项,72+242=252,152+202≠242,故B项不正确;
C项,72+242=252,152+202=252,故C项正确;D项,72+202≠252,242+152≠252,故D项不正确.故选C.
知识点 1 直角三角形的判别方法
A B C D
4.[2020陕西宝鸡期中]如图,在△ABC中,AB=12,BC=13,AC=5,则BC边上的高AD为 ( )
A.12 B.13 C.6013 D.60
?
答案
4.C 【解析】 因为52+122=132,即AC2+AB2=BC2,所以△ABC是直角三角形,所以S△ABC=12AB·AC=12BC·AD,即12×12×5=12×13×AD,所以AD=6013.故选C.
?
知识点 1 直角三角形的判别方法
5.216 【解析】 根据题意,设这个三角形的三边长为9x cm,12x cm,15x cm.因为(9x)2+(12x)2=(15x)2,所以这个三角形是直角三角形.因为该三角形的周长为72 cm,所以9x+12x+15x=72,解得x=2,所以9x=18,12x=24,所以它的面积为12×18×24=216(cm 2).
?
答案
5.如果一个三角形的三边长之比为9∶12∶15,且其周长为72 cm,那么它的面积为 cm2.?
6.[2020云南昆明期末]如图,在锐角三角形ABC中,AB=13,AC=15,点D是BC边上一点,BD=5,AD=12,求BC的长度.
答案
6.【解析】 在△ABD中,AB=13,BD=5,AD=12,
所以BD2+AD2=52+122=169,AB2=132=169,
所以BD2+AD2=AB2,所以∠ADB=∠ADC=90°.
在Rt△ACD中,由勾股定理,得CD2=AC2-AD2=152-122=92,即CD=9.
所以BC=BD+CD=5+9=14.
知识点 1 直角三角形的判别方法
7.下列各组数据,是勾股数的是 ( )
A.13,14,15???????????????B.32,42,52 C.0.5,1.2,1.3 D.12,16,20
?
答案
7.D 【解析】 A项,13,14,15不是整数,故A项不符合题意;B项,92+162≠252,故B项不符合题意;C项,0.5,1.2,1.3不是整数,故C项不符合题意;D项,122+162=202,且是正整数,故D项符合题意.故选D.
?
知识点 2 勾股数
知识点 2 勾股数
8.[2019山东济南槐荫区期末]勾股定理a2+b2=c2本身就是一个关于a,b,c的方程,满足这个方程的正整数解(a,b,c)通常叫做勾股数组.根据该方程可以构造出如下勾股数组:(3,4,5),(5,12,13),(7,24,25),….分析上面勾股数组可以发现:4=1×(3+1),12=2×(5+1),24=3×(7+1),….分析上面规律,第5个勾股数组为 .?
8.(11,60,61) 【解析】 根据题意可得,第n个勾股数组中间的数为n×[(2n+1)+1],第一个数为2n+1,最后一个数为n×[(2n+1)+1]+1,所以第5个勾股数组为(11,60,61).
答案
9.已知一组勾股数中有一个数是5,另外两个数可以是 .?
答案
9.3,4或12,13
知识点 3 勾股定理的逆用
10.直角 【解析】 因为小方格边长均为1,所以BC2=42+62=52,AC2=22+32=13,AB2=12+82=65.在△ABC中,BC2+AC2=52+13=65,AB2=65,所以BC2+AC2=AB2,所以△ABC是直角三角形.
答案
10.正方形网格中的△ABC如图所示,若小方格边长均为1,则△ABC的形状是 三角形.?
11.如图所示的一块地,AD=12 m,CD=9 m,∠ADC=90°,AB=39 m,BC=36 m,求这块地的面积.
答案
11.【解析】 如图,连接AC.
在Rt△ADC中,由勾股定理,得AC2=CD2+AD2=92+122=225,所以AC=15 m.
在△ABC中,AB2=1 521,AC2+BC2=152+362=1 521,
所以AB2=AC2+BC2,所以∠ACB=90°,
所以这块地的面积为S△ABC-S△ACD=12AC·BC-12AD·CD= 12×15×36-12×12×9=270-54=216(m2).
答:这块地的面积是216 m2.
?
知识点3 勾股定理的逆用
1.△ABC的三边长分别为a,b,c,给出下列条件:①∠A=∠B-∠C;②∠A∶∠B∶∠C=3∶4∶5;③a2=(b+c)(b-c);
④a∶b∶c=5∶12∶13.其中能判断△ABC是直角三角形的个数为( )
A.1 B.2 C.3 D.4
答案
1.C 【解析】 ①∠A=∠B-∠C,∠A+∠B+∠C=180°,解得∠B=90°,故△ABC是直角三角形;②∠A∶∠B∶∠C=
3∶4∶5,∠A+∠B+∠C=180°,解得∠A=45°,∠B=60°,∠C=75°,故△ABC不是直角三角形;③因为a2=(b+c)(b-c),所以
a2+c2=b2,故△ABC是直角三角形;④因为a∶b∶c=5∶12∶13,所以a2+b2=c2,故△ABC是直角三角形.所以能判断
△ABC是直角三角形的个数为3.故选C.
2.[2019山东威海文登区期中]给出下列四个说法:
①由于0.3,0.4,0.5不是勾股数,所以以0.3,0.4,0.5为边长的三角形不是直角三角形;
②由于以0.5,1.2,1.3为边长的三角形是直角三角形,所以0.5,1.2,1.3是勾股数;
③若a,b,c是勾股数,且c最大,则一定有a2+b2=c2;
④若三个整数a,b,c(c最大)是直角三角形的三边长,则2a,2b,2c一定是勾股数.
其中正确的是( )
A.①② B.②③ C.③④ D.①④
答案
2.C 【解析】 ①由于0.32+0.42=0.52,所以以0.3,0.4,0.5为边长的三角形是直角三角形,但是0.3,0.4,0.5不是整数,所以0.3,0.4,0.5不是勾股数,故①说法错误;②虽然以0.5,1.2,1.3为边长的三角形是直角三角形,但是0.5,1.2,1.3不是整数,所以0.5,1.2,1.3不是勾股数,故②说法错误;③若a,b,c是勾股数,且c最大,则一定有a2+b2=c2,故③说法正确;④若三个整数a,b,c(c最大)是直角三角形的三边长,则a2+b2=c2,所以(2a)2+(2b)2=(2c)2,所以2a,2b,2c一定是勾股数,故④说法正确.故选C.
3.如图,正方形ABCD是由9个边长为1的小正方形组成,连接AE,AF,则∠EAF= ( )
A.30° B.45° C.60° D.75°
答案
3.B 【解析】 如图,连接EF.根据勾股定理,得AE2=EF2=5,AF2=10.因为5+5=10,所以AE2+EF2=AF2,所以△AEF是等腰直角三角形,所以∠EAF=45°.故选B.
4.如图,在△ABC中,∠ABC=90°,AB=6 cm,AD=24 cm,BC与CD的长度之和为34 cm,其中点C是直线l上的一个动点,则当点C离点B cm时,△ACD是以DC为斜边的直角三角形.?
答案
4.8 【解析】 设BC=x cm,因为BC与CD的长度之和为34 cm,所以CD=(34-x)cm.在△ABC中,∠ABC=90°,AB=6 cm,所以AC2=AB2+BC2=62+x2.因为△ACD是以DC为斜边的直角三角形,AD=24 cm,所以AC2=CD2-AD2=(34-x) 2-242,所以62+x2=(34-x)2-242,解得x=8,即BC=8 cm.
5.[2020江苏连云港期中]如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16.
(1)试说明BD⊥AC;
(2)若E是边AB上的动点,求线段DE的最小值.
答案
5.【解析】 (1)因为AC=21,AD=16,
所以CD=AC-AD=5.
因为BD2+CD2=122+52=169=BC2,
所以∠BDC=90°,即BD⊥AC.
(2)当DE⊥AB时,DE取得最小值,
因为AB2=AD2+BD2=162+122=202,所以AB=20.
因为12AD·DB=12AB·DE,所以DE=16×1220=9.6,
所以线段DE的最小值为9.6.
?
6.在B港口有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里的速度前进,乙船沿南偏东某个角度以每小时15海里的速度前进.2小时后,甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船是沿什么方向航行的吗?
答案
6.【解析】 如图,甲船航行的距离BM=8×2=16(海里),乙船航行的距离BP=15×2=30(海里).
因为162+302=1 156,342=1 156,
所以BM2+BP2=MP2,
所以△MBP为直角三角形,∠MBP=90°,
所以乙船是沿南偏东30°的方向航行的.
7.[2020吉林长春期末]张老师在一次“探究性学习”课中,设计了如下数表:
答案
7.【解析】 (1)n2-1 2n n2+1
(2)以a,b,c为边长的三角形是直角三角形.理由如下:
因为a2+b2=(n2-1)2+(2n)2=n4+2n2+1,c2=(n2+1)2=n4+2n2+1,
所以a2+b2=c2,
所以以a,b,c为边长的三角形是直角三角形.
{5940675A-B579-460E-94D1-54222C63F5DA}n
2
3
4
5
…
a
22-1
32-1
42-1
52-1
…
b
4
6
8
10
…
c
22+1
32+1
42+1
52+1
…
(1)请你分别观察a,b,c与n之间的关系,并用含n(n>1)的代数式表示:a= ;b= ;c= .?
(2)猜想:以a,b,c为边长的三角形是否是直角三角形?为什么?
第三节 勾股定理的应用
第三节
1.[2019河南省实验中学月考]如图,圆柱的底面直径为16π,高为12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S所经过的最短距离为( )
A.10 B.12 C.20 D.14
?
知识点 1 立体图形表面上两点间的最短距离
1.A 【解析】 如图是题中圆柱的侧面展开图的一半,则AS为动点P移动到点S的最短距离.由题意可得,AB=12×16π×π=8,BS=12BC=6,由勾股定理可得,AS=10.故选A.
?
答案
2.[2020吉林长春期末]如图是一个三级台阶,它的每一级的长、宽、高分别为20 dm,3 dm,2 dm.A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为 ( )
A.18 dm B.20 dm C.25 dm D.35 dm
知识点 1 立体图形表面上两点间的最短距离
2.C 【解析】 如图,三级台阶平面展开图为长方形,长为20 dm,宽为(2+3)×3 dm,则蚂蚁沿台阶面爬行到B点的最短路程是线段AB的长.AB2=202+[(2+3)×3]2=252,所以AB=25 dm.故选C.
答案
3. 如图所示是一棱长为3 cm的正方体,把其中两面(下底面和右面)分别均分成3×3个小正方形,其边长都为1 cm.假设一只蚂蚁每秒爬行2 cm,则它从下底面点A沿表面爬行至侧面的点B,最少要用 s.?
知识点 1 立体图形表面上两点间的最短距离
3.2.5 【解析】 因为爬行路径不唯一,所以分情况分别计算,再通过比较确定最短路径.(1)展开前面和右面,由勾股定理,得AB2=(2+3)2+22=29;(2)展开下底面和右面,由勾股定理,得AB2=32+(2+2)2=25;(3)展开下底面和后面,由勾股定理,得AB2=(3+2)2+22=29.因为25<29,所以最短路径为第(2)种情况,所以最短路径为5 cm,所以最少要用5÷2=2.5(s).
答案
4.如图,这是一个供滑板爱好者使用的U型池.该U型池可以看作是一个长方体去掉一个“半圆柱”,中间可供滑行部分的截面是半径为8 m的半圆,其边缘AB=CD=20 m,点E在CD上,CE=2 m.一滑板爱好者要从A点滑到E点,则他滑行的最短距离是多少?(边缘部分的厚度忽略不计,π取3)
知识点 1 立体图形表面上两点间的最短距离
4.【解析】 把“半圆柱”的侧面展开后,连接AE,如图所示.
由题意可知AD=8π=8×3=24(m),
DE=DC-CE=20-2=18(m).
在Rt△ADE中,由勾股定理,得AE2=DE2+AD2=182+242=900,
所以AE=30 m,
所以他滑行的最短距离是30 m.
答案
5.[2019河北保定期末]《九章算术》中的“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”意思是一根竹子,原高1丈(1丈=10尺),中间有一处折断,竹梢恰好抵地,抵地处离竹子底部3尺,则折断处离地面的高度是 ( )
A.3尺 B.4尺 C.3.2尺 D.4.55尺
知识点 2 运用勾股定理解决实际问题
5.D 【解析】 设竹子折断处离地面x尺,根据勾股定理,得x2+32=(10-x) 2,解得x=4.55,所以折断处离地面的高度是4.55尺.故选D.
答案
6.[2020浙江温州期中]如图,一高层住宅发生火灾,消防车立即赶到,升起云梯到火灾窗口.已知云梯伸长26米,云梯底部距地面1.5米(AE=1.5米),距住宅10米(AC=10米),则发生火灾的住户窗口(点B)距离地面 米.?
6.25.5 【解析】 因为AC⊥BC,所以∠ACB=90°,根据勾股定理,得BC2=AB2-AC2=262-102=242,所以BC=24米,所以BD=24+1.5=25.5(米).所以发生火灾的住户窗口距离地面25.5米.
答案
知识点 2 运用勾股定理解决实际问题
7.如图,如果只给你一把带有刻度的直尺,你能否检验∠P是不是直角?简述你的方法,并说明理由.
7.【解析】 能检验.
方法:①在射线PM上截取PA,使得PA为3 cm,确定点A的位置,在射线PN上截取PB,使得PB为4 cm,确定点B的位置;
②连接AB,得△PAB;
③用刻度尺测量AB的长度,如果AB恰为5 cm,则说明∠P是直角,否则,∠P不是直角.
理由如下:
PA=3 cm,PB=4 cm,PA2+PB2=32+42=52,
若AB=5 cm,则PA2+PB2=AB2,
根据上式可知△PAB是直角三角形,∠P是直角.
答案
8.[2019山东济南章丘区期末]公路旁有一块山地正在开发,现有C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围250米内不得进入,在进行爆破时,公路AB段是否需要暂时封锁?请通过计算进行说明.
知识点 2 运用勾股定理解决实际问题
8.【解析】 公路AB段需要暂时封锁.理由如下:
过点C作CD⊥AB于点D.
在Rt△ABC中,∠ACB=90°,BC=400米,AC=300米,
由勾股定理,得AB2=AC2+BC2=3002+4002=5002,所以AB=500米.
因为????△????????????=12AB·CD=12BC·AC,
所以CD=????????·????????????????=400×300500=240(米).
因为240<250,
所以公路AB段需要暂时封锁.
?
答案
1.[2019甘肃兰州外国语学校期末]如图,一架梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙脚C的距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.9米,则梯子顶端A下滑了 ( )
A.0.9米 B.1.3米 C.1.5米 D.2米
答案
1.B 【解析】 在Rt△ACB中,AC2=AB2-BC2=2.52-1.52=4,所以AC=2米.因为BD=0.9米,所以CD=2.4米.在Rt△ECD中,EC2=ED2-CD2=2.52-2.42=0.49,所以EC=0.7米,所以AE=AC-EC=2-0.7=1.3(米).故选B.
2.[2020江苏镇江期中]一根长18 cm的牙刷置于底面直径为5 cm、高为12 cm的圆柱形水杯中,牙刷露在杯子外面的长度为h cm,则h的取值范围是 ( )
A.5
2.C 【解析】 根据题意,易得杯子中牙刷长度的最小值等于杯子的高12 cm.设杯子中牙刷长度的最大值为x cm,由勾股定理可得,52+122=x2,所以x=13.因为牙刷的长为18 cm,所以h的取值范围是18-13≤h≤18-12,即5≤h≤6.故选C.
3.[2020山东济南期末]把一张长方形纸片ABCD按如图所示的方式折叠,使点B和点D重合,折痕为EF.若AB=3 cm,BC=
5 cm,则重叠部分△DEF的面积是 cm2.?
答案
3.5.1 【解析】 由折叠的性质可知,A'D=AB=3 cm,A'E=AE.在Rt△A'DE中,由勾股定理,得A'D2+A'E2=DE2.
设DE=x cm,因为AD=BC=5 cm,所以A'E=AE=AD-DE=(5-x)cm,所以32+(5-x)2=x2,解得x=3.4,即DE=3.4 cm,所以S△DEF=12DE·AB=12×3.4×3=5.1(cm2).
?
4.[2018湖北黄冈中考]如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为 cm(杯壁厚度不计).?
答案
4.20 【解析】 如图,将杯子侧面的一半展开,作点A关于EF的对称点A',连接A'B,则A'B即最短距离.在Rt△A'DB中,由勾股定理,得A'B2=A'D2+BD2=162+122=202,所以A'B=20 cm.
5.[2020辽宁朝阳一中期中]已知某开发区有一块四边形的空地ABCD,如图所示.现计划在空地上种植草皮,经测量,∠A=90°,AB=3 m,BC=12 m,CD=13 m,AD=4 m.若每平方米草皮需要200元,则总共需要投入多少钱?
答案
5.【解析】 如图,连接BD.在Rt△ABD中,由勾股定理,得BD2=AB2+AD2=32+42=52,所以BD=5 m.
在△CBD中,BC2+BD2=122+52=132,
因为CD2=132,所以BC2+BD2=CD2,所以∠DBC=90°,
所以????四边形????????????????=????△????????????+????△????????????=12AD·AB+12DB·BC=12×4×3+12×5×12=36(m2).
36×200=7 200(元),
所以总共需要投入7 200 元.
?
6.如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点H(A,H,B在一条直线上),并新修一条路CH,测得BC=3千米,CH=2.4千米,BH=1.8千米.
(1)问CH是否为从村庄C到河边的最近路线(即CH与AB是否垂直)?请通过计算加以说明.
(2)求原来的路线AC的长.
答案
6.【解析】 (1)CH是从村庄C到河边的最近路线.理由如下:
在△CHB中,CH2+BH2=(2.4)2+(1.8)2=9,BC2=9,
所以CH2+BH2=BC2,所以CH⊥AB,
所以CH是从村庄C到河边的最近路线.
(2)设AC=x千米,
在Rt△ACH中,AC=x千米,AH=(x-1.8)千米,CH=2.4千米,
由勾股定理,得AC 2=AH 2+CH 2,
所以x2=(x-1.8)2+(2.4)2,
解得x=2.5.
答:原来的路线AC的长为2.5千米.
7.一辆装满货物的卡车,其外形高2.5 m,宽1.6 m,某工厂的厂门形状及尺寸如图所示(上部是半圆形,下部是长方形).这辆卡车能否通过该工厂的厂门?
答案
7.【解析】 卡车能通过该工厂的厂门.理由如下:
如图,点D距厂门的中心线0.8 m,过点D作CH⊥AB,与地面交于点H,与厂门上方圆弧交于点C,连接OC.
易知OC=1 m,OD=0.8 m,
在Rt△OCD中,由勾股定理,得CD2=OC2-OD2=12-0.82=0.36,
所以CD=0.6 m,
所以CH=0.6+2.3=2.9(m),
因为2.9>2.5,
所以这辆卡车能通过该工厂的厂门.
易错疑难集训
集训
1.在Rt△ABC中,a,b,c分别是∠A,∠B,∠C的对边,若∠A=90°,则 ( )
A.a2+b2=c2 B.b2+c2=a2 C.c2+a2=b2 D.b+a=c
答案
1.B
易错点 1 思维定式或忽视分类讨论
2.在△ABC中,AB=AC=10,S△ABC=48,求BC边的长.
2.【解析】 根据题意,分两种情况:
(1)若∠A为锐角,如图1所示,
过点C作CD⊥AB于点D,
则∠ADC=∠BDC=90°.
因为AB=AC=10,S△ABC=????????·????????2=48,
所以CD=9.6.
?
答案
图1
在Rt△ADC中,由勾股定理,得AD2=AC2-CD2=102-9.62=2.82,
所以AD=2.8,
所以BD=AB-AD=10-2.8=7.2.
在Rt△BDC中,由勾股定理,得BC2=BD2+DC2=7.22+9.62=122,
所以BC=12.
(2)若∠BAC为钝角,如图2所示,
过点C作CD⊥AB交BA的延长线于点D,则∠D=90°.
按(1)中方法可得CD=9.6,AD=2.8,
所以BD=AB+AD=10+2.8=12.8.
在Rt△BDC中,BC2=BD2+CD2=12.82+9.62=162,
所以BC=16.
综上,BC边的长为12或16.
答案
图2
3.如图,A,B两个小镇在河岸CD的同侧,到河岸的距离分别为AC=10千米,BD=30千米,且CD=30千米.现在要在河边建一自来水厂,向A,B两镇供水,铺设水管的费用为每千米3万元,请你在河岸CD上找到水厂的位置M,使得铺设水管的总费用最少,并求出最少总费用.
答案
3.【解析】 如图,作点A关于CD的对称点A',连接A'B,与CD交于点M,点M即水厂的位置,连接AM,过点A'作A'K⊥BD交BD的延长线于点K,可得DK=A'C=AC=10千米,A'K=CD=30千米,
所以BK=BD+DK=40千米.
由作图可知∠A'KB=90°,
所以在Rt△A'KB中,由勾股定理,得A'B2=A'K2+BK2=302+402=502,
所以AM+BM=A'B=50 千米,
50×3=150(万元),
所以铺设水管的总费用最少为150万元.
易错点 2 确定符合要求的点时,忽视利用对称性
1.如图, 小方格都是边长为 1 的正方形, 则△ABC中BC边上的高为 ( B )
A.1.6 B.1.4 C.1.5 D.2
答案
1.B 【解析】 因为BC2=32+42=52,所以BC=5.因为S△ABC=4×4-12×1×1-12×3×4-12×3×4=72,所以△ABC中BC边上的高=
2×725=1.4.故选B.
?
疑难点 1 勾股定理与网格
2.如图,已知圆柱的底面直径为6π,高AB=3,小虫在圆柱侧面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程的平方为( )
A.18 B.48 C.120 D.72
?
答案
2.D 【解析】 把圆柱侧面展开,展开图如图所示,点A,C的最短距离为线段AC的长.在Rt△ABC中,∠ABC=90°,AB=3,BC=π·6π÷2=3,所以AC2=AB2+BC2=18,所以从C点爬到A点,然后再沿另一面爬回C点,
小虫爬行的最短路程的平方为(2AC)2=4AC2=72.故选D.
?
疑难点 2 最短路径问题
3.[2020山东枣庄山亭区期中]如图所示的长方体透明玻璃鱼缸,假设其长AD=80 cm,高AB=60 cm,水深AE=40 cm.在水面上紧贴内壁的G处有一块面包屑,G在水面线EF上,且EG=60 cm,一只蚂蚁想从鱼缸外的A点沿鱼缸壁爬到鱼缸内的G处吃面包屑,则蚂蚁爬行的最短路程为 cm.?
答案
3.100 【解析】 如图,作点A关于BC的对称点A',连接A'G交BC于点Q,则A'G即最短路程.在Rt△A'EG中,A'E=
80 cm,EG=60 cm,所以A'G2=A'E2+EG2=1002,所以A'G=100 cm,所以最短路程为100 cm.
疑难点 2 最短路径问题
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
