沪科版八年级下册数学 18.1 勾股定理课件 (共16张PPT)
文档属性
| 名称 | 沪科版八年级下册数学 18.1 勾股定理课件 (共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-15 17:25:02 | ||
图片预览


文档简介
(共16张PPT)
18.1勾股定理
相传2500年前,古希腊有位著名的数学家——毕达哥拉斯.有一次在朋友家做客,在宴席上当朋友们都在谈天说地的时候,他却对着朋友家的地砖发呆.他发现其中以一个直角三角形的边长为边做出三个正方形,它们的面积之间似乎有着不平常的关系.
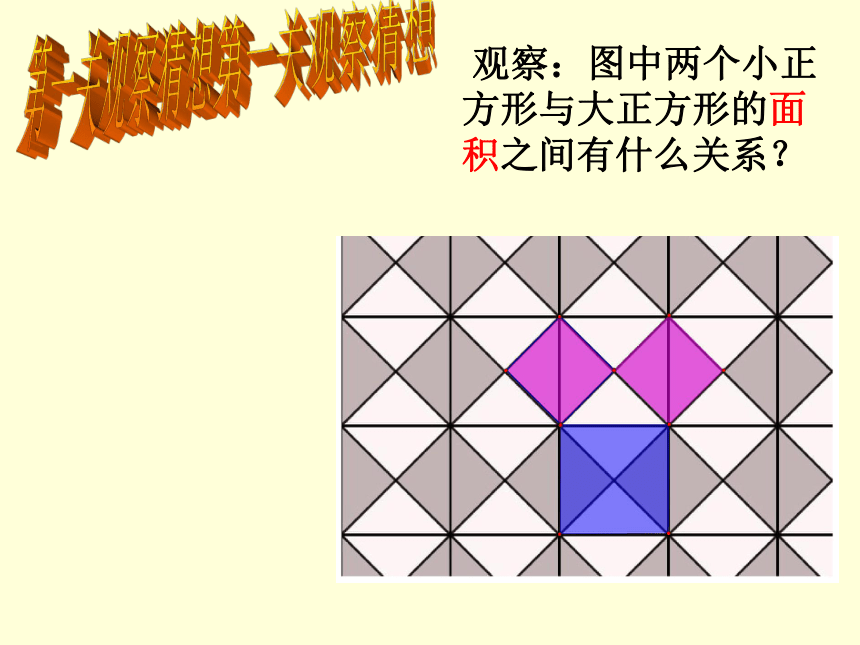
第一关观察猜想
观察:图中两个小正方形与大正方形的面积之间有什么关系?
第一关观察猜想
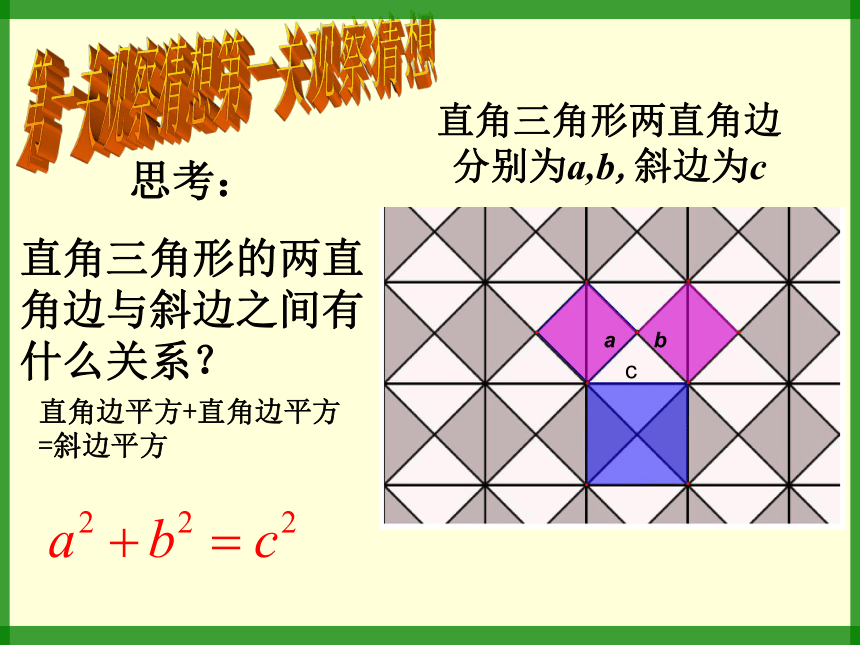
直角三角形两直角边分别为a,b,斜边为c
思考:
直角三角形的两直角边与斜边之间有什么关系?
a
b
c
直角边平方+直角边平方=斜边平方
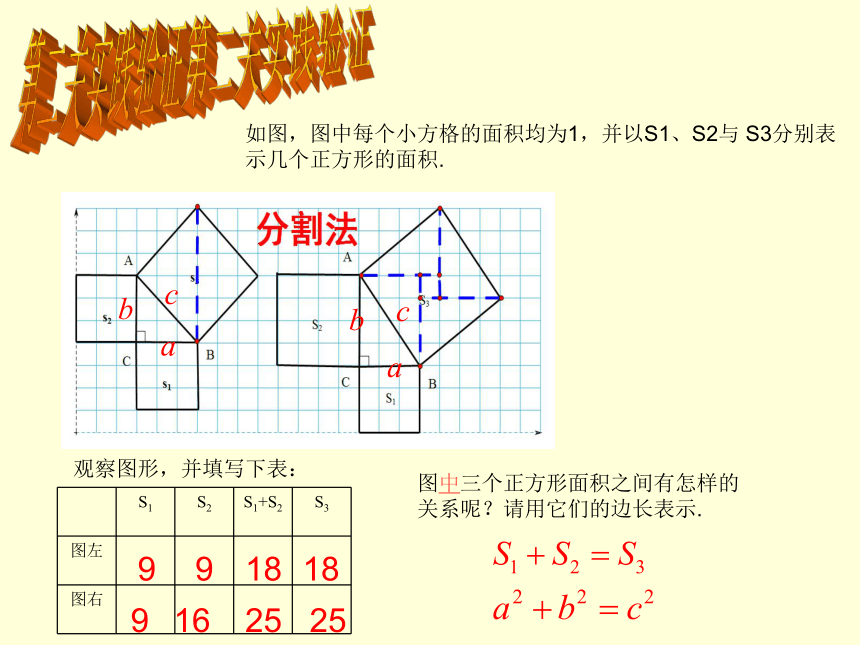
第二关实践验证
如图,图中每个小方格的面积均为1,并以S1、S2与
S3分别表示几个正方形的面积.
观察图形,并填写下表:
图中三个正方形面积之间有怎样的关系呢?请用它们的边长表示.
9
9
18
18
9
16
25
25
S1
S2
S1+S2
S3
图左
图右
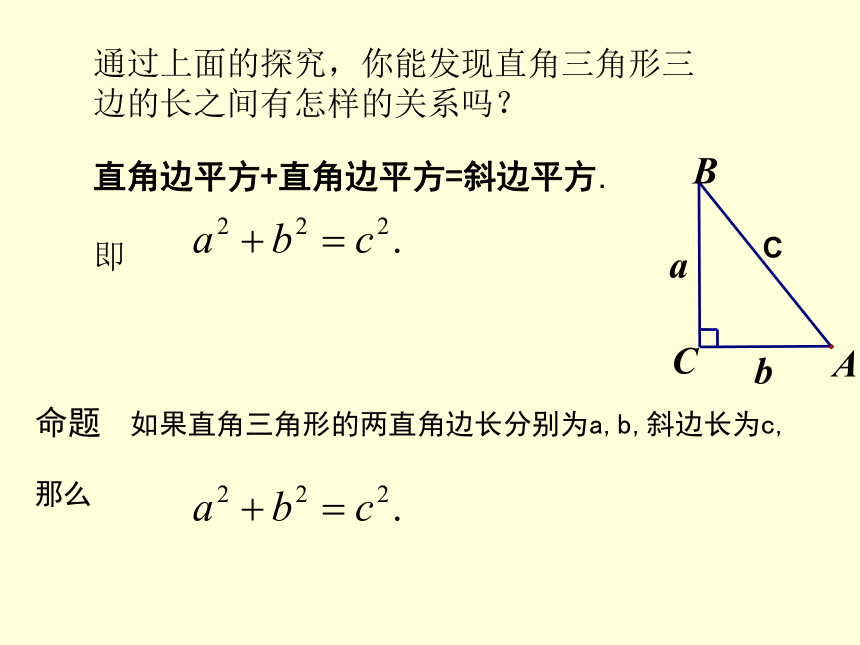
通过上面的探究,你能发现直角三角形三边的长之间有怎样的关系吗?
直角边平方+直角边平方=斜边平方.
即
C
命题
如果直角三角形的两直角边长分别为a,b,斜边长为c,
那么
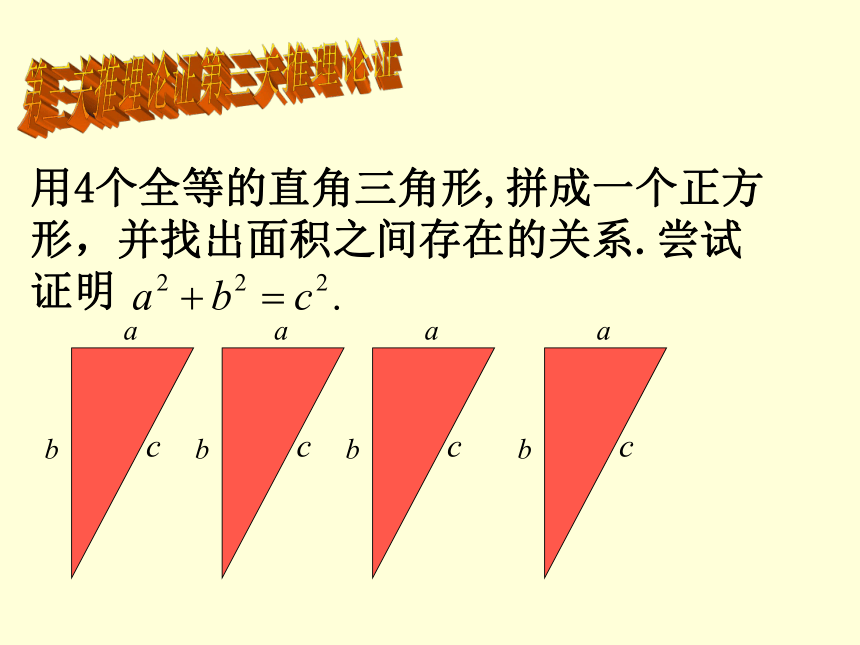
第三关推理论证
毕达哥拉斯定理
百牛定理
直角三角形两条直角边的平方和,等于斜边的平方。
即:
1.成立条件:
在直角三角形中;c为斜边
2.公式变形:
3.作用:
1.知道两条直角边可以求出斜边;
2.知道斜边和一条直角边,可以求另一条直角边。
直角三角形两条直角边的平方和,等于斜边的平方。
例1
求下列直角三角形中未知边的长:
8
x
17
16
20
x
12
5
x
温馨提示:已知直角三角形的两边长,求第三边长时,应选用勾股定理变形公式直接代入计算较为快捷准确!
例2
已知:Rt△ABC中,AB=4,AC=3,则BC=
.
5
或
温馨提示:当直角三角形中斜边或直角边不明确时,其中一较长边可能是直角边,也可能是斜边,这种情况下,一定要进行分类讨论,方能求解.
学以致用
解
例3
1谈谈这节课的收获。
课
堂
小
结:
2
运用“勾股定理”应注意什么问题?
课后作业
课本55页第1、2题.
基训52、53页
18.1勾股定理
相传2500年前,古希腊有位著名的数学家——毕达哥拉斯.有一次在朋友家做客,在宴席上当朋友们都在谈天说地的时候,他却对着朋友家的地砖发呆.他发现其中以一个直角三角形的边长为边做出三个正方形,它们的面积之间似乎有着不平常的关系.
第一关观察猜想
观察:图中两个小正方形与大正方形的面积之间有什么关系?
第一关观察猜想
直角三角形两直角边分别为a,b,斜边为c
思考:
直角三角形的两直角边与斜边之间有什么关系?
a
b
c
直角边平方+直角边平方=斜边平方
第二关实践验证
如图,图中每个小方格的面积均为1,并以S1、S2与
S3分别表示几个正方形的面积.
观察图形,并填写下表:
图中三个正方形面积之间有怎样的关系呢?请用它们的边长表示.
9
9
18
18
9
16
25
25
S1
S2
S1+S2
S3
图左
图右
通过上面的探究,你能发现直角三角形三边的长之间有怎样的关系吗?
直角边平方+直角边平方=斜边平方.
即
C
命题
如果直角三角形的两直角边长分别为a,b,斜边长为c,
那么
第三关推理论证
毕达哥拉斯定理
百牛定理
直角三角形两条直角边的平方和,等于斜边的平方。
即:
1.成立条件:
在直角三角形中;c为斜边
2.公式变形:
3.作用:
1.知道两条直角边可以求出斜边;
2.知道斜边和一条直角边,可以求另一条直角边。
直角三角形两条直角边的平方和,等于斜边的平方。
例1
求下列直角三角形中未知边的长:
8
x
17
16
20
x
12
5
x
温馨提示:已知直角三角形的两边长,求第三边长时,应选用勾股定理变形公式直接代入计算较为快捷准确!
例2
已知:Rt△ABC中,AB=4,AC=3,则BC=
.
5
或
温馨提示:当直角三角形中斜边或直角边不明确时,其中一较长边可能是直角边,也可能是斜边,这种情况下,一定要进行分类讨论,方能求解.
学以致用
解
例3
1谈谈这节课的收获。
课
堂
小
结:
2
运用“勾股定理”应注意什么问题?
课后作业
课本55页第1、2题.
基训52、53页
