人教版(五四制)数学八年级下册 第二十四章 勾股定理 单元练习(Word版 含答案)
文档属性
| 名称 | 人教版(五四制)数学八年级下册 第二十四章 勾股定理 单元练习(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 552.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-15 00:00:00 | ||
图片预览


文档简介
第二十四章
勾股定理
一、选择题
(每小题3分,共计30分)
1.在下列长度的各组线段中,不能构成直角三角形的是(
)
A.3,4,5
B.7,24,25
C.1,1,
D.
2.在平面直角坐标系中,点P(-4,3)到原点的距离是(
)
A.3
B.4
C.5
D.
3.直角三角形ABC中,斜边AB=3,则的值是
(
)
A.6
B.9
C.12
D.18
4.如图,以直角三角形ABC的三边向外作正方形,三个正方形的面积分别为S1
,
S2,
S3,
若S1
=9,S2
=16则S3为(
)
A.5
B.7
C.
25
D.无法确定
5.如图,在△ABC中,AB=AC=5,CD是AB边上的高,BD=1,则BC的长为
(
)
A.3
B.
C.
D.
6.在△ABC中,①若∠B=∠C-∠A,则△ABC是直角三角形;②若a2=(b+c)(b-c),则△ABC是直角三角形;③.若a∶b∶c=5∶4∶3.则△ABC是直角三角形;④若∠A∶∠B∶∠C=
3∶4∶5,则△ABC是直角三角形.
其中错误的个数为
(
)
A.1个
B.2个
C.3个
D.4个
7.如图,四边形ACBD中,∠C=90°,BC=5,,AC=,BD=24,AD=26.则∠CBD的度数为(
)
A.120°
B.135°
C.
150°
D.145°
8.在△ABC中,∠A=30°,∠BCA=105°,AC=6,则BC的长为(
)
A.3
B.
C.
D.
9.在△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为(
)
A.32
B.
42
C.
4或14
D.32或42
下列命题中,逆命题正确的有(
)
①内错角相等,两直线平行;②如果两个角都是直角,那么它们相等;③如果两个实数相等,那么它们的平方相等;④如果三角形的三边长a,b,c,满足,那么这个三角形是直角三角形.
A.1个
B.2个
C.3个
D.4个
二.填空题
(每小题3分,共计30分)
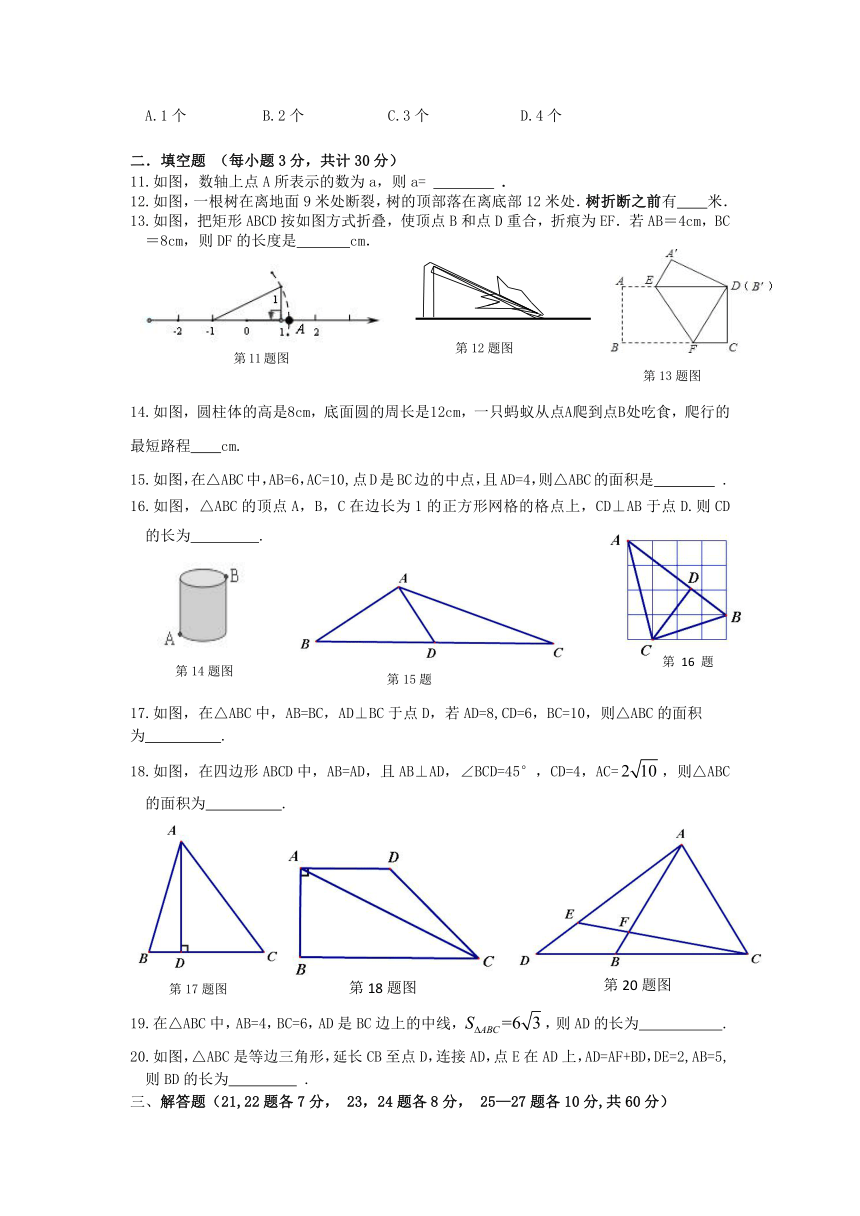
11.如图,数轴上点A所表示的数为a,则a=
.
12.如图,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前有 米.
13.如图,把矩形ABCD按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=4cm,BC=8cm,则DF的长度是
cm.
14.如图,圆柱体的高是8cm,底面圆的周长是12cm,一只蚂蚁从点A爬到点B处吃食,爬行的最短路程
cm.
15.如图,在△ABC中,AB=6,AC=10,点D是BC边的中点,且AD=4,则△ABC的面积是
.
16.如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,CD⊥AB于点D.则CD的长为
.
17.如图,在△ABC中,AB=BC,AD⊥BC于点D,若AD=8,CD=6,BC=10,则△ABC的面积为
.
18.如图,在四边形ABCD中,AB=AD,且AB⊥AD,∠BCD=45°,CD=4,AC=,则△ABC的面积为
.
19.在△ABC中,AB=4,BC=6,AD是BC边上的中线,,则AD的长为
.
20.如图,△ABC是等边三角形,延长CB至点D,连接AD,点E在AD上,AD=AF+BD,DE=2,AB=5,则BD的长为
.
三、解答题(21,22题各7分,
23,24题各8分,
25—27题各10分,共60分)
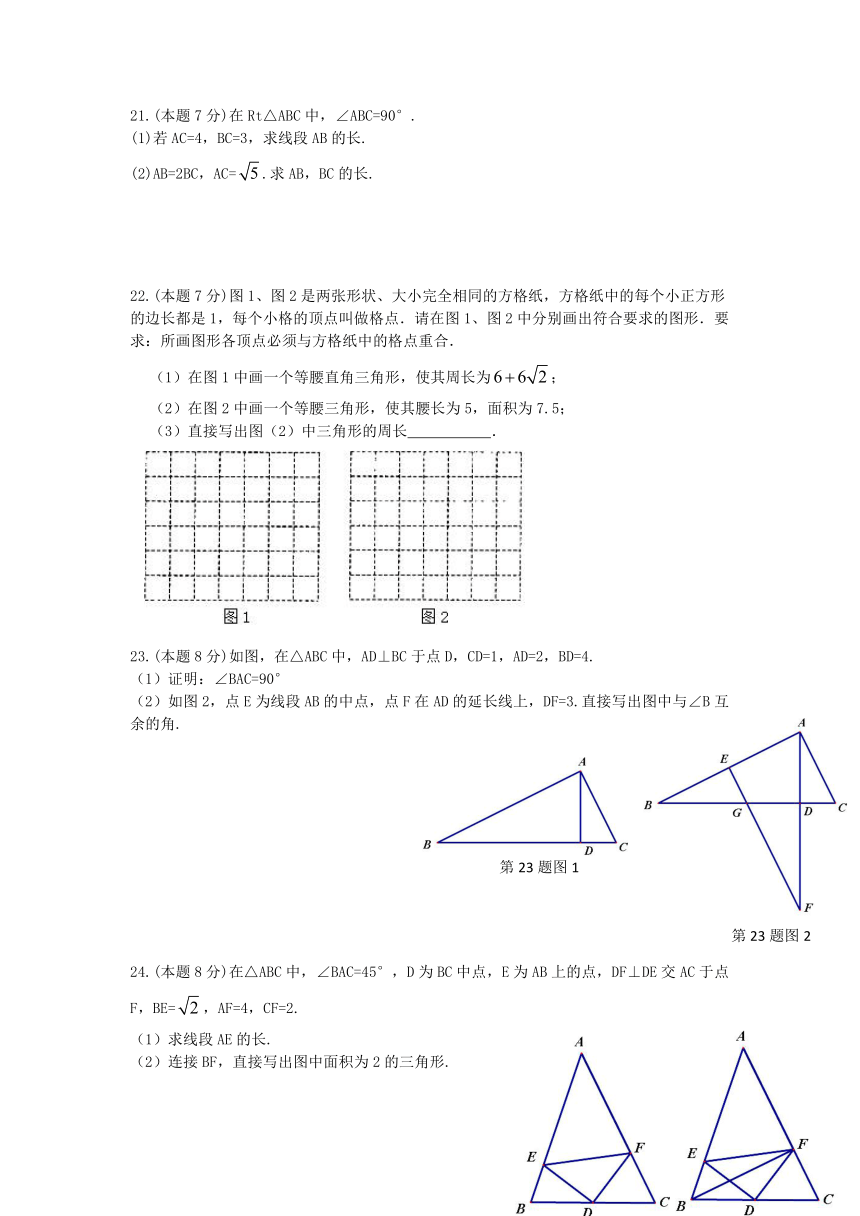
21.(本题7分)在Rt△ABC中,∠ABC=90°.
(1)若AC=4,BC=3,求线段AB的长.
(2)AB=2BC,AC=.求AB,BC的长.
22.(本题7分)图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长都是1,每个小格的顶点叫做格点.请在图1、图2中分别画出符合要求的图形.要求:所画图形各顶点必须与方格纸中的格点重合.
(1)在图1中画一个等腰直角三角形,使其周长为;
(2)在图2中画一个等腰三角形,使其腰长为5,面积为7.5;
(3)直接写出图(2)中三角形的周长
.
23.(本题8分)如图,在△ABC中,AD⊥BC于点D,CD=1,AD=2,BD=4.
(1)证明:∠BAC=90°
(2)如图2,点E为线段AB的中点,点F在AD的延长线上,DF=3.直接写出图中与∠B互余的角.
24.(本题8分)在△ABC中,∠BAC=45°,D为BC中点,E为AB上的点,DF⊥DE交AC于点F,BE=,AF=4,CF=2.
(1)求线段AE的长.
(2)连接BF,直接写出图中面积为2的三角形.
25.(本题10分)如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号)
26.(本题10分)已知四边形ABCD中,对角线AC,BD交于点E,∠BCA=∠BDA,∠ABC=∠CED.
(1)如图(1),求证:AB=AD;
(2)如图(2),点F在BD上,过点B作AC的垂线交AC于点H,交AF的延长线于点G.若∠G=∠ADB,且,求∠CAG的度数;
(3)如图(3),在(2)的条件
下,将EC沿BD翻折,交AB于点M,点N是线段AD上的点,AN=BM,过点N作NP//BG,交BD的延长线于点P,△AME的周长是20,DP=,求线段BD的长.
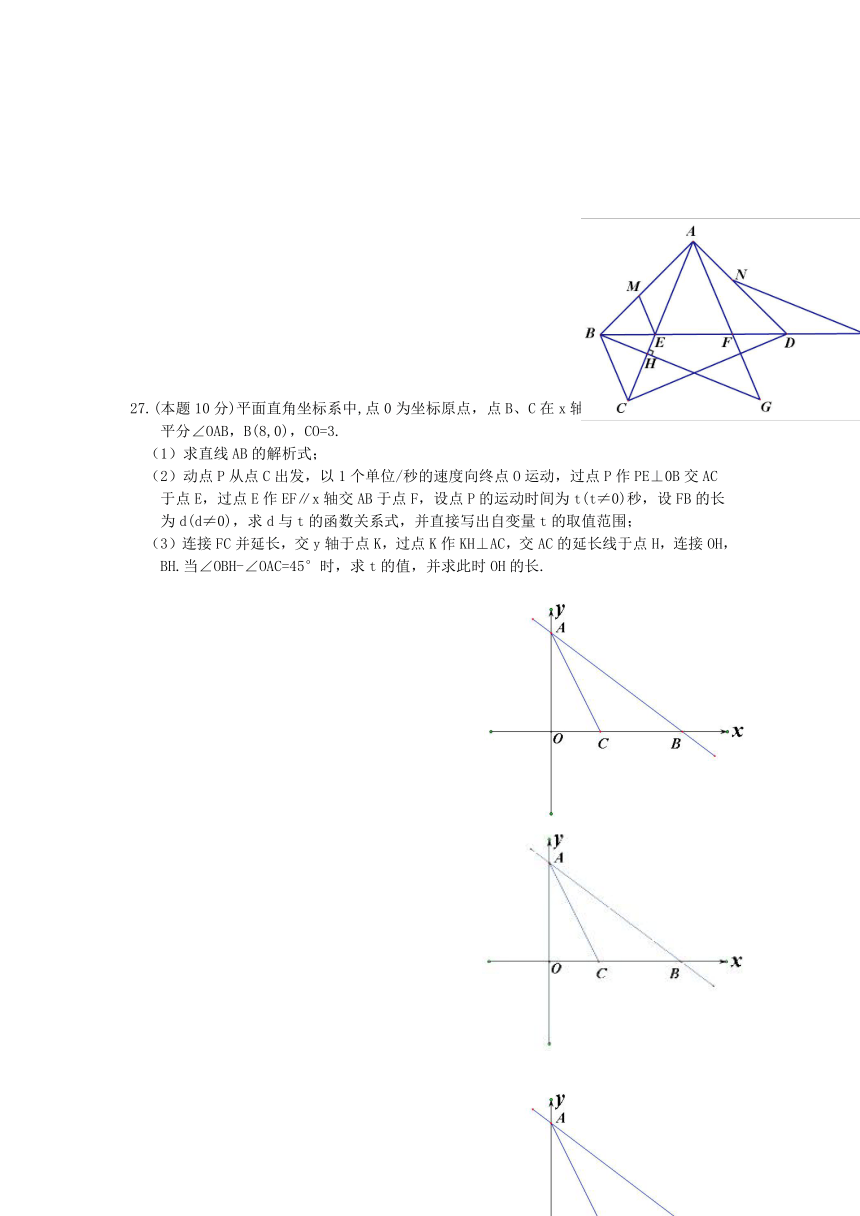
27.(本题10分)平面直角坐标系中,点0为坐标原点,点B、C在x轴上,点A在y轴上,AC平分∠OAB,B(8,0),CO=3.
(1)求直线AB的解析式;
(2)动点P从点C出发,以1个单位/秒的速度向终点O运动,过点P作PE⊥0B交AC于点E,过点E作EF∥x轴交AB于点F,设点P的运动时间为t(t≠0)秒,设FB的长为d(d≠0),求d与t的函数关系式,并直接写出自变量t的取值范围;
(3)连接FC并延长,交y轴于点K,过点K作KH⊥AC,交AC的延长线于点H,连接OH,BH.当∠OBH-∠OAC=45°时,求t的值,并求此时OH的长.
参考答案
第二十四章
勾股定理
一、选择题
1.D
2.C
3.D
4.C
5.C
6.A
7.C
8.C
9.D
10.B
二、填空题
11.
12.24
13.5
14.10
15.24
16.
17.
18.8
19.
20.3
三、解答题
21.解:(1)在Rt△ABC中,∠ABC=90°
∴
∴
解得
:AB=
(2)在Rt△ABC中,∠ABC=90°
∴
∴
解得:
BC=1
∴AB=2BC=2
22.
(3)
23.(1)证明:∵AD⊥BC
∴∠ADB=∠ADC=90°
在Rt△ADC中,AD+CD=AC
∴AC=2+1=5
在Rt△ADB中,AD+BD=AB
∴AB=2+4=25
∵AC+AB=5+20=25
又∵BC=(4+1)=25
∴AC+AB=BC
∴△ABC为直角三角形,∠BAC=90°.
∠EGB,∠FGD,∠C,∠BAD.
24.(1)延长ED至点G,使DG=DE,连接GC,GF
∵点D是线段BC的中点
∴DB=DC
∵∠BDE=∠CDG
∴△BDE≌△CDG(SAS)
∴∠B=∠BCG,FG=FE,CG=BE=
∴∠FCG=∠FCB+∠BCG=∠FCB+∠B=180°-∠A=135°
过点G作GR⊥FC于点R
∠GCR=∠CGR=45°
在Rt△CRG中,∠R=90°
,∴CR=GR=1
在Rt△FGR中,∠FRG=90°
,,
过点F作FH⊥AB于点H
∠A=∠AFH=45°,
在Rt△AFH中,∠FHA=90°,AF=4
,∴AH=FH=
在Rt△FHE中,∠FHE=90°
∴,
(2)△EFB,△DFB,△DFC
25.解:(1)根据题意:得BD∥AE
∴∠ADB=90°,∠BAD=∠ADB=45°∴BD=AB=60米
∴两建筑物底部之间水平距离BD的长度为60米
延长AE、DC交于点F
可证,四边形ABDF为正方形
∴AF=BD=DF=60米
在R△AFC中
∴.FAC=30°
∴AC=2CF,?
即,,
∴建筑物CD的高度为米
26.(1)∵∠BCA=∠BDA
∴∠BEA=∠BDA+∠CAD=∠BCA+∠CBD
∴∠CAD=∠CBD
∵∠CBA=∠CED
∴∠DBA+∠CBD=∠ADE+∠CAD
∴∠DBA=∠ADE
∴BA=AD
作∠F/AB=∠2,使AF/
=AF
可证△F/AB≌△FAD
∴F/B=FD,∠ABF/=∠ADB
设∠ABD=∠ADB=α
∠BAD=180°-2α
∵∠G=∠ADB=α
∴∠HAG=90°-α
∴∠1+∠2=∠BAD-∠HAG=90°-α
∴∠F/AE=∠∠F/AB+∠1=∠2+∠1=∠EAF
可证△F/AE≌△AFE(SAS)
∴F/E=FE
∴△F/BE是直角三角形,且∠F/BE=90°
∴2α=90°,α=45°
∠CAG=45°
设∠DAF=β
∴∠BAC=45°-β
∵∠G=∠ADB=45°,∴∠GBD=∠GAD=β
∵NP//BG,∴∠GBD=∠BPN=β
∴∠BEC=∠ABE+∠BAE=90°-β
∴∠MEB=∠BEC=90°-β,∴∠AEM=2β
∵BM=AN,∴AM=DN
∵∠BAE+∠DAF=∠DNP+∠DPN=45°,∴∠BAE=∠DNP
在NP上截NK=AE
可证△AME≌△NDK(SAS)
∴∠NKD=∠AEM=2β
∵∠NKD=∠KDB+NPD,∴∠KDB=∠NPD=β
∴KD=KP
∵AM+ME+AE=20,∴DN+NK+DK=20
∴DN+NK+PK=20,即DN+NP=20
设DN=2a,NP=20-2a
过点N作NR⊥AD于点R
可求NR=DR=
在Rt△NPR中,∠NRP=90°,
可求a=,∴DN=7,AM=7
过点K作KT⊥DP于点T,
∴DT=PT=
过点M作ML⊥BE于点L
∠LME=90°-∠MEB=90°-(90°-β)=β=∠KDT
∵∠MEL=∠DKT=90°,ME=DK
可证△MEL≌△KDT(AAS)
在Rt△BML中,∠MLB=90°,
可求BM=5,∴AB=12
在Rt△BAD中,
可求BD=
27.(1)过点C作CD⊥AB于点D
∵AC平分∠OAB
∴CO=CD=3
可证△AOC≌△ADC
∵B(8,0)∴OB=8,BC=5
在Rt△BCD中,∠BDC=90°
可求BD=4
设OA=AD=a,AB=a+4
在Rt△AOB中,∠BOA=90°
可求a=6,∴A(0,6)
设直线AB的解析式为y=kx+b
(2)∴A(0,6),C(3,0)
设直线AB的解析式为y=k1x+b1
直线AC的解析式为y=-2x+6
CP=t,OP=3-t
∴点P(3-t,0)
∵EP⊥x轴
∴点E与点P的横坐标相等
将x=3-t代入y=-2x+6
y=2t,∴E(3-t,2t)
∵EF//x轴
,
∴点F与点E的纵坐标相等
将y=2t代入
∴,
∴
过点F作FG⊥OB于点G
∴FG=2t
在Rt△BFG中,∠FGB=90°,
可求
(3)设∠OAC=∠BAC=α
∴∠ACO=90°-α=∠BCH
∵∠OBH-∠OAC=45°,∴∠OBH=45°+α
∴∠AHB=45°
延长KH交AB于点R
∴HR=HK,∠BHR=45°=∠CHB,∠ARH=90°-α=∠BCH
可证△BCH≌△BRH(ASA)
∴BR=BC=5,∴KH=HC,AK=AR=15,OK=9
∴∠CKH=∠KCH=45°
可证∠BFC=∠BCF=45°+α
∴BF=BC=5,∴,
设HK=HC=m
在Rt△AHK中,∠AHK=90°,
可求m=,∴CH=HK==AC
过点H作HM⊥OB于点M
,
可证△ACO≌△HCM(AAS)
∴CM=OC=3,MH=OA=6
在Rt△OMHK中,∠OMH=90°,
可求
勾股定理
一、选择题
(每小题3分,共计30分)
1.在下列长度的各组线段中,不能构成直角三角形的是(
)
A.3,4,5
B.7,24,25
C.1,1,
D.
2.在平面直角坐标系中,点P(-4,3)到原点的距离是(
)
A.3
B.4
C.5
D.
3.直角三角形ABC中,斜边AB=3,则的值是
(
)
A.6
B.9
C.12
D.18
4.如图,以直角三角形ABC的三边向外作正方形,三个正方形的面积分别为S1
,
S2,
S3,
若S1
=9,S2
=16则S3为(
)
A.5
B.7
C.
25
D.无法确定
5.如图,在△ABC中,AB=AC=5,CD是AB边上的高,BD=1,则BC的长为
(
)
A.3
B.
C.
D.
6.在△ABC中,①若∠B=∠C-∠A,则△ABC是直角三角形;②若a2=(b+c)(b-c),则△ABC是直角三角形;③.若a∶b∶c=5∶4∶3.则△ABC是直角三角形;④若∠A∶∠B∶∠C=
3∶4∶5,则△ABC是直角三角形.
其中错误的个数为
(
)
A.1个
B.2个
C.3个
D.4个
7.如图,四边形ACBD中,∠C=90°,BC=5,,AC=,BD=24,AD=26.则∠CBD的度数为(
)
A.120°
B.135°
C.
150°
D.145°
8.在△ABC中,∠A=30°,∠BCA=105°,AC=6,则BC的长为(
)
A.3
B.
C.
D.
9.在△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为(
)
A.32
B.
42
C.
4或14
D.32或42
下列命题中,逆命题正确的有(
)
①内错角相等,两直线平行;②如果两个角都是直角,那么它们相等;③如果两个实数相等,那么它们的平方相等;④如果三角形的三边长a,b,c,满足,那么这个三角形是直角三角形.
A.1个
B.2个
C.3个
D.4个
二.填空题
(每小题3分,共计30分)
11.如图,数轴上点A所表示的数为a,则a=
.
12.如图,一根树在离地面9米处断裂,树的顶部落在离底部12米处.树折断之前有 米.
13.如图,把矩形ABCD按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=4cm,BC=8cm,则DF的长度是
cm.
14.如图,圆柱体的高是8cm,底面圆的周长是12cm,一只蚂蚁从点A爬到点B处吃食,爬行的最短路程
cm.
15.如图,在△ABC中,AB=6,AC=10,点D是BC边的中点,且AD=4,则△ABC的面积是
.
16.如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,CD⊥AB于点D.则CD的长为
.
17.如图,在△ABC中,AB=BC,AD⊥BC于点D,若AD=8,CD=6,BC=10,则△ABC的面积为
.
18.如图,在四边形ABCD中,AB=AD,且AB⊥AD,∠BCD=45°,CD=4,AC=,则△ABC的面积为
.
19.在△ABC中,AB=4,BC=6,AD是BC边上的中线,,则AD的长为
.
20.如图,△ABC是等边三角形,延长CB至点D,连接AD,点E在AD上,AD=AF+BD,DE=2,AB=5,则BD的长为
.
三、解答题(21,22题各7分,
23,24题各8分,
25—27题各10分,共60分)
21.(本题7分)在Rt△ABC中,∠ABC=90°.
(1)若AC=4,BC=3,求线段AB的长.
(2)AB=2BC,AC=.求AB,BC的长.
22.(本题7分)图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长都是1,每个小格的顶点叫做格点.请在图1、图2中分别画出符合要求的图形.要求:所画图形各顶点必须与方格纸中的格点重合.
(1)在图1中画一个等腰直角三角形,使其周长为;
(2)在图2中画一个等腰三角形,使其腰长为5,面积为7.5;
(3)直接写出图(2)中三角形的周长
.
23.(本题8分)如图,在△ABC中,AD⊥BC于点D,CD=1,AD=2,BD=4.
(1)证明:∠BAC=90°
(2)如图2,点E为线段AB的中点,点F在AD的延长线上,DF=3.直接写出图中与∠B互余的角.
24.(本题8分)在△ABC中,∠BAC=45°,D为BC中点,E为AB上的点,DF⊥DE交AC于点F,BE=,AF=4,CF=2.
(1)求线段AE的长.
(2)连接BF,直接写出图中面积为2的三角形.
25.(本题10分)如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号)
26.(本题10分)已知四边形ABCD中,对角线AC,BD交于点E,∠BCA=∠BDA,∠ABC=∠CED.
(1)如图(1),求证:AB=AD;
(2)如图(2),点F在BD上,过点B作AC的垂线交AC于点H,交AF的延长线于点G.若∠G=∠ADB,且,求∠CAG的度数;
(3)如图(3),在(2)的条件
下,将EC沿BD翻折,交AB于点M,点N是线段AD上的点,AN=BM,过点N作NP//BG,交BD的延长线于点P,△AME的周长是20,DP=,求线段BD的长.
27.(本题10分)平面直角坐标系中,点0为坐标原点,点B、C在x轴上,点A在y轴上,AC平分∠OAB,B(8,0),CO=3.
(1)求直线AB的解析式;
(2)动点P从点C出发,以1个单位/秒的速度向终点O运动,过点P作PE⊥0B交AC于点E,过点E作EF∥x轴交AB于点F,设点P的运动时间为t(t≠0)秒,设FB的长为d(d≠0),求d与t的函数关系式,并直接写出自变量t的取值范围;
(3)连接FC并延长,交y轴于点K,过点K作KH⊥AC,交AC的延长线于点H,连接OH,BH.当∠OBH-∠OAC=45°时,求t的值,并求此时OH的长.
参考答案
第二十四章
勾股定理
一、选择题
1.D
2.C
3.D
4.C
5.C
6.A
7.C
8.C
9.D
10.B
二、填空题
11.
12.24
13.5
14.10
15.24
16.
17.
18.8
19.
20.3
三、解答题
21.解:(1)在Rt△ABC中,∠ABC=90°
∴
∴
解得
:AB=
(2)在Rt△ABC中,∠ABC=90°
∴
∴
解得:
BC=1
∴AB=2BC=2
22.
(3)
23.(1)证明:∵AD⊥BC
∴∠ADB=∠ADC=90°
在Rt△ADC中,AD+CD=AC
∴AC=2+1=5
在Rt△ADB中,AD+BD=AB
∴AB=2+4=25
∵AC+AB=5+20=25
又∵BC=(4+1)=25
∴AC+AB=BC
∴△ABC为直角三角形,∠BAC=90°.
∠EGB,∠FGD,∠C,∠BAD.
24.(1)延长ED至点G,使DG=DE,连接GC,GF
∵点D是线段BC的中点
∴DB=DC
∵∠BDE=∠CDG
∴△BDE≌△CDG(SAS)
∴∠B=∠BCG,FG=FE,CG=BE=
∴∠FCG=∠FCB+∠BCG=∠FCB+∠B=180°-∠A=135°
过点G作GR⊥FC于点R
∠GCR=∠CGR=45°
在Rt△CRG中,∠R=90°
,∴CR=GR=1
在Rt△FGR中,∠FRG=90°
,,
过点F作FH⊥AB于点H
∠A=∠AFH=45°,
在Rt△AFH中,∠FHA=90°,AF=4
,∴AH=FH=
在Rt△FHE中,∠FHE=90°
∴,
(2)△EFB,△DFB,△DFC
25.解:(1)根据题意:得BD∥AE
∴∠ADB=90°,∠BAD=∠ADB=45°∴BD=AB=60米
∴两建筑物底部之间水平距离BD的长度为60米
延长AE、DC交于点F
可证,四边形ABDF为正方形
∴AF=BD=DF=60米
在R△AFC中
∴.FAC=30°
∴AC=2CF,?
即,,
∴建筑物CD的高度为米
26.(1)∵∠BCA=∠BDA
∴∠BEA=∠BDA+∠CAD=∠BCA+∠CBD
∴∠CAD=∠CBD
∵∠CBA=∠CED
∴∠DBA+∠CBD=∠ADE+∠CAD
∴∠DBA=∠ADE
∴BA=AD
作∠F/AB=∠2,使AF/
=AF
可证△F/AB≌△FAD
∴F/B=FD,∠ABF/=∠ADB
设∠ABD=∠ADB=α
∠BAD=180°-2α
∵∠G=∠ADB=α
∴∠HAG=90°-α
∴∠1+∠2=∠BAD-∠HAG=90°-α
∴∠F/AE=∠∠F/AB+∠1=∠2+∠1=∠EAF
可证△F/AE≌△AFE(SAS)
∴F/E=FE
∴△F/BE是直角三角形,且∠F/BE=90°
∴2α=90°,α=45°
∠CAG=45°
设∠DAF=β
∴∠BAC=45°-β
∵∠G=∠ADB=45°,∴∠GBD=∠GAD=β
∵NP//BG,∴∠GBD=∠BPN=β
∴∠BEC=∠ABE+∠BAE=90°-β
∴∠MEB=∠BEC=90°-β,∴∠AEM=2β
∵BM=AN,∴AM=DN
∵∠BAE+∠DAF=∠DNP+∠DPN=45°,∴∠BAE=∠DNP
在NP上截NK=AE
可证△AME≌△NDK(SAS)
∴∠NKD=∠AEM=2β
∵∠NKD=∠KDB+NPD,∴∠KDB=∠NPD=β
∴KD=KP
∵AM+ME+AE=20,∴DN+NK+DK=20
∴DN+NK+PK=20,即DN+NP=20
设DN=2a,NP=20-2a
过点N作NR⊥AD于点R
可求NR=DR=
在Rt△NPR中,∠NRP=90°,
可求a=,∴DN=7,AM=7
过点K作KT⊥DP于点T,
∴DT=PT=
过点M作ML⊥BE于点L
∠LME=90°-∠MEB=90°-(90°-β)=β=∠KDT
∵∠MEL=∠DKT=90°,ME=DK
可证△MEL≌△KDT(AAS)
在Rt△BML中,∠MLB=90°,
可求BM=5,∴AB=12
在Rt△BAD中,
可求BD=
27.(1)过点C作CD⊥AB于点D
∵AC平分∠OAB
∴CO=CD=3
可证△AOC≌△ADC
∵B(8,0)∴OB=8,BC=5
在Rt△BCD中,∠BDC=90°
可求BD=4
设OA=AD=a,AB=a+4
在Rt△AOB中,∠BOA=90°
可求a=6,∴A(0,6)
设直线AB的解析式为y=kx+b
(2)∴A(0,6),C(3,0)
设直线AB的解析式为y=k1x+b1
直线AC的解析式为y=-2x+6
CP=t,OP=3-t
∴点P(3-t,0)
∵EP⊥x轴
∴点E与点P的横坐标相等
将x=3-t代入y=-2x+6
y=2t,∴E(3-t,2t)
∵EF//x轴
,
∴点F与点E的纵坐标相等
将y=2t代入
∴,
∴
过点F作FG⊥OB于点G
∴FG=2t
在Rt△BFG中,∠FGB=90°,
可求
(3)设∠OAC=∠BAC=α
∴∠ACO=90°-α=∠BCH
∵∠OBH-∠OAC=45°,∴∠OBH=45°+α
∴∠AHB=45°
延长KH交AB于点R
∴HR=HK,∠BHR=45°=∠CHB,∠ARH=90°-α=∠BCH
可证△BCH≌△BRH(ASA)
∴BR=BC=5,∴KH=HC,AK=AR=15,OK=9
∴∠CKH=∠KCH=45°
可证∠BFC=∠BCF=45°+α
∴BF=BC=5,∴,
设HK=HC=m
在Rt△AHK中,∠AHK=90°,
可求m=,∴CH=HK==AC
过点H作HM⊥OB于点M
,
可证△ACO≌△HCM(AAS)
∴CM=OC=3,MH=OA=6
在Rt△OMHK中,∠OMH=90°,
可求
