2020年人教版(五四学制)八年级下册数学期末培优检测试题(Word版 含答案)
文档属性
| 名称 | 2020年人教版(五四学制)八年级下册数学期末培优检测试题(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 155.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-15 00:00:00 | ||
图片预览




文档简介
期末培优检测试题
一.选择题(满分30分,每小题3分)
1.下列所给方程中,是一元二次方程的是( )
A.2x+y=0 B.x2﹣1=0 C.3﹣x=8 D.y=
2.点A(x1,y1)、B(x2,y2)都在直线y=kx+2(k<0)上,且x1<x2则y1、y2的大小关系是( )
A.y1 =y2 B.y1 <y2 C.y1 >y2 D.y1 ≥y2
3.下列条件中,不能判断一个三角形是直角三角形的是( )
A.三条边的比为2:3:4
B.三条边满足关系a2=b2﹣c2
C.三条边的比为1:1:
D.三个角满足关系∠B+∠C=∠A
4.下列给出的条件中,不能判断四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC B.∠A=∠C,∠B=∠D
C.AB∥CD,AD∥BC D.AB=CD,AD=BC
5.已知关于x的一元二次方程3x2+4x﹣5=0,下列说法正确的是( )
A.方程有两个相等的实数根
B.方程有两个不相等的实数根
C.没有实数根
D.无法确定
6.某农业大镇2018年葡萄总产量为1.2万吨,预计2020年葡萄总产量达到1.6万吨,求葡萄总产量的年平均增长率,设葡萄总产量的年平均增长率为x,则可列方程为( )
A.1.2(1+x)2=1.6 B.1.6(1﹣x)2=1.2
C.1.2(1+2x)=1.6 D.1.2(1+x2)=1.6
7.如果直线y=kx+b经过一、二、四象限,则有( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
8.下列命题中,是真命题的是( )
A.三角形的外心到三角形三边的距离相等
B.顺次连接对角线相等的四边形各边中点所得的四边形是菱形
C.方程x2+2x+3=0有两个不相等的实数根
D.将抛物线y=2x2﹣2向右平移1个单位后得到的抛物线是y=2x2﹣3
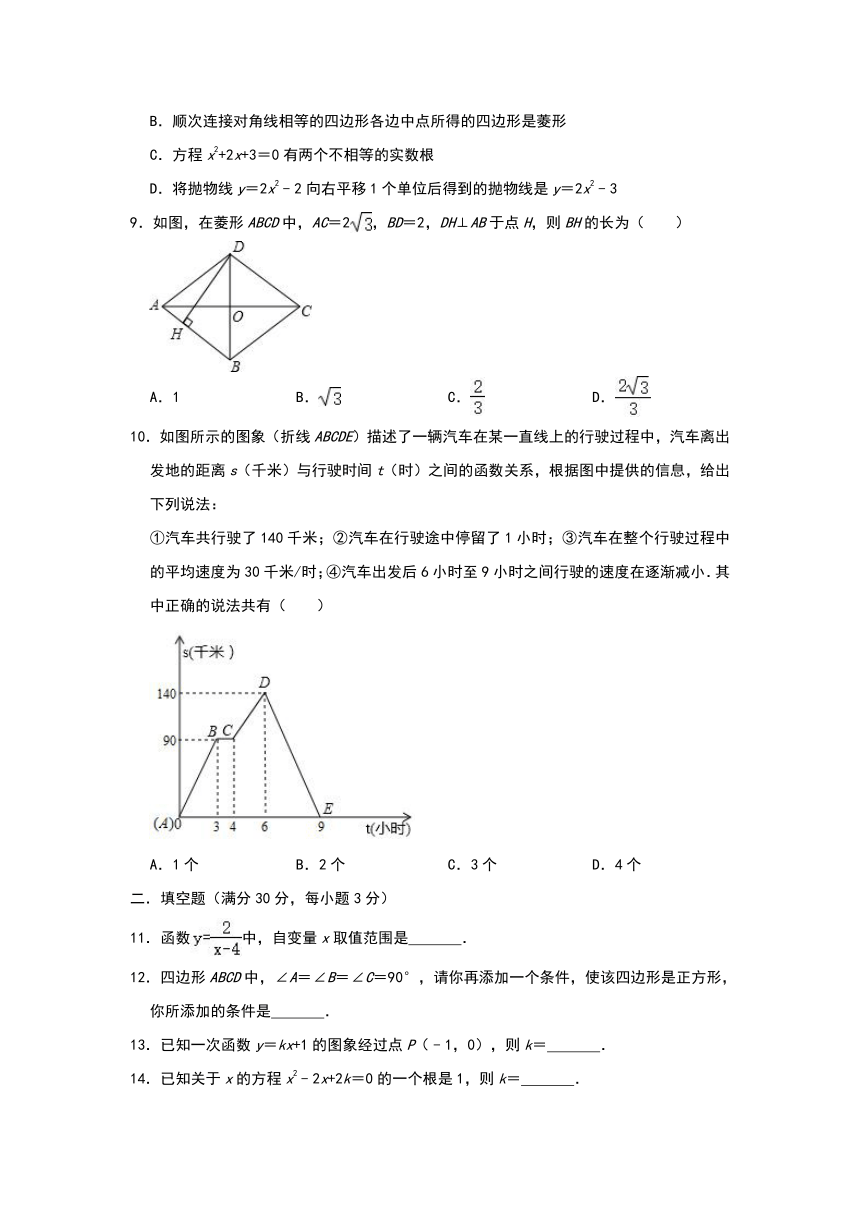
9.如图,在菱形ABCD中,AC=2,BD=2,DH⊥AB于点H,则BH的长为( )
A.1 B. C. D.
10.如图所示的图象(折线ABCDE)描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)与行驶时间t(时)之间的函数关系,根据图中提供的信息,给出下列说法:
①汽车共行驶了140千米;②汽车在行驶途中停留了1小时;③汽车在整个行驶过程中的平均速度为30千米/时;④汽车出发后6小时至9小时之间行驶的速度在逐渐减小.其中正确的说法共有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(满分30分,每小题3分)
11.函数中,自变量x取值范围是 .
12.四边形ABCD中,∠A=∠B=∠C=90°,请你再添加一个条件,使该四边形是正方形,你所添加的条件是 .
13.已知一次函数y=kx+1的图象经过点P(﹣1,0),则k= .
14.已知关于x的方程x2﹣2x+2k=0的一个根是1,则k= .
15.在Rt△ABC中,AC=9,BC=12,则AB2= .
16.当三角形中的一个内角α是另一个内角β的一半时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”为直角三角形,则这个“特征角”的度数为 .
17.在国家积极研发和生产调配下,某种型号的医疗器械连续两年降价,第一年下降20%,第二年下降80%,那么该医疗器械这两年的平均降价率是 .
18.若a,b,c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:
①以a2,b2,c2的长为边的三条线段能组成一个三角形
②以的长为边的三条线段能组成一个三角形
③以a+b,c+h,h的长为边的三条线段能组成直角三角形
④以的长为边的三条线段能组成直角三角形
其中所有正确结论的序号为 .
19.如图,已知一次函数y=kx﹣b与y=x的图象相交于点A(a,1),则关于x的方程(k﹣)x=b的解x= .
20.如图,矩形ABCD中,AB=3,AD=9,将△ABE沿BE翻折得到△A′BE,点A落在矩形ABCD的内部,且∠AA′G=90°,若以点A′、G、C为顶点的三角形是直角三角形,则AE= .
三.解答题
21.(7分)请用合适的方法解方程:
(1)4x2﹣8x+1=0
(2)(x﹣2)(x﹣3)=12
22.(7分)著名台湾魔术师刘谦发明了一个道具,他把下图①中的正方形,分割成两个全等的直角三角形和直角梯形.然后拼成图②中的长方形.
通过计算这两个图形的面积,证明了64=65.请你用学过的数学知识,找到刘谦的破绽.
23.(8分)据我囯古代《周髀算经》记载,公元前1120年商高对周公说,将一根直尺折成一个直角,两端连接得到一个直角三角形,如果勾是3,股是4,那么弦就等于5,后人概括为“勾三,股四、弦五”.像3、4、5这样为三边长能构成直角三角形的三个正整数,称为勾股数.
【应用举例】
观察3,4,5;5,12,13;7,24,25;…,可以发现这些勾股数的勾都是奇数,且从3起就没有间断过,并且
勾为3时,股4=,弦5=;勾为5时,股12=,弦13=;
请仿照上面两组样例,用发现的规律填空:
(1)如果勾为7,则股24= ;弦25= .
(2)如果勾用n(n≥3,且n为奇数)表示时,请用含有n的式子表示股和弦,则股= ;弦= .
(3)继续观察①4,3,5;②6,8,10;③8,15,17;…,可以发现各组的第一个数都是偶数,且从4起也没有间断过.请你直接用m(m为偶数且m≥4)的代数式来表示直角三角形的另一条直角边和弦的长.
24.(8分)如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.若AC=2,CE=4;
(1)求证:四边形ACED是平行四边形.
(2)求BC的长.
25.(10分)元旦期间,小黄自驾游去了离家156千米的黄石矿博园,右图是小黄离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)求小黄出发0.5小时时,离家的距离;
(2)求出AB段的图象的函数解析式;
(3)小黄出发1.5小时时,离目的地还有多少千米?
26.(10分)如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE.
(1)发现:当正方形AEFG绕点A旋转,如图②所示.
①线段DG与BE之间的数量关系是 ;
②直线DG与直线BE之间的位置关系是 ;
(2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,上述结论是否成立,并说明理由.
(3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).
27.(10分)如图1,在平面直角坐标系中,OB=10,F是y轴正半轴上一点.
(1)若OF=2,求直线BF的解析式;
(2)设OF=t,△OBF的面积为s,求s与t的函数关系(直接写出自变量t的取值范围);
(3)如图3,在(2)的条件下,过点B作BA⊥x轴,点C在x轴上,OF=OC,连接AC,CD⊥直线BF于点D,∠ACB=2∠CBD,AC=13,OF=OC,AC.BD交于点E,求此时t的值.
参考答案
一.选择题
1. B.
2. C.
3. A.
4. A.
5. B.
6. A.
7. C.
8. B.
9. A.
10. A.
二.填空题
11. x≠4.
12. AB=BC.
13. 1
14. .
15. 225或63.
16. 45°或30°.
17. 60%.
18.②③.
19. 3.
20. 1或.
三.解答题
21.解:(1)∵a=4,b=﹣8,c=1,
∴△=(﹣8)2﹣4×4×1=48>0,
则x==;
(2)方程整理为一般式,得:x2﹣5x﹣6=0,
则(x﹣6)(x+1)=0,
∴x﹣6=0或x+1=0,
解得:x=6或x=﹣1.
22.解:如图②,过C作CF⊥AB垂足为F,则
,
而tan∠AEB==,
即tan∠BCF>tan∠AEB.
∴∠BCF>∠AEB.
∴B、C、E三点不共线,事实上,∠BCD+∠DCE>180°,
因而图②中间有一条缝,它实际上是个平行四边形,其面积为1.
23.解:(1)依据规律可得,如果勾为7,则股24=(49﹣1),弦25=(49+1),
故答案为:(49﹣1),(49+1);
(2)如果勾用n(n≥3,且n为奇数)表示时,则股=(n2﹣1),弦=(n2+1),
故答案为:(n2﹣1),(n2+1);
(3)根据规律可得,如果a,b,c是符合同样规律的一组勾股数,a=m(m为偶数且m≥4),则另一条直角边b=﹣1,弦c=+1.
24.解:(1)证明:∵∠ACB=90°,DE⊥BC,
∴AC∥DE
又∵CE∥AD
∴四边形ACED是平行四边形.
(2)∵四边形ACED是平行四边形.
∴DE=AC=2.
在Rt△CDE中,由勾股定理得CD===2.
∵D是BC的中点,
∴BC=2CD=4.
25.解:(1)设OA段图象的函数表达式为y=kx.
∵当x=0.8时,y=48,
∴0.8k=48,
∴k=60.
∴y=60x(0≤x≤0.8),
∴当x=0.5时,y=60×0.5=30.
故小黄出发0.5小时时,离家30千米;
(2)设AB段图象的函数表达式为y=k′x+b.
∵A(0.8,48),B(2,156)在AB上,
,
解得,
∴y=90x﹣24(0.8≤x≤2);
(3)∵当x=1.5时,y=90×1.5﹣24=111,
∴156﹣111=45.
故小黄出发1.5小时时,离目的地还有45千米.
26.解:(1)①如图②中,
∵四边形ABCD和四边形AEFG是正方形,
∴AE=AG,AB=AD,∠BAD=∠EAG=90°,
∴∠BAE=∠DAG,
在△ABE和△DAG中,
,
∴△ABE≌△ADG(SAS),
∴BE=DG;
②如图2,延长BE交AD于T,交DG于H.
由①知,△ABE≌△DAG,
∴∠ABE=∠ADG,
∵∠ATB+∠ABE=90°,
∴∠ATB+∠ADG=90°,
∵∠ATB=∠DTH,
∴∠DTH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG,
故答案为:BE=DG,BE⊥DG;
(2)数量关系不成立,DG=2BE,位置关系成立.
如图③中,延长BE交AD于T,交DG于H.
∵四边形ABCD与四边形AEFG都为矩形,
∴∠BAD=∠EAG,
∴∠BAE=∠DAG,
∵AD=2AB,AG=2AE,
∴==,
∴DG=2BE,
∵∠ATB+∠ABE=90°,
∴∠ATB+∠ADG=90°,
∵∠ATB=∠DTH,
∴∠DTH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG;
(3)如图④中,作ET⊥AD于T,GH⊥BA交BA的延长线于H.设ET=x,AT=y.
∴GH=2x,AH=2y,
∴4x2+4y2=4,
∴x2+y2=1,
∴BG2+DE2=(2x)2+(2y+2)2+x2+(4﹣y)2=5x2+5y2+20=25.
27.解:(1)∵OB=10,OF=2,
∴B(﹣10,0),F(0,2),
设直线BF的解析式为y=kx+b,
∵直线y=kx+b经过点B(﹣10,0),F(0,2),
∴,
解得:,
∴直线BF的解析式为y=x+2;
(2)△OBF的面积为S==5t(t>0);
(3)如图,延长AB至点R,使BR=AB,连接CR,延长CD交y轴于点T,过点T,作TM∥x轴交BA的延长线于点M,
过点T作TK⊥CR交RC的延长线于点K,连接RT,
∵AB⊥BC,AB=BR,
∴BC垂直平分AR,
∴AC=CR=13,
∴∠ACB=∠RCB,
设∠CBD=α,则∠ACB=2α,
∵BD⊥CD,
∴∠BDC=90°,
∴∠BCD=90°﹣α,
∵∠ACB=∠RCB=2α,
∴∠ACK=180°﹣4α,
∴∠KCT=∠BCK﹣∠BCD=∠BCA+∠ACK﹣∠BCD=90°﹣α,
∴∠KCT=∠BCD,
∵TK⊥KR,OT⊥OC,
∴OT=TK,
∵TC=TC,
∴Rt△OTC≌Rt△KTC(HL),
∴OC=CK=TK=t,
∵OF=OC,∠BOF=∠TOC,∠FBO=∠OTC,
∴△BOF≌△TOC(AAS),
∴OB=OT=10,
∴TK=10,
∵∠ABO+∠BOT=90°+90°=180°.
∴MB∥OT,
∵MT∥OB,
∴四边形OBMT为平行四边形,
∵OB=OT,∠BOT=90°.
∴四边形OBMT为正方形,
∴MB=MT=OT=10,
∴MT=TK,
∵RT=RT,
∴Rt△RMT≌Rt△RTK(HL),
∴RK=RM=CR+CK=13+t,
∴BR=RM﹣MB=3+t,
∵BC=OB+OC=10+t,
在Rt△BRC中,BR2+BC2=RC2,
∴(3+t)2+(10+t)2=132,
解得:t=2(t=﹣15舍去).
∴t的值为2.
一.选择题(满分30分,每小题3分)
1.下列所给方程中,是一元二次方程的是( )
A.2x+y=0 B.x2﹣1=0 C.3﹣x=8 D.y=
2.点A(x1,y1)、B(x2,y2)都在直线y=kx+2(k<0)上,且x1<x2则y1、y2的大小关系是( )
A.y1 =y2 B.y1 <y2 C.y1 >y2 D.y1 ≥y2
3.下列条件中,不能判断一个三角形是直角三角形的是( )
A.三条边的比为2:3:4
B.三条边满足关系a2=b2﹣c2
C.三条边的比为1:1:
D.三个角满足关系∠B+∠C=∠A
4.下列给出的条件中,不能判断四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC B.∠A=∠C,∠B=∠D
C.AB∥CD,AD∥BC D.AB=CD,AD=BC
5.已知关于x的一元二次方程3x2+4x﹣5=0,下列说法正确的是( )
A.方程有两个相等的实数根
B.方程有两个不相等的实数根
C.没有实数根
D.无法确定
6.某农业大镇2018年葡萄总产量为1.2万吨,预计2020年葡萄总产量达到1.6万吨,求葡萄总产量的年平均增长率,设葡萄总产量的年平均增长率为x,则可列方程为( )
A.1.2(1+x)2=1.6 B.1.6(1﹣x)2=1.2
C.1.2(1+2x)=1.6 D.1.2(1+x2)=1.6
7.如果直线y=kx+b经过一、二、四象限,则有( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
8.下列命题中,是真命题的是( )
A.三角形的外心到三角形三边的距离相等
B.顺次连接对角线相等的四边形各边中点所得的四边形是菱形
C.方程x2+2x+3=0有两个不相等的实数根
D.将抛物线y=2x2﹣2向右平移1个单位后得到的抛物线是y=2x2﹣3
9.如图,在菱形ABCD中,AC=2,BD=2,DH⊥AB于点H,则BH的长为( )
A.1 B. C. D.
10.如图所示的图象(折线ABCDE)描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)与行驶时间t(时)之间的函数关系,根据图中提供的信息,给出下列说法:
①汽车共行驶了140千米;②汽车在行驶途中停留了1小时;③汽车在整个行驶过程中的平均速度为30千米/时;④汽车出发后6小时至9小时之间行驶的速度在逐渐减小.其中正确的说法共有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(满分30分,每小题3分)
11.函数中,自变量x取值范围是 .
12.四边形ABCD中,∠A=∠B=∠C=90°,请你再添加一个条件,使该四边形是正方形,你所添加的条件是 .
13.已知一次函数y=kx+1的图象经过点P(﹣1,0),则k= .
14.已知关于x的方程x2﹣2x+2k=0的一个根是1,则k= .
15.在Rt△ABC中,AC=9,BC=12,则AB2= .
16.当三角形中的一个内角α是另一个内角β的一半时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”为直角三角形,则这个“特征角”的度数为 .
17.在国家积极研发和生产调配下,某种型号的医疗器械连续两年降价,第一年下降20%,第二年下降80%,那么该医疗器械这两年的平均降价率是 .
18.若a,b,c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:
①以a2,b2,c2的长为边的三条线段能组成一个三角形
②以的长为边的三条线段能组成一个三角形
③以a+b,c+h,h的长为边的三条线段能组成直角三角形
④以的长为边的三条线段能组成直角三角形
其中所有正确结论的序号为 .
19.如图,已知一次函数y=kx﹣b与y=x的图象相交于点A(a,1),则关于x的方程(k﹣)x=b的解x= .
20.如图,矩形ABCD中,AB=3,AD=9,将△ABE沿BE翻折得到△A′BE,点A落在矩形ABCD的内部,且∠AA′G=90°,若以点A′、G、C为顶点的三角形是直角三角形,则AE= .
三.解答题
21.(7分)请用合适的方法解方程:
(1)4x2﹣8x+1=0
(2)(x﹣2)(x﹣3)=12
22.(7分)著名台湾魔术师刘谦发明了一个道具,他把下图①中的正方形,分割成两个全等的直角三角形和直角梯形.然后拼成图②中的长方形.
通过计算这两个图形的面积,证明了64=65.请你用学过的数学知识,找到刘谦的破绽.
23.(8分)据我囯古代《周髀算经》记载,公元前1120年商高对周公说,将一根直尺折成一个直角,两端连接得到一个直角三角形,如果勾是3,股是4,那么弦就等于5,后人概括为“勾三,股四、弦五”.像3、4、5这样为三边长能构成直角三角形的三个正整数,称为勾股数.
【应用举例】
观察3,4,5;5,12,13;7,24,25;…,可以发现这些勾股数的勾都是奇数,且从3起就没有间断过,并且
勾为3时,股4=,弦5=;勾为5时,股12=,弦13=;
请仿照上面两组样例,用发现的规律填空:
(1)如果勾为7,则股24= ;弦25= .
(2)如果勾用n(n≥3,且n为奇数)表示时,请用含有n的式子表示股和弦,则股= ;弦= .
(3)继续观察①4,3,5;②6,8,10;③8,15,17;…,可以发现各组的第一个数都是偶数,且从4起也没有间断过.请你直接用m(m为偶数且m≥4)的代数式来表示直角三角形的另一条直角边和弦的长.
24.(8分)如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.若AC=2,CE=4;
(1)求证:四边形ACED是平行四边形.
(2)求BC的长.
25.(10分)元旦期间,小黄自驾游去了离家156千米的黄石矿博园,右图是小黄离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)求小黄出发0.5小时时,离家的距离;
(2)求出AB段的图象的函数解析式;
(3)小黄出发1.5小时时,离目的地还有多少千米?
26.(10分)如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE.
(1)发现:当正方形AEFG绕点A旋转,如图②所示.
①线段DG与BE之间的数量关系是 ;
②直线DG与直线BE之间的位置关系是 ;
(2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,上述结论是否成立,并说明理由.
(3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).
27.(10分)如图1,在平面直角坐标系中,OB=10,F是y轴正半轴上一点.
(1)若OF=2,求直线BF的解析式;
(2)设OF=t,△OBF的面积为s,求s与t的函数关系(直接写出自变量t的取值范围);
(3)如图3,在(2)的条件下,过点B作BA⊥x轴,点C在x轴上,OF=OC,连接AC,CD⊥直线BF于点D,∠ACB=2∠CBD,AC=13,OF=OC,AC.BD交于点E,求此时t的值.
参考答案
一.选择题
1. B.
2. C.
3. A.
4. A.
5. B.
6. A.
7. C.
8. B.
9. A.
10. A.
二.填空题
11. x≠4.
12. AB=BC.
13. 1
14. .
15. 225或63.
16. 45°或30°.
17. 60%.
18.②③.
19. 3.
20. 1或.
三.解答题
21.解:(1)∵a=4,b=﹣8,c=1,
∴△=(﹣8)2﹣4×4×1=48>0,
则x==;
(2)方程整理为一般式,得:x2﹣5x﹣6=0,
则(x﹣6)(x+1)=0,
∴x﹣6=0或x+1=0,
解得:x=6或x=﹣1.
22.解:如图②,过C作CF⊥AB垂足为F,则
,
而tan∠AEB==,
即tan∠BCF>tan∠AEB.
∴∠BCF>∠AEB.
∴B、C、E三点不共线,事实上,∠BCD+∠DCE>180°,
因而图②中间有一条缝,它实际上是个平行四边形,其面积为1.
23.解:(1)依据规律可得,如果勾为7,则股24=(49﹣1),弦25=(49+1),
故答案为:(49﹣1),(49+1);
(2)如果勾用n(n≥3,且n为奇数)表示时,则股=(n2﹣1),弦=(n2+1),
故答案为:(n2﹣1),(n2+1);
(3)根据规律可得,如果a,b,c是符合同样规律的一组勾股数,a=m(m为偶数且m≥4),则另一条直角边b=﹣1,弦c=+1.
24.解:(1)证明:∵∠ACB=90°,DE⊥BC,
∴AC∥DE
又∵CE∥AD
∴四边形ACED是平行四边形.
(2)∵四边形ACED是平行四边形.
∴DE=AC=2.
在Rt△CDE中,由勾股定理得CD===2.
∵D是BC的中点,
∴BC=2CD=4.
25.解:(1)设OA段图象的函数表达式为y=kx.
∵当x=0.8时,y=48,
∴0.8k=48,
∴k=60.
∴y=60x(0≤x≤0.8),
∴当x=0.5时,y=60×0.5=30.
故小黄出发0.5小时时,离家30千米;
(2)设AB段图象的函数表达式为y=k′x+b.
∵A(0.8,48),B(2,156)在AB上,
,
解得,
∴y=90x﹣24(0.8≤x≤2);
(3)∵当x=1.5时,y=90×1.5﹣24=111,
∴156﹣111=45.
故小黄出发1.5小时时,离目的地还有45千米.
26.解:(1)①如图②中,
∵四边形ABCD和四边形AEFG是正方形,
∴AE=AG,AB=AD,∠BAD=∠EAG=90°,
∴∠BAE=∠DAG,
在△ABE和△DAG中,
,
∴△ABE≌△ADG(SAS),
∴BE=DG;
②如图2,延长BE交AD于T,交DG于H.
由①知,△ABE≌△DAG,
∴∠ABE=∠ADG,
∵∠ATB+∠ABE=90°,
∴∠ATB+∠ADG=90°,
∵∠ATB=∠DTH,
∴∠DTH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG,
故答案为:BE=DG,BE⊥DG;
(2)数量关系不成立,DG=2BE,位置关系成立.
如图③中,延长BE交AD于T,交DG于H.
∵四边形ABCD与四边形AEFG都为矩形,
∴∠BAD=∠EAG,
∴∠BAE=∠DAG,
∵AD=2AB,AG=2AE,
∴==,
∴DG=2BE,
∵∠ATB+∠ABE=90°,
∴∠ATB+∠ADG=90°,
∵∠ATB=∠DTH,
∴∠DTH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG;
(3)如图④中,作ET⊥AD于T,GH⊥BA交BA的延长线于H.设ET=x,AT=y.
∴GH=2x,AH=2y,
∴4x2+4y2=4,
∴x2+y2=1,
∴BG2+DE2=(2x)2+(2y+2)2+x2+(4﹣y)2=5x2+5y2+20=25.
27.解:(1)∵OB=10,OF=2,
∴B(﹣10,0),F(0,2),
设直线BF的解析式为y=kx+b,
∵直线y=kx+b经过点B(﹣10,0),F(0,2),
∴,
解得:,
∴直线BF的解析式为y=x+2;
(2)△OBF的面积为S==5t(t>0);
(3)如图,延长AB至点R,使BR=AB,连接CR,延长CD交y轴于点T,过点T,作TM∥x轴交BA的延长线于点M,
过点T作TK⊥CR交RC的延长线于点K,连接RT,
∵AB⊥BC,AB=BR,
∴BC垂直平分AR,
∴AC=CR=13,
∴∠ACB=∠RCB,
设∠CBD=α,则∠ACB=2α,
∵BD⊥CD,
∴∠BDC=90°,
∴∠BCD=90°﹣α,
∵∠ACB=∠RCB=2α,
∴∠ACK=180°﹣4α,
∴∠KCT=∠BCK﹣∠BCD=∠BCA+∠ACK﹣∠BCD=90°﹣α,
∴∠KCT=∠BCD,
∵TK⊥KR,OT⊥OC,
∴OT=TK,
∵TC=TC,
∴Rt△OTC≌Rt△KTC(HL),
∴OC=CK=TK=t,
∵OF=OC,∠BOF=∠TOC,∠FBO=∠OTC,
∴△BOF≌△TOC(AAS),
∴OB=OT=10,
∴TK=10,
∵∠ABO+∠BOT=90°+90°=180°.
∴MB∥OT,
∵MT∥OB,
∴四边形OBMT为平行四边形,
∵OB=OT,∠BOT=90°.
∴四边形OBMT为正方形,
∴MB=MT=OT=10,
∴MT=TK,
∵RT=RT,
∴Rt△RMT≌Rt△RTK(HL),
∴RK=RM=CR+CK=13+t,
∴BR=RM﹣MB=3+t,
∵BC=OB+OC=10+t,
在Rt△BRC中,BR2+BC2=RC2,
∴(3+t)2+(10+t)2=132,
解得:t=2(t=﹣15舍去).
∴t的值为2.
同课章节目录
