1.3.1 公式法同步练习题(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章 因式分解
3 公式法
第1课时
考点突破
考点 用平方差因式分解
例 把下列各式因式分解:
(1); (2);
(3); (4)。
思路引导:有公因式的要先提取公因式,然后再整理成平方差的形式套用平方差公式进行因式分解。
方法归纳
应用平方差公式因式分解时,首先,判断所给多项式是否符合:(1)两项;(2)都是平方项;(3)符号相反,三个条件,然后再“对号入座”套用平方差公式进行因式分解;其次,运用公式前一定要先提取公因式或变形,再套用。
考题训练
1.下列多项式中,能用公式法因式分解的是( )
A. B. C. D.
2.化简:=( )
A. 2 B. 4 C. D.
3.(甘肃)因式分解:=________________。
4.若多项式能用平方差公式因式分解,则单项式M=__________(写一个即可)。
5.(衡阳)已知,,则的值为_________________。
6.利用平方差公式因式分解:
(1); (2); (3)。
巩固练习
1.把多项式因式分解,结果正确的是( )
A. B. C. D.
2.若,则的值是( )
A. 2 B. 3 C. 4 D. 6
3.某同学粗心大意,因式分解时,把等式■=▲)中的两个数字弄污了,则式子中的■,▲对应的一组数字可以是( )
A. 8 ,1 B. 16 ,2 C. 24 ,3 D. 64 ,8
4.(常德)因式分解:___________________。
5.(葫芦岛)因式分解:______________________。
6.(巴彦淖尔)因式分解:_________________________。
7.(株洲)因式分解:__________________________。
8.(济南)请你从下列各式中,任选两式作差,并将得到的式子进行因式分解。
,,1 ,
9.把下列各式因式分解:
(1); (2);
(3); (4).
10.(高青县期末)已知,,则代数式的值为( )
A. -15 B. -2 C. -6 D. 6
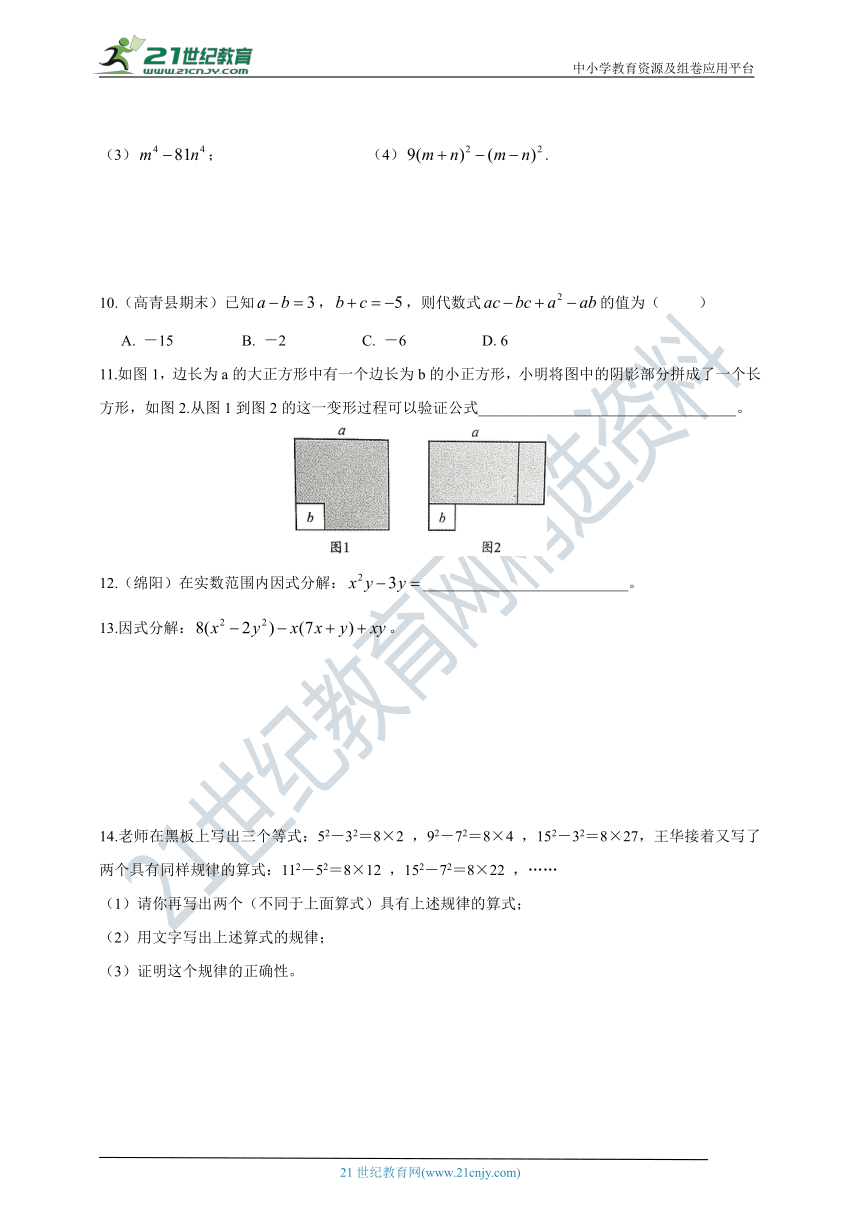
11.如图1,边长为a的大正方形中有一个边长为b的小正方形,小明将图中的阴影部分拼成了一个长方形,如图2.从图1到图2的这一变形过程可以验证公式__________________________________。
12.(绵阳)在实数范围内因式分解:___________________________。
13.因式分解:。
14.老师在黑板上写出三个等式:52-32=8×2 ,92-72=8×4 ,152-32=8×27,王华接着又写了两个具有同样规律的算式:112-52=8×12 ,152-72=8×22 ,……
(1)请你再写出两个(不同于上面算式)具有上述规律的算式;
(2)用文字写出上述算式的规律;
(3)证明这个规律的正确性。
15.在日常生活中经常需要密码,如取款、上网,有一种用“因式分解”法产生的密码,原理是:对于多项式,因式分解的结果是,若取,时,则各个因式的值是:,,,于是就可以把“018162”作为一个六位数的密码,对于多项式,取,时,请用上述方法写出三个密码。
参考答案
考点突破
例 解:(1)
考题训练
1.C 2.C 3. 4.答案不唯一,如-4 , 5.-3
6.解:(1)原式=
(2)原式=
(3)原式=
巩固练习
C 2. C 3. B 4. 5.
7.
8.答案不唯一,如
9.解:(1)原式=
(2)原式=
(3)原式=
(4)原式=
10. C 11. 12.
13.原式=
14.解:(1)答案不唯一,如72-52=8×3 ;92-32=8×9。
(2)规律:任意两个奇数的平方差是8的倍数。
(3)设m,n为整数,两个奇数可表示为2m+1和2n+1,则。
当m ,n同是奇数或偶数时,m-n一定为偶数,所以一定是8的倍数;当m ,n一偶一奇时,则m+n+1一定为偶数,所以一定是8的倍数。所以,任意两个奇数的平方差是8的倍数。
解:①,可得密码103010 ;
②,可得密码101030 ;
③,可得密码301010 .
_21?????????è?????(www.21cnjy.com)_
第一章 因式分解
3 公式法
第1课时
考点突破
考点 用平方差因式分解
例 把下列各式因式分解:
(1); (2);
(3); (4)。
思路引导:有公因式的要先提取公因式,然后再整理成平方差的形式套用平方差公式进行因式分解。
方法归纳
应用平方差公式因式分解时,首先,判断所给多项式是否符合:(1)两项;(2)都是平方项;(3)符号相反,三个条件,然后再“对号入座”套用平方差公式进行因式分解;其次,运用公式前一定要先提取公因式或变形,再套用。
考题训练
1.下列多项式中,能用公式法因式分解的是( )
A. B. C. D.
2.化简:=( )
A. 2 B. 4 C. D.
3.(甘肃)因式分解:=________________。
4.若多项式能用平方差公式因式分解,则单项式M=__________(写一个即可)。
5.(衡阳)已知,,则的值为_________________。
6.利用平方差公式因式分解:
(1); (2); (3)。
巩固练习
1.把多项式因式分解,结果正确的是( )
A. B. C. D.
2.若,则的值是( )
A. 2 B. 3 C. 4 D. 6
3.某同学粗心大意,因式分解时,把等式■=▲)中的两个数字弄污了,则式子中的■,▲对应的一组数字可以是( )
A. 8 ,1 B. 16 ,2 C. 24 ,3 D. 64 ,8
4.(常德)因式分解:___________________。
5.(葫芦岛)因式分解:______________________。
6.(巴彦淖尔)因式分解:_________________________。
7.(株洲)因式分解:__________________________。
8.(济南)请你从下列各式中,任选两式作差,并将得到的式子进行因式分解。
,,1 ,
9.把下列各式因式分解:
(1); (2);
(3); (4).
10.(高青县期末)已知,,则代数式的值为( )
A. -15 B. -2 C. -6 D. 6
11.如图1,边长为a的大正方形中有一个边长为b的小正方形,小明将图中的阴影部分拼成了一个长方形,如图2.从图1到图2的这一变形过程可以验证公式__________________________________。
12.(绵阳)在实数范围内因式分解:___________________________。
13.因式分解:。
14.老师在黑板上写出三个等式:52-32=8×2 ,92-72=8×4 ,152-32=8×27,王华接着又写了两个具有同样规律的算式:112-52=8×12 ,152-72=8×22 ,……
(1)请你再写出两个(不同于上面算式)具有上述规律的算式;
(2)用文字写出上述算式的规律;
(3)证明这个规律的正确性。
15.在日常生活中经常需要密码,如取款、上网,有一种用“因式分解”法产生的密码,原理是:对于多项式,因式分解的结果是,若取,时,则各个因式的值是:,,,于是就可以把“018162”作为一个六位数的密码,对于多项式,取,时,请用上述方法写出三个密码。
参考答案
考点突破
例 解:(1)
考题训练
1.C 2.C 3. 4.答案不唯一,如-4 , 5.-3
6.解:(1)原式=
(2)原式=
(3)原式=
巩固练习
C 2. C 3. B 4. 5.
7.
8.答案不唯一,如
9.解:(1)原式=
(2)原式=
(3)原式=
(4)原式=
10. C 11. 12.
13.原式=
14.解:(1)答案不唯一,如72-52=8×3 ;92-32=8×9。
(2)规律:任意两个奇数的平方差是8的倍数。
(3)设m,n为整数,两个奇数可表示为2m+1和2n+1,则。
当m ,n同是奇数或偶数时,m-n一定为偶数,所以一定是8的倍数;当m ,n一偶一奇时,则m+n+1一定为偶数,所以一定是8的倍数。所以,任意两个奇数的平方差是8的倍数。
解:①,可得密码103010 ;
②,可得密码101030 ;
③,可得密码301010 .
_21?????????è?????(www.21cnjy.com)_
