人教版数学八年级下册 19.1.2 函数的图象课件 (共15张PPT)
文档属性
| 名称 | 人教版数学八年级下册 19.1.2 函数的图象课件 (共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 854.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 14:01:15 | ||
图片预览






文档简介
(共15张PPT)
复习巩固:
1,什么是平面直角坐标系;
2,平面直角坐标系各象限内点的坐标特点;
3,函数图象概念。
函数图象是坐标平面上以自变量的值为横坐标、以对应的函数值为纵坐标的点组成的曲线,函数图象直观地反映了变量之间的对应关系和变化规律.那么,怎样画一个函数的图象呢?
八年级
下册
19.1.2 函数的图象(2)
画函数图象
学习目标:
1.会用描点法画出函数图象,能说出画函数图象的步骤;
2.会判断一个点是否在函数的图象上;
3.能初步通过图象的变化趋势,分析图象中变量变化规律,体会数形结合思想.
学习重点、难点:
重点用描点法画出函数图象。
难点:能初步通过图象的变化趋势,分析图象中变量变化规律
例3 下列式子中,对于
x
每一个确定的值,y
有唯
一的对应值,即
y
是
x
的函数,请画出这些函数的图象.
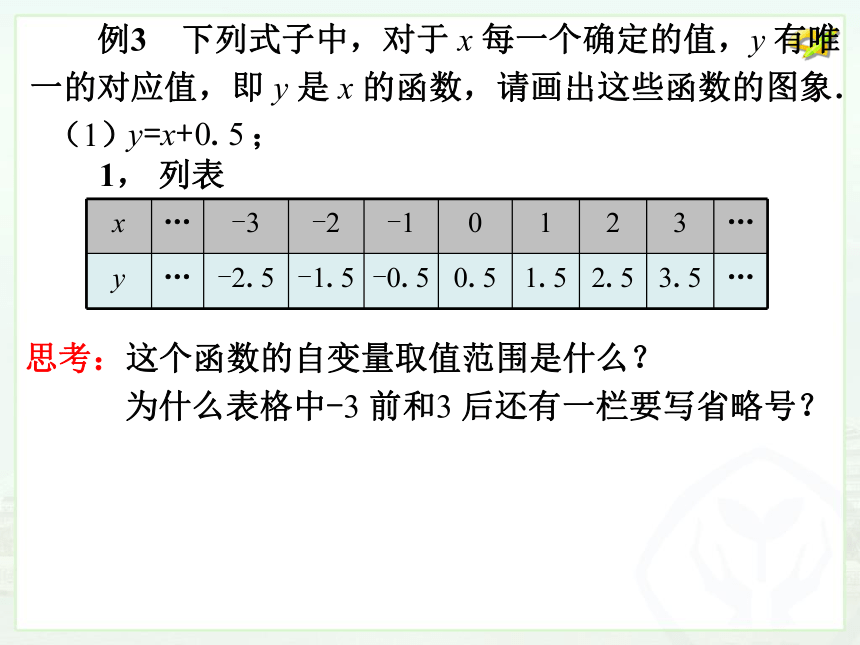
思考:这个函数的自变量取值范围是什么?
为什么表格中-3
前和3
后还有一栏要写省略号?
例3 下列式子中,对于
x
每一个确定的值,y
有唯
一的对应值,即
y
是
x
的函数,请画出这些函数的图象.
(1)
;
1,
列表
x
…
-3
-2
-1
0
1
2
3
…
y
…
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
…
例3 下列式子中,对于
x
每一个确定的值,y
有唯一的对应值,即
y
是
x
的函数,请画出函数
的图象.
1,
列表
2,描点
3,连线
x
…
-3
-2
-1
0
1
2
3
…
y
…
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
…
思考:画出的图象是什么?图象上的点从左向右运动时,
这个点是越来越高还是越来越低?能否用坐标解释这一
图形特点?
练习1
画函数图象的一般步骤:列表、描点、连线,这种画函数图象的方法称为描点法.
归纳
图象特征
——坐标特征
——变量的变化规律
思考
怎样从图象的特征分析中发现函数变化趋势和变化
规律?
小
结
通过这节课的学习你学到
了什么,还有哪些疑问?
作业:教材79页第3题.
作业
再见
复习巩固:
1,什么是平面直角坐标系;
2,平面直角坐标系各象限内点的坐标特点;
3,函数图象概念。
函数图象是坐标平面上以自变量的值为横坐标、以对应的函数值为纵坐标的点组成的曲线,函数图象直观地反映了变量之间的对应关系和变化规律.那么,怎样画一个函数的图象呢?
八年级
下册
19.1.2 函数的图象(2)
画函数图象
学习目标:
1.会用描点法画出函数图象,能说出画函数图象的步骤;
2.会判断一个点是否在函数的图象上;
3.能初步通过图象的变化趋势,分析图象中变量变化规律,体会数形结合思想.
学习重点、难点:
重点用描点法画出函数图象。
难点:能初步通过图象的变化趋势,分析图象中变量变化规律
例3 下列式子中,对于
x
每一个确定的值,y
有唯
一的对应值,即
y
是
x
的函数,请画出这些函数的图象.
思考:这个函数的自变量取值范围是什么?
为什么表格中-3
前和3
后还有一栏要写省略号?
例3 下列式子中,对于
x
每一个确定的值,y
有唯
一的对应值,即
y
是
x
的函数,请画出这些函数的图象.
(1)
;
1,
列表
x
…
-3
-2
-1
0
1
2
3
…
y
…
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
…
例3 下列式子中,对于
x
每一个确定的值,y
有唯一的对应值,即
y
是
x
的函数,请画出函数
的图象.
1,
列表
2,描点
3,连线
x
…
-3
-2
-1
0
1
2
3
…
y
…
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
…
思考:画出的图象是什么?图象上的点从左向右运动时,
这个点是越来越高还是越来越低?能否用坐标解释这一
图形特点?
练习1
画函数图象的一般步骤:列表、描点、连线,这种画函数图象的方法称为描点法.
归纳
图象特征
——坐标特征
——变量的变化规律
思考
怎样从图象的特征分析中发现函数变化趋势和变化
规律?
小
结
通过这节课的学习你学到
了什么,还有哪些疑问?
作业:教材79页第3题.
作业
再见
