人教版数学九年级上册 21.2.2 配方法解一元二次方程(2) (共20张 用WPS打开)
文档属性
| 名称 | 人教版数学九年级上册 21.2.2 配方法解一元二次方程(2) (共20张 用WPS打开) |  | |
| 格式 | zip | ||
| 文件大小 | 440.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 06:56:58 | ||
图片预览








文档简介
(共20张PPT)
---配方法(2)
一元二次方程的解法
(1)
(2)
1、用直接开平方法解下列方程:
开心练一练:
.
一、复习旧知:
2、
(1)
(2)
(3)
=(
+
)2
=(
)2
=(
)2
填上适当的数或式,使下列各等式成立.
大胆试一试:
(
)2
=(
)2
(4)
自主探究
观察(1)(2)看所填的常数与一次项系数之间有什么关系?
3
+4
-2
共同点:
左边:二次项的系数为1时,所填常数等于一次项系数一半的平方。
二、预习检测
想一想:下列方程能用直接开平方法来解吗?
(1)
(2)
X2+6X+9
=
2
把两题转化成
的形式,再利用开平方。
这种方程怎样解?
变形为
的形式.(a为非负常数)
变形为
X2-4x+1=0
(x-2)2=3
?
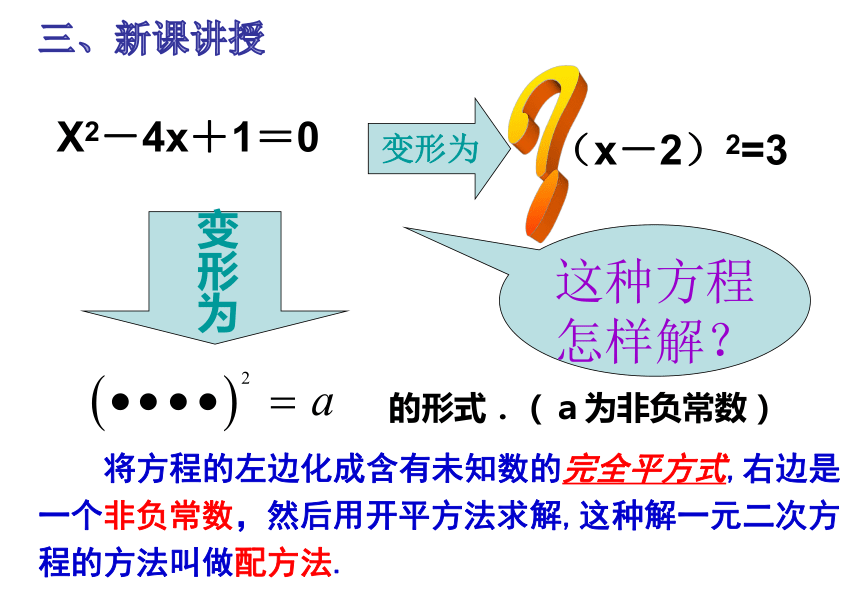
三、新课讲授
将方程的左边化成含有未知数的完全平方式,右边是一个非负常数,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.
问题1:
要使一块矩形场地的长比宽多6m,并且面积为16m2,
场地的长和宽应各是多少?
(1)解:设场地宽为X米,则长为(x+6)米,根据题意得:
整理得:X2+6X-16
=
0
合作交流探究新知
X(X+6)
=
16
移项
两边加上32,使左边配成
左边写成完全平方形式
降次
解:移项,得
配方,得
方程两边同时加上
心动
不如行动
练一练1:
用配方法解方程
2:
你能用配方法解方程
吗?
解:
配方得:
开平方得:
移项得:
∴原方程的解为:
化二次项系数为1得:
二次项系数不为1
怎么办?
想一想用配方法
解一元二次方程
一般有哪些步骤?
0
3
2
1
2
=
-
+
x
x
4
7
4
1
±
=
+
x
一化:把原方程化成
x2+px+q
=
0
的形式。
移项:把常数项移到方程的右边,如x2+px
=-q。
配方:方程两边都加上一次项系数一半的平方。
开方:根据平方根的意义,方程两边开平方。
求解:解一元一次方程。
定解:写出原方程的解。
用配方法解一元二次方程的步骤
方程右边是非负数
x2+px+
(
)2
=
-q+
(
)2
(
x+
)2
=-q+
(
)2
例1:
用配方法解方程
解:
配方得:
开平方得:
移项得:
∴原方程的解为:
四、练习巩固
例2、用配方法解方程:
解:
例3
.
用配方法解方程:
【思路点拨】将二次项系数不为1的一元二次方程两边同除以二次项系数,化成二次项系数为1的一元二次方程,再将方程化成
的形式,直接开方法求解.
解:
归纳总结:
一般地,如果一个一元二次方程通过配方转化成
①
的形式,那么就有:
(1)当p>0时,方程①有两个不等的实数根
;
(2)当p=0时,方程①有两个相等的实数根
;
(3)当p<0时,因为对任何实数x,都有
,所以方程①无实数根。
例4:用配方法解下列方程
解:化为一般形式为
移项,得
配方,得
方程两边同时加上
例5.
二次三项式
的值(
)
A.小于1
B.大于1
C.大于等于1
D.不大于1
【思路点拨】将二次三项式配方,然后根据平方大于等于0,求出最值.
解:∵
C
探究二:利用配方法解一元二次方程
【思路点拨】将方程化成
的形式.
已知实数x,y满足
,
求x,y的值.
解:
直击中考
2、如图,在Rt△ABC中,∠C=90°,AC=8
m,CB=6
m,点P,Q同时由A,B两点出发分别沿AC,BC方向向点C匀速移动,它们的速度都是1
m/s,几秒后△PCQ的面积为Rt△ABC面积的一半?
解:设x秒后△PCQ的面积为Rt△ABC面积的一半.根据题意可列方程:
答:2秒后△PCQ的面积为Rt△ABC面积的一半
(2)移项
(3)配方
(4)开平方
(5)求出方程的解
2、用配方法解一元二次方程
ax2+bx+c=0(a≠0)
的步骤:
1、配方法:
通过配方,将方程的左边化成一个含未
知数的完全平方式,右边是一个非负常数,运用直接开平方求出方程的解的方法。
(1)化二次项系数为1
五、课堂小结
(6)定解
六、布置作业
1、预习下一节内容;
2、练习与习题P16
---配方法(2)
一元二次方程的解法
(1)
(2)
1、用直接开平方法解下列方程:
开心练一练:
.
一、复习旧知:
2、
(1)
(2)
(3)
=(
+
)2
=(
)2
=(
)2
填上适当的数或式,使下列各等式成立.
大胆试一试:
(
)2
=(
)2
(4)
自主探究
观察(1)(2)看所填的常数与一次项系数之间有什么关系?
3
+4
-2
共同点:
左边:二次项的系数为1时,所填常数等于一次项系数一半的平方。
二、预习检测
想一想:下列方程能用直接开平方法来解吗?
(1)
(2)
X2+6X+9
=
2
把两题转化成
的形式,再利用开平方。
这种方程怎样解?
变形为
的形式.(a为非负常数)
变形为
X2-4x+1=0
(x-2)2=3
?
三、新课讲授
将方程的左边化成含有未知数的完全平方式,右边是一个非负常数,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.
问题1:
要使一块矩形场地的长比宽多6m,并且面积为16m2,
场地的长和宽应各是多少?
(1)解:设场地宽为X米,则长为(x+6)米,根据题意得:
整理得:X2+6X-16
=
0
合作交流探究新知
X(X+6)
=
16
移项
两边加上32,使左边配成
左边写成完全平方形式
降次
解:移项,得
配方,得
方程两边同时加上
心动
不如行动
练一练1:
用配方法解方程
2:
你能用配方法解方程
吗?
解:
配方得:
开平方得:
移项得:
∴原方程的解为:
化二次项系数为1得:
二次项系数不为1
怎么办?
想一想用配方法
解一元二次方程
一般有哪些步骤?
0
3
2
1
2
=
-
+
x
x
4
7
4
1
±
=
+
x
一化:把原方程化成
x2+px+q
=
0
的形式。
移项:把常数项移到方程的右边,如x2+px
=-q。
配方:方程两边都加上一次项系数一半的平方。
开方:根据平方根的意义,方程两边开平方。
求解:解一元一次方程。
定解:写出原方程的解。
用配方法解一元二次方程的步骤
方程右边是非负数
x2+px+
(
)2
=
-q+
(
)2
(
x+
)2
=-q+
(
)2
例1:
用配方法解方程
解:
配方得:
开平方得:
移项得:
∴原方程的解为:
四、练习巩固
例2、用配方法解方程:
解:
例3
.
用配方法解方程:
【思路点拨】将二次项系数不为1的一元二次方程两边同除以二次项系数,化成二次项系数为1的一元二次方程,再将方程化成
的形式,直接开方法求解.
解:
归纳总结:
一般地,如果一个一元二次方程通过配方转化成
①
的形式,那么就有:
(1)当p>0时,方程①有两个不等的实数根
;
(2)当p=0时,方程①有两个相等的实数根
;
(3)当p<0时,因为对任何实数x,都有
,所以方程①无实数根。
例4:用配方法解下列方程
解:化为一般形式为
移项,得
配方,得
方程两边同时加上
例5.
二次三项式
的值(
)
A.小于1
B.大于1
C.大于等于1
D.不大于1
【思路点拨】将二次三项式配方,然后根据平方大于等于0,求出最值.
解:∵
C
探究二:利用配方法解一元二次方程
【思路点拨】将方程化成
的形式.
已知实数x,y满足
,
求x,y的值.
解:
直击中考
2、如图,在Rt△ABC中,∠C=90°,AC=8
m,CB=6
m,点P,Q同时由A,B两点出发分别沿AC,BC方向向点C匀速移动,它们的速度都是1
m/s,几秒后△PCQ的面积为Rt△ABC面积的一半?
解:设x秒后△PCQ的面积为Rt△ABC面积的一半.根据题意可列方程:
答:2秒后△PCQ的面积为Rt△ABC面积的一半
(2)移项
(3)配方
(4)开平方
(5)求出方程的解
2、用配方法解一元二次方程
ax2+bx+c=0(a≠0)
的步骤:
1、配方法:
通过配方,将方程的左边化成一个含未
知数的完全平方式,右边是一个非负常数,运用直接开平方求出方程的解的方法。
(1)化二次项系数为1
五、课堂小结
(6)定解
六、布置作业
1、预习下一节内容;
2、练习与习题P16
同课章节目录
