冀教版 九年级上册 25.5 相似三角形的性质课件(共20张PPT)
文档属性
| 名称 | 冀教版 九年级上册 25.5 相似三角形的性质课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 598.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
25.5
相似三角形的性质
学习目标
1.掌握相似三角形的性质定理的内容及证明,使学生进一步理解相似三角形的概念.
2.能运用相似三角形的性质定理来解决有关问题.
3.通过由特殊情况猜想到一般情况,渗透由特殊到一般的数学思想,让学生感受数学的和谐美,并进一步养成严谨科学的学习品质.
(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
(2)如何判定两个三角形相似?
①定义;
②预备定理(平行);
③两个角对应相等的两个三角形相似
④两边对应成比例且夹角相等的两个三角形相似
⑤三边对应成比例的两个三角形相似
⑥直角边和斜边对应成比例的两个三角形相似
A
B
C
A/
B/
C/
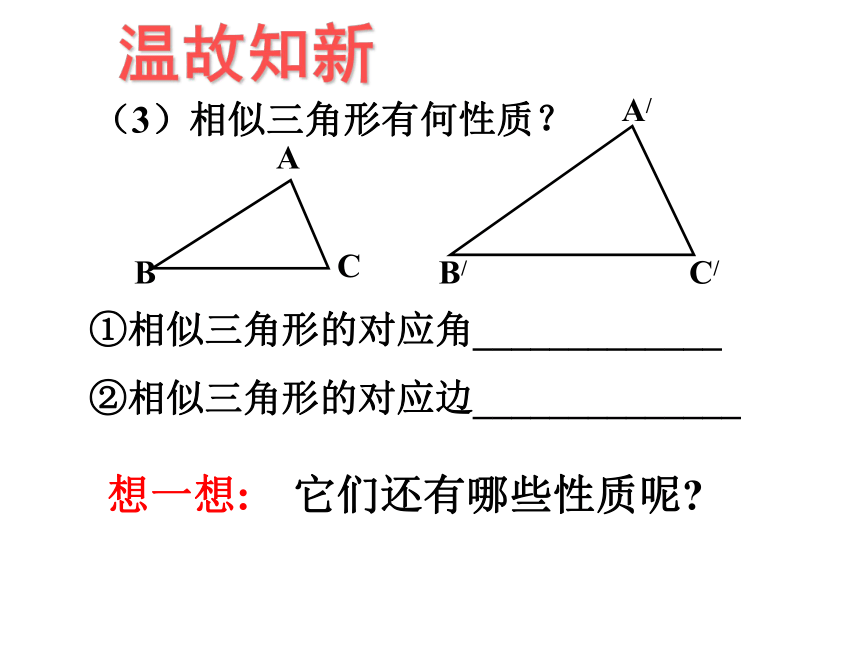
①相似三角形的对应角_____________
②相似三角形的对应边______________
想一想:
它们还有哪些性质呢?
温故知新
(3)相似三角形有何性质?
(1)一个三角形有三条重要线段:
________________
(2)如果两个三角形全等,那么这些对应线段有什么关系?如果两个三角形相似,那么这些对应线段又有什么关系呢?
思考
高、中线、角平分线
A
C
B
A′
B′
C′
∽
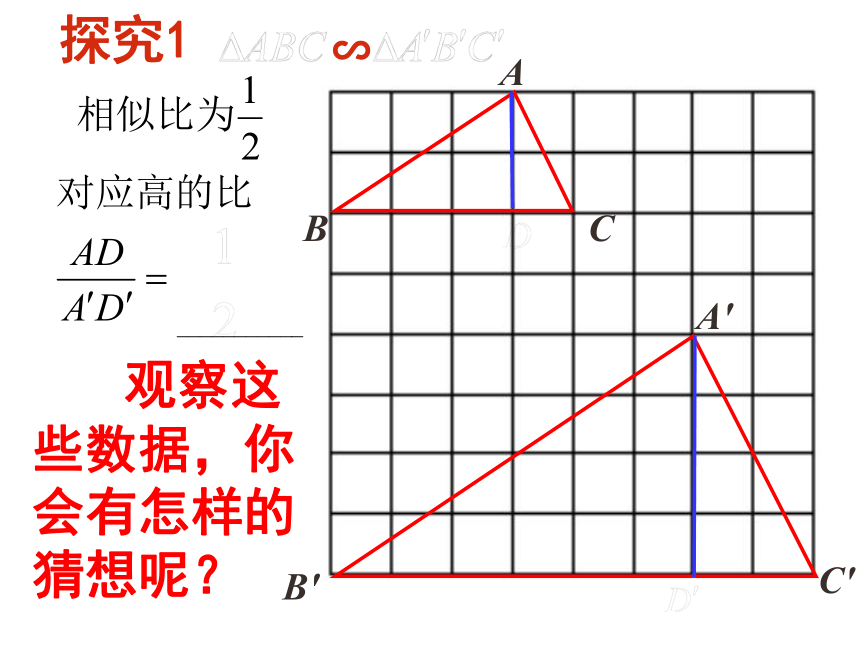
探究1
观察这些数据,你会有怎样的猜想呢?
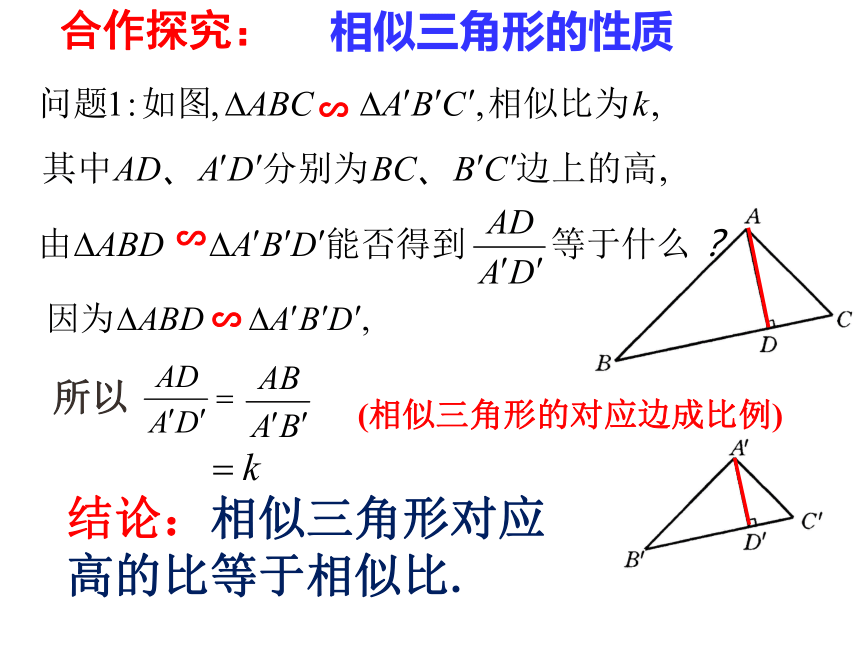
合作探究:
两角对应相等,两三角形相似
∽
∽
已知
所以∠B=∠B′(
)
相似三角形的对应角相等
∽
(
)
相似三角形的性质
合作探究:
∽
所以
(相似三角形的对应边成比例)
∽
∽
相似三角形的性质
结论:相似三角形对应高的比等于相似比.
A
C
B
A′
B′
C′
∽
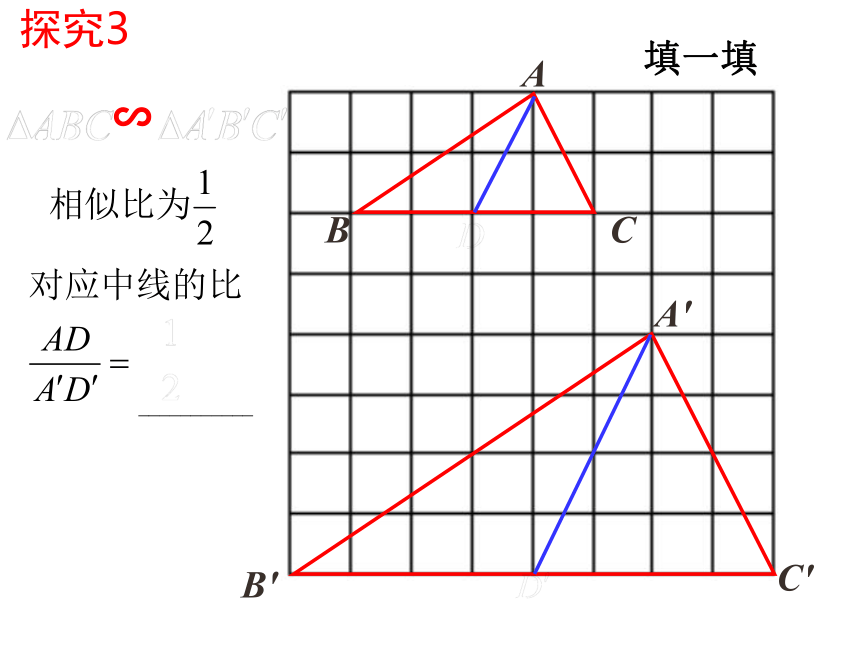
填一填
探究3
A
C
B
A′
B′
C′
∽
填一填
探究3
类似结论
D'
C'
B'
A'
D
C
B
A
∽
探究3
结论:相似三角形对应中线的比等于相似比.
A′
C′
B′
C
B
A
E′
E
∽
类似结论
探究3
结论:相似三角形对应角的角平分线的比等于相似比.
1、相似三角形对应边成____,对应角______.
2、相似三角形对应边高的比、对应中线的比、
对应角平分线的比都等于________.
归纳
相似三角形的性质
比例
相等
相似比
填一填
1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.
2∶
3
2
∶
3
2.两个相似三角形的相似比为1:4,
则对应高的比为_________,对应角的角平分线的比为_________.
1:4
1:4
3.两个相似三角形对应中线的比为
,
则相似比为______,对应高的比为______
.
例1:已知△ABC∽
△A?B
?C
?,BD和B
?D
?分别是△ABC和△A?B?C?中线,且AB=10,A?B?=2,BD=6。求B?D?的长.
解:∵ △ABC∽△A?B?C?
∴
=
=
B?D?=1.2
答:B?D?的长为1.2。
AB
A?B?
BD
B?D?
10
2
6
B?D?
A
B
C
D
A?
B?
C?
D?
1.如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于______.
2.相似三角形对应边的比为2:5,
那么相似比为_______,
对应角的角平分线的比为______,
3∶5
2:5
针对练习:
2:5
3、如果两个三角形相似,相似比为3∶5,那么对应角的角平分线的比等于多少?
4、相似三角形对应边的比为0.4,那么相似比为______,对应角的角平分线的比为______。
3∶5
0.4
0.4
5、若两个三角形的对高之比为4:3,对应中线之比为_____
4
:
3
6、已知△ABC∽△DEF,BG、EH分别是△ABC和
△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
解:∵
△ABC∽△DEF
∴ BC∶EF=BG∶EH
6∶4=4.8∶EH
EH=3.2(cm)
答:EH的长为3.2cm。
A
G
B
C
D
E
F
H
1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
归纳
相似三角形的性质
比例
相等
相似比
课后作业
见课本课后习题第2,3题.
25.5
相似三角形的性质
学习目标
1.掌握相似三角形的性质定理的内容及证明,使学生进一步理解相似三角形的概念.
2.能运用相似三角形的性质定理来解决有关问题.
3.通过由特殊情况猜想到一般情况,渗透由特殊到一般的数学思想,让学生感受数学的和谐美,并进一步养成严谨科学的学习品质.
(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
(2)如何判定两个三角形相似?
①定义;
②预备定理(平行);
③两个角对应相等的两个三角形相似
④两边对应成比例且夹角相等的两个三角形相似
⑤三边对应成比例的两个三角形相似
⑥直角边和斜边对应成比例的两个三角形相似
A
B
C
A/
B/
C/
①相似三角形的对应角_____________
②相似三角形的对应边______________
想一想:
它们还有哪些性质呢?
温故知新
(3)相似三角形有何性质?
(1)一个三角形有三条重要线段:
________________
(2)如果两个三角形全等,那么这些对应线段有什么关系?如果两个三角形相似,那么这些对应线段又有什么关系呢?
思考
高、中线、角平分线
A
C
B
A′
B′
C′
∽
探究1
观察这些数据,你会有怎样的猜想呢?
合作探究:
两角对应相等,两三角形相似
∽
∽
已知
所以∠B=∠B′(
)
相似三角形的对应角相等
∽
(
)
相似三角形的性质
合作探究:
∽
所以
(相似三角形的对应边成比例)
∽
∽
相似三角形的性质
结论:相似三角形对应高的比等于相似比.
A
C
B
A′
B′
C′
∽
填一填
探究3
A
C
B
A′
B′
C′
∽
填一填
探究3
类似结论
D'
C'
B'
A'
D
C
B
A
∽
探究3
结论:相似三角形对应中线的比等于相似比.
A′
C′
B′
C
B
A
E′
E
∽
类似结论
探究3
结论:相似三角形对应角的角平分线的比等于相似比.
1、相似三角形对应边成____,对应角______.
2、相似三角形对应边高的比、对应中线的比、
对应角平分线的比都等于________.
归纳
相似三角形的性质
比例
相等
相似比
填一填
1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.
2∶
3
2
∶
3
2.两个相似三角形的相似比为1:4,
则对应高的比为_________,对应角的角平分线的比为_________.
1:4
1:4
3.两个相似三角形对应中线的比为
,
则相似比为______,对应高的比为______
.
例1:已知△ABC∽
△A?B
?C
?,BD和B
?D
?分别是△ABC和△A?B?C?中线,且AB=10,A?B?=2,BD=6。求B?D?的长.
解:∵ △ABC∽△A?B?C?
∴
=
=
B?D?=1.2
答:B?D?的长为1.2。
AB
A?B?
BD
B?D?
10
2
6
B?D?
A
B
C
D
A?
B?
C?
D?
1.如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于______.
2.相似三角形对应边的比为2:5,
那么相似比为_______,
对应角的角平分线的比为______,
3∶5
2:5
针对练习:
2:5
3、如果两个三角形相似,相似比为3∶5,那么对应角的角平分线的比等于多少?
4、相似三角形对应边的比为0.4,那么相似比为______,对应角的角平分线的比为______。
3∶5
0.4
0.4
5、若两个三角形的对高之比为4:3,对应中线之比为_____
4
:
3
6、已知△ABC∽△DEF,BG、EH分别是△ABC和
△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
解:∵
△ABC∽△DEF
∴ BC∶EF=BG∶EH
6∶4=4.8∶EH
EH=3.2(cm)
答:EH的长为3.2cm。
A
G
B
C
D
E
F
H
1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
归纳
相似三角形的性质
比例
相等
相似比
课后作业
见课本课后习题第2,3题.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
