北师大版九年级上册数学第三章概率的进一步认识素养拓展+中考真题课件(62张PPT)
文档属性
| 名称 | 北师大版九年级上册数学第三章概率的进一步认识素养拓展+中考真题课件(62张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 00:00:00 | ||
图片预览







文档简介
第三章 概率的进一步认识
数学·九年级上册·北师
专题1 概率的计算方法
专项素养拓训
1.在某校运动会4×400 m接力赛中,甲、乙两名同学都是第一棒,参赛同学随机从四个赛道中抽取赛道,则甲、乙两名同学恰好抽到相邻赛道的概率为 ( )
A.316 B.14 C.38 D.12
?
答案
1.D 【解析】 画树状图如下:
?
由树状图可知,共有12种等可能的结果,其中甲、乙两名同学恰好抽到相邻赛道的结果有6种,所以甲、乙两名同学恰好抽到相邻赛道的概率为612=12.故选D.
?
类型1 用树状图或表格求概率
2.甲、乙、丙、丁四人在做踢毽子游戏:第一次由甲将毽子踢给乙、丙、丁中的某一人,从第二次起都由持毽子者将毽子再随机踢给其他三人中的某一人,假设每个人在每一次踢毽子时都不会失误,则第二次踢毽子后,毽子回到甲的概率为? .?
答案
2.13 【解析】 画树状图如下:
?
由树状图可知,共有9种等可能的结果,其中符合要求的结果有3种,所以P(第二次踢毽子后,毽子回到甲)=39=13.
?
类型1 用树状图或表格求概率
3.如图,转盘被等分成4个扇形,转盘上1,2,3,4四个数字分别代表鸡、猴、鼠、羊四种生肖邮票(每种邮票各两枚,鸡年邮票面值“80分”,其他邮票面值都是“1.20元”),转动转盘后,指针每落在某个数字所在的扇形一次就表示获得该种邮票一枚(指针落在分界线时重转).
(1)任意转动转盘一次,获得猴年邮票的概率是? ;?
(2)任意转动转盘两次,求获得的两枚邮票可以邮寄一封需2.40元邮资的信件的概率.
类型1 用树状图或表格求概率
答案
3.【解析】 (1)14
(2)根据题意,列表如下:
由表格可知,共有16种等可能的结果,满足“转动转盘两次,获得的两枚邮票可以邮寄一封需2.40元邮资的信件”(记为事件A)的结果有9种,所以P(A)=916,
即任意转动转盘两次,获得的两枚邮票可以邮寄一封需2.40元邮资的信件的概率是916.
?
类型1 用树状图或表格求概率
4.[2019江苏南京中考]某校计划在暑假第二周的星期一至星期四开展社会实践活动,要求每位学生选择两天参加活动.
(1)甲同学随机选择两天,其中有一天是星期二的概率是多少?
(2)乙同学随机选择连续的两天,其中有一天是星期二的概率是? .?
答案
4.【解析】 (1)根据题意,画树状图如下.
?
?
?
类型1 用树状图或表格求概率
答案
由树状图可知,共有12种等可能的结果,其中有一天是星期二的结果有6种,
故P(其中有一天是星期二)=612=12.
(2)23
乙同学随机选择连续的两天,有3种等可能的结果,即(星期一,星期二),(星期二,星期三),(星期三,星期四),其中有一天是星期二的结果有2种,故P(其中有一天是星期二)=23.
?
类型1 用树状图或表格求概率
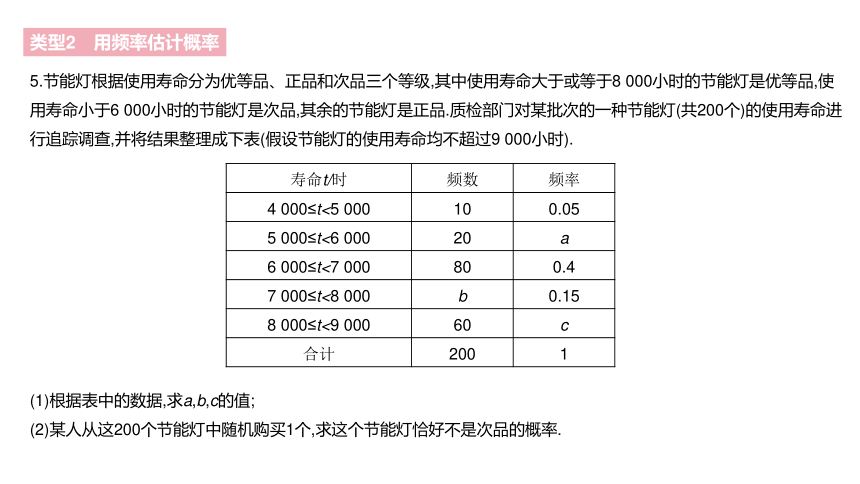
5.节能灯根据使用寿命分为优等品、正品和次品三个等级,其中使用寿命大于或等于8 000小时的节能灯是优等品,使用寿命小于6 000小时的节能灯是次品,其余的节能灯是正品.质检部门对某批次的一种节能灯(共200个)的使用寿命进行追踪调查,并将结果整理成下表(假设节能灯的使用寿命均不超过9 000小时).
(1)根据表中的数据,求a,b,c的值;
(2)某人从这200个节能灯中随机购买1个,求这个节能灯恰好不是次品的概率.
类型2 用频率估计概率
寿命t/时
频数
频率
4 000≤t<5 000
10
0.05
5 000≤t<6 000
20
a
6 000≤t<7 000
80
0.4
7 000≤t<8 000
b
0.15
8 000≤t<9 000
60
c
合计
200
1
答案
5.【解析】 (1)a=20÷200=0.1,b=200×0.15=30,c=60÷200=0.3.
(2)这批节能灯中,优等品有60个,正品有110个,次品有30个.
所以此人购买的这个节能灯恰好不是次品的概率P=110+60200=0.85.
?
类型2 用频率估计概率
专题2 概率的应用
专项素养拓训
6.小敏的爸爸买了一张某项体育比赛的门票,她和哥哥两人都很想去观看,可门票只有一张.读九年级的哥哥想了一个办法,拿了8张扑克牌,将数字为2,3,5,9的四张牌给小敏,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小敏和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌数字相加,若和为偶数,则小敏去;若和为奇数,则哥哥去.
(1)请用画树状图法或列表法求小敏去看比赛的概率;
(2)哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.
类型1 用概率说明事件的合理性
答案
6.【解析】 (1)列表如下:
从表格可知,所有可能出现的结果共有16种,这些结果出现的可能性相等,而和为偶数的结果共有6种,所以小敏去看比赛的概率P=616=38.
?
类型1 用概率说明事件的合理性
答案
(2)不公平.
由(1)得哥哥去看比赛的概率P=1-38=58,
因为38<58,所以哥哥设计的游戏规则不公平.
设计的游戏规则:
规定数字之和小于等于10时小敏(哥哥)去,数字之和大于等于11时哥哥(小敏)去,则两人去看比赛的概率都为12.
(答案不唯一,只要满足两人去看比赛的概率相等即可)
?
类型1 用概率说明事件的合理性
7.某商场为了吸引顾客,举行抽奖活动,并规定顾客每购买100元的商品,就可以随机抽取一张奖券,抽得奖券“紫气东来”“花开富贵”“吉星高照”就可以分别获得100元、50元、20元的购物券,抽得“谢谢惠顾”不赠购物券;若顾客不愿意抽奖,则可以直接获得10元的购物券.小明购买了100元的商品,他看到商场公布的前10 000张奖券的抽奖结果如下:
(1)求“紫气东来”奖券出现的频率;
(2)请你帮助小明判断,抽奖和直接获得购物券,哪种方式更划算?并说明理由.
类型1 用概率说明事件的合理性
奖券种类
紫气东来
花开富贵
吉星高照
谢谢惠顾
出现张数/张
500
1 000
2 000
6 500
答案
7.【解析】 (1)50010?000=120,
∴“紫气东来”奖券出现的频率为120.
(2)抽奖更划算.理由如下:
平均每张奖券获得的购物券金额为100×50010?000+50×1?00010?000+20×2?00010?000+0×6?50010?000=14(元).
∵14>10,∴选择抽奖更划算.
?
类型1 用概率说明事件的合理性
8.[2019湖北恩施州中考]为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级,A级:非常满意;B级:满意;C级:基本满意;D级:不满意),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
?
(1)本次抽样调查测试的建档立卡贫困户的总户数是 ;?
(2)扇形统计图中,∠α的度数是 ,并把条形统计图补充完整;?
类型2 概率与统计的综合
(3)某县建档立卡贫困户有10 000户,如果全部参加这次满意度调查,请估计非常满意的户数约为多少;
(4)调查人员想从5户建档立卡贫困户(分别记为a,b,c,d,e)中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户e的概率.
类型2 概率与统计的综合
答案
8.【解析】 (1)60
(2)54°
C级户数为60-9-21-9=21.
补全条形统计图如图所示:
(3)估计非常满意的户数约为960×10 000=1 500.
?
答案
(4)由题可列如下树状图:
?
由树状图可以看出,所有可能出现的等可能结果共有20种,其中选中贫困户e的结果有8种,
∴P(选中贫困户e)=820=25.
?
类型2 概率与统计的综合
9.现今“微信运动”被越来越多的人关注和喜爱.某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数直方图.
(2)本市约有37 800名教师,用调查的样本数据估计日行走步数超过12 000步(包含12 000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16 000步(包含16 000步)的两名教师与大家分享心得,求被选取的两名教师恰好都在20 000步(包含20 000步)以上的概率.
类型2 概率与统计的综合
步数
人数
频率
0≤x<4 000
8
a
4 000≤x<8 000
15
0.3
8 000≤x<12 000
12
b
12 000≤x<16 000
c
0.2
16 000≤x<20 000
3
0.06
20 000≤x<24 000
d
0.04
答案
9.【解析】 (1)a=850=0.16,b=1250=0.24,c=50×0.2=10,d=50×0.04=2.
补全频数直方图如下:
(2)0.2+0.06+0.04=0.3=30%,37 800×30%=11 340(名).
所以估计日行走步数超过12 000步(包含12 000步)的教师有11 340名.
?
类型2 概率与统计的综合
答案
(3)设日行走步数在16 000≤x<20 000的3名教师分别为A,B,C,
日行走步数在20 000≤x<24 000的2名教师分别为X,Y,列表如下:
由表格可知,一共有20种等可能的结果,其中两名教师恰好都在20 000步(包含20 000步)以上的结果有2种,所以被选取的两名教师恰好都在20 000步(包含20 000步)以上的概率为110.
?
类型2 概率与统计的综合
?
A
B
C
X
Y
A
?
AB
AC
AX
AY
B
BA
?
BC
BX
BY
C
CA
CB
?
CX
CY
X
XA
XB
XC
?
XY
Y
YA
YB
YC
YX
?
综合素养拓训
在互联网大数据时代,数据处理和分析能力逐渐成为必备素养,而数据分析也是数学的核心素养之一.在教材中,数据分析主要以统计和概率来体现,本章就是对概率的进一步认识.对于“概率”的拓展,侧重应用意识和创新意识,例如第1题,以电视台的智力竞答节目为背景,通过分析不同情形发生的概率,使最优途径了然于胸;第2题,通过频率估计概率的模型,探寻估算不规则图形面积的方案,也是核心素养中数学建模方面的体现.
1.[概率帮你做决策]锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就可顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是? ;?
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是? ;?
(3)如果锐锐每道题各用一次“求助”,请用画树状图或者列表的方法来分析他顺利通关的概率.
答案
1.【解析】 (1)14
由题意,知第一道题肯定能答对,第二道题答对的概率为14,所以锐锐通关的概率为14.
(2)16
如果锐锐两次“求助”都在第二道题中使用,易知此时共有6种等可能的结果出现,其中锐锐两道题都答对的结果有1种,所以锐锐能通关的概率为16.
?
答案
(3)如果锐锐每道题各用一次“求助”,分别用A,B表示第一道单选题剩下的2个选项,a,b,c表示第二道单选题剩下的3个选项,
画树状图如图所示:
?
?
?
?
由树状图知,共有6种等可能的结果,锐锐顺利通关的结果只有1种,
所以锐锐顺利通关的概率为16.
?
2.[概率中的方案设计]小红和小明在操场上做游戏,他们先在地上画了半径分别为2 m和3 m的同心圆(如图),然后蒙上眼睛,并在一定距离外向圈内掷小石子,掷中阴影部分时小红胜,否则小明胜,未掷入圈内(半径为3 m的圆内)或掷在边界上重掷.
(1)你认为游戏公平吗?为什么?
(2)游戏结束,小明边走边想:能否用频率估计概率的方法,来估算不规则图形的面积呢?请你设计一个方案,解决这一问题.(要求画出图形,说明设计步骤、原理,并给出计算公式)
答案
2.【解析】 (1)不公平.理由如下:
∵P(掷中阴影部分)=9π?4π9π=59,即小红获胜的概率为59,则小明获胜的概率为49,59≠49,∴游戏不公平.
?
答案
(2)能利用频率估计概率的方法估算不规则图形的面积.
设计方案:①设计一个可测量面积的规则图形将不规则图形围起来(如正方形,其面积为S),如图所示; ?
?
?
?
?
②往图形中掷点(如蒙上眼睛往图形中随意掷小石子,掷在正方形外或边界上不做记录);
③当所掷次数充分大时,记录并统计结果,设掷入正方形内m次,其中n次掷入不规则图形内;
④设不规则图形的面积为S1,用频率估计概率,
即掷入不规则图形内的频率????????≈P(掷入不规则图形内),而P(掷入不规则图形内)=????1????,故????????≈????1????,即S1≈????????????.
?
答案
1.D 【解析】 设正面上的图案是“ ”的3张卡片分别用A1,A2,A3表示,正面上的图案是“?”的卡片用B表示,画树状图如下:
?
?
?
由树状图可知,共有12种等可能的结果,2张卡片正面上的图案相同的结果有6种.故从中随机抽取2张,这2张卡片正面上的图案相同的概率是612=12.故选D.
?
一、选择题
1.[2018河南中考]现有4张卡片,其中3张卡片正面上的图案是“ ”,1张卡片正面上的图案是“?”,它们除此之外完全相同.把这4张卡片背面朝上洗匀,从中随机抽取2张,则这2张卡片正面上的图案相同的概率是 ( )
A.916 B.34 C.38 D.12
?
答案
2.D 【解析】 A项,抛一枚硬币,出现正面朝上的概率为0.5,不符合题中试验的结果;B项,掷一个正六面体的骰子,出现3点朝上的概率为16,不符合题中试验的结果;C项,一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率为0.25,不符合题中试验的结果;D项,从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球的概率为13,符合题中试验的结果.故选D.
?
2.[2018广西玉林中考]某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率折线图如图,则符合这一结果的试验可能是 ( )
A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
答案
3.C 【解析】 根据题意画树状图如下.
?
由树状图可知,共有16种等可能的结果,其中两次抽取的卡片上的数字之积为偶数的结果有12种.故所求概率为1216=34.故选C.
?
3.[2018湖北武汉中考]一个不透明的口袋中装有四张完全相同的卡片,把它们分别标上数字1,2,3,4.随机抽取一张卡片,然后放回,再随机抽取一张卡片,则两次抽取的卡片上的数字之积为偶数的概率是 ( )
A.14 B.12 C.34 D.56
?
答案
4.A 【解析】 m=3÷25%=12.故选A.
4.[2019河北唐山开平区二模]在一个暗箱里放有m个除颜色外其他完全相同的球,这m个球中只有3个黄球,每次将球搅拌均匀后,任意摸出一个球记下颜色后再放回暗箱,通过大量重复试验发现,摸到黄球的频率稳定在25%左右,推算m的值大约是 ( )
A.12 B.9 C.4 D.3
答案
5.B 【解析】 画树状图如下:
?
由树状图可知,共有9种等可能的结果,小强获胜的结果有3种,所以小强获胜的概率是39=13.故选B.
?
5.小强和小华两人玩“剪刀、石头、布”的游戏,随机出手一次,则小强获胜的概率为 ( )
A.16 B.13 C.12 D.23
?
答案
6.B 【解析】 画树状图如图所示:
?
由树状图可知,共有20种等可能的结果,其中点P(m,n)在平面直角坐标系中位于第四象限的结果有4种,所以点P(m,n)在平面直角坐标系中位于第四象限的概率为420=15.故选B.
?
6.[2019山东德州陵城区二模]点P的坐标是(m,n),从-5,-3,0,4,7这五个数中任取一个数作为m的值,再从余下的四个数中任取一个数作为n的值,则点P(m,n)在平面直角坐标系中位于第四象限的概率是 ( )
A.25 B.15 C.14 D.12
?
答案
7.C 【解析】 将题图左边转盘中蓝色部分等分为3份,分别记为蓝a、蓝b、蓝c,红色部分记为红d,将题图右边转盘中红色部分等分为3份,分别记为红1、红2、红3,蓝色部分记为蓝4.列表如下:
由表格可知,共有16种等可能的结果,其中可配成紫色的结果有10种,所以可配成紫色的概率是1016=58.故选C.
?
7.[2019辽宁本溪模拟]用如图所示的两个可以自由转动的转盘做“配紫色”游戏,分别旋转两个转盘,若其中一个转盘转出红色,另一个转盘转出蓝色即可配成紫色,则可配成紫色的概率是 ( )
A.38 B.12
C.58 D.23
?
?
蓝a
蓝b
蓝c
红d
红1
(红1,蓝a)
(红1,蓝b)
(红1,蓝c)
(红1,红d)
红2
(红2,蓝a)
(红2,蓝b)
(红2,蓝c)
(红2,红d)
红3
(红3,蓝a)
(红3,蓝b)
(红3,蓝c)
(红3,红d)
蓝4
(蓝4,蓝a)
(蓝4,蓝b)
(蓝4,蓝c)
(蓝4,红d)
答案
8.B 【解析】 根据题意,列表如下:
由表格可知,共有16种等可能的结果,而落在以A(-2,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)有(-2,0),(0,0),(1,0), (2,0),(0,1),(1,1),(0,2),共7种,所以落在以A(-2,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)的概率是716.故选B.
?
8.如图,一个质地均匀的正四面体的四个面上依次标有数字-2,0,1,2,连续抛掷两次,朝下一面的数字分别作为M点的横、纵坐标,则点M落在以A(-2,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)的概率是 ( )
A.38 B.716 C.12 D.916
?
?
-2
0
1
2
-2
(-2,-2)
(-2,0)
(-2,1)
(-2,2)
0
(0,-2)
(0,0)
(0,1)
(0,2)
1
(1,-2)
(1,0)
(1,1)
(1,2)
2
(2,-2)
(2,0)
(2,1)
(2,2)
答案
9.13 【解析】 根据题意,画树状图如图所示:
?
?
?
从树状图中可以看出,共有6种等可能的情况,积是正数的有2种情况,所以任取两个不同的数,积为正数的概率是26=13.
?
二、填空题
9.从-3,1,-2这三个数中任取两个不同的数,积为正数的概率是? .?
答案
10.14 【解析】 根据题意,列表如下:
∵直线y=mx+n不经过第三象限,m≠0,n≠0,∴直线经过第一、二、四象限,∴m<0,n>0,∴直线y=mx+n不经过第三象限的概率为416=14.
?
10.有四张背面完全相同的卡片,正面上分别标有数字-2,-1,1,2,把这四张卡片背面朝上,洗匀后,随机抽取一张,记下数字为m;放回搅匀,再随机抽取一张卡片,记下数字为n,则y=mx+n不经过第三象限的概率为? .?
答案
11.17 【解析】 ∵|m|≤1,|n|≤3,且m,n都是整数,∴m=-1,0,1;n=-3,-2,-1,0,1,2,3.∵关于x的方程x2+nx+m=0有两个相等的实数根,∴Δ=n2-4m=0.列表如下:
从表格中可看出共有21种等可能的结果,能使Δ=n2-4m=0成立的有序整数(m,n)共有3对,分别为(1,-2),(0,0)和(1,2),故P(关于x的方程x2+nx+m=0有两个相等的实数根)=321=17.
?
11.如果任意选择一对有序整数(m,n),其中|m|≤1,|n|≤3,每一对这样的有序整数被选择的可能性是相等的,那么关于x的方程x2+nx+m=0有两个相等实数根的概率是 .?
三、解答题
12.[2019江苏苏州中考]在一个不透明的盒子中装有4张卡片,4张卡片的正面分别标有数字1,2,3,4,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子中任意抽取一张卡片,恰好抽到标有奇数数字卡片的概率是? ;?
(2)先从盒子中任意抽取一张卡片,再从余下的3张卡片中任意抽取一张卡片,求抽取的2张卡片标有的数字之和大于4的概率.(请用画树状图或列表等方法求解)
答案
12.【解析】 (1)12
(2)根据题意,列表如下:
由表可知,共有12种等可能的结果,其中抽取的2张卡片标有的数字之和大于4的有8种,
所以抽取的2张卡片标有的数字之和大于4的概率为812=23.
?
答案
13.【解析】 (1)12
(2)画树状图如下:
?
?
由树状图可知,共有8种等可能的结果,其中甲至少胜一局的结果有7种.
所以甲队最终获胜的概率为78.
?
13.[2018江苏连云港中考]汤姆斯杯世界男子羽毛球团体赛小组赛比赛规则:两队之间进行五局比赛,其中三局单打,两局双打,五局比赛必须全部打完,赢得三局及以上的队获胜.假如甲、乙两队每局获胜的机会相同.
(1)如果前四局双方战成2∶2,那么甲队最终获胜的概率是 ;?
(2)现甲队在前两局比赛中已取得2∶0的领先,那么甲队最终获胜的概率是多少?
14.[2018内蒙古巴彦淖尔中考]小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A,B,C,D,E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:①玩家只能将小兔从A,B两个出入口放入;②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值4元的小兔玩具,否则应付费3元.
(1)请用画树状图的方法,列举出该游戏的所有可能情况;
(2)小美得到小兔玩具的机会有多大?
(3)假设有125人次玩此游戏,估计游戏设计者可赚多少元.
答案
14.【解析】 (1)根据题意,画树状图如下:
?
?
?
(2)由(1)中的树状图知,共有10种等可能的结果,其中从开始进入的出入口离开的结果有2种.
所以小美玩一次“守株待兔”游戏能得到小兔玩具的概率为210=15.
(3)由(1)中的树状图,可知玩此游戏者获得一只价值4元的小兔玩具的概率为0.2,此游戏设计者能得到3元的概率为0.8.
125×0.8×3-125×0.2×4=200(元),
所以估计游戏设计者可赚200元.
?
15.[2018湖南岳阳中考]为了树立文明乡风,推进社会主义新农村建设,某村决定组建村民文体团队.现围绕“你最喜欢的文体活动项目(每人仅限一项)”在全村范围内随机抽取部分村民进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.
?
?
?
请你根据统计图解答下列问题:
(1)这次参与调查的村民人数为 ;?
(2)请将条形统计图补充完整;
(3)求扇形统计图中,“划龙舟”所在扇形的圆心角的度数;
(4)若在“广场舞、腰鼓、花鼓戏、划龙舟”这四个项目中任选两项组队参加端午节庆典活动,请用列表或画树状图的方法,求恰好选中“花鼓戏、划龙舟”这两个项目的概率.
答案
15.【解析】 (1)120
这次参与调查的村民人数为24÷20%=120.
(2)最喜欢的文体活动项目为广场舞的村民有120-24-15-30-9=42(人),
故补全条形统计图如图所示.
(3)扇形统计图中,“划龙舟”所在扇形的圆心角的度数为360°×30120=90°.
(4)根据题意列表如下:
由表可知,共有12种等可能的结果,其中恰好选中“花鼓戏、划龙舟”这两个项目的结果有2种,
故所求概率为212=16.
?
?
广场舞
腰鼓
花鼓戏
划龙舟
广场舞
?
(广场舞,腰鼓)
(广场舞,花鼓戏)
(广场舞,划龙舟)
腰鼓
(腰鼓,广场舞)
?
(腰鼓,花鼓戏)
(腰鼓,划龙舟)
花鼓戏
(花鼓戏,广场舞)
(花鼓戏,腰鼓)
?
(花鼓戏,划龙舟)
划龙舟
(划龙舟,广场舞)
(划龙舟,腰鼓)
(划龙舟,花鼓戏)
?
第三章 概率的进一步认识中考真题
数学·九年级上册·北师
答案
1.D 【解析】 根据题意,画树状图如下:
?
?
?
由树状图可知,共有12种等可能的结果,任取两个不同的数,使a2+b2>19的结果有4种,∴任取两个不同的数,a2+b2>19的概率是412=13.故选D.
?
1.[2019山东东营中考]从1,2,3,4中任取两个不同的数,分别记为a和b,则a2+b2>19的概率是 ( )
A.12 B.512 C.712 D.13
?
答案
2.D 【解析】 画树状图如下:
?
?
?
?
由树状图可以看出,有36种等可能的结果,其中使a2-4b≥0,即a2≥4b的结果有19种,所以方程x2+ax+b=0有解的概率是1936.故选D.
?
2.[2019湖北荆门中考]投掷一枚质地均匀的骰子两次,向上一面的点数依次记为a,b,那么方程x2+ax+b=0有解的概率是( )
A.12 B.13 C.815 D.1936
?
答案
3.0.4
3.[2019湖南长沙中考]在一个不透明的袋子中有若干个小球,这些球除颜色外无其他差别,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,然后把它重新放回袋中并摇匀,不断重复上述过程.以下是利用计算机模拟的摸球试验统计表:
根据试验所得数据,估计“摸出黑球”的概率是 .(结果保留小数点后一位)?
摸球实验次数
100
1 000
5 000
10 000
50 000
100 000
“摸出黑球”的次数
36
387
2 019
4 009
19 970
40 008
“摸出黑球”的频率(结果保留小数点后三位)
0.360
0.387
0.404
0.401
0.399
0.400
答案
4.49 【解析】 根据题意列表如下:
由表可知,共有9种等可能的结果,其中摸出的2个球颜色相同的结果有4种,所以摸出的2个球颜色相同的概率为49.
?
4.[2019河南中考]现有两个不透明的袋子,一个装有2个红球、1个白球,另一个装有1个黄球、2个红球,这些球除颜色外完全相同.从两个袋子中各随机摸出1个球,摸出的2个球颜色相同的概率是? .?
?
黄
红
红
红
(红,黄)
(红,红)
(红,红)
红
(红,黄)
(红,红)
(红,红)
白
(白,黄)
(白,红)
(白,红)
答案
5.23 【解析】 画树状图如下:
?
?
?
?
?
由树状图可知,共有6种等可能的结果,其中能让灯泡发光的结果有4种,所以能让灯泡发光的概率P=46=23.
?
5.[2019湖南娄底中考]如图,随机闭合开关S1,S2,S3中的两个,能让灯泡发光的概率是? .?
答案
6.【解析】 (1)13
(2)解法一 根据题意,画树状图如下:
?
?
?
?
6.[2019江西中考]为纪念建国70周年,某校举行班级歌咏比赛,歌曲有《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是? ;?
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
答案
由树状图知,共有9种等可能的结果,其中八(1)班和八(2)班抽中不同歌曲的结果有6种,故P(八(1)班和八(2)班抽中不同歌曲)=69=23.
解法二 根据题意,列表如下:
?
?
?
?
?
由表格知,共有9种等可能的结果,其中八(1)班和八(2)班抽中不同歌曲的结果有6种,故P(八(1)班和八(2)班抽中不同歌曲)=69=23.
?
7.[2019河北中考]某球室有三种品牌的4个乒乓球,价格是7,8,9(单位:元)三种,从中随机拿出一个球,已知P(一次拿到8元球)=12.
(1)求这4个球价格的众数;
(2)若甲组已拿走一个7元球训练,乙组准备从剩余3个球中随机拿一个训练.
①所剩的3个球价格的中位数与原来4个球价格的中位数是否相同?并简要说明理由;
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如下表)求乙组两次都拿到8元球的概率.
?
答案
7.【解析】 (1)∵P(一次拿到8元球)=12=24,
∴8元球的个数为2,
∴众数是8.
(2)①相同.理由如下:
∵所剩3个球的价格是8,8,9,
∴中位数是8.
∵原来4个球的价格是7,8,8,9,
∴中位数是8.
故相同.
②根据题意列表如下:
?
?
由表格可知,共有9种等可能的结果,其中乙组两次都拿到8元球的结果有4种,故P(乙组两次都拿到8元球)=49.
?
8.[2018内蒙古赤峰中考]国家为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施.使贫困户的生活条件得到改善,生活质量明显提高.某旗县为了全面了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).
?
?
?
?
?
根据以上信息,解答下列问题:
(1)将图1补充完整;
(2)通过分析,贫困户对扶贫工作的满意度(A,B,C类视为满意)是 ;?
(3)市扶贫办从该旗县甲乡镇3户、乙乡镇2户共5户贫困户中,随机抽取两户进行满意度回访,求这两户贫困户恰好都是同一乡镇的概率.
答案
8.【解析】 (1)被调查的总户数为60÷60%=100,
∴C类别户数为100-(60+20+5)=15.
补全统计图如下:
?
?
?
(2)95%
贫困户对扶贫工作的满意度(A,B,C类视为满意)是60+20+15100×100%=95%.
?
答案
(3)设该旗县甲乡镇3户分别记为甲1,甲2,甲3,乙乡镇2户分别记为乙1,乙2.画树状图如下:
?
?
?
?
由树状图可知,共有20种等可能的结果,其中抽取的两户贫困户恰好都是同一乡镇的有8种结果,
所以抽取的两户贫困户恰好都是同一乡镇的概率为820=25.
?
9.[2019山东济南中考]某学校八年级共400名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下:
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根据数据绘制了如下的表格和统计图:
等级
视力(x)
频数
频率
A
x<4.2
4
0.1
B
4.2≤x≤4.4
12
0.3
C
4.5≤x≤4.7
a
?
D
4.8≤x≤5.0
?
b
E
5.1≤x≤5.3
10
0.25
合计
40
1
根据上面提供的信息,回答下列问题:
(1)统计表中的a= ,b= ;?
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该校八年级学生视力为“E级”的有多少人.
(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用画树状图法或列表法求出恰好选中“1男1女”的概率.
答案
9.【解析】 (1)8 0.15
由题意知C等级的频数a=8,
则C等级对应的频率为8÷40=0.2,
∴b=1-(0.1+0.3+0.2+0.25)=0.15.
(2)D等级对应的频数为40×0.15=6.
补全图形如下:
?
?
?
?
答案
(3)估计该校八年级学生视力为“E级”的有400×0.25=100(人).
(4)列表如下:
由树状图可知,得到所有等可能的情况有12种,其中恰好抽中“1男1女”的情况有8种,
所以恰好选中“1男1女”的概率为812=23.
?
?
男
男
女
女
男
?
(男,男)
(男,女)
(男,女)
男
(男,男)
?
(男,女)
(男,女)
女
(女,男)
(女,男)
?
(女,女)
女
(女,男)
(女,男)
(女,女)
数学·九年级上册·北师
专题1 概率的计算方法
专项素养拓训
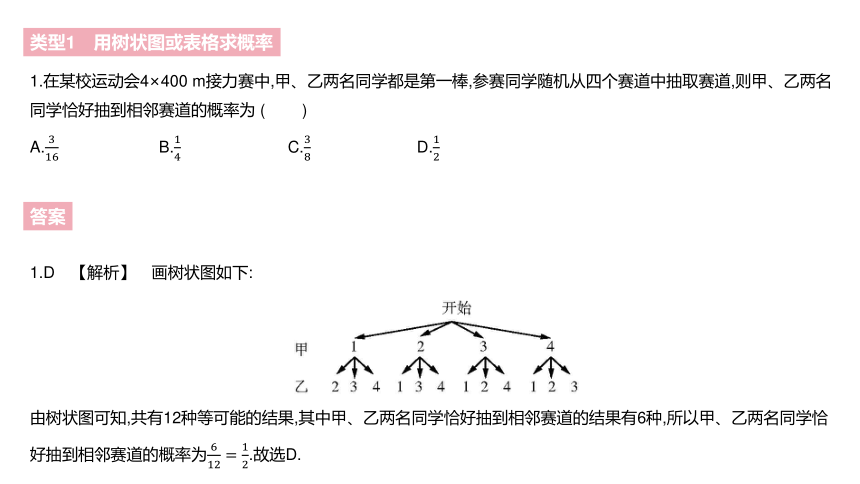
1.在某校运动会4×400 m接力赛中,甲、乙两名同学都是第一棒,参赛同学随机从四个赛道中抽取赛道,则甲、乙两名同学恰好抽到相邻赛道的概率为 ( )
A.316 B.14 C.38 D.12
?
答案
1.D 【解析】 画树状图如下:
?
由树状图可知,共有12种等可能的结果,其中甲、乙两名同学恰好抽到相邻赛道的结果有6种,所以甲、乙两名同学恰好抽到相邻赛道的概率为612=12.故选D.
?
类型1 用树状图或表格求概率
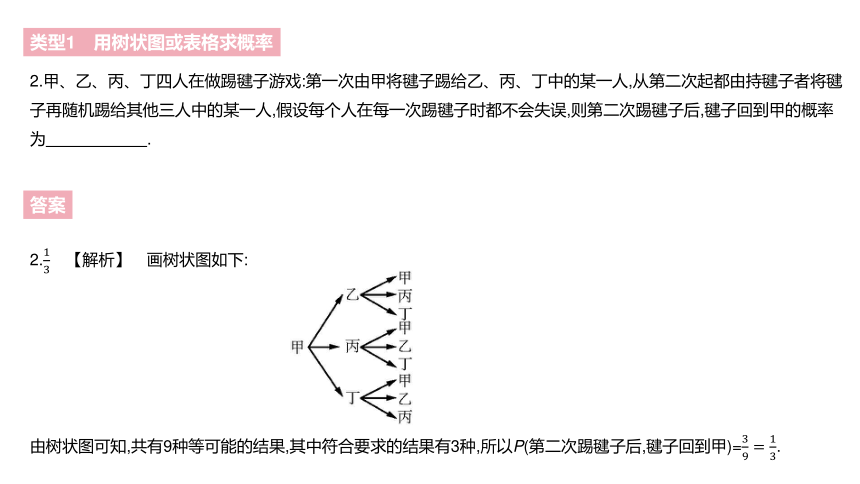
2.甲、乙、丙、丁四人在做踢毽子游戏:第一次由甲将毽子踢给乙、丙、丁中的某一人,从第二次起都由持毽子者将毽子再随机踢给其他三人中的某一人,假设每个人在每一次踢毽子时都不会失误,则第二次踢毽子后,毽子回到甲的概率为? .?
答案
2.13 【解析】 画树状图如下:
?
由树状图可知,共有9种等可能的结果,其中符合要求的结果有3种,所以P(第二次踢毽子后,毽子回到甲)=39=13.
?
类型1 用树状图或表格求概率
3.如图,转盘被等分成4个扇形,转盘上1,2,3,4四个数字分别代表鸡、猴、鼠、羊四种生肖邮票(每种邮票各两枚,鸡年邮票面值“80分”,其他邮票面值都是“1.20元”),转动转盘后,指针每落在某个数字所在的扇形一次就表示获得该种邮票一枚(指针落在分界线时重转).
(1)任意转动转盘一次,获得猴年邮票的概率是? ;?
(2)任意转动转盘两次,求获得的两枚邮票可以邮寄一封需2.40元邮资的信件的概率.
类型1 用树状图或表格求概率
答案
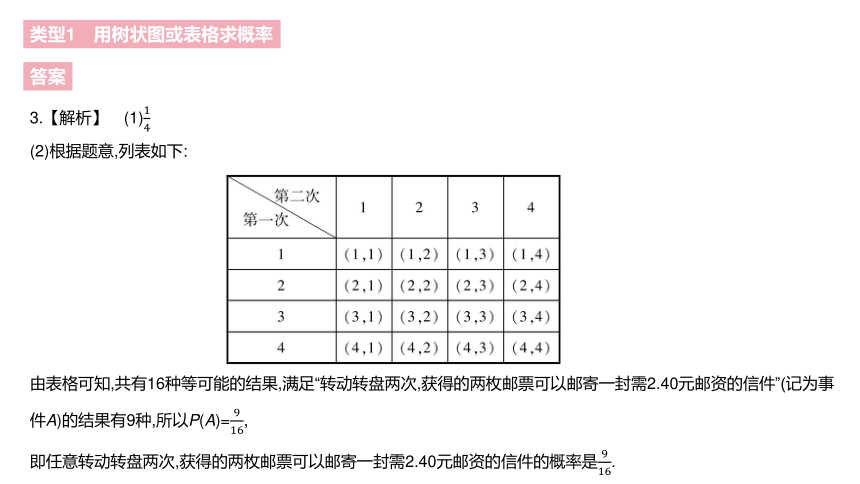
3.【解析】 (1)14
(2)根据题意,列表如下:
由表格可知,共有16种等可能的结果,满足“转动转盘两次,获得的两枚邮票可以邮寄一封需2.40元邮资的信件”(记为事件A)的结果有9种,所以P(A)=916,
即任意转动转盘两次,获得的两枚邮票可以邮寄一封需2.40元邮资的信件的概率是916.
?
类型1 用树状图或表格求概率
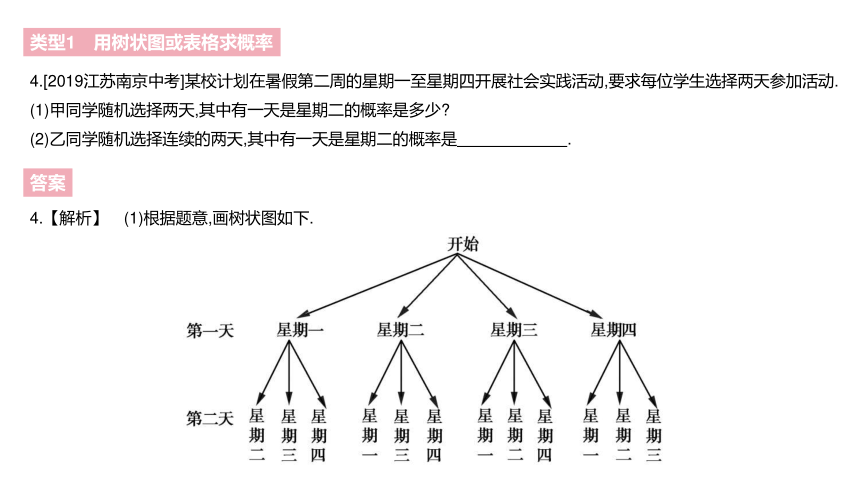
4.[2019江苏南京中考]某校计划在暑假第二周的星期一至星期四开展社会实践活动,要求每位学生选择两天参加活动.
(1)甲同学随机选择两天,其中有一天是星期二的概率是多少?
(2)乙同学随机选择连续的两天,其中有一天是星期二的概率是? .?
答案
4.【解析】 (1)根据题意,画树状图如下.
?
?
?
类型1 用树状图或表格求概率
答案
由树状图可知,共有12种等可能的结果,其中有一天是星期二的结果有6种,
故P(其中有一天是星期二)=612=12.
(2)23
乙同学随机选择连续的两天,有3种等可能的结果,即(星期一,星期二),(星期二,星期三),(星期三,星期四),其中有一天是星期二的结果有2种,故P(其中有一天是星期二)=23.
?
类型1 用树状图或表格求概率
5.节能灯根据使用寿命分为优等品、正品和次品三个等级,其中使用寿命大于或等于8 000小时的节能灯是优等品,使用寿命小于6 000小时的节能灯是次品,其余的节能灯是正品.质检部门对某批次的一种节能灯(共200个)的使用寿命进行追踪调查,并将结果整理成下表(假设节能灯的使用寿命均不超过9 000小时).
(1)根据表中的数据,求a,b,c的值;
(2)某人从这200个节能灯中随机购买1个,求这个节能灯恰好不是次品的概率.
类型2 用频率估计概率
寿命t/时
频数
频率
4 000≤t<5 000
10
0.05
5 000≤t<6 000
20
a
6 000≤t<7 000
80
0.4
7 000≤t<8 000
b
0.15
8 000≤t<9 000
60
c
合计
200
1
答案
5.【解析】 (1)a=20÷200=0.1,b=200×0.15=30,c=60÷200=0.3.
(2)这批节能灯中,优等品有60个,正品有110个,次品有30个.
所以此人购买的这个节能灯恰好不是次品的概率P=110+60200=0.85.
?
类型2 用频率估计概率
专题2 概率的应用
专项素养拓训
6.小敏的爸爸买了一张某项体育比赛的门票,她和哥哥两人都很想去观看,可门票只有一张.读九年级的哥哥想了一个办法,拿了8张扑克牌,将数字为2,3,5,9的四张牌给小敏,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小敏和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌数字相加,若和为偶数,则小敏去;若和为奇数,则哥哥去.
(1)请用画树状图法或列表法求小敏去看比赛的概率;
(2)哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.
类型1 用概率说明事件的合理性
答案
6.【解析】 (1)列表如下:
从表格可知,所有可能出现的结果共有16种,这些结果出现的可能性相等,而和为偶数的结果共有6种,所以小敏去看比赛的概率P=616=38.
?
类型1 用概率说明事件的合理性
答案
(2)不公平.
由(1)得哥哥去看比赛的概率P=1-38=58,
因为38<58,所以哥哥设计的游戏规则不公平.
设计的游戏规则:
规定数字之和小于等于10时小敏(哥哥)去,数字之和大于等于11时哥哥(小敏)去,则两人去看比赛的概率都为12.
(答案不唯一,只要满足两人去看比赛的概率相等即可)
?
类型1 用概率说明事件的合理性
7.某商场为了吸引顾客,举行抽奖活动,并规定顾客每购买100元的商品,就可以随机抽取一张奖券,抽得奖券“紫气东来”“花开富贵”“吉星高照”就可以分别获得100元、50元、20元的购物券,抽得“谢谢惠顾”不赠购物券;若顾客不愿意抽奖,则可以直接获得10元的购物券.小明购买了100元的商品,他看到商场公布的前10 000张奖券的抽奖结果如下:
(1)求“紫气东来”奖券出现的频率;
(2)请你帮助小明判断,抽奖和直接获得购物券,哪种方式更划算?并说明理由.
类型1 用概率说明事件的合理性
奖券种类
紫气东来
花开富贵
吉星高照
谢谢惠顾
出现张数/张
500
1 000
2 000
6 500
答案
7.【解析】 (1)50010?000=120,
∴“紫气东来”奖券出现的频率为120.
(2)抽奖更划算.理由如下:
平均每张奖券获得的购物券金额为100×50010?000+50×1?00010?000+20×2?00010?000+0×6?50010?000=14(元).
∵14>10,∴选择抽奖更划算.
?
类型1 用概率说明事件的合理性
8.[2019湖北恩施州中考]为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级,A级:非常满意;B级:满意;C级:基本满意;D级:不满意),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
?
(1)本次抽样调查测试的建档立卡贫困户的总户数是 ;?
(2)扇形统计图中,∠α的度数是 ,并把条形统计图补充完整;?
类型2 概率与统计的综合
(3)某县建档立卡贫困户有10 000户,如果全部参加这次满意度调查,请估计非常满意的户数约为多少;
(4)调查人员想从5户建档立卡贫困户(分别记为a,b,c,d,e)中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户e的概率.
类型2 概率与统计的综合
答案
8.【解析】 (1)60
(2)54°
C级户数为60-9-21-9=21.
补全条形统计图如图所示:
(3)估计非常满意的户数约为960×10 000=1 500.
?
答案
(4)由题可列如下树状图:
?
由树状图可以看出,所有可能出现的等可能结果共有20种,其中选中贫困户e的结果有8种,
∴P(选中贫困户e)=820=25.
?
类型2 概率与统计的综合
9.现今“微信运动”被越来越多的人关注和喜爱.某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数直方图.
(2)本市约有37 800名教师,用调查的样本数据估计日行走步数超过12 000步(包含12 000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16 000步(包含16 000步)的两名教师与大家分享心得,求被选取的两名教师恰好都在20 000步(包含20 000步)以上的概率.
类型2 概率与统计的综合
步数
人数
频率
0≤x<4 000
8
a
4 000≤x<8 000
15
0.3
8 000≤x<12 000
12
b
12 000≤x<16 000
c
0.2
16 000≤x<20 000
3
0.06
20 000≤x<24 000
d
0.04
答案
9.【解析】 (1)a=850=0.16,b=1250=0.24,c=50×0.2=10,d=50×0.04=2.
补全频数直方图如下:
(2)0.2+0.06+0.04=0.3=30%,37 800×30%=11 340(名).
所以估计日行走步数超过12 000步(包含12 000步)的教师有11 340名.
?
类型2 概率与统计的综合
答案
(3)设日行走步数在16 000≤x<20 000的3名教师分别为A,B,C,
日行走步数在20 000≤x<24 000的2名教师分别为X,Y,列表如下:
由表格可知,一共有20种等可能的结果,其中两名教师恰好都在20 000步(包含20 000步)以上的结果有2种,所以被选取的两名教师恰好都在20 000步(包含20 000步)以上的概率为110.
?
类型2 概率与统计的综合
?
A
B
C
X
Y
A
?
AB
AC
AX
AY
B
BA
?
BC
BX
BY
C
CA
CB
?
CX
CY
X
XA
XB
XC
?
XY
Y
YA
YB
YC
YX
?
综合素养拓训
在互联网大数据时代,数据处理和分析能力逐渐成为必备素养,而数据分析也是数学的核心素养之一.在教材中,数据分析主要以统计和概率来体现,本章就是对概率的进一步认识.对于“概率”的拓展,侧重应用意识和创新意识,例如第1题,以电视台的智力竞答节目为背景,通过分析不同情形发生的概率,使最优途径了然于胸;第2题,通过频率估计概率的模型,探寻估算不规则图形面积的方案,也是核心素养中数学建模方面的体现.
1.[概率帮你做决策]锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就可顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是? ;?
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是? ;?
(3)如果锐锐每道题各用一次“求助”,请用画树状图或者列表的方法来分析他顺利通关的概率.
答案
1.【解析】 (1)14
由题意,知第一道题肯定能答对,第二道题答对的概率为14,所以锐锐通关的概率为14.
(2)16
如果锐锐两次“求助”都在第二道题中使用,易知此时共有6种等可能的结果出现,其中锐锐两道题都答对的结果有1种,所以锐锐能通关的概率为16.
?
答案
(3)如果锐锐每道题各用一次“求助”,分别用A,B表示第一道单选题剩下的2个选项,a,b,c表示第二道单选题剩下的3个选项,
画树状图如图所示:
?
?
?
?
由树状图知,共有6种等可能的结果,锐锐顺利通关的结果只有1种,
所以锐锐顺利通关的概率为16.
?
2.[概率中的方案设计]小红和小明在操场上做游戏,他们先在地上画了半径分别为2 m和3 m的同心圆(如图),然后蒙上眼睛,并在一定距离外向圈内掷小石子,掷中阴影部分时小红胜,否则小明胜,未掷入圈内(半径为3 m的圆内)或掷在边界上重掷.
(1)你认为游戏公平吗?为什么?
(2)游戏结束,小明边走边想:能否用频率估计概率的方法,来估算不规则图形的面积呢?请你设计一个方案,解决这一问题.(要求画出图形,说明设计步骤、原理,并给出计算公式)
答案
2.【解析】 (1)不公平.理由如下:
∵P(掷中阴影部分)=9π?4π9π=59,即小红获胜的概率为59,则小明获胜的概率为49,59≠49,∴游戏不公平.
?
答案
(2)能利用频率估计概率的方法估算不规则图形的面积.
设计方案:①设计一个可测量面积的规则图形将不规则图形围起来(如正方形,其面积为S),如图所示; ?
?
?
?
?
②往图形中掷点(如蒙上眼睛往图形中随意掷小石子,掷在正方形外或边界上不做记录);
③当所掷次数充分大时,记录并统计结果,设掷入正方形内m次,其中n次掷入不规则图形内;
④设不规则图形的面积为S1,用频率估计概率,
即掷入不规则图形内的频率????????≈P(掷入不规则图形内),而P(掷入不规则图形内)=????1????,故????????≈????1????,即S1≈????????????.
?
答案
1.D 【解析】 设正面上的图案是“ ”的3张卡片分别用A1,A2,A3表示,正面上的图案是“?”的卡片用B表示,画树状图如下:
?
?
?
由树状图可知,共有12种等可能的结果,2张卡片正面上的图案相同的结果有6种.故从中随机抽取2张,这2张卡片正面上的图案相同的概率是612=12.故选D.
?
一、选择题
1.[2018河南中考]现有4张卡片,其中3张卡片正面上的图案是“ ”,1张卡片正面上的图案是“?”,它们除此之外完全相同.把这4张卡片背面朝上洗匀,从中随机抽取2张,则这2张卡片正面上的图案相同的概率是 ( )
A.916 B.34 C.38 D.12
?
答案
2.D 【解析】 A项,抛一枚硬币,出现正面朝上的概率为0.5,不符合题中试验的结果;B项,掷一个正六面体的骰子,出现3点朝上的概率为16,不符合题中试验的结果;C项,一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率为0.25,不符合题中试验的结果;D项,从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球的概率为13,符合题中试验的结果.故选D.
?
2.[2018广西玉林中考]某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率折线图如图,则符合这一结果的试验可能是 ( )
A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
答案
3.C 【解析】 根据题意画树状图如下.
?
由树状图可知,共有16种等可能的结果,其中两次抽取的卡片上的数字之积为偶数的结果有12种.故所求概率为1216=34.故选C.
?
3.[2018湖北武汉中考]一个不透明的口袋中装有四张完全相同的卡片,把它们分别标上数字1,2,3,4.随机抽取一张卡片,然后放回,再随机抽取一张卡片,则两次抽取的卡片上的数字之积为偶数的概率是 ( )
A.14 B.12 C.34 D.56
?
答案
4.A 【解析】 m=3÷25%=12.故选A.
4.[2019河北唐山开平区二模]在一个暗箱里放有m个除颜色外其他完全相同的球,这m个球中只有3个黄球,每次将球搅拌均匀后,任意摸出一个球记下颜色后再放回暗箱,通过大量重复试验发现,摸到黄球的频率稳定在25%左右,推算m的值大约是 ( )
A.12 B.9 C.4 D.3
答案
5.B 【解析】 画树状图如下:
?
由树状图可知,共有9种等可能的结果,小强获胜的结果有3种,所以小强获胜的概率是39=13.故选B.
?
5.小强和小华两人玩“剪刀、石头、布”的游戏,随机出手一次,则小强获胜的概率为 ( )
A.16 B.13 C.12 D.23
?
答案
6.B 【解析】 画树状图如图所示:
?
由树状图可知,共有20种等可能的结果,其中点P(m,n)在平面直角坐标系中位于第四象限的结果有4种,所以点P(m,n)在平面直角坐标系中位于第四象限的概率为420=15.故选B.
?
6.[2019山东德州陵城区二模]点P的坐标是(m,n),从-5,-3,0,4,7这五个数中任取一个数作为m的值,再从余下的四个数中任取一个数作为n的值,则点P(m,n)在平面直角坐标系中位于第四象限的概率是 ( )
A.25 B.15 C.14 D.12
?
答案
7.C 【解析】 将题图左边转盘中蓝色部分等分为3份,分别记为蓝a、蓝b、蓝c,红色部分记为红d,将题图右边转盘中红色部分等分为3份,分别记为红1、红2、红3,蓝色部分记为蓝4.列表如下:
由表格可知,共有16种等可能的结果,其中可配成紫色的结果有10种,所以可配成紫色的概率是1016=58.故选C.
?
7.[2019辽宁本溪模拟]用如图所示的两个可以自由转动的转盘做“配紫色”游戏,分别旋转两个转盘,若其中一个转盘转出红色,另一个转盘转出蓝色即可配成紫色,则可配成紫色的概率是 ( )
A.38 B.12
C.58 D.23
?
?
蓝a
蓝b
蓝c
红d
红1
(红1,蓝a)
(红1,蓝b)
(红1,蓝c)
(红1,红d)
红2
(红2,蓝a)
(红2,蓝b)
(红2,蓝c)
(红2,红d)
红3
(红3,蓝a)
(红3,蓝b)
(红3,蓝c)
(红3,红d)
蓝4
(蓝4,蓝a)
(蓝4,蓝b)
(蓝4,蓝c)
(蓝4,红d)
答案
8.B 【解析】 根据题意,列表如下:
由表格可知,共有16种等可能的结果,而落在以A(-2,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)有(-2,0),(0,0),(1,0), (2,0),(0,1),(1,1),(0,2),共7种,所以落在以A(-2,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)的概率是716.故选B.
?
8.如图,一个质地均匀的正四面体的四个面上依次标有数字-2,0,1,2,连续抛掷两次,朝下一面的数字分别作为M点的横、纵坐标,则点M落在以A(-2,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)的概率是 ( )
A.38 B.716 C.12 D.916
?
?
-2
0
1
2
-2
(-2,-2)
(-2,0)
(-2,1)
(-2,2)
0
(0,-2)
(0,0)
(0,1)
(0,2)
1
(1,-2)
(1,0)
(1,1)
(1,2)
2
(2,-2)
(2,0)
(2,1)
(2,2)
答案
9.13 【解析】 根据题意,画树状图如图所示:
?
?
?
从树状图中可以看出,共有6种等可能的情况,积是正数的有2种情况,所以任取两个不同的数,积为正数的概率是26=13.
?
二、填空题
9.从-3,1,-2这三个数中任取两个不同的数,积为正数的概率是? .?
答案
10.14 【解析】 根据题意,列表如下:
∵直线y=mx+n不经过第三象限,m≠0,n≠0,∴直线经过第一、二、四象限,∴m<0,n>0,∴直线y=mx+n不经过第三象限的概率为416=14.
?
10.有四张背面完全相同的卡片,正面上分别标有数字-2,-1,1,2,把这四张卡片背面朝上,洗匀后,随机抽取一张,记下数字为m;放回搅匀,再随机抽取一张卡片,记下数字为n,则y=mx+n不经过第三象限的概率为? .?
答案
11.17 【解析】 ∵|m|≤1,|n|≤3,且m,n都是整数,∴m=-1,0,1;n=-3,-2,-1,0,1,2,3.∵关于x的方程x2+nx+m=0有两个相等的实数根,∴Δ=n2-4m=0.列表如下:
从表格中可看出共有21种等可能的结果,能使Δ=n2-4m=0成立的有序整数(m,n)共有3对,分别为(1,-2),(0,0)和(1,2),故P(关于x的方程x2+nx+m=0有两个相等的实数根)=321=17.
?
11.如果任意选择一对有序整数(m,n),其中|m|≤1,|n|≤3,每一对这样的有序整数被选择的可能性是相等的,那么关于x的方程x2+nx+m=0有两个相等实数根的概率是 .?
三、解答题
12.[2019江苏苏州中考]在一个不透明的盒子中装有4张卡片,4张卡片的正面分别标有数字1,2,3,4,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子中任意抽取一张卡片,恰好抽到标有奇数数字卡片的概率是? ;?
(2)先从盒子中任意抽取一张卡片,再从余下的3张卡片中任意抽取一张卡片,求抽取的2张卡片标有的数字之和大于4的概率.(请用画树状图或列表等方法求解)
答案
12.【解析】 (1)12
(2)根据题意,列表如下:
由表可知,共有12种等可能的结果,其中抽取的2张卡片标有的数字之和大于4的有8种,
所以抽取的2张卡片标有的数字之和大于4的概率为812=23.
?
答案
13.【解析】 (1)12
(2)画树状图如下:
?
?
由树状图可知,共有8种等可能的结果,其中甲至少胜一局的结果有7种.
所以甲队最终获胜的概率为78.
?
13.[2018江苏连云港中考]汤姆斯杯世界男子羽毛球团体赛小组赛比赛规则:两队之间进行五局比赛,其中三局单打,两局双打,五局比赛必须全部打完,赢得三局及以上的队获胜.假如甲、乙两队每局获胜的机会相同.
(1)如果前四局双方战成2∶2,那么甲队最终获胜的概率是 ;?
(2)现甲队在前两局比赛中已取得2∶0的领先,那么甲队最终获胜的概率是多少?
14.[2018内蒙古巴彦淖尔中考]小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A,B,C,D,E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:①玩家只能将小兔从A,B两个出入口放入;②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值4元的小兔玩具,否则应付费3元.
(1)请用画树状图的方法,列举出该游戏的所有可能情况;
(2)小美得到小兔玩具的机会有多大?
(3)假设有125人次玩此游戏,估计游戏设计者可赚多少元.
答案
14.【解析】 (1)根据题意,画树状图如下:
?
?
?
(2)由(1)中的树状图知,共有10种等可能的结果,其中从开始进入的出入口离开的结果有2种.
所以小美玩一次“守株待兔”游戏能得到小兔玩具的概率为210=15.
(3)由(1)中的树状图,可知玩此游戏者获得一只价值4元的小兔玩具的概率为0.2,此游戏设计者能得到3元的概率为0.8.
125×0.8×3-125×0.2×4=200(元),
所以估计游戏设计者可赚200元.
?
15.[2018湖南岳阳中考]为了树立文明乡风,推进社会主义新农村建设,某村决定组建村民文体团队.现围绕“你最喜欢的文体活动项目(每人仅限一项)”在全村范围内随机抽取部分村民进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.
?
?
?
请你根据统计图解答下列问题:
(1)这次参与调查的村民人数为 ;?
(2)请将条形统计图补充完整;
(3)求扇形统计图中,“划龙舟”所在扇形的圆心角的度数;
(4)若在“广场舞、腰鼓、花鼓戏、划龙舟”这四个项目中任选两项组队参加端午节庆典活动,请用列表或画树状图的方法,求恰好选中“花鼓戏、划龙舟”这两个项目的概率.
答案
15.【解析】 (1)120
这次参与调查的村民人数为24÷20%=120.
(2)最喜欢的文体活动项目为广场舞的村民有120-24-15-30-9=42(人),
故补全条形统计图如图所示.
(3)扇形统计图中,“划龙舟”所在扇形的圆心角的度数为360°×30120=90°.
(4)根据题意列表如下:
由表可知,共有12种等可能的结果,其中恰好选中“花鼓戏、划龙舟”这两个项目的结果有2种,
故所求概率为212=16.
?
?
广场舞
腰鼓
花鼓戏
划龙舟
广场舞
?
(广场舞,腰鼓)
(广场舞,花鼓戏)
(广场舞,划龙舟)
腰鼓
(腰鼓,广场舞)
?
(腰鼓,花鼓戏)
(腰鼓,划龙舟)
花鼓戏
(花鼓戏,广场舞)
(花鼓戏,腰鼓)
?
(花鼓戏,划龙舟)
划龙舟
(划龙舟,广场舞)
(划龙舟,腰鼓)
(划龙舟,花鼓戏)
?
第三章 概率的进一步认识中考真题
数学·九年级上册·北师
答案
1.D 【解析】 根据题意,画树状图如下:
?
?
?
由树状图可知,共有12种等可能的结果,任取两个不同的数,使a2+b2>19的结果有4种,∴任取两个不同的数,a2+b2>19的概率是412=13.故选D.
?
1.[2019山东东营中考]从1,2,3,4中任取两个不同的数,分别记为a和b,则a2+b2>19的概率是 ( )
A.12 B.512 C.712 D.13
?
答案
2.D 【解析】 画树状图如下:
?
?
?
?
由树状图可以看出,有36种等可能的结果,其中使a2-4b≥0,即a2≥4b的结果有19种,所以方程x2+ax+b=0有解的概率是1936.故选D.
?
2.[2019湖北荆门中考]投掷一枚质地均匀的骰子两次,向上一面的点数依次记为a,b,那么方程x2+ax+b=0有解的概率是( )
A.12 B.13 C.815 D.1936
?
答案
3.0.4
3.[2019湖南长沙中考]在一个不透明的袋子中有若干个小球,这些球除颜色外无其他差别,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,然后把它重新放回袋中并摇匀,不断重复上述过程.以下是利用计算机模拟的摸球试验统计表:
根据试验所得数据,估计“摸出黑球”的概率是 .(结果保留小数点后一位)?
摸球实验次数
100
1 000
5 000
10 000
50 000
100 000
“摸出黑球”的次数
36
387
2 019
4 009
19 970
40 008
“摸出黑球”的频率(结果保留小数点后三位)
0.360
0.387
0.404
0.401
0.399
0.400
答案
4.49 【解析】 根据题意列表如下:
由表可知,共有9种等可能的结果,其中摸出的2个球颜色相同的结果有4种,所以摸出的2个球颜色相同的概率为49.
?
4.[2019河南中考]现有两个不透明的袋子,一个装有2个红球、1个白球,另一个装有1个黄球、2个红球,这些球除颜色外完全相同.从两个袋子中各随机摸出1个球,摸出的2个球颜色相同的概率是? .?
?
黄
红
红
红
(红,黄)
(红,红)
(红,红)
红
(红,黄)
(红,红)
(红,红)
白
(白,黄)
(白,红)
(白,红)
答案
5.23 【解析】 画树状图如下:
?
?
?
?
?
由树状图可知,共有6种等可能的结果,其中能让灯泡发光的结果有4种,所以能让灯泡发光的概率P=46=23.
?
5.[2019湖南娄底中考]如图,随机闭合开关S1,S2,S3中的两个,能让灯泡发光的概率是? .?
答案
6.【解析】 (1)13
(2)解法一 根据题意,画树状图如下:
?
?
?
?
6.[2019江西中考]为纪念建国70周年,某校举行班级歌咏比赛,歌曲有《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是? ;?
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
答案
由树状图知,共有9种等可能的结果,其中八(1)班和八(2)班抽中不同歌曲的结果有6种,故P(八(1)班和八(2)班抽中不同歌曲)=69=23.
解法二 根据题意,列表如下:
?
?
?
?
?
由表格知,共有9种等可能的结果,其中八(1)班和八(2)班抽中不同歌曲的结果有6种,故P(八(1)班和八(2)班抽中不同歌曲)=69=23.
?
7.[2019河北中考]某球室有三种品牌的4个乒乓球,价格是7,8,9(单位:元)三种,从中随机拿出一个球,已知P(一次拿到8元球)=12.
(1)求这4个球价格的众数;
(2)若甲组已拿走一个7元球训练,乙组准备从剩余3个球中随机拿一个训练.
①所剩的3个球价格的中位数与原来4个球价格的中位数是否相同?并简要说明理由;
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如下表)求乙组两次都拿到8元球的概率.
?
答案
7.【解析】 (1)∵P(一次拿到8元球)=12=24,
∴8元球的个数为2,
∴众数是8.
(2)①相同.理由如下:
∵所剩3个球的价格是8,8,9,
∴中位数是8.
∵原来4个球的价格是7,8,8,9,
∴中位数是8.
故相同.
②根据题意列表如下:
?
?
由表格可知,共有9种等可能的结果,其中乙组两次都拿到8元球的结果有4种,故P(乙组两次都拿到8元球)=49.
?
8.[2018内蒙古赤峰中考]国家为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施.使贫困户的生活条件得到改善,生活质量明显提高.某旗县为了全面了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).
?
?
?
?
?
根据以上信息,解答下列问题:
(1)将图1补充完整;
(2)通过分析,贫困户对扶贫工作的满意度(A,B,C类视为满意)是 ;?
(3)市扶贫办从该旗县甲乡镇3户、乙乡镇2户共5户贫困户中,随机抽取两户进行满意度回访,求这两户贫困户恰好都是同一乡镇的概率.
答案
8.【解析】 (1)被调查的总户数为60÷60%=100,
∴C类别户数为100-(60+20+5)=15.
补全统计图如下:
?
?
?
(2)95%
贫困户对扶贫工作的满意度(A,B,C类视为满意)是60+20+15100×100%=95%.
?
答案
(3)设该旗县甲乡镇3户分别记为甲1,甲2,甲3,乙乡镇2户分别记为乙1,乙2.画树状图如下:
?
?
?
?
由树状图可知,共有20种等可能的结果,其中抽取的两户贫困户恰好都是同一乡镇的有8种结果,
所以抽取的两户贫困户恰好都是同一乡镇的概率为820=25.
?
9.[2019山东济南中考]某学校八年级共400名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下:
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根据数据绘制了如下的表格和统计图:
等级
视力(x)
频数
频率
A
x<4.2
4
0.1
B
4.2≤x≤4.4
12
0.3
C
4.5≤x≤4.7
a
?
D
4.8≤x≤5.0
?
b
E
5.1≤x≤5.3
10
0.25
合计
40
1
根据上面提供的信息,回答下列问题:
(1)统计表中的a= ,b= ;?
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该校八年级学生视力为“E级”的有多少人.
(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用画树状图法或列表法求出恰好选中“1男1女”的概率.
答案
9.【解析】 (1)8 0.15
由题意知C等级的频数a=8,
则C等级对应的频率为8÷40=0.2,
∴b=1-(0.1+0.3+0.2+0.25)=0.15.
(2)D等级对应的频数为40×0.15=6.
补全图形如下:
?
?
?
?
答案
(3)估计该校八年级学生视力为“E级”的有400×0.25=100(人).
(4)列表如下:
由树状图可知,得到所有等可能的情况有12种,其中恰好抽中“1男1女”的情况有8种,
所以恰好选中“1男1女”的概率为812=23.
?
?
男
男
女
女
男
?
(男,男)
(男,女)
(男,女)
男
(男,男)
?
(男,女)
(男,女)
女
(女,男)
(女,男)
?
(女,女)
女
(女,男)
(女,男)
(女,女)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
