北师大版九年级上册数学第六章 反比例函数素养拓展+中考真题课件(60张PPT)
文档属性
| 名称 | 北师大版九年级上册数学第六章 反比例函数素养拓展+中考真题课件(60张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 00:00:00 | ||
图片预览





文档简介
第六章 反比例函数
数学·九年级上册·北师
专题 反比例函数的图象与性质
专项素养拓训
1.[2020安徽二十校联考]如图,点A是反比例函数y=????????(x<0)的图象上一点,过点A作AB⊥x轴,垂足为B,点C为y轴上一点,连接AC,BC.若△ABC的面积为4,则k的值是 ( )
A.4 B.-4 C.8 D.-8
?
答案
1.D 【解析】 如图,连接OA,∵AB⊥x轴,∴OC∥AB,∴S△ABC=S△OAB=12|k|=4,∴|k|=8.∵当x<0时,反比例函数的图象位于第二象限,∴k<0,∴k=-8.故选D.
?
类型1 反比例函数与图形面积
2.如图,双曲线y=-32????(x<0)经过?OABC的对角线的交点D,已知边OC在y轴上,且AC⊥OC于点C,则?OABC的面积是 ( )
A.32 B.94 C.3 D.6
?
答案
2.C 【解析】 ∵AC⊥OC,∴S△CDO=12|k|=12×32=34,∴?OABC的面积为4S△CDO=4×34=3.故选C.
?
类型1 反比例函数与图形面积
3.如图,点C,D在双曲线y=3????(x>0)上,点A,B在x轴上,且OA=AB,CO=CA,DA=DB,则S△OCA+S△ADB= .?
?
答案
3.4 【解析】 如图,过点C作CM⊥x轴于点M,过点D作DN⊥x轴于点N,连接OD,
∵CO=CA,DA=DB,∴OM=AM,AN=BN,∵S△OCM=S△ODN=12|k|=32,∴S△OCA=2S△OCM=3,
∵OA=AB,AN=BN,∴S△AND=12S△OAD=13S△OND=12,∴S△ABD=2S△AND=1,∴S△OCA+S△ADB=3+1=4.
?
类型1 反比例函数与图形面积
4.[2018广东广州中考]一次函数y=ax+b和反比例函数y=?????????????在同一直角坐标系中的大致图象是 ( )
?
答案
4.A 【解析】 易得一次函数y=ax+b与x轴、y轴的交点分别为(-????????,0),(0,b).当a>0时,若b>a>0,则一次函数y=ax+b的图象经过第一、二、三象限,且-????????<-1,反比例函数y=?????????????的图象分布在第二、四象限,故选项B中的图象不符合题意;若a>b>0,则一次函数y=ax+b的图象经过第一、二、三象限,且-????????>-1,反比例函数y=?????????????的图象分布在第一、三象限,故选项A中的图象符合题意;当a<0时,若a<0?
类型2 反比例函数与一次函数
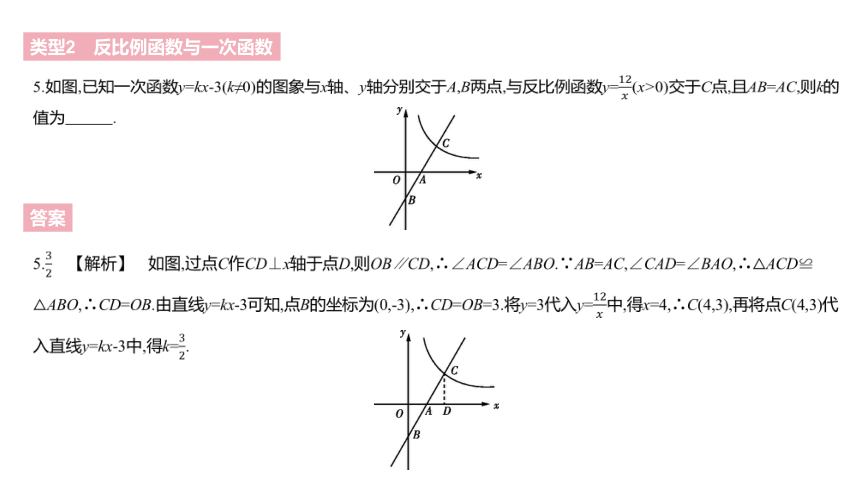
5.如图,已知一次函数y=kx-3(k≠0)的图象与x轴、y轴分别交于A,B两点,与反比例函数y=12????(x>0)交于C点,且AB=AC,则k的值为? .?
?
答案
5.32 【解析】 如图,过点C作CD⊥x轴于点D,则OB∥CD,∴∠ACD=∠ABO.∵AB=AC,∠CAD=∠BAO,∴△ACD≌
△ABO,∴CD=OB.由直线y=kx-3可知,点B的坐标为(0,-3),∴CD=OB=3.将y=3代入y=12????中,得x=4,∴C(4,3),再将点C(4,3)代入直线y=kx-3中,得k=32.
?
类型2 反比例函数与一次函数
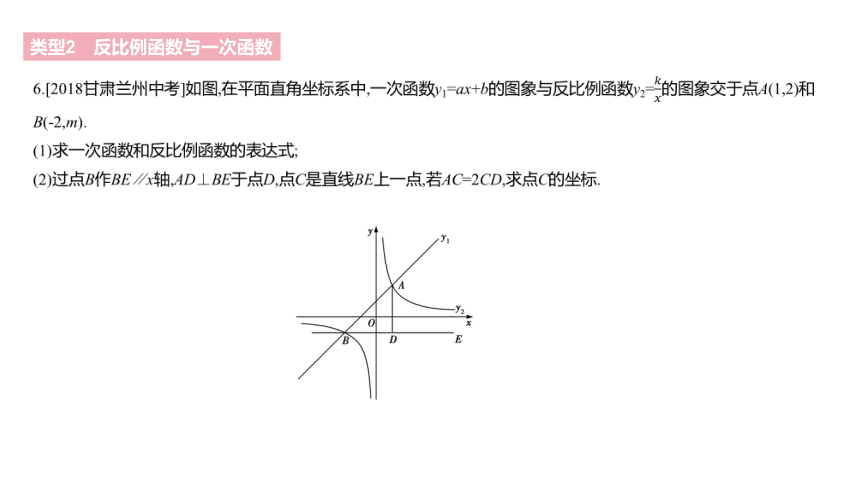
6.[2018甘肃兰州中考]如图,在平面直角坐标系中,一次函数y1=ax+b的图象与反比例函数y2=????????的图象交于点A(1,2)和
B(-2,m).
(1)求一次函数和反比例函数的表达式;
(2)过点B作BE∥x轴,AD⊥BE于点D,点C是直线BE上一点,若AC=2CD,求点C的坐标.
?
类型2 反比例函数与一次函数
答案
6.【解析】 (1)∵点A在反比例函数y2=????????的图象上,
∴k=1×2=2,
故反比例函数的表达式为y2=2????.
∵点B在反比例函数y2=2????的图象上,
∴m=2?2=-1,
故点B的坐标为(-2,-1).
将点A,B的坐标分别代入一次函数的表达式,
得????+????=2,?2????+????=?1,解得????=1,????=1,
故一次函数的表达式为y1=x+1.
?
类型2 反比例函数与一次函数
答案
(2)易得点D的坐标为(1,-1).
设点C的坐标为(n,-1),
则AC=(?????1)2+32,CD=|n-1|.
由AC=2CD,可得AC2=4CD2,即(n-1)2+32=4(n-1)2,
解得n1=1+3,n2=1-3,
故点C的坐标为(1+3,-1)或(1-3,-1).
?
类型2 反比例函数与一次函数
类型3 反比例函数与不等式
7.已知A(-1,y1),B(2,y2)两点在双曲线y=3+2????????上,且y1>y2,则m的取值范围是 ( )
A.m<0 B.m>0
C.m>-32 D.m<-32
?
答案
7.D 【解析】 解法一 由题可知,点A,B位于第二、四象限或第一、三象限,∵-1<2,y1>y2,∴双曲线y=3+2????????位于第二、四象限,∴3+2m<0,即m<-32.故选D.
解法二 将点A(-1,y1),B(2,y2)代入y=3+2????????,得????1=?(3+2????),????2=3+2????2,由y1>y2可得-(3+2m)>3+2????2,解得m<-32.故选D.
?
类型3 反比例函数与不等式
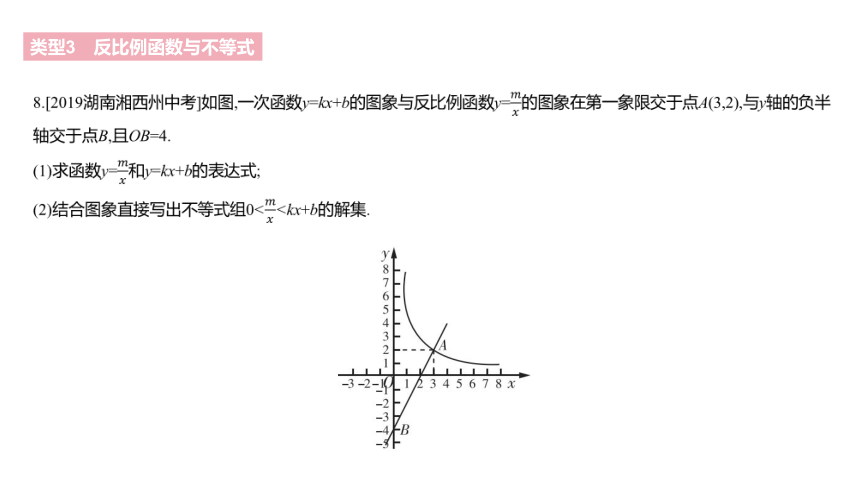
8.[2019湖南湘西州中考]如图,一次函数y=kx+b的图象与反比例函数y=????????的图象在第一象限交于点A(3,2),与y轴的负半轴交于点B,且OB=4.
(1)求函数y=????????和y=kx+b的表达式;
(2)结合图象直接写出不等式组0?
答案
8.【解析】 (1)把点A(3,2)代入反比例函数y=????????,
可得m=3×2=6,
∴反比例函数的表达式为y=6????.
∵OB=4,∴B(0,-4),
把点A(3,2),B(0,-4)代入一次函数y=kx+b,
可得3????+????=2,????=?4,解得????=2,????=?4,
∴一次函数的表达式为y=2x-4.
(2)不等式组03.
?
类型2 反比例函数与一次函数
9.如图,直线y1=-x+4,y2=34x+b都与双曲线y=????????交于点A(1,m),这两条直线分别与x轴交于B,C两点,直线y1=-x+4与双曲线y=????????交另一点D(n,1).
(1)求y与x之间的函数关系式;
(2)写出当x>0时,不等式-x+4(3)若点P在x轴上,连接AP把△ABC的面积分成1∶3两部分,求此时点P的坐标.
?
答案
9.【解析】 (1)把A(1,m)代入y1=-x+4,得m=-1+4=3,
∴点A的坐标为(1,3).
把A(1,3)代入y=????????,得k=1×3=3,
∴y与x之间的函数关系式为y=3????.
?
类型3 反比例函数与不等式
答案
(2)把D(n,1)代入y=3????,得n=3.当x>0时,不等式-x+43.
(3)在y1=-x+4中,令y1=0,得x=4,
∴点B的坐标为(4,0).
把A(1,3)代入y2=34x+b,得3=34+b,
∴b=94,∴y2=34x+94,
令y2=0,得x=-3,∴点C的坐标为(-3,0),∴BC=7.
∵AP把△ABC的面积分成1∶3两部分,
∴CP=14BC=74或BP=14BC=74,
∴OP=3-74=54或OP=4-74=94,
∴此时点P的坐标为(-54,0)或(94,0).
?
类型3 反比例函数与不等式
10.工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料煅烧到800 ℃,然后停止煅烧进行锻造操作.停止煅烧后第8 min时,材料温度降为600 ℃,煅烧时,温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例关系(如图),已知该材料初始温度是32 ℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480 ℃时,需停止操作,那么锻造的操作时间有多长?
?
答案
10.【分析】 根据点A,B的坐标可求得线段AB所在直线的函数关系式,根据点C的坐标可求得锻造阶段的反比例函数关系式,需先求得锻造阶段的关系式才能确定点B的坐标,进而根据函数关系式分析、求解相关实际问题.
【解析】 (1)设锻造时的函数关系式为y=????????(k≠0),
则600=????8,∴k=4 800,
?
类型4 反比例函数在实际问题中的应用
答案
∴y=4?800????.
当y=800时,800=4?800????,解得x=6,
当y=32时,32=480????,解得x=150,
∴点B的坐标为(6,800),锻造时的函数关系式为y=4?800????(6设煅烧时的函数关系式为y=ax+b(a≠0),
则????=32,6????+????=800,解得????=128,????=32,
∴煅烧时的函数关系式为y=128x+32(0≤x≤6).
(2)当x=480时,y=4?800480=10,10-6=4(min),
∴锻造的操作时间有4 min.
?
类型4 反比例函数在实际问题中的应用
11.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(h)变化的图象,其中BC段是双曲线y=????????的一部分.请根据图中信息解答下列问题.
(1)恒温系统在这天保持大棚内温度为18 ℃的时间有多少小时?
(2)求k的值.
(3)当x=16时,大棚内的温度为多少度?
?
类型4 反比例函数在实际问题中的应用
答案
11.【解析】 (1)观察题中图象可知,恒温系统在这天保持大棚内温度为18 ℃的时间为12-2=10(h).
(2)∵点B(12,18)在双曲线y=????????上,∴18=????12,
∴k=216.
(3)当x=16时,y=21616=13.5,
∴当x=16时,大棚内的温度为13.5 ℃.
?
类型4 反比例函数在实际问题中的应用
综合素养拓训
1.[函数与方程之间的转化]已知,直角三角形ABC如图所示放置,∠ABC=90°,AB=10,BC=5,反比例函数y=????????经过点C(m,3).
(1)求点A,B的坐标及m的值.
(2)求反比例函数及直线AB的表达式.
(3)将直线AB上下移动a个单位长度后,与反比例函数的图象只有唯一一个交点,求a的值.
?
答案
1.【解析】 (1)过点C作CE⊥x轴于点E,则CE=3,
∵BC=5,∴BE=52?32=4.
∵∠ABC=90°,∴∠ABO+∠EBC=90°,
又∵∠ABO+∠OAB=90°,∴∠OAB=∠EBC.
∵∠AOB=∠BEC,
∴△AOB∽△BEC,∴????????????????=????????????????,
∴10????????=53,解得BO=6,
∴AO=102?62=8,m=6+4=10,
∴A(0,8),B(6,0),m=10.
?
答案
(2)将C(10,3)代入反比例函数y=????????中,得3=????10,
解得k=30,即y=30????.
设直线AB的表达式为y=k1x+b,
将A(0,8),B(6,0)代入得????=8,0=6????1+????,
解得????1=?43,????=8,即y=-43x+8.
(3)直线AB上下平移a个单位长度后,得y=-43x+8+a,
∵平移后的直线与反比例函数y=30????的图象只有唯一一个交点,
∴方程30????=-43x+8+a,即4x2-3(8+a)x+90=0只有一个根,
∴Δ=9(8+a)2-4×4×90=0,解得a=±410-8.
?
2.[反比例函数与图形相似的结合]如图,已知反比例函数y=????????(x>0)的图象经过点A(1,4)、点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
(1)求该反比例函数的表达式.
(2)求证:△ACB∽△NOM.
(3)若△ACB与△NOM的相似比为2,求点B的坐标及直线AB的函数表达式.
?
答案
2.【解析】 (1) ∵反比例函数y=????????(x>0)的图象经过点A(1,4),
∴k=4×1=4,∴该反比例函数的表达式为y=4????(x>0).
(2)∵点B(m,n)在反比例函数y=4????(x>0)的图象上,
∴n=4????.
易得OM=1,BC=m-1,ON=4????,AC=4-4????,
∴????????????????=?????11=m-1,????????????????=4?4????4????=4?????44=m-1,
∴????????????????=????????????????.
又∵∠ACB=∠MON=90°,
∴△ACB∽△NOM.
?
答案
(3)若△ACB与△NOM的相似比为2,则m-1=2,
∴m=3,∴n=43,∴点B的坐标为(3,43).
设直线AB的函数表达式为y=tx+b,
将点A(1,4)、点B(3,43)代入y=tx+b,
得 4=????+????,43=3????+????,解得????=?43,????=163,
∴直线AB的函数表达式为y=-43x+163.
?
答案
1.D 【解析】 ∵点A的坐标为(2,9),点B的坐标为(6,3),∴当06时,反比例函数图象在一次函数图象的上方,∴当ax+b6.故选D.
?
一、选择题
1.[2019山东济南历城区二模]如图,反比例函数y=????????(x>0)的图象与一次函数y=ax+b的图象交于A(2,9),B(6,3)两点,若ax+bA.26
C.06
?
答案
2.C 【解析】 如图,连接OA,∵AB⊥x轴,∴OC∥AB,∴????△????????????=????△????????????,又∵????△????????????=12|k|=32,∴S△ABC=32.故选C.
?
2.如图,点A在反比例函数y=3????(x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为 ( )
A.3 B.2 C.32 D.1
?
答案
3.D 【解析】 ∵反比例函数的图象经过第一、三象限,∴m>0,故①错误;∵A(-1,h),B(2,k)在图象上,∴h<0,k>0,
∴h3.[2019河北石家庄期末]反比例函数y=????????的图象如图所示,给出以下结论:
①常数m<-2;
②若A(-1,h),B(2,k)在图象上,则h③y随x的增大而减小;
④若P(x,y)在图象上,则P'(-x,-y)也在图象上.
其中正确的是 ( )
A.①② B.③④ C.②③ D.②④
?
答案
4.D 【解析】 ∵点A(1,m)是射线y=65x(x≥0)上一点,∴m=65×1=65,∴A(1,65).∵点A在双曲线y=????????上,∴k=1×65=65,∴反比例函数的表达式为y=65????.∵四边形ABCD是正方形,∴AB=BC=65,∴OC=1+65=115.把x=115代入反比例函数y=65????,得y=611,
∴E(115,611).故选D.
?
4.如图,点A(1,m)是射线y=65x(x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=????????交CD边于点E,则点E的坐标是 ( )
A.(65,35) B.(115,511)
C.(165,516) D.(115,611)
?
答案
5.D 【解析】 如图,连接OA,OB,AB交y轴于点E.∵AB∥x轴,∴AB⊥y轴,∴????△????????????=12×|3|=32,S△OBE=12×|-2|=1,S△OAB=1+32=52, ∴?????????????????????= 2S△OAB=5.故选D.
?
5.如图,点A是反比例函数y=3????(x>0)的图象上任意一点,AB∥x轴交反比例函数y=-2????的图象于点B,以AB为边作?ABCD,其中点C,D在x轴上,则?????????????????????为 ( )?
A.2 B.3
C.4 D.5
?
答案
6.D 【解析】 如图,根据矩形的性质可得????矩形????????????????=????矩形????????????????.∵D(-4,1), ∴OH=4, OG=1,∴????矩形????????????????=OH·OG= 4. 设B(a,b),则OE=a,OF=-b,∴????矩形????????????????=OE·OF=-ab=4,又∵B(a,b)在反比例函数y=????????(k≠0,x>0)的图象上,∴k=ab=-4.故选D.
?
6.[2020辽宁朝阳二模]如图,在平面直角坐标系中,矩形ABCD的对角线AC经过坐标原点O,矩形的边分别平行于坐标轴,点B在反比例函数y=????????(k≠0,x>0)的图象上,点D的坐标为(-4,1),则k的值为 ( )?
A.54 B.-54
C.4 D.-4
?
答案
7.m>12 【解析】 ∵当x112.
?
二、填空题
7.已知点A(x1,y1),B(x2,y2)在反比例函数y=1?2????????的图象上,当x1?
答案
8.50 【解析】 设药物燃烧后y与x之间的关系式为y=????????(x>0),把点(10,6)代入,得6=????10,解得k=60,所以药物燃烧后y关于x的函数表达式为y=60????(x>0).当y=1.2时,由y=60????,得x=50,所以至少需要经过50分钟后,学生才可回到教室.
?
8.为预防传染病,某校定期对教室进行“药熏消毒”,已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与时间x(分)成正比例关系,燃烧后,y与x成反比例关系(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为
6 mg.研究表明,当每立方米空气中含药量低于1.2 mg时,对人体无毒害作用,那么从消毒开始,至少需要经过 分钟后,学生才能回到教室.?
答案
9.2 3 【解析】 如图,过点B作BC⊥y轴于点C,交OA于点D.∵正比例函数y1=k1x的图象与反比例函数y2=????2????(x>0)的图象相交于点A(3,2 3),∴2 3=3k1,2 3=????23,∴k1=2,k2=6, ∴正比例函数的表达式为y1=2x,反比例函数的表达式为y2=6????.∵点B是反比例函数图象上一点,它的横坐标是3,∴y2=63=2,∴B(3,2),∵BC⊥y轴,∴当y1=2时,x=1,∴D(1,2),∴BD=3-1=2, ∴????△????????????=????△????????????+????△????????????=12×2×(2 3-2)+12×2×2=2 3.
?
9.如图,正比例函数y1=k1x的图象与反比例函数y2=????2????(x>0)的图象相交于点A(3,2 3),点B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是 .?
?
答案
10.(3,2) 【解析】 ∵点A的坐标为(0,-1),AB∥x轴,反比例函数y=????????(k≠0)经过?ABCD的顶点B,∴点B的坐标为(-k,-1),
∴AB=CD=-k.设CD与y轴交于点E,∵CD经过点(0,2),∴点E(0,2),∴AE=2+1=3,∵?ABCD的面积是18,∴CD×AE=18,
∴-k×3=18,∴k=-6,∴AB=CD=6,y=-6????,∵CD经过点(0,2),令y=2,可得x=-3,∴点D的坐标为(-3,2),∴DE=3,又∵CD=6,
∴CE=6-3=3,∴C(3,2).
?
10.[2019河南南阳期中]如图,在平面直角坐标系中,反比例函数y=????????(k≠0)的图像经过?ABCD的顶点B,D,点A的坐标为(0,-1),AB∥x轴,CD经过点(0,2),?ABCD的面积是18,则点C的坐标是 .?
?
三、解答题
11.如图,?ABCD放置在平面直角坐标系中,点A,D的坐标分别为(-2,5),(0,1),点B(3,5)在反比例函数y=????????(k>0)的图象上.
(1)求反比例函数的表达式;
(2)求点C的坐标;
(3)将?ABCD沿x轴正方向平移10个单位长度后,判断点C能否落在函数y=????????(k>0)的图象上,并说明理由.
?
答案
11.【解析】 (1)把点B(3,5)代入y=????????(k>0),
得k=3×5=15,
∴反比例函数的表达式为y=15????.
(2)∵四边形ABCD为平行四边形,∴AB=CD,AB∥CD,
∵点A(-2,5),点B(3,5),
∴AB=3+2=5,∴CD=5,
又∵点D(0,1),∴点C坐标为(5,1).
(3)点C能落在函数y=????????(k>0)的图象上.理由如下:
把点C(5,1)沿x轴正方向平移10个单位长度后得到对应点的坐标为(15,1),
又∵当x=15时,y=15????=1,∴平移后,点C落在函数y=????????的图象上.
?
答案
12.【解析】 (1)观察图象,可知当x=7时,y=100.
当0≤x≤7时,设y关于x的函数表达式为y=kx+b,
将点(0,30),(7,100)代入,可得????=30,7????+????=100,解得????=10,????=30,
所以当0≤x≤7时,y关于x的函数表达式为y=10x+30.
?
12.[2019内蒙古鄂尔多斯中考]教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10 ℃,加热到100 ℃停止加热,水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系,直至水温降至30 ℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30 ℃时接通电源,水温y(℃)与时间x(min)的关系如图所示.
(1)分别写出水温上升和下降阶段y与x之间的函数关系式;
(2)怡萱同学想喝高于50 ℃的水,请问她最多需要等待多长时间?
答案
当x>7时,设y关于x的函数表达式为y=????????,
将点(7,100)代入,得100=????7,解得 a=700,
所以当x>7时,y关于x的函数表达式为y=700????.
在水温下降阶段,当y=30时,x=703,
所以y与x之间的函数关系式为y=10????+30(0≤????≤7),700????(7(2)将y=50代入y=10x+30,得x=2,
将y=50代入y=700????,得x=14,
因为14-2=12,703-12=343,
所以怡萱同学想喝高于50 ℃的水,她最多需要等待343 min.
?
答案
13.【解析】 (1)将A(1,m),B(n,1)两点的坐标分别代入反比例函数y2=3????(x>0),
可得m=3,n=3,
∴A(1,3),B(3,1).
把A(1,3),B(3,1)代入一次函数y1=kx+b,
可得3=????+????,1=3????+????,解得????=?1,????=4,
∴一次函数的表达式为y1=-x+4.
?
13.如图,在平面直角坐标中,点O是坐标原点,一次函数y1=kx+b与反比例函数y2=3????(x>0)的图象交于A(1,m),B(n,1)两点.
(1)求一次函数的表达式;
(2)根据图象写出当y1>y2时,x的取值范围;
(3)若P是y轴上一动点,求PA+PB的最小值.
?
答案
(2)观察题中的函数图象,发现:
当1∴当y1>y2时,x的取值范围是1(3)如图,作点A关于y轴的对称点C,连接BC交y轴于点P,则PA+PB的最小值等于BC的长,
过C作y轴的平行线,过B作x轴的平行线,两平行线交于点D,
在Rt△BCD中,BC=????????2+????????2=22+42=25,
∴PA+PB的最小值为25.
?
第六章 反比例函数中考模拟+真题
数学·九年级上册·北师
答案
1.C 【解析】 ∵反比例函数y=????????的图象经过点T(3,8),∴k=3×8=24,∴y=24????.将P(4,6),Q(3,-8),M(2,-12),N(12,48)分别代入y=24????,可得P(4,6),N(12,48)在该函数图象上,∴在该函数图象上的点有2个.故选C.
?
1.[2019江西南昌一模]如图,在平面直角坐标系中,反比例函数y=????????的图象经过点T,则点P(4,6),Q(3,-8),M(2,-12),N(12,48)中,在该函数图象上的有 ( )
A.4个 B.3个 C.2个 D.1个
?
答案
2.C 【解析】 S正方形AOBC-S正方形CDEF=AC2-CF2=(AC-CF)(AC+CF)=BD×AF,根据反比例函数中k的几何意义,可得BD×AF=8.故选C.
2.[2019广西贵港港南区一模]如图,四边形AOBC和四边形CDEF都是正方形,边OA在x轴上,边OB在y轴上,点D在边CB上,反比例函数y=-8????在第二象限的图象经过点E,则正方形AOBC和正方形CDEF的面积之差为 ( )
A.12 B.10 C.8 D.6
?
答案
3.A 【解析】 由题中图象,知k1<0,k2<0,∴k1k2>0,故①错误.∵点A(-2,m),B(1,n)在反比例函数y=????2????的图象上,∴-2m=
n,∴m+12n=0,故②正确.把A(-2,m),B(1,n)代入y=k1x+b,得?2????1+????=????,????1+????=????, 解得????1=?????????3,????=2????+????3,∵-2m=n,∴y=-mx-m,令x=0,得y=-m,令y=0,得x=-1,∴P(-1,0),Q(0,-m),∴OP=1,OQ=m,∴S△AOP=12m,S△BOQ=12m,∴S△AOP=S△BOQ,故③正确.由题中图象,知不等式k1x+b>????2????的解集是x<-2或0?
3.[2019广东揭阳惠来模拟]如图,已知直线y=k1x+b与x轴、y轴相交于P,Q两点,与y=????2????的图象相交于A(-2,m),B(1,n)两点,连接OA,OB,给出下列结论:①k1k2<0;②m+12n=0;③S△AOP=S△BOQ;④不等式k1x+b>????2????的解集是x<-2或0≤x<1.其中正确的是( )
A.②③ B.③④
C.①②③④ D.②③④
?
答案
4.3 【解析】 ∵点A在双曲线y=2????上,点B在双曲线y=5????上,且AB∥y轴,∴设A(m,2????),B(m,5????),∴AB=5?????2????=3????,
∴S?ABCD=3????·m=3.
?
4.[2019江苏无锡模拟]如图,点A在双曲线y=2????上,点B在双曲线y=5????上,且AB∥y轴,C,D在y轴上,若四边形ABCD为平行四边形,则它的面积为 .?
?
答案
5.725 【解析】 设AO的长度为x.因为正方形ADEF的面积为9,所以正方形ADEF的边长为3,所以E(x+3,3).因为BF=53AF,所以BF=53×3=5,所以B(x,8).因为点B、点E在反比例函数y=????????(x>0)的图象上,所以3(x+3)=8x,解得x=95,所以k=95×8=725.
?
5.[2020湖南邵阳模拟]如图,四边形OABC是矩形,四边形ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、点E在反比例函数y=????????(x>0)的图象上,正方形ADEF的面积为9,且BF=53AF,则k的值为? .?
?
答案
6.【解析】 (1)∵反比例函数y=????2????的图象经过点A(-1,2),
∴k2=-1×2=-2,∴反比例函数的表达式为y=-2????.
∵反比例函数y=-2????的图象经过点B(-4,n),
∴-4n=-2,解得n=12,∴点B的坐标为(-4,12).
∵一次函数y=k1x+b的图象经过点A(-1,2),B(-4,12),
?
6.[2019山东菏泽定陶区三模]如图,一次函数y=k1x+b的图象与反比例函数y=????2????(x<0)的图象相交于点A(-1,2),B(-4,n).
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.
?
答案
∴?????1+????=2,?4????1+????=12,解得????1=12,????=52,
∴一次函数的表达式为y=12x+52.
(2)设直线AB与x轴的交点为C,
在y=12x+52中,令y=0,解得x=-5,
∴点C的坐标为(-5,0),∴OC=5.
∴S△AOC=12OC×|yA|=12×5×2=5,
S△BOC=12OC×|yB|=12×5×12=54,
∴S△AOB=S△AOC-S△BOC=5-54=154.
?
答案
(3)如图,作点A关于x轴的对称点A',连接A'B,交x轴于点P,连接AP,此时△PAB的周长最小.
∵点A'和A(-1,2)关于x轴对称,
∴点A'的坐标为(-1,-2).
设直线A'B的函数表达式为y=ax+c,
则?????+????=?2,?4????+????=12,解得????=?56,????=?176,
∴直线A'B的函数表达式为y=-56x-176,
当y=0时,x=-175,
∴点P的坐标为(-175,0).
?
答案
1.B 【解析】 易得y1=4,y2=6,y3=-12.∵-12<4<6,∴y31.[2019天津中考]若点A(-3,y1),B(-2,y2),C(1,y3)都在反比例函数y=-12????的图象上,则y1,y2,y3的大小关系是 ( )
A.y2C.y1?
答案
2.D 【解析】 将点(1,-3)的坐标代入y=-3????,易知A说法正确;由k=-3<0,知双曲线位于第二、四象限,故B说法正确;由反比例函数的对称性,可知反比例函数y=-3????的图象关于直线y=x对称,故C说法正确;由k=-3<0,可知在每个象限内,y随x的增大而增大,故D说法错误.故选D.
?
2.[2019湖北天门中考]反比例函数y=-3????,下列说法不正确的是 ( )
A.图象经过点(1,-3)
B.图象位于第二、四象限
C.图象关于直线y=x对称
D.y随x的增大而增大
?
答案
3.A 【解析】 ∵200×0.50=250×0.40=400×0.25=500×0.20=1 000×0.10=100,∴y关于x的函数表达式为y=100????.
?
3.[2019浙江温州中考]验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表.根据表中数据,可得y关于x的函数表达式为 ( )
A.y=100???? B.y=????100
C.y=400???? D.y=????400
?
近视眼镜的度数y/度
200
250
400
500
1 000
镜片焦距x/米
0.50
0.40
0.25
0.20
0.10
答案
4.C 【解析】 如图,过点A作AE⊥CB,交CB的延长线于点E.∵A,B两点在反比例函数y=????????(x>0)的图象上,且纵坐标分别为4,2,∴A(????4,4),B(????2,2),∴AE=2,BE=????2?????4=????4.∵菱形ABCD的面积为2 5,∴BC×AE=2 5,∴BC=5,∴AB=BC=5,在Rt△AEB中,BE=????????2?????????2=1,∴????4=1,∴k=4.故选C.
?
4.[2019贵州遵义中考]如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y=????????(x>0)的图象经过A,B两点,若菱形ABCD的面积为25,则k的值为 ( )
A.2 B.3 C.4 D.6
?
答案
5.B 【解析】 如图,过点E作EF⊥AD,EG⊥x轴,垂足分别为点F,G.∵四边形ABCD是矩形,∴AE=DE,又∵EF⊥AD,∴AF=DF.在Rt△AOD中,OA=2,OD=4,∴AD=????????2+????????2=
2 5,∴DF=5.∵BD∥OA,∴∠OAD=∠FDE,又∵AOD=∠DFE=90°,∴△AOD∽△DFE,
∴????????????????=????????????????,即????????25=52,解得DE=5,∴S矩形DOGE=5×4=20,即|k|=20,又∵k>0,∴k=20.
?
5.[2019重庆中考A卷]如图,在平面直角坐标系中,矩形ABCD的顶点A,D分别在x轴、y轴上,对角线BD∥x轴,反比例函数y=????????(k>0,x>0)的图象经过矩形对角线的交点E.若点A(2,0),D(0,4),则k的值为 ( )
A.16 B.20 C.32 D.40
?
答案
6.0 【解析】 ∵点A(a,b)在双曲线y=????1????上,∴k1=ab.∵点A与点B关于x轴对称,∴点B的坐标为(a,-b),又∵点B在双曲线y=????2????上,∴k2=-ab,∴k1+k2=ab-ab=0.
?
6.[2019北京中考]在平面直角坐标系xOy中,点A(a,b)(a>0,b>0)在双曲线y=????1????上,点A关于x轴的对称点B在双曲线y=????2????上,则k1+k2的值为 .?
?
答案
7. 4 【解析】 由题意,得E,D在反比例函数的图象上,则S△OCE=12|k|,S△OAD=
12|k|.如图,过点M作MG⊥y轴于点G,作MN⊥x轴于点N,易知四边形ONMG为矩形,则S矩形ONMG=|k|,又∵M为矩形ABCO对角线的交点,则????矩形????????????????=4S矩形ONMG= 4|k|,由于函数图象在第一象限,∴k>0,则????2+????2+12=4k,∴k=4.
?
7.[2019四川眉山中考]如图,反比例函数y=????????(x>0)的图象经过矩形OABC对角线的交点M,分别交AB,BC于点D,E.若四边形ODBE的面积为12,则k的值为 .?
?
8.[2019河南中考]模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)建立函数模型
设矩形相邻两边的长分别为x,y.由矩形的面积为4,得xy=4,即y=4????;由周长为m,得2(x+y)=m,即y=-x+????2.满足要求的(x,y)应是两个函数图象在第 象限内交点的坐标.?
(2)画出函数图象
函数y=4????(x>0)的图象如图所示,而函数y=-x+????2的图象可由直线y=-x平移得到.请在同一直角坐标系中直接画出直线y=
-x.
?
(3)平移直线y=-x,观察函数图象
①当直线平移到与函数y=4????(x>0)的图象有唯一交点(2,2)时,周长m的值为 ;?
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
(4)得出结论
若能生产出面积为4的矩形模具,则周长m的取值范围为 .?
?
答案
8.【解析】 (1)一
(2)画直线y=-x如图所示:
(3)①8
②直线与函数y=4????(x>0)的图象交点还有两种情况:
当有0个交点时,周长m的取值范围是0当有2个交点时,周长m的取值范围是m>8.
(4)m≥8
数学·九年级上册·北师
专题 反比例函数的图象与性质
专项素养拓训
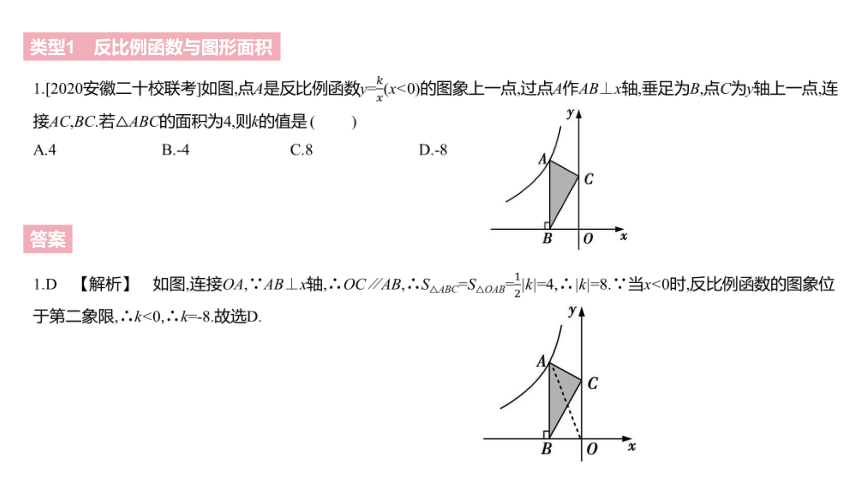
1.[2020安徽二十校联考]如图,点A是反比例函数y=????????(x<0)的图象上一点,过点A作AB⊥x轴,垂足为B,点C为y轴上一点,连接AC,BC.若△ABC的面积为4,则k的值是 ( )
A.4 B.-4 C.8 D.-8
?
答案
1.D 【解析】 如图,连接OA,∵AB⊥x轴,∴OC∥AB,∴S△ABC=S△OAB=12|k|=4,∴|k|=8.∵当x<0时,反比例函数的图象位于第二象限,∴k<0,∴k=-8.故选D.
?
类型1 反比例函数与图形面积
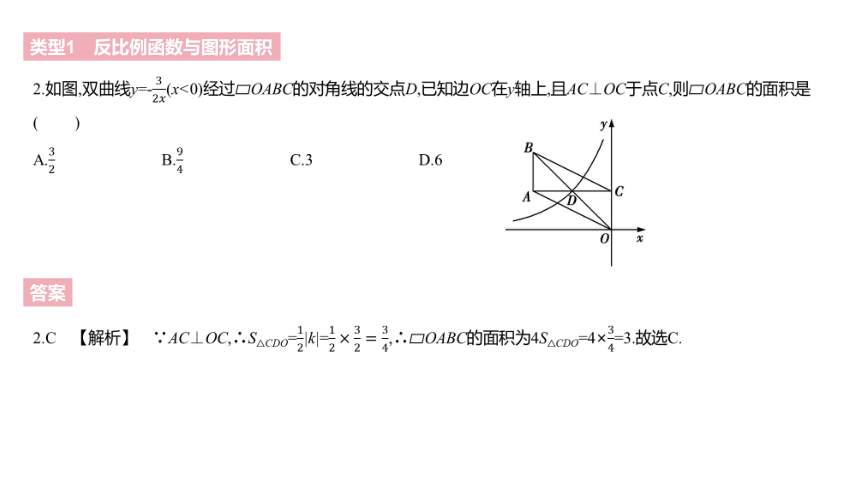
2.如图,双曲线y=-32????(x<0)经过?OABC的对角线的交点D,已知边OC在y轴上,且AC⊥OC于点C,则?OABC的面积是 ( )
A.32 B.94 C.3 D.6
?
答案
2.C 【解析】 ∵AC⊥OC,∴S△CDO=12|k|=12×32=34,∴?OABC的面积为4S△CDO=4×34=3.故选C.
?
类型1 反比例函数与图形面积
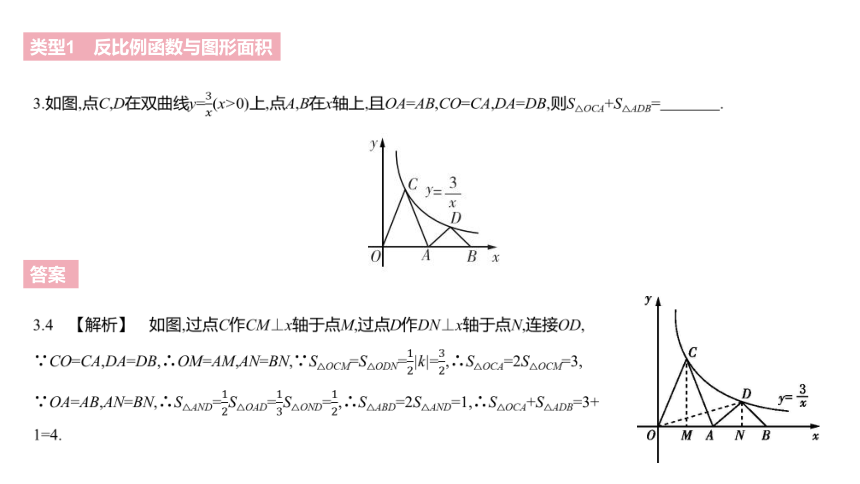
3.如图,点C,D在双曲线y=3????(x>0)上,点A,B在x轴上,且OA=AB,CO=CA,DA=DB,则S△OCA+S△ADB= .?
?
答案
3.4 【解析】 如图,过点C作CM⊥x轴于点M,过点D作DN⊥x轴于点N,连接OD,
∵CO=CA,DA=DB,∴OM=AM,AN=BN,∵S△OCM=S△ODN=12|k|=32,∴S△OCA=2S△OCM=3,
∵OA=AB,AN=BN,∴S△AND=12S△OAD=13S△OND=12,∴S△ABD=2S△AND=1,∴S△OCA+S△ADB=3+1=4.
?
类型1 反比例函数与图形面积
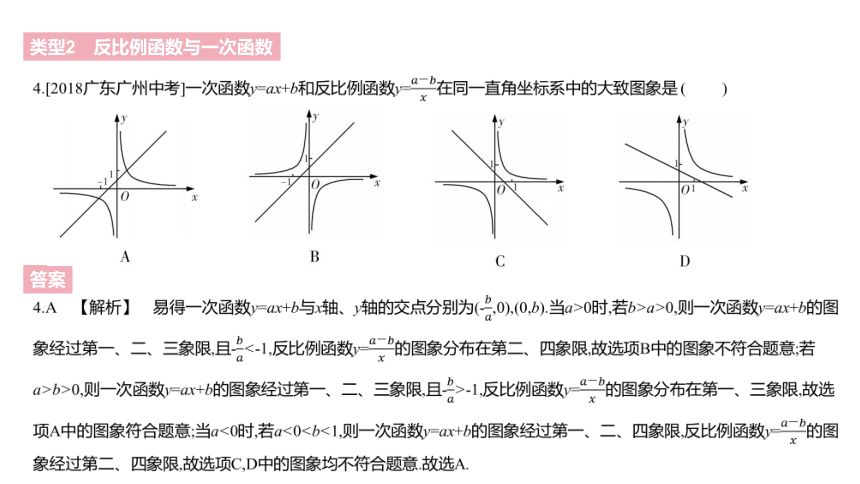
4.[2018广东广州中考]一次函数y=ax+b和反比例函数y=?????????????在同一直角坐标系中的大致图象是 ( )
?
答案
4.A 【解析】 易得一次函数y=ax+b与x轴、y轴的交点分别为(-????????,0),(0,b).当a>0时,若b>a>0,则一次函数y=ax+b的图象经过第一、二、三象限,且-????????<-1,反比例函数y=?????????????的图象分布在第二、四象限,故选项B中的图象不符合题意;若a>b>0,则一次函数y=ax+b的图象经过第一、二、三象限,且-????????>-1,反比例函数y=?????????????的图象分布在第一、三象限,故选项A中的图象符合题意;当a<0时,若a<0
类型2 反比例函数与一次函数
5.如图,已知一次函数y=kx-3(k≠0)的图象与x轴、y轴分别交于A,B两点,与反比例函数y=12????(x>0)交于C点,且AB=AC,则k的值为? .?
?
答案
5.32 【解析】 如图,过点C作CD⊥x轴于点D,则OB∥CD,∴∠ACD=∠ABO.∵AB=AC,∠CAD=∠BAO,∴△ACD≌
△ABO,∴CD=OB.由直线y=kx-3可知,点B的坐标为(0,-3),∴CD=OB=3.将y=3代入y=12????中,得x=4,∴C(4,3),再将点C(4,3)代入直线y=kx-3中,得k=32.
?
类型2 反比例函数与一次函数
6.[2018甘肃兰州中考]如图,在平面直角坐标系中,一次函数y1=ax+b的图象与反比例函数y2=????????的图象交于点A(1,2)和
B(-2,m).
(1)求一次函数和反比例函数的表达式;
(2)过点B作BE∥x轴,AD⊥BE于点D,点C是直线BE上一点,若AC=2CD,求点C的坐标.
?
类型2 反比例函数与一次函数
答案
6.【解析】 (1)∵点A在反比例函数y2=????????的图象上,
∴k=1×2=2,
故反比例函数的表达式为y2=2????.
∵点B在反比例函数y2=2????的图象上,
∴m=2?2=-1,
故点B的坐标为(-2,-1).
将点A,B的坐标分别代入一次函数的表达式,
得????+????=2,?2????+????=?1,解得????=1,????=1,
故一次函数的表达式为y1=x+1.
?
类型2 反比例函数与一次函数
答案
(2)易得点D的坐标为(1,-1).
设点C的坐标为(n,-1),
则AC=(?????1)2+32,CD=|n-1|.
由AC=2CD,可得AC2=4CD2,即(n-1)2+32=4(n-1)2,
解得n1=1+3,n2=1-3,
故点C的坐标为(1+3,-1)或(1-3,-1).
?
类型2 反比例函数与一次函数
类型3 反比例函数与不等式
7.已知A(-1,y1),B(2,y2)两点在双曲线y=3+2????????上,且y1>y2,则m的取值范围是 ( )
A.m<0 B.m>0
C.m>-32 D.m<-32
?
答案
7.D 【解析】 解法一 由题可知,点A,B位于第二、四象限或第一、三象限,∵-1<2,y1>y2,∴双曲线y=3+2????????位于第二、四象限,∴3+2m<0,即m<-32.故选D.
解法二 将点A(-1,y1),B(2,y2)代入y=3+2????????,得????1=?(3+2????),????2=3+2????2,由y1>y2可得-(3+2m)>3+2????2,解得m<-32.故选D.
?
类型3 反比例函数与不等式
8.[2019湖南湘西州中考]如图,一次函数y=kx+b的图象与反比例函数y=????????的图象在第一象限交于点A(3,2),与y轴的负半轴交于点B,且OB=4.
(1)求函数y=????????和y=kx+b的表达式;
(2)结合图象直接写出不等式组0?
答案
8.【解析】 (1)把点A(3,2)代入反比例函数y=????????,
可得m=3×2=6,
∴反比例函数的表达式为y=6????.
∵OB=4,∴B(0,-4),
把点A(3,2),B(0,-4)代入一次函数y=kx+b,
可得3????+????=2,????=?4,解得????=2,????=?4,
∴一次函数的表达式为y=2x-4.
(2)不等式组03.
?
类型2 反比例函数与一次函数
9.如图,直线y1=-x+4,y2=34x+b都与双曲线y=????????交于点A(1,m),这两条直线分别与x轴交于B,C两点,直线y1=-x+4与双曲线y=????????交另一点D(n,1).
(1)求y与x之间的函数关系式;
(2)写出当x>0时,不等式-x+4(3)若点P在x轴上,连接AP把△ABC的面积分成1∶3两部分,求此时点P的坐标.
?
答案
9.【解析】 (1)把A(1,m)代入y1=-x+4,得m=-1+4=3,
∴点A的坐标为(1,3).
把A(1,3)代入y=????????,得k=1×3=3,
∴y与x之间的函数关系式为y=3????.
?
类型3 反比例函数与不等式
答案
(2)把D(n,1)代入y=3????,得n=3.当x>0时,不等式-x+43.
(3)在y1=-x+4中,令y1=0,得x=4,
∴点B的坐标为(4,0).
把A(1,3)代入y2=34x+b,得3=34+b,
∴b=94,∴y2=34x+94,
令y2=0,得x=-3,∴点C的坐标为(-3,0),∴BC=7.
∵AP把△ABC的面积分成1∶3两部分,
∴CP=14BC=74或BP=14BC=74,
∴OP=3-74=54或OP=4-74=94,
∴此时点P的坐标为(-54,0)或(94,0).
?
类型3 反比例函数与不等式
10.工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料煅烧到800 ℃,然后停止煅烧进行锻造操作.停止煅烧后第8 min时,材料温度降为600 ℃,煅烧时,温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例关系(如图),已知该材料初始温度是32 ℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480 ℃时,需停止操作,那么锻造的操作时间有多长?
?
答案
10.【分析】 根据点A,B的坐标可求得线段AB所在直线的函数关系式,根据点C的坐标可求得锻造阶段的反比例函数关系式,需先求得锻造阶段的关系式才能确定点B的坐标,进而根据函数关系式分析、求解相关实际问题.
【解析】 (1)设锻造时的函数关系式为y=????????(k≠0),
则600=????8,∴k=4 800,
?
类型4 反比例函数在实际问题中的应用
答案
∴y=4?800????.
当y=800时,800=4?800????,解得x=6,
当y=32时,32=480????,解得x=150,
∴点B的坐标为(6,800),锻造时的函数关系式为y=4?800????(6
则????=32,6????+????=800,解得????=128,????=32,
∴煅烧时的函数关系式为y=128x+32(0≤x≤6).
(2)当x=480时,y=4?800480=10,10-6=4(min),
∴锻造的操作时间有4 min.
?
类型4 反比例函数在实际问题中的应用
11.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(h)变化的图象,其中BC段是双曲线y=????????的一部分.请根据图中信息解答下列问题.
(1)恒温系统在这天保持大棚内温度为18 ℃的时间有多少小时?
(2)求k的值.
(3)当x=16时,大棚内的温度为多少度?
?
类型4 反比例函数在实际问题中的应用
答案
11.【解析】 (1)观察题中图象可知,恒温系统在这天保持大棚内温度为18 ℃的时间为12-2=10(h).
(2)∵点B(12,18)在双曲线y=????????上,∴18=????12,
∴k=216.
(3)当x=16时,y=21616=13.5,
∴当x=16时,大棚内的温度为13.5 ℃.
?
类型4 反比例函数在实际问题中的应用
综合素养拓训
1.[函数与方程之间的转化]已知,直角三角形ABC如图所示放置,∠ABC=90°,AB=10,BC=5,反比例函数y=????????经过点C(m,3).
(1)求点A,B的坐标及m的值.
(2)求反比例函数及直线AB的表达式.
(3)将直线AB上下移动a个单位长度后,与反比例函数的图象只有唯一一个交点,求a的值.
?
答案
1.【解析】 (1)过点C作CE⊥x轴于点E,则CE=3,
∵BC=5,∴BE=52?32=4.
∵∠ABC=90°,∴∠ABO+∠EBC=90°,
又∵∠ABO+∠OAB=90°,∴∠OAB=∠EBC.
∵∠AOB=∠BEC,
∴△AOB∽△BEC,∴????????????????=????????????????,
∴10????????=53,解得BO=6,
∴AO=102?62=8,m=6+4=10,
∴A(0,8),B(6,0),m=10.
?
答案
(2)将C(10,3)代入反比例函数y=????????中,得3=????10,
解得k=30,即y=30????.
设直线AB的表达式为y=k1x+b,
将A(0,8),B(6,0)代入得????=8,0=6????1+????,
解得????1=?43,????=8,即y=-43x+8.
(3)直线AB上下平移a个单位长度后,得y=-43x+8+a,
∵平移后的直线与反比例函数y=30????的图象只有唯一一个交点,
∴方程30????=-43x+8+a,即4x2-3(8+a)x+90=0只有一个根,
∴Δ=9(8+a)2-4×4×90=0,解得a=±410-8.
?
2.[反比例函数与图形相似的结合]如图,已知反比例函数y=????????(x>0)的图象经过点A(1,4)、点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
(1)求该反比例函数的表达式.
(2)求证:△ACB∽△NOM.
(3)若△ACB与△NOM的相似比为2,求点B的坐标及直线AB的函数表达式.
?
答案
2.【解析】 (1) ∵反比例函数y=????????(x>0)的图象经过点A(1,4),
∴k=4×1=4,∴该反比例函数的表达式为y=4????(x>0).
(2)∵点B(m,n)在反比例函数y=4????(x>0)的图象上,
∴n=4????.
易得OM=1,BC=m-1,ON=4????,AC=4-4????,
∴????????????????=?????11=m-1,????????????????=4?4????4????=4?????44=m-1,
∴????????????????=????????????????.
又∵∠ACB=∠MON=90°,
∴△ACB∽△NOM.
?
答案
(3)若△ACB与△NOM的相似比为2,则m-1=2,
∴m=3,∴n=43,∴点B的坐标为(3,43).
设直线AB的函数表达式为y=tx+b,
将点A(1,4)、点B(3,43)代入y=tx+b,
得 4=????+????,43=3????+????,解得????=?43,????=163,
∴直线AB的函数表达式为y=-43x+163.
?
答案
1.D 【解析】 ∵点A的坐标为(2,9),点B的坐标为(6,3),∴当0
?
一、选择题
1.[2019山东济南历城区二模]如图,反比例函数y=????????(x>0)的图象与一次函数y=ax+b的图象交于A(2,9),B(6,3)两点,若ax+bA.2
C.0
?
答案
2.C 【解析】 如图,连接OA,∵AB⊥x轴,∴OC∥AB,∴????△????????????=????△????????????,又∵????△????????????=12|k|=32,∴S△ABC=32.故选C.
?
2.如图,点A在反比例函数y=3????(x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为 ( )
A.3 B.2 C.32 D.1
?
答案
3.D 【解析】 ∵反比例函数的图象经过第一、三象限,∴m>0,故①错误;∵A(-1,h),B(2,k)在图象上,∴h<0,k>0,
∴h
①常数m<-2;
②若A(-1,h),B(2,k)在图象上,则h
④若P(x,y)在图象上,则P'(-x,-y)也在图象上.
其中正确的是 ( )
A.①② B.③④ C.②③ D.②④
?
答案
4.D 【解析】 ∵点A(1,m)是射线y=65x(x≥0)上一点,∴m=65×1=65,∴A(1,65).∵点A在双曲线y=????????上,∴k=1×65=65,∴反比例函数的表达式为y=65????.∵四边形ABCD是正方形,∴AB=BC=65,∴OC=1+65=115.把x=115代入反比例函数y=65????,得y=611,
∴E(115,611).故选D.
?
4.如图,点A(1,m)是射线y=65x(x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=????????交CD边于点E,则点E的坐标是 ( )
A.(65,35) B.(115,511)
C.(165,516) D.(115,611)
?
答案
5.D 【解析】 如图,连接OA,OB,AB交y轴于点E.∵AB∥x轴,∴AB⊥y轴,∴????△????????????=12×|3|=32,S△OBE=12×|-2|=1,S△OAB=1+32=52, ∴?????????????????????= 2S△OAB=5.故选D.
?
5.如图,点A是反比例函数y=3????(x>0)的图象上任意一点,AB∥x轴交反比例函数y=-2????的图象于点B,以AB为边作?ABCD,其中点C,D在x轴上,则?????????????????????为 ( )?
A.2 B.3
C.4 D.5
?
答案
6.D 【解析】 如图,根据矩形的性质可得????矩形????????????????=????矩形????????????????.∵D(-4,1), ∴OH=4, OG=1,∴????矩形????????????????=OH·OG= 4. 设B(a,b),则OE=a,OF=-b,∴????矩形????????????????=OE·OF=-ab=4,又∵B(a,b)在反比例函数y=????????(k≠0,x>0)的图象上,∴k=ab=-4.故选D.
?
6.[2020辽宁朝阳二模]如图,在平面直角坐标系中,矩形ABCD的对角线AC经过坐标原点O,矩形的边分别平行于坐标轴,点B在反比例函数y=????????(k≠0,x>0)的图象上,点D的坐标为(-4,1),则k的值为 ( )?
A.54 B.-54
C.4 D.-4
?
答案
7.m>12 【解析】 ∵当x1
?
二、填空题
7.已知点A(x1,y1),B(x2,y2)在反比例函数y=1?2????????的图象上,当x1
答案
8.50 【解析】 设药物燃烧后y与x之间的关系式为y=????????(x>0),把点(10,6)代入,得6=????10,解得k=60,所以药物燃烧后y关于x的函数表达式为y=60????(x>0).当y=1.2时,由y=60????,得x=50,所以至少需要经过50分钟后,学生才可回到教室.
?
8.为预防传染病,某校定期对教室进行“药熏消毒”,已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与时间x(分)成正比例关系,燃烧后,y与x成反比例关系(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为
6 mg.研究表明,当每立方米空气中含药量低于1.2 mg时,对人体无毒害作用,那么从消毒开始,至少需要经过 分钟后,学生才能回到教室.?
答案
9.2 3 【解析】 如图,过点B作BC⊥y轴于点C,交OA于点D.∵正比例函数y1=k1x的图象与反比例函数y2=????2????(x>0)的图象相交于点A(3,2 3),∴2 3=3k1,2 3=????23,∴k1=2,k2=6, ∴正比例函数的表达式为y1=2x,反比例函数的表达式为y2=6????.∵点B是反比例函数图象上一点,它的横坐标是3,∴y2=63=2,∴B(3,2),∵BC⊥y轴,∴当y1=2时,x=1,∴D(1,2),∴BD=3-1=2, ∴????△????????????=????△????????????+????△????????????=12×2×(2 3-2)+12×2×2=2 3.
?
9.如图,正比例函数y1=k1x的图象与反比例函数y2=????2????(x>0)的图象相交于点A(3,2 3),点B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是 .?
?
答案
10.(3,2) 【解析】 ∵点A的坐标为(0,-1),AB∥x轴,反比例函数y=????????(k≠0)经过?ABCD的顶点B,∴点B的坐标为(-k,-1),
∴AB=CD=-k.设CD与y轴交于点E,∵CD经过点(0,2),∴点E(0,2),∴AE=2+1=3,∵?ABCD的面积是18,∴CD×AE=18,
∴-k×3=18,∴k=-6,∴AB=CD=6,y=-6????,∵CD经过点(0,2),令y=2,可得x=-3,∴点D的坐标为(-3,2),∴DE=3,又∵CD=6,
∴CE=6-3=3,∴C(3,2).
?
10.[2019河南南阳期中]如图,在平面直角坐标系中,反比例函数y=????????(k≠0)的图像经过?ABCD的顶点B,D,点A的坐标为(0,-1),AB∥x轴,CD经过点(0,2),?ABCD的面积是18,则点C的坐标是 .?
?
三、解答题
11.如图,?ABCD放置在平面直角坐标系中,点A,D的坐标分别为(-2,5),(0,1),点B(3,5)在反比例函数y=????????(k>0)的图象上.
(1)求反比例函数的表达式;
(2)求点C的坐标;
(3)将?ABCD沿x轴正方向平移10个单位长度后,判断点C能否落在函数y=????????(k>0)的图象上,并说明理由.
?
答案
11.【解析】 (1)把点B(3,5)代入y=????????(k>0),
得k=3×5=15,
∴反比例函数的表达式为y=15????.
(2)∵四边形ABCD为平行四边形,∴AB=CD,AB∥CD,
∵点A(-2,5),点B(3,5),
∴AB=3+2=5,∴CD=5,
又∵点D(0,1),∴点C坐标为(5,1).
(3)点C能落在函数y=????????(k>0)的图象上.理由如下:
把点C(5,1)沿x轴正方向平移10个单位长度后得到对应点的坐标为(15,1),
又∵当x=15时,y=15????=1,∴平移后,点C落在函数y=????????的图象上.
?
答案
12.【解析】 (1)观察图象,可知当x=7时,y=100.
当0≤x≤7时,设y关于x的函数表达式为y=kx+b,
将点(0,30),(7,100)代入,可得????=30,7????+????=100,解得????=10,????=30,
所以当0≤x≤7时,y关于x的函数表达式为y=10x+30.
?
12.[2019内蒙古鄂尔多斯中考]教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10 ℃,加热到100 ℃停止加热,水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系,直至水温降至30 ℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30 ℃时接通电源,水温y(℃)与时间x(min)的关系如图所示.
(1)分别写出水温上升和下降阶段y与x之间的函数关系式;
(2)怡萱同学想喝高于50 ℃的水,请问她最多需要等待多长时间?
答案
当x>7时,设y关于x的函数表达式为y=????????,
将点(7,100)代入,得100=????7,解得 a=700,
所以当x>7时,y关于x的函数表达式为y=700????.
在水温下降阶段,当y=30时,x=703,
所以y与x之间的函数关系式为y=10????+30(0≤????≤7),700????(7(2)将y=50代入y=10x+30,得x=2,
将y=50代入y=700????,得x=14,
因为14-2=12,703-12=343,
所以怡萱同学想喝高于50 ℃的水,她最多需要等待343 min.
?
答案
13.【解析】 (1)将A(1,m),B(n,1)两点的坐标分别代入反比例函数y2=3????(x>0),
可得m=3,n=3,
∴A(1,3),B(3,1).
把A(1,3),B(3,1)代入一次函数y1=kx+b,
可得3=????+????,1=3????+????,解得????=?1,????=4,
∴一次函数的表达式为y1=-x+4.
?
13.如图,在平面直角坐标中,点O是坐标原点,一次函数y1=kx+b与反比例函数y2=3????(x>0)的图象交于A(1,m),B(n,1)两点.
(1)求一次函数的表达式;
(2)根据图象写出当y1>y2时,x的取值范围;
(3)若P是y轴上一动点,求PA+PB的最小值.
?
答案
(2)观察题中的函数图象,发现:
当1
过C作y轴的平行线,过B作x轴的平行线,两平行线交于点D,
在Rt△BCD中,BC=????????2+????????2=22+42=25,
∴PA+PB的最小值为25.
?
第六章 反比例函数中考模拟+真题
数学·九年级上册·北师
答案
1.C 【解析】 ∵反比例函数y=????????的图象经过点T(3,8),∴k=3×8=24,∴y=24????.将P(4,6),Q(3,-8),M(2,-12),N(12,48)分别代入y=24????,可得P(4,6),N(12,48)在该函数图象上,∴在该函数图象上的点有2个.故选C.
?
1.[2019江西南昌一模]如图,在平面直角坐标系中,反比例函数y=????????的图象经过点T,则点P(4,6),Q(3,-8),M(2,-12),N(12,48)中,在该函数图象上的有 ( )
A.4个 B.3个 C.2个 D.1个
?
答案
2.C 【解析】 S正方形AOBC-S正方形CDEF=AC2-CF2=(AC-CF)(AC+CF)=BD×AF,根据反比例函数中k的几何意义,可得BD×AF=8.故选C.
2.[2019广西贵港港南区一模]如图,四边形AOBC和四边形CDEF都是正方形,边OA在x轴上,边OB在y轴上,点D在边CB上,反比例函数y=-8????在第二象限的图象经过点E,则正方形AOBC和正方形CDEF的面积之差为 ( )
A.12 B.10 C.8 D.6
?
答案
3.A 【解析】 由题中图象,知k1<0,k2<0,∴k1k2>0,故①错误.∵点A(-2,m),B(1,n)在反比例函数y=????2????的图象上,∴-2m=
n,∴m+12n=0,故②正确.把A(-2,m),B(1,n)代入y=k1x+b,得?2????1+????=????,????1+????=????, 解得????1=?????????3,????=2????+????3,∵-2m=n,∴y=-mx-m,令x=0,得y=-m,令y=0,得x=-1,∴P(-1,0),Q(0,-m),∴OP=1,OQ=m,∴S△AOP=12m,S△BOQ=12m,∴S△AOP=S△BOQ,故③正确.由题中图象,知不等式k1x+b>????2????的解集是x<-2或0
3.[2019广东揭阳惠来模拟]如图,已知直线y=k1x+b与x轴、y轴相交于P,Q两点,与y=????2????的图象相交于A(-2,m),B(1,n)两点,连接OA,OB,给出下列结论:①k1k2<0;②m+12n=0;③S△AOP=S△BOQ;④不等式k1x+b>????2????的解集是x<-2或0≤x<1.其中正确的是( )
A.②③ B.③④
C.①②③④ D.②③④
?
答案
4.3 【解析】 ∵点A在双曲线y=2????上,点B在双曲线y=5????上,且AB∥y轴,∴设A(m,2????),B(m,5????),∴AB=5?????2????=3????,
∴S?ABCD=3????·m=3.
?
4.[2019江苏无锡模拟]如图,点A在双曲线y=2????上,点B在双曲线y=5????上,且AB∥y轴,C,D在y轴上,若四边形ABCD为平行四边形,则它的面积为 .?
?
答案
5.725 【解析】 设AO的长度为x.因为正方形ADEF的面积为9,所以正方形ADEF的边长为3,所以E(x+3,3).因为BF=53AF,所以BF=53×3=5,所以B(x,8).因为点B、点E在反比例函数y=????????(x>0)的图象上,所以3(x+3)=8x,解得x=95,所以k=95×8=725.
?
5.[2020湖南邵阳模拟]如图,四边形OABC是矩形,四边形ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、点E在反比例函数y=????????(x>0)的图象上,正方形ADEF的面积为9,且BF=53AF,则k的值为? .?
?
答案
6.【解析】 (1)∵反比例函数y=????2????的图象经过点A(-1,2),
∴k2=-1×2=-2,∴反比例函数的表达式为y=-2????.
∵反比例函数y=-2????的图象经过点B(-4,n),
∴-4n=-2,解得n=12,∴点B的坐标为(-4,12).
∵一次函数y=k1x+b的图象经过点A(-1,2),B(-4,12),
?
6.[2019山东菏泽定陶区三模]如图,一次函数y=k1x+b的图象与反比例函数y=????2????(x<0)的图象相交于点A(-1,2),B(-4,n).
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.
?
答案
∴?????1+????=2,?4????1+????=12,解得????1=12,????=52,
∴一次函数的表达式为y=12x+52.
(2)设直线AB与x轴的交点为C,
在y=12x+52中,令y=0,解得x=-5,
∴点C的坐标为(-5,0),∴OC=5.
∴S△AOC=12OC×|yA|=12×5×2=5,
S△BOC=12OC×|yB|=12×5×12=54,
∴S△AOB=S△AOC-S△BOC=5-54=154.
?
答案
(3)如图,作点A关于x轴的对称点A',连接A'B,交x轴于点P,连接AP,此时△PAB的周长最小.
∵点A'和A(-1,2)关于x轴对称,
∴点A'的坐标为(-1,-2).
设直线A'B的函数表达式为y=ax+c,
则?????+????=?2,?4????+????=12,解得????=?56,????=?176,
∴直线A'B的函数表达式为y=-56x-176,
当y=0时,x=-175,
∴点P的坐标为(-175,0).
?
答案
1.B 【解析】 易得y1=4,y2=6,y3=-12.∵-12<4<6,∴y3
A.y2
答案
2.D 【解析】 将点(1,-3)的坐标代入y=-3????,易知A说法正确;由k=-3<0,知双曲线位于第二、四象限,故B说法正确;由反比例函数的对称性,可知反比例函数y=-3????的图象关于直线y=x对称,故C说法正确;由k=-3<0,可知在每个象限内,y随x的增大而增大,故D说法错误.故选D.
?
2.[2019湖北天门中考]反比例函数y=-3????,下列说法不正确的是 ( )
A.图象经过点(1,-3)
B.图象位于第二、四象限
C.图象关于直线y=x对称
D.y随x的增大而增大
?
答案
3.A 【解析】 ∵200×0.50=250×0.40=400×0.25=500×0.20=1 000×0.10=100,∴y关于x的函数表达式为y=100????.
?
3.[2019浙江温州中考]验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表.根据表中数据,可得y关于x的函数表达式为 ( )
A.y=100???? B.y=????100
C.y=400???? D.y=????400
?
近视眼镜的度数y/度
200
250
400
500
1 000
镜片焦距x/米
0.50
0.40
0.25
0.20
0.10
答案
4.C 【解析】 如图,过点A作AE⊥CB,交CB的延长线于点E.∵A,B两点在反比例函数y=????????(x>0)的图象上,且纵坐标分别为4,2,∴A(????4,4),B(????2,2),∴AE=2,BE=????2?????4=????4.∵菱形ABCD的面积为2 5,∴BC×AE=2 5,∴BC=5,∴AB=BC=5,在Rt△AEB中,BE=????????2?????????2=1,∴????4=1,∴k=4.故选C.
?
4.[2019贵州遵义中考]如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y=????????(x>0)的图象经过A,B两点,若菱形ABCD的面积为25,则k的值为 ( )
A.2 B.3 C.4 D.6
?
答案
5.B 【解析】 如图,过点E作EF⊥AD,EG⊥x轴,垂足分别为点F,G.∵四边形ABCD是矩形,∴AE=DE,又∵EF⊥AD,∴AF=DF.在Rt△AOD中,OA=2,OD=4,∴AD=????????2+????????2=
2 5,∴DF=5.∵BD∥OA,∴∠OAD=∠FDE,又∵AOD=∠DFE=90°,∴△AOD∽△DFE,
∴????????????????=????????????????,即????????25=52,解得DE=5,∴S矩形DOGE=5×4=20,即|k|=20,又∵k>0,∴k=20.
?
5.[2019重庆中考A卷]如图,在平面直角坐标系中,矩形ABCD的顶点A,D分别在x轴、y轴上,对角线BD∥x轴,反比例函数y=????????(k>0,x>0)的图象经过矩形对角线的交点E.若点A(2,0),D(0,4),则k的值为 ( )
A.16 B.20 C.32 D.40
?
答案
6.0 【解析】 ∵点A(a,b)在双曲线y=????1????上,∴k1=ab.∵点A与点B关于x轴对称,∴点B的坐标为(a,-b),又∵点B在双曲线y=????2????上,∴k2=-ab,∴k1+k2=ab-ab=0.
?
6.[2019北京中考]在平面直角坐标系xOy中,点A(a,b)(a>0,b>0)在双曲线y=????1????上,点A关于x轴的对称点B在双曲线y=????2????上,则k1+k2的值为 .?
?
答案
7. 4 【解析】 由题意,得E,D在反比例函数的图象上,则S△OCE=12|k|,S△OAD=
12|k|.如图,过点M作MG⊥y轴于点G,作MN⊥x轴于点N,易知四边形ONMG为矩形,则S矩形ONMG=|k|,又∵M为矩形ABCO对角线的交点,则????矩形????????????????=4S矩形ONMG= 4|k|,由于函数图象在第一象限,∴k>0,则????2+????2+12=4k,∴k=4.
?
7.[2019四川眉山中考]如图,反比例函数y=????????(x>0)的图象经过矩形OABC对角线的交点M,分别交AB,BC于点D,E.若四边形ODBE的面积为12,则k的值为 .?
?
8.[2019河南中考]模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)建立函数模型
设矩形相邻两边的长分别为x,y.由矩形的面积为4,得xy=4,即y=4????;由周长为m,得2(x+y)=m,即y=-x+????2.满足要求的(x,y)应是两个函数图象在第 象限内交点的坐标.?
(2)画出函数图象
函数y=4????(x>0)的图象如图所示,而函数y=-x+????2的图象可由直线y=-x平移得到.请在同一直角坐标系中直接画出直线y=
-x.
?
(3)平移直线y=-x,观察函数图象
①当直线平移到与函数y=4????(x>0)的图象有唯一交点(2,2)时,周长m的值为 ;?
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
(4)得出结论
若能生产出面积为4的矩形模具,则周长m的取值范围为 .?
?
答案
8.【解析】 (1)一
(2)画直线y=-x如图所示:
(3)①8
②直线与函数y=4????(x>0)的图象交点还有两种情况:
当有0个交点时,周长m的取值范围是0
(4)m≥8
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
