北师大版九年级上册数学第五章 投影与视图素养拓展+中考真题课件(42张PPT)
文档属性
| 名称 | 北师大版九年级上册数学第五章 投影与视图素养拓展+中考真题课件(42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 00:00:00 | ||
图片预览







文档简介
第五章 投影与视图
数学·九年级上册·北师
专题1 平行投影的实际应用
专项素养拓训
1.兴趣小组的同学要测量树的高度,在阳光下,一名同学测得一根长为1 m的竹竿的影长为0.4 m,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,还有一部分落在教学楼的第一级台阶上,如图所示.已知台阶的高度为0.3 m,测得树在地面的影长为4.4 m,落在台阶上的影长为0.2 m,则树高为 .?
答案
1.11.8 m 【解析】 设树高为x m,根据同一时刻物高与影长成正比,得?????0.34.4+0.2=10.4,解得x=11.8,故树高为11.8 m.
?
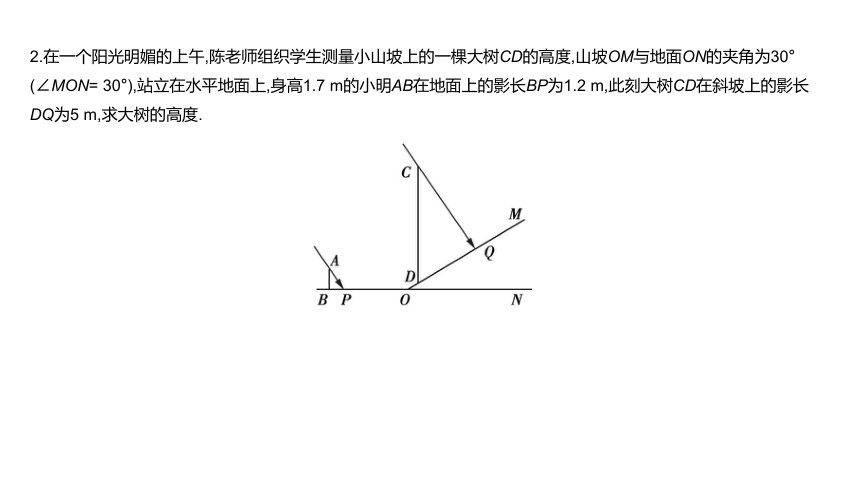
2.在一个阳光明媚的上午,陈老师组织学生测量小山坡上的一棵大树CD的高度,山坡OM与地面ON的夹角为30° (∠MON= 30°),站立在水平地面上,身高1.7 m的小明AB在地面上的影长BP为1.2 m,此刻大树CD在斜坡上的影长DQ为5 m,求大树的高度.
答案
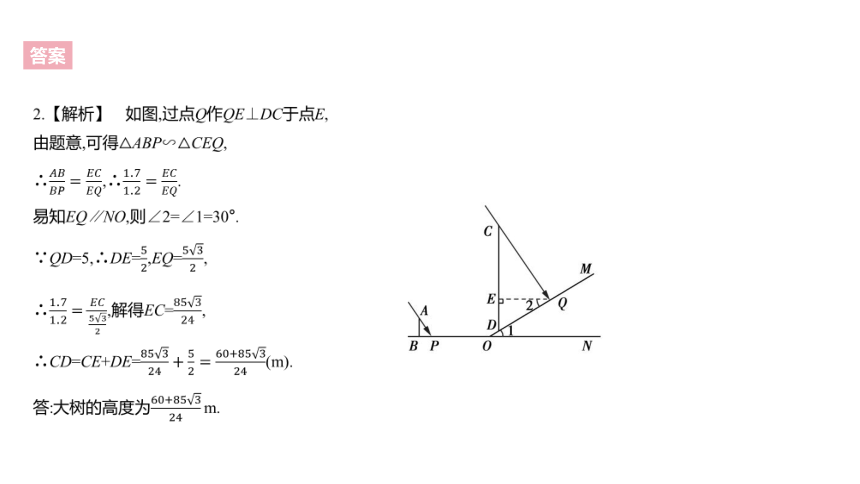
2.【解析】 如图,过点Q作QE⊥DC于点E,
由题意,可得△ABP∽△CEQ,
∴????????????????=????????????????,∴1.71.2=????????????????.
易知EQ∥NO,则∠2=∠1=30°.
∵QD=5,∴DE=52,EQ=532,
∴1.71.2=????????532,解得EC=85324,
∴CD=CE+DE=85324+52=60+85324(m).
答:大树的高度为60+85324 m.
?
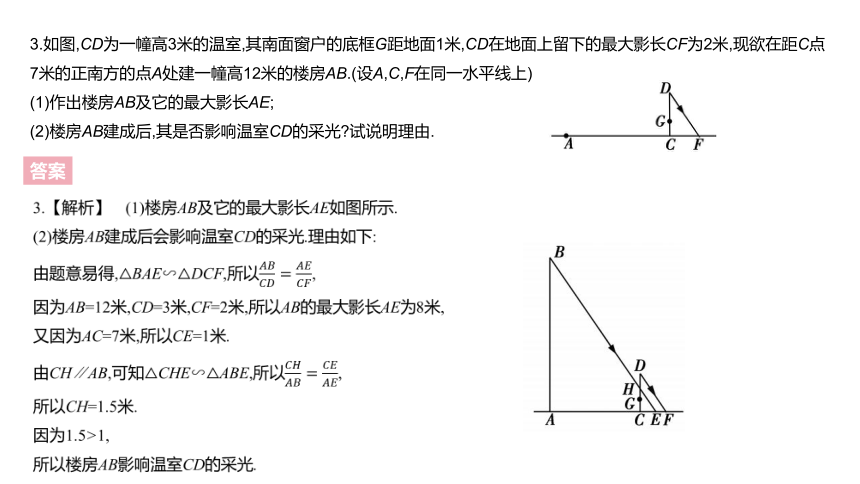
3.如图,CD为一幢高3米的温室,其南面窗户的底框G距地面1米,CD在地面上留下的最大影长CF为2米,现欲在距C点7米的正南方的点A处建一幢高12米的楼房AB.(设A,C,F在同一水平线上)
(1)作出楼房AB及它的最大影长AE;
(2)楼房AB建成后,其是否影响温室CD的采光?试说明理由.
答案
3.【解析】 (1)楼房AB及它的最大影长AE如图所示.
(2)楼房AB建成后会影响温室CD的采光.理由如下:
由题意易得,△BAE∽△DCF,所以????????????????=????????????????,
因为AB=12米,CD=3米,CF=2米,所以AB的最大影长AE为8米,
又因为AC=7米,所以CE=1米.
由CH∥AB,可知△CHE∽△ABE,所以????????????????=????????????????,
所以CH=1.5米.
因为1.5>1,
所以楼房AB影响温室CD的采光.
?
专题2 几何体的三种视图及有关的计算
专项素养拓训
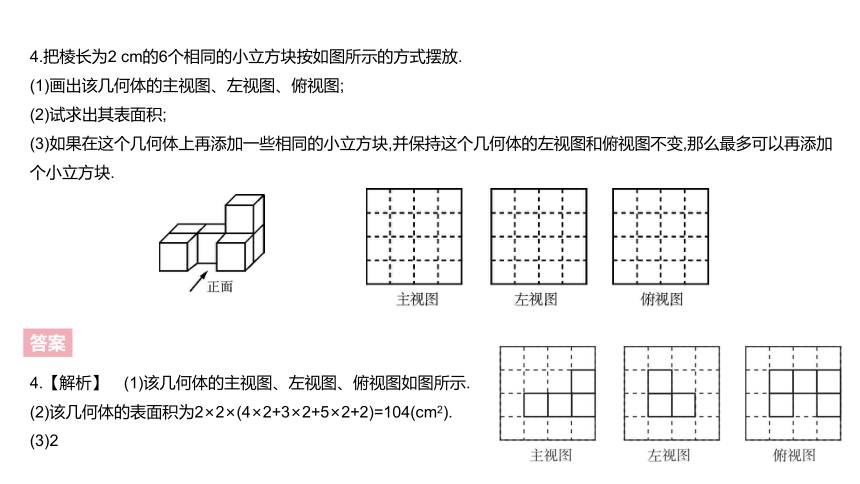
4.把棱长为2 cm的6个相同的小立方块按如图所示的方式摆放.
(1)画出该几何体的主视图、左视图、俯视图;
(2)试求出其表面积;
(3)如果在这个几何体上再添加一些相同的小立方块,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加 个小立方块.?
答案
4.【解析】 (1)该几何体的主视图、左视图、俯视图如图所示.
(2)该几何体的表面积为2×2×(4×2+3×2+5×2+2)=104(cm2).
(3)2
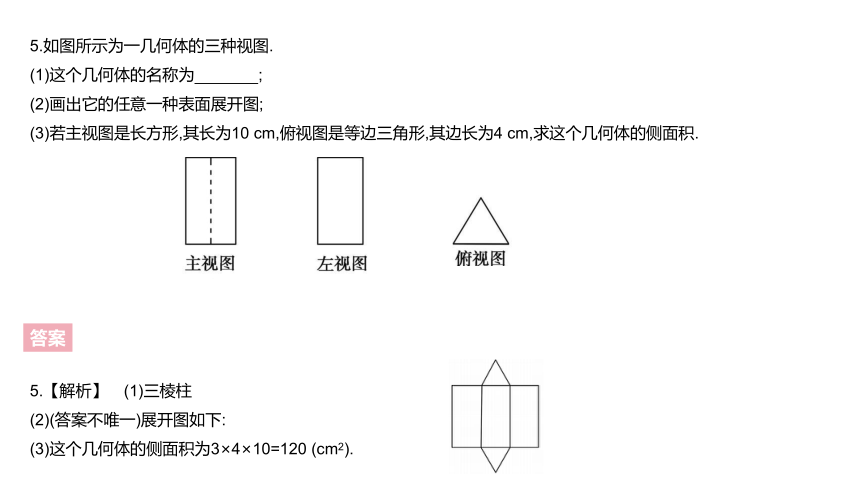
5.如图所示为一几何体的三种视图.
(1)这个几何体的名称为 ;?
(2)画出它的任意一种表面展开图;
(3)若主视图是长方形,其长为10 cm,俯视图是等边三角形,其边长为4 cm,求这个几何体的侧面积.
答案
5.【解析】 (1)三棱柱
(2)(答案不唯一)展开图如下:
(3)这个几何体的侧面积为3×4×10=120 (cm2).
6.(1)如图1是一个组合体,图2是它的两种视图,在横线上填写出两种视图的名称;
(2)根据两种视图中的数据(单位:cm),计算这个组合体的表面积.(π取3.14)
答案
6.【解析】 (1)主 俯
(2)这个组合体的表面积为 2×(8×5+8×2+5×2)+4×π×6≈2×66+4×3.14×6=207.36(cm2).
综合素养拓训
本章通过投影引出物体的三种视图,与高中数学中的三视图联系紧密,意在培养几何直观和空间想象能力,同时在核心素养渗透方面也体现出相应特色.第1题以实际问题为背景,在实际问题中从教学的视角发现问题、提出问题,最终解决问题;第3题和第4题体现了核心素养中的直观想象,构建数学问题的直观模型,探索解决问题的思路,进而形成数学直观,在具体的情境中感悟事物的本质.
1.[三种视图的实际应用]如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是 ( )
答案
1.B 【解析】 因为圆柱的俯视图是一个圆,可以堵住圆形空洞,而它的主视图及左视图都是一个长方形,可以堵住方形的空洞.故选B.
2.[三种视图之间的关系]一个三棱柱的三种视图如图所示,已知主视图、左视图、俯视图的面积分别为12,4,3,则左视图中MN的长为? .?
答案
2.2 【解析】 由题中主视图和左视图的面积可知,俯视图中两直角边长之比为3∶1,设较短直角边长为x,则较长直角边长为3x,因为俯视图的面积为3,所以12x·3x=3,解得x=2或-2(不合题意,舍去),所以MN=2.
?
3.[根据三种视图搭建正方体]如图所示是由一些小立方块搭成的几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,搭成一个大正方体,至少还需要 个小立方块.?
答案
3.54 【解析】 由俯视图得最底层有7个小立方块,结合主视图和左视图得第二层有2个小立方块,第三层有1个小立方块,那么共有小立方块7+2+1=10(个).若搭成大正方体,共需小立方块4×4×4=64(个),所以还需要小立方块64-10=
54(个).
4.[投影问题中的规律探究]学习投影后,小刚、小雯利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6 m的小刚(AB)的影子BC的长是3 m,而小雯(EH)刚好在路灯灯泡的正下方H点,并测得HB=6 m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH;
(3)如果小刚沿BH方向向小雯(点H)走去,当小刚走到BH的中点B1处时,求其影子B1C1的长;当小刚继续走剩下路程的13到B2处时,求其影子B2C2的长;当小刚继续走剩下路程的14到B3处时??按此规律继续走下去,当小刚走剩下路程的1????+1到Bn处时,求其影子BnCn的长.
?
答案
4.【解析】 (1)如图1所示.
(2)由题意,得△ABC∽△GHC.
∴????????????????=????????????????,∴1.6????????=36+3,∴GH=4.8 m.
(3)如图2,由题意,得△A1B1C1∽△GHC1.
∴????1????1????????=????1????1????????1,
设B1C1的长为x m,则1.64.8=????????+3,
∴x=32,即B1C1=32 m.
同理1.64.8=????2????2????2????2+2,∴B2C2=1 m,
∴1.64.8=????????????????????????????????+1????+1×6,∴BnCn=3????+1 m.
?
答案
1.C 【解析】 从左面看该零部件,得到的平面图形是一个长方形且内部含有一个圆,结合选项,知选C.
一、选择题
1.[2019广西柳州中考]如图,这是一个机械零部件,该零部件的左视图是 ( )
答案
2.D
2.[2020河南平顶山期末]在阳光的照射下,一块三角板的投影不会是 ( )
A.线段
B.与原三角形全等的三角形
C.变形的三角形
D.点
答案
3.A 【解析】 “阳马”的俯视图是一个矩形且有一条实对角线,结合选项,知选A.
3.[2019安徽阜阳六校联考]在我国古代数学名著《九章算术》中,将底面为矩形、一条侧棱垂直于底面的四棱锥称之为“阳马”(如图).“阳马”的俯视图是 ( )
答案
4.A 【解析】 主视图是三角形,俯视图是两个矩形,左视图是一个矩形.故选A.
4.[2019江苏常州一模]如图所示的正三棱柱,它的主视图、俯视图、左视图的顺序是 ( )
A.①③② B.②①③ C.③①② D.①②③
答案
5.C
5.将一个棱长为3 cm的大立方体挖去一个棱长为1 cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是 ( )
答案
6.A 【解析】 由BE∥AD,易知△BCE∽△ACD,∴????????????????=????????????????,即11+????????=1.21.2+1.8,∴AB=1.5 m.故选A.
?
6.如图,某一时刻阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8 m,窗户下檐到地面的距离BC=1 m,
EC=1.2 m,那么窗户的高AB为( )
A.1.5 m B.1.6 m
C.1.86 m D.2.16 m
答案
7.C 【解析】 结合主视图,俯视图,左视图,可知底层有5个小立方块,第二层最多有5个小立方块,第三层有1个小立方块,所以搭成这个几何体所用的小立方块的数目最多有11个.故选C.
7.由相同的小立方块组成的几何体的三视图如图所示,则该几何体中小立方块的数目最多为 ( )
?
A.7个 B.9个 C.11个 D.13个
答案
8.D 【解析】 由这个几何体的三视图可知,这个几何体是底面半径为2、高为4的圆柱体的一半,其表面积为π×22+
4×2π+4×4=16+12π.故选D.
8.[2018山东济宁中考]一个几何体的三视图如图所示,则该几何体的表面积是 ( )?
A.24+2π
B.16+4π
C.16+8π
D.16+12π
答案
9.5 【解析】 因为主视图中线段AB=a cm,所以该三棱锥的棱长为a cm,在主视图的三角形中只有底边长为a cm,在左视图的三角形中只有左上方边长为a cm,在俯视图中大三角形的三条边均为a cm,所以三种视图中长度为a cm的线段有5条.
二、填空题
9.[2020四川资阳一诊]图1是一个棱长均相等的三棱锥,它的三种视图如图2所示,若AB=a cm,则在这三种视图中,边长为a cm的线段有 条.?
答案
10.0.81π 【解析】 如图,O,E,F三点共线,OE⊥EB,OF⊥FD,OE=OF-EF=3-1=2(m).易知△OEB∽△OFD,∴????????????????=????????????????,即23=0.6????????,∴FD=0.9 m,∴地面上阴影部分的面积为πFD2=π×0.92=0.81π(m2).
?
10.圆桌正上方的灯泡(看作一个点)发出的光线照射在桌面上后,在地面上形成阴影(圆形)的示意图如图所示.已知桌面的直径为1.2 m,桌面距地面1 m,灯泡距地面3 m,则地面上阴影部分的面积是 m2.(用含π的式子表示)?
答案
11.3或5 【解析】 若要使主视图和原几何体的主视图相同,则可取走的小正方体的序号是3或4或5或7;若要使左视图和原几何体的左视图相同,则可取走的小正方体的序号是1或3或5.故可取走的小正方体的序号是3或5.
11.[2019山东青岛模拟]如图是用8个大小相同的小正方体搭成的几何体,仅在该几何体中取走一个小正方体,使得到的新几何体同时满足两个要求:(1)主视图和原几何体的主视图相同;(2)左视图和原几何体的左视图相同.在不改变其他小正方体位置的前提下,可取走的小正方体的序号是 .?
答案
12.【解析】 (1)主视图和左视图如图所示.?
(2)32
(3)1
三、解答题
12.[2019黑龙江绥化模拟]由一些大小相同、棱长为1的小正方体组成的几何体的俯视图如图所示,小正方形中的数字表示该位置上小正方体的个数.
?
(1)请画出该几何体的主视图和左视图;
(2)若要给这个几何体表面喷上颜色(底面不喷色),则需要喷色的面积为 ;?
(3)在不改变主视图和俯视图的情况下,最多可再添加 个小正方体.?
答案
13.【解析】 如图,设墙上的影高CD落在地面上时的长度为x m,树高为h m.
∵某一时刻测得高为1 m的竹竿的影长为0.9 m,墙上的影高CD为1.2 m,
∴10.9=1.2????,∴x=1.08,
∴树的影长为1.08+2.7=3.78(m),
∴10.9=h3.78,∴h=4.2.
答:他测得的树高为4.2米.
?
13.如图,一位同学想利用树影测量树高(AB),他在某一时刻测得高为1 m的竹竿的影长为0.9 m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD),他先测得留在墙上的影高(CD)为1.2 m,又测得地面部分的影长(BC)为2.7 m,他测得的树高应为多少米?
14.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处.小明测得窗户距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
答案
14.【解析】 如图,连接CD.
∵DO⊥BF,∴∠DOE=90°.
∵OD=0.8 m,OE=0.8 m,
∴∠DEB=45°.
∵AB⊥BF,∴∠BAE=45°,∴AB=BE.
设AB=BE=x m,
∵AB⊥BF,CO⊥BF,∴AB∥CO,
易得△ABF∽△COF,∴????????????????=????????????????,
????????+(3?0.8)=1.2+0.83,解得x=4.4.
经检验,x=4.4是原方程的解,且符合题意.
答:围墙AB的高度是4.4 m.
?
第五章 投影与视图中考真题
数学·九年级上册·北师
答案
1.A
1.[2019江西中考]如图是手提水果篮抽象的几何体,以箭头所指的方向为主视图方向,则它的俯视图为 ( )
答案
2.B
2.[2019江苏扬州中考]如图所示物体的左视图是 ( )
答案
3.B 【解析】 由已知三视图均为边长相等的正方形,得该几何体是正方体.故选B.
3.[2019广西贺州中考]如图是某几何体的三视图,则该几何体是 ( )?
A.长方体 B.正方体 C.三棱柱 D.圆柱
答案
4.A 【解析】 因为S主=x2+2x=x(x+2),S左=x2+x=x(x+1),所以俯视图的长为x+2,宽为x+1,所以S俯=(x+2)(x+1)=x2+3x+2.故选A.
4.[2019河北中考]图2是图1中长方体的三视图,若用S表示面积,且S主=x2+2x,S左=x2+x,则S俯= ( )?
A.x2+3x+2
B.x2+2
C.x2+2x+1
D.2x2+3x
5.[2019河南中考]如图1是由大小相同的小正方体搭成的几何体,将上层的小正方体平移后得到图2.关于平移前后几何体的三视图,下列说法正确的是 ( )
A.主视图相同
B.左视图相同
C.俯视图相同
D.三种视图都不相同
答案
5.C 【解析】 题图1的三视图如图1所示,题图2的三视图如图2所示,所以平移前后几何体的俯视图相同.故选C.
答案
6.B 【解析】 由三视图可知圆柱的底面直径为4,高为6,∴底面半径为2,∴V=22×6×π=24π.故选B.
6.[2019内蒙古包头中考]一个圆柱体的三视图如图所示,若其俯视图为圆,则这个圆柱体的体积为 ( )
A.24
B.24π
C.96
D.96π
答案
7.B 【解析】 由俯视图,可得下面一层有5个正方体,由主视图,可得上面一层最多有4个正方体,所以该组合体中正方体的个数最多是9.故选B.
7.[2019四川宜宾中考]已知一个组合体是由几个相同的正方体叠合在一起组成,该组合体的主视图与俯视图如图所示,则该组合体中正方体的个数最多是 ( )
A.10 B.9
C.8 D.7
8.[2018山东青岛中考]一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有 种.?
答案
8.10 【解析】 由题意知俯视图由9个正方形组成,由主视图和左视图知:①第一行第一列的位置一定是4,第二行第三列的位置一定是3;②一定有2个2,其余有5个1;③最后一行至少有一个2,中间一列至少有一个2.根据2的排列不同,这个几何体的搭法共有10种,如下图所示.
数学·九年级上册·北师
专题1 平行投影的实际应用
专项素养拓训
1.兴趣小组的同学要测量树的高度,在阳光下,一名同学测得一根长为1 m的竹竿的影长为0.4 m,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,还有一部分落在教学楼的第一级台阶上,如图所示.已知台阶的高度为0.3 m,测得树在地面的影长为4.4 m,落在台阶上的影长为0.2 m,则树高为 .?
答案
1.11.8 m 【解析】 设树高为x m,根据同一时刻物高与影长成正比,得?????0.34.4+0.2=10.4,解得x=11.8,故树高为11.8 m.
?
2.在一个阳光明媚的上午,陈老师组织学生测量小山坡上的一棵大树CD的高度,山坡OM与地面ON的夹角为30° (∠MON= 30°),站立在水平地面上,身高1.7 m的小明AB在地面上的影长BP为1.2 m,此刻大树CD在斜坡上的影长DQ为5 m,求大树的高度.
答案
2.【解析】 如图,过点Q作QE⊥DC于点E,
由题意,可得△ABP∽△CEQ,
∴????????????????=????????????????,∴1.71.2=????????????????.
易知EQ∥NO,则∠2=∠1=30°.
∵QD=5,∴DE=52,EQ=532,
∴1.71.2=????????532,解得EC=85324,
∴CD=CE+DE=85324+52=60+85324(m).
答:大树的高度为60+85324 m.
?
3.如图,CD为一幢高3米的温室,其南面窗户的底框G距地面1米,CD在地面上留下的最大影长CF为2米,现欲在距C点7米的正南方的点A处建一幢高12米的楼房AB.(设A,C,F在同一水平线上)
(1)作出楼房AB及它的最大影长AE;
(2)楼房AB建成后,其是否影响温室CD的采光?试说明理由.
答案
3.【解析】 (1)楼房AB及它的最大影长AE如图所示.
(2)楼房AB建成后会影响温室CD的采光.理由如下:
由题意易得,△BAE∽△DCF,所以????????????????=????????????????,
因为AB=12米,CD=3米,CF=2米,所以AB的最大影长AE为8米,
又因为AC=7米,所以CE=1米.
由CH∥AB,可知△CHE∽△ABE,所以????????????????=????????????????,
所以CH=1.5米.
因为1.5>1,
所以楼房AB影响温室CD的采光.
?
专题2 几何体的三种视图及有关的计算
专项素养拓训
4.把棱长为2 cm的6个相同的小立方块按如图所示的方式摆放.
(1)画出该几何体的主视图、左视图、俯视图;
(2)试求出其表面积;
(3)如果在这个几何体上再添加一些相同的小立方块,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加 个小立方块.?
答案
4.【解析】 (1)该几何体的主视图、左视图、俯视图如图所示.
(2)该几何体的表面积为2×2×(4×2+3×2+5×2+2)=104(cm2).
(3)2
5.如图所示为一几何体的三种视图.
(1)这个几何体的名称为 ;?
(2)画出它的任意一种表面展开图;
(3)若主视图是长方形,其长为10 cm,俯视图是等边三角形,其边长为4 cm,求这个几何体的侧面积.
答案
5.【解析】 (1)三棱柱
(2)(答案不唯一)展开图如下:
(3)这个几何体的侧面积为3×4×10=120 (cm2).
6.(1)如图1是一个组合体,图2是它的两种视图,在横线上填写出两种视图的名称;
(2)根据两种视图中的数据(单位:cm),计算这个组合体的表面积.(π取3.14)
答案
6.【解析】 (1)主 俯
(2)这个组合体的表面积为 2×(8×5+8×2+5×2)+4×π×6≈2×66+4×3.14×6=207.36(cm2).
综合素养拓训
本章通过投影引出物体的三种视图,与高中数学中的三视图联系紧密,意在培养几何直观和空间想象能力,同时在核心素养渗透方面也体现出相应特色.第1题以实际问题为背景,在实际问题中从教学的视角发现问题、提出问题,最终解决问题;第3题和第4题体现了核心素养中的直观想象,构建数学问题的直观模型,探索解决问题的思路,进而形成数学直观,在具体的情境中感悟事物的本质.
1.[三种视图的实际应用]如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是 ( )
答案
1.B 【解析】 因为圆柱的俯视图是一个圆,可以堵住圆形空洞,而它的主视图及左视图都是一个长方形,可以堵住方形的空洞.故选B.
2.[三种视图之间的关系]一个三棱柱的三种视图如图所示,已知主视图、左视图、俯视图的面积分别为12,4,3,则左视图中MN的长为? .?
答案
2.2 【解析】 由题中主视图和左视图的面积可知,俯视图中两直角边长之比为3∶1,设较短直角边长为x,则较长直角边长为3x,因为俯视图的面积为3,所以12x·3x=3,解得x=2或-2(不合题意,舍去),所以MN=2.
?
3.[根据三种视图搭建正方体]如图所示是由一些小立方块搭成的几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,搭成一个大正方体,至少还需要 个小立方块.?
答案
3.54 【解析】 由俯视图得最底层有7个小立方块,结合主视图和左视图得第二层有2个小立方块,第三层有1个小立方块,那么共有小立方块7+2+1=10(个).若搭成大正方体,共需小立方块4×4×4=64(个),所以还需要小立方块64-10=
54(个).
4.[投影问题中的规律探究]学习投影后,小刚、小雯利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6 m的小刚(AB)的影子BC的长是3 m,而小雯(EH)刚好在路灯灯泡的正下方H点,并测得HB=6 m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH;
(3)如果小刚沿BH方向向小雯(点H)走去,当小刚走到BH的中点B1处时,求其影子B1C1的长;当小刚继续走剩下路程的13到B2处时,求其影子B2C2的长;当小刚继续走剩下路程的14到B3处时??按此规律继续走下去,当小刚走剩下路程的1????+1到Bn处时,求其影子BnCn的长.
?
答案
4.【解析】 (1)如图1所示.
(2)由题意,得△ABC∽△GHC.
∴????????????????=????????????????,∴1.6????????=36+3,∴GH=4.8 m.
(3)如图2,由题意,得△A1B1C1∽△GHC1.
∴????1????1????????=????1????1????????1,
设B1C1的长为x m,则1.64.8=????????+3,
∴x=32,即B1C1=32 m.
同理1.64.8=????2????2????2????2+2,∴B2C2=1 m,
∴1.64.8=????????????????????????????????+1????+1×6,∴BnCn=3????+1 m.
?
答案
1.C 【解析】 从左面看该零部件,得到的平面图形是一个长方形且内部含有一个圆,结合选项,知选C.
一、选择题
1.[2019广西柳州中考]如图,这是一个机械零部件,该零部件的左视图是 ( )
答案
2.D
2.[2020河南平顶山期末]在阳光的照射下,一块三角板的投影不会是 ( )
A.线段
B.与原三角形全等的三角形
C.变形的三角形
D.点
答案
3.A 【解析】 “阳马”的俯视图是一个矩形且有一条实对角线,结合选项,知选A.
3.[2019安徽阜阳六校联考]在我国古代数学名著《九章算术》中,将底面为矩形、一条侧棱垂直于底面的四棱锥称之为“阳马”(如图).“阳马”的俯视图是 ( )
答案
4.A 【解析】 主视图是三角形,俯视图是两个矩形,左视图是一个矩形.故选A.
4.[2019江苏常州一模]如图所示的正三棱柱,它的主视图、俯视图、左视图的顺序是 ( )
A.①③② B.②①③ C.③①② D.①②③
答案
5.C
5.将一个棱长为3 cm的大立方体挖去一个棱长为1 cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是 ( )
答案
6.A 【解析】 由BE∥AD,易知△BCE∽△ACD,∴????????????????=????????????????,即11+????????=1.21.2+1.8,∴AB=1.5 m.故选A.
?
6.如图,某一时刻阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8 m,窗户下檐到地面的距离BC=1 m,
EC=1.2 m,那么窗户的高AB为( )
A.1.5 m B.1.6 m
C.1.86 m D.2.16 m
答案
7.C 【解析】 结合主视图,俯视图,左视图,可知底层有5个小立方块,第二层最多有5个小立方块,第三层有1个小立方块,所以搭成这个几何体所用的小立方块的数目最多有11个.故选C.
7.由相同的小立方块组成的几何体的三视图如图所示,则该几何体中小立方块的数目最多为 ( )
?
A.7个 B.9个 C.11个 D.13个
答案
8.D 【解析】 由这个几何体的三视图可知,这个几何体是底面半径为2、高为4的圆柱体的一半,其表面积为π×22+
4×2π+4×4=16+12π.故选D.
8.[2018山东济宁中考]一个几何体的三视图如图所示,则该几何体的表面积是 ( )?
A.24+2π
B.16+4π
C.16+8π
D.16+12π
答案
9.5 【解析】 因为主视图中线段AB=a cm,所以该三棱锥的棱长为a cm,在主视图的三角形中只有底边长为a cm,在左视图的三角形中只有左上方边长为a cm,在俯视图中大三角形的三条边均为a cm,所以三种视图中长度为a cm的线段有5条.
二、填空题
9.[2020四川资阳一诊]图1是一个棱长均相等的三棱锥,它的三种视图如图2所示,若AB=a cm,则在这三种视图中,边长为a cm的线段有 条.?
答案
10.0.81π 【解析】 如图,O,E,F三点共线,OE⊥EB,OF⊥FD,OE=OF-EF=3-1=2(m).易知△OEB∽△OFD,∴????????????????=????????????????,即23=0.6????????,∴FD=0.9 m,∴地面上阴影部分的面积为πFD2=π×0.92=0.81π(m2).
?
10.圆桌正上方的灯泡(看作一个点)发出的光线照射在桌面上后,在地面上形成阴影(圆形)的示意图如图所示.已知桌面的直径为1.2 m,桌面距地面1 m,灯泡距地面3 m,则地面上阴影部分的面积是 m2.(用含π的式子表示)?
答案
11.3或5 【解析】 若要使主视图和原几何体的主视图相同,则可取走的小正方体的序号是3或4或5或7;若要使左视图和原几何体的左视图相同,则可取走的小正方体的序号是1或3或5.故可取走的小正方体的序号是3或5.
11.[2019山东青岛模拟]如图是用8个大小相同的小正方体搭成的几何体,仅在该几何体中取走一个小正方体,使得到的新几何体同时满足两个要求:(1)主视图和原几何体的主视图相同;(2)左视图和原几何体的左视图相同.在不改变其他小正方体位置的前提下,可取走的小正方体的序号是 .?
答案
12.【解析】 (1)主视图和左视图如图所示.?
(2)32
(3)1
三、解答题
12.[2019黑龙江绥化模拟]由一些大小相同、棱长为1的小正方体组成的几何体的俯视图如图所示,小正方形中的数字表示该位置上小正方体的个数.
?
(1)请画出该几何体的主视图和左视图;
(2)若要给这个几何体表面喷上颜色(底面不喷色),则需要喷色的面积为 ;?
(3)在不改变主视图和俯视图的情况下,最多可再添加 个小正方体.?
答案
13.【解析】 如图,设墙上的影高CD落在地面上时的长度为x m,树高为h m.
∵某一时刻测得高为1 m的竹竿的影长为0.9 m,墙上的影高CD为1.2 m,
∴10.9=1.2????,∴x=1.08,
∴树的影长为1.08+2.7=3.78(m),
∴10.9=h3.78,∴h=4.2.
答:他测得的树高为4.2米.
?
13.如图,一位同学想利用树影测量树高(AB),他在某一时刻测得高为1 m的竹竿的影长为0.9 m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD),他先测得留在墙上的影高(CD)为1.2 m,又测得地面部分的影长(BC)为2.7 m,他测得的树高应为多少米?
14.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处.小明测得窗户距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
答案
14.【解析】 如图,连接CD.
∵DO⊥BF,∴∠DOE=90°.
∵OD=0.8 m,OE=0.8 m,
∴∠DEB=45°.
∵AB⊥BF,∴∠BAE=45°,∴AB=BE.
设AB=BE=x m,
∵AB⊥BF,CO⊥BF,∴AB∥CO,
易得△ABF∽△COF,∴????????????????=????????????????,
????????+(3?0.8)=1.2+0.83,解得x=4.4.
经检验,x=4.4是原方程的解,且符合题意.
答:围墙AB的高度是4.4 m.
?
第五章 投影与视图中考真题
数学·九年级上册·北师
答案
1.A
1.[2019江西中考]如图是手提水果篮抽象的几何体,以箭头所指的方向为主视图方向,则它的俯视图为 ( )
答案
2.B
2.[2019江苏扬州中考]如图所示物体的左视图是 ( )
答案
3.B 【解析】 由已知三视图均为边长相等的正方形,得该几何体是正方体.故选B.
3.[2019广西贺州中考]如图是某几何体的三视图,则该几何体是 ( )?
A.长方体 B.正方体 C.三棱柱 D.圆柱
答案
4.A 【解析】 因为S主=x2+2x=x(x+2),S左=x2+x=x(x+1),所以俯视图的长为x+2,宽为x+1,所以S俯=(x+2)(x+1)=x2+3x+2.故选A.
4.[2019河北中考]图2是图1中长方体的三视图,若用S表示面积,且S主=x2+2x,S左=x2+x,则S俯= ( )?
A.x2+3x+2
B.x2+2
C.x2+2x+1
D.2x2+3x
5.[2019河南中考]如图1是由大小相同的小正方体搭成的几何体,将上层的小正方体平移后得到图2.关于平移前后几何体的三视图,下列说法正确的是 ( )
A.主视图相同
B.左视图相同
C.俯视图相同
D.三种视图都不相同
答案
5.C 【解析】 题图1的三视图如图1所示,题图2的三视图如图2所示,所以平移前后几何体的俯视图相同.故选C.
答案
6.B 【解析】 由三视图可知圆柱的底面直径为4,高为6,∴底面半径为2,∴V=22×6×π=24π.故选B.
6.[2019内蒙古包头中考]一个圆柱体的三视图如图所示,若其俯视图为圆,则这个圆柱体的体积为 ( )
A.24
B.24π
C.96
D.96π
答案
7.B 【解析】 由俯视图,可得下面一层有5个正方体,由主视图,可得上面一层最多有4个正方体,所以该组合体中正方体的个数最多是9.故选B.
7.[2019四川宜宾中考]已知一个组合体是由几个相同的正方体叠合在一起组成,该组合体的主视图与俯视图如图所示,则该组合体中正方体的个数最多是 ( )
A.10 B.9
C.8 D.7
8.[2018山东青岛中考]一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有 种.?
答案
8.10 【解析】 由题意知俯视图由9个正方形组成,由主视图和左视图知:①第一行第一列的位置一定是4,第二行第三列的位置一定是3;②一定有2个2,其余有5个1;③最后一行至少有一个2,中间一列至少有一个2.根据2的排列不同,这个几何体的搭法共有10种,如下图所示.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
