北师大版九年级上册数学第六章 反比例函数整章同步练习课件(86张PPT)
文档属性
| 名称 | 北师大版九年级上册数学第六章 反比例函数整章同步练习课件(86张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览











文档简介
数学·九年级上册·北师
第六章 反比例函数
1 反比例函数
1.[2019浙江嘉兴期末]下列函数中,能表示y是x的反比例函数的是 ( )
A.y=????2 B.y=-2????
C.y=12????? D.y=1????-2
?
答案
1.B 【解析】 一般地,形如y=????????(k为常数,k≠0)的函数,叫做反比例函数.由此可知B项符合反比例函数的概念.故选B.
?
知识点1 反比例函数的定义
反比例函数的表达式y=????????(k≠0)中,等号的右边是一个分式,分子是不为0的常数k(也叫做比例系数k),分母是自变量x,三个量x,y,k均不为0.
?
2.若y=????+1????是y关于x的反比例函数,则m的取值范围是 ( )
A.m>-1 B.m≠-1
C.m<-1 D.m≠0
?
答案
2.B 【解析】 ∵y=????+1????是y关于x的反比例函数,∴m+1≠0,∴m≠-1.故选B.
?
知识点1 反比例函数的定义
3.在反比例函数y=????????(k是常数,k≠0)中,自变量x的取值范围是 .?
4.反比例函数y=-53????的比例系数为 .?
5.[2019江苏泰州期中]已知y=2x2m-1是y关于x的反比例函数,则m= .?
?
答案
3.x≠0
4.-53
5.0 【解析】 ∵y=2????2?????1是y关于x的反比例函数,∴2m-1=-1,解得m=0.
?
知识点1 反比例函数的定义
6.已知y是x的反比例函数,且x=-2时,y=3,则y与x的函数关系式为 .?
答案
6.y=-6???? 【解析】 设y与x的函数关系式为y=????????(k≠0),因为x=-2时,y=3,所以k=-6,所以y=-6????.
?
知识点2 确定反比例函数的表达式
7.已知函数y=?????2????是y关于x的反比例函数.
(1)求k的取值范围;
(2)当x=2时,y的值为6,求此函数的表达式.
?
答案
7.【解析】 (1)由题意可知,k-2≠0,
解得k≠2.
(2)将x=2,y=6代入,得k-2=xy=12,
∴反比例函数的表达式为y=12????.
?
知识点2 确定反比例函数的表达式
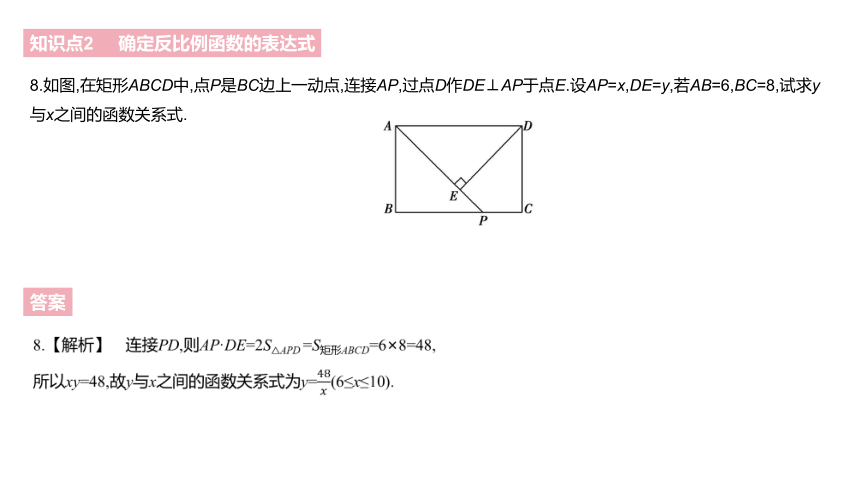
8.如图,在矩形ABCD中,点P是BC边上一动点,连接AP,过点D作DE⊥AP于点E.设AP=x,DE=y,若AB=6,BC=8,试求y与x之间的函数关系式.
答案
8.【解析】 连接PD,则AP·DE=2S△APD =S矩形ABCD=6×8=48,
所以xy=48,故y与x之间的函数关系式为y=48????(6≤x≤10).
?
知识点2 确定反比例函数的表达式
9.下列关系中,两个变量之间为反比例函数关系的是 ( )
A.长40米的绳子减去x米,还剩y米
B.买单价为3元的笔记本x本,花了y元
C.正方形的面积为S,边长为a
D.菱形的面积为20,对角线的长分别为x,y
答案
9.D 【解析】 长40米的绳子减去x米,还剩y米,则y=40-x,不是反比例函数;买单价为3元的笔记本x本,花了y元,则y=3x,不是反比例函数;正方形的面积为S,边长为a,则S=a2,不是反比例函数;菱形的面积为20,对角线的长分别为x,y,则y=40????,是反比例函数.故选D.
?
知识点3 实际问题中的反比例函数关系
10.[2020辽宁大连一模]一司机驾驶汽车从甲地去乙地,他以80km/h的平均速度行驶了4h到达乙地.当他按原路匀速返回时,汽车的速度v(km/h)与时间t(h)的函数关系是 ( )
A.v=320t B.v=320????
C.v=20t D.v=20????
?
答案
10.B 【解析】 根据题意,得甲地到乙地的路程为80×4=320(km),所以汽车的速度v与时间t的函数关系是v=320????.故选B.
?
知识点3 实际问题中的反比例函数关系
11.近视镜的度数y(度)与镜片焦距x(m)成反比例,且200度近视镜的镜片焦距为0.5 m,则y与x之间的函数关系式为 .?
答案
11.y=100???? 【解析】 由题意可设y=????????(k≠0),当x=0.5时,y=200,所以k=100,所以y=100????.
?
知识点3 实际问题中的反比例函数关系
12.已知一个长方体的体积是100 cm3,它的长是 x cm,宽是5 cm,高是y cm.
(1)写出y与x之间的函数关系式;
(2)写出自变量x的取值范围;
(3)当长方体的长是8 cm时,求它的高.
答案
12.【解析】 (1)由题意,得5xy=100,
所以y与x之间的函数关系式为y=20????.
(2)因为长方体的长大于等于长方体的宽,
所以自变量x的取值范围是x≥5.
(3)当x=8时,y=208=2.5,
所以当长方体的长是8 cm时,高是2.5 cm.
?
知识点3 实际问题中的反比例函数关系
在实际问题中,注意自变量的取值范围应符合实际意义.
2 反比例函数的
图象与性质
课时1 反比例函数的图象
课时1
1.在同一平面直角坐标系中,画出反比例函数y=8????与y=-8????的图象.
?
答案
1.【解析】 列表如下:
描点、连线,如图所示.
知识点1 反比例函数图象的画法
答案
画反比例函数图象的注意事项
(1)在列表时,要尽量多取一些数值,这样能多描出一些点,方便连线;(2)连线时,一定要用光滑的曲线,不能用折线;(3)因为反比例函数中的自变量x≠0,函数值y≠0,所以其图象与x轴、y轴都没有交点;(4)要注意图象端点处的延伸性;(5)作出图象后要注明函数的表达式.
知识点1 反比例函数图象的画法
2.反比例函数y=????????(k<0)的大致图象是 ( )
?
答案
2.B 【解析】 反比例函数y=????????(k≠0)的图象是由两支曲线组成的.当k<0时,两支曲线分别位于第二、四象限内.故
选B.
?
知识点2 反比例函数的图象与比例系数k的关系
反比例函数图象的位置是由比例系数k的符号决定的;反之,由双曲线所在位置,也可以推断出k的符号.
3.当x<0时,函数y=4????的图象在 ( )
A.第二、四象限 B.第二象限
C.第一、三象限 D.第三象限
?
答案
3.D 【解析】 因为函数y=4????中,k=4>0,所以当x<0时,函数y=4????的图象在第三象限.故选D.
?
知识点2 反比例函数的图象与比例系数k的关系
4.[2019海南中考]如果反比例函数y=?????2????(a是常数)的图象在第一、三象限,那么a的取值范围是 ( )
A.a<0 B.a>0
C.a<2 D.a>2
?
答案
4.D 【解析】 ∵反比例函数y=?????2????(a是常数)的图象在第一、三象限,∴a-2>0,∴a>2.故选D.
?
知识点2 反比例函数的图象与比例系数k的关系
5.[2019辽宁大连二模]若点A(-2,m)在反比例函数y=2????的图象上,则m的值是 ( )
A.14 B.-14
C.1 D.-1
?
答案
5.D 【解析】 ∵点A(-2,m)在反比例函数y=2????的图象上,∴m=2?2,即m=-1.故选D.
?
知识点3 反比例函数图象上的点的坐标
6.[2019黑龙江哈尔滨中考]点(-1,4)在反比例函数y=????????的图象上,则下列各点在此函数图象上的是 ( )
A.(4,-1) B.(-14,1)
C.(-4,-1) D.(14,2)
?
答案
6.A 【解析】 将点(-1,4)代入y=????????,得k=-4,∴y=-4????,将四个选项的坐标分别代入反比例函数y=-4????中,可知点(4,-1)在函数图象上.故选A.
?
知识点3 反比例函数图象上的点的坐标
7.[2018海南中考]已知反比例函数y=????????的图象经过点P(-1,2),则这个函数的图象位于 ( )
A.第二、三象限
B.第一、三象限
C.第三、四象限
D.第二、四象限
?
答案
7.D 【解析】 将点P(-1,2)代入y=????????,得k=-2<0,所以其图象位于第二、四象限.故选D.
?
知识点3 反比例函数图象上的点的坐标
8.[2018浙江湖州中考]如图,已知直线y=k1x(k1≠0)与反比例函数y=????2????(k2≠0)的图象交于M,N两点.若点M的坐标是(1,2),则点N的坐标是 ( )
A.(-1,-2) B.(-1,2)
C.(1,-2) D.(-2,-1)
?
答案
8.A 【解析】 因为点M,N都在反比例函数的图象上,且两点的连线经过原点,所以M,N关于原点对称.因为点M的坐标是(1,2),所以点N的坐标是(-1,-2).故选A.
知识点4 反比例函数图象的对称性
9.已知点P为反比例函数y=3????的图象上一点,且点P到坐标原点的距离为10,则符合条件的点P有 ( )
A.0个 B.2个
C.4个 D.无数个
?
答案
9.C 【解析】 易知反比例函数y=3????在第一象限内的图象上到坐标原点的距离为10的点为(1,3)和(3,1),根据反比例函数图象的对称性,可知符合条件的点P有4个.故选C.
?
知识点4 反比例函数图象的对称性
1.[2019河北中考]如图,函数y=1????(????>0),?1????(????<0)的图象所在坐标系的原点是 ( )
A.点M
B.点N
C.点P
D.点Q
?
答案
1.A 【解析】 对于y=1????(x>0),其图象位于第一象限;对于y=-1????(x<0),其图象位于第二象限,故所在坐标系的原点是点M.故选A.
?
2.已知反比例函数y=????????的图象如图所示,则k的值可能是 ( )
A.-1 B.12 C.1 D.2
?
答案
2.B 【解析】 因为反比例函数的图象在第一、三象限,所以k>0.因为当x=1时,y<1,所以k<1.故选B.
3.[2019山东济南中考]函数y=-ax+a与y=????????(a≠0)在同一坐标系中的图象可能是 ( )
?
答案
3.D 【解析】 当a>0时,-a<0,y=-ax+a过第一、二、四象限,y=????????位于第一、三象限,无选项符合.当a<0时,-a>0,y=
-ax+a过第一、三、四象限,y=????????(a≠0)位于第二、四象限,只有D符合.故选D.
?
4.[2020广西北部湾经济区一模]如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=????????(x<0)的图象经过顶点B,则k的值为 ( )
A.-12 B.-27 C.-32 D.-36
?
答案
4.C 【解析】 ∵点A的坐标为(-3,4),∴OA=32+42=5.∵四边形OABC是菱形,∴AB=OA=5,AB∥OC,∴点B的坐标为(-8,4).将点B的坐标代入y=????????,得4=?????8,解得k=-32.故选C.
?
5.如图,直线y=x+a-2与双曲线y=4????交于A,B两点,则当线段AB的长度最小时,a的值为 ( )
A.0 B.1
C.2 D.5
?
答案
5.C 【解析】 反比例函数的图象既是轴对称图形又是中心对称图形,只有当A,B,O(坐标原点)三点共线时,才能使线段AB的长度最小,所以直线y=x+a-2过坐标原点,把(0,0)代入 y=x+a-2,得a=2.故选C.
6.对于反比例函数y=4????,下列说法错误的是 ( )
A.它的图象与坐标轴永远不相交
B.它的图象绕原点旋转180°能和本身重合
C.它的图象关于直线y=±x对称
D.它的图象与直线y=-x有两个交点
?
答案
6.D 【解析】 反比例函数y=4????的图象位于第一、三象限,直线y=-x经过第二、四象限,所以直线y=-x与双曲线y=4????无交点,所以选项D中的说法是错误的.故选D.
?
7.[2019辽宁朝阳中考]从点M(-1,6),N(12,12),E(2,-3),F(-3,-2)中任取一点,所取的点恰好在反比例函数y=6????的图象上的概率为? .?
8.已知点A是反比例函数y=2????(x>0)图象上的一点,点A'是点A关于y轴的对称点,当△AOA'为直角三角形时,点A的坐标是 .?
?
答案
7.12 【解析】 ∵k=6,-1×6=-6≠6,12×12=6,2×(-3)=-6≠6,-3×(-2)=6,∴点N,F在反比例函数y=6????的图象上,故所取的点恰好在反比例函数y=6????的图象上的概率为24=12.
8.(2,2) 【解析】 因为点A是反比例函数y=2????(x>0)图象上的一点,所以设点A的坐标为(x,2????).因为点A'是点A关于y轴的对称点,所以OA=OA',又因为△AOA'为直角三角形,所以△AOA'为等腰直角三角形,所以OA与x轴、y轴正半轴的夹角均为45°,所以点A的纵坐标与横坐标相等,即x=2????,又因为x>0,所以x=2,故点A的坐标为(2,2).
?
9.已知反比例函数y=?????7????的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m
的值.
?
答案
9.【解析】 (1)该函数图象的另一支在第三象限.
∵该反比例函数的图象位于第一、三象限,
∴m-7>0,∴m>7,
∴m的取值范围为m>7.
(2)设点A的坐标为(x,y).
∵点B与点A关于x轴对称,
∴点B的坐标为(x,-y).
∵S△OAB=6,∴12·2y·x=6,∴xy=6.
∵点A在反比例函数y=?????7????的图象上,
∴xy=m-7,∴m-7=6,
∴m=13.
?
课时2 反比例函数的性质
课时2
1.下列函数的图象,在每一个象限内,y值随x值的增大而增大的是 ( )
A.y=1???? B.y=-x+1
C.y=12???? D.y=-1????
?
答案
1.D 【解析】 A项,对于反比例函数y=1????,k=1>0,函数的图象在其所在的每一个象限内,y值随x值的增大而减小,不合题意;B项,对于一次函数y=-x+1,k=-1<0,y值随x值的增大而减小,不合题意;C项,对于反比例函数y=12????,k=12>0,函数的图象在其所在的每一个象限内,y值随x值的增大而减小,不合题意;D项,对于反比例函数y=-1????,k=-1<0,函数的图象在其所在的每一个象限内,y值随x值的增大而增大,符合题意.故选D.
?
知识点1 反比例函数的性质
描述反比例函数值的增减情况时,必须指出“在每一象限内”,而不能直接说“当k>0时,y值随x值的增大而减小”.
2.[2020贵州毕节一模]若反比例函数y=3????的图象上有P1(x1,-2),P2(x2,-3)两点,则x1与x2的大小关系是( )
A.x1>x2 B.x1=x2
C.x1?
答案
2.C 【解析】 ∵k=3>0,∴反比例函数y=3????的图象位于第一、三象限,且在每个象限内,y随x的增大而减小.∵-2>
-3,∴x1?
知识点1 反比例函数的性质
3.已知A(1,y1),B(2,y2)两点在反比例函数y=5+2????????的图象上,若y1A.m>0 B.m<0
C.m>-52 D.m<-52
?
答案
3.D 【解析】 因为A(1,y1),B(2,y2)两点在反比例函数y=5+2????????的图象上,且y1?
知识点1 反比例函数的性质
4.[2018湖南衡阳中考]对于反比例函数y=-2????,下列说法不正确的是 ( )
A.图象分布在第二、四象限
B.当x>0时,y随x的增大而增大
C.图象经过点(1,-2)
D.若点A(x1,y1),B(x2,y2)都在图象上,且x1?
答案
4.D 【解析】 ∵-2<0,∴该反比例函数的图象位于第二、四象限,且当x>0时,y随x的增大而增大,故选项A,B中的说法正确.∵1×(-2)=-2,∴其图象经过点(1,-2),故选项C中的说法正确.当点A,B在该反比例函数图象的同一条曲线上时,若x1y2,故选项D中的说法错误.故选D.
知识点1 反比例函数的性质
5.[2019河南焦作一模]已知反比例函数y=2????,当x<-1时,y的取值范围为 .?
?
答案
5.-2?
知识点1 反比例函数的性质
6.反比例函数y=????????的图象如图所示,点A是该函数图象上一点,AB垂直于x轴,垂足是点B,若????△????????????=1,则k的值为 ( )
A.1 B.-1 C.2 D.-2
?
答案
6.D 【解析】 因为点A在反比例函数y=????????的图象上,所以S△AOB=12|k|=1,解得k=±2,又因为反比例函数的图象在第二、四象限,所以k<0,则k=-2.故选D.
?
知识点2 反比例函数中比例系数k的几何意义
借助k的几何意义求反比例函数的表达式
过双曲线y=????????(k≠0)上任意一点作x轴或y轴的垂线,该点与垂足及原点构成的三角形的面积为|????|2.反比例函数表达式的确定,除了根据构成的三角形的面积等于|????|2外,还应看函数图象所在的位置,以便于确定k的符号.
?
7.[2019山东临沂一模]如图,点A是反比例函数y=-6????(x<0)的图象上的一点,过点A作?ABCD,使点B,C在x轴上,点D在y轴上,则?ABCD的面积为 ( )
A.1 B.3 C.6 D.12
?
答案
7.C 【解析】 如图,过点A作AH⊥OB于点H.∵四边形ABCD是平行四边形,∴AD∥OB,
∴?????????????????????=????矩形????????????????.∵点A是反比例函数y=-6????(x<0)的图象上的一点,∴????矩形????????????????=|-6|=
6,∴?????????????????????=6.故选C.
?
知识点2 反比例函数中比例系数k的几何意义
8.如图,过y轴正半轴上的任意一点P作x轴的平行线,分别与反比例函数y=-4????和y=2????的图象交于点A和点B,若点C是x轴上的任意一点,连接AC,BC,则△ABC的面积为 ( )
A.3 B.4
C.5 D.6
?
答案
8.A 【解析】 连接OA,OB,则 S△ABC =S△AOB .因为点B在y=2????的图象上,所以S△OBP =1.因为点A在y=-4????的图象上,所以S△OAP =2,所以S△ABC =S△AOB = S△OBP + S△OAP =3.故选A.
?
知识点2 反比例函数中比例系数k的几何意义
9.[2020湖南永州期中]如图,A,B两点在双曲线y=4????上,分别过A,B两点向x轴、y轴作垂线段,若S阴影=1,则S1 +S2 = ( )
A.8 B.6
C.4 D.2
?
答案
9.B 【解析】 因为A,B两点在双曲线y=4????上,所以矩形ACOD和矩形BEOF的面积均为4.因为S阴影=1,所以S1 =S2 =3,所以S1 +S2 =6.故选B.
?
知识点2 反比例函数中比例系数k的几何意义
10.易错题如图,在平面直角坐标系中,过点M(0,2)的直线与x轴平行且分别与反比例函数y=6????(x>0)和y=????????(x<0)的图象交于P,Q两点.
(1)求点P的坐标;
(2)若△POQ的面积为8,求k的值.
?
知识点2 反比例函数中比例系数k的几何意义
答案
10.【解析】 (1)由题意可得,直线y=2与反比例函数y=6????(x>0)的图象相交于点P,则可设点P的坐标为(a,2),
将点P的坐标(a,2)代入y=6????,解得a=3,
∴点P的坐标为(3,2).
(2) ∵点P在反比例函数y=6????的图象上,
∴S△OPM=12×6=3,
∴S△OQM= S△POQ- S△OPM=8-3=5,
∴|k|=10.
∵函数y=????????(x<0)的图象位于第二象限,∴k<0,
∴k=-10.
?
知识点2 反比例函数中比例系数k的几何意义
1.若在反比例函数y=????+3????图象的每一支上,y都随x的增大而增大,则k的值可以是 ( )
A.-5 B.-2
C.1 D.4
?
答案
1.A 【解析】 因为在反比例函数y=????+3????图象的每一支上,y都随x的增大而增大,所以k+3<0,所以k<-3.故选A.
?
2.易错题[2020天津南开翔宇学校月考]若点(-1,y1),(-14,y2),(12,y3)在函数y=????2+1????(a为常数)的图象上,则函数值y1,y2,y3的大小关系是 ( )
A.y2C.y1?
答案
2.A 【解析】 ∵反比例函数的比例系数a2+1>0,∴函数y=????2+1????(a为常数)的图象位于第一、三象限,且在每个象限内,y随x的增大而减小.∵-1<-14<0,点(-1,y1),(-14,y2)在第三象限,∴y20,点(12,y3)在第一象限,∴y3>0,∴y2?
3.[2019浙江金华模拟]如图,直线y=mx与双曲线y=????????交于点A,B,过点A作AM⊥x轴于点M,连接BM.若S△ABM=2,则k的值是 ( )
A.1 B.2
C.3 D.4
?
答案
3.B 【解析】 由题意得S△ABM=2S△AOM=2,所以S△AOM=12|k|=1,所以k=±2.因为双曲线y=????????位于第一、三象限,所以k>0,所以k=2.故选B.
?
4.如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线y=3????(x>0)上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会 ( )
A.逐渐增大 B.逐渐减小
C.不变 D.先增大后减小
?
答案
4.B 【解析】 设点B的坐标为(a,b),因为点B是双曲线y=3????(x>0)上的一个动点,所以a>0,b>0,纵坐标b随着横坐标a的增大而减小.因为S△OAB=12OA·b,OA为定值,所以当点B的横坐标a逐渐增大时,△OAB的面积逐渐减小.故选B.
?
5.[2018浙江宁波中考]如图,平行于x轴的直线与函数y=????1????(k1>0,x>0), y=????2????(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点.若△ABC的面积为4,则k1-k2的值为 ( )
A.8 B.-8 C.4 D.-4
?
答案
5.A 【解析】 如图,连接AO,BO.∵AB∥x轴,∴S△ABO=S△ABC=4.设AB与y轴交于点D,则S△AOD=12k1,S△BOD=12k2.∵S△AOD-S△BOD=S△ABO,即12k1-12k2=4,∴k1-k2=8.故选A.
?
6.[2019山西临汾期中]如图,点A在双曲线y=1????(x>0)上,点B在双曲线y=3????(x>0)上,且AB∥x轴,C,D在x轴上,若四边形ABCD为矩形,则它的面积为 .?
?
答案
6.2 【解析】 如图,延长BA交y轴于点E.∵AB∥x轴,四边形ABCD为矩形,∴四边形AEOD和四边形BEOC都是矩形.∵点A在双曲线y=1????(x>0)上,
∴矩形AEOD的面积为1.∵点B在双曲线y=3????(x>0)上,∴矩形BEOC的面积为3,∴矩形ABCD的面积为3-1=2.
?
7.易错题[2019广东江门期末]如图,在平面直角坐标系中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=????????(x<0)的图象上,则k的值为 .?
?
答案
7.-6 【解析】 如图,连接AC,交y轴于点D,∵四边形OABC为菱形,∴AC⊥OB,且CD=
AD,BD=OD.∵菱形OABC的面积为12,∴S△CDO=14S菱形OABC=3,∴|k|=6.∵当x<0时,反比例函数图象位于第二象限,∴k<0,∴k=-6.
?
8.如图,在第一象限内,正比例函数y=ax的图象与反比例函数y=????????的图象交于点A(3,2).
(1)试确定上述正比例函数和反比例函数的表达式.
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)点M(m,n)是反比例函数图象上的一动点,其中0?
答案
8.【解析】 (1)∵在第一象限内,正比例函数y=ax的图象与反比例函数y=????????的图象交于点A(3,2),
∴2=3a,2=????3,∴a=23,k=6,
∴正比例函数的表达式为y=23x,
?
答案
反比例函数的表达式为y=6????.
(2)由题中图象,知当0∴当0(3)BM=DM.理由如下:
连接OD.
∵MB∥x轴,AC∥y轴,∠BOC=90°,
∴四边形OCDB为矩形,∴S△BOD =S△COD .
∵点M,A在双曲线y=6????上,∴S△OBM =S△AOC =3,
∴S△ODM =S△AOD .
∵四边形OADM的面积为6,
∴S△ODM =S△OBM =3,∴BM=DM.
?
3 反比例函数的应用
1.[2019江苏淮安中考]当矩形面积一定时,下列图象中能表示它的长y和宽x之间函数关系的是 ( )
答案
1.B 【解析】 设矩形的面积为S(定值),则xy=S,∴y是x的反比例函数(x>0,y>0).故选B.
知识点1 利用反比例函数解决实际问题
在实际问题中要判断其中的两个量是否成反比例,应先根据题意列出函数的表达式.对于实际问题中函数自变量的取值范围,除使表达式有意义外,还要使实际问题有意义.
2.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于120 kPa时,气球将会爆炸,为了安全起见,气球的体积应 ( )
A.不小于54 m3 B.大于54 m3
C.不小于45 m3 D.小于45 m3
?
答案
2.C 【解析】 因为气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,所以可设p=????????(V>0),由题图可知,当V=
1.6时,p=60,所以k=1.6×60=96,所以p=96????(V>0).为了安全起见,气球内的气压应不大于120 kPa,即96????≤120,所以V≥45.故选C.
?
知识点1 利用反比例函数解决实际问题
3.[2020山东济南外国语期中]在一个可以改变容积的密闭容器内,装有一定质量m(kg)的某种气体,当改变容积V(m3)时,气体的密度ρ(kg/m3)也随之改变,ρ与V在一定范围内满足ρ=????????,它的图象如图所示,则该气体的质量为 kg.?
?
答案
3.7 【解析】 因为ρ=????????,所以m=ρV.因为点(5,1.4)在函数图象上,所以m=5×1.4=7(kg).
?
知识点1 利用反比例函数解决实际问题
4.在学校就餐时,往往需要在窗口前排队等待.经调查发现,同学们的舒适度指数y与等待时间x(分)之间存在如下的关系:y=100????(x>0).
(1)若等待时间x为5分钟,求舒适度指数y的值.
(2)舒适度指数不低于10时,同学们才会感觉到舒适,函数y=100????(x>0)的图象如图所示,请根
据图象说明,作为食堂的管理员,让每个在窗口排队的同学最多等待多长时间合适?
?
答案
4.【解析】 (1)将x=5代入y=100????中,得y=1005=20.
答:舒适度指数y的值为20.
(2)当y=10时,x=10010=10,
由图象可知,当y>10时,0所以让每个在窗口排队的同学最多等待10分钟合适.
?
知识点1 利用反比例函数解决实际问题
5.[2018四川遂宁中考]已知一次函数y1=kx+b(k≠0)与反比例函数y2=????????(m≠0)的图象如图所示,则当y1>y2时,自变量x满足的条件是 ( )
A.1B.1≤x≤3
C.x>1
D.x<3
?
答案
5.A 【解析】 由题中图象可得,当1y2,所以自变量x满足的条件是1知识点2 反比例函数与一次函数的综合运用
6.[2019江苏淮安二模]如图,正比例函数y1=-2x的图象与反比例函数y2=????????的图象交于A,B两点,点C在x轴负半轴上,若AC=AO,△ACO的面积为6,则k的值为 ( )
A.3 B.-3
C.-6 D.6
?
答案
6.C 【解析】 由题意,设A(m,-2m),∵AC=AO,∴△ACO是等腰三角形,∴CO=-2m,∴S△ACO=12×(-2m)×(-2m)=6,
m2=3.∵k=-2m2,∴k=-6.故选C.
?
知识点2 反比例函数与一次函数的综合运用
7.[2019四川泸州中考]如图,一次函数y1=ax+b和反比例函数y2=????????的图象相交于A,B两点,则使y1>y2成立的x取值范围是 .?
?
答案
7.x<-2或0知识点2 反比例函数与一次函数的综合运用
8.已知一次函数y=x+m的图象与反比例函数y=????+1????(m≠-1)的图象在第一象限内交于点P(n,3),请你分别求出一次函数和反比例函数的表达式.
?
答案
8.【解析】 ∵一次函数y=x+m的图象与反比例函数y=????+1????(m≠-1)的图象在第一象限内交于点P(n,3),
∴m+n=3且????+1????=3,∴n=1,m=2,
∴一次函数的表达式为y=x+2,反比例函数的表达式为y=3????.
?
知识点2 反比例函数与一次函数的综合运用
1.[2018山东临沂中考]如图,正比例函数y1=k1x与反比例函数y2=????2????的图象相交于A,B两点,其中点A的横坐标为1.当y1A.x<-1或x>1
B.-11
C.-1D.x<-1或0?
答案
1.D 【解析】 因为正比例函数图象、反比例函数图象均关于原点成中心对称,所以点A,B也关于原点成中心对称,所以点B的横坐标为-1,结合题图可知,当y12.[2020吉林长春模拟]如图为某公园“水上滑梯”的侧面图,其中BC段可看成是双曲线的一段,建立如图的坐标系,其中,四边形AOEB是矩形,OA=5米,AB∥OD,且AB=2米,C点距水面的距离CD为1米,则B,C之间的水平距离DE的长度为 ( )
A.5米 B.6米
C.7米 D.8米
答案
2.D 【解析】 ∵四边形AOEB是矩形,∴BE=OA=5米,OE=AB=2米,∴B(2,5).设曲线BC的表达式为y=????????(k>0,x>0),则k=10,∴y=10????(x>0).当y=1时,x=10,∴DE=10-2=8(米).故选D.
?
3.如图,正比例函数y1=k1x和反比例函数y2=????2????的图象交于A(1,2),B两点,给出下列结论:①k1y2时,x>1;④当x<0时,y2随x的增大而减小.其中正确的个数为 ( )
A.0 B.1
C.2 D.3
?
答案
3.C 【解析】 因为正比例函数y1=k1x和反比例函数y2=????2????的图象交于A(1,2),B两点,所以k1=2,k2=2,B(-1,-2),所以k1=k2,所以结论①不正确;由题中图象,可知当x<-1时,y1y2时,x>1或-10,所以当x<0时,y2随x的增大而减小,所以结论④正确.故选C.
?
4.[2019山东聊城中考]如图,点A(32,4),B(3,m)是直线AB与反比例函数y=????????(x>0)图象的两个交点,AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
(1)求直线AB的表达式;
(2)△ABC和△ABD的面积分别为S1,S2,求S2-S1.
?
答案
4.【解析】 (1)把点A(32,4)代入y=????????(x>0),得4=????32,∴n=6,
∴反比例函数的表达式为y=6????(x>0).
将点B(3,m)代入y=6????(x>0),得m=2,∴B(3,2).
设直线AB的表达式为y=kx+b,
∵点A(32,4),B(3,2)是直线AB上的两点,
?
答案
∴32????+????=4,3????+????=2,解得????=?43,????=6,
∴直线AB的表达式为y=-43x+6.
(2)AC=4,点B到AC的距离为3-32=32,
∴S1=12×4×32=3.
设直线AB与y轴的交点为E,可得E(0,6),
∴DE=6-1=5.
易知点A(32,4),B(3,2)到DE的距离分别为32,3,
∴S2=S△BDE-S△AED=12×5×3-12×5×32=154,
∴S2-S1=154-3=34.
?
5.环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的质量浓度超标,即硫化物的质量浓度超过最高允许的1.0 mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的质量浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,其中第3天时硫化物的质量浓度降为4 mg/L.从第3天起所排污水中硫化物的质量浓度y与时间x满足下面表格中的关系:
(1)求整改过程中当0≤x≤3时,硫化物的质量浓度y与时间x的函数表达式;
(2)求整改过程中当x≥3时,硫化物的质量浓度y与时间x的函数表达式;
(3)该企业所排污水中硫化物的质量浓度能否在15天以内不超过最高允许的1.0 mg/L?为什么?
时间x/天
3
4
5
6
8
?
硫化物的质量浓度y/(mg/L)
4
3
2.4
2
1.5
?
答案
5.【解析】 (1)前3天的函数图象是线段AB,设直线AB的函数表达式为y=kx+b,
把(0,10),(3,4)代入y=kx+b,得????=10,3????+????=4,解得????=?2,????=10,
所以当0≤x≤3时,硫化物的质量浓度y与时间x的函数表达式为y=-2x+10.
(2)当x≥3时,由题意可知,硫化物的质量浓度y与时间x成反比例关系,设该函数的表达式为y=????????(k≠0),
把(3,4)代入y=????????(k≠0),得4=????3,所以k=12,
所以当x≥3时,硫化物的质量浓度y与时间x的函数表达式为y=12????.
(3)能.理由如下:
令y=12????=1,则x=12<15,
所以该企业所排污水中硫化物的质量浓度能在15天以内不超过最高允许的1.0 mg/L.
?
易错疑难集训
集训
1.当m= 时,函数y=(m+3)????2?????是反比例函数??
?
答案
1.3 【解析】 因为函数y=(m+3)????2?|?????是反比例函数,所以2-|m|=-1且 m+3≠0,即m=±3且m≠-3,故m=3.
?
易错点 1 忽视反比例函数y=????????中比例系数k的限制条件
?
错解:因为函数y=(m+3)????2??|?????是反比例函数,所以2-|m|=-1,所以m=±3.
分析:解题过程中,忽略条件m+3≠0,从而得到错误答案m=±3.
?
2.如图,已知矩形OABC的面积为6,且反比例函数y=????????的图象经过点B,则k= .?
?
答案
2.-6 【解析】 因为矩形OABC的面积为6,点B在反比例函数y=????????的图象上,且点B在第四象限,所以k=-6.
?
易错点 1 忽视反比例函数y=????????中比例系数k的限制条件
?
错解:6
分析:出现错解的原因是直接由矩形OABC的面积为6,点B在反比例函数y=????????的图象上,得到k=6,忽略了题图中点B在第四象限这一隐含条件.
?
3.已知反比例函数y=(3m-1)????????2?2的图象在所在的每一个象限内,y随x的增大而增大,求该反比例函数的表达式.
?
答案
3.【解析】 ∵反比例函数y=(3m-1)????????2?2的图象在所在的每一个象限内,y随x的增大而增大,
∴????2?2=?1,3?????1<0,解得????=±1,????<13,
∴m=-1,
∴该反比例函数的表达式为y=-4????.
?
易错点 1 忽视反比例函数y=????????中比例系数k的限制条件
?
4.现有面积为20 m2的长方形场地,设其一边长为x m,另一边长为y m,则y与x之间的函数关系式为 ,自变量x的取值范围是 .?
答案
4.y=20???? x>0
?
易错点 2 忽略自变量的实际意义
5.已知一个三角形的面积为4,一边长为x,这条边上的高为y,则y关于x的变化规律用图象表示大致是 ( )
答案
5.C 【解析】 因为三角形的面积为4,一边长为x,这条边上的高为y,所以12xy=4,所以y=8????(x>0).故选C.
?
易错点 2 忽略自变量的实际意义
6.某服装厂承揽了一项生产2 000件衬衫的任务,为了抢抓商机,商家要求在10天内(含10天)供货.
(1) 请你写出服装厂每天生产衬衫的件数y与生产天数x之间的函数关系式.
(2) 由于服装厂加班加点,所以提前2天交货,则服装厂每天多生产多少件?
答案
6.【解析】 (1)所求函数关系式为y=2?000????(0(2)根据题意,得2?00010?2?2?00010=50(件).
答:服装厂每天多生产50件.
?
易错点 2 忽略自变量的实际意义
7.[2019江苏徐州中考]若A(x1,y1),B(x2,y2)都在函数y=2?019????的图象上,且x1<0A.y1y2 D.y1=-y2
?
答案
7.A 【解析】 ∵k=2 019>0,∴该函数图象在第一、三象限,当x<0时,y<0,当x>0时,y>0,∵A(x1,y1),B(x2,y2)都在函数y=2?019????的图象上,且x1<0?
易错点 3 研究函数的增减性时不分象限
8.设A(x1,y1),B(x2,y2)是反比例函数y=-4????的图象上的点,若x1?
答案
8.【解析】 因为反比例函数y=-4????中比例系数k<0,
所以反比例函数y=-4????的图象位于第二、四象限,在每一象限内,y值随x值的增大而增大.
当x1,x2同号时,若x1当x1,x2异号时,若x10,
由k<0,知y1>0>y2.
?
易错点 3 研究函数的增减性时不分象限
错解:因为反比例函数y=-4????中比例系数k<0,所以反比例函数y=-4????的图象位于第二、四象限,y值随x值的增大而增大,所以若x1分析:忽略了A,B两点不在同一象限内这一情况,而直接比较大小.实际上,反比例函数的增减性要依据不同象限进行区分.
?
1.如图,双曲线y=????????与直线y=kx+b交于点M,N,并且点M的坐标为(1,3),点N的纵坐标为-1.根据图象信息可得关于x的方程????????=kx+b的解为 ( )
A.-3,1 B.-3,3 C.-1,1 D.-1,3
?
答案
1.A 【解析】 因为双曲线y=????????与直线y=kx+b交于点M,N,并且点M的坐标为(1,3),所以m=3,双曲线的表达式为y=3????.因为点N的纵坐标为-1,代入双曲线的表达式可得点N的横坐标为-3.由题中图象可得关于x的方程????????=kx+b的解为双曲线y=????????与直线y=kx+b的交点N,M的横坐标,即-3,1.故选A.
?
疑难点 1 反比例函数图象与一次函数图象的交点
2.[2019山东济南莱芜区中考]如图,直线l与x轴,y轴分别交于A,B两点,且与反比例函数y=????????(x>0)的图象交于点C,若S△AOB=S△BOC=1,则k= ( )
A.1 B.2
C.3 D.4
?
答案
2.D 【解析】 如图,过点C作CD⊥x轴于点D,设OB=a(a>0).∵S△AOB=S△BOC, ∴AB=BC.∵S△AOB=1,∴12OA·OB=1, ∴OA=2????.∵CD∥OB,AB=BC, ∴OD=OA=2????, CD=2OB=2a,∴C(2????,2a).∵反比例函数y=????????(x>0)的图象经过点C,∴k=2????×2a=4.故选D.
?
疑难点 1 反比例函数图象与一次函数图象的交点
3.[2019广西贺州一模]下列选项中,阴影部分面积最小的是 ( )
答案
3.C 【解析】 由反比例函数y=????????中比例系数k的几何意义,易知A项和B项中阴影部分的面积都是2.C项中,过点M作MP⊥x轴于点P,过点N作NQ⊥x轴于点Q,则S阴影部分=S梯形NQPM+S△MOP-S△NOQ=12×(1+2)×1+12×1×2-12×2×1=32.D项中,阴影部分的面积为12×1×4=2.故选C.
?
疑难点2 反比例函数y=?????????(k≠0)中比例系数k的几何意义
?
4.如图1,点A是x轴上的一个动点,过点A作x轴的垂线PA交双曲线y=1????于点P,连接OP.
(1)当点A在x轴上的正方向上运动时,Rt△AOP的面积是否发生变化?若不变,请求出Rt△AOP的面积;若变化,请说明理由.
(2)如图2,在x轴上点A的右侧有一点D,过点D作x轴的垂线DB交双曲线y=1????于点B,连接BO交AP于点C,设△AOP的面积为S1,梯形BCAD的面积为S2,则S1与S2的大小关系是S1 S2.(选填“>”“=”或“<”)?
(3)如图3,PO的延长线与双曲线y=1????的另一个交点是F,作FH垂直于x轴,垂足为H,连接AF,PH,试说明四边形APHF的面积为常数.
?
疑难点2 反比例函数y=?????????(k≠0)中比例系数k的几何意义
?
答案
4.【分析】 (1)由于点A是x正半轴上的动点,点P始终在双曲线上,根据反比例函数y=????????中比例系数k的几何意义,可以得出△AOP的面积是否发生变化;(2)利用(1)中的结论,求出△AOP和△BOD的面积,由△AOC是公共部分即可得出S1与S2的大小关系;(3)由双曲线的对称性可知,四边形APHF是平行四边形,又因为△AOP的面积为常数,所以四边形APHF的面积也是常数.
【解析】 (1)Rt△AOP的面积不变.
根据反比例函数y=????????中比例系数k的几何意义,得S△AOP=12.
(2)>
由(1)知S1=12,S2=S△BOD-S△AOC=12-S△AOC,所以S1>S2.
(3)由已知条件可知四边形APHF是平行四边形,则AH,PF互相平分并交于点O,
由(1)知S△AOP=12,所以S四边形APHF=4S△AOP=2.
?
疑难点2 反比例函数y=?????????(k≠0)中比例系数k的几何意义
?
答案
与反比例函数y=????????的图象有关的图形面积问题主要是矩形和三角形的面积问题,以及由矩形和三角形所形成的图形的面积问题,面积的计算方法主要有直接计算、间接计算和变换计算三种,本题主要采用间接计算.解题的关键是理解与运用反比例函数y=????????的比例系数k的几何意义.在解与面积有关的几何图形时,要特别注意点的坐标与线段长度之间的转化关系及符号问题.
?
疑难点2 反比例函数y=?????????(k≠0)中比例系数k的几何意义
第六章 反比例函数
1 反比例函数
1.[2019浙江嘉兴期末]下列函数中,能表示y是x的反比例函数的是 ( )
A.y=????2 B.y=-2????
C.y=12????? D.y=1????-2
?
答案
1.B 【解析】 一般地,形如y=????????(k为常数,k≠0)的函数,叫做反比例函数.由此可知B项符合反比例函数的概念.故选B.
?
知识点1 反比例函数的定义
反比例函数的表达式y=????????(k≠0)中,等号的右边是一个分式,分子是不为0的常数k(也叫做比例系数k),分母是自变量x,三个量x,y,k均不为0.
?
2.若y=????+1????是y关于x的反比例函数,则m的取值范围是 ( )
A.m>-1 B.m≠-1
C.m<-1 D.m≠0
?
答案
2.B 【解析】 ∵y=????+1????是y关于x的反比例函数,∴m+1≠0,∴m≠-1.故选B.
?
知识点1 反比例函数的定义
3.在反比例函数y=????????(k是常数,k≠0)中,自变量x的取值范围是 .?
4.反比例函数y=-53????的比例系数为 .?
5.[2019江苏泰州期中]已知y=2x2m-1是y关于x的反比例函数,则m= .?
?
答案
3.x≠0
4.-53
5.0 【解析】 ∵y=2????2?????1是y关于x的反比例函数,∴2m-1=-1,解得m=0.
?
知识点1 反比例函数的定义
6.已知y是x的反比例函数,且x=-2时,y=3,则y与x的函数关系式为 .?
答案
6.y=-6???? 【解析】 设y与x的函数关系式为y=????????(k≠0),因为x=-2时,y=3,所以k=-6,所以y=-6????.
?
知识点2 确定反比例函数的表达式
7.已知函数y=?????2????是y关于x的反比例函数.
(1)求k的取值范围;
(2)当x=2时,y的值为6,求此函数的表达式.
?
答案
7.【解析】 (1)由题意可知,k-2≠0,
解得k≠2.
(2)将x=2,y=6代入,得k-2=xy=12,
∴反比例函数的表达式为y=12????.
?
知识点2 确定反比例函数的表达式
8.如图,在矩形ABCD中,点P是BC边上一动点,连接AP,过点D作DE⊥AP于点E.设AP=x,DE=y,若AB=6,BC=8,试求y与x之间的函数关系式.
答案
8.【解析】 连接PD,则AP·DE=2S△APD =S矩形ABCD=6×8=48,
所以xy=48,故y与x之间的函数关系式为y=48????(6≤x≤10).
?
知识点2 确定反比例函数的表达式
9.下列关系中,两个变量之间为反比例函数关系的是 ( )
A.长40米的绳子减去x米,还剩y米
B.买单价为3元的笔记本x本,花了y元
C.正方形的面积为S,边长为a
D.菱形的面积为20,对角线的长分别为x,y
答案
9.D 【解析】 长40米的绳子减去x米,还剩y米,则y=40-x,不是反比例函数;买单价为3元的笔记本x本,花了y元,则y=3x,不是反比例函数;正方形的面积为S,边长为a,则S=a2,不是反比例函数;菱形的面积为20,对角线的长分别为x,y,则y=40????,是反比例函数.故选D.
?
知识点3 实际问题中的反比例函数关系
10.[2020辽宁大连一模]一司机驾驶汽车从甲地去乙地,他以80km/h的平均速度行驶了4h到达乙地.当他按原路匀速返回时,汽车的速度v(km/h)与时间t(h)的函数关系是 ( )
A.v=320t B.v=320????
C.v=20t D.v=20????
?
答案
10.B 【解析】 根据题意,得甲地到乙地的路程为80×4=320(km),所以汽车的速度v与时间t的函数关系是v=320????.故选B.
?
知识点3 实际问题中的反比例函数关系
11.近视镜的度数y(度)与镜片焦距x(m)成反比例,且200度近视镜的镜片焦距为0.5 m,则y与x之间的函数关系式为 .?
答案
11.y=100???? 【解析】 由题意可设y=????????(k≠0),当x=0.5时,y=200,所以k=100,所以y=100????.
?
知识点3 实际问题中的反比例函数关系
12.已知一个长方体的体积是100 cm3,它的长是 x cm,宽是5 cm,高是y cm.
(1)写出y与x之间的函数关系式;
(2)写出自变量x的取值范围;
(3)当长方体的长是8 cm时,求它的高.
答案
12.【解析】 (1)由题意,得5xy=100,
所以y与x之间的函数关系式为y=20????.
(2)因为长方体的长大于等于长方体的宽,
所以自变量x的取值范围是x≥5.
(3)当x=8时,y=208=2.5,
所以当长方体的长是8 cm时,高是2.5 cm.
?
知识点3 实际问题中的反比例函数关系
在实际问题中,注意自变量的取值范围应符合实际意义.
2 反比例函数的
图象与性质
课时1 反比例函数的图象
课时1
1.在同一平面直角坐标系中,画出反比例函数y=8????与y=-8????的图象.
?
答案
1.【解析】 列表如下:
描点、连线,如图所示.
知识点1 反比例函数图象的画法
答案
画反比例函数图象的注意事项
(1)在列表时,要尽量多取一些数值,这样能多描出一些点,方便连线;(2)连线时,一定要用光滑的曲线,不能用折线;(3)因为反比例函数中的自变量x≠0,函数值y≠0,所以其图象与x轴、y轴都没有交点;(4)要注意图象端点处的延伸性;(5)作出图象后要注明函数的表达式.
知识点1 反比例函数图象的画法
2.反比例函数y=????????(k<0)的大致图象是 ( )
?
答案
2.B 【解析】 反比例函数y=????????(k≠0)的图象是由两支曲线组成的.当k<0时,两支曲线分别位于第二、四象限内.故
选B.
?
知识点2 反比例函数的图象与比例系数k的关系
反比例函数图象的位置是由比例系数k的符号决定的;反之,由双曲线所在位置,也可以推断出k的符号.
3.当x<0时,函数y=4????的图象在 ( )
A.第二、四象限 B.第二象限
C.第一、三象限 D.第三象限
?
答案
3.D 【解析】 因为函数y=4????中,k=4>0,所以当x<0时,函数y=4????的图象在第三象限.故选D.
?
知识点2 反比例函数的图象与比例系数k的关系
4.[2019海南中考]如果反比例函数y=?????2????(a是常数)的图象在第一、三象限,那么a的取值范围是 ( )
A.a<0 B.a>0
C.a<2 D.a>2
?
答案
4.D 【解析】 ∵反比例函数y=?????2????(a是常数)的图象在第一、三象限,∴a-2>0,∴a>2.故选D.
?
知识点2 反比例函数的图象与比例系数k的关系
5.[2019辽宁大连二模]若点A(-2,m)在反比例函数y=2????的图象上,则m的值是 ( )
A.14 B.-14
C.1 D.-1
?
答案
5.D 【解析】 ∵点A(-2,m)在反比例函数y=2????的图象上,∴m=2?2,即m=-1.故选D.
?
知识点3 反比例函数图象上的点的坐标
6.[2019黑龙江哈尔滨中考]点(-1,4)在反比例函数y=????????的图象上,则下列各点在此函数图象上的是 ( )
A.(4,-1) B.(-14,1)
C.(-4,-1) D.(14,2)
?
答案
6.A 【解析】 将点(-1,4)代入y=????????,得k=-4,∴y=-4????,将四个选项的坐标分别代入反比例函数y=-4????中,可知点(4,-1)在函数图象上.故选A.
?
知识点3 反比例函数图象上的点的坐标
7.[2018海南中考]已知反比例函数y=????????的图象经过点P(-1,2),则这个函数的图象位于 ( )
A.第二、三象限
B.第一、三象限
C.第三、四象限
D.第二、四象限
?
答案
7.D 【解析】 将点P(-1,2)代入y=????????,得k=-2<0,所以其图象位于第二、四象限.故选D.
?
知识点3 反比例函数图象上的点的坐标
8.[2018浙江湖州中考]如图,已知直线y=k1x(k1≠0)与反比例函数y=????2????(k2≠0)的图象交于M,N两点.若点M的坐标是(1,2),则点N的坐标是 ( )
A.(-1,-2) B.(-1,2)
C.(1,-2) D.(-2,-1)
?
答案
8.A 【解析】 因为点M,N都在反比例函数的图象上,且两点的连线经过原点,所以M,N关于原点对称.因为点M的坐标是(1,2),所以点N的坐标是(-1,-2).故选A.
知识点4 反比例函数图象的对称性
9.已知点P为反比例函数y=3????的图象上一点,且点P到坐标原点的距离为10,则符合条件的点P有 ( )
A.0个 B.2个
C.4个 D.无数个
?
答案
9.C 【解析】 易知反比例函数y=3????在第一象限内的图象上到坐标原点的距离为10的点为(1,3)和(3,1),根据反比例函数图象的对称性,可知符合条件的点P有4个.故选C.
?
知识点4 反比例函数图象的对称性
1.[2019河北中考]如图,函数y=1????(????>0),?1????(????<0)的图象所在坐标系的原点是 ( )
A.点M
B.点N
C.点P
D.点Q
?
答案
1.A 【解析】 对于y=1????(x>0),其图象位于第一象限;对于y=-1????(x<0),其图象位于第二象限,故所在坐标系的原点是点M.故选A.
?
2.已知反比例函数y=????????的图象如图所示,则k的值可能是 ( )
A.-1 B.12 C.1 D.2
?
答案
2.B 【解析】 因为反比例函数的图象在第一、三象限,所以k>0.因为当x=1时,y<1,所以k<1.故选B.
3.[2019山东济南中考]函数y=-ax+a与y=????????(a≠0)在同一坐标系中的图象可能是 ( )
?
答案
3.D 【解析】 当a>0时,-a<0,y=-ax+a过第一、二、四象限,y=????????位于第一、三象限,无选项符合.当a<0时,-a>0,y=
-ax+a过第一、三、四象限,y=????????(a≠0)位于第二、四象限,只有D符合.故选D.
?
4.[2020广西北部湾经济区一模]如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=????????(x<0)的图象经过顶点B,则k的值为 ( )
A.-12 B.-27 C.-32 D.-36
?
答案
4.C 【解析】 ∵点A的坐标为(-3,4),∴OA=32+42=5.∵四边形OABC是菱形,∴AB=OA=5,AB∥OC,∴点B的坐标为(-8,4).将点B的坐标代入y=????????,得4=?????8,解得k=-32.故选C.
?
5.如图,直线y=x+a-2与双曲线y=4????交于A,B两点,则当线段AB的长度最小时,a的值为 ( )
A.0 B.1
C.2 D.5
?
答案
5.C 【解析】 反比例函数的图象既是轴对称图形又是中心对称图形,只有当A,B,O(坐标原点)三点共线时,才能使线段AB的长度最小,所以直线y=x+a-2过坐标原点,把(0,0)代入 y=x+a-2,得a=2.故选C.
6.对于反比例函数y=4????,下列说法错误的是 ( )
A.它的图象与坐标轴永远不相交
B.它的图象绕原点旋转180°能和本身重合
C.它的图象关于直线y=±x对称
D.它的图象与直线y=-x有两个交点
?
答案
6.D 【解析】 反比例函数y=4????的图象位于第一、三象限,直线y=-x经过第二、四象限,所以直线y=-x与双曲线y=4????无交点,所以选项D中的说法是错误的.故选D.
?
7.[2019辽宁朝阳中考]从点M(-1,6),N(12,12),E(2,-3),F(-3,-2)中任取一点,所取的点恰好在反比例函数y=6????的图象上的概率为? .?
8.已知点A是反比例函数y=2????(x>0)图象上的一点,点A'是点A关于y轴的对称点,当△AOA'为直角三角形时,点A的坐标是 .?
?
答案
7.12 【解析】 ∵k=6,-1×6=-6≠6,12×12=6,2×(-3)=-6≠6,-3×(-2)=6,∴点N,F在反比例函数y=6????的图象上,故所取的点恰好在反比例函数y=6????的图象上的概率为24=12.
8.(2,2) 【解析】 因为点A是反比例函数y=2????(x>0)图象上的一点,所以设点A的坐标为(x,2????).因为点A'是点A关于y轴的对称点,所以OA=OA',又因为△AOA'为直角三角形,所以△AOA'为等腰直角三角形,所以OA与x轴、y轴正半轴的夹角均为45°,所以点A的纵坐标与横坐标相等,即x=2????,又因为x>0,所以x=2,故点A的坐标为(2,2).
?
9.已知反比例函数y=?????7????的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m
的值.
?
答案
9.【解析】 (1)该函数图象的另一支在第三象限.
∵该反比例函数的图象位于第一、三象限,
∴m-7>0,∴m>7,
∴m的取值范围为m>7.
(2)设点A的坐标为(x,y).
∵点B与点A关于x轴对称,
∴点B的坐标为(x,-y).
∵S△OAB=6,∴12·2y·x=6,∴xy=6.
∵点A在反比例函数y=?????7????的图象上,
∴xy=m-7,∴m-7=6,
∴m=13.
?
课时2 反比例函数的性质
课时2
1.下列函数的图象,在每一个象限内,y值随x值的增大而增大的是 ( )
A.y=1???? B.y=-x+1
C.y=12???? D.y=-1????
?
答案
1.D 【解析】 A项,对于反比例函数y=1????,k=1>0,函数的图象在其所在的每一个象限内,y值随x值的增大而减小,不合题意;B项,对于一次函数y=-x+1,k=-1<0,y值随x值的增大而减小,不合题意;C项,对于反比例函数y=12????,k=12>0,函数的图象在其所在的每一个象限内,y值随x值的增大而减小,不合题意;D项,对于反比例函数y=-1????,k=-1<0,函数的图象在其所在的每一个象限内,y值随x值的增大而增大,符合题意.故选D.
?
知识点1 反比例函数的性质
描述反比例函数值的增减情况时,必须指出“在每一象限内”,而不能直接说“当k>0时,y值随x值的增大而减小”.
2.[2020贵州毕节一模]若反比例函数y=3????的图象上有P1(x1,-2),P2(x2,-3)两点,则x1与x2的大小关系是( )
A.x1>x2 B.x1=x2
C.x1
答案
2.C 【解析】 ∵k=3>0,∴反比例函数y=3????的图象位于第一、三象限,且在每个象限内,y随x的增大而减小.∵-2>
-3,∴x1
知识点1 反比例函数的性质
3.已知A(1,y1),B(2,y2)两点在反比例函数y=5+2????????的图象上,若y1
C.m>-52 D.m<-52
?
答案
3.D 【解析】 因为A(1,y1),B(2,y2)两点在反比例函数y=5+2????????的图象上,且y1
知识点1 反比例函数的性质
4.[2018湖南衡阳中考]对于反比例函数y=-2????,下列说法不正确的是 ( )
A.图象分布在第二、四象限
B.当x>0时,y随x的增大而增大
C.图象经过点(1,-2)
D.若点A(x1,y1),B(x2,y2)都在图象上,且x1
答案
4.D 【解析】 ∵-2<0,∴该反比例函数的图象位于第二、四象限,且当x>0时,y随x的增大而增大,故选项A,B中的说法正确.∵1×(-2)=-2,∴其图象经过点(1,-2),故选项C中的说法正确.当点A,B在该反比例函数图象的同一条曲线上时,若x1
知识点1 反比例函数的性质
5.[2019河南焦作一模]已知反比例函数y=2????,当x<-1时,y的取值范围为 .?
?
答案
5.-2
知识点1 反比例函数的性质
6.反比例函数y=????????的图象如图所示,点A是该函数图象上一点,AB垂直于x轴,垂足是点B,若????△????????????=1,则k的值为 ( )
A.1 B.-1 C.2 D.-2
?
答案
6.D 【解析】 因为点A在反比例函数y=????????的图象上,所以S△AOB=12|k|=1,解得k=±2,又因为反比例函数的图象在第二、四象限,所以k<0,则k=-2.故选D.
?
知识点2 反比例函数中比例系数k的几何意义
借助k的几何意义求反比例函数的表达式
过双曲线y=????????(k≠0)上任意一点作x轴或y轴的垂线,该点与垂足及原点构成的三角形的面积为|????|2.反比例函数表达式的确定,除了根据构成的三角形的面积等于|????|2外,还应看函数图象所在的位置,以便于确定k的符号.
?
7.[2019山东临沂一模]如图,点A是反比例函数y=-6????(x<0)的图象上的一点,过点A作?ABCD,使点B,C在x轴上,点D在y轴上,则?ABCD的面积为 ( )
A.1 B.3 C.6 D.12
?
答案
7.C 【解析】 如图,过点A作AH⊥OB于点H.∵四边形ABCD是平行四边形,∴AD∥OB,
∴?????????????????????=????矩形????????????????.∵点A是反比例函数y=-6????(x<0)的图象上的一点,∴????矩形????????????????=|-6|=
6,∴?????????????????????=6.故选C.
?
知识点2 反比例函数中比例系数k的几何意义
8.如图,过y轴正半轴上的任意一点P作x轴的平行线,分别与反比例函数y=-4????和y=2????的图象交于点A和点B,若点C是x轴上的任意一点,连接AC,BC,则△ABC的面积为 ( )
A.3 B.4
C.5 D.6
?
答案
8.A 【解析】 连接OA,OB,则 S△ABC =S△AOB .因为点B在y=2????的图象上,所以S△OBP =1.因为点A在y=-4????的图象上,所以S△OAP =2,所以S△ABC =S△AOB = S△OBP + S△OAP =3.故选A.
?
知识点2 反比例函数中比例系数k的几何意义
9.[2020湖南永州期中]如图,A,B两点在双曲线y=4????上,分别过A,B两点向x轴、y轴作垂线段,若S阴影=1,则S1 +S2 = ( )
A.8 B.6
C.4 D.2
?
答案
9.B 【解析】 因为A,B两点在双曲线y=4????上,所以矩形ACOD和矩形BEOF的面积均为4.因为S阴影=1,所以S1 =S2 =3,所以S1 +S2 =6.故选B.
?
知识点2 反比例函数中比例系数k的几何意义
10.易错题如图,在平面直角坐标系中,过点M(0,2)的直线与x轴平行且分别与反比例函数y=6????(x>0)和y=????????(x<0)的图象交于P,Q两点.
(1)求点P的坐标;
(2)若△POQ的面积为8,求k的值.
?
知识点2 反比例函数中比例系数k的几何意义
答案
10.【解析】 (1)由题意可得,直线y=2与反比例函数y=6????(x>0)的图象相交于点P,则可设点P的坐标为(a,2),
将点P的坐标(a,2)代入y=6????,解得a=3,
∴点P的坐标为(3,2).
(2) ∵点P在反比例函数y=6????的图象上,
∴S△OPM=12×6=3,
∴S△OQM= S△POQ- S△OPM=8-3=5,
∴|k|=10.
∵函数y=????????(x<0)的图象位于第二象限,∴k<0,
∴k=-10.
?
知识点2 反比例函数中比例系数k的几何意义
1.若在反比例函数y=????+3????图象的每一支上,y都随x的增大而增大,则k的值可以是 ( )
A.-5 B.-2
C.1 D.4
?
答案
1.A 【解析】 因为在反比例函数y=????+3????图象的每一支上,y都随x的增大而增大,所以k+3<0,所以k<-3.故选A.
?
2.易错题[2020天津南开翔宇学校月考]若点(-1,y1),(-14,y2),(12,y3)在函数y=????2+1????(a为常数)的图象上,则函数值y1,y2,y3的大小关系是 ( )
A.y2
答案
2.A 【解析】 ∵反比例函数的比例系数a2+1>0,∴函数y=????2+1????(a为常数)的图象位于第一、三象限,且在每个象限内,y随x的增大而减小.∵-1<-14<0,点(-1,y1),(-14,y2)在第三象限,∴y2
3.[2019浙江金华模拟]如图,直线y=mx与双曲线y=????????交于点A,B,过点A作AM⊥x轴于点M,连接BM.若S△ABM=2,则k的值是 ( )
A.1 B.2
C.3 D.4
?
答案
3.B 【解析】 由题意得S△ABM=2S△AOM=2,所以S△AOM=12|k|=1,所以k=±2.因为双曲线y=????????位于第一、三象限,所以k>0,所以k=2.故选B.
?
4.如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线y=3????(x>0)上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会 ( )
A.逐渐增大 B.逐渐减小
C.不变 D.先增大后减小
?
答案
4.B 【解析】 设点B的坐标为(a,b),因为点B是双曲线y=3????(x>0)上的一个动点,所以a>0,b>0,纵坐标b随着横坐标a的增大而减小.因为S△OAB=12OA·b,OA为定值,所以当点B的横坐标a逐渐增大时,△OAB的面积逐渐减小.故选B.
?
5.[2018浙江宁波中考]如图,平行于x轴的直线与函数y=????1????(k1>0,x>0), y=????2????(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点.若△ABC的面积为4,则k1-k2的值为 ( )
A.8 B.-8 C.4 D.-4
?
答案
5.A 【解析】 如图,连接AO,BO.∵AB∥x轴,∴S△ABO=S△ABC=4.设AB与y轴交于点D,则S△AOD=12k1,S△BOD=12k2.∵S△AOD-S△BOD=S△ABO,即12k1-12k2=4,∴k1-k2=8.故选A.
?
6.[2019山西临汾期中]如图,点A在双曲线y=1????(x>0)上,点B在双曲线y=3????(x>0)上,且AB∥x轴,C,D在x轴上,若四边形ABCD为矩形,则它的面积为 .?
?
答案
6.2 【解析】 如图,延长BA交y轴于点E.∵AB∥x轴,四边形ABCD为矩形,∴四边形AEOD和四边形BEOC都是矩形.∵点A在双曲线y=1????(x>0)上,
∴矩形AEOD的面积为1.∵点B在双曲线y=3????(x>0)上,∴矩形BEOC的面积为3,∴矩形ABCD的面积为3-1=2.
?
7.易错题[2019广东江门期末]如图,在平面直角坐标系中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=????????(x<0)的图象上,则k的值为 .?
?
答案
7.-6 【解析】 如图,连接AC,交y轴于点D,∵四边形OABC为菱形,∴AC⊥OB,且CD=
AD,BD=OD.∵菱形OABC的面积为12,∴S△CDO=14S菱形OABC=3,∴|k|=6.∵当x<0时,反比例函数图象位于第二象限,∴k<0,∴k=-6.
?
8.如图,在第一象限内,正比例函数y=ax的图象与反比例函数y=????????的图象交于点A(3,2).
(1)试确定上述正比例函数和反比例函数的表达式.
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)点M(m,n)是反比例函数图象上的一动点,其中0
答案
8.【解析】 (1)∵在第一象限内,正比例函数y=ax的图象与反比例函数y=????????的图象交于点A(3,2),
∴2=3a,2=????3,∴a=23,k=6,
∴正比例函数的表达式为y=23x,
?
答案
反比例函数的表达式为y=6????.
(2)由题中图象,知当0
连接OD.
∵MB∥x轴,AC∥y轴,∠BOC=90°,
∴四边形OCDB为矩形,∴S△BOD =S△COD .
∵点M,A在双曲线y=6????上,∴S△OBM =S△AOC =3,
∴S△ODM =S△AOD .
∵四边形OADM的面积为6,
∴S△ODM =S△OBM =3,∴BM=DM.
?
3 反比例函数的应用
1.[2019江苏淮安中考]当矩形面积一定时,下列图象中能表示它的长y和宽x之间函数关系的是 ( )
答案
1.B 【解析】 设矩形的面积为S(定值),则xy=S,∴y是x的反比例函数(x>0,y>0).故选B.
知识点1 利用反比例函数解决实际问题
在实际问题中要判断其中的两个量是否成反比例,应先根据题意列出函数的表达式.对于实际问题中函数自变量的取值范围,除使表达式有意义外,还要使实际问题有意义.
2.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于120 kPa时,气球将会爆炸,为了安全起见,气球的体积应 ( )
A.不小于54 m3 B.大于54 m3
C.不小于45 m3 D.小于45 m3
?
答案
2.C 【解析】 因为气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,所以可设p=????????(V>0),由题图可知,当V=
1.6时,p=60,所以k=1.6×60=96,所以p=96????(V>0).为了安全起见,气球内的气压应不大于120 kPa,即96????≤120,所以V≥45.故选C.
?
知识点1 利用反比例函数解决实际问题
3.[2020山东济南外国语期中]在一个可以改变容积的密闭容器内,装有一定质量m(kg)的某种气体,当改变容积V(m3)时,气体的密度ρ(kg/m3)也随之改变,ρ与V在一定范围内满足ρ=????????,它的图象如图所示,则该气体的质量为 kg.?
?
答案
3.7 【解析】 因为ρ=????????,所以m=ρV.因为点(5,1.4)在函数图象上,所以m=5×1.4=7(kg).
?
知识点1 利用反比例函数解决实际问题
4.在学校就餐时,往往需要在窗口前排队等待.经调查发现,同学们的舒适度指数y与等待时间x(分)之间存在如下的关系:y=100????(x>0).
(1)若等待时间x为5分钟,求舒适度指数y的值.
(2)舒适度指数不低于10时,同学们才会感觉到舒适,函数y=100????(x>0)的图象如图所示,请根
据图象说明,作为食堂的管理员,让每个在窗口排队的同学最多等待多长时间合适?
?
答案
4.【解析】 (1)将x=5代入y=100????中,得y=1005=20.
答:舒适度指数y的值为20.
(2)当y=10时,x=10010=10,
由图象可知,当y>10时,0
?
知识点1 利用反比例函数解决实际问题
5.[2018四川遂宁中考]已知一次函数y1=kx+b(k≠0)与反比例函数y2=????????(m≠0)的图象如图所示,则当y1>y2时,自变量x满足的条件是 ( )
A.1
C.x>1
D.x<3
?
答案
5.A 【解析】 由题中图象可得,当1
6.[2019江苏淮安二模]如图,正比例函数y1=-2x的图象与反比例函数y2=????????的图象交于A,B两点,点C在x轴负半轴上,若AC=AO,△ACO的面积为6,则k的值为 ( )
A.3 B.-3
C.-6 D.6
?
答案
6.C 【解析】 由题意,设A(m,-2m),∵AC=AO,∴△ACO是等腰三角形,∴CO=-2m,∴S△ACO=12×(-2m)×(-2m)=6,
m2=3.∵k=-2m2,∴k=-6.故选C.
?
知识点2 反比例函数与一次函数的综合运用
7.[2019四川泸州中考]如图,一次函数y1=ax+b和反比例函数y2=????????的图象相交于A,B两点,则使y1>y2成立的x取值范围是 .?
?
答案
7.x<-2或0
8.已知一次函数y=x+m的图象与反比例函数y=????+1????(m≠-1)的图象在第一象限内交于点P(n,3),请你分别求出一次函数和反比例函数的表达式.
?
答案
8.【解析】 ∵一次函数y=x+m的图象与反比例函数y=????+1????(m≠-1)的图象在第一象限内交于点P(n,3),
∴m+n=3且????+1????=3,∴n=1,m=2,
∴一次函数的表达式为y=x+2,反比例函数的表达式为y=3????.
?
知识点2 反比例函数与一次函数的综合运用
1.[2018山东临沂中考]如图,正比例函数y1=k1x与反比例函数y2=????2????的图象相交于A,B两点,其中点A的横坐标为1.当y1
B.-1
C.-1
答案
1.D 【解析】 因为正比例函数图象、反比例函数图象均关于原点成中心对称,所以点A,B也关于原点成中心对称,所以点B的横坐标为-1,结合题图可知,当y1
A.5米 B.6米
C.7米 D.8米
答案
2.D 【解析】 ∵四边形AOEB是矩形,∴BE=OA=5米,OE=AB=2米,∴B(2,5).设曲线BC的表达式为y=????????(k>0,x>0),则k=10,∴y=10????(x>0).当y=1时,x=10,∴DE=10-2=8(米).故选D.
?
3.如图,正比例函数y1=k1x和反比例函数y2=????2????的图象交于A(1,2),B两点,给出下列结论:①k1
A.0 B.1
C.2 D.3
?
答案
3.C 【解析】 因为正比例函数y1=k1x和反比例函数y2=????2????的图象交于A(1,2),B两点,所以k1=2,k2=2,B(-1,-2),所以k1=k2,所以结论①不正确;由题中图象,可知当x<-1时,y1
?
4.[2019山东聊城中考]如图,点A(32,4),B(3,m)是直线AB与反比例函数y=????????(x>0)图象的两个交点,AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
(1)求直线AB的表达式;
(2)△ABC和△ABD的面积分别为S1,S2,求S2-S1.
?
答案
4.【解析】 (1)把点A(32,4)代入y=????????(x>0),得4=????32,∴n=6,
∴反比例函数的表达式为y=6????(x>0).
将点B(3,m)代入y=6????(x>0),得m=2,∴B(3,2).
设直线AB的表达式为y=kx+b,
∵点A(32,4),B(3,2)是直线AB上的两点,
?
答案
∴32????+????=4,3????+????=2,解得????=?43,????=6,
∴直线AB的表达式为y=-43x+6.
(2)AC=4,点B到AC的距离为3-32=32,
∴S1=12×4×32=3.
设直线AB与y轴的交点为E,可得E(0,6),
∴DE=6-1=5.
易知点A(32,4),B(3,2)到DE的距离分别为32,3,
∴S2=S△BDE-S△AED=12×5×3-12×5×32=154,
∴S2-S1=154-3=34.
?
5.环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的质量浓度超标,即硫化物的质量浓度超过最高允许的1.0 mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的质量浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,其中第3天时硫化物的质量浓度降为4 mg/L.从第3天起所排污水中硫化物的质量浓度y与时间x满足下面表格中的关系:
(1)求整改过程中当0≤x≤3时,硫化物的质量浓度y与时间x的函数表达式;
(2)求整改过程中当x≥3时,硫化物的质量浓度y与时间x的函数表达式;
(3)该企业所排污水中硫化物的质量浓度能否在15天以内不超过最高允许的1.0 mg/L?为什么?
时间x/天
3
4
5
6
8
?
硫化物的质量浓度y/(mg/L)
4
3
2.4
2
1.5
?
答案
5.【解析】 (1)前3天的函数图象是线段AB,设直线AB的函数表达式为y=kx+b,
把(0,10),(3,4)代入y=kx+b,得????=10,3????+????=4,解得????=?2,????=10,
所以当0≤x≤3时,硫化物的质量浓度y与时间x的函数表达式为y=-2x+10.
(2)当x≥3时,由题意可知,硫化物的质量浓度y与时间x成反比例关系,设该函数的表达式为y=????????(k≠0),
把(3,4)代入y=????????(k≠0),得4=????3,所以k=12,
所以当x≥3时,硫化物的质量浓度y与时间x的函数表达式为y=12????.
(3)能.理由如下:
令y=12????=1,则x=12<15,
所以该企业所排污水中硫化物的质量浓度能在15天以内不超过最高允许的1.0 mg/L.
?
易错疑难集训
集训
1.当m= 时,函数y=(m+3)????2?????是反比例函数??
?
答案
1.3 【解析】 因为函数y=(m+3)????2?|?????是反比例函数,所以2-|m|=-1且 m+3≠0,即m=±3且m≠-3,故m=3.
?
易错点 1 忽视反比例函数y=????????中比例系数k的限制条件
?
错解:因为函数y=(m+3)????2??|?????是反比例函数,所以2-|m|=-1,所以m=±3.
分析:解题过程中,忽略条件m+3≠0,从而得到错误答案m=±3.
?
2.如图,已知矩形OABC的面积为6,且反比例函数y=????????的图象经过点B,则k= .?
?
答案
2.-6 【解析】 因为矩形OABC的面积为6,点B在反比例函数y=????????的图象上,且点B在第四象限,所以k=-6.
?
易错点 1 忽视反比例函数y=????????中比例系数k的限制条件
?
错解:6
分析:出现错解的原因是直接由矩形OABC的面积为6,点B在反比例函数y=????????的图象上,得到k=6,忽略了题图中点B在第四象限这一隐含条件.
?
3.已知反比例函数y=(3m-1)????????2?2的图象在所在的每一个象限内,y随x的增大而增大,求该反比例函数的表达式.
?
答案
3.【解析】 ∵反比例函数y=(3m-1)????????2?2的图象在所在的每一个象限内,y随x的增大而增大,
∴????2?2=?1,3?????1<0,解得????=±1,????<13,
∴m=-1,
∴该反比例函数的表达式为y=-4????.
?
易错点 1 忽视反比例函数y=????????中比例系数k的限制条件
?
4.现有面积为20 m2的长方形场地,设其一边长为x m,另一边长为y m,则y与x之间的函数关系式为 ,自变量x的取值范围是 .?
答案
4.y=20???? x>0
?
易错点 2 忽略自变量的实际意义
5.已知一个三角形的面积为4,一边长为x,这条边上的高为y,则y关于x的变化规律用图象表示大致是 ( )
答案
5.C 【解析】 因为三角形的面积为4,一边长为x,这条边上的高为y,所以12xy=4,所以y=8????(x>0).故选C.
?
易错点 2 忽略自变量的实际意义
6.某服装厂承揽了一项生产2 000件衬衫的任务,为了抢抓商机,商家要求在10天内(含10天)供货.
(1) 请你写出服装厂每天生产衬衫的件数y与生产天数x之间的函数关系式.
(2) 由于服装厂加班加点,所以提前2天交货,则服装厂每天多生产多少件?
答案
6.【解析】 (1)所求函数关系式为y=2?000????(0
答:服装厂每天多生产50件.
?
易错点 2 忽略自变量的实际意义
7.[2019江苏徐州中考]若A(x1,y1),B(x2,y2)都在函数y=2?019????的图象上,且x1<0
?
答案
7.A 【解析】 ∵k=2 019>0,∴该函数图象在第一、三象限,当x<0时,y<0,当x>0时,y>0,∵A(x1,y1),B(x2,y2)都在函数y=2?019????的图象上,且x1<0
易错点 3 研究函数的增减性时不分象限
8.设A(x1,y1),B(x2,y2)是反比例函数y=-4????的图象上的点,若x1
答案
8.【解析】 因为反比例函数y=-4????中比例系数k<0,
所以反比例函数y=-4????的图象位于第二、四象限,在每一象限内,y值随x值的增大而增大.
当x1,x2同号时,若x1
由k<0,知y1>0>y2.
?
易错点 3 研究函数的增减性时不分象限
错解:因为反比例函数y=-4????中比例系数k<0,所以反比例函数y=-4????的图象位于第二、四象限,y值随x值的增大而增大,所以若x1
?
1.如图,双曲线y=????????与直线y=kx+b交于点M,N,并且点M的坐标为(1,3),点N的纵坐标为-1.根据图象信息可得关于x的方程????????=kx+b的解为 ( )
A.-3,1 B.-3,3 C.-1,1 D.-1,3
?
答案
1.A 【解析】 因为双曲线y=????????与直线y=kx+b交于点M,N,并且点M的坐标为(1,3),所以m=3,双曲线的表达式为y=3????.因为点N的纵坐标为-1,代入双曲线的表达式可得点N的横坐标为-3.由题中图象可得关于x的方程????????=kx+b的解为双曲线y=????????与直线y=kx+b的交点N,M的横坐标,即-3,1.故选A.
?
疑难点 1 反比例函数图象与一次函数图象的交点
2.[2019山东济南莱芜区中考]如图,直线l与x轴,y轴分别交于A,B两点,且与反比例函数y=????????(x>0)的图象交于点C,若S△AOB=S△BOC=1,则k= ( )
A.1 B.2
C.3 D.4
?
答案
2.D 【解析】 如图,过点C作CD⊥x轴于点D,设OB=a(a>0).∵S△AOB=S△BOC, ∴AB=BC.∵S△AOB=1,∴12OA·OB=1, ∴OA=2????.∵CD∥OB,AB=BC, ∴OD=OA=2????, CD=2OB=2a,∴C(2????,2a).∵反比例函数y=????????(x>0)的图象经过点C,∴k=2????×2a=4.故选D.
?
疑难点 1 反比例函数图象与一次函数图象的交点
3.[2019广西贺州一模]下列选项中,阴影部分面积最小的是 ( )
答案
3.C 【解析】 由反比例函数y=????????中比例系数k的几何意义,易知A项和B项中阴影部分的面积都是2.C项中,过点M作MP⊥x轴于点P,过点N作NQ⊥x轴于点Q,则S阴影部分=S梯形NQPM+S△MOP-S△NOQ=12×(1+2)×1+12×1×2-12×2×1=32.D项中,阴影部分的面积为12×1×4=2.故选C.
?
疑难点2 反比例函数y=?????????(k≠0)中比例系数k的几何意义
?
4.如图1,点A是x轴上的一个动点,过点A作x轴的垂线PA交双曲线y=1????于点P,连接OP.
(1)当点A在x轴上的正方向上运动时,Rt△AOP的面积是否发生变化?若不变,请求出Rt△AOP的面积;若变化,请说明理由.
(2)如图2,在x轴上点A的右侧有一点D,过点D作x轴的垂线DB交双曲线y=1????于点B,连接BO交AP于点C,设△AOP的面积为S1,梯形BCAD的面积为S2,则S1与S2的大小关系是S1 S2.(选填“>”“=”或“<”)?
(3)如图3,PO的延长线与双曲线y=1????的另一个交点是F,作FH垂直于x轴,垂足为H,连接AF,PH,试说明四边形APHF的面积为常数.
?
疑难点2 反比例函数y=?????????(k≠0)中比例系数k的几何意义
?
答案
4.【分析】 (1)由于点A是x正半轴上的动点,点P始终在双曲线上,根据反比例函数y=????????中比例系数k的几何意义,可以得出△AOP的面积是否发生变化;(2)利用(1)中的结论,求出△AOP和△BOD的面积,由△AOC是公共部分即可得出S1与S2的大小关系;(3)由双曲线的对称性可知,四边形APHF是平行四边形,又因为△AOP的面积为常数,所以四边形APHF的面积也是常数.
【解析】 (1)Rt△AOP的面积不变.
根据反比例函数y=????????中比例系数k的几何意义,得S△AOP=12.
(2)>
由(1)知S1=12,S2=S△BOD-S△AOC=12-S△AOC,所以S1>S2.
(3)由已知条件可知四边形APHF是平行四边形,则AH,PF互相平分并交于点O,
由(1)知S△AOP=12,所以S四边形APHF=4S△AOP=2.
?
疑难点2 反比例函数y=?????????(k≠0)中比例系数k的几何意义
?
答案
与反比例函数y=????????的图象有关的图形面积问题主要是矩形和三角形的面积问题,以及由矩形和三角形所形成的图形的面积问题,面积的计算方法主要有直接计算、间接计算和变换计算三种,本题主要采用间接计算.解题的关键是理解与运用反比例函数y=????????的比例系数k的几何意义.在解与面积有关的几何图形时,要特别注意点的坐标与线段长度之间的转化关系及符号问题.
?
疑难点2 反比例函数y=?????????(k≠0)中比例系数k的几何意义
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
