北师大版八年级上册数学第三章位置与坐标素养拓展课件(32张PPT)
文档属性
| 名称 | 北师大版八年级上册数学第三章位置与坐标素养拓展课件(32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 09:22:31 | ||
图片预览









文档简介
第三章·位置与坐标
数学·八年级上册·北师
专项素养拓训
专项 点的坐标
专项
1.点M(m+1,m+3)在y轴上,则点M的坐标为( )
A.(0,-4) B.(4,0) C.(-2,0) D.(0,2)
答案
1.D 【解析】 因为点M(m+1,m+3)在y轴上,所以m+1=0,解得m=-1,所以m+3=-1+3=2,所以点M的坐标为(0,2).故选D.
类型1 点的坐标特征
2.若点A(n-2,n+3)在x轴上,则点B(n-1,n+1)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案
2.C 【解析】 因为点A(n-2,n+3)在x轴上,所以n+3=0,所以n=-3,所以n-1=-4<0,n+1=-2<0,所以点B在第三象限.故选C.
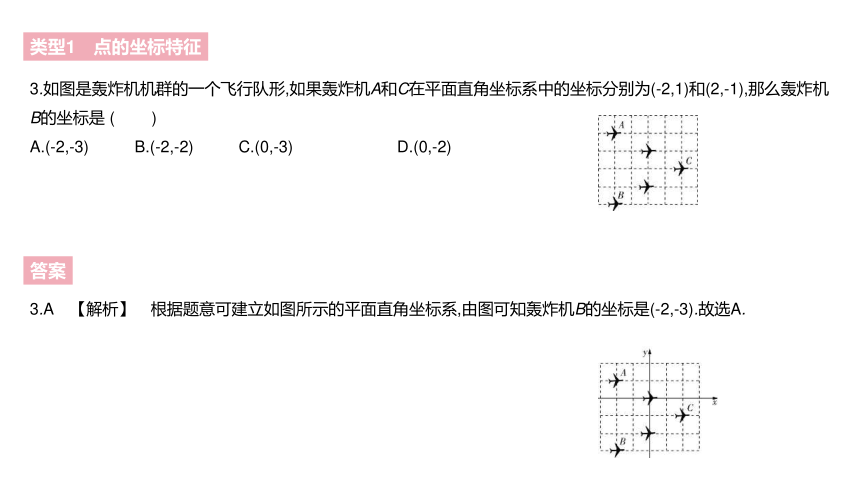
3.如图是轰炸机机群的一个飞行队形,如果轰炸机A和C在平面直角坐标系中的坐标分别为(-2,1)和(2,-1),那么轰炸机B的坐标是 ( )
A.(-2,-3) B.(-2,-2) C.(0,-3) D.(0,-2)
类型1 点的坐标特征
答案
3.A 【解析】 根据题意可建立如图所示的平面直角坐标系,由图可知轰炸机B的坐标是(-2,-3).故选A.
4.[2019湖北武汉黄陂区期末]已知甲、乙、丙三人所在的位置不同,他们三人都以相同的单位长度建立不同的坐标系,甲说:“以我为坐标原点,乙的位置是(4,3)”,丙说:“以我为坐标原点,乙的位置是(-3,-4)”.若以乙为坐标原点,则甲和丙的位置分别是 ( )
A.(3,4),(-3,-4) B.(4,-3),(3,-4)
C.(-3,-4),(4,3) D.(-4,-3),(3,4)
类型1 点的坐标特征
答案
4.D 【解析】 以甲为坐标原点,乙的位置是(4,3),则以乙为坐标原点,甲的位置是(-4,-3);以丙为坐标原点,乙的位置是(-3,-4),则以乙为坐标原点,丙的位置是(3,4).故选D.
5.已知点P到x轴,y轴的距离分别是2和3,且点P关于y轴对称的点在第四象限,则点P的坐标是 .?
类型1 点的坐标特征
答案
5.(-3,-2) 【解析】 因为点P关于y轴对称的点在第四象限,所以点P在第三象限,结合点P到x轴,y轴的距离分别是2和3,可知点P的坐标是(-3,-2).
6.在平面直角坐标系中,点A的坐标是(2,-3),作点A关于x轴的对称点,得到点A',再作点A'关于y轴的对称点,得到点A″,则点A″的坐标是( , ).?
答案
6.-2 3 【解析】 因为点A的坐标是(2,-3),点A'与点A关于x轴对称,所以点A'的坐标为(2,3).因为点A″与点A'关于y轴对称,所以点A″的坐标是(-2,3).
7.在平面直角坐标系中,将点(-b,-a)称为点(a,b)的“关联点”(例如点(-2,-1)是点(1,2)的“关联点”).如果一个点和它的“关联点”在同一象限内,那么这一点在第 象限.?
类型1 点的坐标特征
答案
7.二或四 【解析】 因为(-b,-a)与(a,b)在同一象限,所以-b与a符号相同,-a与b符号相同,所以a,b符号相反,所以这一点在第二象限或第四象限.
8.若点(5-a,a-3)在第一、三象限的角平分线上,求a的值.
答案
8.【解析】 因为点(5-a,a-3)在第一、三象限的角平分线上,所以5-a=a-3,解得a=4.
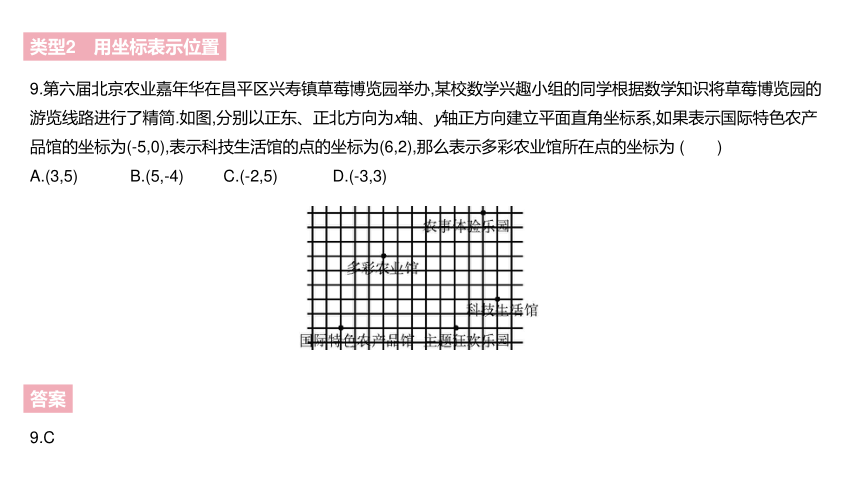
9.第六届北京农业嘉年华在昌平区兴寿镇草莓博览园举办,某校数学兴趣小组的同学根据数学知识将草莓博览园的游览线路进行了精简.如图,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,如果表示国际特色农产品馆的坐标为(-5,0),表示科技生活馆的点的坐标为(6,2),那么表示多彩农业馆所在点的坐标为 ( )
A.(3,5) B.(5,-4) C.(-2,5) D.(-3,3)
类型2 用坐标表示位置
答案
9.C
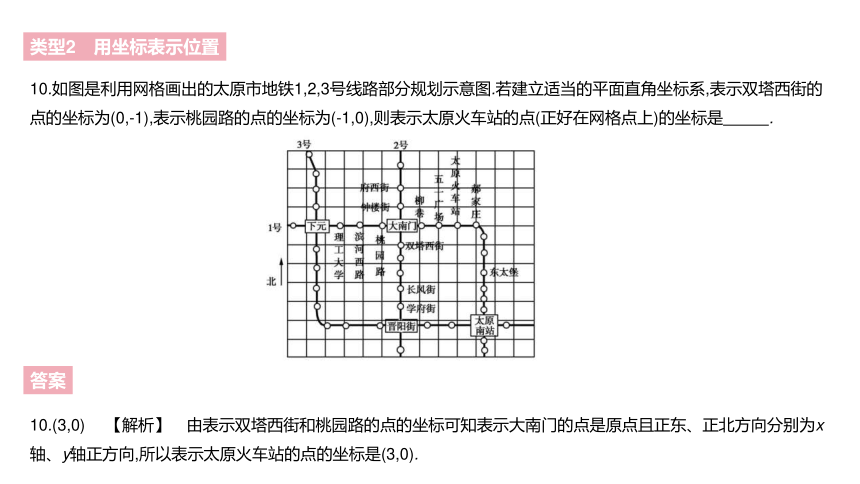
10.如图是利用网格画出的太原市地铁1,2,3号线路部分规划示意图.若建立适当的平面直角坐标系,表示双塔西街的点的坐标为(0,-1),表示桃园路的点的坐标为(-1,0),则表示太原火车站的点(正好在网格点上)的坐标是 .?
类型2 用坐标表示位置
答案
10.(3,0) 【解析】 由表示双塔西街和桃园路的点的坐标可知表示大南门的点是原点且正东、正北方向分别为x轴、y轴正方向,所以表示太原火车站的点的坐标是(3,0).
11.已知A(a,0)和B(0,10)两点,且AB与坐标轴围成的三角形的面积等于20,则a的值为( )
A.2 B.4
C.0或4 D.4或-4
类型3 点的坐标与图形面积
答案
11.D 【解析】 因为A(a,0),B(0,10),所以OA=|a|,OB=10,所以S△AOB=12OA·OB=12×10|a|=20,解得a=±4.故选D.
?
12.如图,已知A(4,3),B(3,b-1),C(1,2),且△ABC关于x轴的对称图形为△A'B'C'.
(1)作出△ABC关于x轴的对称图形△A'B'C';
(2)若点B'(a-1,-1),求a+b的值.
类型3 点的坐标与图形面积
答案
12.【解析】 (1)△A'B'C'如图所示.
(2)因为点B'(a-1,-1)与点B关于x轴对称,
所以a-1=3,b-1=1,
解得a=4,b=2,所以a+b=6.
13.在平面直角坐标系中,已知点A,B的坐标分别为(-3,4),(4,-2).
(1)求点A,B关于y轴的对称点的坐标;
(2)在平面直角坐标系中分别作出点A,B关于x轴的对称点M,N,顺次连接AM,BM,BN,AN,求四边形AMBN的面积.
类型3 点的坐标与图形面积
答案
13.【解析】 (1)根据轴对称的性质,得点A(-3,4)关于y轴的对称点的坐标是(3,4);
点B(4,-2)关于y轴的对称点的坐标是(-4,-2).
(2)因为点M与点A、点N与点B关于x轴对称,
所以M(-3,-4),N(4,2),所以四边形AMBN为梯形.
因为AM,BN平行于y轴,
所以梯形AMBN的高为7,且AM=8,BN=4,
所以S梯形AMBN=12×7×(8+4)=42.
故四边形AMBN的面积为42.
?
综合素养拓训
1.[探究图形变换的点的坐标]如图,已知正方形ABCD的顶点A(1,3),B(1,1),C(3,1),规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位长度”为一次变换,如此这样,连续经过2 020次变换后,正方形ABCD的对角线的交点M的坐标为( )
A.(-2 018,2) B.(-2 018,-2)
C.(-2 017,-2) D.(-2 017,2)
答案
1.A 【解析】 由题意,得变换前点M的坐标为(2,2),第1次变换为M1(1,-2),第2次变换为M2(0,2),第3次变换为M3(-1,
-2),第4次变换为M4(-2,2)……从而得到规律:当n为奇数时,Mn(2-n,-2);当n为偶数时,Mn(2-n,2).所以当n=2 020时,
M2 020(-2 018,2).故选A.
答案
2.D 【解析】 由题意知,P1(1,1),P2(1,2),P3(1,3),P4(1,4),P5(1,5),P6(2,1),P7(2,2),P8(2,3),P9(2,4),P10(2,5),…,观察以上数据,因为2 020÷5=404,所以P2 020的坐标为(404,5).故选D.
2.[探究点的坐标变化规律][2020湖北黄石期末]某校数学课外小组,在坐标纸上为某湿地公园的一块空地设计植树方案如下:第k棵树种植在点Pk(xk,yk)处,x1=1,y1=1,当k≥2时,????????=?????????1+[?????15]?[?????25],????????=?????????1+1?5([?????15]?[?????25]),其中 [a]表示非负实数a的整数部分,例如[2.3]=2,[43]=1,[0.5]=0.按此方案,第2 020棵树种植点的坐标应为( )
A.(6,2 020) B.(2 020,5)
C.(403,5) D.(404,5)
?
答案
3.【解析】 (1)AB=(?3?2)2+(?8?4)2=52+122=13.(2)AB=|-1-5|=6.
(3)能.理由如下:
因为DE=(?3?0)2+(2?6)2=5,EF=[3?(?3)]2+(2?2)2=6,DF=(3?0)2+(2?6)2=5,
所以DE=DF,
又因为52+52≠62,
所以△DEF为等腰三角形.
?
3.[两点间的距离公式]先阅读文字,再回答问题:
已知在平面内有两点P1(x1,y1),P2(x2,y2),则这两点间的距离公式为P1P2=(????2?????1)2+(????2?????1)2.同时,当这两点在同一坐标轴上或所在直线平行于坐标轴时,这两点间的距离公式可简化为|x2-x1|或|y2-y1|.
(1)已知点A(2,4),B(-3,-8),试求A,B两点间的距离;
(2)已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为-1,试求A,B两点间的距离;
(3)已知一个三角形各顶点的坐标为D(0,6),E(-3,2),F(3,2),你能判定此三角形的形状吗?请说明理由.
?
答案
1.B
一、选择题
1.[2020广东广州越秀区期中]下列各点中,位于第四象限的是 ( )
A.(-4,3) B.(4,-3) C.(4,3) D.(-4,-3)
答案
2.D 【解析】 因为点M位于第二象限,所以点M的横坐标为负数,纵坐标为正数.因为点M距离x轴5个单位长度,距离y轴3个单位长度,所以点M的坐标为(-3,5).故选D.
2.[2020山东济南槐荫区期末]已知点M在第二象限,且点M距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为 ( )
A.(5,-3) B.(-5,3) C.(3,-5) D.(-3,5)
答案
3.D
3.[2019浙江金华中考]如图是雷达屏幕在一次探测中发现的多个目标,其中对目标A的位置表述正确的是 ( )
A.在南偏东75°方向处
B.在5 km处
C.在南偏东15°方向5 km处
D.在南偏东75°方向5 km处
答案
4.A 【解析】 由题意可知,-3=m-1,所以m=-2.故选A.
4.[2020辽宁辽阳期末]已知点A(m+2,-3)和点B(4,m-1),若直线AB∥x轴,则m的值为 ( )
A.-2 B.-4 C.2 D.3
答案
5.C 【解析】 根据题意建立如图所示的平面
直角坐标系,所以含弘楼的位置可以表示成(-2,0).故选C.
5.[2020重庆沙坪坝区月考]重庆一中寄宿学校北楼、食堂、含弘楼的位置如图所示,如果北楼的位置用(-1,2)表示,食堂的位置用(2,1)表示,那么含弘楼的位置可以表示成 ( )
A.(0,0) B.(0,4) C.(-2,0) D.(1,5)
答案
6.A 【解析】 因为a2b>0,所以b>0,a>0或a<0,当a>0,b>0时,点P在第一象限;当a<0,b>0时,点P在第二象限.故选A.
6.[2020广东深圳福田区期中]若点P(a,b)满足a2b>0,则点P所在的象限为 ( )
A.第一象限或第二象限
B.第一象限或第四象限
C.第二象限或第三象限
D.第三象限或第四象限
答案
7.B 【解析】 因为点A(-4,3),AB垂直于y轴于点B,所以AB=4,OB=3,所以OA=????????2+????????2=5,所以△ABC的周长为3+4+5=12.故选B.
?
7.在平面直角坐标系中,点A(-4,3),作AB垂直于y轴于点B,则△AOB的周长为 ( )
A.7+7 B.12
C.12或7+7 D.12+7
?
答案
8.A 【解析】 因为小红同学误将点A的横、纵坐标顺序颠倒,写成A(a,b),所以A点的正确坐标为(b,a),因为另一名学生误将点B的坐标写成关于y轴对称的点的坐标,写成B(-b,-a),所以点B的正确坐标为(b,-a),所以A,B两点原来的位置关系是关于x轴对称.故选A.
8.[2019海南三亚期末]小红同学误将点A的横、纵坐标顺序颠倒,写成A(a,b),另一名学生误将点B的坐标写成关于y轴对称的点的坐标,写成B(-b,-a),则A,B两点原来的位置关系是 ( )
A.关于x轴对称
B.关于y轴对称
C.A和B重合
D.以上都不对
答案
9.2 【解析】 因为点A(-3,2m-1)在x轴上,所以2m-1=0,解得m=12.因为点B(n+1,4)在y轴上,所以n+1=0,解得n=-1,所以2m-n=1-(-1)=2.
?
二、填空题
9.[2020广东揭阳期中]已知点A(-3,2m-1)在x轴上,点B(n+1,4)在y轴上,则2m-n= .?
答案
10.8 【解析】 因为点A(a+2,5)与点B(5,b)关于x轴对称,所以a+2=5,b=-5,所以a=3,所以a-b=3+5=8.
10.[2020安徽芜湖期末]已知点A(a+2,5)与点B(5,b)关于x轴对称,则a-b= .?
答案
11.一或四 【解析】 因为A(a,b)在第三象限,所以a<0,b<0,所以-a+1>1,3b+1<1,则点B(-a+1,3b+1)在第一象限或第四象限.
11.若点A(a,b)在第三象限,则点B(-a+1,3b+1)在第 象限.?
答案
12.(-5,-1),(-1,-3),(-3,-4),(-7,-2) 【解析】 如图,因为a,b均为负整数,所以点C在第三象限,
又因为△ABC的面积为2,所以C1(-5,-1),C2(-3,-4),C3(-1,-3),C4(-7,-2)均符合题意.
12.如图,在直角坐标系中,△ABC的面积为2,三个顶点的坐标分别为A(-3,-2),B(-1,-1),C(a,b),且a,b均为负整数,则点C的坐标为 .?
答案
13.【解析】 (1)小莹和小亮的位置如图所示.
(2)(1,3) (1,4)
三、解答题
13.[2019北京大兴区期末]小莹、小亮准备参加中考模拟考试,学校规定考生每人占一张桌子,按考号入座.考号按如图所示的方式贴在桌子上,请回答下面的问题:
(1)小莹的考号是13,小亮的考号是24,在图中对应的“ ”中,请用他们的名字分别标出他们在考场内座位的位置;
(2)某考生座位的位置在第a行和第b列相交的“ ”处,用数对表示是(a,b),那么小莹的位置用数对表示是 ,小亮的位置用数对表示是 .?
答案
14.【解析】 (1)由题图可得,商会大厦的坐标为(-1,2),医院的坐标为(3,1).
(2)路上经过的地方为大剧院,体育公园,购物广场.
14.如图是某市市政府周边的一些建筑,以市政府为坐标原点,建立平面直角坐标系.(每个小方格的边长均为1)
(1)请写出商会大厦和医院的坐标;
(2)王老师在市政府办完事情后,沿(2,0)→(2,-1)→(2,-3)→(0,-3)→(0,-1)→(-2,-1)的路线逛了一下,然后到汽车站坐车回家,写出他路上经过的地方.
答案
15.【解析】 (1)因为AB∥x轴,所以A点和B点的纵坐标相等,
即a+2=4,解得a=2,
所以A(-2,4),B(-1,4),
所以A,B两点间的距离为-1-(-2)=1.
(2)因为CD⊥x轴于点D,CD=3,
所以|b|=3,解得b=3或b=-3,
当b=3时,b-4=-1;当b=-3时,b-4=-7.
所以点C的坐标为(-1,3)或(-7,-3).
15.[2020安徽合肥包河区期中]在平面直角坐标系中,有A(-2,a+2),B(a-3,4),C(b-4,b)三点.
(1)当AB∥x轴时,求A,B两点间的距离;
(2)若CD⊥x轴于点D,且CD=3,求点C的坐标.
16.[2020山东济南市中区期末]如图,在平面直角坐标系中,已知A(0,1),B(2,0),C(4,3).
(1)在如图所示的平面直角坐标系中画出△ABC,则△ABC的面积是 ;?
(2)若点D与点C关于y轴对称,则点D的坐标为 ;?
(3)已知P为x轴上一点,若△ABP的面积为4,求点P的坐标.
答案
16.【解析】 (1)4 △ABC如图所示.
△ABC的面积是3×4-12×1×2-12×2×4-12×2×3=4.
(2)(-4,3)
(3)因为P为x轴上一点,△ABP的面积为4,
所以BP=8,
所以点P的横坐标为2+8=10或2-8=-6,
故点P的坐标为(10,0)或(-6,0).
.
?
17.[2019广东汕头潮南区期末]如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a,b满足?????4+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O—C—B—A—O的线路移动,回到O点,停止移动.
(1)点B的坐标为 ;当点P移动3.5秒时,点P的坐标为 .?
(2)在移动过程中,当点P到x轴的距离为4个单位长度时,求点P移动的时间.
(3)在O—C—B线路的移动过程中,是否存在某个时刻,使△OBP的面积是10 ?若存在,求出点P移动的时间;若不存在,请说明理由.
?
答案
17.【解析】 (1)(4,6) (1,6)
因为?????4+|b-6|=0,
所以a-4=0,b-6=0,解得a=4,b=6,
所以OA=4,OC=6,所以点B的坐标是(4,6).
因为点P从原点出发,以每秒2个单位长度的速度沿着O—C—B—A—O的线路移动,
2×3.5=7,
所以当点P移动3.5秒时,P在线段CB上,离点C的距离是7-6=1,
即点P的坐标是(1,6).
(2)由题意可知,在移动过程中,当点P到x轴的距离为4个单位长度时,存在两种情况,
①当点P在OC上时,点P移动的时间是4÷2=2(秒),
②当点P在BA上时,点P移动的时间是(6+4+2)÷2=6(秒),
故在移动过程中,当点P到x轴的距离为4个单位长度时,点P移动的时间是2秒或6秒.
?
答案
(3)当点P的移动时间为52 秒或103 秒时,△OBP的面积是10.理由如下:
①如图1,当点P在线段OC上时,
因为△OBP的面积是10,
所以12OP×BC=10,即12×4×OP=10,
解得OP=5,5÷2=52,
所以当点P移动的时间为52 秒时,△OBP的面积是10.
②如图2,当点P在CB上时,
因为△OBP的面积是10,
所以12PB×OC=10,即12×6×PB=10,所以PB=103,
所以CP=4-103=23,(6+23)÷2=103,
所以当点P移动的时间为103 秒时,△OBP的面积是10.
综上,当点P的移动时间为52 秒或103 秒时,△OBP的面积是10.
?
图1
图2
数学·八年级上册·北师
专项素养拓训
专项 点的坐标
专项
1.点M(m+1,m+3)在y轴上,则点M的坐标为( )
A.(0,-4) B.(4,0) C.(-2,0) D.(0,2)
答案
1.D 【解析】 因为点M(m+1,m+3)在y轴上,所以m+1=0,解得m=-1,所以m+3=-1+3=2,所以点M的坐标为(0,2).故选D.
类型1 点的坐标特征
2.若点A(n-2,n+3)在x轴上,则点B(n-1,n+1)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案
2.C 【解析】 因为点A(n-2,n+3)在x轴上,所以n+3=0,所以n=-3,所以n-1=-4<0,n+1=-2<0,所以点B在第三象限.故选C.
3.如图是轰炸机机群的一个飞行队形,如果轰炸机A和C在平面直角坐标系中的坐标分别为(-2,1)和(2,-1),那么轰炸机B的坐标是 ( )
A.(-2,-3) B.(-2,-2) C.(0,-3) D.(0,-2)
类型1 点的坐标特征
答案
3.A 【解析】 根据题意可建立如图所示的平面直角坐标系,由图可知轰炸机B的坐标是(-2,-3).故选A.
4.[2019湖北武汉黄陂区期末]已知甲、乙、丙三人所在的位置不同,他们三人都以相同的单位长度建立不同的坐标系,甲说:“以我为坐标原点,乙的位置是(4,3)”,丙说:“以我为坐标原点,乙的位置是(-3,-4)”.若以乙为坐标原点,则甲和丙的位置分别是 ( )
A.(3,4),(-3,-4) B.(4,-3),(3,-4)
C.(-3,-4),(4,3) D.(-4,-3),(3,4)
类型1 点的坐标特征
答案
4.D 【解析】 以甲为坐标原点,乙的位置是(4,3),则以乙为坐标原点,甲的位置是(-4,-3);以丙为坐标原点,乙的位置是(-3,-4),则以乙为坐标原点,丙的位置是(3,4).故选D.
5.已知点P到x轴,y轴的距离分别是2和3,且点P关于y轴对称的点在第四象限,则点P的坐标是 .?
类型1 点的坐标特征
答案
5.(-3,-2) 【解析】 因为点P关于y轴对称的点在第四象限,所以点P在第三象限,结合点P到x轴,y轴的距离分别是2和3,可知点P的坐标是(-3,-2).
6.在平面直角坐标系中,点A的坐标是(2,-3),作点A关于x轴的对称点,得到点A',再作点A'关于y轴的对称点,得到点A″,则点A″的坐标是( , ).?
答案
6.-2 3 【解析】 因为点A的坐标是(2,-3),点A'与点A关于x轴对称,所以点A'的坐标为(2,3).因为点A″与点A'关于y轴对称,所以点A″的坐标是(-2,3).
7.在平面直角坐标系中,将点(-b,-a)称为点(a,b)的“关联点”(例如点(-2,-1)是点(1,2)的“关联点”).如果一个点和它的“关联点”在同一象限内,那么这一点在第 象限.?
类型1 点的坐标特征
答案
7.二或四 【解析】 因为(-b,-a)与(a,b)在同一象限,所以-b与a符号相同,-a与b符号相同,所以a,b符号相反,所以这一点在第二象限或第四象限.
8.若点(5-a,a-3)在第一、三象限的角平分线上,求a的值.
答案
8.【解析】 因为点(5-a,a-3)在第一、三象限的角平分线上,所以5-a=a-3,解得a=4.
9.第六届北京农业嘉年华在昌平区兴寿镇草莓博览园举办,某校数学兴趣小组的同学根据数学知识将草莓博览园的游览线路进行了精简.如图,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,如果表示国际特色农产品馆的坐标为(-5,0),表示科技生活馆的点的坐标为(6,2),那么表示多彩农业馆所在点的坐标为 ( )
A.(3,5) B.(5,-4) C.(-2,5) D.(-3,3)
类型2 用坐标表示位置
答案
9.C
10.如图是利用网格画出的太原市地铁1,2,3号线路部分规划示意图.若建立适当的平面直角坐标系,表示双塔西街的点的坐标为(0,-1),表示桃园路的点的坐标为(-1,0),则表示太原火车站的点(正好在网格点上)的坐标是 .?
类型2 用坐标表示位置
答案
10.(3,0) 【解析】 由表示双塔西街和桃园路的点的坐标可知表示大南门的点是原点且正东、正北方向分别为x轴、y轴正方向,所以表示太原火车站的点的坐标是(3,0).
11.已知A(a,0)和B(0,10)两点,且AB与坐标轴围成的三角形的面积等于20,则a的值为( )
A.2 B.4
C.0或4 D.4或-4
类型3 点的坐标与图形面积
答案
11.D 【解析】 因为A(a,0),B(0,10),所以OA=|a|,OB=10,所以S△AOB=12OA·OB=12×10|a|=20,解得a=±4.故选D.
?
12.如图,已知A(4,3),B(3,b-1),C(1,2),且△ABC关于x轴的对称图形为△A'B'C'.
(1)作出△ABC关于x轴的对称图形△A'B'C';
(2)若点B'(a-1,-1),求a+b的值.
类型3 点的坐标与图形面积
答案
12.【解析】 (1)△A'B'C'如图所示.
(2)因为点B'(a-1,-1)与点B关于x轴对称,
所以a-1=3,b-1=1,
解得a=4,b=2,所以a+b=6.
13.在平面直角坐标系中,已知点A,B的坐标分别为(-3,4),(4,-2).
(1)求点A,B关于y轴的对称点的坐标;
(2)在平面直角坐标系中分别作出点A,B关于x轴的对称点M,N,顺次连接AM,BM,BN,AN,求四边形AMBN的面积.
类型3 点的坐标与图形面积
答案
13.【解析】 (1)根据轴对称的性质,得点A(-3,4)关于y轴的对称点的坐标是(3,4);
点B(4,-2)关于y轴的对称点的坐标是(-4,-2).
(2)因为点M与点A、点N与点B关于x轴对称,
所以M(-3,-4),N(4,2),所以四边形AMBN为梯形.
因为AM,BN平行于y轴,
所以梯形AMBN的高为7,且AM=8,BN=4,
所以S梯形AMBN=12×7×(8+4)=42.
故四边形AMBN的面积为42.
?
综合素养拓训
1.[探究图形变换的点的坐标]如图,已知正方形ABCD的顶点A(1,3),B(1,1),C(3,1),规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位长度”为一次变换,如此这样,连续经过2 020次变换后,正方形ABCD的对角线的交点M的坐标为( )
A.(-2 018,2) B.(-2 018,-2)
C.(-2 017,-2) D.(-2 017,2)
答案
1.A 【解析】 由题意,得变换前点M的坐标为(2,2),第1次变换为M1(1,-2),第2次变换为M2(0,2),第3次变换为M3(-1,
-2),第4次变换为M4(-2,2)……从而得到规律:当n为奇数时,Mn(2-n,-2);当n为偶数时,Mn(2-n,2).所以当n=2 020时,
M2 020(-2 018,2).故选A.
答案
2.D 【解析】 由题意知,P1(1,1),P2(1,2),P3(1,3),P4(1,4),P5(1,5),P6(2,1),P7(2,2),P8(2,3),P9(2,4),P10(2,5),…,观察以上数据,因为2 020÷5=404,所以P2 020的坐标为(404,5).故选D.
2.[探究点的坐标变化规律][2020湖北黄石期末]某校数学课外小组,在坐标纸上为某湿地公园的一块空地设计植树方案如下:第k棵树种植在点Pk(xk,yk)处,x1=1,y1=1,当k≥2时,????????=?????????1+[?????15]?[?????25],????????=?????????1+1?5([?????15]?[?????25]),其中 [a]表示非负实数a的整数部分,例如[2.3]=2,[43]=1,[0.5]=0.按此方案,第2 020棵树种植点的坐标应为( )
A.(6,2 020) B.(2 020,5)
C.(403,5) D.(404,5)
?
答案
3.【解析】 (1)AB=(?3?2)2+(?8?4)2=52+122=13.(2)AB=|-1-5|=6.
(3)能.理由如下:
因为DE=(?3?0)2+(2?6)2=5,EF=[3?(?3)]2+(2?2)2=6,DF=(3?0)2+(2?6)2=5,
所以DE=DF,
又因为52+52≠62,
所以△DEF为等腰三角形.
?
3.[两点间的距离公式]先阅读文字,再回答问题:
已知在平面内有两点P1(x1,y1),P2(x2,y2),则这两点间的距离公式为P1P2=(????2?????1)2+(????2?????1)2.同时,当这两点在同一坐标轴上或所在直线平行于坐标轴时,这两点间的距离公式可简化为|x2-x1|或|y2-y1|.
(1)已知点A(2,4),B(-3,-8),试求A,B两点间的距离;
(2)已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为-1,试求A,B两点间的距离;
(3)已知一个三角形各顶点的坐标为D(0,6),E(-3,2),F(3,2),你能判定此三角形的形状吗?请说明理由.
?
答案
1.B
一、选择题
1.[2020广东广州越秀区期中]下列各点中,位于第四象限的是 ( )
A.(-4,3) B.(4,-3) C.(4,3) D.(-4,-3)
答案
2.D 【解析】 因为点M位于第二象限,所以点M的横坐标为负数,纵坐标为正数.因为点M距离x轴5个单位长度,距离y轴3个单位长度,所以点M的坐标为(-3,5).故选D.
2.[2020山东济南槐荫区期末]已知点M在第二象限,且点M距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为 ( )
A.(5,-3) B.(-5,3) C.(3,-5) D.(-3,5)
答案
3.D
3.[2019浙江金华中考]如图是雷达屏幕在一次探测中发现的多个目标,其中对目标A的位置表述正确的是 ( )
A.在南偏东75°方向处
B.在5 km处
C.在南偏东15°方向5 km处
D.在南偏东75°方向5 km处
答案
4.A 【解析】 由题意可知,-3=m-1,所以m=-2.故选A.
4.[2020辽宁辽阳期末]已知点A(m+2,-3)和点B(4,m-1),若直线AB∥x轴,则m的值为 ( )
A.-2 B.-4 C.2 D.3
答案
5.C 【解析】 根据题意建立如图所示的平面
直角坐标系,所以含弘楼的位置可以表示成(-2,0).故选C.
5.[2020重庆沙坪坝区月考]重庆一中寄宿学校北楼、食堂、含弘楼的位置如图所示,如果北楼的位置用(-1,2)表示,食堂的位置用(2,1)表示,那么含弘楼的位置可以表示成 ( )
A.(0,0) B.(0,4) C.(-2,0) D.(1,5)
答案
6.A 【解析】 因为a2b>0,所以b>0,a>0或a<0,当a>0,b>0时,点P在第一象限;当a<0,b>0时,点P在第二象限.故选A.
6.[2020广东深圳福田区期中]若点P(a,b)满足a2b>0,则点P所在的象限为 ( )
A.第一象限或第二象限
B.第一象限或第四象限
C.第二象限或第三象限
D.第三象限或第四象限
答案
7.B 【解析】 因为点A(-4,3),AB垂直于y轴于点B,所以AB=4,OB=3,所以OA=????????2+????????2=5,所以△ABC的周长为3+4+5=12.故选B.
?
7.在平面直角坐标系中,点A(-4,3),作AB垂直于y轴于点B,则△AOB的周长为 ( )
A.7+7 B.12
C.12或7+7 D.12+7
?
答案
8.A 【解析】 因为小红同学误将点A的横、纵坐标顺序颠倒,写成A(a,b),所以A点的正确坐标为(b,a),因为另一名学生误将点B的坐标写成关于y轴对称的点的坐标,写成B(-b,-a),所以点B的正确坐标为(b,-a),所以A,B两点原来的位置关系是关于x轴对称.故选A.
8.[2019海南三亚期末]小红同学误将点A的横、纵坐标顺序颠倒,写成A(a,b),另一名学生误将点B的坐标写成关于y轴对称的点的坐标,写成B(-b,-a),则A,B两点原来的位置关系是 ( )
A.关于x轴对称
B.关于y轴对称
C.A和B重合
D.以上都不对
答案
9.2 【解析】 因为点A(-3,2m-1)在x轴上,所以2m-1=0,解得m=12.因为点B(n+1,4)在y轴上,所以n+1=0,解得n=-1,所以2m-n=1-(-1)=2.
?
二、填空题
9.[2020广东揭阳期中]已知点A(-3,2m-1)在x轴上,点B(n+1,4)在y轴上,则2m-n= .?
答案
10.8 【解析】 因为点A(a+2,5)与点B(5,b)关于x轴对称,所以a+2=5,b=-5,所以a=3,所以a-b=3+5=8.
10.[2020安徽芜湖期末]已知点A(a+2,5)与点B(5,b)关于x轴对称,则a-b= .?
答案
11.一或四 【解析】 因为A(a,b)在第三象限,所以a<0,b<0,所以-a+1>1,3b+1<1,则点B(-a+1,3b+1)在第一象限或第四象限.
11.若点A(a,b)在第三象限,则点B(-a+1,3b+1)在第 象限.?
答案
12.(-5,-1),(-1,-3),(-3,-4),(-7,-2) 【解析】 如图,因为a,b均为负整数,所以点C在第三象限,
又因为△ABC的面积为2,所以C1(-5,-1),C2(-3,-4),C3(-1,-3),C4(-7,-2)均符合题意.
12.如图,在直角坐标系中,△ABC的面积为2,三个顶点的坐标分别为A(-3,-2),B(-1,-1),C(a,b),且a,b均为负整数,则点C的坐标为 .?
答案
13.【解析】 (1)小莹和小亮的位置如图所示.
(2)(1,3) (1,4)
三、解答题
13.[2019北京大兴区期末]小莹、小亮准备参加中考模拟考试,学校规定考生每人占一张桌子,按考号入座.考号按如图所示的方式贴在桌子上,请回答下面的问题:
(1)小莹的考号是13,小亮的考号是24,在图中对应的“ ”中,请用他们的名字分别标出他们在考场内座位的位置;
(2)某考生座位的位置在第a行和第b列相交的“ ”处,用数对表示是(a,b),那么小莹的位置用数对表示是 ,小亮的位置用数对表示是 .?
答案
14.【解析】 (1)由题图可得,商会大厦的坐标为(-1,2),医院的坐标为(3,1).
(2)路上经过的地方为大剧院,体育公园,购物广场.
14.如图是某市市政府周边的一些建筑,以市政府为坐标原点,建立平面直角坐标系.(每个小方格的边长均为1)
(1)请写出商会大厦和医院的坐标;
(2)王老师在市政府办完事情后,沿(2,0)→(2,-1)→(2,-3)→(0,-3)→(0,-1)→(-2,-1)的路线逛了一下,然后到汽车站坐车回家,写出他路上经过的地方.
答案
15.【解析】 (1)因为AB∥x轴,所以A点和B点的纵坐标相等,
即a+2=4,解得a=2,
所以A(-2,4),B(-1,4),
所以A,B两点间的距离为-1-(-2)=1.
(2)因为CD⊥x轴于点D,CD=3,
所以|b|=3,解得b=3或b=-3,
当b=3时,b-4=-1;当b=-3时,b-4=-7.
所以点C的坐标为(-1,3)或(-7,-3).
15.[2020安徽合肥包河区期中]在平面直角坐标系中,有A(-2,a+2),B(a-3,4),C(b-4,b)三点.
(1)当AB∥x轴时,求A,B两点间的距离;
(2)若CD⊥x轴于点D,且CD=3,求点C的坐标.
16.[2020山东济南市中区期末]如图,在平面直角坐标系中,已知A(0,1),B(2,0),C(4,3).
(1)在如图所示的平面直角坐标系中画出△ABC,则△ABC的面积是 ;?
(2)若点D与点C关于y轴对称,则点D的坐标为 ;?
(3)已知P为x轴上一点,若△ABP的面积为4,求点P的坐标.
答案
16.【解析】 (1)4 △ABC如图所示.
△ABC的面积是3×4-12×1×2-12×2×4-12×2×3=4.
(2)(-4,3)
(3)因为P为x轴上一点,△ABP的面积为4,
所以BP=8,
所以点P的横坐标为2+8=10或2-8=-6,
故点P的坐标为(10,0)或(-6,0).
.
?
17.[2019广东汕头潮南区期末]如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a,b满足?????4+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O—C—B—A—O的线路移动,回到O点,停止移动.
(1)点B的坐标为 ;当点P移动3.5秒时,点P的坐标为 .?
(2)在移动过程中,当点P到x轴的距离为4个单位长度时,求点P移动的时间.
(3)在O—C—B线路的移动过程中,是否存在某个时刻,使△OBP的面积是10 ?若存在,求出点P移动的时间;若不存在,请说明理由.
?
答案
17.【解析】 (1)(4,6) (1,6)
因为?????4+|b-6|=0,
所以a-4=0,b-6=0,解得a=4,b=6,
所以OA=4,OC=6,所以点B的坐标是(4,6).
因为点P从原点出发,以每秒2个单位长度的速度沿着O—C—B—A—O的线路移动,
2×3.5=7,
所以当点P移动3.5秒时,P在线段CB上,离点C的距离是7-6=1,
即点P的坐标是(1,6).
(2)由题意可知,在移动过程中,当点P到x轴的距离为4个单位长度时,存在两种情况,
①当点P在OC上时,点P移动的时间是4÷2=2(秒),
②当点P在BA上时,点P移动的时间是(6+4+2)÷2=6(秒),
故在移动过程中,当点P到x轴的距离为4个单位长度时,点P移动的时间是2秒或6秒.
?
答案
(3)当点P的移动时间为52 秒或103 秒时,△OBP的面积是10.理由如下:
①如图1,当点P在线段OC上时,
因为△OBP的面积是10,
所以12OP×BC=10,即12×4×OP=10,
解得OP=5,5÷2=52,
所以当点P移动的时间为52 秒时,△OBP的面积是10.
②如图2,当点P在CB上时,
因为△OBP的面积是10,
所以12PB×OC=10,即12×6×PB=10,所以PB=103,
所以CP=4-103=23,(6+23)÷2=103,
所以当点P移动的时间为103 秒时,△OBP的面积是10.
综上,当点P的移动时间为52 秒或103 秒时,△OBP的面积是10.
?
图1
图2
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
