北师大版八年级上册数学第三章位置与坐标整章同步教学课件(85张PPT)
文档属性
| 名称 | 北师大版八年级上册数学第三章位置与坐标整章同步教学课件(85张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 09:24:26 | ||
图片预览











文档简介
第三章·位置与坐标
数学·八年级上册·北师
第一节 确定位置
第一节
1.在平面内,确定一个点的位置一般需要的数据个数是 ( )
A.1 B.2 C.3 D.4
答案
1.B
知识点 1 平面内位置的确定
2.[2020山西晋中榆次区期中]若(1,2)表示教室里第1列第2排的位置,则教室里第3列第2排的位置表示为 ( )
A.(2,3) B.(3,2) C.(2,1) D.(3,3)
答案
2.B 【解析】 由(1,2)表示教室里第1列第2排的位置,可知有序数对与列、排的对应关系,所以教室里第3列第2排的位置表示为(3,2).故选B.
知识点 2 行列定位法
3.易错题 某同学的座位号为(2,4),那么该同学所坐的位置是 ( )
A.第2排第4列 B.第4排第2列
C.第6排第2列 D.无法确定
答案
3.D 【解析】 已知座位号为(2,4),但从题中无法获知“2”和“4”分别表示什么,故无法确定该同学的位置.故选D.
4.[2019河南平顶山期中]在海战中,欲确定敌方每艘战舰的位置,需要知道敌方每艘战舰相对我方潜艇的 ( )
A.距离
B.方位角
C.方位角和距离
D.以上都不对
答案
4.C 【解析】 在一个平面内,要表示清楚一个点的位置,要有两个数据,所以从选项中应选方位角和距离.故选C.
知识点 3 “方位角+距离”定位法
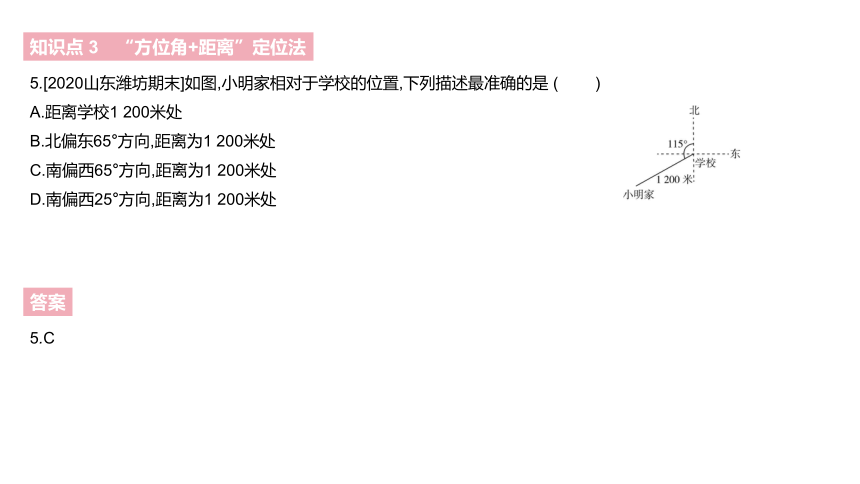
5.[2020山东潍坊期末]如图,小明家相对于学校的位置,下列描述最准确的是 ( )
A.距离学校1 200米处
B.北偏东65°方向,距离为1 200米处
C.南偏西65°方向,距离为1 200米处
D.南偏西25°方向,距离为1 200米处
答案
5.C
知识点 3 “方位角+距离”定位法
6.气象台为了预报台风,首先要确定台风中心的位置,下列说法能确定台风中心位置的是 ( )
A.西太平洋北偏东47°
B.距广州500海里
C.北纬28°,东经36°
D.湛江附近
答案
6.C
知识点 4 经纬定位法
7.如图是沈阳市地区简图的一部分,图中“故宫”“鼓楼”所在的区域分别是 ( )
A.D7,E6 B.D6,E7
C.E7,D6 D.E6,D7
答案
7.C 【解析】 由题图,可知“故宫”所在的位置是E竖排7横行,“鼓楼”所在的位置是D竖排6横行,所以题图中“故宫”“鼓楼”所在的区域分别是E7,D6.故选C
知识点 5 区域定位法
8.如图,请设计一条由学校到博物馆的路线,并分别用“××区”(如A1区)表示这条路线所经过的区域.
答案
8.【解析】 路线:A4区→A3区→A2区→B2区→C2区 →C1区→D1区→D2区.(答案不唯一)
知识点 5 区域定位法
9.做操时,甲、乙、丙的位置如图所示,甲对乙说,如果我的位置用(0,0)来表示,你的位置用(2,1)来表示,那么丙的位置是 ( )
A.(5,4) B.(4,5) C.(3,4) D.(4,3)
答案
9.A 【解析】 根据甲的位置用(0,0)来表示,乙的位置用(2,1)来表示,可以确定从下面数第二行用1来表示,从左面数第三列用2来表示,依此规律,得丙的位置是(5,4).故选A.
知识点 6 方格定位法
1.下列描述不能确定具体位置的是 ( )
A.某电影院1号厅6排7座
B.岳麓山北偏东40度
C.劳动西路428号
D.北纬28度,东经112度
答案
1.B
2.共享单车为我们提供了便捷、环保的出行方式.小白同学在北京植物园打开某共享单车APP,如图,“ ”为小白同学的位置,“★”为检索到的共享单车停放点.为了到达距离最近的共享单车停放点,下列四个区域中,小白同学应该前往的是( )
A.F6 B.F5 C.D5 D.F7
答案
2.A
3.雷达二维平面定位的主要原理:测量目标的两个信息——距离和角度,目标的表示方法为(γ,α),其中,γ表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现.其中,目标A的位置表示为A(5,30°),目标B的位置表示为B(4,150°).用这种方法表示目标C的位置,正确的是 ( )
A.(-3,300°) B.(3,60°)
C.(3,300°) D.(-3,60°)
答案
3.C
4.如图,A在O的北偏东30°方向,距离为5 km处;B在O的南偏东60°方向,距离为5 km处,则B在A的 ( )
A.距离为5 km处
B.南偏东15°方向,距离为52 km处
C.南偏西75°方向,距离为52 km处
D.南偏东15°方向,距离为5 km处
?
答案
4.B 【解析】 由题意可得∠AOB=90°,OA=OB=5 km,所以∠A=∠B=45°,由勾股定理可得AB=52 km.以A为中心,正北、正东方向为正方向建立方位图,结合两直线平行,内错角相等可得B在A的南偏东15°方向,距离为52 km处.故选B.
?
答案
5.(3,1)?(2,1)?(2,2)?(2,3)?(1,3)(答案不唯一)
6.如图,是小明家和学校所在地的简单地图,已知OA=2 km,OB=3.5 km,OP=4 km,点C为OP的中点,回答下列问题:
(1)图中到小明家距离相同的是哪些地方?
(2)请用方位角与距离描述学校、商场、停车场相对于小明家的位置.
答案
6.【解析】 (1)因为点C为OP的中点,
所以OC=12OP=12×4=2(km),
又因为OA=2 km,
所以到小明家距离相同的是学校和公园.
(2)学校在小明家北偏东45°的方向上,且到小明家的距离为2 km,
商场在小明家北偏西30°的方向上,且到小明家的距离为3.5 km,
停车场在小明家南偏东60°的方向上,且到小明家的距离为4 km.
?
7.如图,在4×4的方格中(小正方形的边长为1个单位长度),标有A,B两点.请你用两种不同的方法表述B点相对A点的位置.
答案
7.【解析】 方法1(用有序实数对(a,b)表示):如图,若记A点为(0,0),则B点可记为(3,3).
方法2(用方位角和距离表示): B点位于A点的东北方向(或北偏东45°),距离A点32个单位长度处.
(方法合理即可)
?
第二节 平面直角坐标系
第二节
课时1 平面直角坐标系
课时1
1.关于平面直角坐标系,有以下说法:
①在平面直角坐标系中,水平方向的数轴称为x轴或横轴,铅直方向的数轴称为y轴或纵轴;
②x轴上所有的点的纵坐标都等于0;
③点M(0,1)在平面直角坐标系中的位置是第三象限或第四象限.
其中正确的是 ( )
A.①②③ B.①② C.①③ D.②③
答案
1.B 【解析】 因为点M(0,1)在y轴的正半轴上,故③错误;易知①②正确.故选B.
知识点 1 平面直角坐标系的有关概念
2.如图,图中点A,B,C,D的坐标分别为 .?
答案
2.(3,2),(2,3),(-2,3),(-1,-3)
知识点 1 平面直角坐标系的有关概念
3.[2019湖南株洲中考]在平面直角坐标系中,点A(2,-3)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案
3.D 【解析】 根据平面直角坐标系中点的坐标特征可知,第四象限的点的坐标符号为(+,-).故选D.
知识点 2 各象限内点的坐标的符号特征
4.[2020河南平顶山期中]如图,小手盖住的点的坐标可能为 ( )
A.(5,2) B.(-6,3)
C.(-4,-6) D.(3,-4)
答案
4.C 【解析】 因为小手的位置在第三象限,所以小手盖住的点的横坐标小于0,纵坐标小于0,结合选项知只有(-4,-6)符合第三象限内点的坐标的符号特征.故选C.
知识点 2 各象限内点的坐标的符号特征
5.[2020河南郑州中原区月考]在平面直角坐标系中,点P(a+1,-????-1)在( )
A.x轴上 B.第二象限
C.y轴上 D.第四象限
?
答案
5.D 【解析】 因为????有意义,所以a≥0,所以a+1>0,-????-1<0,所以点P(a+1,-????-1)在第四象限.故选D.
?
知识点 2 各象限内点的坐标的符号特征
6.如果点M(a+b,ab)在第二象限,那么点N(a,b)在第 象限.?
答案
6.三 【解析】 因为点M(a+b,ab)在第二象限,所以a+b<0,ab>0,所以ab同号,且a,b同是负数,即a<0,b<0,所以点N在第三象限.
7.点P(2,-4)到x轴的距离是 ( )
A.2 B.-4 C.-2 D.4
答案
7.D
知识点 3 坐标与距离的关系
8.[2019湖南广益实验中学开学考试]已知在平面直角坐标系中,点P在第二象限,且点P到x轴和y轴的距离分别为6和5,那么点P的坐标为( )
A.(-5,-6) B.(-6,-5) C.(-5,6) D.(-6,5)
答案
8.C 【解析】 根据第二象限内的点的横坐标小于0,纵坐标大于0,且点P到x轴的距离是6,则其纵坐标为6,点P到y轴的距离为5,则其横坐标为-5,所以点P的坐标是(-5,6).故选C.
9.已知平面直角坐标系中有一点M(m-1,2m+3).
(1)当m为何值时,点M到x轴的距离为1?
(2)当m为何值时,点M到y轴的距离为2?
答案
9.【解析】 (1)由题意,得|2m+3|=1,
所以2m+3=1或2m+3=-1,
所以m=-1或m=-2.
(2)由题意,得|m-1|=2,
所以m-1=2或m-1=-2,
所以m=3或m=-1.
知识点 3 坐标与距离的关系
10.建立适当的平面直角坐标系,并在图中描出下列各点:A(2,3),B(-2,3),C(3,-2),D(5,1),E(0,-4),F(-3,0).
答案
10.【解析】 如图所示.
知识点 4 根据坐标描点
1.若点A(a,b)在第四象限,则点B(a,-b)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案
1.A 【解析】 因为点A(a,b)在第四象限,所以a>0,b<0,所以-b>0,所以点B(a,-b)在第一象限.故选A.
2.易错题 [2019山东济宁期中]点P到x轴的距离是2,到y轴的距离是3,且点P在y轴的右侧,则点P的坐标是 ( )
A.(2,3) B.(3,2)或(3,-2)
C.(3,2) D.(2,3)或(2,-3)
答案
2.B 【解析】 因为点P在y轴的右侧,且点P到x轴的距离是2,到y轴的距离是3,所以点P的横坐标是3,纵坐标是2或-2,所以点P的坐标是(3,2)或(3,-2).故选B.
3.关于平面直角坐标系,有以下说法:①坐标平面内的点可以用有序数对来表示;②若a大于0,b不大于0,则点A(2a+1,5b-2)在第三象限;③坐标原点不属于任何象限;④当m≠0时,点P(m2,m)在第四象限.
其中正确的个数为( )
A.1 B.2 C.3 D.4
答案
3.B 【解析】 易知①③正确;若a大于0,b不大于0,则2a+1>0,5b-2<0,所以点A(2a+1,5b-2)在第四象限,故②错误;当m≠0时,m2>0,m可能为正数,也可能为负数,所以点P(m2,m)在第一象限或第四象限,故④错误.综上,可知正确的个数为2.故选B.
4.在平面直角坐标系中,如果mn>0,那么点(m,|n|)在( )
A.第一象限或第二象限
B.第一象限或第三象限
C.第二象限或第四象限
D.第三象限或第四象限
答案
4.A 【解析】 因为mn>0,所以m和n同号.当m和n都是正数时,m>0,|n|>0,所以点(m,|n|)在第一象限;当m,n都是负数时,m<0,|n|>0,所以点(m,|n|)在第二象限.综上,可知点(m,|n|)在第一象限或第二象限.故选A.
5.点A(m+2,3m-5)在第一象限,若点A到x轴的距离是它到y轴的距离的一半,则m的值为 .?
答案
5.125 【解析】 由题意,知点A(m+2,3m-5)到x轴的距离是3m-5,到y轴的距离是m+2,所以3m-5=12(m+2),解得m=125.
?
6.[2020广东汕头期中]已知点P的坐标为(2-a,3a+6),且点P到两坐标轴的距离相等,求点P的坐标.
答案
6.【解析】 因为点P的坐标为(2-a,3a+6),且点P到两坐标轴的距离相等,
所以2-a=3a+6或(2-a)+(3a+6)=0,
解得a=-1或a=-4,
所以点P的坐标为(3,3)或(6,-6).
7.[2020广西崇左期中]如图,已知四边形ABCD.(网格中每个小正方形的边长均为1)
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.
答案
7.【解析】 (1)A(-2,1),B(-3,-2),C(3,-2),D(1,2).
(2)S四边形ABCD=3×3+2×12×1×3+12×2×4=16.
?
8.[2019山东济宁期末]【阅读材料】
平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为[P],即[P]=|x|+|y|,例如点P(1,2)的勾股值[P]=|1|+|2|=3.
【解决问题】
(1)求点A(-2,4),B(2+3,2-3)的勾股值[A],[B];
(2)若点M(x,y)在x轴的上方,其横、纵坐标均为整数,且[M]=3,求点M的坐标.
?
答案
8.【解析】 (1)[A]=|-2|+|4|=2+4=6,
[B]=|2+3|+|2-3|=2+3+3-2=23.
(2)因为点M(x,y)在x轴的上方,所以y>0.
因为点M的横、纵坐标均为整数,且[M]=|x|+|y|=3,
所以当y=1时,x=±2;当y=2时,x=±1;当y=3时,x=0.
所以点M的坐标为(-1,2),(1,2),(-2,1),(2,1)或(0,3).
?
课时2 点的坐标
课时2
1.下列各点不在x轴上的是 ( )
A.(0,1) B.(-1,0) C.(0,0) D.(π,0)
答案
1.A 【解析】 因为在x轴上的点的纵坐标为0,所以(0,1)不在x轴上.故选A.
知识点 1 坐标轴及象限角平分线上的点的坐标特征
2.易错题 已知点C在y轴上,且距离原点5个单位长度,则点C的坐标是 ( )
A.(5,0) B.(0,5) C.(5,0)或(0,5) D.(0,5)或(0,-5)
答案
2.D 【解析】 因为点C在y轴上,所以点C的横坐标为0,又因为点C距离原点5个单位长度,所以满足题意的点C有2个,分别是(0,5),(0,-5).故选D.
3.[2020陕西西安雁塔区期中]已知点M(2x-3,3-x)在第二、四象限的角平分线上,则点M的坐标为 ( )
A.(-3,-3) B.(-1,1) C.(-3,3) D.(3,-3)
答案
3.C 【解析】 因为点M(2x-3,3-x)在第二、四象限的角平分线上,所以2x-3+3-x=0,解得x=0,所以2x-3=-3,3-x=3,所以点M的坐标为(-3,3).故选C.
知识点 1 坐标轴及象限角平分线上的点的坐标特征
4.若点A(a,b),B(b,a)表示同一个点,则这个点在( )
A.第二、四象限的角平分线上 B.平行于x轴的直线上
C.第一、三象限的角平分线上 D.平行于y轴的直线上
答案
4.C 【解析】 因为点A(a,b),B(b,a)表示同一个点,所以它们的横、纵坐标相等,而横、纵坐标相等的点在第一、三象限的角平分线上.故选C.
5.已知平面直角坐标系内有一点M(a,b),且ab=0,则点M的位置一定在 ( )
A.原点上
B.x轴上
C.y轴上
D.坐标轴上
答案
5.D 【解析】 因为ab=0,所以a=0或b=0或a,b均为0.当a=0时,点M在y轴上;当b=0时,点M在x轴上;当a,b均为0时,点M在原点.综上所述,点M在坐标轴上.故选D.
知识点 1 坐标轴及象限角平分线上的点的坐标特征
6.已知点M(-1,3),N(-3,3),则直线MN与x轴、y轴的位置关系分别为( )
A.相交,相交 B.平行,平行
C.垂直,平行 D.平行,垂直
答案
6.D 【解析】 因为点M,N的坐标分别为(-1,3)和(-3,3),所以点M和点N的纵坐标相同,所以直线MN与x轴平行,与y轴垂直.故选D.
知识点 2 与坐标轴平行的直线上的点的坐标特征
7.下列说法正确的是 ( )
A.已知直线AB∥x轴,点A(3,5),点B(m,n),则m=3
B.点(1,-a2)一定在第四象限
C.已知点A(1,-3)与点B(1,3),则直线AB平行于y轴
D.在y轴上的点的横坐标都是0,纵坐标都大于0
答案
7.C 【解析】 A项,直线AB∥x轴,点A(3,5),点B(m,n),则n=5,但不能确定m的值,故说法错误;B项,因为a2≥0,所以-a2≤0,所以点(1,-a2)一定在第四象限或x轴上,故说法错误;D项,在y轴上的点的横坐标都是0,纵坐标为任意实数,故说法错误.故选C.
知识点 2 与坐标轴平行的直线上的点的坐标特征
8.在平面直角坐标系中,若AB∥y轴,AB=3,点A的坐标为(-2,3),则点B的坐标为 ( )
A.(-2,6) B.(1,3)
C.(-2,6)或(-2,0) D.(1,3)或(-5,3)
答案
8.C 【解析】 因为点A(-2,3),AB∥y轴,所以点B的横坐标为-2,又因为AB=3,所以点B的纵坐标为3+3=6或3-3=0,所以点B的坐标为(-2,6)或(-2,0).故选C.
知识点 2 与坐标轴平行的直线上的点的坐标特征
9.如图,四边形ABCD是长方形,AB=3,AD=4.已知点A(-32,-1),则点C的坐标是( )
A.(-3,32) B.(32,-3)
C.(3,32) D.(32,3)
?
答案
9.D 【解析】 因为四边形ABCD是长方形,所以AB=CD=3,AD=BC=4,又因为点C在第一象限,所以点C的坐标为
(-32+3,-1+4),即点C的坐标为(32,3).故选D.
?
知识点 2 与坐标轴平行的直线上的点的坐标特征
10.[2019广东珠海香洲区期末]若点P(m+3,m+1)在平面直角坐标系的x轴上,则m的值为 ( )
A.0 B.-1 C.-2 D.-3
答案
10.B 【解析】 因为点P(m+3,m+1)在x轴上,所以m+1=0,解得m=-1.故选B
知识点 3 根据点的坐标或位置求字母的值
11.已知点A(m+1,-2)和点B(3,m-1),如果直线AB∥x轴,那么m的值为 ,如果直线AB∥y轴,那么m的值为 .?
答案
11.-1 2 【解析】 由直线AB∥x轴,可知m-1=-2,m+1≠3,所以m=-1.由直线AB∥y轴,可知m+1=3,m-1≠-2,所以m=2.
12.已知点P(2m-6,m+2).
(1)若点P在y轴上,则点P的坐标为 .?
(2)若点P的纵坐标比横坐标大6,则点P在第几象限?
(3)若点P在过点A(2,3)且与x轴平行的直线上,求点P的坐标.
知识点 3 根据点的坐标或位置求字母的值
答案
12.【解析】 (1)(0,5)
因为点P在y轴上,所以2m-6=0,解得m=3,所以P点的坐标为(0,5).
(2)根据题意,得2m-6+6=m+2,解得m=2,
所以点P的坐标为(-2,4),所以点P在第二象限.
(3)因为点P在过点A(2,3)且与x轴平行的直线上,
所以点P的纵坐标为3,即m+2=3,解得m=1,
2m-6=-4,所以点P的坐标为(-4,3).
13.在如图所示的平面直角坐标系中,描出下列各点,并依次用线连接起来,看它像什么?
(2,1),(6,1),(6,3),(7,3),(4,6),(1,3),(2,3),(2,1).
答案
13.【解析】 描点、连线,如图所示,它的形状像一座小房子.
知识点 4 根据点的坐标描点连线构成图形
课时3 建立直角坐标系求坐标
课时3
1.如图,正方形ABCD的边长为4,请你建立适当的平面直角坐标系,写出各个顶点的坐标.
答案
1.【解析】 以点A为坐标原点,以AB所在的直线为x轴,AD所在的直线为y轴建立如图所示的平面直角坐标系,
则点A,B,C,D的坐标分别是(0,0),(4,0),(4,4),(0,4).(答案不唯一)
知识点 1 建立适当的平面直角坐标系求点的坐标
2.如图,若在象棋盘上建立平面直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),则“炮”位于点 ( )
A.(1,3) B.(-2,0)
C.(-1,2) D.(-2,2)
答案
2.B 【解析】 因为“将”位于点(1,-2),“象”位于点(3,-2),所以建立的平面直角坐标系如图所示,则“炮”位于点(-2,0).故选B.
知识点 2 确定有关点的位置
3.如图是利用平面直角坐标系画出的天安门广场的平面示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示天安门广场上国旗台的点的坐标为(0,2.5),表示中国国家博物馆的点的坐标为(4,1),则表示下列建筑的点的坐标正确的是( )
A.天安门(0,4)
B.人民大会堂(-4,1)
C.毛主席纪念堂(-1,-3)
D.正阳门(0,-5)
答案
3.B 【解析】 建立如图所示的平面直角坐标系,则天安门(0,5),
人民大会堂(-4,1),毛主席纪念堂(0,-3),正阳门(0,-5.5).故选B.
知识点 2 确定有关点的位置
4.[2019河北保定竞秀区一模]嘉嘉和淇淇下棋,嘉嘉执圆形棋子,淇淇执方形棋子.如图,棋盘中心的圆形棋子的位置用(-1,1)表示,右下角的圆形棋子的位置用(0,0)表示,若淇淇将第4枚方形棋子放入棋盘后,所有棋子构成的图形是轴对称图形,则淇淇放的方形棋子的位置可能是 ( )
A.(-1,2) B.(-1,-1) C.(0,2) D.(1,3)
答案
4.A 【解析】 根据已知两枚棋子的位置建立如图所示的平面直角坐标系,根据题图
可知,要再放入一枚方形棋子使得所有棋子构成的图形是轴对称图形,放的方形棋子应
在棋盘中心的圆形棋子的上方相邻点处,所以所放方形棋子的位置坐标为(-1,2).故选A.
知识点 2 确定有关点的位置
5.已知A,B,C三点的坐标分别为(0,3),(4,0),(-4,0).则△ABC的面积为 .?
答案
5.12 【解析】 建立平面直角坐标系如图所示.由点A,B,C的坐标可知BC=8,OA=3,所以△ABC的面积为12×8×3=12.
?
知识点 3 求平面直角坐标系中图形的面积
6.已知在平面直角坐标系中有三点A(-2,1),B(3,1),C(2,3).请回答如下问题:
(1)在如图所示的平面直角坐标系内描出点A,B,C的位置;
(2)求出以A,B,C三点为顶点的三角形的面积;
(3)在y轴上是否存在点P,使以A,B,P三点为顶点的三角形的面积为10?若存在,直接写出点P的坐标;若不存在,请说明理由.
知识点 3 求平面直角坐标系中图形的面积
答案
6.【解析】 (1)点A,B,C的位置如图所示.
(2)如图,连接AB,BC,AC.
依题意,得AB∥x轴,且AB=3-(-2)=5,
所以S△ABC=12×5×2=5.
(3)存在.点P的坐标为(0,5)或(0,-3).
因为AB=5,S△ABP=10,
所以点P到AB的距离为4,
又因为点P在y轴上,
所以点P的坐标为(0,5)或(0,-3).
?
1.[2019福建南平期末]在平面直角坐标系中,点A,B,C,D,E,F的位置如图所示,如果点E的坐标是(-3,0),点F的坐标是(3,0),那么在第三象限内的点是 ( )
A.点A B.点B C.点C D.点D
答案
1.C 【解析】 如图,连接EF,过EF的中点作EF的垂线GH,因为点E的坐标是(-3,0),点F的坐标是(3,0),所以GH所在直线为y轴,EF所在直线为x轴,所以在第三象限内的点是点C.故选C.
2.已知点A(0,0),B(4,0),点C在y轴上,且△ABC的面积为5,则点C的坐标为 ( )
A.(0,52)
B.(0,-52)
C.(0,52)或(0,-52)
D.无法确定
?
答案
2.C 【解析】 由题意知,以点A为坐标原点,分别以AB所在直线为x轴,过点A且垂直AB的直线为y轴建立平面直角坐标系.因为A(0,0),B(4,0),所以AB=4.因为△ABC的面积为5,点C在y轴上,所以12AB·AC=5,所以AC=52.设点C的纵坐标为y,则|y|=52,所以y=52或y=-52,所以点C的坐标为(0,52)或(0,-52).故选C.
?
3.星期天,小李和小张相约到文化广场游玩,出发前,他们每人带了一张利用平面直角坐标系画的示意图,如图所示,其中行政办公楼的坐标是(-4,3),南城百货的坐标是(2,-3).
(1)请根据上述信息,画出这个平面直角坐标系;
(2)写出示意图中体育馆、升旗台、北部湾俱乐部、盘龙苑小区、国际大酒店的坐标;
(3)小李跟小张说他现在的位置坐标是(-2,-2),请你在图中用字母A标出小李的位置.
答案
3.【解析】 (1)如图所示(图1).
(2)体育馆(-9,4),升旗台(-4,2),北部湾俱乐部(-7,-1),盘龙苑小区(-5,-3),国际大酒店(0,0).
(3)小李的位置A如图所示(图2).
图1 图2
4.如图为草房的示意图,AB的长为15米,房檐CD的长为20米,门宽EF为6米,CD到地面的距离为18米,请你建立适当的平面直角坐标系,并写出A,B,C,D,E,F的坐标.
答案
4.【解析】 根据题意,可以以AB的中点为坐标原点,AB所在直线为x轴,AB的垂直平分线为y轴,建立如图所示的平面直角坐标系.
因为AB=15米,且在x轴上,A点在负半轴上,B点在正半轴上,
所以A(-7.5,0),B(7.5,0).
因为CD=20米,CD到地面的距离为18米,
所以C(-10,18),D(10,18).
因为EF在x轴上,E点在负半轴上,F点在正半轴上,EF=6米,
所以E(-3,0),F(3,0).(答案不唯一)
5.如图,A(-4,0),B(6,0),C(2,4),D(-3,2).
(1)求四边形ABCD的面积;
(2)在y轴上找一点P,使△APB的面积等于四边形ABCD的面积的一半.求点P的坐标.
答案
5.【解析】 (1)如图,分别过C,D两点作x轴的垂线,垂足分别为E,F,
则S四边形ABCD=S△ADF+S梯形CDFE+S△BCE=12AF·DF+12FE·
(DF+CE)+12BE·CE=12×1×2+12×5×(2+4)+12×4×4=24.
(2)设△APB的边AB上的高为h,
则由S△APB=12S四边形ABCD,
得12×10×h=12×24,
解得h=2.4,
又因为点P在y轴上,
所以点P的坐标为(0,2.4)或(0,-2.4).
?
6.如图,在Rt△OAB中,斜边OB在x轴的正半轴上,直角顶点A在第四象限内,S△OAB=20,OA∶AB=1∶2.求A,B两点的坐标.
答案
6.【解析】 由OA∶AB=1∶2,可设OA=x(x>0),则AB=2x.
在Rt△OAB中,根据勾股定理,可得OB=????????2+????????2=5x,
因为S△OAB=20=12OA·AB,所以20=12x·2x,
所以x2=20,所以x=25,
所以OB=5×25=10,
所以点B的坐标是(10,0).
如图,过点A作AC⊥OB于点C,
因为S△OAB=12BO·AC=20,
所以AC=4,
又因为点A在第四象限,所以点A的纵坐标为-4.
在Rt△AOC中,OA=25,AC=4,
由勾股定理,得OC=????????2?????????2=2,
所以点A的横坐标是2,所以点A的坐标为(2,-4).
?
易错疑难集训
集训
1.在平面直角坐标系中,点A(5,-7)到x轴的距离是 .?
答案
1.7
易错点 1 混淆坐标顺序、坐标与点到坐标轴的距离之间的关系
2.如图,若用(2,3)表示点A的位置,则点C的位置可表示成 ,(7,7)表示点 的位置.?
答案
2.(6,2) E
3.如图,在长方形OABC中,OA=3,OC=4,则点B的坐标是 .?
答案
3.(-4,3) 【解析】 由题图可知,点B在第二象限,所以点B的横坐标为负数,纵坐标为正数.由于AB=OC=4,所以点B的横坐标为-4,又因为BC=OA=3,所以点B的纵坐标为3,所以点B的坐标是(-4,3).
易错点 1 混淆坐标顺序、坐标与点到坐标轴的距离之间的关系
4.[2019河北张家口桥东区期中]已知点P(2-a,3)到两坐标轴的距离相等,则a的值为 ( )
A.3 B.-1 C.-1或5 D.-3
答案
4.C 【解析】 因为点P(2-a,3)到两坐标轴的距离相等,所以2-a=3或2-a=-3,所以a=-1或a=5.故选C.
易错点 2 因考虑不全面出现漏解
答案
5.B 【解析】 由(x+y)2=x2+y2-2,可得xy=-1,所以x,y异号,所以点M在第二象限或第四象限.故选B.
5.若点M(x,y)满足(x+y)2=x2+y2-2,则点M所在的象限是 ( )
A.第一象限或第三象限
B.第二象限或第四象限
C.第一象限或第二象限
D.不能确定
答案
6.已知点M(3,-2)与点M'(x,y)在同一条平行于x轴的直线上,且点M'到y轴的距离等于4,那么点M'的坐标是 ( )
A.(4,2)或(-4,2)
B.(4,-2)或(-4,-2)
C.(4,-2)或(-5,-2)
D.(4,-2)或(-1,-2)
6.B 【解析】 因为点M(3,-2)与点M'(x,y)在同一条平行于x轴的直线上,所以M'的纵坐标为-2,又因为点M'到y轴的距离等于4,所以点M'的横坐标为4或-4,所以点M'的坐标为(4,-2)或(-4,-2).故选B.
易错点 2 因考虑不全面出现漏解
答案
7.求符合下列条件的点B的坐标.
(1)已知点A(2,0),AB=4,点B和点A在同一坐标轴上,求点B的坐标;
(2)已知点A(0,0),AB=4,点B和点A在同一坐标轴上,求点B的坐标.
7.【解析】 (1)根据题意,得点B在x轴上,分两种情况讨论:
①当点B在点A的左侧时,因为点A(2,0),AB=4,
所以点B的坐标为(-2,0);
②当点B在点A的右侧时,因为点A(2,0),AB=4,
所以点B的坐标为(6,0).
综上,点B的坐标为(-2,0)或(6,0).
(2)根据题意,得点B可能在x轴上,也可能在y轴上.
①当点B在x轴上时,点B的坐标为(4,0)或(-4,0);
②当点B在y轴上时,点B的坐标为(0,4)或(0,-4).
综上,点B的坐标为(4,0),(-4,0),(0,4)或(0,-4).
易错点 2 因考虑不全面出现漏解
答案
1.[2020山东枣庄山亭区期中]已知点P(a,b)在第四象限,且点P到x轴的距离为3,到y轴的距离为6,则点P的坐标是 ( )
A.(3,-6)
B.(6,-3)
C.(-3,6)
D.(-3,3)或(-6,6)
答案
1.B 【解析】 因为点P(a,b)在第四象限,且到x轴的距离为3,到y轴的距离为6,所以点的横坐标是6,纵坐标是-3,所以点P的坐标为(6,-3).故选B.
疑难点 1 确定点的位置
2.[2020福建福州模拟]已知点A(m,n)在第二象限,则点B(|m|,-n)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案
2.D 【解析】 因为点A(m,n)在第二象限,所以m<0,n>0,所以|m|>0,-n<0,所以点B在第四象限.故选D.
疑难点 1 确定点的位置
3.在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点……则边长为8的正方形内部的整点的个数为( )
A.64 B.49 C.36 D.25
答案
3.B 【解析】 边长为1的正方形内部有1个整点,1×1;边长为2的正方形内部有1个整点,1×1;边长为3的正方形内部有9个整点,3×3;边长为4的正方形内部有9个整点,3×3;边长为5的正方形内部有25个整点,5×5;边长为6的正方形内部有25个整点,5×5;边长为7的正方形内部有49个整点,7×7,所以边长为8的正方形内部整点的个数为7×7=49.故选B.
疑难点 2 点的坐标规律探究
4.将正整数按以下规律排列:
第一列 第二列 第三列 第四列 第五列……
第一行 1 4 5 16 …
第二行 2 3 6 15 …
第三行 9 8 7 14 …
第四行 10 11 12 13 …
第五行 … … … … …
……
数2在第二行、第一列,与有序数对(2,1)对应;数5与(1,3)对应;数14与(3,4)对应;根据这一规律,数2 020对应的有序数对为 .?
疑难点 2 点的坐标规律探究
答案
4.(45,6) 【解析】 将正整数按从小到大的顺序用“→”排列.先找到第奇数行、第一列的数的规律,再推测出2 020对应的有序数对.观察下表,可发现:第奇数行、第一列的数等于该行行数的平方,即第一行、第一列的数为12=1,第三行、第一列的数为32=9,第五行、第一列的数为52=25……因为452=2 025,2 025-2 020=5,所以2 020在第45行第6列,所以数
2 020对应的有序数对为(45,6).
……
第三节 轴对称与坐标变化
第三节
1.点P1(1,-7)和P2(-1,-7)的位置关系是 ( )
A.关于x轴对称
B.关于y轴对称
C.关于原点对称
D.以上都不对
答案
1.B 【解析】 因为P1,P2两点的纵坐标相同,横坐标互为相反数,所以点P1(1,-7)和P2(-1,-7)关于y轴对称.故选B.
知识点 1 关于x轴、y轴对称的点的坐标特征
2.[2019江苏泰州姜堰区期中]在平面直角坐标系中,点A(-2,-3)关于x轴对称的点的坐标是( )
A.(-2,-3)
B.(-2,3)
C.(2,-3)
D.(2,3)
答案
2.B 【解析】 关于x轴对称的两个点的横坐标相同,纵坐标互为相反数,所以点A(-2,-3)关于x轴对称的点的坐标是
(-2,3).故选B.
知识点 1 关于x轴、y轴对称的点的坐标特征
3.[2020广东惠州期末]在平面直角坐标系中,点P(-3,1)关于y轴的对称点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案
3.A 【解析】 点P(-3,1)关于y轴的对称点的坐标为(3,1),(3,1)在第一象限.故选A.
知识点 1 关于x轴、y轴对称的点的坐标特征
4.[2020山东临沂期末]在平面直角坐标系中,若点P(-3,a)与点Q(b,-4)关于x轴对称,则a+b的值为 ( )
A.-7 B.7 C.1 D.-1
答案
4.C 【解析】 因为点P(-3,a)与点Q(b,-4)关于x轴对称,所以b=-3,a=4,所以a+b=-3+4=1.故选C.
知识点 1 关于x轴、y轴对称的点的坐标特征
5.若点P(a,b)关于y轴的对称点是P1,而点P1关于x轴的对称点是P2,已知点P2的坐标为(-3,4),则a= ,b= .?
答案
5.3 -4 【解析】 由题意知点P1和P2(-3,4)关于x轴对称,所以点P1的坐标为(-3,-4),又因为点P(a,b)和点P1(-3,-4)关于y轴对称,所以点P的坐标为(3,-4),所以a=3,b=-4.
6.(1)请在图中画出△ABC关于y轴对称的图形△A'B'C'(其中A',B',C'分别是A,B,C的对应点,不写画法);
(2)直接写出A',B',C'三点的坐标:A'( , ),B'( , ),C'( , ).?
答案
6.【解析】 (1)画出△A'B'C'如图所示.
(2)2 3 3 1 -1 -2
知识点 2 与坐标对称有关的作图
7.如图,△ABC在正方形网格中,每个小正方形的边长均为1,若点A的坐标为(0,3),按要求回答下列问题:
(1)在图中建立适当的平面直角坐标系,并写出点B和点C的坐标;
(2)作出△ABC关于x轴对称的图形△A'B'C'.(不用写作法)
答案
7.【解析】 (1)建立平面直角坐标系如图所示.
点B和点C的坐标分别为(-3,-1),(1,1).
(2)△A'B'C'如图所示.
知识点 2 与坐标对称有关的作图
8.在平面直角坐标系中,△ABC的位置如图所示.
(1)写出A,B,C三点的坐标;
(2)若△ABC各顶点的横坐标不变,纵坐标都乘以-1,请你
在同一平面直角坐标系中描出对应的点A',B',C',并依次
连接这三个点,所得的△A'B'C'与△ABC有怎样的位置关系?
答案
8.【解析】 (1)由题图,可知A,B,C三点的坐标分别是(3,4),(1,2),(5,1).
(2)△A'B'C'如图所示.
△A'B'C'与△ABC的位置关系是关于x轴对称.
知识点3 图形的坐标变化与图形对称的关系
1.将平面直角坐标系中某个图形上的各个点的横坐标都乘以-1,纵坐标不变,所得图形与原图形的位置关系是 ( )
A.关于x轴对称
B.关于y轴对称
C.关于原点对称
D.重合
答案
1.B 【解析】 因为各个点的纵坐标不变,横坐标都乘以-1,即纵坐标相同,横坐标互为相反数,所以所得图形与原图形关于y轴对称.故选B.
2.在平面直角坐标系中,若点P(x,y)在第二象限,且|x|-1=0,y2-4=0,则点P关于坐标原点对称的点P'的坐标是 ( )
A.(-1,-2) B.(1,-2) C.(-1,2) D.(1,2)
答案
2.B 【解析】 因为点P(x,y)在第二象限,且|x|-1=0,y2-4=0,所以x=-1,y=2,所以点P的坐标为(-1,2),所以点P关于坐标原点对称的点P'的坐标是(1,-2).故选B.
3.[2020四川南充嘉陵区期中]已知点P(a-1,5)和Q(2,b-1)关于x轴对称,则(a+b)2 020的值为 .?
答案
3.1 【解析】 因为点P(a-1,5)和Q(2,b-1)关于x轴对称,所以a-1=2,b-1=-5,所以a=3,b=-4,所以(a+b)2 020=(3-4)2 020=1.
4.已知△ABC在平面直角坐标系中的位置如图所示,若△A'B'C'与△ABC关于y轴对称,则点A的对应点A'的坐标是 .?
答案
4.(3,2) 【解析】 由题图可知,点A的坐标为(-3,2),所以点A关于y轴的对应点A'的坐标是(3,2).
5.如图,已知等边三角形ABC的边长为3,写出点A,B,C的坐标,并画出△ABC关于y轴对称的图形△A1B1C1.
答案
5.【解析】 如图,过点A作高AD,可得BD=32,AD=332,
所以A(32,332),B(0,0),C(3,0).
△ABC关于y轴对称的图形△A1B1C1如图所示.
?
6.在棋盘中建立平面直角坐标系,三颗棋子A,O,B的位置的坐标分别是(-1,1),(0,0),(1,0).
(1)如图1,添加棋子C,使四颗棋子A,O,B,C组成一个轴对称图形,请写出棋子C的位置的坐标,并在图中画出该图形的对称轴;
(2)在图2中的其他格点位置添加一颗棋子P,使四颗棋子A,O,B,P成为轴对称图形,请直接写出棋子P的位置的坐标.(写出2个即可)
答案
6.【解析】 (1)如图1所示,棋子C的位置的坐标为(-1,2),A,O,B,C四颗棋子组成等腰梯形,直线l为该图形的对称轴.
(2)如图2所示,P(0,-1),P'(-1,-1)都符合题意.(答案不唯一)
图1 图2
图1 图2
7.[2020湖北恩施州期末]如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;
(2)如果点P的坐标是(-a,0)(07.【解析】 (1)因为△ABC关于y轴的对称图形是△A1B1C1,
所以A1(2,0),B1(1,0),C1(1,2),
因为△A1B1C1关于直线l的对称图形是△A2B2C2,
所以△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2).
(2)如图,因为P(-a,0)(0因为P1与P2关于直线l:x=3对称,所以设P2(m,0),
所以????+????2=3,即m=6-a,所以P2(6-a,0),
所以PP2=6-a-(-a)=6-a+a=6.
?
答案
数学·八年级上册·北师
第一节 确定位置
第一节
1.在平面内,确定一个点的位置一般需要的数据个数是 ( )
A.1 B.2 C.3 D.4
答案
1.B
知识点 1 平面内位置的确定
2.[2020山西晋中榆次区期中]若(1,2)表示教室里第1列第2排的位置,则教室里第3列第2排的位置表示为 ( )
A.(2,3) B.(3,2) C.(2,1) D.(3,3)
答案
2.B 【解析】 由(1,2)表示教室里第1列第2排的位置,可知有序数对与列、排的对应关系,所以教室里第3列第2排的位置表示为(3,2).故选B.
知识点 2 行列定位法
3.易错题 某同学的座位号为(2,4),那么该同学所坐的位置是 ( )
A.第2排第4列 B.第4排第2列
C.第6排第2列 D.无法确定
答案
3.D 【解析】 已知座位号为(2,4),但从题中无法获知“2”和“4”分别表示什么,故无法确定该同学的位置.故选D.
4.[2019河南平顶山期中]在海战中,欲确定敌方每艘战舰的位置,需要知道敌方每艘战舰相对我方潜艇的 ( )
A.距离
B.方位角
C.方位角和距离
D.以上都不对
答案
4.C 【解析】 在一个平面内,要表示清楚一个点的位置,要有两个数据,所以从选项中应选方位角和距离.故选C.
知识点 3 “方位角+距离”定位法
5.[2020山东潍坊期末]如图,小明家相对于学校的位置,下列描述最准确的是 ( )
A.距离学校1 200米处
B.北偏东65°方向,距离为1 200米处
C.南偏西65°方向,距离为1 200米处
D.南偏西25°方向,距离为1 200米处
答案
5.C
知识点 3 “方位角+距离”定位法
6.气象台为了预报台风,首先要确定台风中心的位置,下列说法能确定台风中心位置的是 ( )
A.西太平洋北偏东47°
B.距广州500海里
C.北纬28°,东经36°
D.湛江附近
答案
6.C
知识点 4 经纬定位法
7.如图是沈阳市地区简图的一部分,图中“故宫”“鼓楼”所在的区域分别是 ( )
A.D7,E6 B.D6,E7
C.E7,D6 D.E6,D7
答案
7.C 【解析】 由题图,可知“故宫”所在的位置是E竖排7横行,“鼓楼”所在的位置是D竖排6横行,所以题图中“故宫”“鼓楼”所在的区域分别是E7,D6.故选C
知识点 5 区域定位法
8.如图,请设计一条由学校到博物馆的路线,并分别用“××区”(如A1区)表示这条路线所经过的区域.
答案
8.【解析】 路线:A4区→A3区→A2区→B2区→C2区 →C1区→D1区→D2区.(答案不唯一)
知识点 5 区域定位法
9.做操时,甲、乙、丙的位置如图所示,甲对乙说,如果我的位置用(0,0)来表示,你的位置用(2,1)来表示,那么丙的位置是 ( )
A.(5,4) B.(4,5) C.(3,4) D.(4,3)
答案
9.A 【解析】 根据甲的位置用(0,0)来表示,乙的位置用(2,1)来表示,可以确定从下面数第二行用1来表示,从左面数第三列用2来表示,依此规律,得丙的位置是(5,4).故选A.
知识点 6 方格定位法
1.下列描述不能确定具体位置的是 ( )
A.某电影院1号厅6排7座
B.岳麓山北偏东40度
C.劳动西路428号
D.北纬28度,东经112度
答案
1.B
2.共享单车为我们提供了便捷、环保的出行方式.小白同学在北京植物园打开某共享单车APP,如图,“ ”为小白同学的位置,“★”为检索到的共享单车停放点.为了到达距离最近的共享单车停放点,下列四个区域中,小白同学应该前往的是( )
A.F6 B.F5 C.D5 D.F7
答案
2.A
3.雷达二维平面定位的主要原理:测量目标的两个信息——距离和角度,目标的表示方法为(γ,α),其中,γ表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现.其中,目标A的位置表示为A(5,30°),目标B的位置表示为B(4,150°).用这种方法表示目标C的位置,正确的是 ( )
A.(-3,300°) B.(3,60°)
C.(3,300°) D.(-3,60°)
答案
3.C
4.如图,A在O的北偏东30°方向,距离为5 km处;B在O的南偏东60°方向,距离为5 km处,则B在A的 ( )
A.距离为5 km处
B.南偏东15°方向,距离为52 km处
C.南偏西75°方向,距离为52 km处
D.南偏东15°方向,距离为5 km处
?
答案
4.B 【解析】 由题意可得∠AOB=90°,OA=OB=5 km,所以∠A=∠B=45°,由勾股定理可得AB=52 km.以A为中心,正北、正东方向为正方向建立方位图,结合两直线平行,内错角相等可得B在A的南偏东15°方向,距离为52 km处.故选B.
?
答案
5.(3,1)?(2,1)?(2,2)?(2,3)?(1,3)(答案不唯一)
6.如图,是小明家和学校所在地的简单地图,已知OA=2 km,OB=3.5 km,OP=4 km,点C为OP的中点,回答下列问题:
(1)图中到小明家距离相同的是哪些地方?
(2)请用方位角与距离描述学校、商场、停车场相对于小明家的位置.
答案
6.【解析】 (1)因为点C为OP的中点,
所以OC=12OP=12×4=2(km),
又因为OA=2 km,
所以到小明家距离相同的是学校和公园.
(2)学校在小明家北偏东45°的方向上,且到小明家的距离为2 km,
商场在小明家北偏西30°的方向上,且到小明家的距离为3.5 km,
停车场在小明家南偏东60°的方向上,且到小明家的距离为4 km.
?
7.如图,在4×4的方格中(小正方形的边长为1个单位长度),标有A,B两点.请你用两种不同的方法表述B点相对A点的位置.
答案
7.【解析】 方法1(用有序实数对(a,b)表示):如图,若记A点为(0,0),则B点可记为(3,3).
方法2(用方位角和距离表示): B点位于A点的东北方向(或北偏东45°),距离A点32个单位长度处.
(方法合理即可)
?
第二节 平面直角坐标系
第二节
课时1 平面直角坐标系
课时1
1.关于平面直角坐标系,有以下说法:
①在平面直角坐标系中,水平方向的数轴称为x轴或横轴,铅直方向的数轴称为y轴或纵轴;
②x轴上所有的点的纵坐标都等于0;
③点M(0,1)在平面直角坐标系中的位置是第三象限或第四象限.
其中正确的是 ( )
A.①②③ B.①② C.①③ D.②③
答案
1.B 【解析】 因为点M(0,1)在y轴的正半轴上,故③错误;易知①②正确.故选B.
知识点 1 平面直角坐标系的有关概念
2.如图,图中点A,B,C,D的坐标分别为 .?
答案
2.(3,2),(2,3),(-2,3),(-1,-3)
知识点 1 平面直角坐标系的有关概念
3.[2019湖南株洲中考]在平面直角坐标系中,点A(2,-3)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案
3.D 【解析】 根据平面直角坐标系中点的坐标特征可知,第四象限的点的坐标符号为(+,-).故选D.
知识点 2 各象限内点的坐标的符号特征
4.[2020河南平顶山期中]如图,小手盖住的点的坐标可能为 ( )
A.(5,2) B.(-6,3)
C.(-4,-6) D.(3,-4)
答案
4.C 【解析】 因为小手的位置在第三象限,所以小手盖住的点的横坐标小于0,纵坐标小于0,结合选项知只有(-4,-6)符合第三象限内点的坐标的符号特征.故选C.
知识点 2 各象限内点的坐标的符号特征
5.[2020河南郑州中原区月考]在平面直角坐标系中,点P(a+1,-????-1)在( )
A.x轴上 B.第二象限
C.y轴上 D.第四象限
?
答案
5.D 【解析】 因为????有意义,所以a≥0,所以a+1>0,-????-1<0,所以点P(a+1,-????-1)在第四象限.故选D.
?
知识点 2 各象限内点的坐标的符号特征
6.如果点M(a+b,ab)在第二象限,那么点N(a,b)在第 象限.?
答案
6.三 【解析】 因为点M(a+b,ab)在第二象限,所以a+b<0,ab>0,所以ab同号,且a,b同是负数,即a<0,b<0,所以点N在第三象限.
7.点P(2,-4)到x轴的距离是 ( )
A.2 B.-4 C.-2 D.4
答案
7.D
知识点 3 坐标与距离的关系
8.[2019湖南广益实验中学开学考试]已知在平面直角坐标系中,点P在第二象限,且点P到x轴和y轴的距离分别为6和5,那么点P的坐标为( )
A.(-5,-6) B.(-6,-5) C.(-5,6) D.(-6,5)
答案
8.C 【解析】 根据第二象限内的点的横坐标小于0,纵坐标大于0,且点P到x轴的距离是6,则其纵坐标为6,点P到y轴的距离为5,则其横坐标为-5,所以点P的坐标是(-5,6).故选C.
9.已知平面直角坐标系中有一点M(m-1,2m+3).
(1)当m为何值时,点M到x轴的距离为1?
(2)当m为何值时,点M到y轴的距离为2?
答案
9.【解析】 (1)由题意,得|2m+3|=1,
所以2m+3=1或2m+3=-1,
所以m=-1或m=-2.
(2)由题意,得|m-1|=2,
所以m-1=2或m-1=-2,
所以m=3或m=-1.
知识点 3 坐标与距离的关系
10.建立适当的平面直角坐标系,并在图中描出下列各点:A(2,3),B(-2,3),C(3,-2),D(5,1),E(0,-4),F(-3,0).
答案
10.【解析】 如图所示.
知识点 4 根据坐标描点
1.若点A(a,b)在第四象限,则点B(a,-b)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案
1.A 【解析】 因为点A(a,b)在第四象限,所以a>0,b<0,所以-b>0,所以点B(a,-b)在第一象限.故选A.
2.易错题 [2019山东济宁期中]点P到x轴的距离是2,到y轴的距离是3,且点P在y轴的右侧,则点P的坐标是 ( )
A.(2,3) B.(3,2)或(3,-2)
C.(3,2) D.(2,3)或(2,-3)
答案
2.B 【解析】 因为点P在y轴的右侧,且点P到x轴的距离是2,到y轴的距离是3,所以点P的横坐标是3,纵坐标是2或-2,所以点P的坐标是(3,2)或(3,-2).故选B.
3.关于平面直角坐标系,有以下说法:①坐标平面内的点可以用有序数对来表示;②若a大于0,b不大于0,则点A(2a+1,5b-2)在第三象限;③坐标原点不属于任何象限;④当m≠0时,点P(m2,m)在第四象限.
其中正确的个数为( )
A.1 B.2 C.3 D.4
答案
3.B 【解析】 易知①③正确;若a大于0,b不大于0,则2a+1>0,5b-2<0,所以点A(2a+1,5b-2)在第四象限,故②错误;当m≠0时,m2>0,m可能为正数,也可能为负数,所以点P(m2,m)在第一象限或第四象限,故④错误.综上,可知正确的个数为2.故选B.
4.在平面直角坐标系中,如果mn>0,那么点(m,|n|)在( )
A.第一象限或第二象限
B.第一象限或第三象限
C.第二象限或第四象限
D.第三象限或第四象限
答案
4.A 【解析】 因为mn>0,所以m和n同号.当m和n都是正数时,m>0,|n|>0,所以点(m,|n|)在第一象限;当m,n都是负数时,m<0,|n|>0,所以点(m,|n|)在第二象限.综上,可知点(m,|n|)在第一象限或第二象限.故选A.
5.点A(m+2,3m-5)在第一象限,若点A到x轴的距离是它到y轴的距离的一半,则m的值为 .?
答案
5.125 【解析】 由题意,知点A(m+2,3m-5)到x轴的距离是3m-5,到y轴的距离是m+2,所以3m-5=12(m+2),解得m=125.
?
6.[2020广东汕头期中]已知点P的坐标为(2-a,3a+6),且点P到两坐标轴的距离相等,求点P的坐标.
答案
6.【解析】 因为点P的坐标为(2-a,3a+6),且点P到两坐标轴的距离相等,
所以2-a=3a+6或(2-a)+(3a+6)=0,
解得a=-1或a=-4,
所以点P的坐标为(3,3)或(6,-6).
7.[2020广西崇左期中]如图,已知四边形ABCD.(网格中每个小正方形的边长均为1)
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.
答案
7.【解析】 (1)A(-2,1),B(-3,-2),C(3,-2),D(1,2).
(2)S四边形ABCD=3×3+2×12×1×3+12×2×4=16.
?
8.[2019山东济宁期末]【阅读材料】
平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为[P],即[P]=|x|+|y|,例如点P(1,2)的勾股值[P]=|1|+|2|=3.
【解决问题】
(1)求点A(-2,4),B(2+3,2-3)的勾股值[A],[B];
(2)若点M(x,y)在x轴的上方,其横、纵坐标均为整数,且[M]=3,求点M的坐标.
?
答案
8.【解析】 (1)[A]=|-2|+|4|=2+4=6,
[B]=|2+3|+|2-3|=2+3+3-2=23.
(2)因为点M(x,y)在x轴的上方,所以y>0.
因为点M的横、纵坐标均为整数,且[M]=|x|+|y|=3,
所以当y=1时,x=±2;当y=2时,x=±1;当y=3时,x=0.
所以点M的坐标为(-1,2),(1,2),(-2,1),(2,1)或(0,3).
?
课时2 点的坐标
课时2
1.下列各点不在x轴上的是 ( )
A.(0,1) B.(-1,0) C.(0,0) D.(π,0)
答案
1.A 【解析】 因为在x轴上的点的纵坐标为0,所以(0,1)不在x轴上.故选A.
知识点 1 坐标轴及象限角平分线上的点的坐标特征
2.易错题 已知点C在y轴上,且距离原点5个单位长度,则点C的坐标是 ( )
A.(5,0) B.(0,5) C.(5,0)或(0,5) D.(0,5)或(0,-5)
答案
2.D 【解析】 因为点C在y轴上,所以点C的横坐标为0,又因为点C距离原点5个单位长度,所以满足题意的点C有2个,分别是(0,5),(0,-5).故选D.
3.[2020陕西西安雁塔区期中]已知点M(2x-3,3-x)在第二、四象限的角平分线上,则点M的坐标为 ( )
A.(-3,-3) B.(-1,1) C.(-3,3) D.(3,-3)
答案
3.C 【解析】 因为点M(2x-3,3-x)在第二、四象限的角平分线上,所以2x-3+3-x=0,解得x=0,所以2x-3=-3,3-x=3,所以点M的坐标为(-3,3).故选C.
知识点 1 坐标轴及象限角平分线上的点的坐标特征
4.若点A(a,b),B(b,a)表示同一个点,则这个点在( )
A.第二、四象限的角平分线上 B.平行于x轴的直线上
C.第一、三象限的角平分线上 D.平行于y轴的直线上
答案
4.C 【解析】 因为点A(a,b),B(b,a)表示同一个点,所以它们的横、纵坐标相等,而横、纵坐标相等的点在第一、三象限的角平分线上.故选C.
5.已知平面直角坐标系内有一点M(a,b),且ab=0,则点M的位置一定在 ( )
A.原点上
B.x轴上
C.y轴上
D.坐标轴上
答案
5.D 【解析】 因为ab=0,所以a=0或b=0或a,b均为0.当a=0时,点M在y轴上;当b=0时,点M在x轴上;当a,b均为0时,点M在原点.综上所述,点M在坐标轴上.故选D.
知识点 1 坐标轴及象限角平分线上的点的坐标特征
6.已知点M(-1,3),N(-3,3),则直线MN与x轴、y轴的位置关系分别为( )
A.相交,相交 B.平行,平行
C.垂直,平行 D.平行,垂直
答案
6.D 【解析】 因为点M,N的坐标分别为(-1,3)和(-3,3),所以点M和点N的纵坐标相同,所以直线MN与x轴平行,与y轴垂直.故选D.
知识点 2 与坐标轴平行的直线上的点的坐标特征
7.下列说法正确的是 ( )
A.已知直线AB∥x轴,点A(3,5),点B(m,n),则m=3
B.点(1,-a2)一定在第四象限
C.已知点A(1,-3)与点B(1,3),则直线AB平行于y轴
D.在y轴上的点的横坐标都是0,纵坐标都大于0
答案
7.C 【解析】 A项,直线AB∥x轴,点A(3,5),点B(m,n),则n=5,但不能确定m的值,故说法错误;B项,因为a2≥0,所以-a2≤0,所以点(1,-a2)一定在第四象限或x轴上,故说法错误;D项,在y轴上的点的横坐标都是0,纵坐标为任意实数,故说法错误.故选C.
知识点 2 与坐标轴平行的直线上的点的坐标特征
8.在平面直角坐标系中,若AB∥y轴,AB=3,点A的坐标为(-2,3),则点B的坐标为 ( )
A.(-2,6) B.(1,3)
C.(-2,6)或(-2,0) D.(1,3)或(-5,3)
答案
8.C 【解析】 因为点A(-2,3),AB∥y轴,所以点B的横坐标为-2,又因为AB=3,所以点B的纵坐标为3+3=6或3-3=0,所以点B的坐标为(-2,6)或(-2,0).故选C.
知识点 2 与坐标轴平行的直线上的点的坐标特征
9.如图,四边形ABCD是长方形,AB=3,AD=4.已知点A(-32,-1),则点C的坐标是( )
A.(-3,32) B.(32,-3)
C.(3,32) D.(32,3)
?
答案
9.D 【解析】 因为四边形ABCD是长方形,所以AB=CD=3,AD=BC=4,又因为点C在第一象限,所以点C的坐标为
(-32+3,-1+4),即点C的坐标为(32,3).故选D.
?
知识点 2 与坐标轴平行的直线上的点的坐标特征
10.[2019广东珠海香洲区期末]若点P(m+3,m+1)在平面直角坐标系的x轴上,则m的值为 ( )
A.0 B.-1 C.-2 D.-3
答案
10.B 【解析】 因为点P(m+3,m+1)在x轴上,所以m+1=0,解得m=-1.故选B
知识点 3 根据点的坐标或位置求字母的值
11.已知点A(m+1,-2)和点B(3,m-1),如果直线AB∥x轴,那么m的值为 ,如果直线AB∥y轴,那么m的值为 .?
答案
11.-1 2 【解析】 由直线AB∥x轴,可知m-1=-2,m+1≠3,所以m=-1.由直线AB∥y轴,可知m+1=3,m-1≠-2,所以m=2.
12.已知点P(2m-6,m+2).
(1)若点P在y轴上,则点P的坐标为 .?
(2)若点P的纵坐标比横坐标大6,则点P在第几象限?
(3)若点P在过点A(2,3)且与x轴平行的直线上,求点P的坐标.
知识点 3 根据点的坐标或位置求字母的值
答案
12.【解析】 (1)(0,5)
因为点P在y轴上,所以2m-6=0,解得m=3,所以P点的坐标为(0,5).
(2)根据题意,得2m-6+6=m+2,解得m=2,
所以点P的坐标为(-2,4),所以点P在第二象限.
(3)因为点P在过点A(2,3)且与x轴平行的直线上,
所以点P的纵坐标为3,即m+2=3,解得m=1,
2m-6=-4,所以点P的坐标为(-4,3).
13.在如图所示的平面直角坐标系中,描出下列各点,并依次用线连接起来,看它像什么?
(2,1),(6,1),(6,3),(7,3),(4,6),(1,3),(2,3),(2,1).
答案
13.【解析】 描点、连线,如图所示,它的形状像一座小房子.
知识点 4 根据点的坐标描点连线构成图形
课时3 建立直角坐标系求坐标
课时3
1.如图,正方形ABCD的边长为4,请你建立适当的平面直角坐标系,写出各个顶点的坐标.
答案
1.【解析】 以点A为坐标原点,以AB所在的直线为x轴,AD所在的直线为y轴建立如图所示的平面直角坐标系,
则点A,B,C,D的坐标分别是(0,0),(4,0),(4,4),(0,4).(答案不唯一)
知识点 1 建立适当的平面直角坐标系求点的坐标
2.如图,若在象棋盘上建立平面直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),则“炮”位于点 ( )
A.(1,3) B.(-2,0)
C.(-1,2) D.(-2,2)
答案
2.B 【解析】 因为“将”位于点(1,-2),“象”位于点(3,-2),所以建立的平面直角坐标系如图所示,则“炮”位于点(-2,0).故选B.
知识点 2 确定有关点的位置
3.如图是利用平面直角坐标系画出的天安门广场的平面示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示天安门广场上国旗台的点的坐标为(0,2.5),表示中国国家博物馆的点的坐标为(4,1),则表示下列建筑的点的坐标正确的是( )
A.天安门(0,4)
B.人民大会堂(-4,1)
C.毛主席纪念堂(-1,-3)
D.正阳门(0,-5)
答案
3.B 【解析】 建立如图所示的平面直角坐标系,则天安门(0,5),
人民大会堂(-4,1),毛主席纪念堂(0,-3),正阳门(0,-5.5).故选B.
知识点 2 确定有关点的位置
4.[2019河北保定竞秀区一模]嘉嘉和淇淇下棋,嘉嘉执圆形棋子,淇淇执方形棋子.如图,棋盘中心的圆形棋子的位置用(-1,1)表示,右下角的圆形棋子的位置用(0,0)表示,若淇淇将第4枚方形棋子放入棋盘后,所有棋子构成的图形是轴对称图形,则淇淇放的方形棋子的位置可能是 ( )
A.(-1,2) B.(-1,-1) C.(0,2) D.(1,3)
答案
4.A 【解析】 根据已知两枚棋子的位置建立如图所示的平面直角坐标系,根据题图
可知,要再放入一枚方形棋子使得所有棋子构成的图形是轴对称图形,放的方形棋子应
在棋盘中心的圆形棋子的上方相邻点处,所以所放方形棋子的位置坐标为(-1,2).故选A.
知识点 2 确定有关点的位置
5.已知A,B,C三点的坐标分别为(0,3),(4,0),(-4,0).则△ABC的面积为 .?
答案
5.12 【解析】 建立平面直角坐标系如图所示.由点A,B,C的坐标可知BC=8,OA=3,所以△ABC的面积为12×8×3=12.
?
知识点 3 求平面直角坐标系中图形的面积
6.已知在平面直角坐标系中有三点A(-2,1),B(3,1),C(2,3).请回答如下问题:
(1)在如图所示的平面直角坐标系内描出点A,B,C的位置;
(2)求出以A,B,C三点为顶点的三角形的面积;
(3)在y轴上是否存在点P,使以A,B,P三点为顶点的三角形的面积为10?若存在,直接写出点P的坐标;若不存在,请说明理由.
知识点 3 求平面直角坐标系中图形的面积
答案
6.【解析】 (1)点A,B,C的位置如图所示.
(2)如图,连接AB,BC,AC.
依题意,得AB∥x轴,且AB=3-(-2)=5,
所以S△ABC=12×5×2=5.
(3)存在.点P的坐标为(0,5)或(0,-3).
因为AB=5,S△ABP=10,
所以点P到AB的距离为4,
又因为点P在y轴上,
所以点P的坐标为(0,5)或(0,-3).
?
1.[2019福建南平期末]在平面直角坐标系中,点A,B,C,D,E,F的位置如图所示,如果点E的坐标是(-3,0),点F的坐标是(3,0),那么在第三象限内的点是 ( )
A.点A B.点B C.点C D.点D
答案
1.C 【解析】 如图,连接EF,过EF的中点作EF的垂线GH,因为点E的坐标是(-3,0),点F的坐标是(3,0),所以GH所在直线为y轴,EF所在直线为x轴,所以在第三象限内的点是点C.故选C.
2.已知点A(0,0),B(4,0),点C在y轴上,且△ABC的面积为5,则点C的坐标为 ( )
A.(0,52)
B.(0,-52)
C.(0,52)或(0,-52)
D.无法确定
?
答案
2.C 【解析】 由题意知,以点A为坐标原点,分别以AB所在直线为x轴,过点A且垂直AB的直线为y轴建立平面直角坐标系.因为A(0,0),B(4,0),所以AB=4.因为△ABC的面积为5,点C在y轴上,所以12AB·AC=5,所以AC=52.设点C的纵坐标为y,则|y|=52,所以y=52或y=-52,所以点C的坐标为(0,52)或(0,-52).故选C.
?
3.星期天,小李和小张相约到文化广场游玩,出发前,他们每人带了一张利用平面直角坐标系画的示意图,如图所示,其中行政办公楼的坐标是(-4,3),南城百货的坐标是(2,-3).
(1)请根据上述信息,画出这个平面直角坐标系;
(2)写出示意图中体育馆、升旗台、北部湾俱乐部、盘龙苑小区、国际大酒店的坐标;
(3)小李跟小张说他现在的位置坐标是(-2,-2),请你在图中用字母A标出小李的位置.
答案
3.【解析】 (1)如图所示(图1).
(2)体育馆(-9,4),升旗台(-4,2),北部湾俱乐部(-7,-1),盘龙苑小区(-5,-3),国际大酒店(0,0).
(3)小李的位置A如图所示(图2).
图1 图2
4.如图为草房的示意图,AB的长为15米,房檐CD的长为20米,门宽EF为6米,CD到地面的距离为18米,请你建立适当的平面直角坐标系,并写出A,B,C,D,E,F的坐标.
答案
4.【解析】 根据题意,可以以AB的中点为坐标原点,AB所在直线为x轴,AB的垂直平分线为y轴,建立如图所示的平面直角坐标系.
因为AB=15米,且在x轴上,A点在负半轴上,B点在正半轴上,
所以A(-7.5,0),B(7.5,0).
因为CD=20米,CD到地面的距离为18米,
所以C(-10,18),D(10,18).
因为EF在x轴上,E点在负半轴上,F点在正半轴上,EF=6米,
所以E(-3,0),F(3,0).(答案不唯一)
5.如图,A(-4,0),B(6,0),C(2,4),D(-3,2).
(1)求四边形ABCD的面积;
(2)在y轴上找一点P,使△APB的面积等于四边形ABCD的面积的一半.求点P的坐标.
答案
5.【解析】 (1)如图,分别过C,D两点作x轴的垂线,垂足分别为E,F,
则S四边形ABCD=S△ADF+S梯形CDFE+S△BCE=12AF·DF+12FE·
(DF+CE)+12BE·CE=12×1×2+12×5×(2+4)+12×4×4=24.
(2)设△APB的边AB上的高为h,
则由S△APB=12S四边形ABCD,
得12×10×h=12×24,
解得h=2.4,
又因为点P在y轴上,
所以点P的坐标为(0,2.4)或(0,-2.4).
?
6.如图,在Rt△OAB中,斜边OB在x轴的正半轴上,直角顶点A在第四象限内,S△OAB=20,OA∶AB=1∶2.求A,B两点的坐标.
答案
6.【解析】 由OA∶AB=1∶2,可设OA=x(x>0),则AB=2x.
在Rt△OAB中,根据勾股定理,可得OB=????????2+????????2=5x,
因为S△OAB=20=12OA·AB,所以20=12x·2x,
所以x2=20,所以x=25,
所以OB=5×25=10,
所以点B的坐标是(10,0).
如图,过点A作AC⊥OB于点C,
因为S△OAB=12BO·AC=20,
所以AC=4,
又因为点A在第四象限,所以点A的纵坐标为-4.
在Rt△AOC中,OA=25,AC=4,
由勾股定理,得OC=????????2?????????2=2,
所以点A的横坐标是2,所以点A的坐标为(2,-4).
?
易错疑难集训
集训
1.在平面直角坐标系中,点A(5,-7)到x轴的距离是 .?
答案
1.7
易错点 1 混淆坐标顺序、坐标与点到坐标轴的距离之间的关系
2.如图,若用(2,3)表示点A的位置,则点C的位置可表示成 ,(7,7)表示点 的位置.?
答案
2.(6,2) E
3.如图,在长方形OABC中,OA=3,OC=4,则点B的坐标是 .?
答案
3.(-4,3) 【解析】 由题图可知,点B在第二象限,所以点B的横坐标为负数,纵坐标为正数.由于AB=OC=4,所以点B的横坐标为-4,又因为BC=OA=3,所以点B的纵坐标为3,所以点B的坐标是(-4,3).
易错点 1 混淆坐标顺序、坐标与点到坐标轴的距离之间的关系
4.[2019河北张家口桥东区期中]已知点P(2-a,3)到两坐标轴的距离相等,则a的值为 ( )
A.3 B.-1 C.-1或5 D.-3
答案
4.C 【解析】 因为点P(2-a,3)到两坐标轴的距离相等,所以2-a=3或2-a=-3,所以a=-1或a=5.故选C.
易错点 2 因考虑不全面出现漏解
答案
5.B 【解析】 由(x+y)2=x2+y2-2,可得xy=-1,所以x,y异号,所以点M在第二象限或第四象限.故选B.
5.若点M(x,y)满足(x+y)2=x2+y2-2,则点M所在的象限是 ( )
A.第一象限或第三象限
B.第二象限或第四象限
C.第一象限或第二象限
D.不能确定
答案
6.已知点M(3,-2)与点M'(x,y)在同一条平行于x轴的直线上,且点M'到y轴的距离等于4,那么点M'的坐标是 ( )
A.(4,2)或(-4,2)
B.(4,-2)或(-4,-2)
C.(4,-2)或(-5,-2)
D.(4,-2)或(-1,-2)
6.B 【解析】 因为点M(3,-2)与点M'(x,y)在同一条平行于x轴的直线上,所以M'的纵坐标为-2,又因为点M'到y轴的距离等于4,所以点M'的横坐标为4或-4,所以点M'的坐标为(4,-2)或(-4,-2).故选B.
易错点 2 因考虑不全面出现漏解
答案
7.求符合下列条件的点B的坐标.
(1)已知点A(2,0),AB=4,点B和点A在同一坐标轴上,求点B的坐标;
(2)已知点A(0,0),AB=4,点B和点A在同一坐标轴上,求点B的坐标.
7.【解析】 (1)根据题意,得点B在x轴上,分两种情况讨论:
①当点B在点A的左侧时,因为点A(2,0),AB=4,
所以点B的坐标为(-2,0);
②当点B在点A的右侧时,因为点A(2,0),AB=4,
所以点B的坐标为(6,0).
综上,点B的坐标为(-2,0)或(6,0).
(2)根据题意,得点B可能在x轴上,也可能在y轴上.
①当点B在x轴上时,点B的坐标为(4,0)或(-4,0);
②当点B在y轴上时,点B的坐标为(0,4)或(0,-4).
综上,点B的坐标为(4,0),(-4,0),(0,4)或(0,-4).
易错点 2 因考虑不全面出现漏解
答案
1.[2020山东枣庄山亭区期中]已知点P(a,b)在第四象限,且点P到x轴的距离为3,到y轴的距离为6,则点P的坐标是 ( )
A.(3,-6)
B.(6,-3)
C.(-3,6)
D.(-3,3)或(-6,6)
答案
1.B 【解析】 因为点P(a,b)在第四象限,且到x轴的距离为3,到y轴的距离为6,所以点的横坐标是6,纵坐标是-3,所以点P的坐标为(6,-3).故选B.
疑难点 1 确定点的位置
2.[2020福建福州模拟]已知点A(m,n)在第二象限,则点B(|m|,-n)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案
2.D 【解析】 因为点A(m,n)在第二象限,所以m<0,n>0,所以|m|>0,-n<0,所以点B在第四象限.故选D.
疑难点 1 确定点的位置
3.在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点……则边长为8的正方形内部的整点的个数为( )
A.64 B.49 C.36 D.25
答案
3.B 【解析】 边长为1的正方形内部有1个整点,1×1;边长为2的正方形内部有1个整点,1×1;边长为3的正方形内部有9个整点,3×3;边长为4的正方形内部有9个整点,3×3;边长为5的正方形内部有25个整点,5×5;边长为6的正方形内部有25个整点,5×5;边长为7的正方形内部有49个整点,7×7,所以边长为8的正方形内部整点的个数为7×7=49.故选B.
疑难点 2 点的坐标规律探究
4.将正整数按以下规律排列:
第一列 第二列 第三列 第四列 第五列……
第一行 1 4 5 16 …
第二行 2 3 6 15 …
第三行 9 8 7 14 …
第四行 10 11 12 13 …
第五行 … … … … …
……
数2在第二行、第一列,与有序数对(2,1)对应;数5与(1,3)对应;数14与(3,4)对应;根据这一规律,数2 020对应的有序数对为 .?
疑难点 2 点的坐标规律探究
答案
4.(45,6) 【解析】 将正整数按从小到大的顺序用“→”排列.先找到第奇数行、第一列的数的规律,再推测出2 020对应的有序数对.观察下表,可发现:第奇数行、第一列的数等于该行行数的平方,即第一行、第一列的数为12=1,第三行、第一列的数为32=9,第五行、第一列的数为52=25……因为452=2 025,2 025-2 020=5,所以2 020在第45行第6列,所以数
2 020对应的有序数对为(45,6).
……
第三节 轴对称与坐标变化
第三节
1.点P1(1,-7)和P2(-1,-7)的位置关系是 ( )
A.关于x轴对称
B.关于y轴对称
C.关于原点对称
D.以上都不对
答案
1.B 【解析】 因为P1,P2两点的纵坐标相同,横坐标互为相反数,所以点P1(1,-7)和P2(-1,-7)关于y轴对称.故选B.
知识点 1 关于x轴、y轴对称的点的坐标特征
2.[2019江苏泰州姜堰区期中]在平面直角坐标系中,点A(-2,-3)关于x轴对称的点的坐标是( )
A.(-2,-3)
B.(-2,3)
C.(2,-3)
D.(2,3)
答案
2.B 【解析】 关于x轴对称的两个点的横坐标相同,纵坐标互为相反数,所以点A(-2,-3)关于x轴对称的点的坐标是
(-2,3).故选B.
知识点 1 关于x轴、y轴对称的点的坐标特征
3.[2020广东惠州期末]在平面直角坐标系中,点P(-3,1)关于y轴的对称点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案
3.A 【解析】 点P(-3,1)关于y轴的对称点的坐标为(3,1),(3,1)在第一象限.故选A.
知识点 1 关于x轴、y轴对称的点的坐标特征
4.[2020山东临沂期末]在平面直角坐标系中,若点P(-3,a)与点Q(b,-4)关于x轴对称,则a+b的值为 ( )
A.-7 B.7 C.1 D.-1
答案
4.C 【解析】 因为点P(-3,a)与点Q(b,-4)关于x轴对称,所以b=-3,a=4,所以a+b=-3+4=1.故选C.
知识点 1 关于x轴、y轴对称的点的坐标特征
5.若点P(a,b)关于y轴的对称点是P1,而点P1关于x轴的对称点是P2,已知点P2的坐标为(-3,4),则a= ,b= .?
答案
5.3 -4 【解析】 由题意知点P1和P2(-3,4)关于x轴对称,所以点P1的坐标为(-3,-4),又因为点P(a,b)和点P1(-3,-4)关于y轴对称,所以点P的坐标为(3,-4),所以a=3,b=-4.
6.(1)请在图中画出△ABC关于y轴对称的图形△A'B'C'(其中A',B',C'分别是A,B,C的对应点,不写画法);
(2)直接写出A',B',C'三点的坐标:A'( , ),B'( , ),C'( , ).?
答案
6.【解析】 (1)画出△A'B'C'如图所示.
(2)2 3 3 1 -1 -2
知识点 2 与坐标对称有关的作图
7.如图,△ABC在正方形网格中,每个小正方形的边长均为1,若点A的坐标为(0,3),按要求回答下列问题:
(1)在图中建立适当的平面直角坐标系,并写出点B和点C的坐标;
(2)作出△ABC关于x轴对称的图形△A'B'C'.(不用写作法)
答案
7.【解析】 (1)建立平面直角坐标系如图所示.
点B和点C的坐标分别为(-3,-1),(1,1).
(2)△A'B'C'如图所示.
知识点 2 与坐标对称有关的作图
8.在平面直角坐标系中,△ABC的位置如图所示.
(1)写出A,B,C三点的坐标;
(2)若△ABC各顶点的横坐标不变,纵坐标都乘以-1,请你
在同一平面直角坐标系中描出对应的点A',B',C',并依次
连接这三个点,所得的△A'B'C'与△ABC有怎样的位置关系?
答案
8.【解析】 (1)由题图,可知A,B,C三点的坐标分别是(3,4),(1,2),(5,1).
(2)△A'B'C'如图所示.
△A'B'C'与△ABC的位置关系是关于x轴对称.
知识点3 图形的坐标变化与图形对称的关系
1.将平面直角坐标系中某个图形上的各个点的横坐标都乘以-1,纵坐标不变,所得图形与原图形的位置关系是 ( )
A.关于x轴对称
B.关于y轴对称
C.关于原点对称
D.重合
答案
1.B 【解析】 因为各个点的纵坐标不变,横坐标都乘以-1,即纵坐标相同,横坐标互为相反数,所以所得图形与原图形关于y轴对称.故选B.
2.在平面直角坐标系中,若点P(x,y)在第二象限,且|x|-1=0,y2-4=0,则点P关于坐标原点对称的点P'的坐标是 ( )
A.(-1,-2) B.(1,-2) C.(-1,2) D.(1,2)
答案
2.B 【解析】 因为点P(x,y)在第二象限,且|x|-1=0,y2-4=0,所以x=-1,y=2,所以点P的坐标为(-1,2),所以点P关于坐标原点对称的点P'的坐标是(1,-2).故选B.
3.[2020四川南充嘉陵区期中]已知点P(a-1,5)和Q(2,b-1)关于x轴对称,则(a+b)2 020的值为 .?
答案
3.1 【解析】 因为点P(a-1,5)和Q(2,b-1)关于x轴对称,所以a-1=2,b-1=-5,所以a=3,b=-4,所以(a+b)2 020=(3-4)2 020=1.
4.已知△ABC在平面直角坐标系中的位置如图所示,若△A'B'C'与△ABC关于y轴对称,则点A的对应点A'的坐标是 .?
答案
4.(3,2) 【解析】 由题图可知,点A的坐标为(-3,2),所以点A关于y轴的对应点A'的坐标是(3,2).
5.如图,已知等边三角形ABC的边长为3,写出点A,B,C的坐标,并画出△ABC关于y轴对称的图形△A1B1C1.
答案
5.【解析】 如图,过点A作高AD,可得BD=32,AD=332,
所以A(32,332),B(0,0),C(3,0).
△ABC关于y轴对称的图形△A1B1C1如图所示.
?
6.在棋盘中建立平面直角坐标系,三颗棋子A,O,B的位置的坐标分别是(-1,1),(0,0),(1,0).
(1)如图1,添加棋子C,使四颗棋子A,O,B,C组成一个轴对称图形,请写出棋子C的位置的坐标,并在图中画出该图形的对称轴;
(2)在图2中的其他格点位置添加一颗棋子P,使四颗棋子A,O,B,P成为轴对称图形,请直接写出棋子P的位置的坐标.(写出2个即可)
答案
6.【解析】 (1)如图1所示,棋子C的位置的坐标为(-1,2),A,O,B,C四颗棋子组成等腰梯形,直线l为该图形的对称轴.
(2)如图2所示,P(0,-1),P'(-1,-1)都符合题意.(答案不唯一)
图1 图2
图1 图2
7.[2020湖北恩施州期末]如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;
(2)如果点P的坐标是(-a,0)(0
所以A1(2,0),B1(1,0),C1(1,2),
因为△A1B1C1关于直线l的对称图形是△A2B2C2,
所以△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2).
(2)如图,因为P(-a,0)(0
所以????+????2=3,即m=6-a,所以P2(6-a,0),
所以PP2=6-a-(-a)=6-a+a=6.
?
答案
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
