北师大版八年级上册数学第二章实数素养拓展+中考真题课件(59张PPT)
文档属性
| 名称 | 北师大版八年级上册数学第二章实数素养拓展+中考真题课件(59张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 00:00:00 | ||
图片预览










文档简介
第二章·实数
数学·八年级上册·北师
专项素养拓训
专项一 比较实数的大小
专项
1.比较-2与-6的大小.
?
答案
1.【解析】 因为2<6,所以2<6,所以-2>-6.
?
类型 1 平方法
2.比较13+5与15+3的大小.
?
答案
2.【解析】 (13+5)2=13+265+5=18+265,
(15+3)2=15+245+3=18+245,
因为18+265>18+245,
所以13+5>15+3.
?
3.[2020广东广州期中]课堂上,老师出了一道题,比较19?23与23的大小.
小明的解法如下:
解:19?23-23=19?2?23=19?43,
因为42=16<19,所以19>4,所以19-4>0.
所以19?43>0,所以19?23>23.
我们把这种比较大小的方法称为作差法.
(1)根据上述材料填空.(在横线上填“>”“=”或“<” )
①若a-b>0,则a b;?②若a-b=0,则a b;?③若a-b<0,则a b.?
(2)利用上述方法比较9?224与23的大小.
?
类型 2 作差法
答案
3.【解析】 (1)①> ②= ③<
(2)9?224-23=27?322?812=19?32212=19?19812,
因为192=361>198,所以19>198,
所以19-198>0,所以19?19812>0,
所以9?224>23.
?
4.比较????+1????+2与????+2????+3的大小.
?
类型 3 作商法
答案
4.【解析】 因为????+1????+2÷????+2????+3=????+1????+2×????+3????+2=(????+1)(????+3)(????+2)?2=????+3+4????????+4+4????<1,????+1????+2>0,????+2????+3>0,
所以????+1????+2?
5.已知0A.x<1????C.x2?
类型 4 特殊值法
答案
5.C 【解析】 本题直接比较大小比较困难,可以采用特殊值法求解,取x=14,则1????=4,x2=116,????=12.因为116<14<12<4,所以x2?
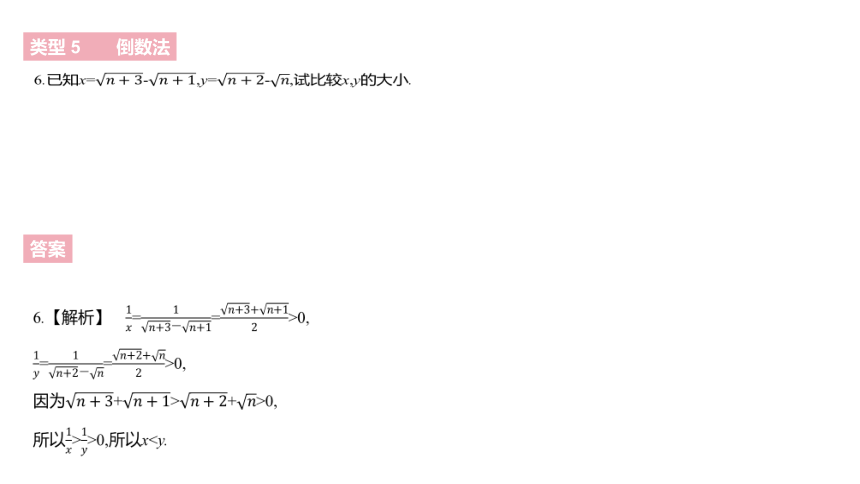
6.已知x=????+3-????+1,y=????+2-????,试比较x,y的大小.
?
类型 5 倒数法
答案
6.【解析】 1????=1????+3?????+1=????+3+????+12>0,
1????=1????+2?????=????+2+????2>0,
因为????+3+????+1>????+2+????>0,
所以1????>1????>0,所以x?
专项二 非负数应用的常见题型
专项
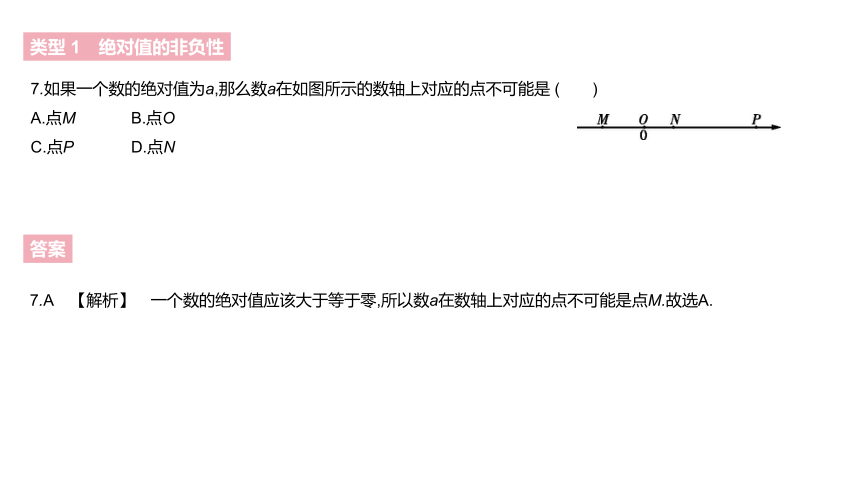
7.如果一个数的绝对值为a,那么数a在如图所示的数轴上对应的点不可能是 ( )
A.点M B.点O
C.点P D.点N
类型 1 绝对值的非负性
答案
7.A 【解析】 一个数的绝对值应该大于等于零,所以数a在数轴上对应的点不可能是点M.故选A.
8.若(y+2)2=a-1,则a的值可以是 ( )
A.-2 B.-1 C.0 D.1
类型 2 偶次方的非负性
答案
8.D 【解析】 由题意,得a-1≥0,所以a≥1.故选D.
9.当式子2????+1的值取最小值时,a 的值为( )
A.0 B.-12 C.-1 D.1
?
类型 3 算术平方根的非负性
答案
9.B 【解析】 因为2????+1≥0,所以当式子2????+1的值取最小值时,2????+1=0,所以2a+1=0,所以a的值为-12.故选B.
?
10.[2020贵州铜仁期末]若?????2+n2+2n+1=0,则mn=( )
A.12 B.-12 C.2 D.-2
?
答案
10.A 【解析】 因为?????2+n2+2n+1=0,所以?????2+(n+1)2=0,所以m-2=0,n+1=0,所以m=2,n=-1,所以mn=2-1=12.故选A.
?
11.若3?????4-4?3????=|12x-y|,求4(x+y)的立方根.
?
类型 3 算术平方根的非负性
答案
11.【解析】 由题意可知,3x-4≥0且4-3x≥0,则x≥43且x≤43,
所以x=43,所以|12x-y|=0,所以y=23.
所以4(x+y)=8,其立方根为38=2.
?
12.[2020北京房山区期中]已知|2 019-m|+?????2?020=m,求m-2 0192的值.
?
类型 3 算术平方根的非负性
答案
12.【解析】 因为m-2 020≥0,所以m≥2 020,所以2 019-m≤-1,
所以|2 019-m|+?????2?020=m可化为m-2 019+?????2?020=m,
所以?????2?020=2 019,所以m-2 020=2 0192,
所以m-2 0192=2 020.
?
专项三 二次根式的常见题型
专项
13.计算:
(1)(232-12)(82+23);
(2)(3+2-6)2-(2-3+6)2;
(3)(1+2-3)(1-2+3);
(4)6÷(3+2)+(3+2)÷6.
?
类型 1 二次根式的运算
答案
13.【解析】 (1)(232-12)(82+23)
=232×82+232×23-12×82-12×23
=23+2-1-33
=1+533.
?
答案
(2)(3+2-6)2-(2-3+6)2
=(3+2-6+2-3+6)(3+2-6-2+3-6)
=2 2(2 3-2 6)
=4 6-8 3.
(3)(1+2-3)(1-2+3)
=[1+(2-3)][1-(2-3)]
=1-(2-3)2
=1-5+2 6
=2 6-4.
(4)6÷(3+2)+(3+2)÷6
=63+2+3+26
=6(3?2)(3+2)(3?2)+(3+2)×66×6
=3 2-2 3+22+33
=722-533.
?
14.已知a+1????=1+10,求a2+1????2的值.
?
类型2 二次根式的化简求值
答案
14.【解析】 a2+1????2=(a+1????)2-2
=(1+10)2-2
=9+210.
?
15.[2020甘肃白银期中]已知x=12?3,y=12+3,求x2-3xy+y2的值.
?
类型2 二次根式的化简求值
答案
15.【解析】 x=12?3=2+3(2?3)(2+3)=2+3,
y=12+3=2?3(2+3)(2?3)=2-3,
所以x2-3xy+y2=(x-y)2-xy=(2+3-2+3)2-(2+3)(2-3)=12-1=11.
?
16.已知:a,b,c满足(a-8)2+?????5+|c-32|=0.
(1)求a,b,c的值;
(2)试问以a,b,c为边能否构成三角形?若能构成三角形,求出三角形的周长;若不能构成三角形,请说明理由.
?
类型3 二次根式的运算与三角形知识的结合
答案
16.【解析】 (1)根据题意,得a-8=0,b-5=0,c-3 2=0,
解得a=8=2 2,b=5,c=3 2.
(2)能构成三角形.
因为2 2+3 2=5 2>5>3 2-2 2,
所以以a,b,c为边能构成三角形,
三角形的周长为22+5+32=52+5.
?
综合素养拓训
素养解读
本章内容贯通初高中数学,学习实数与二次根式,有助于培养学生的数感和符号意识.同时,基于旧知识的探究式学习,也有助于培养学生发现问题、提出问题的意识,逐渐形成解决问题的能力.例如第2题,需要在熟练掌握算术平方根的基础上,尝试利用逆运算解决问题;第4题,面对形式复杂的问题时,可以通过观察发现式子的异同,进而利用构造法将问题简单化;第5题,通过材料给出新方法,考查阅读理解能力,对综合素养要求较高.
1.[分类讨论化简二次根式]设a,b为非零实数,则????|????|+????2????所有可能的值为( )
A.±2 B.±1或0
C.±2或0 D.±2或±1
?
答案
1.C 【解析】 ①a,b同号时,????|????|,????2????也同号,即同为1或-1,故此时????|????|+????2????=±2;②a,b异号时,????|????|,????2????也异号,即一个是1,另一个是-1,故此时????|????|+????2????=0.故选C.
?
2.[算术平方根与规律探究]对于任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[3]=1,现对72进行如下操作:72 [72]=8 [8]=2 [2]=1,这样对72需进行3次操作后变为1.类似地,对81需进行 次操作后变为1;需进行3次操作后变为1的所有正整数中,最大的数是 .?
?
答案
2.3 255 【解析】 81 [81]=9 [9]=3 [3]=1,所以对81需进行3次操作后变为1.算术平方根的整数部分为1的最大正整数为3,算术平方根的整数部分为3的最大正整数为15,算术平方根的整数部分为15的最大正整数为255,所以需进行3次操作后变为1的所有正整数中,最大的数是255.
?
3.[二次根式与勾股定理]如图,S1,S2,S3,…分别表示各个三角形的面积,仔细观察,并认真分析各式,然后解答问题.
O????22=12+12=2,S1=12;
O????32=12+(2)2=3,S2=22;
O????42=12+(3)2=4,S3=32;
…
(1)用含n(n是正整数)的式子表示OA2n+1和Sn;
(2)若一个三角形的面积是5,通过计算说明它是第几个三角形.
?
答案
3.【解析】 (1)O????????+12=12+(????)2=n+1,Sn=????2.
(2)当Sn=????2=5时,????=25=4×5=20,即n=20,
所以它是第20个三角形.
?
4.[巧用构造法化简二次根式]化简:(2+3+5)2+(2+3-5)2+(2-3+5)2+(-2+3+5)2.
?
答案
4.【解析】 设x=2+3,y=2-3,则x2+y2=10,
(2+3+5)2+(2+3-5)2+(2-3+5)2+(-2+3+5)2
=(x+5)2+(x-5)2+(y+5)2+(-y+5)2
=(x2+25x+5)+(x2-25x+5)+(y2+25y+5)+(y2-25y+5)
=2(x2+y2)+20
=40.
?
5.[形如????±????????形式的二次根式的化简]先阅读下面的解题过程,然后再解答.
形如????±2????的化简,我们只要找到两个数a,b,使a+b=m,ab=n,即(????)2+(????)2=m,????·????=????,那么便有:????±2????=(????±????)2=????±????(a>b≥0).
例如化简:7+43.
解:首先把7+43化为7+212,这里m=7,n=12,
由于4+3=7,4×3=12,所以(4)2+(3)2=7,4×3=12,
所以7+43=7+212=(4+3)2=2+3.
根据上述方法化简:13?242.
?
答案
5.【解析】 根据题意,可知m=13,n=42,
由于7+6=13,7×6=42,
所以(7)2+(6)2=13,7×6=42,
所以13?242=(7)2+(6)2?2×7×6=(7?6)2=7-6.
?
答案
1.D 【解析】 无理数有5,-π,60.123 45…(小数部分由相继的正整数组成),共3个.故选D.
?
一、选择题
1.[2020山东菏泽期中]给出下列各数:-52,0.212 121 21,1.21,5,|-2|,9,-π,2.003 003 003…(相邻两个3之间有2个0),60.123 45…(小数部分由相继的正整数组成),其中属于无理数的有( )
A.6个 B.5个 C.4个 D.3个
?
答案
2.C 【解析】 38=2,2的平方根是±2.故选C.
?
2.[2020辽宁辽阳期末]38的平方根是( )
A.2 B.-2 C.±2 D.±2
?
答案
3.A 【解析】 12-3=23-3=3.故选A.
?
3.[2019甘肃兰州中考]计算:12-3=( )
A.3 B.2 3 C.3 D.4 3
?
答案
4.C 【解析】 -4没有算术平方根,故A项错误;4是16的算术平方根,故B项错误;1的平方根是±1,故D项错误.故选C.
4.[2020陕西西安雁塔区月考]下列说法正确的是 ( )
A.2是-4的算术平方根
B.±4是16的算术平方根
C.-6是(-6)2的平方根
D.1的平方根是它本身
答案
5.C 【解析】 (7-3)(7+3)-(3+6)2=7-3-(3+62+6)=-5-62.故选C.
?
5.计算(7-3)(7+3)-(3+6)2的结果是( )
A.-5
B.-5-3 2
C.-5-6 2
D.-3-2
?
答案
6.D 【解析】 因为(32)2<3<4,即32<3<2,所以与3对应的点距离最近的是点D.故选D.
?
6.[2020北京延庆区期末]如图,数轴上A,B,C,D四点中,与3对应的点距离最近的是( )
A.点A B.点B
C.点C D.点D
?
答案
7.C 【解析】 18-89=32-223=723,A选项成立,不符合题意;2+23=83=223,B选项成立,不符合题意;8+182=22+322=522,C选项不成立,符合题意;13+2=3?2(3+2)(3?2)=3-2,D选项成立,不符合题意.故选C.
?
7.[2019山东聊城中考]下列各式不成立的是 ( )
A.18-89=73 2
B.2+23=223
C.8+182=4+9=5
D.13+2=3-2
?
答案
8.A 【解析】 因为4<7<9,所以2<7<3,所以a=2,b=7-2,所以(4+7)(a-b)=(4+7)(4-7)=42-(7)2=16-7=9.
?
8.[2020辽宁朝阳双塔区期中]若a是7的整数部分,b是7的小数部分,则代数式(4+7)(a-b)的值为( )
A.9 B.2+7
C.7 D.4-7
?
答案
9.2 【解析】 24×13-4×18=24×13-4×24=22-2=2.
?
二、填空题
9.[2020四川遂宁期末]计算:24×13-4×18= .?
?
答案
10.2 【解析】 由题意,得256=16,16=4,4=2,2是无理数,所以输出的y等于2.
?
10.[2020吉林长春期末]有一个数值转换器,原理如图所示,当输入的x=256时,输出的y等于? .?
答案
11.等边 【解析】 因为三角形的三边a,b,c满足?????????+(b-c)2=0,所以a-b=0,b-c=0,解得a=b,b=c,所以a=b=c,所以该三角形是等边三角形.
?
11.[2020四川宜宾期中]若三角形的三边a,b,c满足?????????+(b-c)2=0,则三角形是 三角形.?
?
答案
12.2 0182?0182?019 【解析】 1+112+122+1+122+132+1+132+142+…+1+12?0182+12?0192=1+(1-12)+1+(12-13)+…+1+(12?018-12?019)=2 018+1-12+12-13+13-14+…+12?018-12?019=2 0182?0182?019.
?
12.[2019山东枣庄中考]观察下列各式:
1+112+122=1+11×2=1+(1-12),
1+122+132=1+12×3=1+(12-13),
1+132+142=1+13×4=1+(13-14),
…
请利用你发现的规律,计算:
1+112+122+1+122+132+1+132+142+…+1+12?0182+12?0192,
其结果为 .?
?
答案
13.【解析】 (1)-12+|3-2|-(3-7)0
=-1+2-3-1
=-3.
(2)12-22-613+18
=23-22-23+32
=2.
(3)50÷5+(23+2)(23-2)
=50÷5+12-2
=10+10.
(4)12+3+2+3-(3-1)2
=2-3+2+3-(4-23)
=23.
?
三、解答题
13.[2020江苏无锡惠山区期中]计算:
(1)-12+|3-2|-(3-7)0;(2)-12-2 2-613+18;(3)50÷5+(2 3+2)(2 3-2);(4)12+3+2+3-(3-1)2.
?
答案
14.【解析】 (1)因为a2=4,所以a=±2,
因为b的算术平方根为3,所以b=9,
所以a+b=-2+9=7或a+b=2+9=11.
综上,a+b的值为7或11.
(2)因为x是25的平方根,所以x=±5,
因为y是16的算术平方根,所以y=4,
因为x所以x-y=-5-4=-9.
14.[2019江西宜春期中](1)如果a2=4,b的算术平方根为3,求a+b的值;
(2)已知x是25的平方根,y是16的算术平方根,且x答案
15.【解析】 (1)23?7=2(3+7)(3?7)(3+7)=2(3+7)2=3+7.
(2)因为a=13+22=3?22(3+22)(3?22)=3-2 2,
所以a-3=-2 2,所以(a-3)2=8,即a2-6a+9=8,
所以a2-6a=-1,
所以2a2-12a+1=2(a2-6a)+1=2×(-1)+1=-1.
?
15.[2019河北唐山一模]在解决问题“已知a=12?1,求3a2-6a-1的值”时,小明是这样解答的:
因为a=12?1=2+1(2?1)(2+1)=2+1,
所以a-1=2,所以(a-1)2=2,即a2-2a+1=2,
所以a2-2a=1,所以3a2-6a=3,
所以3a2-6a-1=2.
请你根据小明的解答过程,解决下列问题:
(1)化简:23?7.
(2)若a=13+22,求2a2-12a+1的值.
?
16.有一块长方形木板,木工采用如图所示的方法,在木板上截出两个面积分别为18 dm2和32 dm2的正方形木板.
(1)求剩余木板的面积;
(2)如果木工想从剩余的木板中截出长为1.5 dm,宽为1 dm的长方形木条,最多能截出多少块这样的木条?
答案
16.【解析】 (1)因为两个正方形的面积分别为18 dm2和32 dm2,
所以这两个正方形的边长分别为32 dm和42 dm,
所以剩余木板的面积为(42-32)×32=6(dm2).
(2)由(1)可得,剩余木板的长为32dm,宽为4 2-3 2=2(dm),
因为4<32<4.5,1<2<2,
所以从剩余的木板中截出长为1.5 dm,宽为1 dm的长方形木条,最多能截出2块.
?
第二章·实数中考模拟+真题
数学·八年级上册·北师
答案
1.B 【解析】 因为150????=5×5×2×3????,150????(0?
1.[2019湖北潜江一模]如果150????(0A.3个 B.4个 C.5个 D.6个
?
答案
2.B 【解析】53-27=53-3 3=2 3,因为3<2 3<4,所以表示53-27的点应在线段BC上.故选B.
?
2.[2019重庆九龙坡区模拟]如图,表示53-27的点应在( )
A.线段AB上 B.线段BC上
C.线段CD上 D.线段DE上
?
答案
3.D 【解析】 根据题意,得c-3=0且b-2=0,解得c=3,b=2,则a的取值范围是3-23.[2020福建龙岩永定区期中]若a,b,c为△ABC的三边长,且满足|c-3|+?????2=0,则a的值不可以为( )
A.2 B.3 C.4 D.5
?
答案
4.2 【解析】 x2+2x+1=(x+1)2,当x=2-1时,原式=(2)2=2.
?
4.[2020河南一模]若x=2-1,则x2+2x+1= .?
?
答案
5.3 【解析】 根据题意,得8※4=8+48?4=232=3.
?
5.[2020湖南益阳期末]对于任意不相等的两个实数a,b,定义运算※如下:a※b=????+?????????????,如3※2=3+23?2=5.那么8※4=???????? .?
?
答案
6.4 【解析】 因为f(m)=[2?????3]-[????5],所以f(-6)=[2?(?6)3]-[?65]=2-(-2)=4.
?
6.[2019四川成都武侯区模拟]定义[x]表示不超过实数x的最大整数,例如[0.82]=0,[6]=6,[-135]=-3,[-7]=-7.若规定:对于实数m,f(m)=[2?????3]-[????5].例如f(7)=[2?73]-[75]=[-53]-[75]=-2-1=-3,则f(-6)= .?
?
答案
7.【解析】 |3-2|+(12)-1-(5+1)(5-1)
=2-3+2-(5-1)
=2-3+2-5+1
=-3.
?
7.[2019四川宜宾翠屏区二片区期中]计算:|3-2|+(12)-1-(5+1)(5-1).
?
答案
8.【解析】 (1)因为5a+2的立方根是3,
所以5a+2=27,所以a=5.
因为3a+b-1的算术平方根是4,
所以3a+b-1=14+b=16,所以b=2.
因为c是13的整数部分,3<13<4,
所以c=3.
(2)将a=5,b=2,c=3代入3a-b+c,得3a-b+c=16,
所以3a-b+c的平方根是±4.
?
8.[2020河南洛阳期中]已知5a+2的立方根是3,3a+b-1的算术平方根是4,c是13的整数部分.
(1)求a,b,c的值;
(2)求3a-b+c的平方根.
?
答案
9.【解析】 (1)>
16?2=1×(6+2)(6?2)(6+2)=6+22, 15?3=1×(5+3)(5?3)(5+3)=5+32,
因为6+2>5+3,所以16?2>15?3.
?
9.[2019重庆九龙坡区模拟]阅读材料:
黑白双雄,纵横江湖;双剑合璧,天下无敌.这是武侠小说中的常见描述,其意是指两个人合在一起,取长补短,威力无比,在二次根式中也有这种相辅相成的“对子”,如(5+3)(5-3)=-4,(3+2)(3-2)=1,它们的积不含根号,我们说这两个因式互为有理化因式,其中一个是另一个的有理数因式.
解决问题:
(1)比较大小:16?2 15?3.(用“>”“< ”或“=”填空)?
(2)若实数x,y满足(x+????2+2?019)(y+????2+2?019)=2 019,求x+y+2 019的值.
?
答案
(2)因为(x+????2+2?019)(y+????2+2?019)=2 019,
所以x+????2+2?019=2?019????+????2+2?019,
所以x+????2+2?019=????2+2?019-y①,
同理得y+????2+2?019=????2+2?019-x②,
所以①+②,得x+y+????2+2?019+????2+2?019=????2+2?019+????2+2?019-(x+y),
所以x+y=0,所以x+y+2 019=2 019.
?
答案
1.B 【解析】 38=2,有理数有38,43,共2个.故选B.
?
1.[2019山东日照中考]在实数38,????3,12,43中有理数有( )
A.1个 B.2个 C.3个 D.4个
?
答案
2.B 【解析】 12=22,4=2,12=23,所以A,C,D不是最简二次根式.故选B.
?
2.[2019广西河池中考]下列式子中,为最简二次根式的是 ( )
A.12 B.2 C.4 D.12
?
答案
3.B 【解析】 -2的倒数的平方为(-12)2=12.故选B.
?
3.[2019湖北荆门中考]-2的倒数的平方是( )
A.2 B.12 C.-2 D.-12
?
答案
4.B
4.[2019江苏南京中考]面积为4的正方形的边长是 ( )
A.4的平方根
B.4的算术平方根
C.4开平方的结果
D.4的立方根
答案
5.D 【解析】 由8xmy与6x3yn的和是单项式,得m=3,n=1,所以(m+n)3=(3+1)3=64,64的平方根为±8.故选D.
5.[2019山东滨州中考]若8xmy与6x3yn的和是单项式,则(m+n)3的平方根为 ( )
A.4 B.8 C.±4 D.±8
答案
6.B 【解析】 310与-25的被开方数不同,不能合并,故A项错误;711×(117÷111)=711×117×11=
711×117×11=11,故B项正确;(75-15)÷3=(53-15)÷3=5-5,故C项错误;1318-389=2-22=-2,
故D项错误.故选B.
?
6.[2018山东聊城中考]下列计算正确的是 ( )
A.3 10-2 5=5
B.711 ×(117÷111)=11
C.(75-15)÷3=25
D.1318-389=2
?
答案
7.A 【解析】 因为25<30<1214,所以5<30<112,即与30最接近的整数是5,因为x是整数,所以当|x-30|取最小值时,x的值是5.故选A.
?
7.[2019四川绵阳中考]已知x是整数,当|x-30|取最小值时,x的值是( )
A.5 B.6 C.7 D.8
?
答案
8.D 【解析】 设x=6?33-6+33,因为6+33>6?33,所以x<0,所以x2=6-33-2(6?33)(6+33)+6+33,所以x2=12-2×3=6,所以x=-6.因为3?23+2=5-26,所以3?23+2+6?33-6+33=5-26-6=5-36.故选D.
?
8.[2019湖北随州中考]“分母有理化”是我们常用的一种化简的方法,如:2+32?3=(2+3)(2+3)(2?3)(2+3)=7+4 3,除此之外,我们也可以用平方之后再开方的方式来化简一些有特点的无理数,如:对于3+5-3?5,设x=3+5-3?5,易知3+5>3?5,故x>0,由x2=(3+5-3?5)2=3+5+3-5-2(3+5)(3?5)=2,解得x=2,即3+5-3?5=2.根据以上方法,化简3?23+2+6?33-6+33后的结果为( )
A.5+3 6 B.5+6 C.5-6 D.5-3 6
?
答案
9.5+2 【解析】 (5-2)2 018(5+2)2 019=[(5-2)(5+2)]2 018×(5+2)=(5-4)2 018×(5+2)=5+2.
?
9.[2019江苏扬州中考]计算:(5-2)2 018(5+2)2 019的结果是 .?
?
答案
10.13-242=(7-6)2 【解析】 由题意,得第n(n≥1,且n为整数)个等式为(2n+1)-2 ????(????+1)=(????+1-????)2,所以第6个等式为13-242=(7-6)2.
?
10.[2019湖南益阳中考]观察下列等式:
①3-22=(2-1)2,
②5-26=(3-2)2,
③7-212=(4-3)2,
…
请你根据以上规律,写出第6个等式 .?
?
答案
11.【解析】 12+|1-3|-(-1)
=23+3-1+1
=33.
?
11.[2019浙江台州中考]计算:12+|1-3|-(-1).
?
答案
12.【解析】 (π-3.14)0-(12)-2+327-8
=1-4+3-22
=-22.
?
12.[2019四川达州中考]计算:(π-3.14)0-(12)-2+327-8.
?
答案
13.【解析】 (3-2)2+12+613
=3+4-43+23+6×33
=7.
?
13.[2019辽宁大连中考]计算:(3-2)2+12+613.
数学·八年级上册·北师
专项素养拓训
专项一 比较实数的大小
专项
1.比较-2与-6的大小.
?
答案
1.【解析】 因为2<6,所以2<6,所以-2>-6.
?
类型 1 平方法
2.比较13+5与15+3的大小.
?
答案
2.【解析】 (13+5)2=13+265+5=18+265,
(15+3)2=15+245+3=18+245,
因为18+265>18+245,
所以13+5>15+3.
?
3.[2020广东广州期中]课堂上,老师出了一道题,比较19?23与23的大小.
小明的解法如下:
解:19?23-23=19?2?23=19?43,
因为42=16<19,所以19>4,所以19-4>0.
所以19?43>0,所以19?23>23.
我们把这种比较大小的方法称为作差法.
(1)根据上述材料填空.(在横线上填“>”“=”或“<” )
①若a-b>0,则a b;?②若a-b=0,则a b;?③若a-b<0,则a b.?
(2)利用上述方法比较9?224与23的大小.
?
类型 2 作差法
答案
3.【解析】 (1)①> ②= ③<
(2)9?224-23=27?322?812=19?32212=19?19812,
因为192=361>198,所以19>198,
所以19-198>0,所以19?19812>0,
所以9?224>23.
?
4.比较????+1????+2与????+2????+3的大小.
?
类型 3 作商法
答案
4.【解析】 因为????+1????+2÷????+2????+3=????+1????+2×????+3????+2=(????+1)(????+3)(????+2)?2=????+3+4????????+4+4????<1,????+1????+2>0,????+2????+3>0,
所以????+1????+2?
5.已知0
类型 4 特殊值法
答案
5.C 【解析】 本题直接比较大小比较困难,可以采用特殊值法求解,取x=14,则1????=4,x2=116,????=12.因为116<14<12<4,所以x2
6.已知x=????+3-????+1,y=????+2-????,试比较x,y的大小.
?
类型 5 倒数法
答案
6.【解析】 1????=1????+3?????+1=????+3+????+12>0,
1????=1????+2?????=????+2+????2>0,
因为????+3+????+1>????+2+????>0,
所以1????>1????>0,所以x
专项二 非负数应用的常见题型
专项
7.如果一个数的绝对值为a,那么数a在如图所示的数轴上对应的点不可能是 ( )
A.点M B.点O
C.点P D.点N
类型 1 绝对值的非负性
答案
7.A 【解析】 一个数的绝对值应该大于等于零,所以数a在数轴上对应的点不可能是点M.故选A.
8.若(y+2)2=a-1,则a的值可以是 ( )
A.-2 B.-1 C.0 D.1
类型 2 偶次方的非负性
答案
8.D 【解析】 由题意,得a-1≥0,所以a≥1.故选D.
9.当式子2????+1的值取最小值时,a 的值为( )
A.0 B.-12 C.-1 D.1
?
类型 3 算术平方根的非负性
答案
9.B 【解析】 因为2????+1≥0,所以当式子2????+1的值取最小值时,2????+1=0,所以2a+1=0,所以a的值为-12.故选B.
?
10.[2020贵州铜仁期末]若?????2+n2+2n+1=0,则mn=( )
A.12 B.-12 C.2 D.-2
?
答案
10.A 【解析】 因为?????2+n2+2n+1=0,所以?????2+(n+1)2=0,所以m-2=0,n+1=0,所以m=2,n=-1,所以mn=2-1=12.故选A.
?
11.若3?????4-4?3????=|12x-y|,求4(x+y)的立方根.
?
类型 3 算术平方根的非负性
答案
11.【解析】 由题意可知,3x-4≥0且4-3x≥0,则x≥43且x≤43,
所以x=43,所以|12x-y|=0,所以y=23.
所以4(x+y)=8,其立方根为38=2.
?
12.[2020北京房山区期中]已知|2 019-m|+?????2?020=m,求m-2 0192的值.
?
类型 3 算术平方根的非负性
答案
12.【解析】 因为m-2 020≥0,所以m≥2 020,所以2 019-m≤-1,
所以|2 019-m|+?????2?020=m可化为m-2 019+?????2?020=m,
所以?????2?020=2 019,所以m-2 020=2 0192,
所以m-2 0192=2 020.
?
专项三 二次根式的常见题型
专项
13.计算:
(1)(232-12)(82+23);
(2)(3+2-6)2-(2-3+6)2;
(3)(1+2-3)(1-2+3);
(4)6÷(3+2)+(3+2)÷6.
?
类型 1 二次根式的运算
答案
13.【解析】 (1)(232-12)(82+23)
=232×82+232×23-12×82-12×23
=23+2-1-33
=1+533.
?
答案
(2)(3+2-6)2-(2-3+6)2
=(3+2-6+2-3+6)(3+2-6-2+3-6)
=2 2(2 3-2 6)
=4 6-8 3.
(3)(1+2-3)(1-2+3)
=[1+(2-3)][1-(2-3)]
=1-(2-3)2
=1-5+2 6
=2 6-4.
(4)6÷(3+2)+(3+2)÷6
=63+2+3+26
=6(3?2)(3+2)(3?2)+(3+2)×66×6
=3 2-2 3+22+33
=722-533.
?
14.已知a+1????=1+10,求a2+1????2的值.
?
类型2 二次根式的化简求值
答案
14.【解析】 a2+1????2=(a+1????)2-2
=(1+10)2-2
=9+210.
?
15.[2020甘肃白银期中]已知x=12?3,y=12+3,求x2-3xy+y2的值.
?
类型2 二次根式的化简求值
答案
15.【解析】 x=12?3=2+3(2?3)(2+3)=2+3,
y=12+3=2?3(2+3)(2?3)=2-3,
所以x2-3xy+y2=(x-y)2-xy=(2+3-2+3)2-(2+3)(2-3)=12-1=11.
?
16.已知:a,b,c满足(a-8)2+?????5+|c-32|=0.
(1)求a,b,c的值;
(2)试问以a,b,c为边能否构成三角形?若能构成三角形,求出三角形的周长;若不能构成三角形,请说明理由.
?
类型3 二次根式的运算与三角形知识的结合
答案
16.【解析】 (1)根据题意,得a-8=0,b-5=0,c-3 2=0,
解得a=8=2 2,b=5,c=3 2.
(2)能构成三角形.
因为2 2+3 2=5 2>5>3 2-2 2,
所以以a,b,c为边能构成三角形,
三角形的周长为22+5+32=52+5.
?
综合素养拓训
素养解读
本章内容贯通初高中数学,学习实数与二次根式,有助于培养学生的数感和符号意识.同时,基于旧知识的探究式学习,也有助于培养学生发现问题、提出问题的意识,逐渐形成解决问题的能力.例如第2题,需要在熟练掌握算术平方根的基础上,尝试利用逆运算解决问题;第4题,面对形式复杂的问题时,可以通过观察发现式子的异同,进而利用构造法将问题简单化;第5题,通过材料给出新方法,考查阅读理解能力,对综合素养要求较高.
1.[分类讨论化简二次根式]设a,b为非零实数,则????|????|+????2????所有可能的值为( )
A.±2 B.±1或0
C.±2或0 D.±2或±1
?
答案
1.C 【解析】 ①a,b同号时,????|????|,????2????也同号,即同为1或-1,故此时????|????|+????2????=±2;②a,b异号时,????|????|,????2????也异号,即一个是1,另一个是-1,故此时????|????|+????2????=0.故选C.
?
2.[算术平方根与规律探究]对于任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[3]=1,现对72进行如下操作:72 [72]=8 [8]=2 [2]=1,这样对72需进行3次操作后变为1.类似地,对81需进行 次操作后变为1;需进行3次操作后变为1的所有正整数中,最大的数是 .?
?
答案
2.3 255 【解析】 81 [81]=9 [9]=3 [3]=1,所以对81需进行3次操作后变为1.算术平方根的整数部分为1的最大正整数为3,算术平方根的整数部分为3的最大正整数为15,算术平方根的整数部分为15的最大正整数为255,所以需进行3次操作后变为1的所有正整数中,最大的数是255.
?
3.[二次根式与勾股定理]如图,S1,S2,S3,…分别表示各个三角形的面积,仔细观察,并认真分析各式,然后解答问题.
O????22=12+12=2,S1=12;
O????32=12+(2)2=3,S2=22;
O????42=12+(3)2=4,S3=32;
…
(1)用含n(n是正整数)的式子表示OA2n+1和Sn;
(2)若一个三角形的面积是5,通过计算说明它是第几个三角形.
?
答案
3.【解析】 (1)O????????+12=12+(????)2=n+1,Sn=????2.
(2)当Sn=????2=5时,????=25=4×5=20,即n=20,
所以它是第20个三角形.
?
4.[巧用构造法化简二次根式]化简:(2+3+5)2+(2+3-5)2+(2-3+5)2+(-2+3+5)2.
?
答案
4.【解析】 设x=2+3,y=2-3,则x2+y2=10,
(2+3+5)2+(2+3-5)2+(2-3+5)2+(-2+3+5)2
=(x+5)2+(x-5)2+(y+5)2+(-y+5)2
=(x2+25x+5)+(x2-25x+5)+(y2+25y+5)+(y2-25y+5)
=2(x2+y2)+20
=40.
?
5.[形如????±????????形式的二次根式的化简]先阅读下面的解题过程,然后再解答.
形如????±2????的化简,我们只要找到两个数a,b,使a+b=m,ab=n,即(????)2+(????)2=m,????·????=????,那么便有:????±2????=(????±????)2=????±????(a>b≥0).
例如化简:7+43.
解:首先把7+43化为7+212,这里m=7,n=12,
由于4+3=7,4×3=12,所以(4)2+(3)2=7,4×3=12,
所以7+43=7+212=(4+3)2=2+3.
根据上述方法化简:13?242.
?
答案
5.【解析】 根据题意,可知m=13,n=42,
由于7+6=13,7×6=42,
所以(7)2+(6)2=13,7×6=42,
所以13?242=(7)2+(6)2?2×7×6=(7?6)2=7-6.
?
答案
1.D 【解析】 无理数有5,-π,60.123 45…(小数部分由相继的正整数组成),共3个.故选D.
?
一、选择题
1.[2020山东菏泽期中]给出下列各数:-52,0.212 121 21,1.21,5,|-2|,9,-π,2.003 003 003…(相邻两个3之间有2个0),60.123 45…(小数部分由相继的正整数组成),其中属于无理数的有( )
A.6个 B.5个 C.4个 D.3个
?
答案
2.C 【解析】 38=2,2的平方根是±2.故选C.
?
2.[2020辽宁辽阳期末]38的平方根是( )
A.2 B.-2 C.±2 D.±2
?
答案
3.A 【解析】 12-3=23-3=3.故选A.
?
3.[2019甘肃兰州中考]计算:12-3=( )
A.3 B.2 3 C.3 D.4 3
?
答案
4.C 【解析】 -4没有算术平方根,故A项错误;4是16的算术平方根,故B项错误;1的平方根是±1,故D项错误.故选C.
4.[2020陕西西安雁塔区月考]下列说法正确的是 ( )
A.2是-4的算术平方根
B.±4是16的算术平方根
C.-6是(-6)2的平方根
D.1的平方根是它本身
答案
5.C 【解析】 (7-3)(7+3)-(3+6)2=7-3-(3+62+6)=-5-62.故选C.
?
5.计算(7-3)(7+3)-(3+6)2的结果是( )
A.-5
B.-5-3 2
C.-5-6 2
D.-3-2
?
答案
6.D 【解析】 因为(32)2<3<4,即32<3<2,所以与3对应的点距离最近的是点D.故选D.
?
6.[2020北京延庆区期末]如图,数轴上A,B,C,D四点中,与3对应的点距离最近的是( )
A.点A B.点B
C.点C D.点D
?
答案
7.C 【解析】 18-89=32-223=723,A选项成立,不符合题意;2+23=83=223,B选项成立,不符合题意;8+182=22+322=522,C选项不成立,符合题意;13+2=3?2(3+2)(3?2)=3-2,D选项成立,不符合题意.故选C.
?
7.[2019山东聊城中考]下列各式不成立的是 ( )
A.18-89=73 2
B.2+23=223
C.8+182=4+9=5
D.13+2=3-2
?
答案
8.A 【解析】 因为4<7<9,所以2<7<3,所以a=2,b=7-2,所以(4+7)(a-b)=(4+7)(4-7)=42-(7)2=16-7=9.
?
8.[2020辽宁朝阳双塔区期中]若a是7的整数部分,b是7的小数部分,则代数式(4+7)(a-b)的值为( )
A.9 B.2+7
C.7 D.4-7
?
答案
9.2 【解析】 24×13-4×18=24×13-4×24=22-2=2.
?
二、填空题
9.[2020四川遂宁期末]计算:24×13-4×18= .?
?
答案
10.2 【解析】 由题意,得256=16,16=4,4=2,2是无理数,所以输出的y等于2.
?
10.[2020吉林长春期末]有一个数值转换器,原理如图所示,当输入的x=256时,输出的y等于? .?
答案
11.等边 【解析】 因为三角形的三边a,b,c满足?????????+(b-c)2=0,所以a-b=0,b-c=0,解得a=b,b=c,所以a=b=c,所以该三角形是等边三角形.
?
11.[2020四川宜宾期中]若三角形的三边a,b,c满足?????????+(b-c)2=0,则三角形是 三角形.?
?
答案
12.2 0182?0182?019 【解析】 1+112+122+1+122+132+1+132+142+…+1+12?0182+12?0192=1+(1-12)+1+(12-13)+…+1+(12?018-12?019)=2 018+1-12+12-13+13-14+…+12?018-12?019=2 0182?0182?019.
?
12.[2019山东枣庄中考]观察下列各式:
1+112+122=1+11×2=1+(1-12),
1+122+132=1+12×3=1+(12-13),
1+132+142=1+13×4=1+(13-14),
…
请利用你发现的规律,计算:
1+112+122+1+122+132+1+132+142+…+1+12?0182+12?0192,
其结果为 .?
?
答案
13.【解析】 (1)-12+|3-2|-(3-7)0
=-1+2-3-1
=-3.
(2)12-22-613+18
=23-22-23+32
=2.
(3)50÷5+(23+2)(23-2)
=50÷5+12-2
=10+10.
(4)12+3+2+3-(3-1)2
=2-3+2+3-(4-23)
=23.
?
三、解答题
13.[2020江苏无锡惠山区期中]计算:
(1)-12+|3-2|-(3-7)0;(2)-12-2 2-613+18;(3)50÷5+(2 3+2)(2 3-2);(4)12+3+2+3-(3-1)2.
?
答案
14.【解析】 (1)因为a2=4,所以a=±2,
因为b的算术平方根为3,所以b=9,
所以a+b=-2+9=7或a+b=2+9=11.
综上,a+b的值为7或11.
(2)因为x是25的平方根,所以x=±5,
因为y是16的算术平方根,所以y=4,
因为x
14.[2019江西宜春期中](1)如果a2=4,b的算术平方根为3,求a+b的值;
(2)已知x是25的平方根,y是16的算术平方根,且x
15.【解析】 (1)23?7=2(3+7)(3?7)(3+7)=2(3+7)2=3+7.
(2)因为a=13+22=3?22(3+22)(3?22)=3-2 2,
所以a-3=-2 2,所以(a-3)2=8,即a2-6a+9=8,
所以a2-6a=-1,
所以2a2-12a+1=2(a2-6a)+1=2×(-1)+1=-1.
?
15.[2019河北唐山一模]在解决问题“已知a=12?1,求3a2-6a-1的值”时,小明是这样解答的:
因为a=12?1=2+1(2?1)(2+1)=2+1,
所以a-1=2,所以(a-1)2=2,即a2-2a+1=2,
所以a2-2a=1,所以3a2-6a=3,
所以3a2-6a-1=2.
请你根据小明的解答过程,解决下列问题:
(1)化简:23?7.
(2)若a=13+22,求2a2-12a+1的值.
?
16.有一块长方形木板,木工采用如图所示的方法,在木板上截出两个面积分别为18 dm2和32 dm2的正方形木板.
(1)求剩余木板的面积;
(2)如果木工想从剩余的木板中截出长为1.5 dm,宽为1 dm的长方形木条,最多能截出多少块这样的木条?
答案
16.【解析】 (1)因为两个正方形的面积分别为18 dm2和32 dm2,
所以这两个正方形的边长分别为32 dm和42 dm,
所以剩余木板的面积为(42-32)×32=6(dm2).
(2)由(1)可得,剩余木板的长为32dm,宽为4 2-3 2=2(dm),
因为4<32<4.5,1<2<2,
所以从剩余的木板中截出长为1.5 dm,宽为1 dm的长方形木条,最多能截出2块.
?
第二章·实数中考模拟+真题
数学·八年级上册·北师
答案
1.B 【解析】 因为150????=5×5×2×3????,150????(0
1.[2019湖北潜江一模]如果150????(0
?
答案
2.B 【解析】53-27=53-3 3=2 3,因为3<2 3<4,所以表示53-27的点应在线段BC上.故选B.
?
2.[2019重庆九龙坡区模拟]如图,表示53-27的点应在( )
A.线段AB上 B.线段BC上
C.线段CD上 D.线段DE上
?
答案
3.D 【解析】 根据题意,得c-3=0且b-2=0,解得c=3,b=2,则a的取值范围是3-2
A.2 B.3 C.4 D.5
?
答案
4.2 【解析】 x2+2x+1=(x+1)2,当x=2-1时,原式=(2)2=2.
?
4.[2020河南一模]若x=2-1,则x2+2x+1= .?
?
答案
5.3 【解析】 根据题意,得8※4=8+48?4=232=3.
?
5.[2020湖南益阳期末]对于任意不相等的两个实数a,b,定义运算※如下:a※b=????+?????????????,如3※2=3+23?2=5.那么8※4=???????? .?
?
答案
6.4 【解析】 因为f(m)=[2?????3]-[????5],所以f(-6)=[2?(?6)3]-[?65]=2-(-2)=4.
?
6.[2019四川成都武侯区模拟]定义[x]表示不超过实数x的最大整数,例如[0.82]=0,[6]=6,[-135]=-3,[-7]=-7.若规定:对于实数m,f(m)=[2?????3]-[????5].例如f(7)=[2?73]-[75]=[-53]-[75]=-2-1=-3,则f(-6)= .?
?
答案
7.【解析】 |3-2|+(12)-1-(5+1)(5-1)
=2-3+2-(5-1)
=2-3+2-5+1
=-3.
?
7.[2019四川宜宾翠屏区二片区期中]计算:|3-2|+(12)-1-(5+1)(5-1).
?
答案
8.【解析】 (1)因为5a+2的立方根是3,
所以5a+2=27,所以a=5.
因为3a+b-1的算术平方根是4,
所以3a+b-1=14+b=16,所以b=2.
因为c是13的整数部分,3<13<4,
所以c=3.
(2)将a=5,b=2,c=3代入3a-b+c,得3a-b+c=16,
所以3a-b+c的平方根是±4.
?
8.[2020河南洛阳期中]已知5a+2的立方根是3,3a+b-1的算术平方根是4,c是13的整数部分.
(1)求a,b,c的值;
(2)求3a-b+c的平方根.
?
答案
9.【解析】 (1)>
16?2=1×(6+2)(6?2)(6+2)=6+22, 15?3=1×(5+3)(5?3)(5+3)=5+32,
因为6+2>5+3,所以16?2>15?3.
?
9.[2019重庆九龙坡区模拟]阅读材料:
黑白双雄,纵横江湖;双剑合璧,天下无敌.这是武侠小说中的常见描述,其意是指两个人合在一起,取长补短,威力无比,在二次根式中也有这种相辅相成的“对子”,如(5+3)(5-3)=-4,(3+2)(3-2)=1,它们的积不含根号,我们说这两个因式互为有理化因式,其中一个是另一个的有理数因式.
解决问题:
(1)比较大小:16?2 15?3.(用“>”“< ”或“=”填空)?
(2)若实数x,y满足(x+????2+2?019)(y+????2+2?019)=2 019,求x+y+2 019的值.
?
答案
(2)因为(x+????2+2?019)(y+????2+2?019)=2 019,
所以x+????2+2?019=2?019????+????2+2?019,
所以x+????2+2?019=????2+2?019-y①,
同理得y+????2+2?019=????2+2?019-x②,
所以①+②,得x+y+????2+2?019+????2+2?019=????2+2?019+????2+2?019-(x+y),
所以x+y=0,所以x+y+2 019=2 019.
?
答案
1.B 【解析】 38=2,有理数有38,43,共2个.故选B.
?
1.[2019山东日照中考]在实数38,????3,12,43中有理数有( )
A.1个 B.2个 C.3个 D.4个
?
答案
2.B 【解析】 12=22,4=2,12=23,所以A,C,D不是最简二次根式.故选B.
?
2.[2019广西河池中考]下列式子中,为最简二次根式的是 ( )
A.12 B.2 C.4 D.12
?
答案
3.B 【解析】 -2的倒数的平方为(-12)2=12.故选B.
?
3.[2019湖北荆门中考]-2的倒数的平方是( )
A.2 B.12 C.-2 D.-12
?
答案
4.B
4.[2019江苏南京中考]面积为4的正方形的边长是 ( )
A.4的平方根
B.4的算术平方根
C.4开平方的结果
D.4的立方根
答案
5.D 【解析】 由8xmy与6x3yn的和是单项式,得m=3,n=1,所以(m+n)3=(3+1)3=64,64的平方根为±8.故选D.
5.[2019山东滨州中考]若8xmy与6x3yn的和是单项式,则(m+n)3的平方根为 ( )
A.4 B.8 C.±4 D.±8
答案
6.B 【解析】 310与-25的被开方数不同,不能合并,故A项错误;711×(117÷111)=711×117×11=
711×117×11=11,故B项正确;(75-15)÷3=(53-15)÷3=5-5,故C项错误;1318-389=2-22=-2,
故D项错误.故选B.
?
6.[2018山东聊城中考]下列计算正确的是 ( )
A.3 10-2 5=5
B.711 ×(117÷111)=11
C.(75-15)÷3=25
D.1318-389=2
?
答案
7.A 【解析】 因为25<30<1214,所以5<30<112,即与30最接近的整数是5,因为x是整数,所以当|x-30|取最小值时,x的值是5.故选A.
?
7.[2019四川绵阳中考]已知x是整数,当|x-30|取最小值时,x的值是( )
A.5 B.6 C.7 D.8
?
答案
8.D 【解析】 设x=6?33-6+33,因为6+33>6?33,所以x<0,所以x2=6-33-2(6?33)(6+33)+6+33,所以x2=12-2×3=6,所以x=-6.因为3?23+2=5-26,所以3?23+2+6?33-6+33=5-26-6=5-36.故选D.
?
8.[2019湖北随州中考]“分母有理化”是我们常用的一种化简的方法,如:2+32?3=(2+3)(2+3)(2?3)(2+3)=7+4 3,除此之外,我们也可以用平方之后再开方的方式来化简一些有特点的无理数,如:对于3+5-3?5,设x=3+5-3?5,易知3+5>3?5,故x>0,由x2=(3+5-3?5)2=3+5+3-5-2(3+5)(3?5)=2,解得x=2,即3+5-3?5=2.根据以上方法,化简3?23+2+6?33-6+33后的结果为( )
A.5+3 6 B.5+6 C.5-6 D.5-3 6
?
答案
9.5+2 【解析】 (5-2)2 018(5+2)2 019=[(5-2)(5+2)]2 018×(5+2)=(5-4)2 018×(5+2)=5+2.
?
9.[2019江苏扬州中考]计算:(5-2)2 018(5+2)2 019的结果是 .?
?
答案
10.13-242=(7-6)2 【解析】 由题意,得第n(n≥1,且n为整数)个等式为(2n+1)-2 ????(????+1)=(????+1-????)2,所以第6个等式为13-242=(7-6)2.
?
10.[2019湖南益阳中考]观察下列等式:
①3-22=(2-1)2,
②5-26=(3-2)2,
③7-212=(4-3)2,
…
请你根据以上规律,写出第6个等式 .?
?
答案
11.【解析】 12+|1-3|-(-1)
=23+3-1+1
=33.
?
11.[2019浙江台州中考]计算:12+|1-3|-(-1).
?
答案
12.【解析】 (π-3.14)0-(12)-2+327-8
=1-4+3-22
=-22.
?
12.[2019四川达州中考]计算:(π-3.14)0-(12)-2+327-8.
?
答案
13.【解析】 (3-2)2+12+613
=3+4-43+23+6×33
=7.
?
13.[2019辽宁大连中考]计算:(3-2)2+12+613.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
