北师大版八年级上册数学第五章二元一次方程组素养拓展+中考真题课件(55张PPT)
文档属性
| 名称 | 北师大版八年级上册数学第五章二元一次方程组素养拓展+中考真题课件(55张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 00:00:00 | ||
图片预览



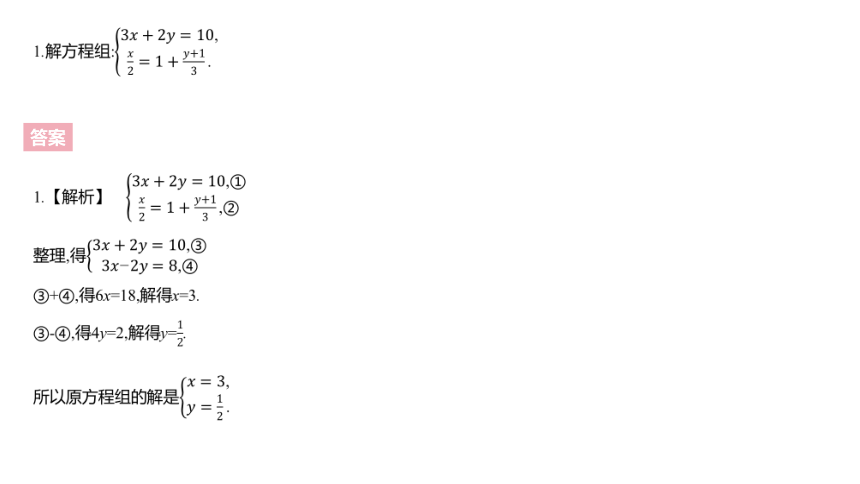

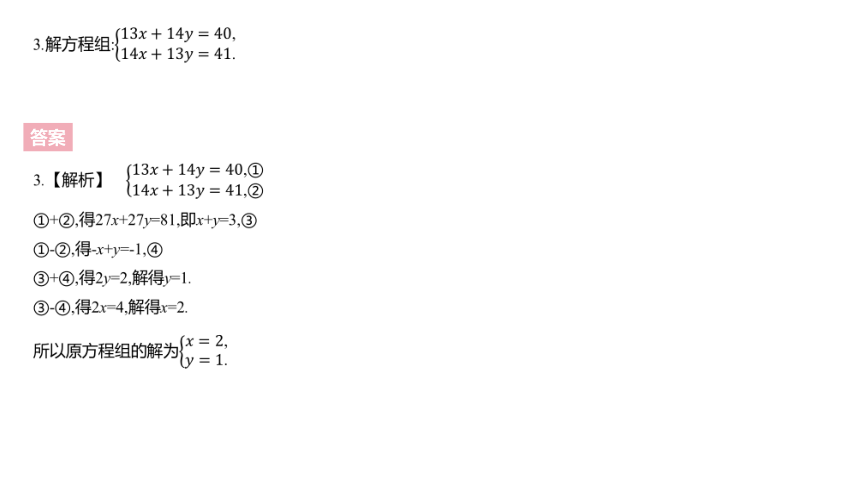






文档简介
第五章·二元一次方程组
数学·八年级上册·北师
专项素养拓训
专项一 二元一次方程组的解法
专项
1.解方程组:3????+2????=10,????2=1+????+13.
?
答案
1.【解析】 3????+2????=10,①????2=1+????+13,②
整理,得3????+2????=10,③3?????2????=8,④
③+④,得6x=18,解得x=3.
③-④,得4y=2,解得y=12.
所以原方程组的解是????=3,????=12.
?
2.解方程组:23(2????+????)=4,34????+56(2????+????)=8.
?
答案
2.【解析】 23(2????+????)=4,①34????+56(2????+????)=8,②
由①,得2x+y=6,③
把③代入②,得34x+56×6=8,解得x=4.
把x=4代入③,得8+y=6,解得y=-2.
所以原方程组的解为????=4,????=?2.
?
3.解方程组:13????+14????=40,14????+13????=41.
?
答案
3.【解析】 13????+14????=40,①14????+13????=41,②
①+②,得27x+27y=81,即x+y=3,③
①-②,得-x+y=-1,④
③+④,得2y=2,解得y=1.
③-④,得2x=4,解得x=2.
所以原方程组的解为????=2,????=1.
?
4.解方程组:3(????+????)+2(?????????)=10,????+????4+?????????2=72.
?
答案
4.【解析】 令x+y=a,x-y=b,
则原方程组可变形为3????+2????=10,①????4+????2=72,②
整理,得3????+2????=10,③????+2????=14,④
③-④,得2a=-4,解得a=-2.
把a=-2代入④,得-2+2b=14,解得b=8.
所以????+????=?2,?????????=8,解得????=3,????=?5.
所以原方程组的解为????=3,????=?5.
?
专项二 利用二元一次方程组求解字母或代数式的值
专项
5.若????=1,????=1和????=2,????=?1是方程mx+ny=6的两组解,则m,n的值分别为( )
A.-4,-2 B.2,4 C.4,2 D.-2,-4
?
答案
5.C 【解析】 根据题意,得????+????=6,①2?????????=6,②①+②,得3m=12,解得m=4.把m=4代入①,得n=2.故选C.
?
6.如果 ????=????,????=???? 是方程x-3y=-3的一组解,那么代数式 5-a+3b的值是( )
A.8 B.5 C.2 D.0
?
答案
6.A 【解析】 把x=a,y=b代入x-3y=-3,可得a-3b=-3,所以5-a+3b=5-(a-3b)=5+3=8.故选A.
7.[2019浙江杭州西湖区模拟]若关于x,y的方程组4????+3????=10,?????????(?????1)????=?8 的解中x的值比y的值的相反数大2,则k为( )
A.-3 B.-2 C.-1 D.1
?
答案
7.C 【解析】 因为x的值比y的值的相反数大2,所以x-(-y)=x+y=2,根据题意,得????+????=2,4????+3????=10,解得????=4,????=?2.把????=4,????=?2 代入kx-(k-1)y=-8,得4k+2(k-1)=-8,解得k=-1.故选C.
?
8.[2019湖南长沙期中]甲、乙两人同求关于x,y的二元一次方程ax-by=7的整数解,甲正确地求得一组解为????=1,????=?1,乙把ax-by=7看成ax-by=1,求得另一组解为????=1,????=2, 求a+2b的平方根.
?
答案
8.【解析】 根据题意,得????+????=7,①?????2????=1,②
①-②,得3b=6,所以b=2,
把b=2代入①,
得a=5.
所以a+2b=9,9的平方根为±3.
?
专项三 二元一次方程组与一次函数的综合应用
专项
9.[2020江苏扬州期中]直线l与直线y=2x+1的交点的横坐标为2,与直线y=-x+2的交点的纵坐标为1,则直线l对应的函数表达式是 .?
答案
9.y=4x-3 【解析】 在直线y=2x+1中,令x=2,得y=5,在y=-x+2中,令y=1,得x=1,所以直线l经过点(2,5),(1,1).设直线l对应的函数表达式是y=kx+b,所以2????+????=5,????+????=1, 解得????=4,????=?3,故直线l对应的函数表达式是y=4x-3.
?
10.[2019广西桂林期末]某商店在节日期间开展优惠促销活动:凡购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)之间的函数关系如图所示,则图中a的值是 .?
答案
10.340 【解析】 当x≥200时,设y与x的函数关系式为y=kx+b,所以200????+????=200,500????+????=410,解得????=0.7,????=60,所以y=0.7x+60(x≥200).当x=400时,y=340,所以题图中a的值为340.
?
11.如图,在平面直角坐标系中,直线a与x轴,y轴分别交于A,B两点,且直线a上所有点的坐标都适合二元一次方程4x-3y=-6,直线b与x轴,y轴分别交于C,D两点,且直线b上所有点的坐标都适合二元一次方程x-2y=1,直线a与b交于点E.
(1)分别求出点A,D的坐标;
(2)求四边形AODE的面积.
答案
11.【解析】 (1)因为直线a上所有点的坐标都适合二元一次方程4x-3y=-6,
所以当y=0时,x=-32,所以点A的坐标为(-32,0).
因为直线b上所有点的坐标都适合二元一次方程x-2y=1,
所以当x=0时,y=-12,所以点D的坐标为(0,-12).
(2)由题意易知,点C的坐标(1,0).
由4?????3????=?6,?????2????=1, 得????=?3,????=?2, 所以点E的坐标为(-3,-2).
则S四边形AODE =S△ACE -S△ODC =12×(32+1)×2-12×12×1=94.
?
12.某校一课外小组准备进行“绿色环保”的宣传活动,需要制作宣传单,校园附近有甲、乙两家印刷社,制作此种宣传单的收费标准如下.
甲印刷社的收费y(元)与印数x(张)的函数关系如下表:
乙印刷社的收费方式为:500张以内(含500张),按每张0.20元收费;超过500张的部分,按每张0.10元收费.
(1)根据表中规律,写出甲印刷社的收费y(元)与印数x(张)之间的函数关系式;
(2)若该小组在甲、乙两家印刷社共印制400张宣传单,用去65元,问在甲、乙两家印刷社各印制多少张?
(3)活动结束后,市民反应良好,该小组决定再加印800张宣传单,若在甲、乙印刷社中选一家,则该小组选择哪家印刷社比较划算?
{5940675A-B579-460E-94D1-54222C63F5DA}印数x/张
…
100
200
300
…
收费y/元
…
15
30
45
…
答案
12.【解析】 (1)由题意设甲印刷社的收费y(元)与印数x(张)之间的函数关系式为y=kx+b,
由题意,得15=100????+????,30=200????+????,
解得????=0.15,????=0,
所以甲印刷社的收费y(元)与印数x(张)之间的函数关系式为y=0.15x.
(2)设在甲印刷社印制a张,则在乙印刷社印制(400-a)张,
由题意,得0.15a+0.2(400-a)=65,解得a=300,
400-300=100(张),
所以在甲印刷社印制300张,在乙印刷社印制100张.
(3)在甲印刷社印制的费用为0.15×800=120(元).
在乙印刷社印制的费用为500×0.2+0.1×(800-500)=130(元).
因为120<130,
所以该小组选择甲印刷社比较划算.
?
综合素养拓训
素养解读
数学建模是对现实问题进行数学抽象,用数学语言表达问题,用数学方法构建模型解决问题的素养.数学建模过程主要包括:在实际情境中从数学的视角发现问题、提出问题、分析问题、建立模型、计算求解、检验结果,最终解决实际问题.本章在学习和理解二元一次方程组并经历和体验其工具作用的过程中,锻炼思维、培养建模能力,发展模型思想和应用意识.如第1题,根据绝对值的性质,探究含绝对值的方程组的解的组数,培养学生的分类讨论思想;第2题,通过设元构建二元一次方程组解决实际问题,关注数学建模和方程思想;第4题,利用换元法解方程组,培养学生分析问题、解决问题的能力.
1.[探究方程组解的组数]方程组|????|?????=10,?????|????|=4的解的组数是( )
A.1 B.2 C.3 D.4
?
答案
1.A 【解析】 当x>0,y>0时,方程组变形得?????????=10,?????????=4,无解;当x>0,y<0时,方程组变形得?????????=10,①????+????=4,②①+②得2x=14,解得x=7,②-①得2y=-6, 解得y=-3,则方程组的解为????=7,????=?3;当x<0,y>0时,方程组变形得??????????=10,③?????????=4,④③+④得-2y=14, 解得y=-7<0,舍去;当x<0,y<0时,方程组变形得????+????=?10,????+????=4,无解.综上,方程组的解的组数是1.故选A.
?
2.[方程组与几何图形问题的综合]如图,分别用火柴棍连续搭建等边三角形和正六边形,公共边只用一根火柴棍.如果搭建等边三角形和正六边形共用了2 020根火柴棍,并且等边三角形的个数比正六边形的个数多8,那么连续搭建的等边三角形的个数是 ( )
A.222 B.280 C.286 D.294
答案
2.D 【解析】 设连续搭建等边三角形x个,连续搭建正六边形 y个.由题意,得2????+1+5????+1=2?020,?????????=8,解得????=294,????=286.故选D.
?
3.[二元一次方程组的解与系数之间的关系]根据要求,解答下列问题.
(1)解下列方程组(直接写出方程组的解即可):
①????+2????=3,2????+????=3的解为 ;?
②3????+2????=10,2????+3????=10的解为? ;?
③2?????????=4,?????+2????=4的解为? .?
(2)以上每个方程组的解中,x值与y值的大小关系为 .?
(3)请你构造一个具有以上外形特征的方程组,并直接写出它的解.
?
答案
3.【解析】 (1)①????=1,????=1②????=2,????=2③????=4,????=4
(2)x=y
(3)3????+2????=25,2????+3????=25的解为????=5,????=5.(答案不唯一)
?
4.[换元法解方程组]三个同学同时解一道题:若方程组????1????+????1????=????1,????2????+????2????=????2的解是????=3,????=4,求方程组3????1????+2????1????=5????1,3????2????+2????2????=5????2的解.
三个人各自提出不同的想法:
甲说:“这个题目好像条件不够,不能求出它的解.”
乙说:“它们的系数有一定的规律,可以试试.”
丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元的方法来解决呢?”
参考他们的讨论,你认为这个题目应该怎么解?
?
答案
4.【解析】 按照丙的想法,将第二个方程组3????1????+2????1????=5????1,3????2????+2????2????=5????2变形为????1(35????)+????1(25????)=????1,????2(35????)+????2(25????)=????2,
再由方程组????1????+????1????=????1,????2????+????2????=????2的解是????=3,????=4,可得35????=3,25????=4,解得????=5,????=10,
所以方程组3????1????+2????1????=5????1,3????2????+2????2????=5????2的解是????=5,????=10.
?
答案
1.A 【解析】 根据题意,知|2m-3|=1,m-2≠0,所以m=1.故选A.
一、选择题
1.若x|2m-3|+(m-2)y=8是关于x,y的二元一次方程,则m的值是 ( )
A.1 B.2 C.1或2 D.任何数
答案
2.C
2.利用加减消元法解方程组2????+5????=?10,①5?????3????=6②时,下列说法正确的是( )
A.要消去y,可以将①×5+②×3
B.要消去x,可以将①×3+②×(-5)
C.要消去y,可以将①×3+②×5
D.要消去x,可以将①×5+②×2
?
答案
3.C 【解析】 把????=1,????=4代入二元一次方程ax+y=7中,得a+4=7,解得a=3.故选C.
?
3.若????=1,????=4是关于x,y的二元一次方程ax+y=7的解,则a的值为( )
A.1 B.2 C.3 D.4
?
答案
4.C 【解析】 两式相减,得x+3y=-2,所以2(x+3y)=-4,即2x+6y=-4.故选C.
4.[2019广西贺州中考]已知方程组2????+????=3,?????2????=5, 则2x+6y的值是( )
A.-2 B.2 C.-4 D.4
?
答案
5.A 【解析】 设直线PQ对应的一次函数的表达式为y=kx+b,因为直线PQ经过点P(-20,5),Q(10,20),所以?20????+????=5,10????+????=20, 解得????=12,????=15, 所以直线PQ对应的一次函数的表达式为y=12x+15.故选A.
?
5.[2019河北沧州期末]直线PQ上两点的坐标分别是P(-20,5),Q(10,20),则直线PQ对应的一次函数的表达式为 ( )
A.y=12x+15 B.y=2x
C.y=12x-15 D.y=3x-10
?
答案
6.A 【解析】 将????=1,????=?1与????=2,????=2代入二元一次方程ax+by+2=0,可得?????????+2=0,2????+2????+2=0,解得????=?32,????=12,则二元一次方程为-32x+12y+2=0,经检验得A项仍为此方程的解.故选A.
?
6.如果二元一次方程ax+by+2=0有两组解????=1,????=?1与????=2,????=2,那么下面四个选项中仍是这个方程的解的是( )
A.????=3,????=5 B.????=5,????=3
C.????=6,????=2 D.????=4,????=4
?
答案
7.B 【解析】 因为?????3?????1+|x-2y+2|=0,所以?????3????=1,?????2????=?2, 解得????=?8,????=?3, 所以x-4y=-8+12=4,4的平方根是±2.故选B.
?
7.已知x,y满足?????3?????1+|x-2y+2|=0,则x-4y的平方根为( )
A.2 B.±2 C.4 D.±4
?
答案
8.A 【解析】 设甲工厂5月份的用水量是x吨,乙工厂5月份的用水量是y吨,根据题意,得????+????=200,(1?15%)????+(1?10%)????=174, 解得????=120,????=80. 所以甲工厂5月份的用水量是120吨,乙工厂5月份的用水量是80吨.
?
8.[2019湖北潜江期末]5月份,甲、乙两个工厂用水量共为200吨.两工厂积极响应国家号召,采取节水措施.6月份,甲工厂用水量比5月份减少了15%,乙工厂用水量比5月份减少了10%,两个工厂6月份用水量共为174吨,则甲、乙两个工厂5月份的用水量分别是( )
A.120吨,80吨 B.80吨,120吨
C.140吨,60吨 D.60吨,140吨
答案
9.????=1,????=2 【解析】 因为直线y=x+1经过点M(1,b),所以b=1+1=2,所以M(1,2),所以关于x,y的方程组????+1=????,?????????????=???? 的解为????=1,????=2.
?
二、填空题
9.如图,直线y=x+1与直线y=mx-n相交于点M(1,b),则关于x,y的方程组????+1=????,?????????????=???? 的解为? .?
?
答案
10.????+4.5=????,?????1=12????
?
10.[2019湖北咸宁中考]《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”如果设木条长x尺,绳子长y尺,可列方程组为? .?
答案
11.1 【解析】 2????+3????=4,①3????+2????=2?????3,②①+②,得5(x+y)=2m+1,解得x+y=2????+15.因为x+y=35,所以2????+15=35,解得m=1.
?
11.[2019四川南充高坪区模拟]若关于x,y的方程组2????+3????=4,3????+2????=2?????3 的解满足x+y=35,则m= .?
?
答案
12.823 【解析】 如图,设直线AB的表达式为y=kx+b.根据题意可知,点A的坐标为(15,40),将点A(15,40),B(18,21)代入,得15????+????=40,18????+????=21, 解得????=?193,????=135, 所以直线AB的表达式为y=-193x+135,将x=17代入,得y=823.
?
12.某洗衣机洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分)之间的关系如图所示,已知清洗时间为11分钟,则排水2分钟时洗衣机中剩下的水量为??????? 升.?
?
答案
13.【解析】 (1)因为关于x,y的二元一次方程组????+????=3,????????+????????=8 与方程组?????????=1,?????????????????=4 有相同的解,
所以????+????=3,?????????=1的解就是这个相同的解,
所以这个相同的解为????=2,????=1.
(2)由(1)知,????=2,????=1是????????+????????=8,?????????????????=4的解,所以2????+????=8,2?????????=4,
解得????=3,????=2, 所以m-n=3-2=1.
?
三、解答题
13.若关于x,y的二元一次方程组????+????=3,????????+????????=8 与方程组?????????=1,?????????????????=4 有相同的解.
(1)求这个相同的解;
(2)求m-n的值.
?
答案
14.【解析】 (1)因为点C在直线l1:y=2x-2上,
所以2=2m-2,所以m=2,所以点C的坐标为(2,2).
因为点C(2,2),B(3,1)在直线l2上,
所以2????+????=2,3????+????=1,解得????=?1,????=4,
所以直线l2的表达式为y=-x+4.
(2)由题意知A(4,0),D(1,0),
所以AD=4-1=3,所以S△ADC=12×3×2=3.
(3)????=2,????=2.
?
14.如图,直线l1的表达式为y=2x-2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B(3,1),直线l1,l2交于点C(m,2).
(1)求直线l2的表达式;
(2)求△ADC的面积;
(3)写出关于x,y的二元一次方程组????=2?????2,????=????????+???? 的解.
?
15.[2019内蒙古呼和浩特中考]滴滴快车是一种便捷的出行工具,计价规则如下表:
小王与小张各自乘坐滴滴快车,在同一地点约见,已知到达约见地点时他们的实际行车里程分别为6公里与8.5公里,两人付给滴滴快车的乘车费相同.
(1)求这两辆滴滴快车的实际行车时间相差多少分钟;
(2)实际乘车时间较少的人,由于出发时间比另一人早,所以提前到达约见地点在大厅等候.已知他等候另一人的时间是他自己实际乘车时间的1.5倍,且比另一人的实际乘车时间的一半多8.5分钟,计算俩人各自的实际乘车时间.
{5940675A-B579-460E-94D1-54222C63F5DA}计费项目
里程费
时长费
远途费
价格
1.8元/公里
0.3元/分
0.8元/公里
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收0.8元.
答案
15.【解析】 设小王的实际行车时间为x分钟,小张的实际行车时间为y分钟.
(1)由题意,得1.8×6+0.3x=1.8×8.5+0.3y+0.8×(8.5-7),
所以0.3(x-y)=5.7,所以x-y=19.
所以这两辆滴滴快车的实际行车时间相差19分钟.
(2)由(1)及题意,得?????????=19,1.5????=12????+8.5,
解得????=37,????=18.
所以小王的实际乘车时间为37分钟,小张的实际乘车时间为18分钟.
?
16.某地植物园从正门到侧门有一条小路,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6 h后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2 h,然后按原路原速匀速返回侧门.甲、乙到侧门的距离y(km)与出发时间x(h)之间的函数关系如图所示.根据图象信息解答下列问题:
(1)求甲在休息前,y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求甲、乙第一次相遇的时间;
(3)直接写出乙回到侧门时,甲到侧门的距离.
答案
16.【解析】 (1)设甲在休息前,y与x之间的函数关系式是y=kx+b,
将(0,12),(1,7)代入,
得????=12,????+????=7, 解得????=?5,????=12,
所以甲在休息前,y与x之间的函数关系式是y=-5x+12(0≤x≤1.2).
(2)由题意知,乙从侧门到正门对应的函数表达式为y=12x,
由????=12????,????=?5????+12, 得x=1217.
答:甲、乙第一次相遇的时间是1217 h.
(3)乙回到侧门时,甲到侧门的距离是4 km.
设甲休息后对应的函数表达式为y=mx+n,
将x=1.2代入y=-5x+12,得y=6,
所以甲休息后对应的函数图象过点(1.8,6),(3,0),
所以1.8????+????=6,3????+????=0, 解得????=?5,????=15,
即甲休息后对应的函数表达式为y=-5x+15(1.8≤x≤3),
将x=2.2代入y=-5x+15,得y=4,
即乙回到侧门时,甲到侧门的距离是4 km.
?
第五章·二元一次方程组中考模拟+真题
数学·八年级上册 ·北师
答案
1.B 【解析】 将????=?2,????=3分别代入四个选项中.A项,3-4×(-2)=11≠-5;B项,2×(-2)-3×3=-13;C项,3≠2×(-2)+5;D项,
-2≠3-1.故选B.
?
1.[2020浙江杭州上城区二模]已知二元一次方程组????+????=1,( )的解是????=?2,????=3,则括号内的方程可能是( )
A.y-4x=-5 B.2x-3y=-13
C.y=2x+5 D.x=y-1
?
答案
2.D 【解析】 根据题意,将????=2,????=1代入????????+????????=7,?????????????????=1,得2????+????=7,①?????+2????=1,②①+②,得m+3n=8.故选D.
?
2.[2019甘肃金昌期末]已知????=2,????=1是二元一次方程组????????+????????=7,?????????????????=1的解,则m+3n的值是( )
A.4 B.6 C.7 D.8
?
答案
3.A 【解析】 将x=1代入x+y=3,得y=2.将x=1,y=2代入x+py=0,得1+2p=0,解得p=-12.故选A.
?
3.[2020浙江杭州下城区期中]关于x,y的方程组????+????????=0,????+????=3的解是????=1,????=▲,其中y的值被盖住了,不过仍能求出p的值是( )
A.-12 B.12 C.-14 D.14
?
答案
4.A 【解析】 由题意,得????+2????=1,2?????????=7,解得????=3,????=?1.故选A.
?
4.[2019辽宁铁岭模拟]为确保信息安全,信息需加密传输,发送方将明文加密文件传输给接收方,接收方收到密文后解密还原为明文.已知某种加密规则为明文a,b对应密文a+2b,2a-b.例如:明文1,2对应密文5,0.当接收方收到的密文是1,7时,解密得到的明文a,b分别是 ( )
A.3,-1 B.1,-3
C.-3,1 D.-1,3
答案
5.6 【解析】 设103路公交车的行驶速度为x米/分,小明的行走速度为y米/分,同向行驶的相邻两辆103路公交车间的间距为s米.根据题意得7?????7????=????,5????+5????=????, 解得x=6y.
?
5.[2020黑龙江哈尔滨模拟]小明沿街匀速行走,发现每隔7分钟从背后驶过一辆103路公交车,每隔5分钟从迎面驶来一辆103路公交车,假设每辆103路公交车行驶速度相同,而且103路公交车总站每隔固定时间发一辆车,那么103路公交车行驶速度是小明行走速度的 倍.?
6.[2019河北承德期末]阅读材料:善于思考的小军在解方程组2????+5????=3,①4????+11????=5②时,采用了一种“整体代换”的解法.
解:将②变形,得4x+10y+y=5,
即2(2x+5y)+y=5.③
把①代入③,得2×3+y=5,解得y=-1.
把y=-1代入①,得2x-5=3,解得x=4.
所以原方程组的解为????=4,????=?1.
请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组3?????2????=5,①9?????4????=19;②
(2)已知x,y满足方程组3????2?2????????+12????2=47,①2????2+????????+8????2=36.②
(i)求x2+4y2的值;
(ii)求1????+12????的值.
?
答案
6.【解析】 (1)将②变形,得3(3x-2y)+2y=19,③
把①代入③,得3×5+2y=19,解得y=2.
把y=2代入①,得3x-4=5,解得x=3.
所以原方程组的解为????=3,????=2.
(2)(i)由②,得2(x2+4y2)+xy=36,
所以xy=36-2(x2+4y2).③
由①,得3(x2+4y2)-2xy=47,④
把③代入④,得3(x2+4y2)-2[36-2(x2+4y2)]=47,
所以x2+4y2=17.
(ii)由(i)得xy=36-2(x2+4y2)=36-2×17=2.
所以(x+2y)2=x2+4y2+4xy=17+8=25,
所以x+2y=±5,
所以1????+12????=????+2????2????????=±54.
?
答案
1.D 【解析】 3????+2????=7,①6?????2????=11,②①+②,得9x=18,解得x=2.将x=2代入①,解得y=12,所以方程组的解是????=2,????=12.
?
1.[2019天津中考]方程组3????+2????=7,6?????2????=11的解是( )
A.????=?1,????=5 B.????=1,????=2
C.????=3,????=?1 D.????=2,????=12
?
答案
2.D 【解析】 由“津津乘坐这种出租车走了7 km,付了16元”,可列方程x+(7-2)y=16;由“盼盼乘坐这种出租车走了13 km,付了28元”,可列方程x+(13-2)y=28.联立两方程即可.
2.[2019湖南邵阳中考]某出租车起步价所包含的路程为0~2 km,超过2 km的部分按每千米另收费.津津乘坐这种出租车走了7 km,付了16元;盼盼乘坐这种出租车走了13 km,付了28元.设这种出租车的起步价为x元,超过2 km后每千米收费y元,则下列方程组正确的是 ( )
A.????+7????=16,????+13????=28 B.????+(7?2)????=16,????+13????=28
C.????+7????=16,????+(13?2)????=28 D.????+(7?2)????=16,????+(13?2)????=28
?
答案
3.2 【解析】 ????+2????=?????1,①2????+????=5????+4,② ①+②,得3x+3y=6k+3,所以x+y=2k+1,因为x+y=5,所以2k+1=5,解得k=2.
?
3.[2019四川眉山中考]已知关于x,y的方程组????+2????=?????1,2????+????=5????+4 的解满足x+y=5,则k的值为 .?
?
答案
4.【解析】 ????+3????=7,①?????3????=1,②
①+②,得2x=8,解得x=4.
将x=4代入②,得4-3y=1,
解得y=1.
所以原方程组的解为????=4,????=1.
?
4.[2019湖南怀化中考]解二元一次方程组:????+3????=7,?????3????=1.
?
5.[2019浙江金华中考]解方程组:3?????4(?????2????)=5,?????2????=1.
?
答案
5.【解析】 解法一 3?????4(?????2????)=5,①?????2????=1,②将①化简,得-x+8y=5③,②+③,得y=1,将y=1代入②,得x=3,所以????=3,????=1.
解法二 将②代入①,可得3x-4=5,所以x=3,将x=3代入②,可得y=1,所以原方程组的解为????=3,????=1.
?
6.[2019山东枣庄中考]对于实数a,b,定义关于“ ”的一种运算:a b=2a+b.例如3 4=2×3+4=10.
(1)求4 (-3)的值;
(2)若x (-y)=2,(2y) x=-1,求x+y的值.
答案
6.【解析】 (1)根据题意,得4 (-3)=2×4-3=5.
(2)根据题意,得2?????????=2,①????+4????=?1,②
①+②,得3x+3y=1,
所以x+y=13.
?
7.[2019甘肃白银中考]小甘到文具超市去买文具.请你根据如图中的对话信息,求中性笔和笔记本的单价分别是多少元?
答案
7.【解析】 设中性笔和笔记本的单价分别是x元,y元.
根据题意,得12????+20????=112,12????+20????=144,
解得????=2,????=6.
答:中性笔和笔记本的单价分别是2元,6元.
?
8.[2019山东烟台中考]亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
答案
8.【解析】 (1)设计划调配36座新能源客车x辆,该大学共有y名志愿者.
根据题意,得36????+2=????,22(????+4)?2=????, 解得????=6,????=218.
答:计划调配36座新能源客车6辆,该大学共有218名志愿者.
(2)设需调配36座新能源客车m辆,22座新能源客车n辆.
根据题意,得36m+22n=218,所以n=109?18????11.
因为m,n均为正整数,所以????=3,????=5.
答:需调配36座新能源客车3辆,22座新能源客车5辆.
数学·八年级上册·北师
专项素养拓训
专项一 二元一次方程组的解法
专项
1.解方程组:3????+2????=10,????2=1+????+13.
?
答案
1.【解析】 3????+2????=10,①????2=1+????+13,②
整理,得3????+2????=10,③3?????2????=8,④
③+④,得6x=18,解得x=3.
③-④,得4y=2,解得y=12.
所以原方程组的解是????=3,????=12.
?
2.解方程组:23(2????+????)=4,34????+56(2????+????)=8.
?
答案
2.【解析】 23(2????+????)=4,①34????+56(2????+????)=8,②
由①,得2x+y=6,③
把③代入②,得34x+56×6=8,解得x=4.
把x=4代入③,得8+y=6,解得y=-2.
所以原方程组的解为????=4,????=?2.
?
3.解方程组:13????+14????=40,14????+13????=41.
?
答案
3.【解析】 13????+14????=40,①14????+13????=41,②
①+②,得27x+27y=81,即x+y=3,③
①-②,得-x+y=-1,④
③+④,得2y=2,解得y=1.
③-④,得2x=4,解得x=2.
所以原方程组的解为????=2,????=1.
?
4.解方程组:3(????+????)+2(?????????)=10,????+????4+?????????2=72.
?
答案
4.【解析】 令x+y=a,x-y=b,
则原方程组可变形为3????+2????=10,①????4+????2=72,②
整理,得3????+2????=10,③????+2????=14,④
③-④,得2a=-4,解得a=-2.
把a=-2代入④,得-2+2b=14,解得b=8.
所以????+????=?2,?????????=8,解得????=3,????=?5.
所以原方程组的解为????=3,????=?5.
?
专项二 利用二元一次方程组求解字母或代数式的值
专项
5.若????=1,????=1和????=2,????=?1是方程mx+ny=6的两组解,则m,n的值分别为( )
A.-4,-2 B.2,4 C.4,2 D.-2,-4
?
答案
5.C 【解析】 根据题意,得????+????=6,①2?????????=6,②①+②,得3m=12,解得m=4.把m=4代入①,得n=2.故选C.
?
6.如果 ????=????,????=???? 是方程x-3y=-3的一组解,那么代数式 5-a+3b的值是( )
A.8 B.5 C.2 D.0
?
答案
6.A 【解析】 把x=a,y=b代入x-3y=-3,可得a-3b=-3,所以5-a+3b=5-(a-3b)=5+3=8.故选A.
7.[2019浙江杭州西湖区模拟]若关于x,y的方程组4????+3????=10,?????????(?????1)????=?8 的解中x的值比y的值的相反数大2,则k为( )
A.-3 B.-2 C.-1 D.1
?
答案
7.C 【解析】 因为x的值比y的值的相反数大2,所以x-(-y)=x+y=2,根据题意,得????+????=2,4????+3????=10,解得????=4,????=?2.把????=4,????=?2 代入kx-(k-1)y=-8,得4k+2(k-1)=-8,解得k=-1.故选C.
?
8.[2019湖南长沙期中]甲、乙两人同求关于x,y的二元一次方程ax-by=7的整数解,甲正确地求得一组解为????=1,????=?1,乙把ax-by=7看成ax-by=1,求得另一组解为????=1,????=2, 求a+2b的平方根.
?
答案
8.【解析】 根据题意,得????+????=7,①?????2????=1,②
①-②,得3b=6,所以b=2,
把b=2代入①,
得a=5.
所以a+2b=9,9的平方根为±3.
?
专项三 二元一次方程组与一次函数的综合应用
专项
9.[2020江苏扬州期中]直线l与直线y=2x+1的交点的横坐标为2,与直线y=-x+2的交点的纵坐标为1,则直线l对应的函数表达式是 .?
答案
9.y=4x-3 【解析】 在直线y=2x+1中,令x=2,得y=5,在y=-x+2中,令y=1,得x=1,所以直线l经过点(2,5),(1,1).设直线l对应的函数表达式是y=kx+b,所以2????+????=5,????+????=1, 解得????=4,????=?3,故直线l对应的函数表达式是y=4x-3.
?
10.[2019广西桂林期末]某商店在节日期间开展优惠促销活动:凡购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)之间的函数关系如图所示,则图中a的值是 .?
答案
10.340 【解析】 当x≥200时,设y与x的函数关系式为y=kx+b,所以200????+????=200,500????+????=410,解得????=0.7,????=60,所以y=0.7x+60(x≥200).当x=400时,y=340,所以题图中a的值为340.
?
11.如图,在平面直角坐标系中,直线a与x轴,y轴分别交于A,B两点,且直线a上所有点的坐标都适合二元一次方程4x-3y=-6,直线b与x轴,y轴分别交于C,D两点,且直线b上所有点的坐标都适合二元一次方程x-2y=1,直线a与b交于点E.
(1)分别求出点A,D的坐标;
(2)求四边形AODE的面积.
答案
11.【解析】 (1)因为直线a上所有点的坐标都适合二元一次方程4x-3y=-6,
所以当y=0时,x=-32,所以点A的坐标为(-32,0).
因为直线b上所有点的坐标都适合二元一次方程x-2y=1,
所以当x=0时,y=-12,所以点D的坐标为(0,-12).
(2)由题意易知,点C的坐标(1,0).
由4?????3????=?6,?????2????=1, 得????=?3,????=?2, 所以点E的坐标为(-3,-2).
则S四边形AODE =S△ACE -S△ODC =12×(32+1)×2-12×12×1=94.
?
12.某校一课外小组准备进行“绿色环保”的宣传活动,需要制作宣传单,校园附近有甲、乙两家印刷社,制作此种宣传单的收费标准如下.
甲印刷社的收费y(元)与印数x(张)的函数关系如下表:
乙印刷社的收费方式为:500张以内(含500张),按每张0.20元收费;超过500张的部分,按每张0.10元收费.
(1)根据表中规律,写出甲印刷社的收费y(元)与印数x(张)之间的函数关系式;
(2)若该小组在甲、乙两家印刷社共印制400张宣传单,用去65元,问在甲、乙两家印刷社各印制多少张?
(3)活动结束后,市民反应良好,该小组决定再加印800张宣传单,若在甲、乙印刷社中选一家,则该小组选择哪家印刷社比较划算?
{5940675A-B579-460E-94D1-54222C63F5DA}印数x/张
…
100
200
300
…
收费y/元
…
15
30
45
…
答案
12.【解析】 (1)由题意设甲印刷社的收费y(元)与印数x(张)之间的函数关系式为y=kx+b,
由题意,得15=100????+????,30=200????+????,
解得????=0.15,????=0,
所以甲印刷社的收费y(元)与印数x(张)之间的函数关系式为y=0.15x.
(2)设在甲印刷社印制a张,则在乙印刷社印制(400-a)张,
由题意,得0.15a+0.2(400-a)=65,解得a=300,
400-300=100(张),
所以在甲印刷社印制300张,在乙印刷社印制100张.
(3)在甲印刷社印制的费用为0.15×800=120(元).
在乙印刷社印制的费用为500×0.2+0.1×(800-500)=130(元).
因为120<130,
所以该小组选择甲印刷社比较划算.
?
综合素养拓训
素养解读
数学建模是对现实问题进行数学抽象,用数学语言表达问题,用数学方法构建模型解决问题的素养.数学建模过程主要包括:在实际情境中从数学的视角发现问题、提出问题、分析问题、建立模型、计算求解、检验结果,最终解决实际问题.本章在学习和理解二元一次方程组并经历和体验其工具作用的过程中,锻炼思维、培养建模能力,发展模型思想和应用意识.如第1题,根据绝对值的性质,探究含绝对值的方程组的解的组数,培养学生的分类讨论思想;第2题,通过设元构建二元一次方程组解决实际问题,关注数学建模和方程思想;第4题,利用换元法解方程组,培养学生分析问题、解决问题的能力.
1.[探究方程组解的组数]方程组|????|?????=10,?????|????|=4的解的组数是( )
A.1 B.2 C.3 D.4
?
答案
1.A 【解析】 当x>0,y>0时,方程组变形得?????????=10,?????????=4,无解;当x>0,y<0时,方程组变形得?????????=10,①????+????=4,②①+②得2x=14,解得x=7,②-①得2y=-6, 解得y=-3,则方程组的解为????=7,????=?3;当x<0,y>0时,方程组变形得??????????=10,③?????????=4,④③+④得-2y=14, 解得y=-7<0,舍去;当x<0,y<0时,方程组变形得????+????=?10,????+????=4,无解.综上,方程组的解的组数是1.故选A.
?
2.[方程组与几何图形问题的综合]如图,分别用火柴棍连续搭建等边三角形和正六边形,公共边只用一根火柴棍.如果搭建等边三角形和正六边形共用了2 020根火柴棍,并且等边三角形的个数比正六边形的个数多8,那么连续搭建的等边三角形的个数是 ( )
A.222 B.280 C.286 D.294
答案
2.D 【解析】 设连续搭建等边三角形x个,连续搭建正六边形 y个.由题意,得2????+1+5????+1=2?020,?????????=8,解得????=294,????=286.故选D.
?
3.[二元一次方程组的解与系数之间的关系]根据要求,解答下列问题.
(1)解下列方程组(直接写出方程组的解即可):
①????+2????=3,2????+????=3的解为 ;?
②3????+2????=10,2????+3????=10的解为? ;?
③2?????????=4,?????+2????=4的解为? .?
(2)以上每个方程组的解中,x值与y值的大小关系为 .?
(3)请你构造一个具有以上外形特征的方程组,并直接写出它的解.
?
答案
3.【解析】 (1)①????=1,????=1②????=2,????=2③????=4,????=4
(2)x=y
(3)3????+2????=25,2????+3????=25的解为????=5,????=5.(答案不唯一)
?
4.[换元法解方程组]三个同学同时解一道题:若方程组????1????+????1????=????1,????2????+????2????=????2的解是????=3,????=4,求方程组3????1????+2????1????=5????1,3????2????+2????2????=5????2的解.
三个人各自提出不同的想法:
甲说:“这个题目好像条件不够,不能求出它的解.”
乙说:“它们的系数有一定的规律,可以试试.”
丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元的方法来解决呢?”
参考他们的讨论,你认为这个题目应该怎么解?
?
答案
4.【解析】 按照丙的想法,将第二个方程组3????1????+2????1????=5????1,3????2????+2????2????=5????2变形为????1(35????)+????1(25????)=????1,????2(35????)+????2(25????)=????2,
再由方程组????1????+????1????=????1,????2????+????2????=????2的解是????=3,????=4,可得35????=3,25????=4,解得????=5,????=10,
所以方程组3????1????+2????1????=5????1,3????2????+2????2????=5????2的解是????=5,????=10.
?
答案
1.A 【解析】 根据题意,知|2m-3|=1,m-2≠0,所以m=1.故选A.
一、选择题
1.若x|2m-3|+(m-2)y=8是关于x,y的二元一次方程,则m的值是 ( )
A.1 B.2 C.1或2 D.任何数
答案
2.C
2.利用加减消元法解方程组2????+5????=?10,①5?????3????=6②时,下列说法正确的是( )
A.要消去y,可以将①×5+②×3
B.要消去x,可以将①×3+②×(-5)
C.要消去y,可以将①×3+②×5
D.要消去x,可以将①×5+②×2
?
答案
3.C 【解析】 把????=1,????=4代入二元一次方程ax+y=7中,得a+4=7,解得a=3.故选C.
?
3.若????=1,????=4是关于x,y的二元一次方程ax+y=7的解,则a的值为( )
A.1 B.2 C.3 D.4
?
答案
4.C 【解析】 两式相减,得x+3y=-2,所以2(x+3y)=-4,即2x+6y=-4.故选C.
4.[2019广西贺州中考]已知方程组2????+????=3,?????2????=5, 则2x+6y的值是( )
A.-2 B.2 C.-4 D.4
?
答案
5.A 【解析】 设直线PQ对应的一次函数的表达式为y=kx+b,因为直线PQ经过点P(-20,5),Q(10,20),所以?20????+????=5,10????+????=20, 解得????=12,????=15, 所以直线PQ对应的一次函数的表达式为y=12x+15.故选A.
?
5.[2019河北沧州期末]直线PQ上两点的坐标分别是P(-20,5),Q(10,20),则直线PQ对应的一次函数的表达式为 ( )
A.y=12x+15 B.y=2x
C.y=12x-15 D.y=3x-10
?
答案
6.A 【解析】 将????=1,????=?1与????=2,????=2代入二元一次方程ax+by+2=0,可得?????????+2=0,2????+2????+2=0,解得????=?32,????=12,则二元一次方程为-32x+12y+2=0,经检验得A项仍为此方程的解.故选A.
?
6.如果二元一次方程ax+by+2=0有两组解????=1,????=?1与????=2,????=2,那么下面四个选项中仍是这个方程的解的是( )
A.????=3,????=5 B.????=5,????=3
C.????=6,????=2 D.????=4,????=4
?
答案
7.B 【解析】 因为?????3?????1+|x-2y+2|=0,所以?????3????=1,?????2????=?2, 解得????=?8,????=?3, 所以x-4y=-8+12=4,4的平方根是±2.故选B.
?
7.已知x,y满足?????3?????1+|x-2y+2|=0,则x-4y的平方根为( )
A.2 B.±2 C.4 D.±4
?
答案
8.A 【解析】 设甲工厂5月份的用水量是x吨,乙工厂5月份的用水量是y吨,根据题意,得????+????=200,(1?15%)????+(1?10%)????=174, 解得????=120,????=80. 所以甲工厂5月份的用水量是120吨,乙工厂5月份的用水量是80吨.
?
8.[2019湖北潜江期末]5月份,甲、乙两个工厂用水量共为200吨.两工厂积极响应国家号召,采取节水措施.6月份,甲工厂用水量比5月份减少了15%,乙工厂用水量比5月份减少了10%,两个工厂6月份用水量共为174吨,则甲、乙两个工厂5月份的用水量分别是( )
A.120吨,80吨 B.80吨,120吨
C.140吨,60吨 D.60吨,140吨
答案
9.????=1,????=2 【解析】 因为直线y=x+1经过点M(1,b),所以b=1+1=2,所以M(1,2),所以关于x,y的方程组????+1=????,?????????????=???? 的解为????=1,????=2.
?
二、填空题
9.如图,直线y=x+1与直线y=mx-n相交于点M(1,b),则关于x,y的方程组????+1=????,?????????????=???? 的解为? .?
?
答案
10.????+4.5=????,?????1=12????
?
10.[2019湖北咸宁中考]《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”如果设木条长x尺,绳子长y尺,可列方程组为? .?
答案
11.1 【解析】 2????+3????=4,①3????+2????=2?????3,②①+②,得5(x+y)=2m+1,解得x+y=2????+15.因为x+y=35,所以2????+15=35,解得m=1.
?
11.[2019四川南充高坪区模拟]若关于x,y的方程组2????+3????=4,3????+2????=2?????3 的解满足x+y=35,则m= .?
?
答案
12.823 【解析】 如图,设直线AB的表达式为y=kx+b.根据题意可知,点A的坐标为(15,40),将点A(15,40),B(18,21)代入,得15????+????=40,18????+????=21, 解得????=?193,????=135, 所以直线AB的表达式为y=-193x+135,将x=17代入,得y=823.
?
12.某洗衣机洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分)之间的关系如图所示,已知清洗时间为11分钟,则排水2分钟时洗衣机中剩下的水量为??????? 升.?
?
答案
13.【解析】 (1)因为关于x,y的二元一次方程组????+????=3,????????+????????=8 与方程组?????????=1,?????????????????=4 有相同的解,
所以????+????=3,?????????=1的解就是这个相同的解,
所以这个相同的解为????=2,????=1.
(2)由(1)知,????=2,????=1是????????+????????=8,?????????????????=4的解,所以2????+????=8,2?????????=4,
解得????=3,????=2, 所以m-n=3-2=1.
?
三、解答题
13.若关于x,y的二元一次方程组????+????=3,????????+????????=8 与方程组?????????=1,?????????????????=4 有相同的解.
(1)求这个相同的解;
(2)求m-n的值.
?
答案
14.【解析】 (1)因为点C在直线l1:y=2x-2上,
所以2=2m-2,所以m=2,所以点C的坐标为(2,2).
因为点C(2,2),B(3,1)在直线l2上,
所以2????+????=2,3????+????=1,解得????=?1,????=4,
所以直线l2的表达式为y=-x+4.
(2)由题意知A(4,0),D(1,0),
所以AD=4-1=3,所以S△ADC=12×3×2=3.
(3)????=2,????=2.
?
14.如图,直线l1的表达式为y=2x-2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B(3,1),直线l1,l2交于点C(m,2).
(1)求直线l2的表达式;
(2)求△ADC的面积;
(3)写出关于x,y的二元一次方程组????=2?????2,????=????????+???? 的解.
?
15.[2019内蒙古呼和浩特中考]滴滴快车是一种便捷的出行工具,计价规则如下表:
小王与小张各自乘坐滴滴快车,在同一地点约见,已知到达约见地点时他们的实际行车里程分别为6公里与8.5公里,两人付给滴滴快车的乘车费相同.
(1)求这两辆滴滴快车的实际行车时间相差多少分钟;
(2)实际乘车时间较少的人,由于出发时间比另一人早,所以提前到达约见地点在大厅等候.已知他等候另一人的时间是他自己实际乘车时间的1.5倍,且比另一人的实际乘车时间的一半多8.5分钟,计算俩人各自的实际乘车时间.
{5940675A-B579-460E-94D1-54222C63F5DA}计费项目
里程费
时长费
远途费
价格
1.8元/公里
0.3元/分
0.8元/公里
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收0.8元.
答案
15.【解析】 设小王的实际行车时间为x分钟,小张的实际行车时间为y分钟.
(1)由题意,得1.8×6+0.3x=1.8×8.5+0.3y+0.8×(8.5-7),
所以0.3(x-y)=5.7,所以x-y=19.
所以这两辆滴滴快车的实际行车时间相差19分钟.
(2)由(1)及题意,得?????????=19,1.5????=12????+8.5,
解得????=37,????=18.
所以小王的实际乘车时间为37分钟,小张的实际乘车时间为18分钟.
?
16.某地植物园从正门到侧门有一条小路,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6 h后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2 h,然后按原路原速匀速返回侧门.甲、乙到侧门的距离y(km)与出发时间x(h)之间的函数关系如图所示.根据图象信息解答下列问题:
(1)求甲在休息前,y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求甲、乙第一次相遇的时间;
(3)直接写出乙回到侧门时,甲到侧门的距离.
答案
16.【解析】 (1)设甲在休息前,y与x之间的函数关系式是y=kx+b,
将(0,12),(1,7)代入,
得????=12,????+????=7, 解得????=?5,????=12,
所以甲在休息前,y与x之间的函数关系式是y=-5x+12(0≤x≤1.2).
(2)由题意知,乙从侧门到正门对应的函数表达式为y=12x,
由????=12????,????=?5????+12, 得x=1217.
答:甲、乙第一次相遇的时间是1217 h.
(3)乙回到侧门时,甲到侧门的距离是4 km.
设甲休息后对应的函数表达式为y=mx+n,
将x=1.2代入y=-5x+12,得y=6,
所以甲休息后对应的函数图象过点(1.8,6),(3,0),
所以1.8????+????=6,3????+????=0, 解得????=?5,????=15,
即甲休息后对应的函数表达式为y=-5x+15(1.8≤x≤3),
将x=2.2代入y=-5x+15,得y=4,
即乙回到侧门时,甲到侧门的距离是4 km.
?
第五章·二元一次方程组中考模拟+真题
数学·八年级上册 ·北师
答案
1.B 【解析】 将????=?2,????=3分别代入四个选项中.A项,3-4×(-2)=11≠-5;B项,2×(-2)-3×3=-13;C项,3≠2×(-2)+5;D项,
-2≠3-1.故选B.
?
1.[2020浙江杭州上城区二模]已知二元一次方程组????+????=1,( )的解是????=?2,????=3,则括号内的方程可能是( )
A.y-4x=-5 B.2x-3y=-13
C.y=2x+5 D.x=y-1
?
答案
2.D 【解析】 根据题意,将????=2,????=1代入????????+????????=7,?????????????????=1,得2????+????=7,①?????+2????=1,②①+②,得m+3n=8.故选D.
?
2.[2019甘肃金昌期末]已知????=2,????=1是二元一次方程组????????+????????=7,?????????????????=1的解,则m+3n的值是( )
A.4 B.6 C.7 D.8
?
答案
3.A 【解析】 将x=1代入x+y=3,得y=2.将x=1,y=2代入x+py=0,得1+2p=0,解得p=-12.故选A.
?
3.[2020浙江杭州下城区期中]关于x,y的方程组????+????????=0,????+????=3的解是????=1,????=▲,其中y的值被盖住了,不过仍能求出p的值是( )
A.-12 B.12 C.-14 D.14
?
答案
4.A 【解析】 由题意,得????+2????=1,2?????????=7,解得????=3,????=?1.故选A.
?
4.[2019辽宁铁岭模拟]为确保信息安全,信息需加密传输,发送方将明文加密文件传输给接收方,接收方收到密文后解密还原为明文.已知某种加密规则为明文a,b对应密文a+2b,2a-b.例如:明文1,2对应密文5,0.当接收方收到的密文是1,7时,解密得到的明文a,b分别是 ( )
A.3,-1 B.1,-3
C.-3,1 D.-1,3
答案
5.6 【解析】 设103路公交车的行驶速度为x米/分,小明的行走速度为y米/分,同向行驶的相邻两辆103路公交车间的间距为s米.根据题意得7?????7????=????,5????+5????=????, 解得x=6y.
?
5.[2020黑龙江哈尔滨模拟]小明沿街匀速行走,发现每隔7分钟从背后驶过一辆103路公交车,每隔5分钟从迎面驶来一辆103路公交车,假设每辆103路公交车行驶速度相同,而且103路公交车总站每隔固定时间发一辆车,那么103路公交车行驶速度是小明行走速度的 倍.?
6.[2019河北承德期末]阅读材料:善于思考的小军在解方程组2????+5????=3,①4????+11????=5②时,采用了一种“整体代换”的解法.
解:将②变形,得4x+10y+y=5,
即2(2x+5y)+y=5.③
把①代入③,得2×3+y=5,解得y=-1.
把y=-1代入①,得2x-5=3,解得x=4.
所以原方程组的解为????=4,????=?1.
请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组3?????2????=5,①9?????4????=19;②
(2)已知x,y满足方程组3????2?2????????+12????2=47,①2????2+????????+8????2=36.②
(i)求x2+4y2的值;
(ii)求1????+12????的值.
?
答案
6.【解析】 (1)将②变形,得3(3x-2y)+2y=19,③
把①代入③,得3×5+2y=19,解得y=2.
把y=2代入①,得3x-4=5,解得x=3.
所以原方程组的解为????=3,????=2.
(2)(i)由②,得2(x2+4y2)+xy=36,
所以xy=36-2(x2+4y2).③
由①,得3(x2+4y2)-2xy=47,④
把③代入④,得3(x2+4y2)-2[36-2(x2+4y2)]=47,
所以x2+4y2=17.
(ii)由(i)得xy=36-2(x2+4y2)=36-2×17=2.
所以(x+2y)2=x2+4y2+4xy=17+8=25,
所以x+2y=±5,
所以1????+12????=????+2????2????????=±54.
?
答案
1.D 【解析】 3????+2????=7,①6?????2????=11,②①+②,得9x=18,解得x=2.将x=2代入①,解得y=12,所以方程组的解是????=2,????=12.
?
1.[2019天津中考]方程组3????+2????=7,6?????2????=11的解是( )
A.????=?1,????=5 B.????=1,????=2
C.????=3,????=?1 D.????=2,????=12
?
答案
2.D 【解析】 由“津津乘坐这种出租车走了7 km,付了16元”,可列方程x+(7-2)y=16;由“盼盼乘坐这种出租车走了13 km,付了28元”,可列方程x+(13-2)y=28.联立两方程即可.
2.[2019湖南邵阳中考]某出租车起步价所包含的路程为0~2 km,超过2 km的部分按每千米另收费.津津乘坐这种出租车走了7 km,付了16元;盼盼乘坐这种出租车走了13 km,付了28元.设这种出租车的起步价为x元,超过2 km后每千米收费y元,则下列方程组正确的是 ( )
A.????+7????=16,????+13????=28 B.????+(7?2)????=16,????+13????=28
C.????+7????=16,????+(13?2)????=28 D.????+(7?2)????=16,????+(13?2)????=28
?
答案
3.2 【解析】 ????+2????=?????1,①2????+????=5????+4,② ①+②,得3x+3y=6k+3,所以x+y=2k+1,因为x+y=5,所以2k+1=5,解得k=2.
?
3.[2019四川眉山中考]已知关于x,y的方程组????+2????=?????1,2????+????=5????+4 的解满足x+y=5,则k的值为 .?
?
答案
4.【解析】 ????+3????=7,①?????3????=1,②
①+②,得2x=8,解得x=4.
将x=4代入②,得4-3y=1,
解得y=1.
所以原方程组的解为????=4,????=1.
?
4.[2019湖南怀化中考]解二元一次方程组:????+3????=7,?????3????=1.
?
5.[2019浙江金华中考]解方程组:3?????4(?????2????)=5,?????2????=1.
?
答案
5.【解析】 解法一 3?????4(?????2????)=5,①?????2????=1,②将①化简,得-x+8y=5③,②+③,得y=1,将y=1代入②,得x=3,所以????=3,????=1.
解法二 将②代入①,可得3x-4=5,所以x=3,将x=3代入②,可得y=1,所以原方程组的解为????=3,????=1.
?
6.[2019山东枣庄中考]对于实数a,b,定义关于“ ”的一种运算:a b=2a+b.例如3 4=2×3+4=10.
(1)求4 (-3)的值;
(2)若x (-y)=2,(2y) x=-1,求x+y的值.
答案
6.【解析】 (1)根据题意,得4 (-3)=2×4-3=5.
(2)根据题意,得2?????????=2,①????+4????=?1,②
①+②,得3x+3y=1,
所以x+y=13.
?
7.[2019甘肃白银中考]小甘到文具超市去买文具.请你根据如图中的对话信息,求中性笔和笔记本的单价分别是多少元?
答案
7.【解析】 设中性笔和笔记本的单价分别是x元,y元.
根据题意,得12????+20????=112,12????+20????=144,
解得????=2,????=6.
答:中性笔和笔记本的单价分别是2元,6元.
?
8.[2019山东烟台中考]亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
答案
8.【解析】 (1)设计划调配36座新能源客车x辆,该大学共有y名志愿者.
根据题意,得36????+2=????,22(????+4)?2=????, 解得????=6,????=218.
答:计划调配36座新能源客车6辆,该大学共有218名志愿者.
(2)设需调配36座新能源客车m辆,22座新能源客车n辆.
根据题意,得36m+22n=218,所以n=109?18????11.
因为m,n均为正整数,所以????=3,????=5.
答:需调配36座新能源客车3辆,22座新能源客车5辆.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
