北师大版七年级上册数学:第四章 基本平面图形素养拓展+中考真题课件(31张PPT)
文档属性
| 名称 | 北师大版七年级上册数学:第四章 基本平面图形素养拓展+中考真题课件(31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 10:42:02 | ||
图片预览







文档简介
第四章 基本平面图形
数学·七年级上册·北师
专题1 直线、线段、角的计数问题
专项素养拓训
1.平面内不重合的两个点确定一条直线,不同的三个点最多确定3条直线,则平面内不同的10个点最多可以确定 条直线.?
答案
1.45 【解析】 不同的10个点中,每个点最多可以和其他9个点构成9条直线,共有10个点,且每个点被算了两次,所以直线总数最多为10×92=45(条).
?
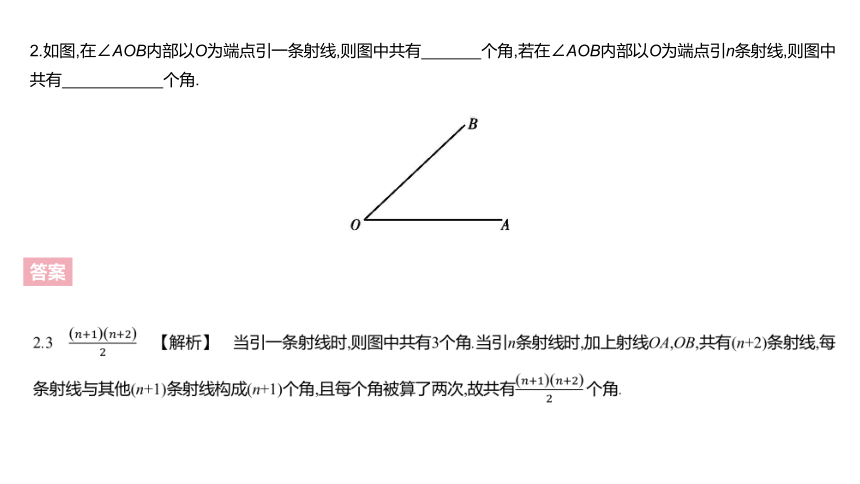
2.如图,在∠AOB内部以O为端点引一条射线,则图中共有 个角,若在∠AOB内部以O为端点引n条射线,则图中共有 个角.?
答案
2.3 (????+1)(????+2)2 【解析】 当引一条射线时,则图中共有3个角.当引n条射线时,加上射线OA,OB,共有(n+2)条射线,每条射线与其他(n+1)条射线构成(n+1)个角,且每个角被算了两次,故共有(????+1)(????+2)2 个角.
?
3.为丰富师生的课余生活,某地区的五所学校联合举行教师篮球赛和学生联谊活动,每校派一支教工篮球队,各派10名学生参加联谊活动.
(1)若篮球赛采取单循环比赛(每两支队伍之间只进行一场比赛),则篮球赛共进行了 场;?
(2)学生联谊活动中,全体同学制作了手工小礼品,活动结束,全体同学互赠手工小礼品(每两个同学之间都互赠,数量刚好够赠送),则本次活动共制作了 件小礼品.?
答案
3.(1)10;(2)2 450 【解析】 (1)由题意,得5×42=10(场);(2)由题意得,50×(50-1)=2 450(件).
?
专题2 线段的有关计算
专项素养拓训
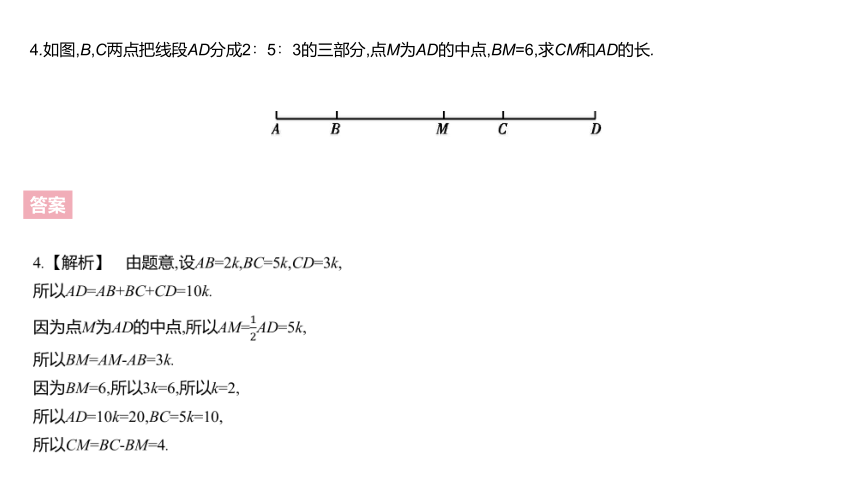
4.如图,B,C两点把线段AD分成2∶5∶3的三部分,点M为AD的中点,BM=6,求CM和AD的长.
答案
4.【解析】 由题意,设AB=2k,BC=5k,CD=3k,
所以AD=AB+BC+CD=10k.
因为点M为AD的中点,所以AM=12AD=5k,
所以BM=AM-AB=3k.
因为BM=6,所以3k=6,所以k=2,
所以AD=10k=20,BC=5k=10,
所以CM=BC-BM=4.
?
5.[2020湖北武汉青山区期末]已知线段AB上有M,N两点,AB=18,AM∶BM=1∶2,MN=5,点C为BN的中点,求BC的长.
答案
5.【解析】 因为AB=18,AM∶BM=1∶2,
所以AM=6,BM=12.
分两种情况:
如图1,因为MN=5,所以BN=12-5=7,
因为点C为BN的中点,所以BC=12BN=3.5.
如图2,因为MN=5,所以BN=12+5=17,
因为点C为BN的中点,所以BC=12BN=8.5.
综上所述,BC=3.5或8.5.
?
专题3 与角平分线有关的问题
专项素养拓训
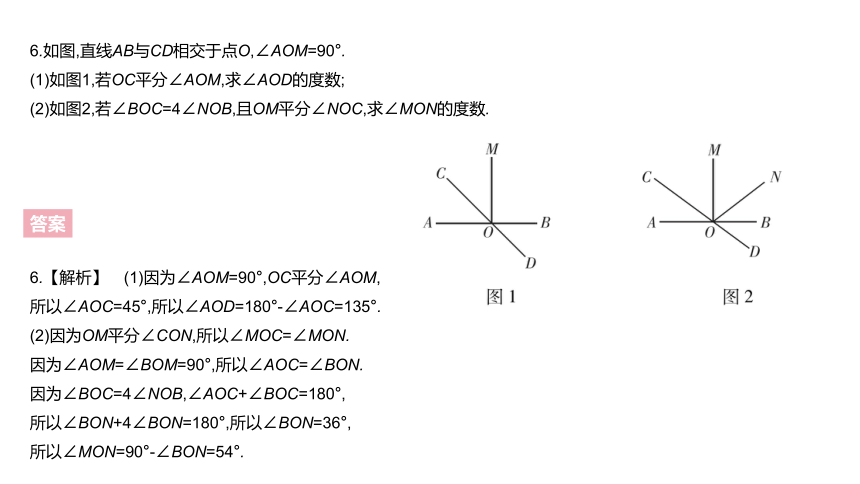
6.如图,直线AB与CD相交于点O,∠AOM=90°.
(1)如图1,若OC平分∠AOM,求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数.
答案
6.【解析】 (1)因为∠AOM=90°,OC平分∠AOM,
所以∠AOC=45°,所以∠AOD=180°-∠AOC=135°.
(2)因为OM平分∠CON,所以∠MOC=∠MON.
因为∠AOM=∠BOM=90°,所以∠AOC=∠BON.
因为∠BOC=4∠NOB,∠AOC+∠BOC=180°,
所以∠BON+4∠BON=180°,所以∠BON=36°,
所以∠MON=90°-∠BON=54°.
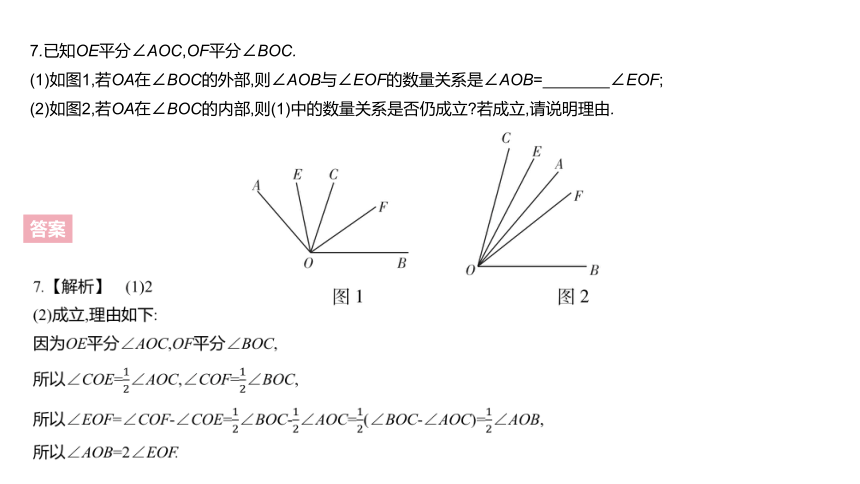
7.已知OE平分∠AOC,OF平分∠BOC.
(1)如图1,若OA在∠BOC的外部,则∠AOB与∠EOF的数量关系是∠AOB= ∠EOF;?
(2)如图2,若OA在∠BOC的内部,则(1)中的数量关系是否仍成立?若成立,请说明理由.
答案
7.【解析】 (1)2
(2)成立,理由如下:
因为OE平分∠AOC,OF平分∠BOC,
所以∠COE=12∠AOC,∠COF=12∠BOC,
所以∠EOF=∠COF-∠COE=12∠BOC-12∠AOC=12(∠BOC-∠AOC)=12∠AOB,
所以∠AOB=2∠EOF.
?
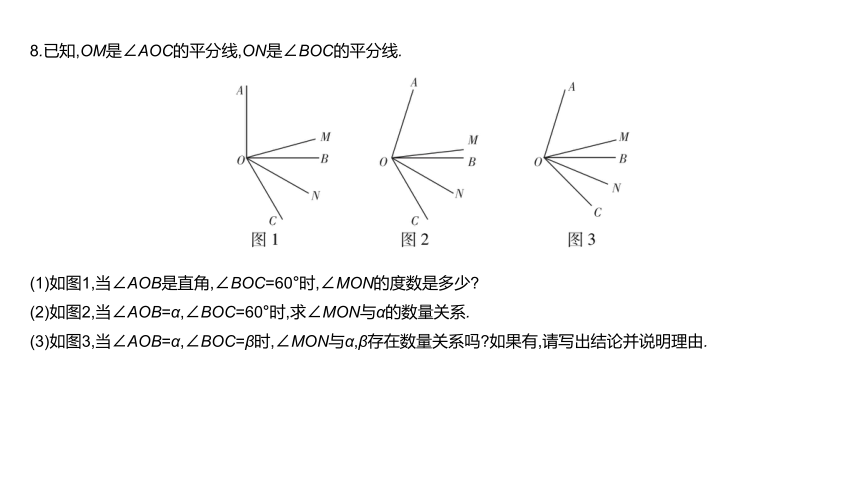
8.已知,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,求∠MON与α的数量关系.
(3)如图3,当∠AOB=α,∠BOC=β时,∠MON与α,β存在数量关系吗?如果有,请写出结论并说明理由.
答案
8.【解析】 (1)因为∠AOB=90°,∠BOC=60°,
所以∠AOC=∠AOB+∠BOC=150°.
因为OM是∠AOC的平分线,ON是∠BOC的平分线,
所以∠COM=12∠AOC=75°,∠CON=12∠BOC=30°,
所以∠MON=∠COM-∠CON=45°.
(2)易知∠AOC=∠AOB+∠BOC=α+60°.
因为OM是∠AOC的平分线,ON是∠BOC的平分线,
所以∠COM=12∠AOC=12α+30°,∠CON=12∠BOC=30°,
所以∠MON=∠COM-∠CON=12α.
?
答案
(3)∠MON只和α有关,和β无关,∠MON=12α.理由如下:
易知∠AOC=∠AOB+∠BOC=α+β.
因为OM是∠AOC的平分线,ON是∠BOC的平分线,
所以∠COM=12∠AOC=12α+12β,∠CON=12∠BOC=12β,
所以∠MON=∠COM-∠CON=12α,
所以∠MON只和α有关,和β无关,∠MON=12α.
?
综合素养拓训
本章引入基本平面图形,用点线刻画物体模型,是几何知识体系中最基本的内容之一,也是后续学习三角形、四边形等知识的基础.将线段、角等作为载体,通过与线段中点、角平分线等相关的计算问题,渗透转化思想、分类讨论思想、方程思想,增强运用图形思考问题的意识,提升数形结合能力.
1.[2019山东济南市中区期末]【新知理解】
如图1,点C在线段AB上,图中有三条线段,分别为线段AB,AC和BC,若其中一条线段的长度是另外一条线段的2倍,则称点C是线段AB的“巧点”.
(1)线段的中点 这条线段的“巧点”(填“是”或“不是”).?
(2)若线段AB=12 cm,点C是线段AB的“巧点”,则AC= cm.?
【解决问题】
(3)如图2,已知AB=12 cm,动点P从点A出发,以2 cm/s的速度沿AB向点B运动,点Q从点B出发,以1 cm/s的速度沿BA向点A运动,点P,Q同时出发,当其中一点到达终点时,运动停止.设运动的时间为t s,当t为何值时,点P为线段AQ的“巧点”,并说明理由.
答案
1.【解析】 (1)是
(2)4,6或8
①当AB=2AC时,AC=6 cm;②当AC=2BC时,因为AC+BC=AB=12 cm,所以AC=8 cm;③当BC=2AC时,BC=8 cm,AC=4 cm.综上,AC=4 cm,6 cm或8 cm.
(3)由题意知,AP=2t cm,BQ=t cm,所以AQ=(12-t)cm,
因为点P为AQ的“巧点”,所以点P在线段AQ上,
①当AQ=2AP时,12-t=4t,所以t=125;
②当AP=2PQ时,AP=23AQ,即2t=23(12-t),所以t=3;
③当PQ=2AP时,AP=13AQ,即2t=13(12-t),所以t=127.
所以当t为125,3或127时,点P为线段AQ的“巧点”.
?
本题是一道“新定义”的题,做题的关键是要搞懂什么是“巧点”.由于一条直线上的三个点共构成了三条线段,而“巧点”只是两条线段的数量关系,所以这里需要进行分类讨论:哪两条线段满足“巧点”关系?哪条线段是另一条线段的2倍?
2.[探究角之间的数量关系]如图,O为直线AB上一点,∠BOC=α.
(1)如图1,若α=40°,OD平分∠AOC,∠DOE=90°,求∠AOE的度数;
(2)如图2,若∠AOD=13∠AOC,∠DOE=60°,请用α表示∠AOE的度数;
(3)如图3,若∠AOD=1????∠AOC,∠DOE=180°????(n≥2,且n为正整数),请用α和n表示∠AOE的度数.(直接写出结果)
?
答案
2.【解析】 (1)因为∠BOC=40°,所以∠AOC=180°-∠BOC=140°,
又因为OD平分∠AOC,
所以∠AOD=∠DOC=12∠AOC=70°.
因为∠DOE=90°,所以∠AOE=90°-70°=20°.
(2)设∠AOD=x,则∠DOC=2x,∠BOC=180°-3x=α,
所以x=180°?????3,
所以∠AOE=60°-x=60°-180°?????3=13α.
(3)∠AOE=????????.
设∠AOD=y,则∠DOC=(n-1)y,∠BOC=180°-ny=α,
所以y=180°?????????,所以∠AOE=180°?????180°?????????=????????.
?
答案
1.C 【解析】 因为一副三角尺有30°,45°,60°,90°,所以能用三角尺画出30°,60°,75° .故选C.
一、选择题
1.用一副三角尺可以画出许多不同的角度,以下角度不能用三角尺画出的是 ( )
A.75° B.60° C.40° D.30°
答案
2.B 【解析】 因为∠BAF=60°,所以∠FAD=90°-60°=30°.因为∠DAE=∠FAE,所以∠DAE=12×30°=15°.故选B.
?
2.如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,那么∠DAE等于 ( )
A.10°
B.15°
C.20°
D.30°
答案
3.A 【解析】 如图,因为A岛在C岛的北偏西15°方向,所以∠1=15°.因为∠ACB=90°,所以∠2=180°-∠1-∠ACB=180°-15°-90°=75°,故B岛在C岛的南偏西75°方向.故选A.
3.如图,一张地图上标记了A,B,C三个小岛,已知A岛在C岛的北偏西15°方向,若∠ACB=90°,则B岛在C岛的 ( )
A.南偏西75°方向
B.南偏西65°方向
C.南偏西60°方向
D.南偏西30°方向
答案
4.C 【解析】 因为BC=12AB,所以BC=13AC.因为D为线段AC的中点,所以CD=12AC,所以BD=16AC.因为BD=2,所以AC=2×6=12,所以AB=AD+BD=12AC+BD=12×12+2=8.故选C.
?
4.[2020浙江杭州期末]如图,将线段AB延长至点C,使BC=12AB,D为线段AC的中点,若BD=2,则线段AB的长为 ( )
A.4
B.6
C.8
D.12
?
答案
5.96 【解析】 因为∠BOC=120°,所以甲、丙两个扇形的圆心角的度数和为240°,因为甲、丙两个扇形的面积之比为3∶2,所以∠AOC=240°×23+2=96°.
?
二、填空题
5.[2020山东青岛崂山区期末]如图,将一个圆分割成三个扇形,若甲、丙两个扇形的面积之比为3∶2,∠BOC=120°,则∠AOC= °. ?
答案
6.36 【解析】 由∠AOB+∠BOC=∠BOC+∠COD知∠AOB=∠COD,设∠AOB=2α,则∠AOD=7α,故∠AOB+∠BOC=∠AOD-∠COD=7α-2α=5α=90°,解得α=18°,故∠COD=36°.
6.如图,∠AOC与∠BOD都是直角,且∠AOB∶∠AOD=2∶7,则∠COD= °.?
答案
7.22.5 【解析】 因为时钟指示14时15分时,分针指到3,时针指到2与3之间的某个位置,时针从2到这个位置经过了15分钟,时针每分钟转0.5°,所以转过7.5°,所以时针和分针所成的锐角是30°-7.5°=22.5°.
7.[2020四川遂宁安居区期末]已知某学校下午上课的时间为14时15分,则此时刻时钟上的时针与分针的夹角为 °.?
答案
8.180或144 【解析】 因为AP∶BP=4∶5,所以设AP=4x(x>0)cm,BP=5x cm,则AB=9x cm.因为剪断后的各段绳子中最长的一段为80 cm,所以8x=80或10x=80,解得x=10或x=8,则18x=180或144,所以绳子的原长为180 cm或144 cm.
8.[2020湖北武汉江汉区期末]如图,把一根绳子对折后得到的图形为线段AB,从点P处把绳子剪断,若AP∶BP=4∶5,剪断后的各段绳子中最长的一段为80 cm,则绳子的原长为 cm.?
答案
9.【解析】 (1)如图所示.
(2)因为DE=AC,DE=3,所以AC=3.
因为点C是线段AB的中点,BD=AB,所以BD=AB=2AC=6,
所以BE=BD+DE=6+3=9.
(3)CD=BE.理由如下:
因为C是线段AB的中点,所以CB=AC,
又因为DE=AC,所以CB=DE,
所以CB+BD=DE+BD,即CD=BE.
三、解答题
9.[2020河南焦作期末]如图,点C是线段AB的中点,延长线段AB至点D,使BD=AB,延长AD至点E,使DE=AC.
(1)依照题意补全图形;
(2)若DE=3,求线段AB,BE的长;
(3)请写出图中与BE相等的线段,并说明理由.
10.[2020湖南长沙期末]已知点O是直线AB上一点,∠COE=60°,OF是∠AOE的平分线.
(1)如图1,点C,E在直线AB的同侧,且OF在∠COE的内部,∠BOE-2∠COF=α,求α的大小;
(2)如图2,当点C与点E,F在直线AB的两侧,(1)中的结论是否仍然成立?请说明理由;
(3)将图2中的射线OF绕点O顺时针旋转m°(0?
答案
10.【解析】 (1)设∠AOC=β,则∠BOE=180°-(60°+β)=120°-β.
因为OF是∠AOE的平分线,所以∠COF=12∠AOE-∠AOC=12(60°+β)-β=30°-12β,
所以∠BOE-2∠COF=120°-β-2(30°-12β)=60°,即α=60°.
(2)(1)中的结论仍然成立.理由如下:
因为OF是∠AOE的平分线,所以∠COF=∠COE-∠EOF=60°-12∠AOE,而∠BOE=180°-∠AOE,
故∠BOE-2∠COF=180°-∠AOE-2(60°-12∠AOE)=60°,即α=60°.
(3)(75+7????4)°
通过比较,可判断出射线OD只可能在∠BOE的内部,如图所示.
∠DOE=180°-∠BOD-∠AOE=180°-(45-3????4)°-(60°-n°)=(75+7????4)°.
?
第四章 基本平面图形中考真题
数学·七年级上册·北师
答案
1.A
1.[2019吉林中考]曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光.如图,A,B两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是 ( )
A.两点之间,线段最短
B.平行于同一条直线的两条直线平行
C.垂线段最短
D.两点确定一条直线
2.[2017河北中考]如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能是 ( )
A.北偏东55°
B.北偏西55°
C.北偏东35°
D.北偏西35°
答案
2.D 【解析】 如图1,当乙的航向是北偏东55°时,甲、乙两船不会相撞;如图2,当乙的航向是北偏西55°时,由于甲、乙两船等速航行,故甲、乙两船不会相撞;如图3,当乙的航向是北偏东35°时,甲、乙两船不会相撞;如图4,当乙的航向是北偏西35°时,由于甲、乙两船等速航行,故甲、乙两船会相撞.故选D.
答案
3.B 【解析】 因为钟面分成12个大格,每格的度数为30°,所以钟表上10点整时,时针与分针所成的角是60°.故选B.
3.[2019广西梧州中考]如图,钟表上10点整时,时针与分针所成的角是 ( )
A.30°
B.60°
C.90°
D.120°
答案
4.C 【解析】 因为数轴上点A,B,M表示的数分别是a,2a,9,点M为线段AB的中点,所以9-a=2a-9,所以a=6.故选C.
4.[2019贵州贵阳中考]数轴上点A,B,M表示的数分别是a,2a,9,点M为线段AB的中点,则a的值是 ( )
A.3 B.4.5 C.6 D.18
答案
5.111°20' 【解析】 45°39'+65°41'=45°+65°+39'+41'=110°+80'=111°20'.
5.[2017内蒙古兴安盟中考]计算:45°39'+65°41'= .?
6.[2019山东日照中考]如图,已知AB=8 cm,BD=3 cm,C为AB的中点,则线段CD的长为 cm.?
6.1
答案
7.150°42' 【解析】 由题意得,∠AOC=∠AOB-∠BOC=180°-29°18'=150°42'.
7.[2018云南昆明中考]如图,过直线AB上一点O作射线OC,∠BOC=29°18',则∠AOC的度数为 .?
答案
8.4-12?????2 【解析】 因为OA=4,所以第一次跳动到OA的中点A1处时,OA1=12×4=2;第二次从A1点跳动到A2处,OA2= (12)2×4;第三次从A2点跳动到A3处,OA3=(12)3×4??跳动n次后,OAn=(12)n×4=12?????2.故线段AnA的长度为4-12?????2(n≥3,n是整数).
?
8.[2019山东聊城中考]数轴上O,A两点的距离为4,一动点P从点A出发,按以下规律跳动:第1次跳动到AO的中点A1处,第2次从A1点跳动到A1O的中点A2处,第3次从A2点跳动到A2O的中点A3处,按照这样的规律继续跳动到点A4,A5,A6,?,An处,那么线段AnA的长度为 (n≥3,n是整数).?
答案
9.【解析】 (1)以B为原点,点A,C分别对应-2,1.
p=-2+0+1=-1.
以C为原点,p=(-1-2)+(-1)+0=-4.
(2)p=(-28-1-2)+(-28-1)+(-28)=-88.
9.[2017河北中考]在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示.设点A,B,C所对应数的和是p.
(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?
(2)若原点O在图中数轴上点C的右边,且CO=28,求p.
数学·七年级上册·北师
专题1 直线、线段、角的计数问题
专项素养拓训
1.平面内不重合的两个点确定一条直线,不同的三个点最多确定3条直线,则平面内不同的10个点最多可以确定 条直线.?
答案
1.45 【解析】 不同的10个点中,每个点最多可以和其他9个点构成9条直线,共有10个点,且每个点被算了两次,所以直线总数最多为10×92=45(条).
?
2.如图,在∠AOB内部以O为端点引一条射线,则图中共有 个角,若在∠AOB内部以O为端点引n条射线,则图中共有 个角.?
答案
2.3 (????+1)(????+2)2 【解析】 当引一条射线时,则图中共有3个角.当引n条射线时,加上射线OA,OB,共有(n+2)条射线,每条射线与其他(n+1)条射线构成(n+1)个角,且每个角被算了两次,故共有(????+1)(????+2)2 个角.
?
3.为丰富师生的课余生活,某地区的五所学校联合举行教师篮球赛和学生联谊活动,每校派一支教工篮球队,各派10名学生参加联谊活动.
(1)若篮球赛采取单循环比赛(每两支队伍之间只进行一场比赛),则篮球赛共进行了 场;?
(2)学生联谊活动中,全体同学制作了手工小礼品,活动结束,全体同学互赠手工小礼品(每两个同学之间都互赠,数量刚好够赠送),则本次活动共制作了 件小礼品.?
答案
3.(1)10;(2)2 450 【解析】 (1)由题意,得5×42=10(场);(2)由题意得,50×(50-1)=2 450(件).
?
专题2 线段的有关计算
专项素养拓训
4.如图,B,C两点把线段AD分成2∶5∶3的三部分,点M为AD的中点,BM=6,求CM和AD的长.
答案
4.【解析】 由题意,设AB=2k,BC=5k,CD=3k,
所以AD=AB+BC+CD=10k.
因为点M为AD的中点,所以AM=12AD=5k,
所以BM=AM-AB=3k.
因为BM=6,所以3k=6,所以k=2,
所以AD=10k=20,BC=5k=10,
所以CM=BC-BM=4.
?
5.[2020湖北武汉青山区期末]已知线段AB上有M,N两点,AB=18,AM∶BM=1∶2,MN=5,点C为BN的中点,求BC的长.
答案
5.【解析】 因为AB=18,AM∶BM=1∶2,
所以AM=6,BM=12.
分两种情况:
如图1,因为MN=5,所以BN=12-5=7,
因为点C为BN的中点,所以BC=12BN=3.5.
如图2,因为MN=5,所以BN=12+5=17,
因为点C为BN的中点,所以BC=12BN=8.5.
综上所述,BC=3.5或8.5.
?
专题3 与角平分线有关的问题
专项素养拓训
6.如图,直线AB与CD相交于点O,∠AOM=90°.
(1)如图1,若OC平分∠AOM,求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数.
答案
6.【解析】 (1)因为∠AOM=90°,OC平分∠AOM,
所以∠AOC=45°,所以∠AOD=180°-∠AOC=135°.
(2)因为OM平分∠CON,所以∠MOC=∠MON.
因为∠AOM=∠BOM=90°,所以∠AOC=∠BON.
因为∠BOC=4∠NOB,∠AOC+∠BOC=180°,
所以∠BON+4∠BON=180°,所以∠BON=36°,
所以∠MON=90°-∠BON=54°.
7.已知OE平分∠AOC,OF平分∠BOC.
(1)如图1,若OA在∠BOC的外部,则∠AOB与∠EOF的数量关系是∠AOB= ∠EOF;?
(2)如图2,若OA在∠BOC的内部,则(1)中的数量关系是否仍成立?若成立,请说明理由.
答案
7.【解析】 (1)2
(2)成立,理由如下:
因为OE平分∠AOC,OF平分∠BOC,
所以∠COE=12∠AOC,∠COF=12∠BOC,
所以∠EOF=∠COF-∠COE=12∠BOC-12∠AOC=12(∠BOC-∠AOC)=12∠AOB,
所以∠AOB=2∠EOF.
?
8.已知,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,求∠MON与α的数量关系.
(3)如图3,当∠AOB=α,∠BOC=β时,∠MON与α,β存在数量关系吗?如果有,请写出结论并说明理由.
答案
8.【解析】 (1)因为∠AOB=90°,∠BOC=60°,
所以∠AOC=∠AOB+∠BOC=150°.
因为OM是∠AOC的平分线,ON是∠BOC的平分线,
所以∠COM=12∠AOC=75°,∠CON=12∠BOC=30°,
所以∠MON=∠COM-∠CON=45°.
(2)易知∠AOC=∠AOB+∠BOC=α+60°.
因为OM是∠AOC的平分线,ON是∠BOC的平分线,
所以∠COM=12∠AOC=12α+30°,∠CON=12∠BOC=30°,
所以∠MON=∠COM-∠CON=12α.
?
答案
(3)∠MON只和α有关,和β无关,∠MON=12α.理由如下:
易知∠AOC=∠AOB+∠BOC=α+β.
因为OM是∠AOC的平分线,ON是∠BOC的平分线,
所以∠COM=12∠AOC=12α+12β,∠CON=12∠BOC=12β,
所以∠MON=∠COM-∠CON=12α,
所以∠MON只和α有关,和β无关,∠MON=12α.
?
综合素养拓训
本章引入基本平面图形,用点线刻画物体模型,是几何知识体系中最基本的内容之一,也是后续学习三角形、四边形等知识的基础.将线段、角等作为载体,通过与线段中点、角平分线等相关的计算问题,渗透转化思想、分类讨论思想、方程思想,增强运用图形思考问题的意识,提升数形结合能力.
1.[2019山东济南市中区期末]【新知理解】
如图1,点C在线段AB上,图中有三条线段,分别为线段AB,AC和BC,若其中一条线段的长度是另外一条线段的2倍,则称点C是线段AB的“巧点”.
(1)线段的中点 这条线段的“巧点”(填“是”或“不是”).?
(2)若线段AB=12 cm,点C是线段AB的“巧点”,则AC= cm.?
【解决问题】
(3)如图2,已知AB=12 cm,动点P从点A出发,以2 cm/s的速度沿AB向点B运动,点Q从点B出发,以1 cm/s的速度沿BA向点A运动,点P,Q同时出发,当其中一点到达终点时,运动停止.设运动的时间为t s,当t为何值时,点P为线段AQ的“巧点”,并说明理由.
答案
1.【解析】 (1)是
(2)4,6或8
①当AB=2AC时,AC=6 cm;②当AC=2BC时,因为AC+BC=AB=12 cm,所以AC=8 cm;③当BC=2AC时,BC=8 cm,AC=4 cm.综上,AC=4 cm,6 cm或8 cm.
(3)由题意知,AP=2t cm,BQ=t cm,所以AQ=(12-t)cm,
因为点P为AQ的“巧点”,所以点P在线段AQ上,
①当AQ=2AP时,12-t=4t,所以t=125;
②当AP=2PQ时,AP=23AQ,即2t=23(12-t),所以t=3;
③当PQ=2AP时,AP=13AQ,即2t=13(12-t),所以t=127.
所以当t为125,3或127时,点P为线段AQ的“巧点”.
?
本题是一道“新定义”的题,做题的关键是要搞懂什么是“巧点”.由于一条直线上的三个点共构成了三条线段,而“巧点”只是两条线段的数量关系,所以这里需要进行分类讨论:哪两条线段满足“巧点”关系?哪条线段是另一条线段的2倍?
2.[探究角之间的数量关系]如图,O为直线AB上一点,∠BOC=α.
(1)如图1,若α=40°,OD平分∠AOC,∠DOE=90°,求∠AOE的度数;
(2)如图2,若∠AOD=13∠AOC,∠DOE=60°,请用α表示∠AOE的度数;
(3)如图3,若∠AOD=1????∠AOC,∠DOE=180°????(n≥2,且n为正整数),请用α和n表示∠AOE的度数.(直接写出结果)
?
答案
2.【解析】 (1)因为∠BOC=40°,所以∠AOC=180°-∠BOC=140°,
又因为OD平分∠AOC,
所以∠AOD=∠DOC=12∠AOC=70°.
因为∠DOE=90°,所以∠AOE=90°-70°=20°.
(2)设∠AOD=x,则∠DOC=2x,∠BOC=180°-3x=α,
所以x=180°?????3,
所以∠AOE=60°-x=60°-180°?????3=13α.
(3)∠AOE=????????.
设∠AOD=y,则∠DOC=(n-1)y,∠BOC=180°-ny=α,
所以y=180°?????????,所以∠AOE=180°?????180°?????????=????????.
?
答案
1.C 【解析】 因为一副三角尺有30°,45°,60°,90°,所以能用三角尺画出30°,60°,75° .故选C.
一、选择题
1.用一副三角尺可以画出许多不同的角度,以下角度不能用三角尺画出的是 ( )
A.75° B.60° C.40° D.30°
答案
2.B 【解析】 因为∠BAF=60°,所以∠FAD=90°-60°=30°.因为∠DAE=∠FAE,所以∠DAE=12×30°=15°.故选B.
?
2.如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,那么∠DAE等于 ( )
A.10°
B.15°
C.20°
D.30°
答案
3.A 【解析】 如图,因为A岛在C岛的北偏西15°方向,所以∠1=15°.因为∠ACB=90°,所以∠2=180°-∠1-∠ACB=180°-15°-90°=75°,故B岛在C岛的南偏西75°方向.故选A.
3.如图,一张地图上标记了A,B,C三个小岛,已知A岛在C岛的北偏西15°方向,若∠ACB=90°,则B岛在C岛的 ( )
A.南偏西75°方向
B.南偏西65°方向
C.南偏西60°方向
D.南偏西30°方向
答案
4.C 【解析】 因为BC=12AB,所以BC=13AC.因为D为线段AC的中点,所以CD=12AC,所以BD=16AC.因为BD=2,所以AC=2×6=12,所以AB=AD+BD=12AC+BD=12×12+2=8.故选C.
?
4.[2020浙江杭州期末]如图,将线段AB延长至点C,使BC=12AB,D为线段AC的中点,若BD=2,则线段AB的长为 ( )
A.4
B.6
C.8
D.12
?
答案
5.96 【解析】 因为∠BOC=120°,所以甲、丙两个扇形的圆心角的度数和为240°,因为甲、丙两个扇形的面积之比为3∶2,所以∠AOC=240°×23+2=96°.
?
二、填空题
5.[2020山东青岛崂山区期末]如图,将一个圆分割成三个扇形,若甲、丙两个扇形的面积之比为3∶2,∠BOC=120°,则∠AOC= °. ?
答案
6.36 【解析】 由∠AOB+∠BOC=∠BOC+∠COD知∠AOB=∠COD,设∠AOB=2α,则∠AOD=7α,故∠AOB+∠BOC=∠AOD-∠COD=7α-2α=5α=90°,解得α=18°,故∠COD=36°.
6.如图,∠AOC与∠BOD都是直角,且∠AOB∶∠AOD=2∶7,则∠COD= °.?
答案
7.22.5 【解析】 因为时钟指示14时15分时,分针指到3,时针指到2与3之间的某个位置,时针从2到这个位置经过了15分钟,时针每分钟转0.5°,所以转过7.5°,所以时针和分针所成的锐角是30°-7.5°=22.5°.
7.[2020四川遂宁安居区期末]已知某学校下午上课的时间为14时15分,则此时刻时钟上的时针与分针的夹角为 °.?
答案
8.180或144 【解析】 因为AP∶BP=4∶5,所以设AP=4x(x>0)cm,BP=5x cm,则AB=9x cm.因为剪断后的各段绳子中最长的一段为80 cm,所以8x=80或10x=80,解得x=10或x=8,则18x=180或144,所以绳子的原长为180 cm或144 cm.
8.[2020湖北武汉江汉区期末]如图,把一根绳子对折后得到的图形为线段AB,从点P处把绳子剪断,若AP∶BP=4∶5,剪断后的各段绳子中最长的一段为80 cm,则绳子的原长为 cm.?
答案
9.【解析】 (1)如图所示.
(2)因为DE=AC,DE=3,所以AC=3.
因为点C是线段AB的中点,BD=AB,所以BD=AB=2AC=6,
所以BE=BD+DE=6+3=9.
(3)CD=BE.理由如下:
因为C是线段AB的中点,所以CB=AC,
又因为DE=AC,所以CB=DE,
所以CB+BD=DE+BD,即CD=BE.
三、解答题
9.[2020河南焦作期末]如图,点C是线段AB的中点,延长线段AB至点D,使BD=AB,延长AD至点E,使DE=AC.
(1)依照题意补全图形;
(2)若DE=3,求线段AB,BE的长;
(3)请写出图中与BE相等的线段,并说明理由.
10.[2020湖南长沙期末]已知点O是直线AB上一点,∠COE=60°,OF是∠AOE的平分线.
(1)如图1,点C,E在直线AB的同侧,且OF在∠COE的内部,∠BOE-2∠COF=α,求α的大小;
(2)如图2,当点C与点E,F在直线AB的两侧,(1)中的结论是否仍然成立?请说明理由;
(3)将图2中的射线OF绕点O顺时针旋转m°(0
答案
10.【解析】 (1)设∠AOC=β,则∠BOE=180°-(60°+β)=120°-β.
因为OF是∠AOE的平分线,所以∠COF=12∠AOE-∠AOC=12(60°+β)-β=30°-12β,
所以∠BOE-2∠COF=120°-β-2(30°-12β)=60°,即α=60°.
(2)(1)中的结论仍然成立.理由如下:
因为OF是∠AOE的平分线,所以∠COF=∠COE-∠EOF=60°-12∠AOE,而∠BOE=180°-∠AOE,
故∠BOE-2∠COF=180°-∠AOE-2(60°-12∠AOE)=60°,即α=60°.
(3)(75+7????4)°
通过比较,可判断出射线OD只可能在∠BOE的内部,如图所示.
∠DOE=180°-∠BOD-∠AOE=180°-(45-3????4)°-(60°-n°)=(75+7????4)°.
?
第四章 基本平面图形中考真题
数学·七年级上册·北师
答案
1.A
1.[2019吉林中考]曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光.如图,A,B两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是 ( )
A.两点之间,线段最短
B.平行于同一条直线的两条直线平行
C.垂线段最短
D.两点确定一条直线
2.[2017河北中考]如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能是 ( )
A.北偏东55°
B.北偏西55°
C.北偏东35°
D.北偏西35°
答案
2.D 【解析】 如图1,当乙的航向是北偏东55°时,甲、乙两船不会相撞;如图2,当乙的航向是北偏西55°时,由于甲、乙两船等速航行,故甲、乙两船不会相撞;如图3,当乙的航向是北偏东35°时,甲、乙两船不会相撞;如图4,当乙的航向是北偏西35°时,由于甲、乙两船等速航行,故甲、乙两船会相撞.故选D.
答案
3.B 【解析】 因为钟面分成12个大格,每格的度数为30°,所以钟表上10点整时,时针与分针所成的角是60°.故选B.
3.[2019广西梧州中考]如图,钟表上10点整时,时针与分针所成的角是 ( )
A.30°
B.60°
C.90°
D.120°
答案
4.C 【解析】 因为数轴上点A,B,M表示的数分别是a,2a,9,点M为线段AB的中点,所以9-a=2a-9,所以a=6.故选C.
4.[2019贵州贵阳中考]数轴上点A,B,M表示的数分别是a,2a,9,点M为线段AB的中点,则a的值是 ( )
A.3 B.4.5 C.6 D.18
答案
5.111°20' 【解析】 45°39'+65°41'=45°+65°+39'+41'=110°+80'=111°20'.
5.[2017内蒙古兴安盟中考]计算:45°39'+65°41'= .?
6.[2019山东日照中考]如图,已知AB=8 cm,BD=3 cm,C为AB的中点,则线段CD的长为 cm.?
6.1
答案
7.150°42' 【解析】 由题意得,∠AOC=∠AOB-∠BOC=180°-29°18'=150°42'.
7.[2018云南昆明中考]如图,过直线AB上一点O作射线OC,∠BOC=29°18',则∠AOC的度数为 .?
答案
8.4-12?????2 【解析】 因为OA=4,所以第一次跳动到OA的中点A1处时,OA1=12×4=2;第二次从A1点跳动到A2处,OA2= (12)2×4;第三次从A2点跳动到A3处,OA3=(12)3×4??跳动n次后,OAn=(12)n×4=12?????2.故线段AnA的长度为4-12?????2(n≥3,n是整数).
?
8.[2019山东聊城中考]数轴上O,A两点的距离为4,一动点P从点A出发,按以下规律跳动:第1次跳动到AO的中点A1处,第2次从A1点跳动到A1O的中点A2处,第3次从A2点跳动到A2O的中点A3处,按照这样的规律继续跳动到点A4,A5,A6,?,An处,那么线段AnA的长度为 (n≥3,n是整数).?
答案
9.【解析】 (1)以B为原点,点A,C分别对应-2,1.
p=-2+0+1=-1.
以C为原点,p=(-1-2)+(-1)+0=-4.
(2)p=(-28-1-2)+(-28-1)+(-28)=-88.
9.[2017河北中考]在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示.设点A,B,C所对应数的和是p.
(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?
(2)若原点O在图中数轴上点C的右边,且CO=28,求p.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
