北师大版七年级上册数学:第三章 整式及其加减同步习题课件(141张PPT)
文档属性
| 名称 | 北师大版七年级上册数学:第三章 整式及其加减同步习题课件(141张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 10:36:09 | ||
图片预览











文档简介
第三章 整式及其加减
数学·七年级上册·北师
1 字母表示数
1.“比a的3倍小1的数”可以表示为 ( )
A.3(a-1) B.3a-1
C.3a+1 D.3(a+1)
答案
1.B 【解析】 A项为“比a小1的数的3倍”,C项为“比a的3倍大1的数”,D项为“比a大1的数的3倍”.故选B.
知识点1 用字母表示数或数量关系
2.[2019山东泰安期中]设某数为m,则3????2?52表示 ( )
A.某数的3倍的平方减去5除以2
B.某数平方的3倍与5的差的一半
C.某数的平方的3倍减5的一半
D.某数的平方与5的差的3倍除以2
?
答案
2.B
知识点1 用字母表示数或数量关系
3.[2019广西桂林期末]用字母x,y表示两个数,则x,y两数的平方的和减去两数积的2倍为 .?
4.易错题 一个三位数,百位数字是a,十位数字是b,个位数字是c,则这个三位数可表示为 .?
答案
3.x2+y2-2xy 【解析】 x,y两数的平方的和为x2+y2,x,y两数的积的2倍为2xy,所以x,y两数的平方的和减去两数积的2倍为x2+y2-2xy.
知识点1 用字母表示数或数量关系
4.100a+10b+c
本题易将这个三位数错误地表示为abc.实际上abc表示a,b,c三个数相乘.
5.如果长方形的长为m,宽为n,那么该长方形的周长是 ,面积是 .?
6.若一个圆的半径为r-8,则该圆的面积S= ( )
A.πr2 B.2π(r-8)
C.π2(r-8) D.π(r-8)2
答案
5.2(m+n) mn 【解析】 长方形的周长公式:周长=2×(长+宽).长方形的面积公式:面积=长×宽.所以题中长方形的周长为2(m+n),面积为mn.
知识点2 用字母表示图形的周长、面积
6.D
7.[2020江西赣州期中]如图,阴影部分的面积可表示为( )
A.ab+bc
B.c(b-d)+d(a-c)
C.ad+c(b-d)
D.ab-cd
答案
7.C 【解析】 如图,阴影部分的面积等于图中两个长方形面积的和,即ad+c(b-d).故选C.
知识点2 用字母表示图形的周长、面积
用字母表示图形的面积问题的解题策略
解决有关图形的面积问题时,一要注意观察图形的特征,二要注意相关图形面积的表示.有时直接计算图形的面积,如长方形、三角形的面积;有时间接计算图形的面积,如通过图形的割补等,化不规则图形为规则图形.
8.[2020湖北孝感期末]某种商品的标价为x元/件,进价为400元/件,在商场开展的促销活动中,该商品按8折销售,那么每件可获利 ( )
A.(8x-400)元 B.(400×8-x)元
C.(0.8x-400)元 D.(400×0.8-x)元
答案
8.C
知识点3 用字母表示数的实际应用
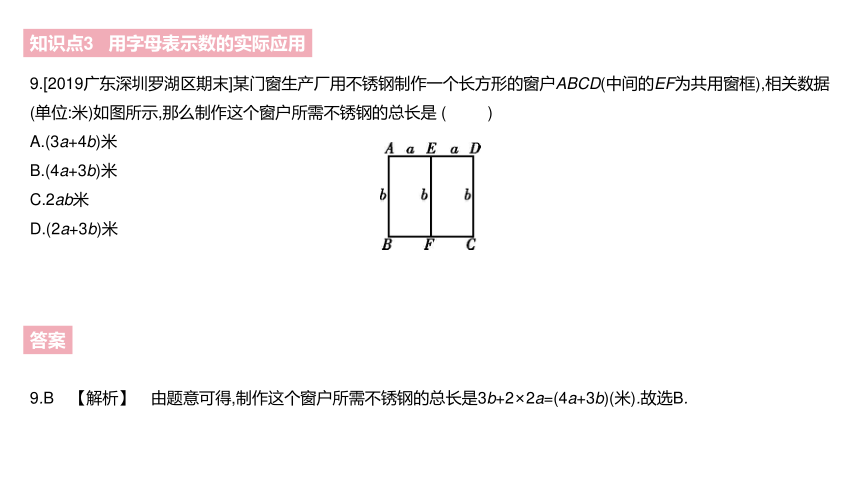
9.[2019广东深圳罗湖区期末]某门窗生产厂用不锈钢制作一个长方形的窗户ABCD(中间的EF为共用窗框),相关数据(单位:米)如图所示,那么制作这个窗户所需不锈钢的总长是 ( )
A.(3a+4b)米
B.(4a+3b)米
C.2ab米
D.(2a+3b)米
答案
9.B 【解析】 由题意可得,制作这个窗户所需不锈钢的总长是3b+2×2a=(4a+3b)(米).故选B.
知识点3 用字母表示数的实际应用
10.某班共有54名学生,在一次考试中,该班28名男生的总分是m分,26名女生的平均分是n分,则这个班学生的平均分是 ( )
A.28????+26????54 分 B.????+26????54 分
C.????+????54 分 D.28(????+????)54 分
?
答案
10.B 【解析】 因为28名男生的总分是m分,26名女生的平均分是n分,所以该班学生的总分是(m+26n)分,所以这个班学生的平均分是????+26????54 分.故选B.
?
知识点3 用字母表示数的实际应用
11.[2020北京昌平区期末]在2019年世界杯上,中国女排最终以11战全胜积32分的成绩成功卫冕.比赛的积分规则为:比赛中以3-0或者3-1取胜的球队积3分,负队积0分;比赛中以3-2取胜的球队积2分,负队积1分.某队以3-1胜了a场,以3-2胜了b场,以2-3负了c场,则该队的积分为 .?
答案
11.3a+2b+c
知识点3 用字母表示数的实际应用
12.填空:
(1)m支某种铅笔的售价为n元,则5支该种铅笔的售价为 元;?
(2)轮船在静水中的速度为x千米/时,水流速度为a千米/时,则该轮船逆流航行3小时的路程是 千米.?
答案
12.(1)5????????;(2)3(x-a) 【解析】 (1)由题意,得每支铅笔的售价为???????? 元,则5支该种铅笔的售价为5???????? 元;(2)由题意,得轮船逆流航行的速度为(x-a)千米/时,则逆流航行3小时的路程是3(x-a)千米.
?
知识点3 用字母表示数的实际应用
13.[2020黑龙江哈尔滨道里区期末]观察一列数13,36,512,724,?,则第六个数是 .?
?
答案
13.1196 【解析】 经过观察知第n个数是2?????13×2?????1,所以第六个数是113×25=1196.
?
知识点4 用字母表示数字、图形的变化规律
14.如图所示的图形都是由同样大小的小圆圈按一定规律组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈??按此规律,则第 个图形中小圆圈的个数为 .?
答案
14.3+3n 【解析】 观察题中图形,得第①个图形中小圆圈的个数是3+3×1=6,第②个图形中小圆圈的个数是3+3× 2=9,第③个图形中小圆圈的个数是3+3×3=12??所以第 个图形中小圆圈的个数是3+3n.
知识点4 用字母表示数字、图形的变化规律
2 代数式
课时1 代数式
课时1
1.下列式子中,不属于代数式的是 ( )
A.a+3 B.2mn C.????+23 D.x>y
?
答案
1.D
知识点1 代数式的概念
2.下列各式中, 是代数式.(填序号)?
①2mn-1;②S=12(a+b);③b+1>a;④a;⑤????+????????;⑥7.
?
答案
2.①④⑤⑥ 【解析】 代数式只能用运算符号连接,②中有等号,③中有大于号,故②③不是代数式.
知识点1 代数式的概念
3.下列是数与字母相乘,书写规范的是 ( )
A.1×a B.-1×a
C.a×(-1) D.-a
答案
3.D
知识点2 代数式的书写规则
4.[2019四川成都七中初中学校期中]下列式子中,符合代数式的书写要求的是 ( )
A.112c B.a×b×c÷2
C.3x·y÷2 D.52xy
?
答案
4.D 【解析】 A项,112c应写成32c;B项,a×b×c÷2应写成12abc;C项,3x·y÷2应写成32xy;D项,52xy符合代数式的书写要求.故选D.
?
知识点2 代数式的书写规则
5.a是一个三位数,b是一个一位数,把a放在b的右边组成一个四位数,这个四位数是 ( )
A.ba B.100b+a
C.1 000b+a D.10b+a
答案
5.C 【解析】 依题意,知千位上的数字是b,所以这个四位数是1 000b+a.故选C.
知识点3 列代数式
6.用代数式表示:
(1)汽车每小时行驶70千米,t小时行驶 千米;?
(2)哥哥今年m岁,哥哥比妹妹大n岁,妹妹今年 岁;?
(3)现有b棵树排成a行,则平均每行有 棵树;?
(4)x的5倍与y的13的差的立方是 .?
?
答案
6.(1)70t;(2)(m-n);(3)????????;(4)(5x-13y)3
?
知识点3 列代数式
7.某班学生参加艺术节演出,需购买A,B两种衬衫共80件,其中A种衬衫买了c件,A,B两种衬衫的价格分别为每件a元和b元,则一共花了 元.?
答案
7.[ac+b(80-c)] 【解析】 因为A种衬衫买了c件,所以B种衬衫买了(80-c)件,所以一共花了[ac+b(80-c)]元.
知识点3 列代数式
8.[2020河南新乡期末]某商场经销一种品牌的电视机,每台的进价为x元,商场将进价提高20%后作为零售价进行销售,过了一段时间,商场又以9折优惠价进行促销活动.这时这种品牌的电视机每台的售价是 元.(用含x的代数式表示)?
答案
8.(1+20%)×0.9x
知识点3 列代数式
9.某商店举办促销活动,将原价x元/件的商品以0.6(x-10)元/件出售,则下列说法中,能正确表达该商店促销方法的是 ( )
A.原价减去10元后再打6折
B.原价打6折后再减去10元
C.原价减去10元后再打4折
D.原价打4折后再减去10元
答案
9.A
知识点4 代数式的实际意义
10.[2019江苏扬州期中]体育委员带了100元钱去买体育用品,已知一个足球a元,一个篮球b元,则代数式100-3a-2b表示的意义为 .?
答案
10.体育委员买3个足球和2个篮球后剩余的钱数 【解析】 因为买一个足球a元,一个篮球b元,所以3a表示体育委员买3个足球所用钱数,2b表示买2个篮球所用钱数,所以代数式100-3a-2b表示体育委员买3个足球和2个篮球后剩余的钱数.
知识点4 代数式的实际意义
11.某工厂第一车间有x人,第二车间比第一车间人数的12少10人,现在根据工作需要,从第二车间调出10人到第一车间,请列代数式表示(不需要化简):
(1)两个车间共有多少人?
(2)调动后第一车间的人数比第二车间的人数多几人?
?
答案
11.【解析】 (1)由题意知,第二车间有(12x-10)人,
所以两个车间共有(x+12x-10)人.
(2)由题意知,调动后第一车间有(x+10)人,第二车间有(12x-20)人,
所以调动后第一车间的人数比第二车间的人数多[(x+10)-(12x-20)]人.
?
知识点5 利用代数式解决实际问题
12.某公园的成人票每张50元,儿童票每张30元.甲旅游团有a名成人和b名儿童,乙旅游团的成人数是甲旅游团的2倍,儿童数是甲旅游团的12.
(1)用含a,b的代数式表示乙旅游团的总人数;
(2)用含a,b的代数式表示甲、乙两个旅游团的门票总费用.(不需要化简)
?
答案
12.【解析】 (1)依题意得,乙旅游团的总人数为2a+12b.
(2)甲旅游团的门票总费用为(50a+30b)元,
乙旅游团的门票总费用为(100a+15b)元,
所以甲、乙两个旅游团的门票总费用为(50a+30b+100a+15b)元.
?
知识点5 利用代数式解决实际问题
1.[2020福建厦门期中]能用代数式a+0.3a表示含义的是 ( )
A.妈妈在超市购买物品共需a元,结账时买塑料袋又花了0.3元,妈妈共花了多少元
B.一个长方形的长是a米,宽是0.3a米,这个长方形的周长是多少米
C.小明骑自行车的速度是a千米/时,行驶0.3a小时后,小明所行驶的路程是多少千米
D.一套商品房原价为a万元,现提价30%,那么现在这套商品房的售价是多少万元
答案
1.D 【解析】 A项,根据题意得,妈妈共花了(a+0.3)元,故A项不合题意;B项,根据题意得,这个长方形的周长是2(a+ 0.3a)米,故B项不合题意;C项,根据题意得,小明所行驶的路程是a×0.3a千米,故C项不合题意.故选D.
2.[2018安徽中考]据省统计局发布,2017年我省有效发明专利数比2016年增长22.1%.假定2018年的年增长率保持不变,2016年和2018年我省有效发明专利分别为a万件和b万件,则 ( )
A.b=(1+22.1%×2)a
B.b=(1+22.1%)2a
C.b=(1+22.1%)×2a
D.b=22.1%×2a
答案
2.B
3.为了做一个试管架,在长为a cm(a>6)的木板上钻3个相同的小孔(如图),每个小孔的直径为2 cm,则用含a的代数式表示x为 ( )
A.?????34
B.????+34
C.?????64
D.????+64
?
答案
3.C 【解析】 由题意得,x=?????2×34,即x=?????64.故选C.
?
4.王阿姨以每个m元的价格买进苹果100个,现以每个比进价多20%的价格卖出70个后,再以每个比进价低n元的价格将剩下的30个卖出,则全部苹果共卖得的金额是 ( )
A.[70m+30(m-n)]元
B.[70×(1+20%)m+30(m-n)]元
C.[70×(1+20%)m+30n]元
D.[100×(1+20%)m-30(m-n)]元
答案
4.B 【解析】 由题意得,先卖出的70个苹果的单价是(1+20%)m元,剩下的30个苹果卖出的单价是(m-n)元.全部苹果共卖得的金额=先卖出的70个苹果的总价+剩下的30个苹果卖出的总价,即[70×(1+20%)m+30(m-n)]元.故选B.
5.[2020浙江宁波期中]某市出租车的起步价为10元(行驶里程不超过3千米),另收取燃油附加费1元,超过3千米以后,每增加1千米,加价1.8元.若某人乘出租车行驶里程为P(P>3,且P为整数)千米,则所需费用是 元.?
6.[2020广东梅州期末]某文具店销售一种羽毛球拍和羽毛球,球拍每副标价120元,羽毛球每个标价4元,近期该店开展促销活动,活动期间向客户提供的优惠方案为:买一副球拍送5个羽毛球.某人到该店买球拍20副,a(a>100,且a为整数)个羽毛球,则需付款 元.?
答案
5.[11+1.8(p-3)]
6.[2 400+4(a-100)] 【解析】 120×20+4(a-20×5)=[2 400+4(a-100)](元).
7.整理一批图书,如果由一个人单独整理要用60 h.现先由一部分人整理1 h,随后增加15人和他们一起又整理了2 h,假设每个人的工作效率相同,设先安排的整理人员有x人.
(1)用代数式表示x人1 h的工作量;
(2)用代数式表示增加15人后一起整理2 h的工作量.
答案
7.【解析】 (1)把总工作量看作1,
由题意得,每个人1 h的工作量是160,则x人1 h的工作量是????60.
(2)增加15人后,(x+15)人一起整理2 h的工作量为2(????+15)60,即????+1530.
?
8.[2019湖北十堰期末]某超市在春节期间对顾客实行优惠,规定如下:
(1)王老师一次性购物600元,他实际付款 元;?
(2)某顾客在该超市一次性购物x元,当x小于500但不小于200时,他实际付款 元,当x大于或等于500时,他实际付款 元;(用含x的代数式表示)?
(3)如果王老师两次购物合计820元,第一次购物a(200一次性购物
优惠办法
低于200元
不予优惠
低于500元但
不低于200元
9折优惠
不低于500元
其中500元部分给予9折优惠,
超过500元部分给予8折优惠
答案
8.【解析】 (1)530
根据题意,得他实际付款500×0.9+(600-500)×0.8=530(元).
(2)0.9x [450+0.8(x-500)]
当x小于500但不小于200时,实际付款=购物款×0.9=0.9x(元);当x大于或等于500时,实际付款=500×0.9+购物款超过500元的部分×0.8=500×0.9+(x-500)×0.8=[450+0.8(x-500)](元).
(3)由题意知,第二次购物大于500元,
所以两次购物王老师实际付款=0.9a+500×0.9+0.8(820-a-500)=[0.9a+450+0.8(320-a)](元).
所以两次购物王老师实际付款[0.9a+450+0.8(320-a)]元.
课时2 代数式的值
课时2
1.[2019海南中考]当m=-1时,代数式2m+3的值是 ( )
A.-1 B.0 C.1 D.2
答案
1.C 【解析】 将m=-1代入,得2m+3=2×(-1)+3=1.故选C.
知识点1 求代数式的值
2.[2020四川眉山期末]当x=1时,代数式px3+qx+1的值为2 020,则当x=-1时,代数式px3+qx+1的值为 ( )
A.-2 017 B.-2 019 C.-2 018 D.2 019
答案
2.C 【解析】 当x=1时,代数式px3+qx+1的值为2 020,所以p+q=2019.当x=-1时,px3+qx+1=-p-q+1=-(p+q)+1=-2 019+ 1=-2 018.故选C.
知识点1 求代数式的值
3.[2020江西赣州期末]如图是一个运算程序的示意图,若开始输入x的值为81,则第2 020次输出的结果为 ( )
A.3
B.27
C.9
D.1
答案
3.D 【解析】 第1次,13×81=27;第2次,13×27=9;第3次,13×9=3;第4次,13×3=1;第5次,1+2=3;第6次,13×3=1??依此可知,从第4次开始,运算输出的结果依次是1,3,1,3??因为(2 020-3)÷2=1 008??1,所以第2 020次输出的结果为1.故选D.
?
知识点1 求代数式的值
解决周期性规律问题的步骤
第一步:分析并找准循环周期及一个循环周期内图形变换或数据变化的特点.第二步:用所求数据除以循环周期数,观察商和余数.第三步:结合问题及余数确定答案.
4.若a,b互为倒数,x,y互为相反数,则代数式4(x+y)+5ab+3 的值为 .?
5.如果|5-a|+(b+3)2=0,那么代数式1????(1-2b)的值为 .?
6.[2020湖北孝感期末]已知代数式4x2-2x+3=5,那么代数式2x2-x+2 019= .?
?
答案
4.8 【解析】 因为a,b互为倒数,x,y互为相反数,所以ab=1,x+y=0.因此4(x+y)+5ab+3=0+5+3=8.
知识点1 求代数式的值
5.75 【解析】 由|5-a|+(b+3)2=0,可知5-a=0,b+3=0,所以a=5,b=-3,所以1????(1-2b)=15×[1-2×(-3)]=75.
?
6.2 020 【解析】 因为4x2-2x+3=5,所以2x2-x=1,所以2x2-x+2 019=1+2 019=2 020.
7.先填表,再回答问题:
(1)当x为何值时,代数式2x-1的值等于5?
(2)已知有两个x的值使代数式-3x和x2的值相等,请你找出这两个x的值.
(3)随着x值的逐渐增大,代数式2x-1,-3x和x2的值是如何变化的?(写出结论即可,无需说明理由)
知识点1 求代数式的值
x
-3
-2
-1
0
1
2
3
2x-1
?
?
?
?
?
?
?
-3x
?
?
?
?
?
?
?
x2
?
?
?
?
?
?
?
答案
7.【解析】 填表如下:
(1)根据表格得,当x=3时,代数式2x-1的值等于5.
(2)根据表格得,当x=0或x=-3时,代数式-3x和x2的值相等.
(3)随着x值的逐渐增大,代数式2x-1的值逐渐增大;代数式-3x的值逐渐减小;代数式x2的值先减小再增大.
知识点1 求代数式的值
x
-3
-2
-1
0
1
2
3
2x-1
-7
-5
-3
-1
1
3
5
-3x
9
6
3
0
-3
-6
-9
x2
9
4
1
0
1
4
9
8.一个塑料直角三角形模具,形状和尺寸如图所示.
(1)求阴影部分的面积;(用含a,b,r的代数式表示)
(2)当a=5 cm,b=4 cm,r=1 cm时,计算阴影部分的面积.
答案
8.【解析】 (1)根据直角三角形的面积公式,得直角三角形的面积是12ab,
因为圆的面积是πr2,
所以阴影部分的面积是12ab-πr2.
(2)当a=5 cm,b=4 cm,r=1 cm时,
12ab-πr2=12×5×4-π×12=(10-π)(cm2).
故阴影部分的面积为(10-π)cm2.
?
知识点2 利用求代数式的值解决实际问题
9.某家具厂生产一种餐桌和椅子,餐桌每张定价为500元,椅子每把定价为160元.厂方在开展促销活动期间,向客户提供两种优惠方案.
方案一:每买一张餐桌就赠送一把椅子.
方案二:餐桌和椅子都按定价的80%付款.
某餐厅计划添置100张餐桌和x把椅子.
(1)若x>100,请用含x的代数式分别把两种方案的费用表示出来.
(2)已知x=300,如果两种方案可以同时使用,请帮助餐厅设计一种最省钱的方案.
知识点2 利用求代数式的值解决实际问题
答案
9.【解析】 (1)当x>100时,
方案一:100×500+160×(x-100)=160x+34 000.
方案二:(100×500+160x)×80%=128x+40 000.
答:方案一、方案二的费用分别为(160x+34 000)元、(128x+40 000)元.
(2)当x=300时,
①按方案一购买:500×100+160×200=82 000(元).
②按方案二购买:(100×500+160×300)×80%=78 400(元).
③先按方案一购买100张餐桌,同时送100把椅子,再按方案二购买200把椅子,
即100×500+160×200×80%=75 600(元).
因为82 000>78 400>75 600,
所以先按方案一购买100张餐桌,同时送100把椅子,再按方案二购买200把椅子最省钱.
知识点2 利用求代数式的值解决实际问题
3 整式
1.易错题[2020上海市实验学校月考]给出下列代数式:①-12a,②????3,③????2+????2,④????2π,⑤x2y.其中单项式的个数为 ( )
A.2 B.3 C.4 D.5
?
答案
1.C 【解析】 ①②④⑤属于单项式,共有4个.③????2+????2实质上是????22+????2,不是单项式.故选C.
?
知识点1 单项式
判断一个代数式是不是单项式,关键是看该代数式是不是单独的一个数或一个字母或数与字母的乘积,含有加、减运算或分母中含有字母的式子均不是单项式.
2.易错题[2019甘肃平凉期末]单项式-ab2的系数是 ( )
A.-1 B.1 C.2 D.3
答案
2.A
知识点1 单项式
本题容易误认为-ab2的系数是1而错选B,需要注意,单项式的系数包括符号.
3.[2019上海浦东新区期末]下列各单项式的次数为5的是 ( )
A.4x2y2 B.17x4ya
C.2a3b2 D.6x3y5
?
答案
3.C 【解析】 A项,4x2y2的次数是4,故A项不合题意;B项,17x4ya的次数是6,故B项不合题意;C项,2a3b2的次数是5,故C项符合题意;D项,6x3y5的次数是8,故D项不合题意.故选C.
?
知识点1 单项式
4.下列说法中,正确的是 ( )
A.单项式一定是含字母的代数式
B.单项式a没有系数
C.-y的次数是0
D.单项式-π2x2y的系数是-π2,次数是3
答案
4.D 【解析】 单独一个数也是单项式,A项不正确;当单项式的系数为1时,可以省略不写,所以单项式a的系数为1,B项不正确;-y的次数是1,C项不正确.故选D.
知识点1 单项式
5.单项式0.5x4+my与6xy12的次数相同,求m的值.
答案
5.【解析】 因为单项式0.5x4+my的次数是4+m+1=m+5,6xy12的次数是1+12=13,所以m+5=13,所以m=8.
知识点1 单项式
6.[2019湖南长沙开福区期中]下列代数式中,多项式的个数是 ( )
(1)a;(2)2x2+2xy+y2;(3)a+1;(4)a2-1????;
(5)-14(x+y).
A.1 B.2 C.3 D.4
?
答案
6.C 【解析】 单独一个字母是单项式,故(1)不是多项式;(4)中分母中含有字母,不是几个单项式的和的形式,故(4)不是多项式;(2)(3)(5)都是多项式.故选C.
知识点2 多项式
7.[2020江苏苏州期末]多项式m3n4-5m3n5+3的项数和次数分别为 ( )
A.2,7 B.3,8 C.2,8 D.3,7
答案
7.B 【解析】 多项式m3n4-5m3n5+3的各项分别是m3n4,-5m3n5,3,故项数是3,次数是8.故选B.
知识点2 多项式
8.[2020安徽合肥庐阳区期末]二次三项式2x2-3x-1的二次项系数、一次项系数、常数项分别是 ( )
A.2,-3,-1 B.2,3,1
C.2,3,-1 D.2,-3,1
答案
8.A 【解析】 二次三项式2x2-3x-1的二次项系数、一次项系数、常数项分别是2,-3,-1.故选A.
知识点2 多项式
9.[2019江西抚州临川区期中]多项式3x|m|y2+(m+2)x2y-1是关于x,y的四次三项式,则m的值为 .?
答案
9.2 【解析】 因为关于x,y的多项式3x|m|y2+(m+2)x2y-1是四次三项式,所以|m|+2=4,m+2≠0,所以m=2.
知识点2 多项式
10.[2020上海静安区月考]下列代数式中,是整式的有 ( )
2x+y,13a2b,?????????π,1????(x2-2xy+1),0,πx+14y.
A.4个 B.5个 C.6个 D.7个
?
答案
10.B 【解析】 2x+y,13a2b,?????????π,0,πx+14y是整式,共有5个.故选B.
?
知识点3 整式
11.下列说法中,错误的是 ( )
A.m是单项式也是整式
B.12(m-n)是多项式也是整式
C.整式一定是单项式
D.整式不一定是多项式
?
答案
11.C 【解析】 单项式和多项式统称为整式.故选C.
知识点3 整式
12.小王购买了一套房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),用含x,y的式子表示地面总面积.
答案
12.【解析】 由题图,得地面共由四部分组成,其总面积是6x+3×2+4×3+2y=(6x+2y+18)(m2).
知识点3 整式
1.[2020福建漳州期末]下列说法中,正确的是 ( )
A.单项式π????2????4的系数是14,次数是4
B.单项式m的次数是1,没有系数
C.在12x3,?????????π,5????4????,0中,整式有2个
D.多项式2x2+xy2+3是三次三项式
?
答案
1.D 【解析】 A项,单项式π????2????4的系数是π4,次数是3,此项错误;B项,单项式m的次数是1,系数是1,此项错误;C项,在12x3,?????????π,5????4????,0中,整式有12x3,?????????π,0,共3个,此项错误.故选D.
?
2.[2019江苏盐城盐都区期中]如果一个多项式中各项的次数都相同,那么这个多项式叫做齐次多项式.如:x3+3xy2+4xyz+2y3是3次齐次多项式.若ax+3b2-6ab3c2是齐次多项式,则x的值为 ( )
A.-1 B.0 C.1 D.2
答案
2.C 【解析】 由题意,得x+3+2=6,解得x=1.故选C.
根据新定义,使多项式中每一项的次数相等,便可确定字母指数的值.
3.如果一个多项式的次数是5,那么这个多项式的任何一项的次数 ( )
A.都小于5 B.都等于5
C.都不小于5 D.都不大于5
答案
3.D 【解析】 多项式中次数最高的项的次数叫做这个多项式的次数.所以如果一个多项式的次数是5,那么这个多项式的任何一项的次数都不大于5.故选D.
4.观察下列多项式:2a+b;3a+b2;4a+b3;5a+b4;?.则第n个多项式为 .?
答案
4.(n+1)a+bn 【解析】 观察发现,每个多项式都是二项式.字母a的系数从2开始依次增加1,字母b的指数从1开始依次增加1,所以第n个多项式为(n+1)a+bn.
5.[2020辽宁葫芦岛连山区期末]如图,在一块长为a、宽为2b的长方形铁皮中,剪掉两个以2b为直径的半圆.
(1)求剩下铁皮的面积.(用含a,b的式子表示)
(2)(1)中所得的式子是单项式还是多项式?如果是多项式,请指出是几次几项式.
答案
5.【解析】 (1)长方形的面积为2ab,两个半圆的面积和为πb2,
所以剩下铁皮的面积为2ab-πb2.
(2)2ab-πb2是多项式,是二次二项式.
6.若关于x的多项式(m-2)x3+3x2+(3-n)x+1不含三次项及一次项,请你确定m,n的值,并求出mn+(m-n)2 019的值.
答案
6.【解析】 因为关于x的多项式(m-2)x3+3x2+(3-n)x+1不含三次项及一次项,
所以m-2=0,3-n=0,所以m=2,n=3.
当m=2,n=3时,
mn+(m-n)2 019=23+(-1)2 019=8-1=7.
若一个多项式不含某项,则该项的系数为0;若一个多项式的值与某字母的取值无关,则该多项式中含这个字母的项的系数为0.
7.若关于x,y的多项式4xy2-5x3y4+(m-5)x5y3-2与多项式-2xny4+6xy-3x-7的次数相同,且次数最高的项的系数也相同,求m,n的值.
答案
7.【解析】 易知多项式-2xny4+6xy-3x-7中次数最高的项一定是-2xny4,
对于多项式4xy2-5x3y4+(m-5)x5y3-2,
若m=5,则次数最高的项为-5x3y4,
因为-5≠-2,所以多项式4xy2-5x3y4+(m-5)x5y3-2中次数最高的项为(m-5)x5y3,
所以5+3=n+4,m-5=-2,
所以n=4,m=3.
8.对于整式(n-1)xm+2-3x2+2x(其中m是大于-2的整数).
(1)若n=2,且该整式是关于x的三次三项式,求m的值;
(2)若该整式是关于x的二次单项式,求m,n的值;
(3)若该整式是关于x的二次二项式,则m,n要满足什么条件?
答案
8.【解析】 (1)当n=2时,整式为xm+2-3x2+2x,
因为该整式是关于x的三次三项式,
所以m+2=3,解得m=1.
(2)因为该整式是关于x的二次单项式,
所以m+2=1,n-1=-2,
解得m=-1,n=-1.
(3)因为该整式是关于x的二次二项式,
所以m,n要满足n=1,m为大于-2的任意整数,或m=-1,n≠-1,或m=0,n≠4.
4 整式的加减
课时1 合并同类项
课时1
1.[2019湖南株洲中考]下列各式中,与3x2y3是同类项的是 ( )
A.2x5 B.3x3y2 C.-12x2y3 D.-13y5
?
答案
1.C 【解析】 -12x2y3与3x2y3所含字母相同,均为x,y,且字母x的指数都是2,字母y的指数都是3,所以-12x2y3与3x2y3是同类项.故选C.
?
知识点1 同类项
2.[2020辽宁沈阳期末]下列各组式子中,不是同类项的是 ( )
A.34与43 B.-mn与3nm
C.-0.1m2n与13m2n D.m2n3与n2m3
?
答案
2.D 【解析】 A项,34与43都是数,所以它们是同类项;B项,-mn与3nm所含的字母相同,并且相同字母的指数也分别相同,所以它们是同类项;C项,-0.1m2n与13m2n所含的字母相同,并且相同字母的指数也分别相同,所以它们是同类项;D项,虽然m2n3与n2m3所含的字母相同,但是相同字母的指数不同,所以它们不是同类项.故选D.
?
知识点1 同类项
3.[2020辽宁丹东期末]已知代数式-3am-1b6和16ab2n是同类项,则m-n的值是 ( )
A.-1 B.-2 C.-3 D.0
?
答案
3.A 【解析】 因为代数式-3am-1b6和16ab2n是同类项,所以m-1=1,2n=6,所以m=2,n=3,所以m-n=2-3=-1.故选A.
?
知识点1 同类项
4.将下列各式填在相应的横线上:
a,3ab,3a2b,2ba2,a2,b2,13ba,2.5a2b,4ab2,a2b2,????????4,-2????2????5,-23b2a.
a2b的同类项: .?
-ab的同类项: .?
2 020ab2的同类项: .?
?
答案
4.3a2b,2ba2,2.5a2b,-2????2????5 3ab,13ba,????????4 4ab2,-23b2a
?
知识点1 同类项
5.[2020江苏苏州期末]计算3x2y3-5y3x2的结果是 ( )
A.2x2y3 B.2x3y2 C.-2x3y2 D.-2x2y3
答案
5.D 【解析】 3x2y3-5y3x2=(3-5)x2y3=-2x2y3.故选D.
知识点2 合并同类项
6.[2020江苏苏州期末]下列运算正确的是 ( )
A.3a+2b=5ab B.a+a=a2
C.2ab-ab=2 D.a2b-3ba2=-2a2b
答案
6.D 【解析】 A项,3a与2b不是同类项,不能合并,故A项错误;B项,a+a=2a,故B项错误;C项,2ab-ab=ab,故C项错误.故选D.
知识点2 合并同类项
7.关于多项式xyz2-1+3xy+z2xy-2xyz2-3xy的值,下列说法正确的是 ( )
A.无论x,y,z取何值,都是一个常数
B.x取不同值时,其值也不同
C.y取不同值时,其值也不同
D.z取不同值时,其值也不同
答案
7.A 【解析】 xyz2-1+3xy+z2xy-2xyz2-3xy=(xyz2+z2xy-2xyz2)+(3xy-3xy)-1=-1,所以该多项式的值与x,y,z的取值无关.故选A.
知识点2 合并同类项
8.[2019湖北鄂州鄂城区期中]已知mx2yn-1+4x2y9=0(其中x≠0,y≠0),则m+n= .?
答案
8.6 【解析】 由题意可知,mx2yn-1与4x2y9是同类项,且系数互为相反数,所以n-1=9,m=-4,所以n=10,所以m+n=6.
知识点2 合并同类项
9.合并下列各式中的同类项.
(1)a+3a-2a;
(2)3x2-5y-2x2+1+3y.
答案
9.【解析】 (1)a+3a-2a
=(1+3-2)a
=2a.
(2)3x2-5y-2x2+1+3y
=(3-2)x2+(-5+3)y+1
=x2-2y+1.
知识点2 合并同类项
10.先化简,再求值:
(1)2x2-5x3-4x+5+6x-x2+5x3-8,其中x=-2;
(2)a3-5a2b+3ab2-3b3+2b3-3b2a-5a2b-2a3,其中a=-1,b=2.
答案
10.【解析】 (1)2x2-5x3-4x+5+6x-x2+5x3-8
=(-5x3+5x3)+(2x2-x2)+(-4x+6x)+(5-8)
=x2+2x-3.
当x=-2时,原式=(-2)2+2×(-2)-3=-3.
(2)a3-5a2b+3ab2-3b3+2b3-3b2a-5a2b-2a3
=(a3-2a3)+(-5a2b-5a2b)+(3ab2-3b2a)+(-3b3+2b3)
=-a3-10a2b-b3.
当a=-1,b=2时,原式=-(-1)3-10×(-1)2×2-23=-27.
知识点2 合并同类项
1.给出下列合并同类项的运算:①5a5-4a5=1;②3x+3y=6xy;③-ax+ax=0;④ a3+a4=a7;⑤-m2n+13nm2=-23m2n;⑥ 2xy2+x2y= 3xy2.
其中正确的有 ( )
A.2个 B.3个 C.4个 D.5个
?
答案
1.A 【解析】 ①5a5-4a5=a5 ,错误;②3x与3y不是同类项,不能合并,错误;③-ax+ax=(-1+1)ax=0,正确;④a3与a4不是同类项,不能合并,错误;⑤-m2n+13nm2=(-1+13)m2n=-23m2n,正确;⑥2xy2与x2y不是同类项,不能合并,错误.故正确的有2个.故选A.
?
2.计算-3(x-2y)+4(x-2y)的结果是 ( )
A.x-2y B.x+2y
C.-x-2y D.-x+2y
答案
2.A 【解析】 -3(x-2y)+4(x-2y)=(-3+4)(x-2y)=x-2y.故选A.
3.已知单项式3xa+1y4与-2yb-2x3是同类项,则下列单项式中,与它们是同类项的是 ( )
A.-5xb-3y4 B.3xby4
C.xay4 D.-xayb+1
答案
3.A 【解析】 由3xa+1y4与-2yb-2x3是同类项,得a+1=3,b-2=4,所以a=2,b=6,即原单项式为3x3y4与-2x3y4.选项A,
-5xb-3y4= -5x3y4,与它们是同类项.故选A.
4.如果单项式x2ym+2与xny的和仍然是一个单项式,那么(m+n)2 019等于 ( )
A.1 B.-1 C.2 019 D.-2 019
答案
4.A 【解析】 因为单项式x2ym+2与xny的和仍然是一个单项式,所以单项式x2ym+2与xny是同类项,所以n=2,m+2=1,所以m=-1,所以(m+n)2 019=1.故选A.
5.[2019吉林四平期末]已知关于x,y的多项式-3kx2+xy-3y2+x2-6合并后不含x2项,则k等于 ( )
A.0 B.-13 C.13 D.3
?
答案
5.C 【解析】 -3kx2+xy-3y2+x2-6=-3kx2+x2+xy-3y2-6=(1-3k)x2+xy-3y2-6,由于该多项式不含x2项,所以1-3k=0,所以k=13.故选C.
?
6.若|1-a|+|b-2|=0,则2a3+b3+3a3-2b3的值为 .?
7.[2020江苏无锡滨湖区期中]已知关于x,y的多项式mx3+3nxy2-2x3+xy2+2x-y不含三次项,那么nm= .?
答案
6.-3 【解析】 根据题意,得1-a=0,b-2=0,所以a=1,b=2.因为2a3+b3+3a3-2b3=(2+3)a3+(1-2)b3=5a3-b3,所以原式=5×13-23=5-8=-3.
7.19 【解析】 因为mx3+3nxy2-2x3+xy2+2x-y=(m-2)x3+(3n+1)xy2+2x-y,且该多项式不含三次项,所以m-2=0且3n+1=0,解得m=2,n=-13,则nm=(-13)2=19.
?
8.已知x-y=3,求多项式14(x-y)2-0.3(x-y)+0.75(x-y)2+310(x-y)-2(x-y)+7的值.
?
答案
8.【解析】 14(x-y)2-0.3(x-y)+0.75(x-y)2+310(x-y)-2(x-y)+7
=(14+0.75)(x-y)2+(-0.3+310-2)(x-y)+7
=(x-y)2-2(x-y)+7.
因为x-y=3,
所以原式=32-2×3+7=10.
?
9.“囧”曾经是一个风靡网络的流行词,像一个人脸郁闷的神情.如图,将边长为a的正方形纸片剪去两个一样的小直角三角形和一个小长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x,y,小长方形的长和宽也分别为x,y.
(1)用含a,x,y的式子表示“囧”字图案的面积S;
(2)当a=7,x=3.14,y=2时,求S的值.
答案
9.【解析】 (1)S=a2-12xy×2-xy=a2-2xy.
(2)当a=7,x=3.14,y=2时,
S=a2-2xy=72-2×3.14×2=49-12.56=36.44.
?
10.关于x,y的多项式2x2+7xy+3y2+x2-kxy+5y2,老师提出了两个问题,第一个问题:当k为何值时,多项式中不含xy项?第二个问题:在第一个问题的前提下,如果x=2,y=-1,多项式的值是多少?
(1)小明同学很快就完成了第一个问题,请你把你的解答写在下面.
(2)在做第二个问题时,小虎同学把y=-1,错看成y=1,可是他得到的最后结果却是正确的,你知道这是为什么吗?
答案
10.【解析】 (1)2x2+7xy+3y2+x2-kxy+5y2
=(2x2+x2)+(3y2+5y2)+(7xy-kxy)
=3x2+8y2+(7-k)xy.
所以只要7-k=0,这个多项式就不含xy项,
即k=7时,多项式中不含xy项.
(2)在第一个问题的前提下原多项式为3x2+8y2.
当x=2,y=-1时,原式=3×22+8×(-1)2=12+8=20.
当x=2,y=1时,原式=3×22+8×12=12+8=20.
所以小虎同学的最后结果是正确的.
课时2 去括号
课时2
1.[2020河北石家庄期末]下列去括号运算正确的是 ( )
A.-(x-y+z)=-x-y-z
B.x-(y-z)=x-y-z
C.x-(x+y)=x-x+y
D.-(a-b)-(-c-d)=-a+b+c+d
答案
1.D 【解析】 A项,-(x-y+z)=-x+y-z,故此项错误;B项,x-(y-z)=x-y+z,故此项错误;C项,x-(x+y)=x-x-y=-y,故此项错误.故选D.
知识点1 去括号法则
2.下列运算正确的是 ( )
A.-2(3x-1)=-6x-1
B.-2(3x-1)=-6x+1
C.-2(3x-1)=-6x-2
D.-2(3x-1)=-6x+2
答案
2.D
知识点1 去括号法则
3.下列各式中,去括号错误的个数为 ( )
①a+(b+c)=a+b+c;
②a-(b+c-d)=a-b-c+d;
③a+2(b-c)=a+2b-c;
④a2-[-(a+b)]=a2-a+b.
A.1 B.2 C.3 D.4
答案
3.B 【解析】 a+2(b-c)=a+2b-2c,③错误;a2-[-(a+b)]=a2+a+b,④错误.故错误的个数为2.故选B.
知识点1 去括号法则
4.化简-x2+(2x2-3x)-5(x2+x-2)的结果是 .?
答案
4.-4x2-8x+10 【解析】 -x2+(2x2-3x)-5(x2+x-2)=-x2+2x2-3x-5x2-5x+10=-4x2-8x+10.
知识点1 去括号法则
5.化简下列各式:
(1)-3(2x2-xy)+4(x2+xy-6);
(2)3x-[5x-(12x-4)].
?
答案
5.【解析】 (1)-3(2x2-xy)+4(x2+xy-6)
=-6x2+3xy+4x2+4xy-24
=-2x2+7xy-24.
(2)3x-[5x-(12x-4)]
=3x-(5x-12x+4)
=3x-5x+12x-4
=-32x-4.
?
知识点1 去括号法则
6.已知关于x,y的多项式x2-2kxy-3(x2-12xy+x)不含x,y的乘积项,则k的值为( )
A.-18 B.18 C.0 D.16
答案
6.B 【解析】 x2-2kxy-3(x2-12xy+x)= x2-2kxy-3x2+36xy-3x=-2x2+(36-2k)xy-3x,因为多项式x2-2kxy-3(x2-12xy+x)不含x,y的乘积项,所以36-2k=0,所以k=18.故选B.
知识点2 去括号法则的应用
7.当a是整数时,整式a3-3a2+7a+7+(3-2a+3a2-a3)一定是 ( )
A.3的倍数 B.4的倍数
C.5的倍数 D.7的倍数
答案
7.C 【解析】 a3-3a2+7a+7+(3-2a+3a2-a3)=a3-3a2+7a+7+3-2a+3a2-a3=5a+10=5(a+2),因为a是整数,所以该整式一定是5的倍数.故选C.
知识点2 去括号法则的应用
8.[2020广东深圳盐田区期末]一个长方形的周长为6a+4b,相邻的两边中一边的长为2a-b,则另一边的长为 .?
答案
8.a+3b 【解析】 根据题意,得另一边的长为12(6a+4b)-(2a-b)=3a+2b-2a+b=a+3b.
?
知识点2 去括号法则的应用
9.[2019福建厦门期中]先化简,再求值:x2-3(2x2-4y)+2(x2-y),其中x=-2,y=15.
?
答案
9.【解析】 x2-3(2x2-4y)+2(x2-y)
=x2-6x2+12y+2x2-2y
=-3x2+10y.
当x=-2,y=15时,
原式=-3×(-2)2+10×15=-3×4+2=-10.
?
知识点2 去括号法则的应用
10.[2020甘肃庆阳期中]有理数a,b,c在数轴上的对应点的位置如图所示.
(1)用“>”或“<”填空:c-b 0,a-b 0,a+c 0.?
(2)化简:|c-b|+|a-b|-|a+c|.
答案
10.【解析】 (1)> < >
(2)|c-b|+|a-b|-|a+c|=c-b-(a-b)-(a+c)=-2a.
知识点2 去括号法则的应用
课时3 整式的加减
课时3
1.[2020河北秦皇岛期末]一个多项式与x2-2x+1的和是3x-2,则这个多项式为 ( )
A.x2-5x+3 B.-x2+x-1
C.-x2+5x-3 D.x2-5x-13
答案
1.C 【解析】 由题意得,这个多项式为3x-2-(x2-2x+1)=3x-2-x2+2x-1=-x2+5x-3.故选C.
知识点 整式的加减
2.如果多项式N减去-3x+5,再加上x2-x-7后得5x2-3x-1,那么N为 ( )
A.4x2+5x+11 B.4x2-5x-11
C.4x2-5x+11 D.4x2+5x-11
答案
2.C 【解析】 由题意得,N-(-3x+5)+(x2-x-7)=5x2-3x-1,所以N=(5x2-3x-1)+(-3x+5)-(x2-x-7)=5x2-3x-1-3x+5-x2+x+7=4x2-5x+11.故选C.
知识点 整式的加减
3.若(ax2-2xy+y2)-(-ax2+bxy+2y2)=6x2-9xy+cy2成立,则a,b,c的值分别为 ( )
A.3,-7,-1 B.-3,7,-1
C.3,7,-1 D.-3,-7,1
答案
3.C 【解析】 (ax2-2xy+y2)-(-ax2+bxy+2y2)=ax2-2xy+????2+????????2-bxy-2y2=2ax2-(b+2)xy-y2=6x2-9xy+cy2,所以2a=6,
-(b+2)=-9,c=-1,解得a=3,b=7,c=-1.故选C.
?
知识点 整式的加减
4.设M=x2-8x+22,N=-x2-8x-3,那么M与N的大小关系是 ( )
A.M>N B.M=N
C.M答案
4.A 【解析】 因为M=x2-8x+22,N=-x2-8x-3,所以M-N=x2-8x+22-(-x2-8x-3)=x2-8x+22+x2+8x+3=2x2+25>0,所以M>N.故选A.
知识点 整式的加减
5.一个两位数x,个位上的数字是a,十位上的数字是b,交换个位与十位上的数字得到一个新的两位数y,则下列各数一定能整除x-y的是 ( )
A.11 B.9 C.5 D.2
答案
5.B 【解析】 根据题意得,x=10b+a,y=10a+b,所以x-y=10b+a-(10a+b)=10(b-a)-(b-a)=9(b-a),所以9一定能整除x-y.故选B.
知识点 整式的加减
6.[2020福建龙岩期末]某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n(m>n)元的价格进了同样的60包茶叶,如果商家以每包????+????2 元的价格卖出这些茶叶,则卖完后,这家商店 ( )
A.盈利了 B.亏损了
C.不盈不亏 D.盈亏不能确定
?
答案
6.A 【解析】 根据题意,得在甲批发市场进的茶叶的利润为40(????+????2-m)=20(m+n)-40m=(20n-20m)(元),在乙批发市场进的茶叶的利润为60(????+????2-n)=30(m+n)-60n=(30m-30n)(元),所以该商店的总利润为20n-20m+30m-30n=10m-10n= 10(m- n)(元),因为m>n,所以m-n>0,即10(m-n)>0,则这家商店盈利了.故选A.
?
知识点 整式的加减
7.[2020重庆渝北区期末]先化简,再求值:3x2y-[xy2-2(2xy2-3x2y)+x2y]+4xy2,其中(x+2)2+|y+1|=0.
答案
7.【解析】 3x2y-[xy2-2(2xy2-3x2y)+x2y]+4xy2
=3x2y-(xy2-4xy2+6x2y+x2y)+4xy2
=3x2y-xy2+4xy2-6x2y-x2y+4xy2
=-4x2y+7xy2.
因为(x+2)2+|y+1|=0,所以x=-2,y=-1.
当x=-2,y=-1时,
原式=-4×(-2)2×(-1)+7×(-2)×(-1)2=16-14=2.
知识点 整式的加减
8.[2020河北石家庄期末]小丽放学回家后准备完成下面的题目:化简(□x2-6x+8)+(6x-5x2-2),发现系数“□”印刷不清楚.
(1)她把“□”猜成3,请你化简(3x2-6x+8)+(6x-5x2-2);
(2)她妈妈说:你猜错了,我看到该题的答案是常数.通过计算说明原题中“□”是什么.
答案
8.【解析】 (1)(3x2-6x+8)+(6x-5x2-2)=3x2-6x+8+6x-5x2-2=-2x2+6.
(2)设“□”是a,
则(□x2-6x+8)+(6x-5x2-2)=(ax2-6x+8)+(6x-5x2-2)=ax2-6x+8+6x-5x2-2=(a-5)x2+6.
因为答案是常数,所以a-5=0,
所以a=5.
知识点 整式的加减
9.已知A=3a2b-2ab2+abc,小明错将“2A-B”看成“2A+B”,算得结果C=4a2b-3ab2+4abc.
(1)计算B的表达式;
(2)小强说正确结果的大小与c的取值无关,对吗?请说明理由.
(3)若b=15,a=18,求正确结果的代数式的值.
?
知识点 整式的加减
答案
9.【解析】 (1)因为2A+B=C,
所以B=C-2A
=4a2b-3ab2+4abc-2(3a2b-2ab2+abc)
=4a2b-3ab2+4abc-6a2b+4ab2-2abc
=-2a2b+ab2+2abc.
(2)对.理由如下:
2A-B=2(3a2b-2ab2+abc)-(-2a2b+ab2+2abc)
=6a2b-4ab2+2abc+2a2b-ab2-2abc
=8a2b-5ab2.
因为正确结果中不含c,所以小强的说法对,正确结果的大小与c无关.
(3)将b=15,a=18代入(2)中的代数式,
得8a2b-5ab2=8×(18)2×15-5×18×(15)2=0.
?
知识点 整式的加减
10.[2020湖北宜昌期中]把正方体(图1)沿着某些棱边剪开,就可以得到正方体的表面展开图,如图2所示.在图1的正方体中,每个面上都写了一个含有字母x的整式,相对两个面上的整式之和都等于4x-7,且A+D=0.(说明:A,B,C,D都表示含有字母x的整式)请回答下面问题:
(1)把图1的正方体沿着某些棱剪开得到它的表面展开图(图2),要剪开 条棱;?
(2)整式B+C= ;?
(3)计算图2中D和“?”所表示的整式.
答案
10.【解析】 (1)7
(2)4x-7
(3)D=4x-7-(2x2-x+1)=4x-7-2x2+x-1=-2x2+5x-8.
A=-D=2x2-5x+8.
“?”=4x-7-(2x2-5x+8)=4x-7-2x2+5x-8=-2x2+9x-15.
知识点 整式的加减
易错疑难集训
集训
1.[2019江苏南京玄武区期末]单项式-3π????2????38的系数与次数分别为 ( )
A.-3和5 B.-38和5
C.-38和6 D.-38π和5
?
答案
1.D
易错点1 基本概念不明
当单项式或多项式中含有π时,不要认为π是字母,它是一个数,因此涉及有关单项式的系数或次数的问题时,π可以作为系数或系数的一部分,而π的指数不能用来计算次数.
2.多项式3x6+2x2y-5y2+2x4y3是 次 项式.?
答案
2.七 四
易错点1 基本概念不明
错解:六 四
分析:x的最高次数是6,而次数最高的项是2x4y3,次数是7.这里错把x的最高次数看成多项式的次数.
3.式子5?????3????4是单项式,还是多项式?
?
答案
3.【解析】 5?????3????4是多项式.
?
易错点1 基本概念不明
本题的易错之处是将分子5x-3y看作一个整体,而误认为5?????3????4是单项式.式子5?????3????4实质上就是54x-34y,由于54x-34y是多项式,所以5?????3????4是多项式.
?
4.计算:4xy2+12x2y+5x2y-12xy2-5.
?
答案
4.【解析】 4xy2+12x2y+5x2y-12xy2-5
=(4-12)xy2+(12+5)x2y-5
=72xy2+112x2y-5.
?
易错点1 基本概念不明
本题的易错之处是将12x2y与-12xy2看作同类项,从而产生错解.
?
合并同类项之前要根据定义确定同类项,不要找错,也不要重复或遗漏,合并时要注意系数的符号.
5.下列说法中,错误的是 ( )
A.代数式x2+y2的意义是x,y的平方的和
B.代数式5(x+y)的意义是5与(x+y)的积
C.x的5倍与y的和的一半,用代数式表示为5x+????2
D.比x的2倍多3的数,用代数式表示为2x+3
?
答案
5.C 【解析】 x的5倍与y的和的一半,用代数式表示为5????+????2.故选C.
?
易错点2 列代数式时弄错运算顺序
6.用代数式表示“a与b的3倍的和除以c”为 .?
答案
6.????+3????????
?
易错点2 列代数式时弄错运算顺序
错解:3(????+????)????或a+3????????
分析:列代数式的关键是审清题意,弄清运算顺序,同时还要注意“除”和“除以”的区别.本题的运算顺序是先“3倍”,再求“和”,最后“除以”.
?
7.计算:(5x2-2x+3)-3(x2-2x+1).
答案
7.【解析】 (5x2-2x+3)-3(x2-2x+1)
=5x2-2x+3-3x2+6x-3
=2x2+4x.
易错点3 去括号时漏乘或符号错误
本题的易错之处是去第二个括号时没有改变括号内各项的符号或括号内的部分项漏乘3.
在去括号的时候,一定要注意括号前面的系数要与括号内的每一项都相乘,当括号外面是负号时,要改变括号内各项的符号.
8.[2020山东青岛崂山区期中]先化简,再求值:A=3a2b-ab2,B=ab2+3a2b,其中a=12,b=13.求5A-B的值.
?
答案
8.【解析】 5A-B=5(3a2b-ab2)-(ab2+3a2b)
=15a2b-5ab2-ab2-3a2b
=12a2b-6ab2.
当a=12,b=13时,
原式=12×14×13-6×12×19=1-13=23.
?
易错点3 去括号时漏乘或符号错误
1.若3x2-2x+b与x2+bx-1的和不含x项,试求b的值,及它们的和,并证明不论x取何值,它们的和总是正数.
答案
1.【解析】 (3x2-2x+b)+(x2+bx-1)
=3x2-2x+b+x2+bx-1
=4x2+(b-2)x+(b-1).
由题意得b-2=0,解得b=2.
所以3x2-2x+b与x2+bx-1的和是4x2+1.
因为任何数的平方都是非负数,所以4x2+1≥1,
所以不论x取何值,它们的和总是正数.
疑难点1 利用单项式的特点求相关字母的值
2.设a表示一个两位数,b表示一个三位数,把a放在b的左边,组成一个五位数x,把b放在a的左边,组成一个五位数y,试问9能否整除x-y?请说明理由.
答案
2.【解析】 9能整除x-y.理由如下:
由题意得,x=1 000a+b,y=100b+a,
所以x-y=1 000a+b-100b-a=999a-99b=9(111a-11b),
因为a,b都是整数,
所以9能整除9(111a-11b),即9能整除x-y.
疑难点2 利用整式的加减解决数字问题
解决本题首先要用字母a,b将x,y表示出来,并寻找9和x-y之间的关系.解题的关键有两点:一是正确用a,b表示出x-y;二是对表示出来的整式进行合理变形.
5 探索与表达规律
课时1 探索数字和图形中的规律
课时1
1.如图所示是某月的日历图.
(1)求日历图中画出的位于楼梯形中的三个数的和.
(2)用代数式表示位于楼梯形中的三个数的和.
(3)若位于这样的楼梯形中的三个数的和等于72,则这三个数分别是多少?
(4)位于这样的楼梯形中的三个数的和可以是57吗?若可以,请求出这三个数;若不可以,请说明理由.
知识点1 探索日历图中的规律
星期日
星期一
星期二
星期三
星期四
星期五
星期六
?
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
?
?
?
答案
1.【解析】 (1)8+14+20=42.
(2)设这三个数中中间的一个数为n,
则另外两个数分别为n-6,n+6,
所以这三个数的和为(n-6)+n+(n+6)=3n.
(3)令3n=72,则n=24,所以n-6=18,n+6=30,
即这三个数分别是18,24,30.
(4)不可以.理由如下:
令3n=57,则n=19,所以n-6=13,n+6=25,
因为13和19在此日历图中位于同一行,不能构成“楼梯”,
所以位于这样的楼梯形中的三个数的和不可以是57.
知识点1 探索日历图中的规律
日历图中的规律
在日历图中,一般可以从横行、竖列、斜列三个方向去寻找规律,也可以从其他角度去探索规律.①横行:相邻两数相差1.②竖列:相邻两数相差7.③斜列:从左上到右下的斜列相邻两数相差8,从右上到左下的斜列相邻两数相差6.
2.观察下列图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星??按此规律,图形⑧中星星的颗数是( )
A.43
B.45
C.51
D.53
答案
2.C 【解析】 设图形 中星星的颗数是an(n为正整数),因为 a1=2,a2=6=a1+4,a3=11=a2+5,a4=17=a3+6,所以a5= a4+7=24,a6=a5+8=32,a7=a6+9=41,a8=a7+10=51.故选C.
知识点2 探索图形中的规律
3.[2019青海中考]如图,将图1中的菱形剪开得到图2,图中共有4个四边形;将图2中的一个四边形剪开得到图3,图中共有7个四边形;如此剪下去,第5个图中共有 个四边形??,第n个图中共有 个四边形.?
答案
3.13 (3n-2) 【解析】 第1个图形中四边形的个数为1,第2个图形中四边形的个数为4=1+3,第3个图形中四边形的个数为7=1+3×2,第4个图形四边形的个数为10=1+3×3??第n个图形中四边形的个数为1+3(n-1)=(3n-2)(个),当n=5时, 3n-2=13.
知识点2 探索图形中的规律
4.[2020山东日照期中]按一定规律排列的一列数依次为-3,6,-11,18,-27,?,则这列数中第9个数及第n(n为正整数)个数分别是 ( )
A.83,-n2+2
B.-83,(-1)n(n2+2)
C.83,(-1)n(n2+2)
D.-83,-n2+2
答案
4.B 【解析】 根据数的变化规律可得,第1个数:-3=(-1)1(12+2);第2个数:6=(-1)2(22+2);第3个数:-11=(-1)3(32+2)??所以第9个数为(-1)9(92+2)=-83,第n个数为(-1)n(n2+2).故选B.
知识点3 探索数字中的规律
5.[2020江苏连云港期中]根据图中数字的规律,则x+y的值是 ( )
?
?
A.729 B.550 C.593 D.738
答案
5.C 【解析】 根据图中数字的规律,得5=22+1,12=5×2+2;17=42+1,72=17×4+4;37=62+1,228=37×6+6;所以x=82+ 1= 65,y=65×8+8=528,所以x+y=65+528=593.故选C.
知识点3 探索数字中的规律
6.观察表格,解答下列问题.
?
(1)求用“ ”框出的五个数的和;
(2)用“ ”任意框出五个数,用代数式表示这五个数的和;
(3)若用“ ”框出的五个数中最上边的数为97,求这五个数的和.
知识点3 探索数字中的规律
答案
6.【解析】 (1)10+25+28+31+46=140.
(2)设中间那个数为n ,
则这五个数的和为(n-18)+(n-3)+n+(n+3)+(n+18)=5n.
(3)这五个数中,最中间那个数为97+18=115,
结合(2)知,这五个数的和为115×5=575.
知识点3 探索数字中的规律
课时2 借助运算解释规律和现象
课时2
1.[2020辽宁鞍山期末]请先观察下列算式,再填空:32-12=8×1,52-32=8×2,72-52=8×3,92-72=8×4,?,通过观察归纳,第
2 020个算式是 . ?
答案
1.4 0412-4 0392=8×2 020 【解析】 根据题意知,第n个算式的左边是(2n+1)2-(2n-1)2,右边是8n,所以第2 020个算式是4 0412-4 0392=8×2 020.
2.[2019广西河池中考]a1,a2,a3,a4,a5,a6,?,是一列数,已知第1个数a1=4,第5个数a5=5,且任意三个相邻的数之和为15,则第2 019个数a2 019的值是 .?
答案
2.6 【解析】 由任意三个相邻的数之和是15可知a1+a2+a3=15,a2+a3+a4=15,a3+a4+a5=15,?,an+an+1+an+2=15,可以推出a1=a4=a7=?=a3n+1,a2=a5=a8=?=a3n+2,a3=a6=a9=?=a3n,所以a2=a5=5,则4+5+a3=15,解得a3=6,所以这列数以4,5,6为一个循环,因为2 019÷3=673,所以a2 019=a3=6.
3.[2020福建厦门外国语学校月考]从2开始,连续的偶数相加,它们和的情况如下表:
(1)若n=7,则S的值为 .?
(2)根据表中的规律猜想:用含n的式子表示S的公式为S=2+4+6+8+?+2n= .?
(3)根据(2)中总结的规律计算300+302+304+?+2 016+2 018+2 020的值.
加数的个数n
和S
1
2=1×2
2
2+4=6=2×3
3
2+4+6=12=3×4
4
2+4+6+8=20=4×5
5
2+4+6+8+10=30=5×6
?
?
答案
3.【解析】 (1)56
(2)n(n+1)
(3)300+302+304+?+2 016+2 018+2 020
=(2+4+6+?+2020)-(2+4+6+?+298)
=1 010×1 011-149×150
=998 760.
4.小明对蔚蔚说:“蔚蔚,你现在在脑子里想好一个整数,然后将这个数乘2加7,把结果再乘3减21.”蔚蔚按照小明的要求做好后,小明很得意地告诉蔚蔚说:“现在你所得的数一定是6的倍数.”蔚蔚非常惊讶,但很快明白了其中的道理,亲爱的同学,你能告诉大家是为什么吗?请你也像小明一样编一个类似的游戏,并说明其中的道理.
答案
4.【解析】 设这个整数是a,则(a×2+7)×3-21=6a,
所以所得的数一定是6的倍数.
所编游戏:一个整数,将这个数乘3减9,把结果再乘5加45,最后结果一定是15的倍数.
说明:设这个整数为b,则(b×3-9)×5+45=15b,所以所得的数一定是15的倍数.(答案不唯一)
5.观察下列三行数.
0,3,8,15,24,?; ①
2,5,10,17,26,?; ②
0,6,16,30,48,?. ③
(1)请写出第①行数是按什么规律排列的.
(2)第②,③行数分别与第①行数对比,有什么关系?
(3)取每行的第n个数,求这三个数的和.
答案
5.【解析】 (1)观察发现:0=12-1,3=22-1,8=32-1,15=42-1,24=52-1,?,
可得第①行数的排列规律:第n个数为n2-1.
(2)第②行的数是第①行相应的数加2得到的,第③行的数是第①行相应的数的2倍.
(3)根据题意,所求的和为(n2-1)+[(n2-1)+2]+2(n2-1)=n2-1+n2-1+2+2n2-2=4n2-2.
6.观察下列等式:
第1个等式:a1=11×3=12×(1 ??13);
第2个等式:a2=13×5=12×(13?15);
第3个等式:a3=15×7=12×(15?17);
?
请按以上规律解答下列问题:
(1)列出第5个等式:a5= ;?
(2)计算a1+a2+a3+a4+a5的结果.
(3)计算a1+a2+a3+?+an的结果.
?
答案
6.【解析】 (1)19×11=12×(19?111)
?
答案
(2)a1+a2+a3+a4+a5
=12×(1 ??13)+12×(13?15)+12×(15?17)+12×(17?19)+12×(19?111)
=12×(1 ??13+13?15+15?17+17?19+19?111)
=12×(1 ??111)
=12×1011
=511.
(3)a1+a2+a3+?+an
=12×(1 ??13)+12×(13?15)+12×(15?17)+?+12(12?????1?12????+1)
=12[(1 ??13)+(13?15)+(15?17)+?+(12?????1?12????+1)]
=12(1 ??13+13?15+15?17+?+12?????1?12????+1)
=12(1 ??12????+1).
数学·七年级上册·北师
1 字母表示数
1.“比a的3倍小1的数”可以表示为 ( )
A.3(a-1) B.3a-1
C.3a+1 D.3(a+1)
答案
1.B 【解析】 A项为“比a小1的数的3倍”,C项为“比a的3倍大1的数”,D项为“比a大1的数的3倍”.故选B.
知识点1 用字母表示数或数量关系
2.[2019山东泰安期中]设某数为m,则3????2?52表示 ( )
A.某数的3倍的平方减去5除以2
B.某数平方的3倍与5的差的一半
C.某数的平方的3倍减5的一半
D.某数的平方与5的差的3倍除以2
?
答案
2.B
知识点1 用字母表示数或数量关系
3.[2019广西桂林期末]用字母x,y表示两个数,则x,y两数的平方的和减去两数积的2倍为 .?
4.易错题 一个三位数,百位数字是a,十位数字是b,个位数字是c,则这个三位数可表示为 .?
答案
3.x2+y2-2xy 【解析】 x,y两数的平方的和为x2+y2,x,y两数的积的2倍为2xy,所以x,y两数的平方的和减去两数积的2倍为x2+y2-2xy.
知识点1 用字母表示数或数量关系
4.100a+10b+c
本题易将这个三位数错误地表示为abc.实际上abc表示a,b,c三个数相乘.
5.如果长方形的长为m,宽为n,那么该长方形的周长是 ,面积是 .?
6.若一个圆的半径为r-8,则该圆的面积S= ( )
A.πr2 B.2π(r-8)
C.π2(r-8) D.π(r-8)2
答案
5.2(m+n) mn 【解析】 长方形的周长公式:周长=2×(长+宽).长方形的面积公式:面积=长×宽.所以题中长方形的周长为2(m+n),面积为mn.
知识点2 用字母表示图形的周长、面积
6.D
7.[2020江西赣州期中]如图,阴影部分的面积可表示为( )
A.ab+bc
B.c(b-d)+d(a-c)
C.ad+c(b-d)
D.ab-cd
答案
7.C 【解析】 如图,阴影部分的面积等于图中两个长方形面积的和,即ad+c(b-d).故选C.
知识点2 用字母表示图形的周长、面积
用字母表示图形的面积问题的解题策略
解决有关图形的面积问题时,一要注意观察图形的特征,二要注意相关图形面积的表示.有时直接计算图形的面积,如长方形、三角形的面积;有时间接计算图形的面积,如通过图形的割补等,化不规则图形为规则图形.
8.[2020湖北孝感期末]某种商品的标价为x元/件,进价为400元/件,在商场开展的促销活动中,该商品按8折销售,那么每件可获利 ( )
A.(8x-400)元 B.(400×8-x)元
C.(0.8x-400)元 D.(400×0.8-x)元
答案
8.C
知识点3 用字母表示数的实际应用
9.[2019广东深圳罗湖区期末]某门窗生产厂用不锈钢制作一个长方形的窗户ABCD(中间的EF为共用窗框),相关数据(单位:米)如图所示,那么制作这个窗户所需不锈钢的总长是 ( )
A.(3a+4b)米
B.(4a+3b)米
C.2ab米
D.(2a+3b)米
答案
9.B 【解析】 由题意可得,制作这个窗户所需不锈钢的总长是3b+2×2a=(4a+3b)(米).故选B.
知识点3 用字母表示数的实际应用
10.某班共有54名学生,在一次考试中,该班28名男生的总分是m分,26名女生的平均分是n分,则这个班学生的平均分是 ( )
A.28????+26????54 分 B.????+26????54 分
C.????+????54 分 D.28(????+????)54 分
?
答案
10.B 【解析】 因为28名男生的总分是m分,26名女生的平均分是n分,所以该班学生的总分是(m+26n)分,所以这个班学生的平均分是????+26????54 分.故选B.
?
知识点3 用字母表示数的实际应用
11.[2020北京昌平区期末]在2019年世界杯上,中国女排最终以11战全胜积32分的成绩成功卫冕.比赛的积分规则为:比赛中以3-0或者3-1取胜的球队积3分,负队积0分;比赛中以3-2取胜的球队积2分,负队积1分.某队以3-1胜了a场,以3-2胜了b场,以2-3负了c场,则该队的积分为 .?
答案
11.3a+2b+c
知识点3 用字母表示数的实际应用
12.填空:
(1)m支某种铅笔的售价为n元,则5支该种铅笔的售价为 元;?
(2)轮船在静水中的速度为x千米/时,水流速度为a千米/时,则该轮船逆流航行3小时的路程是 千米.?
答案
12.(1)5????????;(2)3(x-a) 【解析】 (1)由题意,得每支铅笔的售价为???????? 元,则5支该种铅笔的售价为5???????? 元;(2)由题意,得轮船逆流航行的速度为(x-a)千米/时,则逆流航行3小时的路程是3(x-a)千米.
?
知识点3 用字母表示数的实际应用
13.[2020黑龙江哈尔滨道里区期末]观察一列数13,36,512,724,?,则第六个数是 .?
?
答案
13.1196 【解析】 经过观察知第n个数是2?????13×2?????1,所以第六个数是113×25=1196.
?
知识点4 用字母表示数字、图形的变化规律
14.如图所示的图形都是由同样大小的小圆圈按一定规律组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈??按此规律,则第 个图形中小圆圈的个数为 .?
答案
14.3+3n 【解析】 观察题中图形,得第①个图形中小圆圈的个数是3+3×1=6,第②个图形中小圆圈的个数是3+3× 2=9,第③个图形中小圆圈的个数是3+3×3=12??所以第 个图形中小圆圈的个数是3+3n.
知识点4 用字母表示数字、图形的变化规律
2 代数式
课时1 代数式
课时1
1.下列式子中,不属于代数式的是 ( )
A.a+3 B.2mn C.????+23 D.x>y
?
答案
1.D
知识点1 代数式的概念
2.下列各式中, 是代数式.(填序号)?
①2mn-1;②S=12(a+b);③b+1>a;④a;⑤????+????????;⑥7.
?
答案
2.①④⑤⑥ 【解析】 代数式只能用运算符号连接,②中有等号,③中有大于号,故②③不是代数式.
知识点1 代数式的概念
3.下列是数与字母相乘,书写规范的是 ( )
A.1×a B.-1×a
C.a×(-1) D.-a
答案
3.D
知识点2 代数式的书写规则
4.[2019四川成都七中初中学校期中]下列式子中,符合代数式的书写要求的是 ( )
A.112c B.a×b×c÷2
C.3x·y÷2 D.52xy
?
答案
4.D 【解析】 A项,112c应写成32c;B项,a×b×c÷2应写成12abc;C项,3x·y÷2应写成32xy;D项,52xy符合代数式的书写要求.故选D.
?
知识点2 代数式的书写规则
5.a是一个三位数,b是一个一位数,把a放在b的右边组成一个四位数,这个四位数是 ( )
A.ba B.100b+a
C.1 000b+a D.10b+a
答案
5.C 【解析】 依题意,知千位上的数字是b,所以这个四位数是1 000b+a.故选C.
知识点3 列代数式
6.用代数式表示:
(1)汽车每小时行驶70千米,t小时行驶 千米;?
(2)哥哥今年m岁,哥哥比妹妹大n岁,妹妹今年 岁;?
(3)现有b棵树排成a行,则平均每行有 棵树;?
(4)x的5倍与y的13的差的立方是 .?
?
答案
6.(1)70t;(2)(m-n);(3)????????;(4)(5x-13y)3
?
知识点3 列代数式
7.某班学生参加艺术节演出,需购买A,B两种衬衫共80件,其中A种衬衫买了c件,A,B两种衬衫的价格分别为每件a元和b元,则一共花了 元.?
答案
7.[ac+b(80-c)] 【解析】 因为A种衬衫买了c件,所以B种衬衫买了(80-c)件,所以一共花了[ac+b(80-c)]元.
知识点3 列代数式
8.[2020河南新乡期末]某商场经销一种品牌的电视机,每台的进价为x元,商场将进价提高20%后作为零售价进行销售,过了一段时间,商场又以9折优惠价进行促销活动.这时这种品牌的电视机每台的售价是 元.(用含x的代数式表示)?
答案
8.(1+20%)×0.9x
知识点3 列代数式
9.某商店举办促销活动,将原价x元/件的商品以0.6(x-10)元/件出售,则下列说法中,能正确表达该商店促销方法的是 ( )
A.原价减去10元后再打6折
B.原价打6折后再减去10元
C.原价减去10元后再打4折
D.原价打4折后再减去10元
答案
9.A
知识点4 代数式的实际意义
10.[2019江苏扬州期中]体育委员带了100元钱去买体育用品,已知一个足球a元,一个篮球b元,则代数式100-3a-2b表示的意义为 .?
答案
10.体育委员买3个足球和2个篮球后剩余的钱数 【解析】 因为买一个足球a元,一个篮球b元,所以3a表示体育委员买3个足球所用钱数,2b表示买2个篮球所用钱数,所以代数式100-3a-2b表示体育委员买3个足球和2个篮球后剩余的钱数.
知识点4 代数式的实际意义
11.某工厂第一车间有x人,第二车间比第一车间人数的12少10人,现在根据工作需要,从第二车间调出10人到第一车间,请列代数式表示(不需要化简):
(1)两个车间共有多少人?
(2)调动后第一车间的人数比第二车间的人数多几人?
?
答案
11.【解析】 (1)由题意知,第二车间有(12x-10)人,
所以两个车间共有(x+12x-10)人.
(2)由题意知,调动后第一车间有(x+10)人,第二车间有(12x-20)人,
所以调动后第一车间的人数比第二车间的人数多[(x+10)-(12x-20)]人.
?
知识点5 利用代数式解决实际问题
12.某公园的成人票每张50元,儿童票每张30元.甲旅游团有a名成人和b名儿童,乙旅游团的成人数是甲旅游团的2倍,儿童数是甲旅游团的12.
(1)用含a,b的代数式表示乙旅游团的总人数;
(2)用含a,b的代数式表示甲、乙两个旅游团的门票总费用.(不需要化简)
?
答案
12.【解析】 (1)依题意得,乙旅游团的总人数为2a+12b.
(2)甲旅游团的门票总费用为(50a+30b)元,
乙旅游团的门票总费用为(100a+15b)元,
所以甲、乙两个旅游团的门票总费用为(50a+30b+100a+15b)元.
?
知识点5 利用代数式解决实际问题
1.[2020福建厦门期中]能用代数式a+0.3a表示含义的是 ( )
A.妈妈在超市购买物品共需a元,结账时买塑料袋又花了0.3元,妈妈共花了多少元
B.一个长方形的长是a米,宽是0.3a米,这个长方形的周长是多少米
C.小明骑自行车的速度是a千米/时,行驶0.3a小时后,小明所行驶的路程是多少千米
D.一套商品房原价为a万元,现提价30%,那么现在这套商品房的售价是多少万元
答案
1.D 【解析】 A项,根据题意得,妈妈共花了(a+0.3)元,故A项不合题意;B项,根据题意得,这个长方形的周长是2(a+ 0.3a)米,故B项不合题意;C项,根据题意得,小明所行驶的路程是a×0.3a千米,故C项不合题意.故选D.
2.[2018安徽中考]据省统计局发布,2017年我省有效发明专利数比2016年增长22.1%.假定2018年的年增长率保持不变,2016年和2018年我省有效发明专利分别为a万件和b万件,则 ( )
A.b=(1+22.1%×2)a
B.b=(1+22.1%)2a
C.b=(1+22.1%)×2a
D.b=22.1%×2a
答案
2.B
3.为了做一个试管架,在长为a cm(a>6)的木板上钻3个相同的小孔(如图),每个小孔的直径为2 cm,则用含a的代数式表示x为 ( )
A.?????34
B.????+34
C.?????64
D.????+64
?
答案
3.C 【解析】 由题意得,x=?????2×34,即x=?????64.故选C.
?
4.王阿姨以每个m元的价格买进苹果100个,现以每个比进价多20%的价格卖出70个后,再以每个比进价低n元的价格将剩下的30个卖出,则全部苹果共卖得的金额是 ( )
A.[70m+30(m-n)]元
B.[70×(1+20%)m+30(m-n)]元
C.[70×(1+20%)m+30n]元
D.[100×(1+20%)m-30(m-n)]元
答案
4.B 【解析】 由题意得,先卖出的70个苹果的单价是(1+20%)m元,剩下的30个苹果卖出的单价是(m-n)元.全部苹果共卖得的金额=先卖出的70个苹果的总价+剩下的30个苹果卖出的总价,即[70×(1+20%)m+30(m-n)]元.故选B.
5.[2020浙江宁波期中]某市出租车的起步价为10元(行驶里程不超过3千米),另收取燃油附加费1元,超过3千米以后,每增加1千米,加价1.8元.若某人乘出租车行驶里程为P(P>3,且P为整数)千米,则所需费用是 元.?
6.[2020广东梅州期末]某文具店销售一种羽毛球拍和羽毛球,球拍每副标价120元,羽毛球每个标价4元,近期该店开展促销活动,活动期间向客户提供的优惠方案为:买一副球拍送5个羽毛球.某人到该店买球拍20副,a(a>100,且a为整数)个羽毛球,则需付款 元.?
答案
5.[11+1.8(p-3)]
6.[2 400+4(a-100)] 【解析】 120×20+4(a-20×5)=[2 400+4(a-100)](元).
7.整理一批图书,如果由一个人单独整理要用60 h.现先由一部分人整理1 h,随后增加15人和他们一起又整理了2 h,假设每个人的工作效率相同,设先安排的整理人员有x人.
(1)用代数式表示x人1 h的工作量;
(2)用代数式表示增加15人后一起整理2 h的工作量.
答案
7.【解析】 (1)把总工作量看作1,
由题意得,每个人1 h的工作量是160,则x人1 h的工作量是????60.
(2)增加15人后,(x+15)人一起整理2 h的工作量为2(????+15)60,即????+1530.
?
8.[2019湖北十堰期末]某超市在春节期间对顾客实行优惠,规定如下:
(1)王老师一次性购物600元,他实际付款 元;?
(2)某顾客在该超市一次性购物x元,当x小于500但不小于200时,他实际付款 元,当x大于或等于500时,他实际付款 元;(用含x的代数式表示)?
(3)如果王老师两次购物合计820元,第一次购物a(200
优惠办法
低于200元
不予优惠
低于500元但
不低于200元
9折优惠
不低于500元
其中500元部分给予9折优惠,
超过500元部分给予8折优惠
答案
8.【解析】 (1)530
根据题意,得他实际付款500×0.9+(600-500)×0.8=530(元).
(2)0.9x [450+0.8(x-500)]
当x小于500但不小于200时,实际付款=购物款×0.9=0.9x(元);当x大于或等于500时,实际付款=500×0.9+购物款超过500元的部分×0.8=500×0.9+(x-500)×0.8=[450+0.8(x-500)](元).
(3)由题意知,第二次购物大于500元,
所以两次购物王老师实际付款=0.9a+500×0.9+0.8(820-a-500)=[0.9a+450+0.8(320-a)](元).
所以两次购物王老师实际付款[0.9a+450+0.8(320-a)]元.
课时2 代数式的值
课时2
1.[2019海南中考]当m=-1时,代数式2m+3的值是 ( )
A.-1 B.0 C.1 D.2
答案
1.C 【解析】 将m=-1代入,得2m+3=2×(-1)+3=1.故选C.
知识点1 求代数式的值
2.[2020四川眉山期末]当x=1时,代数式px3+qx+1的值为2 020,则当x=-1时,代数式px3+qx+1的值为 ( )
A.-2 017 B.-2 019 C.-2 018 D.2 019
答案
2.C 【解析】 当x=1时,代数式px3+qx+1的值为2 020,所以p+q=2019.当x=-1时,px3+qx+1=-p-q+1=-(p+q)+1=-2 019+ 1=-2 018.故选C.
知识点1 求代数式的值
3.[2020江西赣州期末]如图是一个运算程序的示意图,若开始输入x的值为81,则第2 020次输出的结果为 ( )
A.3
B.27
C.9
D.1
答案
3.D 【解析】 第1次,13×81=27;第2次,13×27=9;第3次,13×9=3;第4次,13×3=1;第5次,1+2=3;第6次,13×3=1??依此可知,从第4次开始,运算输出的结果依次是1,3,1,3??因为(2 020-3)÷2=1 008??1,所以第2 020次输出的结果为1.故选D.
?
知识点1 求代数式的值
解决周期性规律问题的步骤
第一步:分析并找准循环周期及一个循环周期内图形变换或数据变化的特点.第二步:用所求数据除以循环周期数,观察商和余数.第三步:结合问题及余数确定答案.
4.若a,b互为倒数,x,y互为相反数,则代数式4(x+y)+5ab+3 的值为 .?
5.如果|5-a|+(b+3)2=0,那么代数式1????(1-2b)的值为 .?
6.[2020湖北孝感期末]已知代数式4x2-2x+3=5,那么代数式2x2-x+2 019= .?
?
答案
4.8 【解析】 因为a,b互为倒数,x,y互为相反数,所以ab=1,x+y=0.因此4(x+y)+5ab+3=0+5+3=8.
知识点1 求代数式的值
5.75 【解析】 由|5-a|+(b+3)2=0,可知5-a=0,b+3=0,所以a=5,b=-3,所以1????(1-2b)=15×[1-2×(-3)]=75.
?
6.2 020 【解析】 因为4x2-2x+3=5,所以2x2-x=1,所以2x2-x+2 019=1+2 019=2 020.
7.先填表,再回答问题:
(1)当x为何值时,代数式2x-1的值等于5?
(2)已知有两个x的值使代数式-3x和x2的值相等,请你找出这两个x的值.
(3)随着x值的逐渐增大,代数式2x-1,-3x和x2的值是如何变化的?(写出结论即可,无需说明理由)
知识点1 求代数式的值
x
-3
-2
-1
0
1
2
3
2x-1
?
?
?
?
?
?
?
-3x
?
?
?
?
?
?
?
x2
?
?
?
?
?
?
?
答案
7.【解析】 填表如下:
(1)根据表格得,当x=3时,代数式2x-1的值等于5.
(2)根据表格得,当x=0或x=-3时,代数式-3x和x2的值相等.
(3)随着x值的逐渐增大,代数式2x-1的值逐渐增大;代数式-3x的值逐渐减小;代数式x2的值先减小再增大.
知识点1 求代数式的值
x
-3
-2
-1
0
1
2
3
2x-1
-7
-5
-3
-1
1
3
5
-3x
9
6
3
0
-3
-6
-9
x2
9
4
1
0
1
4
9
8.一个塑料直角三角形模具,形状和尺寸如图所示.
(1)求阴影部分的面积;(用含a,b,r的代数式表示)
(2)当a=5 cm,b=4 cm,r=1 cm时,计算阴影部分的面积.
答案
8.【解析】 (1)根据直角三角形的面积公式,得直角三角形的面积是12ab,
因为圆的面积是πr2,
所以阴影部分的面积是12ab-πr2.
(2)当a=5 cm,b=4 cm,r=1 cm时,
12ab-πr2=12×5×4-π×12=(10-π)(cm2).
故阴影部分的面积为(10-π)cm2.
?
知识点2 利用求代数式的值解决实际问题
9.某家具厂生产一种餐桌和椅子,餐桌每张定价为500元,椅子每把定价为160元.厂方在开展促销活动期间,向客户提供两种优惠方案.
方案一:每买一张餐桌就赠送一把椅子.
方案二:餐桌和椅子都按定价的80%付款.
某餐厅计划添置100张餐桌和x把椅子.
(1)若x>100,请用含x的代数式分别把两种方案的费用表示出来.
(2)已知x=300,如果两种方案可以同时使用,请帮助餐厅设计一种最省钱的方案.
知识点2 利用求代数式的值解决实际问题
答案
9.【解析】 (1)当x>100时,
方案一:100×500+160×(x-100)=160x+34 000.
方案二:(100×500+160x)×80%=128x+40 000.
答:方案一、方案二的费用分别为(160x+34 000)元、(128x+40 000)元.
(2)当x=300时,
①按方案一购买:500×100+160×200=82 000(元).
②按方案二购买:(100×500+160×300)×80%=78 400(元).
③先按方案一购买100张餐桌,同时送100把椅子,再按方案二购买200把椅子,
即100×500+160×200×80%=75 600(元).
因为82 000>78 400>75 600,
所以先按方案一购买100张餐桌,同时送100把椅子,再按方案二购买200把椅子最省钱.
知识点2 利用求代数式的值解决实际问题
3 整式
1.易错题[2020上海市实验学校月考]给出下列代数式:①-12a,②????3,③????2+????2,④????2π,⑤x2y.其中单项式的个数为 ( )
A.2 B.3 C.4 D.5
?
答案
1.C 【解析】 ①②④⑤属于单项式,共有4个.③????2+????2实质上是????22+????2,不是单项式.故选C.
?
知识点1 单项式
判断一个代数式是不是单项式,关键是看该代数式是不是单独的一个数或一个字母或数与字母的乘积,含有加、减运算或分母中含有字母的式子均不是单项式.
2.易错题[2019甘肃平凉期末]单项式-ab2的系数是 ( )
A.-1 B.1 C.2 D.3
答案
2.A
知识点1 单项式
本题容易误认为-ab2的系数是1而错选B,需要注意,单项式的系数包括符号.
3.[2019上海浦东新区期末]下列各单项式的次数为5的是 ( )
A.4x2y2 B.17x4ya
C.2a3b2 D.6x3y5
?
答案
3.C 【解析】 A项,4x2y2的次数是4,故A项不合题意;B项,17x4ya的次数是6,故B项不合题意;C项,2a3b2的次数是5,故C项符合题意;D项,6x3y5的次数是8,故D项不合题意.故选C.
?
知识点1 单项式
4.下列说法中,正确的是 ( )
A.单项式一定是含字母的代数式
B.单项式a没有系数
C.-y的次数是0
D.单项式-π2x2y的系数是-π2,次数是3
答案
4.D 【解析】 单独一个数也是单项式,A项不正确;当单项式的系数为1时,可以省略不写,所以单项式a的系数为1,B项不正确;-y的次数是1,C项不正确.故选D.
知识点1 单项式
5.单项式0.5x4+my与6xy12的次数相同,求m的值.
答案
5.【解析】 因为单项式0.5x4+my的次数是4+m+1=m+5,6xy12的次数是1+12=13,所以m+5=13,所以m=8.
知识点1 单项式
6.[2019湖南长沙开福区期中]下列代数式中,多项式的个数是 ( )
(1)a;(2)2x2+2xy+y2;(3)a+1;(4)a2-1????;
(5)-14(x+y).
A.1 B.2 C.3 D.4
?
答案
6.C 【解析】 单独一个字母是单项式,故(1)不是多项式;(4)中分母中含有字母,不是几个单项式的和的形式,故(4)不是多项式;(2)(3)(5)都是多项式.故选C.
知识点2 多项式
7.[2020江苏苏州期末]多项式m3n4-5m3n5+3的项数和次数分别为 ( )
A.2,7 B.3,8 C.2,8 D.3,7
答案
7.B 【解析】 多项式m3n4-5m3n5+3的各项分别是m3n4,-5m3n5,3,故项数是3,次数是8.故选B.
知识点2 多项式
8.[2020安徽合肥庐阳区期末]二次三项式2x2-3x-1的二次项系数、一次项系数、常数项分别是 ( )
A.2,-3,-1 B.2,3,1
C.2,3,-1 D.2,-3,1
答案
8.A 【解析】 二次三项式2x2-3x-1的二次项系数、一次项系数、常数项分别是2,-3,-1.故选A.
知识点2 多项式
9.[2019江西抚州临川区期中]多项式3x|m|y2+(m+2)x2y-1是关于x,y的四次三项式,则m的值为 .?
答案
9.2 【解析】 因为关于x,y的多项式3x|m|y2+(m+2)x2y-1是四次三项式,所以|m|+2=4,m+2≠0,所以m=2.
知识点2 多项式
10.[2020上海静安区月考]下列代数式中,是整式的有 ( )
2x+y,13a2b,?????????π,1????(x2-2xy+1),0,πx+14y.
A.4个 B.5个 C.6个 D.7个
?
答案
10.B 【解析】 2x+y,13a2b,?????????π,0,πx+14y是整式,共有5个.故选B.
?
知识点3 整式
11.下列说法中,错误的是 ( )
A.m是单项式也是整式
B.12(m-n)是多项式也是整式
C.整式一定是单项式
D.整式不一定是多项式
?
答案
11.C 【解析】 单项式和多项式统称为整式.故选C.
知识点3 整式
12.小王购买了一套房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),用含x,y的式子表示地面总面积.
答案
12.【解析】 由题图,得地面共由四部分组成,其总面积是6x+3×2+4×3+2y=(6x+2y+18)(m2).
知识点3 整式
1.[2020福建漳州期末]下列说法中,正确的是 ( )
A.单项式π????2????4的系数是14,次数是4
B.单项式m的次数是1,没有系数
C.在12x3,?????????π,5????4????,0中,整式有2个
D.多项式2x2+xy2+3是三次三项式
?
答案
1.D 【解析】 A项,单项式π????2????4的系数是π4,次数是3,此项错误;B项,单项式m的次数是1,系数是1,此项错误;C项,在12x3,?????????π,5????4????,0中,整式有12x3,?????????π,0,共3个,此项错误.故选D.
?
2.[2019江苏盐城盐都区期中]如果一个多项式中各项的次数都相同,那么这个多项式叫做齐次多项式.如:x3+3xy2+4xyz+2y3是3次齐次多项式.若ax+3b2-6ab3c2是齐次多项式,则x的值为 ( )
A.-1 B.0 C.1 D.2
答案
2.C 【解析】 由题意,得x+3+2=6,解得x=1.故选C.
根据新定义,使多项式中每一项的次数相等,便可确定字母指数的值.
3.如果一个多项式的次数是5,那么这个多项式的任何一项的次数 ( )
A.都小于5 B.都等于5
C.都不小于5 D.都不大于5
答案
3.D 【解析】 多项式中次数最高的项的次数叫做这个多项式的次数.所以如果一个多项式的次数是5,那么这个多项式的任何一项的次数都不大于5.故选D.
4.观察下列多项式:2a+b;3a+b2;4a+b3;5a+b4;?.则第n个多项式为 .?
答案
4.(n+1)a+bn 【解析】 观察发现,每个多项式都是二项式.字母a的系数从2开始依次增加1,字母b的指数从1开始依次增加1,所以第n个多项式为(n+1)a+bn.
5.[2020辽宁葫芦岛连山区期末]如图,在一块长为a、宽为2b的长方形铁皮中,剪掉两个以2b为直径的半圆.
(1)求剩下铁皮的面积.(用含a,b的式子表示)
(2)(1)中所得的式子是单项式还是多项式?如果是多项式,请指出是几次几项式.
答案
5.【解析】 (1)长方形的面积为2ab,两个半圆的面积和为πb2,
所以剩下铁皮的面积为2ab-πb2.
(2)2ab-πb2是多项式,是二次二项式.
6.若关于x的多项式(m-2)x3+3x2+(3-n)x+1不含三次项及一次项,请你确定m,n的值,并求出mn+(m-n)2 019的值.
答案
6.【解析】 因为关于x的多项式(m-2)x3+3x2+(3-n)x+1不含三次项及一次项,
所以m-2=0,3-n=0,所以m=2,n=3.
当m=2,n=3时,
mn+(m-n)2 019=23+(-1)2 019=8-1=7.
若一个多项式不含某项,则该项的系数为0;若一个多项式的值与某字母的取值无关,则该多项式中含这个字母的项的系数为0.
7.若关于x,y的多项式4xy2-5x3y4+(m-5)x5y3-2与多项式-2xny4+6xy-3x-7的次数相同,且次数最高的项的系数也相同,求m,n的值.
答案
7.【解析】 易知多项式-2xny4+6xy-3x-7中次数最高的项一定是-2xny4,
对于多项式4xy2-5x3y4+(m-5)x5y3-2,
若m=5,则次数最高的项为-5x3y4,
因为-5≠-2,所以多项式4xy2-5x3y4+(m-5)x5y3-2中次数最高的项为(m-5)x5y3,
所以5+3=n+4,m-5=-2,
所以n=4,m=3.
8.对于整式(n-1)xm+2-3x2+2x(其中m是大于-2的整数).
(1)若n=2,且该整式是关于x的三次三项式,求m的值;
(2)若该整式是关于x的二次单项式,求m,n的值;
(3)若该整式是关于x的二次二项式,则m,n要满足什么条件?
答案
8.【解析】 (1)当n=2时,整式为xm+2-3x2+2x,
因为该整式是关于x的三次三项式,
所以m+2=3,解得m=1.
(2)因为该整式是关于x的二次单项式,
所以m+2=1,n-1=-2,
解得m=-1,n=-1.
(3)因为该整式是关于x的二次二项式,
所以m,n要满足n=1,m为大于-2的任意整数,或m=-1,n≠-1,或m=0,n≠4.
4 整式的加减
课时1 合并同类项
课时1
1.[2019湖南株洲中考]下列各式中,与3x2y3是同类项的是 ( )
A.2x5 B.3x3y2 C.-12x2y3 D.-13y5
?
答案
1.C 【解析】 -12x2y3与3x2y3所含字母相同,均为x,y,且字母x的指数都是2,字母y的指数都是3,所以-12x2y3与3x2y3是同类项.故选C.
?
知识点1 同类项
2.[2020辽宁沈阳期末]下列各组式子中,不是同类项的是 ( )
A.34与43 B.-mn与3nm
C.-0.1m2n与13m2n D.m2n3与n2m3
?
答案
2.D 【解析】 A项,34与43都是数,所以它们是同类项;B项,-mn与3nm所含的字母相同,并且相同字母的指数也分别相同,所以它们是同类项;C项,-0.1m2n与13m2n所含的字母相同,并且相同字母的指数也分别相同,所以它们是同类项;D项,虽然m2n3与n2m3所含的字母相同,但是相同字母的指数不同,所以它们不是同类项.故选D.
?
知识点1 同类项
3.[2020辽宁丹东期末]已知代数式-3am-1b6和16ab2n是同类项,则m-n的值是 ( )
A.-1 B.-2 C.-3 D.0
?
答案
3.A 【解析】 因为代数式-3am-1b6和16ab2n是同类项,所以m-1=1,2n=6,所以m=2,n=3,所以m-n=2-3=-1.故选A.
?
知识点1 同类项
4.将下列各式填在相应的横线上:
a,3ab,3a2b,2ba2,a2,b2,13ba,2.5a2b,4ab2,a2b2,????????4,-2????2????5,-23b2a.
a2b的同类项: .?
-ab的同类项: .?
2 020ab2的同类项: .?
?
答案
4.3a2b,2ba2,2.5a2b,-2????2????5 3ab,13ba,????????4 4ab2,-23b2a
?
知识点1 同类项
5.[2020江苏苏州期末]计算3x2y3-5y3x2的结果是 ( )
A.2x2y3 B.2x3y2 C.-2x3y2 D.-2x2y3
答案
5.D 【解析】 3x2y3-5y3x2=(3-5)x2y3=-2x2y3.故选D.
知识点2 合并同类项
6.[2020江苏苏州期末]下列运算正确的是 ( )
A.3a+2b=5ab B.a+a=a2
C.2ab-ab=2 D.a2b-3ba2=-2a2b
答案
6.D 【解析】 A项,3a与2b不是同类项,不能合并,故A项错误;B项,a+a=2a,故B项错误;C项,2ab-ab=ab,故C项错误.故选D.
知识点2 合并同类项
7.关于多项式xyz2-1+3xy+z2xy-2xyz2-3xy的值,下列说法正确的是 ( )
A.无论x,y,z取何值,都是一个常数
B.x取不同值时,其值也不同
C.y取不同值时,其值也不同
D.z取不同值时,其值也不同
答案
7.A 【解析】 xyz2-1+3xy+z2xy-2xyz2-3xy=(xyz2+z2xy-2xyz2)+(3xy-3xy)-1=-1,所以该多项式的值与x,y,z的取值无关.故选A.
知识点2 合并同类项
8.[2019湖北鄂州鄂城区期中]已知mx2yn-1+4x2y9=0(其中x≠0,y≠0),则m+n= .?
答案
8.6 【解析】 由题意可知,mx2yn-1与4x2y9是同类项,且系数互为相反数,所以n-1=9,m=-4,所以n=10,所以m+n=6.
知识点2 合并同类项
9.合并下列各式中的同类项.
(1)a+3a-2a;
(2)3x2-5y-2x2+1+3y.
答案
9.【解析】 (1)a+3a-2a
=(1+3-2)a
=2a.
(2)3x2-5y-2x2+1+3y
=(3-2)x2+(-5+3)y+1
=x2-2y+1.
知识点2 合并同类项
10.先化简,再求值:
(1)2x2-5x3-4x+5+6x-x2+5x3-8,其中x=-2;
(2)a3-5a2b+3ab2-3b3+2b3-3b2a-5a2b-2a3,其中a=-1,b=2.
答案
10.【解析】 (1)2x2-5x3-4x+5+6x-x2+5x3-8
=(-5x3+5x3)+(2x2-x2)+(-4x+6x)+(5-8)
=x2+2x-3.
当x=-2时,原式=(-2)2+2×(-2)-3=-3.
(2)a3-5a2b+3ab2-3b3+2b3-3b2a-5a2b-2a3
=(a3-2a3)+(-5a2b-5a2b)+(3ab2-3b2a)+(-3b3+2b3)
=-a3-10a2b-b3.
当a=-1,b=2时,原式=-(-1)3-10×(-1)2×2-23=-27.
知识点2 合并同类项
1.给出下列合并同类项的运算:①5a5-4a5=1;②3x+3y=6xy;③-ax+ax=0;④ a3+a4=a7;⑤-m2n+13nm2=-23m2n;⑥ 2xy2+x2y= 3xy2.
其中正确的有 ( )
A.2个 B.3个 C.4个 D.5个
?
答案
1.A 【解析】 ①5a5-4a5=a5 ,错误;②3x与3y不是同类项,不能合并,错误;③-ax+ax=(-1+1)ax=0,正确;④a3与a4不是同类项,不能合并,错误;⑤-m2n+13nm2=(-1+13)m2n=-23m2n,正确;⑥2xy2与x2y不是同类项,不能合并,错误.故正确的有2个.故选A.
?
2.计算-3(x-2y)+4(x-2y)的结果是 ( )
A.x-2y B.x+2y
C.-x-2y D.-x+2y
答案
2.A 【解析】 -3(x-2y)+4(x-2y)=(-3+4)(x-2y)=x-2y.故选A.
3.已知单项式3xa+1y4与-2yb-2x3是同类项,则下列单项式中,与它们是同类项的是 ( )
A.-5xb-3y4 B.3xby4
C.xay4 D.-xayb+1
答案
3.A 【解析】 由3xa+1y4与-2yb-2x3是同类项,得a+1=3,b-2=4,所以a=2,b=6,即原单项式为3x3y4与-2x3y4.选项A,
-5xb-3y4= -5x3y4,与它们是同类项.故选A.
4.如果单项式x2ym+2与xny的和仍然是一个单项式,那么(m+n)2 019等于 ( )
A.1 B.-1 C.2 019 D.-2 019
答案
4.A 【解析】 因为单项式x2ym+2与xny的和仍然是一个单项式,所以单项式x2ym+2与xny是同类项,所以n=2,m+2=1,所以m=-1,所以(m+n)2 019=1.故选A.
5.[2019吉林四平期末]已知关于x,y的多项式-3kx2+xy-3y2+x2-6合并后不含x2项,则k等于 ( )
A.0 B.-13 C.13 D.3
?
答案
5.C 【解析】 -3kx2+xy-3y2+x2-6=-3kx2+x2+xy-3y2-6=(1-3k)x2+xy-3y2-6,由于该多项式不含x2项,所以1-3k=0,所以k=13.故选C.
?
6.若|1-a|+|b-2|=0,则2a3+b3+3a3-2b3的值为 .?
7.[2020江苏无锡滨湖区期中]已知关于x,y的多项式mx3+3nxy2-2x3+xy2+2x-y不含三次项,那么nm= .?
答案
6.-3 【解析】 根据题意,得1-a=0,b-2=0,所以a=1,b=2.因为2a3+b3+3a3-2b3=(2+3)a3+(1-2)b3=5a3-b3,所以原式=5×13-23=5-8=-3.
7.19 【解析】 因为mx3+3nxy2-2x3+xy2+2x-y=(m-2)x3+(3n+1)xy2+2x-y,且该多项式不含三次项,所以m-2=0且3n+1=0,解得m=2,n=-13,则nm=(-13)2=19.
?
8.已知x-y=3,求多项式14(x-y)2-0.3(x-y)+0.75(x-y)2+310(x-y)-2(x-y)+7的值.
?
答案
8.【解析】 14(x-y)2-0.3(x-y)+0.75(x-y)2+310(x-y)-2(x-y)+7
=(14+0.75)(x-y)2+(-0.3+310-2)(x-y)+7
=(x-y)2-2(x-y)+7.
因为x-y=3,
所以原式=32-2×3+7=10.
?
9.“囧”曾经是一个风靡网络的流行词,像一个人脸郁闷的神情.如图,将边长为a的正方形纸片剪去两个一样的小直角三角形和一个小长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x,y,小长方形的长和宽也分别为x,y.
(1)用含a,x,y的式子表示“囧”字图案的面积S;
(2)当a=7,x=3.14,y=2时,求S的值.
答案
9.【解析】 (1)S=a2-12xy×2-xy=a2-2xy.
(2)当a=7,x=3.14,y=2时,
S=a2-2xy=72-2×3.14×2=49-12.56=36.44.
?
10.关于x,y的多项式2x2+7xy+3y2+x2-kxy+5y2,老师提出了两个问题,第一个问题:当k为何值时,多项式中不含xy项?第二个问题:在第一个问题的前提下,如果x=2,y=-1,多项式的值是多少?
(1)小明同学很快就完成了第一个问题,请你把你的解答写在下面.
(2)在做第二个问题时,小虎同学把y=-1,错看成y=1,可是他得到的最后结果却是正确的,你知道这是为什么吗?
答案
10.【解析】 (1)2x2+7xy+3y2+x2-kxy+5y2
=(2x2+x2)+(3y2+5y2)+(7xy-kxy)
=3x2+8y2+(7-k)xy.
所以只要7-k=0,这个多项式就不含xy项,
即k=7时,多项式中不含xy项.
(2)在第一个问题的前提下原多项式为3x2+8y2.
当x=2,y=-1时,原式=3×22+8×(-1)2=12+8=20.
当x=2,y=1时,原式=3×22+8×12=12+8=20.
所以小虎同学的最后结果是正确的.
课时2 去括号
课时2
1.[2020河北石家庄期末]下列去括号运算正确的是 ( )
A.-(x-y+z)=-x-y-z
B.x-(y-z)=x-y-z
C.x-(x+y)=x-x+y
D.-(a-b)-(-c-d)=-a+b+c+d
答案
1.D 【解析】 A项,-(x-y+z)=-x+y-z,故此项错误;B项,x-(y-z)=x-y+z,故此项错误;C项,x-(x+y)=x-x-y=-y,故此项错误.故选D.
知识点1 去括号法则
2.下列运算正确的是 ( )
A.-2(3x-1)=-6x-1
B.-2(3x-1)=-6x+1
C.-2(3x-1)=-6x-2
D.-2(3x-1)=-6x+2
答案
2.D
知识点1 去括号法则
3.下列各式中,去括号错误的个数为 ( )
①a+(b+c)=a+b+c;
②a-(b+c-d)=a-b-c+d;
③a+2(b-c)=a+2b-c;
④a2-[-(a+b)]=a2-a+b.
A.1 B.2 C.3 D.4
答案
3.B 【解析】 a+2(b-c)=a+2b-2c,③错误;a2-[-(a+b)]=a2+a+b,④错误.故错误的个数为2.故选B.
知识点1 去括号法则
4.化简-x2+(2x2-3x)-5(x2+x-2)的结果是 .?
答案
4.-4x2-8x+10 【解析】 -x2+(2x2-3x)-5(x2+x-2)=-x2+2x2-3x-5x2-5x+10=-4x2-8x+10.
知识点1 去括号法则
5.化简下列各式:
(1)-3(2x2-xy)+4(x2+xy-6);
(2)3x-[5x-(12x-4)].
?
答案
5.【解析】 (1)-3(2x2-xy)+4(x2+xy-6)
=-6x2+3xy+4x2+4xy-24
=-2x2+7xy-24.
(2)3x-[5x-(12x-4)]
=3x-(5x-12x+4)
=3x-5x+12x-4
=-32x-4.
?
知识点1 去括号法则
6.已知关于x,y的多项式x2-2kxy-3(x2-12xy+x)不含x,y的乘积项,则k的值为( )
A.-18 B.18 C.0 D.16
答案
6.B 【解析】 x2-2kxy-3(x2-12xy+x)= x2-2kxy-3x2+36xy-3x=-2x2+(36-2k)xy-3x,因为多项式x2-2kxy-3(x2-12xy+x)不含x,y的乘积项,所以36-2k=0,所以k=18.故选B.
知识点2 去括号法则的应用
7.当a是整数时,整式a3-3a2+7a+7+(3-2a+3a2-a3)一定是 ( )
A.3的倍数 B.4的倍数
C.5的倍数 D.7的倍数
答案
7.C 【解析】 a3-3a2+7a+7+(3-2a+3a2-a3)=a3-3a2+7a+7+3-2a+3a2-a3=5a+10=5(a+2),因为a是整数,所以该整式一定是5的倍数.故选C.
知识点2 去括号法则的应用
8.[2020广东深圳盐田区期末]一个长方形的周长为6a+4b,相邻的两边中一边的长为2a-b,则另一边的长为 .?
答案
8.a+3b 【解析】 根据题意,得另一边的长为12(6a+4b)-(2a-b)=3a+2b-2a+b=a+3b.
?
知识点2 去括号法则的应用
9.[2019福建厦门期中]先化简,再求值:x2-3(2x2-4y)+2(x2-y),其中x=-2,y=15.
?
答案
9.【解析】 x2-3(2x2-4y)+2(x2-y)
=x2-6x2+12y+2x2-2y
=-3x2+10y.
当x=-2,y=15时,
原式=-3×(-2)2+10×15=-3×4+2=-10.
?
知识点2 去括号法则的应用
10.[2020甘肃庆阳期中]有理数a,b,c在数轴上的对应点的位置如图所示.
(1)用“>”或“<”填空:c-b 0,a-b 0,a+c 0.?
(2)化简:|c-b|+|a-b|-|a+c|.
答案
10.【解析】 (1)> < >
(2)|c-b|+|a-b|-|a+c|=c-b-(a-b)-(a+c)=-2a.
知识点2 去括号法则的应用
课时3 整式的加减
课时3
1.[2020河北秦皇岛期末]一个多项式与x2-2x+1的和是3x-2,则这个多项式为 ( )
A.x2-5x+3 B.-x2+x-1
C.-x2+5x-3 D.x2-5x-13
答案
1.C 【解析】 由题意得,这个多项式为3x-2-(x2-2x+1)=3x-2-x2+2x-1=-x2+5x-3.故选C.
知识点 整式的加减
2.如果多项式N减去-3x+5,再加上x2-x-7后得5x2-3x-1,那么N为 ( )
A.4x2+5x+11 B.4x2-5x-11
C.4x2-5x+11 D.4x2+5x-11
答案
2.C 【解析】 由题意得,N-(-3x+5)+(x2-x-7)=5x2-3x-1,所以N=(5x2-3x-1)+(-3x+5)-(x2-x-7)=5x2-3x-1-3x+5-x2+x+7=4x2-5x+11.故选C.
知识点 整式的加减
3.若(ax2-2xy+y2)-(-ax2+bxy+2y2)=6x2-9xy+cy2成立,则a,b,c的值分别为 ( )
A.3,-7,-1 B.-3,7,-1
C.3,7,-1 D.-3,-7,1
答案
3.C 【解析】 (ax2-2xy+y2)-(-ax2+bxy+2y2)=ax2-2xy+????2+????????2-bxy-2y2=2ax2-(b+2)xy-y2=6x2-9xy+cy2,所以2a=6,
-(b+2)=-9,c=-1,解得a=3,b=7,c=-1.故选C.
?
知识点 整式的加减
4.设M=x2-8x+22,N=-x2-8x-3,那么M与N的大小关系是 ( )
A.M>N B.M=N
C.M
4.A 【解析】 因为M=x2-8x+22,N=-x2-8x-3,所以M-N=x2-8x+22-(-x2-8x-3)=x2-8x+22+x2+8x+3=2x2+25>0,所以M>N.故选A.
知识点 整式的加减
5.一个两位数x,个位上的数字是a,十位上的数字是b,交换个位与十位上的数字得到一个新的两位数y,则下列各数一定能整除x-y的是 ( )
A.11 B.9 C.5 D.2
答案
5.B 【解析】 根据题意得,x=10b+a,y=10a+b,所以x-y=10b+a-(10a+b)=10(b-a)-(b-a)=9(b-a),所以9一定能整除x-y.故选B.
知识点 整式的加减
6.[2020福建龙岩期末]某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n(m>n)元的价格进了同样的60包茶叶,如果商家以每包????+????2 元的价格卖出这些茶叶,则卖完后,这家商店 ( )
A.盈利了 B.亏损了
C.不盈不亏 D.盈亏不能确定
?
答案
6.A 【解析】 根据题意,得在甲批发市场进的茶叶的利润为40(????+????2-m)=20(m+n)-40m=(20n-20m)(元),在乙批发市场进的茶叶的利润为60(????+????2-n)=30(m+n)-60n=(30m-30n)(元),所以该商店的总利润为20n-20m+30m-30n=10m-10n= 10(m- n)(元),因为m>n,所以m-n>0,即10(m-n)>0,则这家商店盈利了.故选A.
?
知识点 整式的加减
7.[2020重庆渝北区期末]先化简,再求值:3x2y-[xy2-2(2xy2-3x2y)+x2y]+4xy2,其中(x+2)2+|y+1|=0.
答案
7.【解析】 3x2y-[xy2-2(2xy2-3x2y)+x2y]+4xy2
=3x2y-(xy2-4xy2+6x2y+x2y)+4xy2
=3x2y-xy2+4xy2-6x2y-x2y+4xy2
=-4x2y+7xy2.
因为(x+2)2+|y+1|=0,所以x=-2,y=-1.
当x=-2,y=-1时,
原式=-4×(-2)2×(-1)+7×(-2)×(-1)2=16-14=2.
知识点 整式的加减
8.[2020河北石家庄期末]小丽放学回家后准备完成下面的题目:化简(□x2-6x+8)+(6x-5x2-2),发现系数“□”印刷不清楚.
(1)她把“□”猜成3,请你化简(3x2-6x+8)+(6x-5x2-2);
(2)她妈妈说:你猜错了,我看到该题的答案是常数.通过计算说明原题中“□”是什么.
答案
8.【解析】 (1)(3x2-6x+8)+(6x-5x2-2)=3x2-6x+8+6x-5x2-2=-2x2+6.
(2)设“□”是a,
则(□x2-6x+8)+(6x-5x2-2)=(ax2-6x+8)+(6x-5x2-2)=ax2-6x+8+6x-5x2-2=(a-5)x2+6.
因为答案是常数,所以a-5=0,
所以a=5.
知识点 整式的加减
9.已知A=3a2b-2ab2+abc,小明错将“2A-B”看成“2A+B”,算得结果C=4a2b-3ab2+4abc.
(1)计算B的表达式;
(2)小强说正确结果的大小与c的取值无关,对吗?请说明理由.
(3)若b=15,a=18,求正确结果的代数式的值.
?
知识点 整式的加减
答案
9.【解析】 (1)因为2A+B=C,
所以B=C-2A
=4a2b-3ab2+4abc-2(3a2b-2ab2+abc)
=4a2b-3ab2+4abc-6a2b+4ab2-2abc
=-2a2b+ab2+2abc.
(2)对.理由如下:
2A-B=2(3a2b-2ab2+abc)-(-2a2b+ab2+2abc)
=6a2b-4ab2+2abc+2a2b-ab2-2abc
=8a2b-5ab2.
因为正确结果中不含c,所以小强的说法对,正确结果的大小与c无关.
(3)将b=15,a=18代入(2)中的代数式,
得8a2b-5ab2=8×(18)2×15-5×18×(15)2=0.
?
知识点 整式的加减
10.[2020湖北宜昌期中]把正方体(图1)沿着某些棱边剪开,就可以得到正方体的表面展开图,如图2所示.在图1的正方体中,每个面上都写了一个含有字母x的整式,相对两个面上的整式之和都等于4x-7,且A+D=0.(说明:A,B,C,D都表示含有字母x的整式)请回答下面问题:
(1)把图1的正方体沿着某些棱剪开得到它的表面展开图(图2),要剪开 条棱;?
(2)整式B+C= ;?
(3)计算图2中D和“?”所表示的整式.
答案
10.【解析】 (1)7
(2)4x-7
(3)D=4x-7-(2x2-x+1)=4x-7-2x2+x-1=-2x2+5x-8.
A=-D=2x2-5x+8.
“?”=4x-7-(2x2-5x+8)=4x-7-2x2+5x-8=-2x2+9x-15.
知识点 整式的加减
易错疑难集训
集训
1.[2019江苏南京玄武区期末]单项式-3π????2????38的系数与次数分别为 ( )
A.-3和5 B.-38和5
C.-38和6 D.-38π和5
?
答案
1.D
易错点1 基本概念不明
当单项式或多项式中含有π时,不要认为π是字母,它是一个数,因此涉及有关单项式的系数或次数的问题时,π可以作为系数或系数的一部分,而π的指数不能用来计算次数.
2.多项式3x6+2x2y-5y2+2x4y3是 次 项式.?
答案
2.七 四
易错点1 基本概念不明
错解:六 四
分析:x的最高次数是6,而次数最高的项是2x4y3,次数是7.这里错把x的最高次数看成多项式的次数.
3.式子5?????3????4是单项式,还是多项式?
?
答案
3.【解析】 5?????3????4是多项式.
?
易错点1 基本概念不明
本题的易错之处是将分子5x-3y看作一个整体,而误认为5?????3????4是单项式.式子5?????3????4实质上就是54x-34y,由于54x-34y是多项式,所以5?????3????4是多项式.
?
4.计算:4xy2+12x2y+5x2y-12xy2-5.
?
答案
4.【解析】 4xy2+12x2y+5x2y-12xy2-5
=(4-12)xy2+(12+5)x2y-5
=72xy2+112x2y-5.
?
易错点1 基本概念不明
本题的易错之处是将12x2y与-12xy2看作同类项,从而产生错解.
?
合并同类项之前要根据定义确定同类项,不要找错,也不要重复或遗漏,合并时要注意系数的符号.
5.下列说法中,错误的是 ( )
A.代数式x2+y2的意义是x,y的平方的和
B.代数式5(x+y)的意义是5与(x+y)的积
C.x的5倍与y的和的一半,用代数式表示为5x+????2
D.比x的2倍多3的数,用代数式表示为2x+3
?
答案
5.C 【解析】 x的5倍与y的和的一半,用代数式表示为5????+????2.故选C.
?
易错点2 列代数式时弄错运算顺序
6.用代数式表示“a与b的3倍的和除以c”为 .?
答案
6.????+3????????
?
易错点2 列代数式时弄错运算顺序
错解:3(????+????)????或a+3????????
分析:列代数式的关键是审清题意,弄清运算顺序,同时还要注意“除”和“除以”的区别.本题的运算顺序是先“3倍”,再求“和”,最后“除以”.
?
7.计算:(5x2-2x+3)-3(x2-2x+1).
答案
7.【解析】 (5x2-2x+3)-3(x2-2x+1)
=5x2-2x+3-3x2+6x-3
=2x2+4x.
易错点3 去括号时漏乘或符号错误
本题的易错之处是去第二个括号时没有改变括号内各项的符号或括号内的部分项漏乘3.
在去括号的时候,一定要注意括号前面的系数要与括号内的每一项都相乘,当括号外面是负号时,要改变括号内各项的符号.
8.[2020山东青岛崂山区期中]先化简,再求值:A=3a2b-ab2,B=ab2+3a2b,其中a=12,b=13.求5A-B的值.
?
答案
8.【解析】 5A-B=5(3a2b-ab2)-(ab2+3a2b)
=15a2b-5ab2-ab2-3a2b
=12a2b-6ab2.
当a=12,b=13时,
原式=12×14×13-6×12×19=1-13=23.
?
易错点3 去括号时漏乘或符号错误
1.若3x2-2x+b与x2+bx-1的和不含x项,试求b的值,及它们的和,并证明不论x取何值,它们的和总是正数.
答案
1.【解析】 (3x2-2x+b)+(x2+bx-1)
=3x2-2x+b+x2+bx-1
=4x2+(b-2)x+(b-1).
由题意得b-2=0,解得b=2.
所以3x2-2x+b与x2+bx-1的和是4x2+1.
因为任何数的平方都是非负数,所以4x2+1≥1,
所以不论x取何值,它们的和总是正数.
疑难点1 利用单项式的特点求相关字母的值
2.设a表示一个两位数,b表示一个三位数,把a放在b的左边,组成一个五位数x,把b放在a的左边,组成一个五位数y,试问9能否整除x-y?请说明理由.
答案
2.【解析】 9能整除x-y.理由如下:
由题意得,x=1 000a+b,y=100b+a,
所以x-y=1 000a+b-100b-a=999a-99b=9(111a-11b),
因为a,b都是整数,
所以9能整除9(111a-11b),即9能整除x-y.
疑难点2 利用整式的加减解决数字问题
解决本题首先要用字母a,b将x,y表示出来,并寻找9和x-y之间的关系.解题的关键有两点:一是正确用a,b表示出x-y;二是对表示出来的整式进行合理变形.
5 探索与表达规律
课时1 探索数字和图形中的规律
课时1
1.如图所示是某月的日历图.
(1)求日历图中画出的位于楼梯形中的三个数的和.
(2)用代数式表示位于楼梯形中的三个数的和.
(3)若位于这样的楼梯形中的三个数的和等于72,则这三个数分别是多少?
(4)位于这样的楼梯形中的三个数的和可以是57吗?若可以,请求出这三个数;若不可以,请说明理由.
知识点1 探索日历图中的规律
星期日
星期一
星期二
星期三
星期四
星期五
星期六
?
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
?
?
?
答案
1.【解析】 (1)8+14+20=42.
(2)设这三个数中中间的一个数为n,
则另外两个数分别为n-6,n+6,
所以这三个数的和为(n-6)+n+(n+6)=3n.
(3)令3n=72,则n=24,所以n-6=18,n+6=30,
即这三个数分别是18,24,30.
(4)不可以.理由如下:
令3n=57,则n=19,所以n-6=13,n+6=25,
因为13和19在此日历图中位于同一行,不能构成“楼梯”,
所以位于这样的楼梯形中的三个数的和不可以是57.
知识点1 探索日历图中的规律
日历图中的规律
在日历图中,一般可以从横行、竖列、斜列三个方向去寻找规律,也可以从其他角度去探索规律.①横行:相邻两数相差1.②竖列:相邻两数相差7.③斜列:从左上到右下的斜列相邻两数相差8,从右上到左下的斜列相邻两数相差6.
2.观察下列图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星??按此规律,图形⑧中星星的颗数是( )
A.43
B.45
C.51
D.53
答案
2.C 【解析】 设图形 中星星的颗数是an(n为正整数),因为 a1=2,a2=6=a1+4,a3=11=a2+5,a4=17=a3+6,所以a5= a4+7=24,a6=a5+8=32,a7=a6+9=41,a8=a7+10=51.故选C.
知识点2 探索图形中的规律
3.[2019青海中考]如图,将图1中的菱形剪开得到图2,图中共有4个四边形;将图2中的一个四边形剪开得到图3,图中共有7个四边形;如此剪下去,第5个图中共有 个四边形??,第n个图中共有 个四边形.?
答案
3.13 (3n-2) 【解析】 第1个图形中四边形的个数为1,第2个图形中四边形的个数为4=1+3,第3个图形中四边形的个数为7=1+3×2,第4个图形四边形的个数为10=1+3×3??第n个图形中四边形的个数为1+3(n-1)=(3n-2)(个),当n=5时, 3n-2=13.
知识点2 探索图形中的规律
4.[2020山东日照期中]按一定规律排列的一列数依次为-3,6,-11,18,-27,?,则这列数中第9个数及第n(n为正整数)个数分别是 ( )
A.83,-n2+2
B.-83,(-1)n(n2+2)
C.83,(-1)n(n2+2)
D.-83,-n2+2
答案
4.B 【解析】 根据数的变化规律可得,第1个数:-3=(-1)1(12+2);第2个数:6=(-1)2(22+2);第3个数:-11=(-1)3(32+2)??所以第9个数为(-1)9(92+2)=-83,第n个数为(-1)n(n2+2).故选B.
知识点3 探索数字中的规律
5.[2020江苏连云港期中]根据图中数字的规律,则x+y的值是 ( )
?
?
A.729 B.550 C.593 D.738
答案
5.C 【解析】 根据图中数字的规律,得5=22+1,12=5×2+2;17=42+1,72=17×4+4;37=62+1,228=37×6+6;所以x=82+ 1= 65,y=65×8+8=528,所以x+y=65+528=593.故选C.
知识点3 探索数字中的规律
6.观察表格,解答下列问题.
?
(1)求用“ ”框出的五个数的和;
(2)用“ ”任意框出五个数,用代数式表示这五个数的和;
(3)若用“ ”框出的五个数中最上边的数为97,求这五个数的和.
知识点3 探索数字中的规律
答案
6.【解析】 (1)10+25+28+31+46=140.
(2)设中间那个数为n ,
则这五个数的和为(n-18)+(n-3)+n+(n+3)+(n+18)=5n.
(3)这五个数中,最中间那个数为97+18=115,
结合(2)知,这五个数的和为115×5=575.
知识点3 探索数字中的规律
课时2 借助运算解释规律和现象
课时2
1.[2020辽宁鞍山期末]请先观察下列算式,再填空:32-12=8×1,52-32=8×2,72-52=8×3,92-72=8×4,?,通过观察归纳,第
2 020个算式是 . ?
答案
1.4 0412-4 0392=8×2 020 【解析】 根据题意知,第n个算式的左边是(2n+1)2-(2n-1)2,右边是8n,所以第2 020个算式是4 0412-4 0392=8×2 020.
2.[2019广西河池中考]a1,a2,a3,a4,a5,a6,?,是一列数,已知第1个数a1=4,第5个数a5=5,且任意三个相邻的数之和为15,则第2 019个数a2 019的值是 .?
答案
2.6 【解析】 由任意三个相邻的数之和是15可知a1+a2+a3=15,a2+a3+a4=15,a3+a4+a5=15,?,an+an+1+an+2=15,可以推出a1=a4=a7=?=a3n+1,a2=a5=a8=?=a3n+2,a3=a6=a9=?=a3n,所以a2=a5=5,则4+5+a3=15,解得a3=6,所以这列数以4,5,6为一个循环,因为2 019÷3=673,所以a2 019=a3=6.
3.[2020福建厦门外国语学校月考]从2开始,连续的偶数相加,它们和的情况如下表:
(1)若n=7,则S的值为 .?
(2)根据表中的规律猜想:用含n的式子表示S的公式为S=2+4+6+8+?+2n= .?
(3)根据(2)中总结的规律计算300+302+304+?+2 016+2 018+2 020的值.
加数的个数n
和S
1
2=1×2
2
2+4=6=2×3
3
2+4+6=12=3×4
4
2+4+6+8=20=4×5
5
2+4+6+8+10=30=5×6
?
?
答案
3.【解析】 (1)56
(2)n(n+1)
(3)300+302+304+?+2 016+2 018+2 020
=(2+4+6+?+2020)-(2+4+6+?+298)
=1 010×1 011-149×150
=998 760.
4.小明对蔚蔚说:“蔚蔚,你现在在脑子里想好一个整数,然后将这个数乘2加7,把结果再乘3减21.”蔚蔚按照小明的要求做好后,小明很得意地告诉蔚蔚说:“现在你所得的数一定是6的倍数.”蔚蔚非常惊讶,但很快明白了其中的道理,亲爱的同学,你能告诉大家是为什么吗?请你也像小明一样编一个类似的游戏,并说明其中的道理.
答案
4.【解析】 设这个整数是a,则(a×2+7)×3-21=6a,
所以所得的数一定是6的倍数.
所编游戏:一个整数,将这个数乘3减9,把结果再乘5加45,最后结果一定是15的倍数.
说明:设这个整数为b,则(b×3-9)×5+45=15b,所以所得的数一定是15的倍数.(答案不唯一)
5.观察下列三行数.
0,3,8,15,24,?; ①
2,5,10,17,26,?; ②
0,6,16,30,48,?. ③
(1)请写出第①行数是按什么规律排列的.
(2)第②,③行数分别与第①行数对比,有什么关系?
(3)取每行的第n个数,求这三个数的和.
答案
5.【解析】 (1)观察发现:0=12-1,3=22-1,8=32-1,15=42-1,24=52-1,?,
可得第①行数的排列规律:第n个数为n2-1.
(2)第②行的数是第①行相应的数加2得到的,第③行的数是第①行相应的数的2倍.
(3)根据题意,所求的和为(n2-1)+[(n2-1)+2]+2(n2-1)=n2-1+n2-1+2+2n2-2=4n2-2.
6.观察下列等式:
第1个等式:a1=11×3=12×(1 ??13);
第2个等式:a2=13×5=12×(13?15);
第3个等式:a3=15×7=12×(15?17);
?
请按以上规律解答下列问题:
(1)列出第5个等式:a5= ;?
(2)计算a1+a2+a3+a4+a5的结果.
(3)计算a1+a2+a3+?+an的结果.
?
答案
6.【解析】 (1)19×11=12×(19?111)
?
答案
(2)a1+a2+a3+a4+a5
=12×(1 ??13)+12×(13?15)+12×(15?17)+12×(17?19)+12×(19?111)
=12×(1 ??13+13?15+15?17+17?19+19?111)
=12×(1 ??111)
=12×1011
=511.
(3)a1+a2+a3+?+an
=12×(1 ??13)+12×(13?15)+12×(15?17)+?+12(12?????1?12????+1)
=12[(1 ??13)+(13?15)+(15?17)+?+(12?????1?12????+1)]
=12(1 ??13+13?15+15?17+?+12?????1?12????+1)
=12(1 ??12????+1).
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
