北师大版七年级上册数学第二章有理数及其运算素养拓展+中考真题课件(57张PPT)
文档属性
| 名称 | 北师大版七年级上册数学第二章有理数及其运算素养拓展+中考真题课件(57张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 887.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-16 00:00:00 | ||
图片预览










文档简介
第二章 有理数及其运算
数学·七年级上册·北师
专题1 数轴
专项素养拓训
1.[2020广西钦州期末]如图,数轴上点P表示的有理数是a,若a+b>0,则有理数b在数轴上对应的点可能是 ( )
A.E
B.F
C.M
D.N
答案
1.D 【解析】 由题中数轴可知-20,则b>|a|,则只有点N表示的数符合题意.故选D.
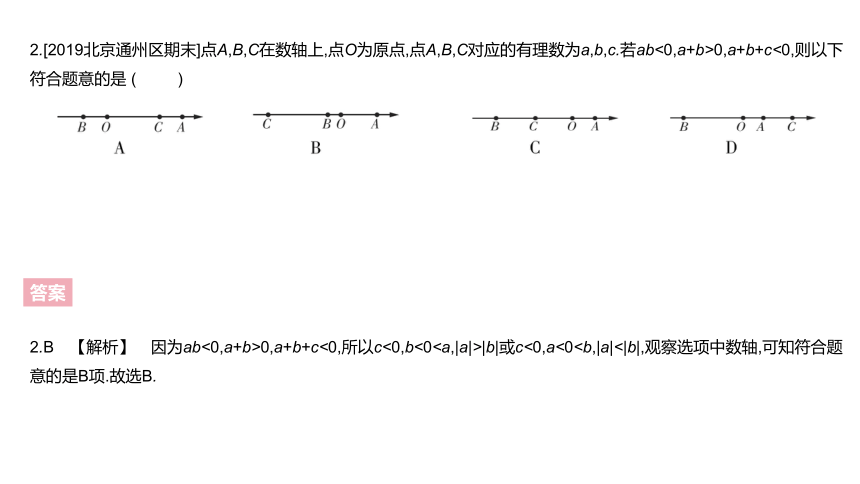
2.[2019北京通州区期末]点A,B,C在数轴上,点O为原点,点A,B,C对应的有理数为a,b,c.若ab<0,a+b>0,a+b+c<0,则以下符合题意的是 ( )
答案
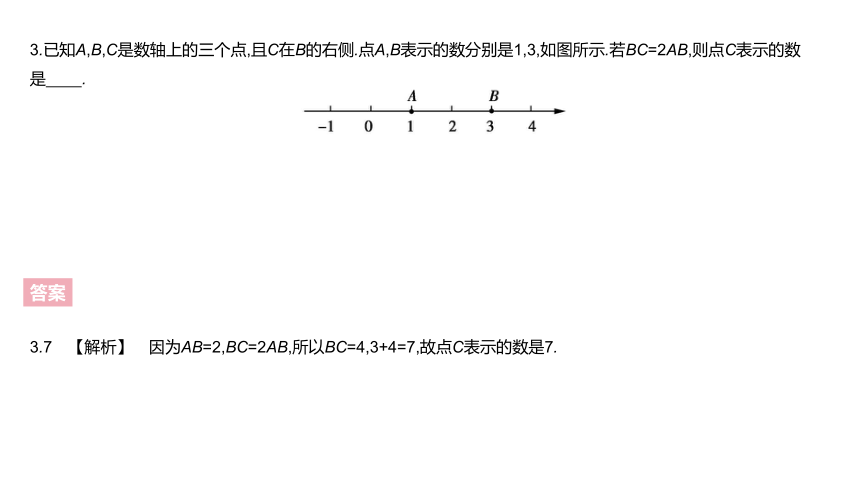
2.B 【解析】 因为ab<0,a+b>0,a+b+c<0,所以c<0,b<0|b|或c<0,a<03.已知A,B,C是数轴上的三个点,且C在B的右侧.点A,B表示的数分别是1,3,如图所示.若BC=2AB,则点C表示的数是 .?
答案
3.7 【解析】 因为AB=2,BC=2AB,所以BC=4,3+4=7,故点C表示的数是7.
4.数轴上点M,N表示的数的绝对值相等,点P表示的数为-3,且点P与点M之间的距离为5,求点M,N所表示的数.
答案
4.【解析】 分两种情况:
(1)当点M在点P的左侧时,点M表示的数是-8,
因为点M,N表示的数的绝对值相等,所以点N表示的数是8;
(2)当点M在点P的右侧时,点M表示的数是2,
因为点M,N表示的数的绝对值相等,所以点N表示的数是-2.
综上所述,点M,N所表示的数为-8,8或2,-2.
专题2 有理数的运算
专项素养拓训
5.计算:
(1)(-557)+(-612)+(-1427)-(-16.5); (2)(-0.5)-(-314)+2.75-(+712).
?
答案
5.【解析】 (1)(-557)+(-612)+(-1427)-(-16.5)
=[(-557)+(-1427)]+[(-6.5)-(-16.5)]
=-20+10
=-10.
(2)(-0.5)-(-314)+2.75-(+712)
=[-12+(-712)]+(314+234)
=-8+6
=-2.
?
类型1 有理数的混合运算
6.计算:
(1)-12 020-(1-12)÷|3-(-3)2|;
(2)(-2)2×0.25-4÷[(12)2-38]-40.
?
类型1 有理数的混合运算
答案
6.【解析】 (1)-12 020-(1-12)÷|3-(-3)2|
=-1-12÷|3-9|
=-1-12÷|-6|
=-1-112
=-1112.
(2)(-2)2×0.25-4÷[(12)2-38]-40
=4×0.25-4÷(14?38)-40
=1-4÷(-18)-40
=1+32-40
=-7.
?
类型1 有理数的混合运算
7.计算:
(1)991718×(-9);
(2)45×(-513)-(-35)×(-513)-513×(-135).
?
类型2 乘法分配律的运用
答案
7.【解析】 (1)991718×(-9)
=(100-118)×(-9)
=-900+12
=-89912.
(2)45×(-513)-(-35)×(-513)-513×(-135)
=-45×513?35×513+513×135
=513×[(-45)-35+135]
=513×15
=113.
?
类型2 乘法分配律的运用
8.先阅读并填空,再解答问题.
我们知道11×2=1-12,12×3=12?13,13×4=13?14,
那么14×5= ,12?018×2?019= .?
利用上述式子中的规律计算:
(1)12+16+112+120+130+142+156+172;
(2)12×4+14×6+16×8+?+12?018×2?020.
?
类型3 运算律解答规律问题
答案
8.【解析】 14?15 12?018?12?019
(1)12+16+112+120+130+142+156+172
=11×2+12×3+13×4+14×5+15×6+16×7+17×8+18×9
?
答案
=1-12+12?13+?+18?19
=1-19
=89.
(2)12×4+14×6+16×8+?+12?018×2?020
=12×(12?14+?+12?018?12?020)
=12×(12?12?020)
=1?0094?040.
?
类型3 运算律解答规律问题
通过阅读题目中给出的解题方法,设法将每个分数转化为两个分数的差,再将相邻的两个数互相抵消,从而使问题得到解决.
综合素养拓训
有理数是整个初中阶段最基础和最重要的内容之一,学习本章内容有助于培养数感和数学运算能力.数感主要是指关于数与数量、数量关系、运算结果估计等方面的感悟,建立数感有助于理解现实生活中数的意义,理解或表述具体情境中的数量关系.数学运算是指在明晰运算对象的基础上,依据运算法则解决问题的过程.数学运算是数学活动的基本形式,也是演绎推理的一种形式,是得到数学结果的重要手段,也是数学学科核心素养之一.
1.[利用数字变化规律解决实际问题]一个容器装有1升水,按照如下要求把水倒出:第1次倒出12 升水,第2次倒出的水量是12 升的13 ,第3次倒出的水量是13 升的14,第4次倒出的水量是14 升的15 ??按照这种倒水的方法,倒了10次后容器内剩余的水量是 ( )
A.18 升 B.19 升 C.110 升 D.111 升
?
答案
1.D 【解析】 根据题意列出算式为1-12?12×13?13×14-?-110×111=1-12-(12?13)-(13?14)-?-(110?111)=1-12?12+13?13+14-?-110+111=111(升).故选D.
?
2.规定一种运算: =ad-bc.例如: =2×5-3×4=-2,请你按照这种运算的规定,计算
的值.
答案
2.【解析】 根据题意,得 =1×0.5-(-3)×2=0.5+6=6.5,
(?1)2?020 41.25 ?9=(-1)2 020×(-9)-4×1.25=-9-5=-14.
所以 +(?1)2?020 41.25 ?9=6.5-14=-7.5.
?
3.阅读理解题:从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
(1)可知●= ,○= ,x= .?
(2)试判断第2 019个格子中的数是多少,并给出相应的理由.
(3)判断:前n个格子中所填整数之和是否可能为2 020?若能,求出n的值;若不能,请说明理由.
(4)若从前n个格子中任取两个数并用大数减去小数得到差值,而后将所有的这样的差值累加起来称为前n项的累差值.例如前3项的累差值为|1-●|+|1-○|+|●-○|.则前3项的累差值为 .若取前10项,则前10项的累差值为多少?(请给出必要的计算过程)?
1
●
○
x
7
?
?
?
-3
?
?
答案
3.【解析】 (1)7 -3 1
(2)第2 019个格子中的数是-3.
由于题格中的数依次是1,7,-3,1,7,-3,?,每3个数循环一次,而 2 019 能被3整除,故第2 019个数为-3.
(3)能.由1+7+(-3)=5,而2 020÷5=404,
得n=404×3=1 212.
(4)20
前10项的累差值为210.
由于前10个数中1出现了4次,而7与-3各出现了3次,
所以前10项的累差值为|1-7|×4×3+|1-(-3)|×4×3+|7-(-3)|×3×3=210.
答案
1.B
一、选择题
1.如果向北走2 m,记作+2 m,那么-5 m表示 ( )
A.向东走5 m B.向南走5 m
C.向西走5 m D.向北走5 m
答案
2.A
2.下列每个选项中的两个数,互为相反数的是 ( )
A.4和-4 B.-3和13
C.|-2|和2 D.|-2|和12
?
答案
3.A
3.[2018浙江宁波中考]在-3,-1,0,1这四个数中,最小的数是 ( )
A.-3 B.-1 C.0 D.1
答案
4.C 【解析】 A项,-(-3)=3,-|-3|=-3,所以A项不符合题意;B项,-22=-4,(-2)2=4,所以B项不符合题意;C项,(-2)3=-8,-23=
-8,所以C项符合题意;D项,223=43,(23)2=49,所以D项不符合题意.故选C.
?
4.下列各对数中,相等的一对数是 ( )
A.-(-3)与-|-3| B.-22与(-2)2
C.(-2)3与-23 D.223与(23)2
?
答案
5.B 【解析】 整数分为正整数、0和负整数,故①错误;0等于它的相反数,故②错误;如果a大于b,那么a的倒数不一定小于b的倒数,例如1>0,但是0没有倒数,不能说1的倒数小于0的倒数,所以⑤错误.故选B.
5.给出下列说法:
①整数分为正整数和负整数;
②任何数都不等于它的相反数;
③一个数的绝对值越大,它在数轴上表示的点离原点越远;
④互为相反数的两个数的同一偶数次方相等;
⑤如果a大于b,那么a的倒数小于b的倒数.
其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
答案
6.D 【解析】 A项,(-5.8)-(-5.8)=(-5.8)+5.8=0,故A项错误;B项,-42÷14×4=-16×4×4=-256,故B项错误;C项,-23×(-3)2=
-8×9=-72,故C项错误;D项,[(-5)2+4×(-5)]×(-3)2=5×9=45,故D项正确.故选D.
?
6.[2020山东枣庄期中]下列各式中,计算正确的是 ( )
A.(-5.8)-(-5.8)=-11.6
B.-42÷14×4=-16
C.-23×(-3)2=72
D.[(-5)2+4×(-5)]×(-3)2=45
?
答案
7.A 【解析】 由题中数轴知c0,a+c<0,b-a<0,bc>0.故选A.
7.有理数a,b,c在数轴上的对应点的位置如图所示,则下列结论正确的是 ( )
A.a+b>0
B.a+c=0
C.b-a>0
D.bc<0
答案
8.A 【解析】 由题意得,(-3)⊕4=-3×4-(-3)=-12+3=-9.故选A.
8.定义新运算:a⊕b=ab-a.例如3⊕2=3×2-3=3.则(-3)⊕4= ( )
A.-9 B.12 C.-15 D.4
答案
9.1.2×1011
二、填空题
9. [2018黑龙江龙东地区中考]人民日报2018年2月23日报道,2017年黑龙江粮食总产量达到1 203.76亿斤,成功超越1 200亿斤,连续七年居全国首位,将1 200亿斤用科学记数法表示为 斤.?
10.如图是计算机计算程序,若开始输入x=-2,则最后输出的结果是 .?
10.-17 【解析】 根据题意可知,(-2)×4-(-3)=-8+3=-5,再把-5代入计算,(-5)×4-(-3)=-20+3=-17<-5,即-17为输出结果.
答案
11.2 500米 【解析】 (24-4)÷0.8×100=20÷0.8×100=25×100=2 500(米).
11.在某地区,夏季高山上的温度从山脚起每升高100米平均降低0.8 ℃,已知山脚的温度是24 ℃,山顶的温度是4 ℃,这座山的高度是 .?
12.已知a,b互为相反数,c,d互为倒数,x的绝对值是2,则3x-(a+b+cd)x= .?
12.±4 【解析】 因为a,b互为相反数,c,d互为倒数,x的绝对值是2,所以a+b=0,cd=1,|x|=2,所以x=±2.当x=2时,3x-(a+ b+cd)x=6-2=4;当x=-2时,3x-(a+b+cd)x=-6+2=-4.综上,3x-(a+b+cd)x=±4.
答案
13.【解析】 (1)正数集合:{227,2 019,?};
(2)负数集合:{-4,-|-43| ,-3.14,-(+5),?};
(3)整数集合:{-4,0,2 019,-(+5),?};
(4)分数集合:{-|-43|,227,-3.14,?}.
?
三、解答题
13.把下列各数分别填入相应的集合中:
-4,-|-43|,0,227,-3.14,2 019,-(+5).
(1)正数集合:{ ?};
(2)负数集合: { ?};
(3)整数集合: { ?};
(4)分数集合: { ?}.
?
答案
14.【解析】 (1)100÷(-2)2-(-2)÷(-23)
=100÷4-3
=25-3
=22.
?
14. 计算:
(1)100÷(-2)2-(-2)÷(-23);
(2)(-12)2+12×(23-|23-2|);
(3)(-3.75)+2.85+(-114)+(-12)+3.15+(-2.5);
(4)[212-(38+16?34)×24]÷5×(-1)2 021.
?
答案
(2)(-12)2+12×(23-|23-2|)
=14+12×(23-2+23)
=14+12×(-23)
=14?13
=-112.
(3)(-3.75)+2.85+(-114)+(-12)+3.15+(-2.5)
=[(-3.75)+(-114)]+2.85+3.15+(-2.5)+(-12)
=-5+6+(-3)
=-2.
?
答案
(4)[212-(38+16?34)×24]÷5×(-1)2 021
=[212-(38×24+16×24-34×24)]÷5×(-1)2 021
=(212-9-4+18)×(-15)
=-12-1
=-112.
?
15.如图,数轴上两点A,B分别位于原点O的两侧,OA=OB=m,点A,B对应的数分别为a,b,点P为数轴上一点,设点P对应的数与a的和为x.
(1)a+b= ;?
(2)若m=1,点P在点B的右侧,BP=2,写出点P对应的数,并求出x的值;
(3)若m=2,点P在点A的左侧,BP=19,求x的值.
答案
15.【解析】 (1)0
(2)若m=1,则a=-1,b=1,
因为点P在点B的右侧,BP=2,
所以点P对应的数为3,
所以x=-1+3=2.
(3)若m=2,则a=-2,b=2.
因为点P在点A的左侧,BP=19,
所以点P对应的数为-17,
所以x=-2+(-17)=-19.
16.某风景区在10月1日至10月8日这八天中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数).
(1)10月1日至10月5日这五天中,每天到该风景区的游客人数最多的是10月 日.?
(2)若9月30日的游客人数为2万人,10月8日到该风景区的游客人数与9月30日的游客人数持平,则上表中“■”表示的数应是多少?
(3)若9月30日的游客人数为2万人,求10月1日至10月5日这五天的游客总人数.
日期
10月
1日
10月
2日
10月
3日
10月
4日
10月
5日
10月
6日
10月
7日
10月
8日
人数变
化/万人
1.2
-0.2
0.8
-0.4
0.6
0.2
■
-1.2
答案
16.【解析】 (1)5
(2)因为9月30日的游客人数为2万人,
所以10月8日的游客人数也为2万人,
而10月8日的游客人数比前一天减少了1.2万人,
故10月7日的游客人数为3.2万人,
因为到10月6日的游客人数为2+1.2-0.2+0.8-0.4+0.6+0.2=4.2(万人),
所以题表中“■”表示的数应是-1.
(3)10月1日至10月5日这五天的游客总人数是(2+1.2)+(3.2-0.2)+(3+0.8)+(3.8-0.4)+(3.4+0.6)=17.4(万人).
第二章 有理数及其运算中考模拟+真题
数学·七年级上册·北师
答案
1.D 【解析】 因为|a-2|+(b+3)2=0,所以a=2,b=-3,所以ba=(-3)2=9.故选D.
1.[2020广东肇庆一模]已知|a-2|+(b+3)2=0,则ba的值是 ( )
A.-6 B.6 C.-9 D.9
答案
2.C
2.[2020河南郑州一模]华为Mate 30 5G系列手机是近期相当火爆的5G国产手机,它采用的麒麟990 5G芯片在指甲盖大小的尺寸上集成了103亿个晶体管,将103亿用科学记数法表示为 ( )
A.1.03×109 B.10.3×109
C.1.03×1010 D.1.03×1011
答案
3.B 【解析】 根据题中数轴,可得a<00,a+b>0,????????<0.故选B.
?
3.[2020宁夏银川兴庆区二模]已知点A,B在数轴上的位置如图所示,其表示的数分别是a和b,给出以下结论:
(1)b-a<0;(2)|a|<|b|;(3)a+b>0;(4)????????>0.
其中正确的是 ( )
A.(1)(2)
B.(2)(3)
C.(3)(4)
D.(1)(4)
?
答案
4.B
4.[2020河北模拟]利用运算律简便计算52×(-999)+49×(-999)+999正确的是 ( )
A.-999×(52+49)=-999×101=-100 899
B.-999×(52+49-1)=-999×100=-99 900
C.-999×(52+49+1)=-999×102=-101 898
D.-999×(52+49-99)=-999×2=-1 998
答案
5.D 【解析】 因为a,b互为相反数,且都不为0,所以a+b=0,????????=-1,所以(a-1+b)(1-????????)=(-1)×[1-(-1)]=(-1)×2=-2.故选D.
?
5.[2020四川绵阳期末]若a,b互为相反数,且都不为0,则(a-1+b)(1-????????)的值为 ( )
A.0 B.-1 C.1 D.-2
?
答案
6.【解析】 (1)5+48÷22×(-14)-1
=5+48÷4×(-14)-1
=5-3-1
=1.
(2)(-2)2×0.25-4÷[(12)2-38]-40
=4×0.25-4÷(-18)-40
=1+32-40
=-7.
?
6.[2019北京期末]计算:
(1)5+48÷22×(-14)-1;
(2)(-2)2×0.25-4÷[(12)2-38]-40.
?
7.[2020江苏南通模拟]如图,在一条不完整的数轴上,一动点A向左移动4个单位长度到达点B,再向右移动7个单位长度到达点C.
(1)若点A表示的数为0,求点B、点C表示的数;
(2)若点C表示的数为5,求点B、点A表示的数;
(3)若点A,C表示的数互为相反数,求点B表示的数.
答案
7.【解析】 (1)若点A表示的数为0,
因为0-4=-4,所以点B表示的数为-4,
因为-4+7=3,所以点C表示的数为3.
(2)若点C表示的数为5,
因为5-7=-2,所以点B表示的数为-2,
因为-2+4=2,所以点A表示的数为2.
(3)若点A,C表示的数互为相反数,
因为7-4=3,所以点A表示的数为-1.5,
因为-1.5-4=-5.5,所以点B表示的数为-5.5.
答案
8.【解析】 (1)如图所示.
(2)2-(-1)=3(km).
所以小彬家与学校之间的距离是3 km.
(3)小明一共跑了(2+1.5+1)×2=9(km),
9 000÷250=36(min).
答:小明跑步一共用了36 min.
8.[2020山东济宁任城区期中]小明早晨跑步,他从自己家出发,向东跑了2 km到达小彬家,继续向东跑了1.5 km到达小红家,然后又向西跑了4.5 km到达学校,最后向东跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1 km,在如图所示的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250 m/min,那么小明跑步一共用了多长时间?
答案
1.A
1.[2019海南中考]如果收入100元记作+100元,那么支出100元记作 ( )
A.-100元 B.+100元
C.-200元 D.+200元
答案
2.B
2.[2019辽宁沈阳中考]2019年1月1日起我国开始贯彻《国务院关于印发个人所得税专项附加扣除暂行办法的通知》的要求,此次减税范围广,其中有6 500万人减税70%以上,将数据6 500用科学记数法表示为 ( )
A.6.5×102 B.6.5×103
C.65×103 D.0.65×104
答案
3.A 【解析】 由题意得,四个排球质量偏差的绝对值分别为0.6,0.7,2.5,3.5,绝对值最小的为0.6,最接近标准.故选A.
3.[2019内蒙古呼和浩特中考]如图,检测排球,其中质量超过标准的克数记为正数,不足的克数记为负数,下面检测过的四个排球,在其上方标注了检测结果,其中质量最接近标准的一个是 ( )
?
A B C D
答案
4.C 【解析】 由“两个负数,绝对值大的反而小”及“正数大于负数,0大于负数,正数大于0”,可知-1<-12<0<2,故最小的有理数是-1.故选C.
?
4.[2019辽宁鞍山中考]在有理数2,0,-1,-12中,最小的是 ( )
A.2 B.0 C.-1 D.-12
?
答案
5.C 【解析】 温差=最高气温-最低气温.星期一的温差为10-3=7(℃);星期二的温差为12-0=12(℃);星期三的温差为11-(-2)=13(℃);星期四的温差为9-(-3)=12(℃).故选C.
5.[2019浙江金华中考]某地一周前四天每天的最高气温与最低气温如下表,则这四天中温差最大的是 ( )
A.星期一 B.星期二 C.星期三 D.星期四
星期
一
二
三
四
最高气温
10 ℃
12 ℃
11 ℃
9 ℃
最低气温
3 ℃
0 ℃
-2 ℃
-3 ℃
答案
6.C 【解析】 根据题中数轴知m|n|,故A,D项错误;因为m|n|,所以|m|>-n,-m>|n|,故B项错误,C项正确.故选C.
6.[2019黑龙江大庆中考]数m,n在数轴上的对应点如图所示,则下列各式子正确的是 ( )
?A.m>n
B.-n>|m|
C.-m>|n|
D.|m|<|n|
答案
7.-3
7.[2019四川攀枝花中考]|-3|的相反数是 .?
8.[2019山东聊城中考]计算:(-13?12)÷54= .?
?
8.-23 【解析】 (-13?12)÷54=(-56)×45=-23.
?
答案
9.【解析】 -5×2+3÷13-(-1)
=-10+9+1
=0.
?
9.[2019广西梧州中考]计算:-5×2+3÷13-(-1).
?
答案
10.【解析】 (1)1+2-6-9=3-15=-12.
(2)因为1÷2×6=3,
所以3□9=-6,
所以□内是-.
(3)-20.
当原式为1-2×6-9时,计算所得数最小,为-20.
10.[2019河北中考]有一个填写运算符号的游戏:在“1□2□6□9”中的每个□内,填入+,-,×,÷中的某一个(可重复使用),然后计算结果.
(1)计算:1+2-6-9.
(2)若1÷2×6□9=-6,请推算□内的符号.
(3)在“1□2□6-9”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
数学·七年级上册·北师
专题1 数轴
专项素养拓训
1.[2020广西钦州期末]如图,数轴上点P表示的有理数是a,若a+b>0,则有理数b在数轴上对应的点可能是 ( )
A.E
B.F
C.M
D.N
答案
1.D 【解析】 由题中数轴可知-2
2.[2019北京通州区期末]点A,B,C在数轴上,点O为原点,点A,B,C对应的有理数为a,b,c.若ab<0,a+b>0,a+b+c<0,则以下符合题意的是 ( )
答案
2.B 【解析】 因为ab<0,a+b>0,a+b+c<0,所以c<0,b<0
答案
3.7 【解析】 因为AB=2,BC=2AB,所以BC=4,3+4=7,故点C表示的数是7.
4.数轴上点M,N表示的数的绝对值相等,点P表示的数为-3,且点P与点M之间的距离为5,求点M,N所表示的数.
答案
4.【解析】 分两种情况:
(1)当点M在点P的左侧时,点M表示的数是-8,
因为点M,N表示的数的绝对值相等,所以点N表示的数是8;
(2)当点M在点P的右侧时,点M表示的数是2,
因为点M,N表示的数的绝对值相等,所以点N表示的数是-2.
综上所述,点M,N所表示的数为-8,8或2,-2.
专题2 有理数的运算
专项素养拓训
5.计算:
(1)(-557)+(-612)+(-1427)-(-16.5); (2)(-0.5)-(-314)+2.75-(+712).
?
答案
5.【解析】 (1)(-557)+(-612)+(-1427)-(-16.5)
=[(-557)+(-1427)]+[(-6.5)-(-16.5)]
=-20+10
=-10.
(2)(-0.5)-(-314)+2.75-(+712)
=[-12+(-712)]+(314+234)
=-8+6
=-2.
?
类型1 有理数的混合运算
6.计算:
(1)-12 020-(1-12)÷|3-(-3)2|;
(2)(-2)2×0.25-4÷[(12)2-38]-40.
?
类型1 有理数的混合运算
答案
6.【解析】 (1)-12 020-(1-12)÷|3-(-3)2|
=-1-12÷|3-9|
=-1-12÷|-6|
=-1-112
=-1112.
(2)(-2)2×0.25-4÷[(12)2-38]-40
=4×0.25-4÷(14?38)-40
=1-4÷(-18)-40
=1+32-40
=-7.
?
类型1 有理数的混合运算
7.计算:
(1)991718×(-9);
(2)45×(-513)-(-35)×(-513)-513×(-135).
?
类型2 乘法分配律的运用
答案
7.【解析】 (1)991718×(-9)
=(100-118)×(-9)
=-900+12
=-89912.
(2)45×(-513)-(-35)×(-513)-513×(-135)
=-45×513?35×513+513×135
=513×[(-45)-35+135]
=513×15
=113.
?
类型2 乘法分配律的运用
8.先阅读并填空,再解答问题.
我们知道11×2=1-12,12×3=12?13,13×4=13?14,
那么14×5= ,12?018×2?019= .?
利用上述式子中的规律计算:
(1)12+16+112+120+130+142+156+172;
(2)12×4+14×6+16×8+?+12?018×2?020.
?
类型3 运算律解答规律问题
答案
8.【解析】 14?15 12?018?12?019
(1)12+16+112+120+130+142+156+172
=11×2+12×3+13×4+14×5+15×6+16×7+17×8+18×9
?
答案
=1-12+12?13+?+18?19
=1-19
=89.
(2)12×4+14×6+16×8+?+12?018×2?020
=12×(12?14+?+12?018?12?020)
=12×(12?12?020)
=1?0094?040.
?
类型3 运算律解答规律问题
通过阅读题目中给出的解题方法,设法将每个分数转化为两个分数的差,再将相邻的两个数互相抵消,从而使问题得到解决.
综合素养拓训
有理数是整个初中阶段最基础和最重要的内容之一,学习本章内容有助于培养数感和数学运算能力.数感主要是指关于数与数量、数量关系、运算结果估计等方面的感悟,建立数感有助于理解现实生活中数的意义,理解或表述具体情境中的数量关系.数学运算是指在明晰运算对象的基础上,依据运算法则解决问题的过程.数学运算是数学活动的基本形式,也是演绎推理的一种形式,是得到数学结果的重要手段,也是数学学科核心素养之一.
1.[利用数字变化规律解决实际问题]一个容器装有1升水,按照如下要求把水倒出:第1次倒出12 升水,第2次倒出的水量是12 升的13 ,第3次倒出的水量是13 升的14,第4次倒出的水量是14 升的15 ??按照这种倒水的方法,倒了10次后容器内剩余的水量是 ( )
A.18 升 B.19 升 C.110 升 D.111 升
?
答案
1.D 【解析】 根据题意列出算式为1-12?12×13?13×14-?-110×111=1-12-(12?13)-(13?14)-?-(110?111)=1-12?12+13?13+14-?-110+111=111(升).故选D.
?
2.规定一种运算: =ad-bc.例如: =2×5-3×4=-2,请你按照这种运算的规定,计算
的值.
答案
2.【解析】 根据题意,得 =1×0.5-(-3)×2=0.5+6=6.5,
(?1)2?020 41.25 ?9=(-1)2 020×(-9)-4×1.25=-9-5=-14.
所以 +(?1)2?020 41.25 ?9=6.5-14=-7.5.
?
3.阅读理解题:从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
(1)可知●= ,○= ,x= .?
(2)试判断第2 019个格子中的数是多少,并给出相应的理由.
(3)判断:前n个格子中所填整数之和是否可能为2 020?若能,求出n的值;若不能,请说明理由.
(4)若从前n个格子中任取两个数并用大数减去小数得到差值,而后将所有的这样的差值累加起来称为前n项的累差值.例如前3项的累差值为|1-●|+|1-○|+|●-○|.则前3项的累差值为 .若取前10项,则前10项的累差值为多少?(请给出必要的计算过程)?
1
●
○
x
7
?
?
?
-3
?
?
答案
3.【解析】 (1)7 -3 1
(2)第2 019个格子中的数是-3.
由于题格中的数依次是1,7,-3,1,7,-3,?,每3个数循环一次,而 2 019 能被3整除,故第2 019个数为-3.
(3)能.由1+7+(-3)=5,而2 020÷5=404,
得n=404×3=1 212.
(4)20
前10项的累差值为210.
由于前10个数中1出现了4次,而7与-3各出现了3次,
所以前10项的累差值为|1-7|×4×3+|1-(-3)|×4×3+|7-(-3)|×3×3=210.
答案
1.B
一、选择题
1.如果向北走2 m,记作+2 m,那么-5 m表示 ( )
A.向东走5 m B.向南走5 m
C.向西走5 m D.向北走5 m
答案
2.A
2.下列每个选项中的两个数,互为相反数的是 ( )
A.4和-4 B.-3和13
C.|-2|和2 D.|-2|和12
?
答案
3.A
3.[2018浙江宁波中考]在-3,-1,0,1这四个数中,最小的数是 ( )
A.-3 B.-1 C.0 D.1
答案
4.C 【解析】 A项,-(-3)=3,-|-3|=-3,所以A项不符合题意;B项,-22=-4,(-2)2=4,所以B项不符合题意;C项,(-2)3=-8,-23=
-8,所以C项符合题意;D项,223=43,(23)2=49,所以D项不符合题意.故选C.
?
4.下列各对数中,相等的一对数是 ( )
A.-(-3)与-|-3| B.-22与(-2)2
C.(-2)3与-23 D.223与(23)2
?
答案
5.B 【解析】 整数分为正整数、0和负整数,故①错误;0等于它的相反数,故②错误;如果a大于b,那么a的倒数不一定小于b的倒数,例如1>0,但是0没有倒数,不能说1的倒数小于0的倒数,所以⑤错误.故选B.
5.给出下列说法:
①整数分为正整数和负整数;
②任何数都不等于它的相反数;
③一个数的绝对值越大,它在数轴上表示的点离原点越远;
④互为相反数的两个数的同一偶数次方相等;
⑤如果a大于b,那么a的倒数小于b的倒数.
其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
答案
6.D 【解析】 A项,(-5.8)-(-5.8)=(-5.8)+5.8=0,故A项错误;B项,-42÷14×4=-16×4×4=-256,故B项错误;C项,-23×(-3)2=
-8×9=-72,故C项错误;D项,[(-5)2+4×(-5)]×(-3)2=5×9=45,故D项正确.故选D.
?
6.[2020山东枣庄期中]下列各式中,计算正确的是 ( )
A.(-5.8)-(-5.8)=-11.6
B.-42÷14×4=-16
C.-23×(-3)2=72
D.[(-5)2+4×(-5)]×(-3)2=45
?
答案
7.A 【解析】 由题中数轴知c
7.有理数a,b,c在数轴上的对应点的位置如图所示,则下列结论正确的是 ( )
A.a+b>0
B.a+c=0
C.b-a>0
D.bc<0
答案
8.A 【解析】 由题意得,(-3)⊕4=-3×4-(-3)=-12+3=-9.故选A.
8.定义新运算:a⊕b=ab-a.例如3⊕2=3×2-3=3.则(-3)⊕4= ( )
A.-9 B.12 C.-15 D.4
答案
9.1.2×1011
二、填空题
9. [2018黑龙江龙东地区中考]人民日报2018年2月23日报道,2017年黑龙江粮食总产量达到1 203.76亿斤,成功超越1 200亿斤,连续七年居全国首位,将1 200亿斤用科学记数法表示为 斤.?
10.如图是计算机计算程序,若开始输入x=-2,则最后输出的结果是 .?
10.-17 【解析】 根据题意可知,(-2)×4-(-3)=-8+3=-5,再把-5代入计算,(-5)×4-(-3)=-20+3=-17<-5,即-17为输出结果.
答案
11.2 500米 【解析】 (24-4)÷0.8×100=20÷0.8×100=25×100=2 500(米).
11.在某地区,夏季高山上的温度从山脚起每升高100米平均降低0.8 ℃,已知山脚的温度是24 ℃,山顶的温度是4 ℃,这座山的高度是 .?
12.已知a,b互为相反数,c,d互为倒数,x的绝对值是2,则3x-(a+b+cd)x= .?
12.±4 【解析】 因为a,b互为相反数,c,d互为倒数,x的绝对值是2,所以a+b=0,cd=1,|x|=2,所以x=±2.当x=2时,3x-(a+ b+cd)x=6-2=4;当x=-2时,3x-(a+b+cd)x=-6+2=-4.综上,3x-(a+b+cd)x=±4.
答案
13.【解析】 (1)正数集合:{227,2 019,?};
(2)负数集合:{-4,-|-43| ,-3.14,-(+5),?};
(3)整数集合:{-4,0,2 019,-(+5),?};
(4)分数集合:{-|-43|,227,-3.14,?}.
?
三、解答题
13.把下列各数分别填入相应的集合中:
-4,-|-43|,0,227,-3.14,2 019,-(+5).
(1)正数集合:{ ?};
(2)负数集合: { ?};
(3)整数集合: { ?};
(4)分数集合: { ?}.
?
答案
14.【解析】 (1)100÷(-2)2-(-2)÷(-23)
=100÷4-3
=25-3
=22.
?
14. 计算:
(1)100÷(-2)2-(-2)÷(-23);
(2)(-12)2+12×(23-|23-2|);
(3)(-3.75)+2.85+(-114)+(-12)+3.15+(-2.5);
(4)[212-(38+16?34)×24]÷5×(-1)2 021.
?
答案
(2)(-12)2+12×(23-|23-2|)
=14+12×(23-2+23)
=14+12×(-23)
=14?13
=-112.
(3)(-3.75)+2.85+(-114)+(-12)+3.15+(-2.5)
=[(-3.75)+(-114)]+2.85+3.15+(-2.5)+(-12)
=-5+6+(-3)
=-2.
?
答案
(4)[212-(38+16?34)×24]÷5×(-1)2 021
=[212-(38×24+16×24-34×24)]÷5×(-1)2 021
=(212-9-4+18)×(-15)
=-12-1
=-112.
?
15.如图,数轴上两点A,B分别位于原点O的两侧,OA=OB=m,点A,B对应的数分别为a,b,点P为数轴上一点,设点P对应的数与a的和为x.
(1)a+b= ;?
(2)若m=1,点P在点B的右侧,BP=2,写出点P对应的数,并求出x的值;
(3)若m=2,点P在点A的左侧,BP=19,求x的值.
答案
15.【解析】 (1)0
(2)若m=1,则a=-1,b=1,
因为点P在点B的右侧,BP=2,
所以点P对应的数为3,
所以x=-1+3=2.
(3)若m=2,则a=-2,b=2.
因为点P在点A的左侧,BP=19,
所以点P对应的数为-17,
所以x=-2+(-17)=-19.
16.某风景区在10月1日至10月8日这八天中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数).
(1)10月1日至10月5日这五天中,每天到该风景区的游客人数最多的是10月 日.?
(2)若9月30日的游客人数为2万人,10月8日到该风景区的游客人数与9月30日的游客人数持平,则上表中“■”表示的数应是多少?
(3)若9月30日的游客人数为2万人,求10月1日至10月5日这五天的游客总人数.
日期
10月
1日
10月
2日
10月
3日
10月
4日
10月
5日
10月
6日
10月
7日
10月
8日
人数变
化/万人
1.2
-0.2
0.8
-0.4
0.6
0.2
■
-1.2
答案
16.【解析】 (1)5
(2)因为9月30日的游客人数为2万人,
所以10月8日的游客人数也为2万人,
而10月8日的游客人数比前一天减少了1.2万人,
故10月7日的游客人数为3.2万人,
因为到10月6日的游客人数为2+1.2-0.2+0.8-0.4+0.6+0.2=4.2(万人),
所以题表中“■”表示的数应是-1.
(3)10月1日至10月5日这五天的游客总人数是(2+1.2)+(3.2-0.2)+(3+0.8)+(3.8-0.4)+(3.4+0.6)=17.4(万人).
第二章 有理数及其运算中考模拟+真题
数学·七年级上册·北师
答案
1.D 【解析】 因为|a-2|+(b+3)2=0,所以a=2,b=-3,所以ba=(-3)2=9.故选D.
1.[2020广东肇庆一模]已知|a-2|+(b+3)2=0,则ba的值是 ( )
A.-6 B.6 C.-9 D.9
答案
2.C
2.[2020河南郑州一模]华为Mate 30 5G系列手机是近期相当火爆的5G国产手机,它采用的麒麟990 5G芯片在指甲盖大小的尺寸上集成了103亿个晶体管,将103亿用科学记数法表示为 ( )
A.1.03×109 B.10.3×109
C.1.03×1010 D.1.03×1011
答案
3.B 【解析】 根据题中数轴,可得a<0
?
3.[2020宁夏银川兴庆区二模]已知点A,B在数轴上的位置如图所示,其表示的数分别是a和b,给出以下结论:
(1)b-a<0;(2)|a|<|b|;(3)a+b>0;(4)????????>0.
其中正确的是 ( )
A.(1)(2)
B.(2)(3)
C.(3)(4)
D.(1)(4)
?
答案
4.B
4.[2020河北模拟]利用运算律简便计算52×(-999)+49×(-999)+999正确的是 ( )
A.-999×(52+49)=-999×101=-100 899
B.-999×(52+49-1)=-999×100=-99 900
C.-999×(52+49+1)=-999×102=-101 898
D.-999×(52+49-99)=-999×2=-1 998
答案
5.D 【解析】 因为a,b互为相反数,且都不为0,所以a+b=0,????????=-1,所以(a-1+b)(1-????????)=(-1)×[1-(-1)]=(-1)×2=-2.故选D.
?
5.[2020四川绵阳期末]若a,b互为相反数,且都不为0,则(a-1+b)(1-????????)的值为 ( )
A.0 B.-1 C.1 D.-2
?
答案
6.【解析】 (1)5+48÷22×(-14)-1
=5+48÷4×(-14)-1
=5-3-1
=1.
(2)(-2)2×0.25-4÷[(12)2-38]-40
=4×0.25-4÷(-18)-40
=1+32-40
=-7.
?
6.[2019北京期末]计算:
(1)5+48÷22×(-14)-1;
(2)(-2)2×0.25-4÷[(12)2-38]-40.
?
7.[2020江苏南通模拟]如图,在一条不完整的数轴上,一动点A向左移动4个单位长度到达点B,再向右移动7个单位长度到达点C.
(1)若点A表示的数为0,求点B、点C表示的数;
(2)若点C表示的数为5,求点B、点A表示的数;
(3)若点A,C表示的数互为相反数,求点B表示的数.
答案
7.【解析】 (1)若点A表示的数为0,
因为0-4=-4,所以点B表示的数为-4,
因为-4+7=3,所以点C表示的数为3.
(2)若点C表示的数为5,
因为5-7=-2,所以点B表示的数为-2,
因为-2+4=2,所以点A表示的数为2.
(3)若点A,C表示的数互为相反数,
因为7-4=3,所以点A表示的数为-1.5,
因为-1.5-4=-5.5,所以点B表示的数为-5.5.
答案
8.【解析】 (1)如图所示.
(2)2-(-1)=3(km).
所以小彬家与学校之间的距离是3 km.
(3)小明一共跑了(2+1.5+1)×2=9(km),
9 000÷250=36(min).
答:小明跑步一共用了36 min.
8.[2020山东济宁任城区期中]小明早晨跑步,他从自己家出发,向东跑了2 km到达小彬家,继续向东跑了1.5 km到达小红家,然后又向西跑了4.5 km到达学校,最后向东跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1 km,在如图所示的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250 m/min,那么小明跑步一共用了多长时间?
答案
1.A
1.[2019海南中考]如果收入100元记作+100元,那么支出100元记作 ( )
A.-100元 B.+100元
C.-200元 D.+200元
答案
2.B
2.[2019辽宁沈阳中考]2019年1月1日起我国开始贯彻《国务院关于印发个人所得税专项附加扣除暂行办法的通知》的要求,此次减税范围广,其中有6 500万人减税70%以上,将数据6 500用科学记数法表示为 ( )
A.6.5×102 B.6.5×103
C.65×103 D.0.65×104
答案
3.A 【解析】 由题意得,四个排球质量偏差的绝对值分别为0.6,0.7,2.5,3.5,绝对值最小的为0.6,最接近标准.故选A.
3.[2019内蒙古呼和浩特中考]如图,检测排球,其中质量超过标准的克数记为正数,不足的克数记为负数,下面检测过的四个排球,在其上方标注了检测结果,其中质量最接近标准的一个是 ( )
?
A B C D
答案
4.C 【解析】 由“两个负数,绝对值大的反而小”及“正数大于负数,0大于负数,正数大于0”,可知-1<-12<0<2,故最小的有理数是-1.故选C.
?
4.[2019辽宁鞍山中考]在有理数2,0,-1,-12中,最小的是 ( )
A.2 B.0 C.-1 D.-12
?
答案
5.C 【解析】 温差=最高气温-最低气温.星期一的温差为10-3=7(℃);星期二的温差为12-0=12(℃);星期三的温差为11-(-2)=13(℃);星期四的温差为9-(-3)=12(℃).故选C.
5.[2019浙江金华中考]某地一周前四天每天的最高气温与最低气温如下表,则这四天中温差最大的是 ( )
A.星期一 B.星期二 C.星期三 D.星期四
星期
一
二
三
四
最高气温
10 ℃
12 ℃
11 ℃
9 ℃
最低气温
3 ℃
0 ℃
-2 ℃
-3 ℃
答案
6.C 【解析】 根据题中数轴知m
6.[2019黑龙江大庆中考]数m,n在数轴上的对应点如图所示,则下列各式子正确的是 ( )
?A.m>n
B.-n>|m|
C.-m>|n|
D.|m|<|n|
答案
7.-3
7.[2019四川攀枝花中考]|-3|的相反数是 .?
8.[2019山东聊城中考]计算:(-13?12)÷54= .?
?
8.-23 【解析】 (-13?12)÷54=(-56)×45=-23.
?
答案
9.【解析】 -5×2+3÷13-(-1)
=-10+9+1
=0.
?
9.[2019广西梧州中考]计算:-5×2+3÷13-(-1).
?
答案
10.【解析】 (1)1+2-6-9=3-15=-12.
(2)因为1÷2×6=3,
所以3□9=-6,
所以□内是-.
(3)-20.
当原式为1-2×6-9时,计算所得数最小,为-20.
10.[2019河北中考]有一个填写运算符号的游戏:在“1□2□6□9”中的每个□内,填入+,-,×,÷中的某一个(可重复使用),然后计算结果.
(1)计算:1+2-6-9.
(2)若1÷2×6□9=-6,请推算□内的符号.
(3)在“1□2□6-9”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
